 |
Reference documentation for deal.II version 9.2.0
|
 |
Reference documentation for deal.II version 9.2.0
|
This tutorial depends on step-33, step-40.
| Table of contents | |
|---|---|
\(^\dagger\)Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-NA0003525. This document describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.
This tutorial presents a first-order scheme for solving compressible Euler's equations that is based on three ingredients: a collocation-type discretization of Euler's equations in the context of finite elements; a graph-viscosity stabilization based on a guaranteed upper bound of the local wave speed; and explicit time-stepping. As such, the ideas and techniques presented in this tutorial step are drastically different from those used in step-33, which focuses on the use of automatic differentiation. From a programming perspective this tutorial will focus on a number of techniques found in large-scale computations: hybrid thread-MPI parallelization; efficient local numbering of degrees of freedom; concurrent post-processing and write-out of results using worker threads; as well as checkpointing and restart.
It should be noted that first-order schemes in the context of hyperbolic conservation laws require prohibitively many degrees of freedom to resolve certain key features of the simulated fluid, and thus, typically only serve as elementary building blocks in higher-order schemes [32]. However, we hope that the reader still finds the tutorial step to be a good starting point (in particular with respect to the programming techniques) before jumping into full research codes such as the second-order scheme discussed in [32].
The compressible Euler's equations of gas dynamics are written in conservative form as follows:
\begin{align} \mathbf{u}_t + \text{div} \, \mathbb{f}(\mathbf{u}) = \boldsymbol{0} , \end{align}
where \(\mathbf{u}(\textbf{x},t):\mathbb{R}^{d} \times \mathbb{R} \rightarrow \mathbb{R}^{d+2}\), and \(\mathbb{f}(\mathbf{u}):\mathbb{R}^{d+2} \rightarrow \mathbb{R}^{(d+2) \times d}\), and \(d \geq 1\) is the space dimension. We say that \(\mathbf{u} \in \mathbb{R}^{d+2}\) is the state and \(\mathbb{f}(\mathbf{u}) \in \mathbb{R}^{(d+2) \times d}\) is the flux of the system. In the case of Euler's equations the state is given by \(\textbf{u} = [\rho, \textbf{m},E]^{\top}\): where \(\rho \in \mathbb{R}^+\) denotes the density, \(\textbf{m} \in \mathbb{R}^d\) is the momentum, and \(E \in \mathbb{R}^+\) is the total energy of the system. The flux of the system \(\mathbb{f}(\mathbf{u})\) is defined as
\begin{align*} \mathbb{f}(\textbf{u}) = \begin{bmatrix} \textbf{m}^\top \\ \rho^{-1} \textbf{m} \otimes \textbf{m} + \mathbb{I} p\\ \tfrac{\textbf{m}^\top}{\rho} (E + p) \end{bmatrix}, \end{align*}
where \(\mathbb{I} \in \mathbb{R}^{d \times d}\) is the identity matrix and \(\otimes\) denotes the tensor product. Here, we have introduced the pressure \(p\) that, in general, is defined by a closed-form equation of state. In this tutorial we limit the discussion to the class of polytropic ideal gases for which the pressure is given by
\begin{align*} p = p(\textbf{u}) := (\gamma -1) \Big(E - \tfrac{|\textbf{m}|^2}{2\,\rho} \Big), \end{align*}
where the factor \(\gamma \in (1,5/3]\) denotes the ratio of specific heats.
Hyperbolic conservation laws, such as
\begin{align*} \mathbf{u}_t + \text{div} \, \mathbb{f}(\mathbf{u}) = \boldsymbol{0}, \end{align*}
pose a significant challenge with respect to solution theory. An evident observation is that rewriting the equation in variational form and testing with the solution itself does not lead to an energy estimate because the pairing \(\langle \text{div} \, \mathbb{f}(\mathbf{u}), \mathbf{u}\rangle\) (understood as the \(L^2(\Omega)\) inner product or duality pairing) is not guaranteed to be non-negative. Notions such as energy-stability or \(L^2(\Omega)\)-stability are (in general) meaningless in this context.
Historically, the most fruitful step taken in order to deepen the understanding of hyperbolic conservation laws was to assume that the solution is formally defined as \(\mathbf{u} := \lim_{\epsilon \rightarrow 0^+} \mathbf{u}^{\epsilon}\) where \(\mathbf{u}^{\epsilon}\) is the solution of the parabolic regularization
\begin{align} \mathbf{u}_t^{\epsilon} + \text{div} \, \mathbb{f}(\mathbf{u}^{\epsilon}) - {\epsilon} \Delta \mathbf{u}^{\epsilon} = 0. \end{align}
Such solutions, which are understood as the solution recovered in the zero-viscosity limit, are often referred to as viscosity solutions. (This is, because physically \(\epsilon\) can be understood as related to the viscosity of the fluid, i.e., a quantity that indicates the amount of friction neighboring gas particles moving at different speeds exert on each other. The Euler equations themselves are derived under the assumption of no friction, but can physically be expected to describe the limiting case of vanishing friction or viscosity.) Global existence and uniqueness of such solutions is an open issue. However, we know at least that if such viscosity solutions exists they have to satisfy the constraint \(\textbf{u}(\mathbf{x},t) \in \mathcal{B}\) for all \(\mathbf{x} \in \Omega\) and \(t \geq 0\) where
\begin{align} \mathcal{B} = \big\{ \textbf{u} = [\rho, \textbf{m},E]^{\top} \in \mathbb{R}^{d+2} \, \big | \ \rho > 0 \, , \ \ E - \tfrac{|\textbf{m}|^2}{2 \rho} > 0 \, , \ s(\mathbf{u}) \geq \min_{x \in \Omega} s(\mathbf{u}_0(\mathbf{x})) \big\}. \end{align}
Here, \(s(\mathbf{u})\) denotes the specific entropy
\begin{align} s(\mathbf{u}) = \ln \Big(\frac{p(\mathbf{u})}{\rho^{\gamma}}\Big). \end{align}
We will refer to \(\mathcal{B}\) as the invariant set of Euler's equations. In other words, a state \(\mathbf{u}(\mathbf{x},t)\in\mathcal{B}\) obeys positivity of the density, positivity of the internal energy, and a local minimum principle on the specific entropy. This condition is a simplified version of a class of pointwise stability constraints satisfied by the exact (viscosity) solution. By pointwise we mean that the constraint has to be satisfied at every point of the domain, not just in an averaged (integral, or high order moments) sense.
In context of a numerical approximation, a violation of such a constraint has dire consequences: it almost surely leads to catastrophic failure of the numerical scheme, loss of hyperbolicity, and overall, loss of well-posedness of the (discrete) problem. It would also mean that we have computed something that can not be interpreted physically. (For example, what are we to make of a computed solution with a negative density?) In the following we will formulate a scheme that ensures that the discrete approximation of \(\mathbf{u}(\mathbf{x},t)\) remains in \(\mathcal{B}\).
Following step-9, step-12, and step-33, at this point it might look tempting to base a discretization of Euler's equations on a (semi-discrete) variational formulation:
\begin{align*} (\partial_t\mathbf{u}_{h},\textbf{v}_h)_{L^2(\Omega)} - ( \mathbb{f}(\mathbf{u}_{h}) ,\text{grad} \, \textbf{v}_{h})_{L^2(\Omega)} + s_h(\mathbf{u}_{h},\textbf{v}_h)_{L^2(\Omega)} = \boldsymbol{0} \quad\forall \textbf{v}_h \in \mathbb{V}_h. \end{align*}
Here, \(\mathbb{V}_h\) is an appropriate finite element space, and \(s_h(\cdot,\cdot)_{L^2(\Omega)}\) is some linear stabilization method (possibly complemented with some ad-hoc shock-capturing technique, see for instance Chapter 5 of [24] and references therein). Most time-dependent discretization approaches described in the deal.II tutorials are based on such a (semi-discrete) variational approach. Fundamentally, from an analysis perspective, variational discretizations are conceived to provide some notion of global (integral) stability, meaning an estimate of the form
\begin{align*} |\!|\!| \mathbf{u}_{h}(t) |\!|\!| \leq |\!|\!| \mathbf{u}_{h}(0) |\!|\!| \end{align*}
holds true, where \(|\!|\!| \cdot |\!|\!| \) could represent the \(L^2(\Omega)\)-norm or, more generally, some discrete (possibly mesh dependent) energy-norm. Variational discretizations of hyperbolic conservation laws have been very popular since the mid eighties, in particular combined with SUPG-type stabilization and/or upwinding techniques (see the early work of [15] and [39]). They have proven to be some of the best approaches for simulations in the subsonic shockless regime and similarly benign situations.
However, in the transonic and supersonic regime, and shock-hydrodynamics applications the use of variational schemes might be questionable. In fact, at the time of this writing, most shock-hydrodynamics codes are still firmly grounded on finite volume methods. The main reason for failure of variational schemes in such extreme regimes is the lack of pointwise stability. This stems from the fact that a priori bounds on integrated quantities (e.g. integrals of moments) have in general no implications on pointwise properties of the solution. While some of these problems might be alleviated by the (perpetual) chase of the right shock capturing scheme, finite difference-like and finite volume schemes still have an edge in many regards.
In this tutorial step we therefore depart from variational schemes. We will present a completely algebraic formulation (with the flavor of a collocation-type scheme) that preserves constraints pointwise, i.e.,
\begin{align*} \textbf{u}_h(\mathbf{x}_i,t) \in \mathcal{B} \;\text{at every node}\;\mathbf{x}_i\;\text{of the mesh}. \end{align*}
Contrary to finite difference/volume schemes, the scheme implemented in this step maximizes the use of finite element software infrastructure, works on any mesh, in any space dimension, and is theoretically guaranteed to always work, all the time, no exception. This illustrates that deal.II can be used far beyond the context of variational schemes in Hilbert spaces and that a large number of classes, modules and namespaces from deal.II can be adapted for such a purpose.
Let \(\mathbb{V}_h\) be scalar-valued finite dimensional space spanned by a basis \(\{\phi_i\}_{i \in \mathcal{V}}\) where: \(\phi_i:\Omega \rightarrow \mathbb{R}\) and \(\mathcal{V}\) is the set of all indices (nonnegative integers) identifying each scalar Degree of Freedom (DOF) in the mesh. Therefore a scalar finite element functional \(u_h \in \mathbb{V}_h\) can be written as \(u_h = \sum_{i \in \mathcal{V}} U_i \phi_i\) with \(U_i \in \mathbb{R}\). We introduce the notation for vector-valued approximation spaces \(\pmb{\mathbb{V}}_h := \{\mathbb{V}_h\}^{d+2}\). Let \(\mathbf{u}_h \in \pmb{\mathbb{V}}_h\), then it can be written as \(\mathbf{u}_h = \sum_{i \in \mathcal{V}} \mathbf{U}_i \phi_i\) where \(\mathbf{U}_i \in \mathbb{R}^{d+2}\) and \(\phi_i\) is a scalar-valued shape function.
We will use the usual Lagrange finite elements: let \(\{\mathbf{x}_i\}_{i \in \mathcal{V}}\) denote the set of all support points (see thisglossary entry"), where \(\mathbf{x}_i \in \mathbb{R}^d\). Then each index \(i \in \mathcal{V}\) uniquely identifies a support point \(\mathbf{x}_i\), as well as a scalar-valued shape function \(\phi_i\). With this notation at hand we can define the (explicit time stepping) scheme as:
\begin{align*} m_i \frac{\mathbf{U}_i^{n+1} - \mathbf{U}_i^{n}}{\tau} + \sum_{j \in \mathcal{I}(i)} \mathbb{f}(\mathbf{U}_j^{n})\cdot \mathbf{c}_{ij} - \sum_{j \in \mathcal{I}(i)} d_{ij} \mathbf{U}_j^{n} = \boldsymbol{0} \, , \end{align*}
where
The definition of \(\lambda_{\text{max}} (\mathbf{U},\mathbf{V}, \textbf{n})\) is far from trivial and we will postpone the precise definition in order to focus first on some algorithmic and implementation questions. We note that
Consider the following pseudo-code, illustrating a possible straight forward strategy for computing the solution \(\textbf{U}^{n+1}\) at a new time \(t_{n+1} = t_n + \tau_n\) given a known state \(\textbf{U}^{n}\) at time \(t_n\):
\begin{align*} &\textbf{for } i \in \mathcal{V} \\ &\ \ \ \ \{\mathbf{c}_{ij}\}_{j \in \mathcal{I}(i)} \leftarrow \mathtt{gather\_cij\_vectors} (\textbf{c}, \mathcal{I}(i)) \\ &\ \ \ \ \{\textbf{U}_j^n\}_{j \in \mathcal{I}(i)} \leftarrow \mathtt{gather\_state\_vectors} (\textbf{U}^n, \mathcal{I}(i)) \\ &\ \ \ \ \ \textbf{U}_i^{n+1} \leftarrow \mathbf{U}_i^{n} \\ &\ \ \ \ \textbf{for } j \in \mathcal{I}(i)\backslash\{i\} \\ &\ \ \ \ \ \ \ \ \texttt{compute } d_{ij} \\ &\ \ \ \ \ \ \ \ \texttt{compute } \mathbb{f}(\mathbf{U}_j^{n}) \\ &\ \ \ \ \ \ \ \ \textbf{U}_i^{n+1} \leftarrow \textbf{U}_i^{n+1} - \frac{\tau_n}{m_i} \mathbb{f}(\mathbf{U}_j^{n})\cdot \mathbf{c}_{ij} + d_{ij} \mathbf{U}_j^{n} \\ &\ \ \ \ \textbf{end} \\ &\ \ \ \ \mathtt{scatter\_updated\_state} (\textbf{U}_i^{n+1}) \\ &\textbf{end} \end{align*}
We note here that:
The actual implementation will deviate from above code in one key aspect: the time-step size \(\tau\) has to be chosen subject to a CFL condition
\begin{align*} \tau_n = c_{\text{cfl}}\,\min_{ i\in\mathcal{V}}\left(\frac{m_i}{-2\,d_{ii}^{n}}\right), \end{align*}
where \(0<c_{\text{cfl}}\le1\) is a chosen constant. This will require to compute all \(d_{ij}\) in a separate step prior to actually performing above update. The core principle remains unchanged, though: we do not loop over cells but rather over all edges of the sparsity graph.
In the example considered in this tutorial step we use three different types of boundary conditions: essential-like boundary conditions (we prescribe a state at the left boundary of our domain), outflow boundary conditions (also called "do-nothing" boundary conditions) at the right boundary of the domain, and "reflecting" boundary conditions \(\mathbf{m} \cdot \boldsymbol{\nu} = 0\) (also called "slip" boundary conditions) at the top, bottom, and surface of the obstacle. We will not discuss much about essential and "do-nothing" boundary conditions since their implementation is relatively easy and the reader will be able to pick-up the implementation directly from the (documented) source code. In this portion of the introduction we will focus only on the "reflecting" boundary conditions which are somewhat more tricky.
For the case of the reflecting boundary conditions we will proceed as follows:
\begin{align*} \mathbf{m}_i \dealcoloneq \mathbf{m}_i - (\widehat{\boldsymbol{\nu}}_i \cdot \mathbf{m}_i) \widehat{\boldsymbol{\nu}}_i \ \ \text{for all }\mathbf{x}_i \in \partial\Omega^r \end{align*}
that removes the normal component of \(\mathbf{m}\). Here the definition of nodal normal \(\widehat{\boldsymbol{\nu}}_i\) is very much arbitrary (there is no unique definition) but it should be consistent upon refinement with the underlying geometry.This is approach is usually called "explicit treatment of boundary conditions". The well seasoned finite element person might find this approach questionable. No doubt, when solving parabolic, or elliptic equations, we typically enforce essential (Dirichlet-like) boundary conditions by making them part of the approximation space \(\mathbb{V}\), and treat natural (e.g. Neumann) boundary conditions as part of the variational formulation. We also know that explicit treatment of boundary conditions (in the context of parabolic PDEs) almost surely leads to catastrophic consequences. However, in the context of nonlinear hyperbolic equations we have that:
If \(\mathbf{u}_t + \text{div} \, \mathbb{f}(\mathbf{u}) = \boldsymbol{0}\) represents Euler's equation with reflecting boundary conditions on the entirety of the boundary (i.e. \(\partial\Omega^r \equiv \partial\Omega\)) and we integrate in space and time \(\int_{\Omega}\int_{t_1}^{t_2}\) we would obtain
\begin{align*} \int_{\Omega} \rho(\mathbf{x},t_2) \, \mathrm{d}\mathbf{x} = \int_{\Omega} \rho(\mathbf{x},t_1) \, \mathrm{d}\mathbf{x} \ , \ \ \int_{\Omega} E(\mathbf{x},t_2) \, \mathrm{d}\mathbf{x} = \int_{\Omega} E(\mathbf{x},t_1) \, \mathrm{d}\mathbf{x} \ , \ \ \int_{\Omega} \mathbf{m}(\mathbf{x},t_2) \, \mathrm{d}\mathbf{x} = \int_{\Omega} \mathbf{m}(\mathbf{x},t_1) \, \mathrm{d}\mathbf{x} + \int_{t_1}^{t_2} \! \int_{\partial\Omega} p \boldsymbol{\nu} \, \mathrm{d}\mathbf{s} \mathrm{d}t\, . \end{align*}
Note that momentum is not a conserved quantity (interaction with walls leads to momentum gain/loss). Even though we will not use reflecting boundary conditions in the entirety of the domain, we would like to know that our implementation of boundary conditions is consistent with the conservation properties mentioned above. In order to guarantee such conservation property it is necessary to modify the values of the vectors \(\mathbf{c}_{ij}\) as follows
\begin{align*} \mathbf{c}_{ij} \dealcoloneq \mathbf{c}_{ij} + \int_{\partial \Omega^r} (\boldsymbol{\nu}_j - \boldsymbol{\nu}(\mathbf{s})) \phi_i \phi_j \, \mathrm{d}\mathbf{s} \ \ \text{whenever both }\mathbf{x}_i\text{ and }\mathbf{x}_j \text{ lie on the boundary} \end{align*}
This consistent modification of the \(\mathbf{c}_{ij}\) is a direct consequence of simple integration by parts arguments, see page 12 of [32] for more details.
The set of include files is quite standard. The most intriguing part is the fact that we will rely solely on deal.II data structures for MPI parallelization, in particular parallel::distributed::Triangulation and LinearAlgebra::distributed::Vector included through distributed/tria.h and lac/la_parallel_vector.h. Instead of a Trilinos, or PETSc specific matrix class, we will use a non-distributed SparseMatrix (lac/sparse_matrix.h) to store the local part of the \(\mathbf{c}_{ij}\), \(\mathbf{n}_{ij}\) and \(d_{ij}\) matrices.
In addition to above deal.II specific includes, we also include four boost headers. The first two are for binary archives that we will use for implementing a check-pointing and restart mechanism.
The last two header files are for creating custom iterator ranges over integer intervals.
For std::isnan, std::isinf, std::ifstream, std::async, and std::future
We begin our actual implementation by declaring all classes with their data structures and methods upfront. In contrast to previous example steps we use a more fine-grained encapsulation of concepts, data structures, and parameters into individual classes. A single class thus usually centers around either a single data structure (such as the Triangulation) in the Discretization class, or a single method (such as the make_one_step() function of the TimeStepping class). We typically declare parameter variables and scratch data object private and make methods and data structures used by other classes public.
We also note that the vast majority of classes is derived from ParameterAcceptor. This facilitates the population of all the global parameters into a single (global) ParameterHandler. More explanations about the use of inheritance from ParameterAcceptor as a global subscription mechanism can be found in step-60.
We start with defining a number of types::boundary_id constants used throughout the tutorial step. This allows us to refer to boundary types by a mnemonic (such as do_nothing) rather than a numerical value.
Discretization classThe class Discretization contains all data structures concerning the mesh (triangulation) and discretization (mapping, finite element, quadrature) of the problem. As mentioned, we use the ParameterAcceptor class to automatically populate problem-specific parameters, such as the geometry information (length, etc.) or the refinement level (refinement) from a parameter file. This requires us to split the initialization of data structures into two functions: We initialize everything that does not depend on parameters in the constructor, and defer the creation of the mesh to the setup() method that can be called once all parameters are read in via ParameterAcceptor::initialize().
OfflineData classThe class OfflineData contains pretty much all components of the discretization that do not evolve in time, in particular, the DoFHandler, SparsityPattern, boundary maps, the lumped mass matrix, \(\mathbf{c}_{ij}\) and \(\mathbf{n}_{ij}\) matrices. Here, the term offline refers to the fact that all the class members of OfflineData have well-defined values independent of the current time step. This means that they can be initialized ahead of time (at time step zero) and are not meant to be modified at any later time step. For instance, the sparsity pattern should not change as we advance in time (we are not doing any form of adaptivity in space). Similarly, the entries of the lumped mass matrix should not be modified as we advance in time either.
We also compute and store a boundary_normal_map that contains a map from a global index of type types::global_dof_index of a boundary degree of freedom to a tuple consisting of a normal vector, the boundary id, and the position associated with the degree of freedom. We have to compute and store this geometric information in this class because we won't have access to geometric (or cell-based) information later on in the algebraic loops over the sparsity pattern.
setup() (and assemble()) method as for the class Discretization.ProblemDescription classThe member functions of this class are utility functions and data structures specific to Euler's equations:
state_type is used for the states \(\mathbf{U}_i^n\)flux_type is used for the fluxes \(\mathbb{f}(\mathbf{U}_j^n)\).momentum function extracts \(\textbf{m}\) out of the state vector \([\rho,\textbf{m},E]\) and stores it in a Tensor<1, dim>.internal_energy function computes \(E - \frac{|\textbf{m}|^2}{2\rho}\) from a given state vector \([\rho,\textbf{m},E]\).The purpose of the class members component_names, pressure, and speed_of_sound is evident from their names. We also provide a function compute_lambda_max(), that computes the wave speed estimate mentioned above, \(\lambda_{max}(\mathbf{U},\mathbf{V},\mathbf{n})\), which is used in the computation of the \(d_{ij}\) matrix.
DEAL_II_ALWAYS_INLINE macro expands to a (compiler specific) pragma that ensures that the corresponding function defined in this class is always inlined, i.e., the function body is put in place for every invocation of the function, and no call (and code indirection) is generated. This is stronger than the inline keyword, which is more or less a (mild) suggestion to the compiler that the programmer thinks it would be beneficial to inline the function. DEAL_II_ALWAYS_INLINE should only be used rarely and with caution in situations such as this one, where we actually know (due to benchmarking) that inlining the function in question improves performance.Finally, we observe that this is the only class in this tutorial step that is tied to a particular "physics" or "hyperbolic conservation law" (in this case Euler's equations). All the other classes are primarily "discretization" classes, very much agnostic of the particular physics being solved.
InitialValues classThe class InitialValues's only public data attribute is a std::function initial_state that computes the initial state of a given point and time. This function is used for populating the initial flow field as well as setting Dirichlet boundary conditions (at inflow boundaries) explicitly in every time step.
For the purpose of this example step we simply implement a homogeneous uniform flow field for which the direction and a 1D primitive state (density, velocity, pressure) are read from the parameter file.
It would be desirable to initialize the class in a single shot: initialize/set the parameters and define the class members that depend on these default parameters. However, since we do not know the actual values for the parameters, this would be sort of meaningless and unsafe in general (we would like to have mechanisms to check the consistency of the input parameters). Instead of defining another setup() method to be called (by-hand) after the call to ParameterAcceptor::initialize() we provide an "implementation" for the class member parse_parameters_call_back() which is automatically called when invoking ParameterAcceptor::initialize() for every class that inherits from ParameterAceptor.
We declare a private callback function that will be wired up to the ParameterAcceptor::parse_parameters_call_back signal.
TimeStepping classWith the OfflineData and ProblemDescription classes at hand we can now implement the explicit time-stepping scheme that was introduced in the discussion above. The main method of the TimeStepping class is make_one_step(vector_type &U, double t) that takes a reference to a state vector U and a time point t (as input arguments) computes the updated solution, stores it in the vector temp, swaps its contents with the vector U, and returns the chosen step-size \(\tau\).
The other important method is prepare() which primarily sets the proper partition and sparsity pattern for the temporary vector temp and the matrix dij_matrix respectively.
SchlierenPostprocessor classAt its core, the Schlieren class implements the class member compute_schlieren(). The main purpose of this class member is to compute an auxiliary finite element field schlieren, that is defined at each node by
\[ \text{schlieren}[i] = e^{\beta \frac{ |\nabla r_i| - \min_j |\nabla r_j| }{\max_j |\nabla r_j| - \min_j |\nabla r_j| } }, \]
where \(r\) can in principle be any scalar quantity. In practice though, the density is a natural candidate, viz. \(r \dealcoloneq \rho\). Schlieren postprocessing is a standard method for enhancing the contrast of a visualization inspired by actual experimental X-ray and shadowgraphy techniques of visualization. (See step-67 for another example where we create a Schlieren plot.)
MainLoop classNow, all that is left to do is to chain the methods implemented in the TimeStepping, InitialValues, and SchlierenPostprocessor classes together. We do this in a separate class MainLoop that contains an object of every class and again reads in a number of parameters with the help of the ParameterAcceptor class.
The first major task at hand is the typical triplet of grid generation, setup of data structures, and assembly. A notable novelty in this example step is the use of the ParameterAcceptor class that we use to populate parameter values: we first initialize the ParameterAcceptor class by calling its constructor with a string subsection denoting the correct subsection in the parameter file. Then, in the constructor body every parameter value is initialized to a sensible default value and registered with the ParameterAcceptor class with a call to ParameterAcceptor::add_parameter().
Note that in the previous constructor we only passed the MPI communicator to the triangulation but we still have not initialized the underlying geometry/mesh. As mentioned earlier, we have to postpone this task to the setup() function that gets called after the ParameterAcceptor::initialize() function has populated all parameter variables with the final values read from the parameter file.
The setup() function is the last class member that has to be implemented. It creates the actual triangulation that is a benchmark configuration consisting of a channel with a disk obstacle, see [32]. We construct the geometry by modifying the mesh generated by GridGenerator::hyper_cube_with_cylindrical_hole(). We refer to step-49, step-53, and step-54 for an overview how to create advanced meshes. We first create 4 temporary (non distributed) coarse triangulations that we stitch together with the GridGenerator::merge_triangulation() function. We center the disk at \((0,0)\) with a diameter of disk_diameter. The lower left corner of the channel has coordinates (-disk_position, -height/2) and the upper right corner has (length-disk_position, height/2).
We have to fix up the left edge that is currently located at \(x=-\)disk_diameter and has to be shifted to \(x=-\)disk_position. As a last step the boundary has to be colorized with Boundaries::do_nothing on the right, dirichlet on the left and free_slip on the upper and lower outer boundaries and the obstacle.
Not much is done in the constructor of OfflineData other than initializing the corresponding class members in the initialization list.
Now we can initialize the DoFHandler, extract the IndexSet objects for locally owned and locally relevant DOFs, and initialize a Utilities::MPI::Partitioner object that is needed for distributed vectors.
We are now in a position to create the sparsity pattern for our matrices. There are quite a few peculiarities that need a detailed explanation. We avoid using a distributed matrix class (as for example provided by Trilinos or PETSc) and instead rely on deal.II's own SparseMatrix object to store the local part of all matrices. This design decision is motivated by the fact that (a) we actually never perform a matrix-vector multiplication, and (b) we can always assemble the local part of a matrix exclusively on a given MPI rank. Instead, we will compute nonlinear updates while iterating over (the local part) of a connectivity stencil; a task for which deal.II's own SparsityPattern is specifically optimized for.
This design consideration has a caveat, though. What makes the deal.II SparseMatrix class fast is the compressed row storage (CSR) used in the SparsityPattern (see Sparsity patterns). This, unfortunately, does not play nicely with a global distributed index range because a sparsity pattern with CSR cannot contain "holes" in the index range. The distributed matrices offered by deal.II avoid this by translating from a global index range into a contiguous local index range. But this is precisely the type of index manipulation we want to avoid in our iteration over the stencil because it creates a measurable overhead.
The Utilities::MPI::Partitioner class already implements the translation from a global index range to a contiguous local (per MPI rank) index range: we don't have to reinvent the wheel. We just need to use that translation capability (once and only once) in order to create a "local" sparsity pattern for the contiguous index range \([0,\)n_locally_relevant \()\). That capability can be invoked by the Utilities::MPI::Partitioner::global_to_local() function. Once the sparsity pattern is created using local indices, all that is left to do is to ensure that (when implementing our scatter and gather auxiliary functions) we always access elements of a distributed vector by a call to LinearAlgebra::distributed::Vector::local_element(). This way we avoid index translations altogether and operate exclusively with local indices.
We have to create the "local" sparsity pattern by hand. We therefore loop over all locally owned and ghosted cells (see GlossArtificialCell) and extract the (global) dof_indices associated with the cell DOFs and renumber them using partitioner->global_to_local(index).
n_locally_owned \()\). However, in the case of a ghosted dof (i.e. not locally owned) the situation is quite different, since the global indices associated with ghosted DOFs will not be (in general) a contiguous set of integers.This concludes the setup of the DoFHandler and SparseMatrix objects. Next, we have to assemble various matrices. We define a number of helper functions and data structures in an anonymous namespace.
CopyData class that will be used to assemble the offline data matrices using WorkStream. It acts as a container: it is just a struct where WorkStream stores the local cell contributions. Note that it also contains a class member local_boundary_normal_map used to store the local contributions required to compute the normals at the boundary.
Next we introduce a number of helper functions that are all concerned about reading and writing matrix and vector entries. They are mainly motivated by providing slightly more efficient code and syntactic sugar for otherwise somewhat tedious code.
The first function we introduce, get_entry(), will be used to read the value stored at the entry pointed by a SparsityPattern iterator it of matrix. The function works around a small deficiency in the SparseMatrix interface: The SparsityPattern is concerned with all index operations of the sparse matrix stored in CRS format. As such the iterator already knows the global index of the corresponding matrix entry in the low-level vector stored in the SparseMatrix object. Due to the lack of an interface in the SparseMatrix for accessing the element directly with a SparsityPattern iterator, we unfortunately have to create a temporary SparseMatrix iterator. We simply hide this in the get_entry() function.
The set_entry() helper is the inverse operation of get_value(): Given an iterator and a value, it sets the entry pointed to by the iterator in the matrix.
gather_get_entry(): we note that \(\mathbf{c}_{ij} \in \mathbb{R}^d\). If \(d=2\) then \(\mathbf{c}_{ij} = [\mathbf{c}_{ij}^1,\mathbf{c}_{ij}^2]^\top\). Which basically implies that we need one matrix per space dimension to store the \(\mathbf{c}_{ij}\) vectors. Similar observation follows for the matrix \(\mathbf{n}_{ij}\). The purpose of gather_get_entry() is to retrieve those entries and store them into a Tensor<1, dim> for our convenience.
gather() (first interface): this first function signature, having three input arguments, will be used to retrieve the individual components (i,l) of a matrix. The functionality of gather_get_entry() and gather() is very much the same, but their context is different: the function gather() does not rely on an iterator (that actually knows the value pointed to) but rather on the indices (i,l) of the entry in order to retrieve its actual value. We should expect gather() to be slightly more expensive than gather_get_entry(). The use of gather() will be limited to the task of computing the algebraic viscosity \(d_{ij}\) in the particular case that when both \(i\) and \(j\) lie at the boundary.
(i,l) entry of a matrix (say for instance Trilinos or PETSc matrices) is in general unacceptably expensive. Here is where we might want to keep an eye on complexity: we want this operation to have constant complexity, which is the case of the current implementation using deal.II matrices.gather() (second interface): this second function signature having two input arguments will be used to gather the state at a node i and return it as a Tensor<1,problem_dimension> for our convenience.
scatter(): this function has three input arguments, the first one is meant to be a "global object" (say a locally owned or locally relevant vector), the second argument which could be a Tensor<1,problem_dimension>, and the last argument which represents a index of the global object. This function will be primarily used to write the updated nodal values, stored as Tensor<1,problem_dimension>, into the global objects.
We are now in a position to assemble all matrices stored in OfflineData: the lumped mass entries \(m_i\), the vector-valued matrices \(\mathbf{c}_{ij}\) and \(\mathbf{n}_{ij} = \frac{\mathbf{c}_{ij}}{|\mathbf{c}_{ij}|}\), and the boundary normals \(\boldsymbol{\nu}_i\).
In order to exploit thread parallelization we use the WorkStream approach detailed in the Parallel computing with multiple processors accessing shared memory. As customary this requires definition of
scratch_data.local_assemble_system() function that actually computes the local (i.e. current cell) contributions from the scratch data.CopyData<dim>().copy_local_to_global() in charge of actually coping these local contributions into the global objects (matrices and/or vectors)Most of the following lines are spent in the definition of the worker local_assemble_system() and the copy data routine copy_local_to_global(). There is not much to say about the WorkStream framework since the vast majority of ideas are reasonably well-documented in step-9, step-13 and step-32 among others.
Finally, assuming that \(\mathbf{x}_i\) is a support point at the boundary, the (nodal) normals are defined as:
\begin{align*} \widehat{\boldsymbol{\nu}}_i \dealcoloneq \frac{\boldsymbol{\nu}_i}{|\boldsymbol{\nu}_i|} \ \text{ where } \boldsymbol{\nu}_i \dealcoloneq \sum_{T \subset \text{supp}(\phi_i)} \sum_{F \subset \partial T \cap \partial \Omega} \sum_{\mathbf{x}_{q,F}} \nu(\mathbf{x}_{q,F}) \phi_i(\mathbf{x}_{q,F}). \end{align*}
Here \(T\) denotes elements, \(\text{supp}(\phi_i)\) the support of the shape function \(\phi_i\), \(F\) are faces of the element \(T\), and \(\mathbf{x}_{q,F}\) are quadrature points on such face. Note that this formula for \(\widehat{\boldsymbol{\nu}}_i\) is nothing else than some form of weighted averaging. Other more sophisticated definitions for \(\nu_i\) are possible but none of them have much influence in theory or practice.
What follows is the initialization of the scratch data required by WorkStream
We compute the local contributions for the lumped mass matrix entries \(m_i\) and and vectors \(c_{ij}\) in the usual fashion:
Now we have to compute the boundary normals. Note that the following loop does not do much unless the element has faces on the boundary of the domain.
Note that "normal" will only represent the contributions from one of the faces in the support of the shape function phi_j. So we cannot normalize this local contribution right here, we have to take it "as is", store it and pass it to the copy data routine. The proper normalization requires an additional loop on nodes. This is done in the copy function below.
Last, we provide a copy_local_to_global function as required for the WorkStream
At this point in time we are done with the computation of \(m_i\) and \(\mathbf{c}_{ij}\), but so far the matrix nij_matrix contains just a copy of the matrix cij_matrix. That's not what we really want: we have to normalize its entries. In addition, we have not filled the entries of the matrix norm_matrix and the vectors stored in the map OfflineData<dim>::BoundaryNormalMap are not normalized.
In principle, this is just offline data, it doesn't make much sense to over-optimize their computation, since their cost will get amortized over the many time steps that we are going to use. However, computing/storing the entries of the matrix norm_matrix and the normalization of nij_matrix are perfect to illustrate thread-parallel node-loops:
From an algebraic point of view, this is equivalent to: visiting every row in the matrix and for each one of these rows execute a loop on the columns. Node-loops is a core theme of this tutorial step (see the pseudo-code in the introduction) that will repeat over and over again. That's why this is the right time to introduce them.
We have the thread parallelization capability parallel::apply_to_subranges() that is somehow more general than the WorkStream framework. In particular, parallel::apply_to_subranges() can be used for our node-loops. This functionality requires four input arguments which we explain in detail (for the specific case of our thread-parallel node loops):
indices.begin() points to a row index.indices.end() points to a numerically higher row index.on_subranges(i1,i2) (where i1 and i2 define a sub-range within the range spanned by the end and begin iterators defined in the two previous bullets) applies an operation to every iterator in such subrange. We may as well call on_subranges the "worker".A minor caveat here is that the iterators indices.begin() and indices.end() supplied to parallel::apply_to_subranges() have to be random access iterators: internally, parallel::apply_to_subranges() will break the range defined by the indices.begin() and indices.end() iterators into subranges (we want to be able to read any entry in those subranges with constant complexity). In order to provide such iterators we resort to std_cxx20::ranges::iota_view.
The bulk of the following piece of code is spent defining the "worker" on_subranges: i.e. the operation applied at each row of the sub-range. Given a fixed row_index we want to visit every column/entry in such row. In order to execute such columns-loops we use std::for_each from the standard library, where:
sparsity_pattern.begin(row_index) gives us an iterator starting at the first column of the row,sparsity_pattern.end(row_index) is an iterator pointing at the last column of the row,std::for_each is the operation applied at each nonzero entry (a lambda expression in this case) of such row.We note that, parallel::apply_to_subranges() will operate on disjoint sets of rows (the subranges) and our goal is to write into these rows. Because of the simple nature of the operations we want to carry out (computation and storage of normals, and normalization of the \(\mathbf{c}_{ij}\) of entries) threads cannot conflict attempting to write the same entry (we do not need a scheduler).
First column-loop: we compute and store the entries of the matrix norm_matrix and write normalized entries into the matrix nij_matrix:
Finally, we normalize the vectors stored in OfflineData<dim>::BoundaryNormalMap. This operation has not been thread parallelized as it would neither illustrate any important concept nor lead to any noticeable speed gain.
As commented in the introduction (see section titled "Stable boundary conditions and conservation properties") we use three different types of boundary conditions: essential-like boundary conditions (we prescribe a state in the left portion of our domain), outflow boundary conditions (also called "do-nothing" boundary conditions) in the right portion of the domain, and "reflecting" boundary conditions (also called "free slip" boundary conditions). With these boundary conditions we should not expect any form of conservation to hold.
However, if we were to use reflecting boundary conditions \(\mathbf{m} \cdot \boldsymbol{\nu}_i =0\) on the entirety of the boundary we should preserve the density and total (mechanical) energy. This requires us to modify the \(\mathbf{c}_{ij}\) vectors at the boundary as follows [32] :
\begin{align*} \mathbf{c}_{ij} \, +\!\!= \int_{\partial \Omega} (\boldsymbol{\nu}_j - \boldsymbol{\nu}(\mathbf{s})) \phi_i \phi_j \, \mathrm{d}\mathbf{s} \ \text{whenever} \ \mathbf{x}_i \text{ and } \mathbf{x}_j \text{ lie in the boundary.} \end{align*}
The ideas repeat themselves: we use WorkStream in order to compute this correction, most of the following code is about the definition of the worker local_assemble_system().
At this point we are very much done with anything related to offline data.
In this section we describe the implementation of the class members of the ProblemDescription class. Most of the code here is specific to the compressible Euler's equations with an ideal gas law. If we wanted to re-purpose step-69 for a different conservation law (say for: instance the shallow water equation) most of the implementation of this class would have to change. But most of the other classes (in particular those defining loop structures) would remain unchanged.
We start by implementing a number of small member functions for computing momentum, internal_energy, pressure, speed_of_sound, and the flux f of the system. The functionality of each one of these functions is self-explanatory from their names.
Now we discuss the computation of \(\lambda_{\text{max}} (\mathbf{U}_i^{n},\mathbf{U}_j^{n}, \textbf{n}_{ij})\). The analysis and derivation of sharp upper-bounds of maximum wavespeeds of Riemann problems is a very technical endeavor and we cannot include an advanced discussion about it in this tutorial. In this portion of the documentation we will limit ourselves to sketch the main functionality of our implementation functions and point to specific academic references in order to help the (interested) reader trace the source (and proper mathematical justification) of these ideas.
In general, obtaining a sharp guaranteed upper-bound on the maximum wavespeed requires solving a quite expensive scalar nonlinear problem. This is typically done with an iterative solver. In order to simplify the presentation in this example step we decided not to include such an iterative scheme. Instead, we will just use an initial guess as a guess for an upper bound on the maximum wavespeed. More precisely, equations (2.11) (3.7), (3.8) and (4.3) of [30] are enough to define a guaranteed upper bound on the maximum wavespeed. This estimate is returned by a call to the function lambda_max_two_rarefaction(). At its core the construction of such an upper bound uses the so-called two-rarefaction approximation for the intermediate pressure \(p^*\), see for instance Equation (4.46), page 128 in [63].
The estimate returned by lambda_max_two_rarefaction() is guaranteed to be an upper bound, it is in general quite sharp, and overall sufficient for our purposes. However, for some specific situations (in particular when one of states is close to vacuum conditions) such an estimate will be overly pessimistic. That's why we used a second estimate to avoid this degeneracy that will be invoked by a call to the function lambda_max_expansion(). The most important function here is compute_lambda_max() which takes the minimum between the estimates returned by lambda_max_two_rarefaction() and lambda_max_expansion().
We start again by defining a couple of helper functions:
The first function takes a state U and a unit vector n_ij and computes the projected 1D state in direction of the unit vector.
For this, we have to change the momentum to \(\textbf{m}\cdot n_{ij}\) and have to subtract the kinetic energy of the perpendicular part from the total energy:
We return the 1D state in primitive variables instead of conserved quantities. The return array consists of density \(\rho\), velocity \(u\), pressure \(p\) and local speed of sound \(a\):
At this point we also define two small functions that return the positive and negative part of a double.
Next, we need two local wavenumbers that are defined in terms of a primitive state \([\rho, u, p, a]\) and a given pressure \(p^\ast\) [31] Eqn. (3.7):
\begin{align*} \lambda^- = u - a\,\sqrt{1 + \frac{\gamma+1}{2\gamma} \left(\frac{p^\ast-p}{p}\right)_+} \end{align*}
Here, the \((\cdot)_{+}\) denotes the positive part of the given argument.
Analougously [31] Eqn. (3.8):
\begin{align*} \lambda^+ = u + a\,\sqrt{1 + \frac{\gamma+1}{2\gamma} \left(\frac{p^\ast-p}{p}\right)_+} \end{align*}
All that is left to do is to compute the maximum of \(\lambda^-\) and \(\lambda^+\) computed from the left and right primitive state ([31] Eqn. (2.11)), where \(p^\ast\) is given by [31] Eqn (4.3):
We compute the second upper bound of the maximal wavespeed that is, in general, not as sharp as the two-rarefaction estimate. But it will save the day in the context of near vacuum conditions when the two-rarefaction approximation might attain extreme values:
\begin{align*} \lambda_{\text{exp}} = \max(u_i,u_j) + 5. \max(a_i, a_j). \end{align*}
The following is the main function that we are going to call in order to compute \(\lambda_{\text{max}} (\mathbf{U}_i^{n},\mathbf{U}_j^{n}, \textbf{n}_{ij})\). We simply compute both maximal wavespeed estimates and return the minimum.
We conclude this section by defining static arrays component_names that contain strings describing the component names of our state vector. We have template specializations for dimensions one, two and three, that are used later in DataOut for naming the corresponding components:
The last preparatory step, before we discuss the implementation of the forward Euler scheme, is to briefly implement the InitialValues class.
In the constructor we initialize all parameters with default values, declare all parameters for the ParameterAcceptor class and connect the parse_parameters_call_back slot to the respective signal.
The parse_parameters_call_back slot will be invoked from ParameterAceptor after the call to ParameterAcceptor::initialize(). In that regard, its use is appropriate for situations where the parameters have to be postprocessed (in some sense) or some consistency condition between the parameters has to be checked.
So far the constructor of InitialValues has defined default values for the two private members initial_direction and initial_1d_state and added them to the parameter list. But we have not defined an implementation of the only public member that we really care about, which is initial_state() (the function that we are going to call to actually evaluate the initial solution at the mesh nodes). At the top of the function, we have to ensure that the provided initial direction is not the zero vector.
parse_parameters_call_back and defined a class member setup() in order to define the implementation of initial_state(). But for illustrative purposes we want to document a different way here and use the call back signal from ParameterAcceptor.Next, we implement the initial_state function object with a lambda function computing a uniform flow field. For this we have to translate a given primitive 1d state (density \(\rho\), velocity \(u\), and pressure \(p\)) into a conserved n-dimensional state (density \(\rho\), momentum \(\mathbf{m}\), and total energy \(E\)).
The constructor of the TimeStepping class does not contain any surprising code:
In the class member prepare() we initialize the temporary vector temp and the matrix dij_matrix. The vector temp will be used to store the solution update temporarily before its contents is swapped with the old vector.
It is now time to implement the forward Euler step. Given a (writable reference) to the old state U at time \(t\) we update the state U in place and return the chosen time-step size. We first declare a number of read-only references to various different variables and data structures. We do this is mainly to have shorter variable names (e.g., sparsity instead of offline_data->sparsity_pattern).
Step 1: Computing the \(d_{ij}\) graph viscosity matrix.
It is important to highlight that the viscosity matrix has to be symmetric, i.e., \(d_{ij} = d_{ji}\). In this regard we note here that \(\int_{\Omega} \nabla \phi_j \phi_i \, \mathrm{d}\mathbf{x}= - \int_{\Omega} \nabla \phi_i \phi_j \, \mathrm{d}\mathbf{x}\) (or equivalently \(\mathbf{c}_{ij} = - \mathbf{c}_{ji}\)) provided either \(\mathbf{x}_i\) or \(\mathbf{x}_j\) is a support point located away from the boundary. In this case we can check that \(\lambda_{\text{max}} (\mathbf{U}_i^{n}, \mathbf{U}_j^{n}, \textbf{n}_{ij}) = \lambda_{\text{max}} (\mathbf{U}_j^{n}, \mathbf{U}_i^{n},\textbf{n}_{ji})\) by construction, which guarantees the property \(d_{ij} = d_{ji}\).
However, if both support points \(\mathbf{x}_i\) or \(\mathbf{x}_j\) happen to lie on the boundary, then, the equalities \(\mathbf{c}_{ij} = - \mathbf{c}_{ji}\) and \(\lambda_{\text{max}} (\mathbf{U}_i^{n}, \mathbf{U}_j^{n}, \textbf{n}_{ij}) = \lambda_{\text{max}} (\mathbf{U}_j^{n}, \mathbf{U}_i^{n}, \textbf{n}_{ji})\) do not necessarily hold true. The only mathematically safe solution for this dilemma is to compute both of them \(d_{ij}\) and \(d_{ji}\) and take the maximum.
Overall, the computation of \(d_{ij}\) is quite expensive. In order to save some computing time we exploit the fact that the viscosity matrix has to be symmetric (as mentioned above): we only compute the upper-triangular entries of \(d_{ij}\) and copy the corresponding entries to the lower-triangular counterpart.
We use again parallel::apply_to_subranges() for thread-parallel for loops. Pretty much all the ideas for parallel traversal that we introduced when discussing the assembly of the matrix norm_matrix and the normalization of nij_matrix above are used here again.
We define again a "worker" function on_subranges that computes the viscosity \(d_{ij}\) for a subrange [i1, i2) of column indices:
For a given column index i we iterate over the columns of the sparsity pattern from sparsity.begin(i) to sparsity.end(i):
We only compute \(d_{ij}\) if \(j < i\) (upper triangular entries) and later copy the values over to \(d_{ji}\).
If both support points happen to be at the boundary we have to compute \(d_{ji}\) as well and then take \(\max(d_{ij},d_{ji})\). After this we can finally set the upper triangular and lower triangular entries.
Step 2: Compute diagonal entries \(d_{ii}\) and \(\tau_{\text{max}}\).
So far we have computed all off-diagonal entries of the matrix dij_matrix. We still have to fill its diagonal entries defined as \(d_{ii}^n = - \sum_{j \in \mathcal{I}(i)\backslash \{i\}} d_{ij}^n\). We use again parallel::apply_to_subranges() for this purpose. While computing the \(d_{ii}\)s we also determine the largest admissible time-step, which is defined as
\[ \tau_n \dealcoloneq c_{\text{cfl}}\,\min_{i\in\mathcal{V}} \left(\frac{m_i}{-2\,d_{ii}^{n}}\right) \, . \]
Note that the operation \(\min_{i \in \mathcal{V}}\) is intrinsically global, it operates on all nodes: first we have to take the minimum over all threads (of a given node) and then we have to take the minimum over all MPI processes. In the current implementation:
tau_max (per node) as std::atomic<double>. The internal implementation of std::atomic will take care of guarding any possible race condition when more than one thread attempts to read and/or write tau_max at the same time.Utilities::MPI::min.on_subranges() will be executed on every thread individually. The variable tau_max_on_subrange is thus stored thread locally.
We store the negative sum of the d_ij entries at the diagonal position
and compute the maximal local time-step size tau:
tau_max_on_subrange contains the largest possible time-step size computed for the (thread local) subrange. At this point we have to synchronize the value over all threads. This is were we use the std::atomic<double> compare exchange update mechanism:
After all threads have finished we can simply synchronize the value over all MPI processes:
This is a good point to verify that the computed tau_max is indeed a valid floating point number.
Step 3: Perform update.
At this point, we have computed all viscosity coefficients \(d_{ij}\) and we know the maximal admissible time-step size \(\tau_{\text{max}}\). This means we can now compute the update:
\[ \mathbf{U}_i^{n+1} = \mathbf{U}_i^{n} - \frac{\tau_{\text{max}} }{m_i} \sum_{j \in \mathcal{I}(i)} (\mathbb{f}(\mathbf{U}_j^{n}) - \mathbb{f}(\mathbf{U}_i^{n})) \cdot \mathbf{c}_{ij} - d_{ij} (\mathbf{U}_j^{n} - \mathbf{U}_i^{n}) \]
This update formula is slightly different from what was discussed in the introduction (in the pseudo-code). However, it can be shown that both equations are algebraically equivalent (they will produce the same numerical values). We favor this second formula since it has natural cancellation properties that might help avoid numerical artifacts.
Step 4: Fix up boundary states.
As a last step in the Forward Euler method, we have to fix up all boundary states. As discussed in the intro we
Here, we compute the correction
\[ \mathbf{m}_i \dealcoloneq \mathbf{m}_i - (\boldsymbol{\nu}_i \cdot \mathbf{m}_i) \boldsymbol{\nu}_i, \]
which removes the normal component of \(\mathbf{m}\).
We only iterate over the locally owned subset:
On free slip boundaries we remove the normal component of the momentum:
On Dirichlet boundaries we enforce initial conditions strongly:
Step 5: We now update the ghost layer over all MPI ranks, swap the temporary vector with the solution vector U (that will get returned by reference) and return the chosen time-step size \(\tau_{\text{max}}\):
At various intervals we will output the current state U of the solution together with a so-called Schlieren plot. The constructor of the SchlierenPostprocessor class again contains no surprises. We simply supply default values to and register two parameters:
Again, the prepare() function initializes two temporary the vectors (r and schlieren).
We now discuss the implementation of the class member SchlierenPostprocessor<dim>::compute_schlieren(), which basically takes a component of the state vector U and computes the Schlieren indicator for such component (the formula of the Schlieren indicator can be found just before the declaration of the class SchlierenPostprocessor). We start by noting that this formula requires the "nodal gradients" \(\nabla r_j\). However, nodal values of gradients are not defined for \(\mathcal{C}^0\) finite element functions. More generally, pointwise values of gradients are not defined for \(W^{1,p}(\Omega)\) functions. The simplest technique we can use to recover gradients at nodes is weighted-averaging i.e.
\[ \nabla r_j \dealcoloneq \frac{1}{\int_{S_i} \omega_i(\mathbf{x}) \, \mathrm{d}\mathbf{x}} \int_{S_i} r_h(\mathbf{x}) \omega_i(\mathbf{x}) \, \mathrm{d}\mathbf{x} \ \ \ \ \ \mathbf{(*)} \]
where \(S_i\) is the support of the shape function \(\phi_i\), and \(\omega_i(\mathbf{x})\) is the weight. The weight could be any positive function such as \(\omega_i(\mathbf{x}) \equiv 1\) (that would allow us to recover the usual notion of mean value). But as usual, the goal is to reuse the off-line data as much as possible. In this sense, the most natural choice of weight is \(\omega_i = \phi_i\). Inserting this choice of weight and the expansion \(r_h(\mathbf{x}) = \sum_{j \in \mathcal{V}} r_j \phi_j(\mathbf{x})\) into \(\mathbf{(*)}\) we get :
\[ \nabla r_j \dealcoloneq \frac{1}{m_i} \sum_{j \in \mathcal{I}(i)} r_j \mathbf{c}_{ij} \ \ \ \ \ \mathbf{(**)} \, . \]
Using this last formula we can recover averaged nodal gradients without resorting to any form of quadrature. This idea aligns quite well with the whole spirit of edge-based schemes (or algebraic schemes) where we want to operate on matrices and vectors as directly as it could be possible avoiding by all means assembly of bilinear forms, cell-loops, quadrature, or any other intermediate construct/operation between the input arguments (the state from the previous time-step) and the actual matrices and vectors required to compute the update.
The second thing to note is that we have to compute global minimum and maximum \(\max_j |\nabla r_j|\) and \(\min_j |\nabla r_j|\). Following the same ideas used to compute the time step size in the class member TimeStepping%<dim%>::step() we define \(\max_j |\nabla r_j|\) and \(\min_j |\nabla r_j|\) as atomic doubles in order to resolve any conflicts between threads. As usual, we use Utilities::MPI::max() and Utilities::MPI::min() to find the global maximum/minimum among all MPI processes.
Finally, it is not possible to compute the Schlieren indicator in a single loop over all nodes. The entire operation requires two loops over nodes:
\[ \text{schlieren}[i] = e^{\beta \frac{ |\nabla r_i| - \min_j |\nabla r_j| }{\max_j |\nabla r_j| - \min_j |\nabla r_j| } } \, . \]
This means that we will have to define two workers on_subranges for each one of these stages.
We define the r_i_max and r_i_min in the current MPI process as atomic doubles in order to avoid race conditions between threads:
First loop: compute the averaged gradient at each node and the global maxima and minima of the gradients.
We fix up the gradient r_i at free slip boundaries similarly to how we fixed up boundary states in the forward Euler step. This avoids sharp, artificial gradients in the Schlieren plot at free slip boundaries and is a purely cosmetic choice.
We remind the reader that we are not interested in the nodal gradients per se. We only want their norms in order to compute the Schlieren indicator (weighted with the lumped mass matrix \(m_i\)):
We compare the current_r_i_max and current_r_i_min (in the current subrange) with r_i_max and r_i_min (for the current MPI process) and update them if necessary:
And synchronize r_i_max and r_i_min over all MPI processes.
Second loop: we now have the vector r and the scalars r_i_max and r_i_min at our disposal. We are thus in a position to actually compute the Schlieren indicator.
And finally, exchange ghost elements.
With all classes implemented it is time to create an instance of Discretization<dim>, OfflineData<dim>, InitialValues<dim>, TimeStepping<dim>, and SchlierenPostprocessor<dim>, and run the forward Euler step in a loop.
In the constructor of MainLoop<dim> we now initialize an instance of all classes, and declare a number of parameters controlling output. Most notable, we declare a boolean parameter resume that will control whether the program attempts to restart from an interrupted computation, or not.
We start by implementing a helper function print_head() in an anonymous namespace that is used to output messages in the terminal with some nice formatting.
With print_head in place it is now time to implement the MainLoop<dim>::run() that contains the main loop of our program.
We start by reading in parameters and initializing all objects. We note here that the call to ParameterAcceptor::initialize reads in all parameters from the parameter file (whose name is given as a string argument). ParameterAcceptor handles a global ParameterHandler that is initialized with subsections and parameter declarations for all class instances that are derived from ParameterAceptor. The call to initialize enters the subsection for each each derived class, and sets all variables that were added using ParameterAcceptor::add_parameter()
Next we create the triangulation, assemble all matrices, set up scratch space, and initialize the DataOut<dim> object:
We will store the current time and state in the variable t and vector U:
By default the boolean resume is set to false, i.e. the following code snippet is not run. However, if resume==true we indicate that we have indeed an interrupted computation and the program shall restart by reading in an old state consisting of t, output_cycle, and U from a checkpoint file. These checkpoint files will be created in the output() routine discussed below.
We use a boost::archive to store and read in the contents the checkpointed state.
it1 iterates over all components of the state vector U. We read in every entry of the component in sequence and update the ghost layer afterwards:
With either the initial state set up, or an interrupted state restored it is time to enter the main loop:
We first print an informative status message
and then perform a single forward Euler step. Note that the state vector U is updated in place and that time_stepping.make_one_step() returns the chosen step size.
Post processing, generating output and writing out the current state is a CPU and IO intensive task that we cannot afford to do every time step - in particular with explicit time stepping. We thus only schedule output by calling the output() function if we are past a threshold set by output_granularity.
We wait for any remaining background output thread to finish before printing a summary and exiting.
The interpolate_initial_values takes an initial time "t" as input argument and populates a state vector U with the help of the InitialValues<dim>::initial_state object.
The function signature of InitialValues<dim>::initial_state is not quite right for VectorTools::interpolate(). We work around this issue by, first, creating a lambda function that for a given position x returns just the value of the ith component. This lambda in turn is converted to a Function with the help of the ScalarFunctionFromFunctionObject wrapper.
Writing out the final vtk files is quite an IO intensive task that can stall the main loop for a while. In order to avoid this we use an asynchronous IO strategy by creating a background thread that will perform IO while the main loop is allowed to continue. In order for this to work we have to be mindful of two things:
output_worker thread, we have to create a copy of the state vector U. We store it in the vector output_vector.If the asynchronous writeback option is set we launch a background thread performing all the slow IO to disc. In that case we have to make sure that the background thread actually finished running. If not, we have to wait to for it to finish. We launch said background thread with std::async() that returns a std::future object. This std::future object contains the return value of the function, which is in our case simply void.
At this point we make a copy of the state vector, run the schlieren postprocessor, and run DataOut<dim>::build_patches() The actual output code is standard: We create a DataOut instance, attach all data vectors we want to output and call DataOut<dim>::build_patches(). There is one twist, however. In order to perform asynchronous IO on a background thread we create the DataOut<dim> object as a shared pointer that we pass on to the worker thread to ensure that once we exit this function and the worker thread finishes the DataOut<dim> object gets destroyed again.
Next we create a lambda function for the background thread. We capture the this pointer as well as most of the arguments of the output function by value so that we have access to them inside the lambda function.
We checkpoint the current state by doing the precise inverse operation to what we discussed for the resume logic:
If the asynchronous writeback option is set we launch a new background thread with the help of std::async function. The function returns a std::future object that we can use to query the status of the background thread. At this point we can return from the output() function and resume with the time stepping in the main loop - the thread will run in the background.
And finally, the main function.
Running the program with default parameters in release mode takes about 1 minute on a 4 core machine (with hyperthreading):
# mpirun -np 4 ./step-69 | tee output
Reading parameters and allocating objects... done
####################################################
######### #########
######### create triangulation #########
######### #########
####################################################
Number of active cells: 36864
####################################################
######### #########
######### compute offline data #########
######### #########
####################################################
Number of degrees of freedom: 37376
####################################################
######### #########
######### set up time step #########
######### #########
####################################################
####################################################
######### #########
######### interpolate initial values #########
######### #########
######### #########
####################################################
TimeLoop<dim>::interpolate_initial_values(t = 0)
TimeLoop<dim>::output(t = 0, checkpoint = 0)
####################################################
######### #########
######### enter main loop #########
######### #########
######### #########
####################################################
####################################################
######### #########
######### Cycle 000001 (0.0%) #########
######### at time t = 0.00000000 #########
######### #########
####################################################
[...]
####################################################
######### #########
######### Cycle 007553 (100.0%) #########
######### at time t = 3.99984036 #########
######### #########
####################################################
TimeLoop<dim>::output(t = 4.00038, checkpoint = 1)
+------------------------------------------------------------------------+------------+------------+
| Total CPU time elapsed since start | 357s | |
| | | |
| Section | no. calls | CPU time | % of total |
+------------------------------------------------------------+-----------+------------+------------+
| discretization - setup | 1 | 0.113s | 0% |
| offline_data - assemble lumped mass matrix, and c_ij | 1 | 0.167s | 0% |
| offline_data - compute |c_ij|, and n_ij | 1 | 0.00255s | 0% |
| offline_data - create sparsity pattern and set up matrices | 1 | 0.0224s | 0% |
| offline_data - distribute dofs | 1 | 0.0617s | 0% |
| offline_data - fix slip boundary c_ij | 1 | 0.0329s | 0% |
| schlieren_postprocessor - compute schlieren plot | 201 | 0.811s | 0.23% |
| schlieren_postprocessor - prepare scratch space | 1 | 7.6e-05s | 0% |
| time_loop - setup scratch space | 1 | 0.127s | 0% |
| time_loop - stalled output | 200 | 0.000685s | 0% |
| time_step - 1 compute d_ij | 7553 | 240s | 67% |
| time_step - 2 compute d_ii, and tau_max | 7553 | 11.5s | 3.2% |
| time_step - 3 perform update | 7553 | 101s | 28% |
| time_step - 4 fix boundary states | 7553 | 0.724s | 0.2% |
| time_step - prepare scratch space | 1 | 0.00245s | 0% |
+------------------------------------------------------------+-----------+------------+------------+
One thing that becomes evident is the fact that the program spends two thirds of the execution time computing the graph viscosity d_ij and about a third of the execution time in performing the update, where computing the flux \(f(U)\) is the expensive operation. The preset default resolution is about 37k gridpoints, which amounts to about 148k spatial degrees of freedom in 2D. An animated schlieren plot of the solution looks as follows:

It is evident that 37k gridpoints for the first-order method is nowhere near the resolution needed to resolve any flow features. For comparison, here is a "reference" computation with a second-order method and about 9.5M gridpoints:
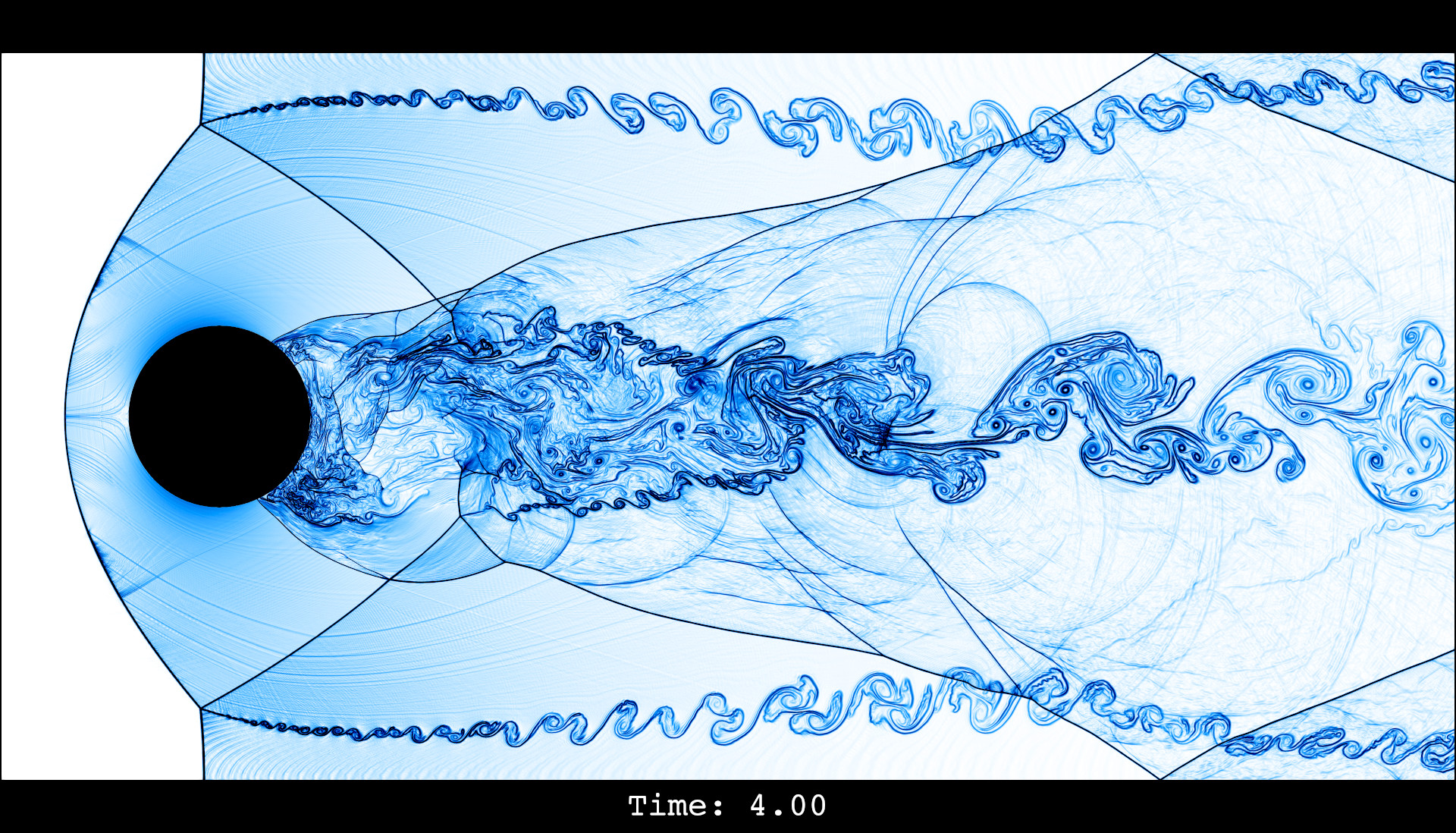
So, we give the first-order method a second chance and run it with about 2.4M gridpoints on a small compute server:
# mpirun -np 16 ./step-69 | tee output
[...]
####################################################
######### #########
######### Cycle 070216 (100.0%) #########
######### at time t = 3.99999231 #########
######### #########
####################################################
TimeLoop<dim>::output(t = 4.00006, checkpoint = 1)
[...]
+------------------------------------------------------------------------+------------+------------+
| Total wallclock time elapsed since start | 6.75e+03s | |
| | | |
| Section | no. calls | wall time | % of total |
+------------------------------------------------------------+-----------+------------+------------+
| discretization - setup | 1 | 1.97s | 0% |
| offline_data - assemble lumped mass matrix, and c_ij | 1 | 1.19s | 0% |
| offline_data - compute |c_ij|, and n_ij | 1 | 0.0172s | 0% |
| offline_data - create sparsity pattern and set up matrices | 1 | 0.413s | 0% |
| offline_data - distribute dofs | 1 | 1.05s | 0% |
| offline_data - fix slip boundary c_ij | 1 | 0.252s | 0% |
| schlieren_postprocessor - compute schlieren plot | 201 | 1.82s | 0% |
| schlieren_postprocessor - prepare scratch space | 1 | 0.000497s | 0% |
| time_loop - setup scratch space | 1 | 1.45s | 0% |
| time_loop - stalled output | 200 | 0.00342s | 0% |
| time_step - 1 compute d_ij | 70216 | 4.38e+03s | 65% |
| time_step - 2 compute d_ii, and tau_max | 70216 | 419s | 6.2% |
| time_step - 3 perform update | 70216 | 1.87e+03s | 28% |
| time_step - 4 fix boundary states | 70216 | 24s | 0.36% |
| time_step - prepare scratch space | 1 | 0.0227s | 0% |
+------------------------------------------------------------+-----------+------------+------------+
And with the following result:

That's substantially better, although of course at the price of having run the code for roughly 2 hours on 16 cores.
 1.8.17
1.8.17