 |
Reference documentation for deal.II version 9.2.0
|
 |
Reference documentation for deal.II version 9.2.0
|
This tutorial depends on step-12.
This program was written for fun by David Neckels (NCAR) while working at Sandia (on the Wyoming Express bus to and from Corrales each day). The main purpose was to better understand Euler flow. The code solves the basic Euler equations of gas dynamics, by using a fully implicit Newton iteration (inspired by Sandia's Aria code). The code may be configured by an input file to run different simulations on different meshes, with differing boundary conditions.
The original code and documentation was later slightly modified by Wolfgang Bangerth to make it more modular and allow replacing the parts that are specific to the Euler equations by other hyperbolic conservation laws without too much trouble.
The equations that describe the movement of a compressible, inviscid gas (the so-called Euler equations of gas dynamics) are a basic system of conservation laws. In spatial dimension \(d\) they read
\[ \partial_t \mathbf{w} + \nabla \cdot \mathbf{F}(\mathbf{w}) = \mathbf{G}(\mathbf w), \]
with the solution \(\mathbf{w}=(\rho v_1,\ldots,\rho v_d,\rho, E)^{\top}\) consisting of \(\rho\) the fluid density, \({\mathbf v}=(v_1,\ldots v_d)^T\) the flow velocity (and thus \(\rho\mathbf v\) being the linear momentum density), and \(E\) the energy density of the gas. We interpret the equations above as \(\partial_t \mathbf{w}_i + \nabla \cdot \mathbf{F}_i(\mathbf{w}) = \mathbf G_i(\mathbf w)\), \(i=1,\ldots,dim+2\).
For the Euler equations, the flux matrix \(\mathbf F\) (or system of flux functions) is defined as (shown here for the case \(d=3\))
\begin{eqnarray*} \mathbf F(\mathbf w) = \left( \begin{array}{ccc} \rho v_1^2+p & \rho v_2v_1 & \rho v_3v_1 \\ \rho v_1v_2 & \rho v_2^2+p & \rho v_3v_2 \\ \rho v_1v_3 & \rho v_2v_3 & \rho v_3^2+p \\ \rho v_1 & \rho v_2 & \rho v_3 \\ (E+p) v_1 & (E+p) v_2 & (E+p) v_3 \end{array} \right), \end{eqnarray*}
and we will choose as particular right hand side forcing only the effects of gravity, described by
\begin{eqnarray*} \mathbf G(\mathbf w) = \left( \begin{array}{c} g_1\rho \\ g_2\rho \\ g_3\rho \\ 0 \\ \rho \mathbf g \cdot \mathbf v \end{array} \right), \end{eqnarray*}
where \(\mathbf g=(g_1,g_2,g_3)^T\) denotes the gravity vector. With this, the entire system of equations reads:
\begin{eqnarray*} \partial_t (\rho v_i) + \sum_{s=1}^d \frac{\partial(\rho v_i v_s + \delta_{is} p)}{\partial x_s} &=& g_i \rho, \qquad i=1,\dots,d, \\ \partial_t \rho + \sum_{s=1}^d \frac{\partial(\rho v_s)}{\partial x_s} &=& 0, \\ \partial_t E + \sum_{s=1}^d \frac{\partial((E+p)v_s)}{\partial x_s} &=& \rho \mathbf g \cdot \mathbf v. \end{eqnarray*}
These equations describe, respectively, the conservation of momentum, mass, and energy. The system is closed by a relation that defines the pressure: \(p = (\gamma -1)(E-\frac{1}{2} \rho |\mathbf v|^2)\). For the constituents of air (mainly nitrogen and oxygen) and other diatomic gases, the ratio of specific heats is \(\gamma=1.4\).
This problem obviously falls into the class of vector-valued problems. A general overview of how to deal with these problems in deal.II can be found in the Handling vector valued problems module.
Discretization happens in the usual way, taking into account that this is a hyperbolic problem in the same style as the simple one discussed in step-12: We choose a finite element space \(V_h\), and integrate our conservation law against our (vector-valued) test function \(\mathbf{z} \in V_h\). We then integrate by parts and approximate the boundary flux with a numerical flux \(\mathbf{H}\),
\begin{eqnarray*} &&\int_{\Omega} (\partial_t \mathbf{w}, \mathbf{z}) + (\nabla \cdot \mathbf{F}(\mathbf{w}), \mathbf{z}) \\ &\approx &\int_{\Omega} (\partial_t \mathbf{w}, \mathbf{z}) - (\mathbf{F}(\mathbf{w}), \nabla \mathbf{z}) + h^{\eta}(\nabla \mathbf{w} , \nabla \mathbf{z}) + \int_{\partial \Omega} (\mathbf{H}(\mathbf{w}^+, \mathbf{w}^-, \mathbf{n}), \mathbf{z}^+), \end{eqnarray*}
where a superscript \(+\) denotes the interior trace of a function, and \(-\) represents the outer trace. The diffusion term \(h^{\eta}(\nabla \mathbf{w} , \nabla \mathbf{z})\) is introduced strictly for stability, where \(h\) is the mesh size and \(\eta\) is a parameter prescribing how much diffusion to add.
On the boundary, we have to say what the outer trace \(\mathbf{w}^-\) is. Depending on the boundary condition, we prescribe either of the following:
More information on these issues can be found, for example, in Ralf Hartmann's PhD thesis ("Adaptive Finite Element Methods for the Compressible Euler Equations", PhD thesis, University of Heidelberg, 2002).
We use a time stepping scheme to substitute the time derivative in the above equations. For simplicity, we define \( \mathbf{B}({\mathbf{w}_{n}})(\mathbf z) \) as the spatial residual at time step \(n\) :
\begin{eqnarray*} \mathbf{B}(\mathbf{w}_{n})(\mathbf z) &=& - \int_{\Omega} \left(\mathbf{F}(\mathbf{w}_n), \nabla\mathbf{z}\right) + h^{\eta}(\nabla \mathbf{w}_n , \nabla \mathbf{z}) \\ && + \int_{\partial \Omega} \left(\mathbf{H}(\mathbf{w}_n^+, \mathbf{w}^-(\mathbf{w}_n^+), \mathbf{n}), \mathbf{z}\right) - \int_{\Omega} \left(\mathbf{G}(\mathbf{w}_n), \mathbf{z}\right) . \end{eqnarray*}
At each time step, our full discretization is thus that the residual applied to any test function \(\mathbf z\) equals zero:
\begin{eqnarray*} R(\mathbf{W}_{n+1})(\mathbf z) &=& \int_{\Omega} \left(\frac{{\mathbf w}_{n+1} - \mathbf{w}_n}{\delta t}, \mathbf{z}\right)+ \theta \mathbf{B}({\mathbf{w}}_{n+1}) + (1-\theta) \mathbf{B}({\mathbf w}_{n}) \\ &=& 0 \end{eqnarray*}
where \( \theta \in [0,1] \) and \(\mathbf{w}_i = \sum_k \mathbf{W}_i^k \mathbf{\phi}_k\). Choosing \(\theta=0\) results in the explicit (forward) Euler scheme, \(\theta=1\) in the stable implicit (backward) Euler scheme, and \(\theta=\frac 12\) in the Crank-Nicolson scheme.
In the implementation below, we choose the Lax-Friedrichs flux for the function \(\mathbf H\), i.e. \(\mathbf{H}(\mathbf{a},\mathbf{b},\mathbf{n}) = \frac{1}{2}(\mathbf{F}(\mathbf{a})\cdot \mathbf{n} + \mathbf{F}(\mathbf{b})\cdot \mathbf{n} + \alpha (\mathbf{a} - \mathbf{b}))\), where \(\alpha\) is either a fixed number specified in the input file, or where \(\alpha\) is a mesh dependent value. In the latter case, it is chosen as \(\frac{h}{2\delta T}\) with \(h\) the diameter of the face to which the flux is applied, and \(\delta T\) the current time step.
With these choices, equating the residual to zero results in a nonlinear system of equations \(R(\mathbf{W}_{n+1})=0\). We solve this nonlinear system by a Newton iteration (in the same way as explained in step-15), i.e. by iterating
\begin{eqnarray*} R'(\mathbf{W}^k_{n+1},\delta \mathbf{W}_{n+1}^k)(\mathbf z) & = & - R(\mathbf{W}^{k}_{n+1})(\mathbf z) \qquad \qquad \forall \mathbf z\in V_h \\ \mathbf{W}^{k+1}_{n+1} &=& \mathbf{W}^k_{n+1} + \delta \mathbf{W}^k_{n+1}, \end{eqnarray*}
until \(|R(\mathbf{W}^k_{n+1})|\) (the residual) is sufficiently small. By testing with the nodal basis of a finite element space instead of all \(\mathbf z\), we arrive at a linear system for \(\delta \mathbf W\):
\begin{eqnarray*} \mathbf R'(\mathbf{W}^k_{n+1})\delta \mathbf{W}^k_{n+1} & = & - \mathbf R(\mathbf{W}^{k}_{n+1}). \end{eqnarray*}
This linear system is, in general, neither symmetric nor has any particular definiteness properties. We will either use a direct solver or Trilinos' GMRES implementation to solve it. As will become apparent from the results shown below, this fully implicit iteration converges very rapidly (typically in 3 steps) and with the quadratic convergence order expected from a Newton method.
Since computing the Jacobian matrix \(\mathbf R'(\mathbf W^k)\) is a terrible beast, we use an automatic differentiation package, Sacado, to do this. Sacado is a package within the Trilinos framework and offers a C++ template class Sacado::Fad::DFad (Fad standing for "forward automatic
differentiation") that supports basic arithmetic operators and functions such as sqrt, sin, cos, pow, etc. In order to use this feature, one declares a collection of variables of this type and then denotes some of this collection as degrees of freedom, the rest of the variables being functions of the independent variables. These variables are used in an algorithm, and as the variables are used, their sensitivities with respect to the degrees of freedom are continuously updated.
One can imagine that for the full Jacobian matrix as a whole, this could be prohibitively expensive: the number of independent variables are the \(\mathbf W^k\), the dependent variables the elements of the vector \(\mathbf R(\mathbf W^k)\). Both of these vectors can easily have tens of thousands of elements or more. However, it is important to note that not all elements of \(\mathbf R\) depend on all elements of \(\mathbf W^k\): in fact, an entry in \(\mathbf R\) only depends on an element of \(\mathbf W^k\) if the two corresponding shape functions overlap and couple in the weak form.
Specifically, it is wise to define a minimum set of independent AD variables that the residual on the current cell may possibly depend on: on every element, we define those variables as independent that correspond to the degrees of freedom defined on this cell (or, if we have to compute jump terms between cells, that correspond to degrees of freedom defined on either of the two adjacent cells), and the dependent variables are the elements of the local residual vector. Not doing this, i.e. defining all elements of \(\mathbf W^k\) as independent, will result a very expensive computation of a lot of zeros: the elements of the local residual vector are independent of almost all elements of the solution vector, and consequently their derivatives are zero; however, trying to compute these zeros can easily take 90% or more of the compute time of the entire program, as shown in an experiment inadvertently made by a student a few years after this program was first written.
Coming back to the question of computing the Jacobian automatically: The author has used this approach side by side with a hand coded Jacobian for the incompressible Navier-Stokes problem and found the Sacado approach to be just as fast as using a hand coded Jacobian, but infinitely simpler and less error prone: Since using the auto-differentiation requires only that one code the residual \(R(\mathbf{W})\), ensuring code correctness and maintaining code becomes tremendously more simple – the Jacobian matrix \(\mathbf R'\) is computed by essentially the same code that also computes the residual \(\mathbf R\).
All this said, here's a very simple example showing how Sacado can be used:
The output are the derivatives \(\frac{\partial c(a,b)}{\partial a}, \frac{\partial c(a,b)}{\partial b}\) of \(c(a,b)=2a+\cos(ab)\) at \(a=1,b=2\).
It should be noted that Sacado provides more auto-differentiation capabilities than the small subset used in this program. However, understanding the example above is enough to understand the use of Sacado in this Euler flow program.
The program uses either the Aztec iterative solvers, or the Amesos sparse direct solver, both provided by the Trilinos package. This package is inherently designed to be used in a parallel program, however, it may be used in serial just as easily, as is done here. The Epetra package is the basic vector/matrix library upon which the solvers are built. This very powerful package can be used to describe the parallel distribution of a vector, and to define sparse matrices that operate on these vectors. Please view the commented code for more details on how these solvers are used within the example.
The example uses an ad hoc refinement indicator that shows some usefulness in shock-type problems, and in the downhill flow example included. We refine according to the squared gradient of the density. Hanging nodes are handled by computing the numerical flux across cells that are of differing refinement levels, rather than using the AffineConstraints class as in all other tutorial programs so far. In this way, the example combines the continuous and DG methodologies. It also simplifies the generation of the Jacobian because we do not have to track constrained degrees of freedom through the automatic differentiation used to compute it.
Further, we enforce a maximum number of refinement levels to keep refinement under check. It is the author's experience that for adaptivity for a time dependent problem, refinement can easily lead the simulation to a screeching halt, because of time step restrictions if the mesh becomes too fine in any part of the domain, if care is not taken. The amount of refinement is limited in the example by letting the user specify the maximum level of refinement that will be present anywhere in the mesh. In this way, refinement tends not to slow the simulation to a halt. This, of course, is purely a heuristic strategy, and if the author's advisor heard about it, the author would likely be exiled forever from the finite element error estimation community.
We use an input file deck to drive the simulation. In this way, we can alter the boundary conditions and other important properties of the simulation without having to recompile. For more information on the format, look at the results section, where we describe an example input file in more detail.
In previous example programs, we have usually hard-coded the initial and boundary conditions. In this program, we instead use the expression parser class FunctionParser so that we can specify a generic expression in the input file and have it parsed at run time — this way, we can change initial conditions without the need to recompile the program. Consequently, no classes named InitialConditions or BoundaryConditions will be declared in the program below.
The implementation of this program is split into three essential parts:
The EulerEquations class that encapsulates everything that completely describes the specifics of the Euler equations. This includes the flux matrix \(\mathbf F(\mathbf W)\), the numerical flux \(\mathbf F(\mathbf W^+,\mathbf W^-,\mathbf n)\), the right hand side \(\mathbf G(\mathbf W)\), boundary conditions, refinement indicators, postprocessing the output, and similar things that require knowledge of the meaning of the individual components of the solution vectors and the equations.
A namespace that deals with everything that has to do with run-time parameters.
ConservationLaw class that deals with time stepping, outer nonlinear and inner linear solves, assembling the linear systems, and the top-level logic that drives all this. The reason for this approach is that it separates the various concerns in a program: the ConservationLaw is written in such a way that it would be relatively straightforward to adapt it to a different set of equations: One would simply re-implement the members of the EulerEquations class for some other hyperbolic equation, or augment the existing equations by additional ones (for example by advecting additional variables, or by adding chemistry, etc). Such modifications, however, would not affect the time stepping, or the nonlinear solvers if correctly done, and consequently nothing in the ConservationLaw would have to be modified.
Similarly, if we wanted to improve on the linear or nonlinear solvers, or on the time stepping scheme (as hinted at the end of the results section), then this would not require changes in the EulerEquations at all.
First a standard set of deal.II includes. Nothing special to comment on here:
Then, as mentioned in the introduction, we use various Trilinos packages as linear solvers as well as for automatic differentiation. These are in the following include files.
Since deal.II provides interfaces to the basic Trilinos matrices, preconditioners and solvers, we include them similarly as deal.II linear algebra structures.
Sacado is the automatic differentiation package within Trilinos, which is used to find the Jacobian for a fully implicit Newton iteration:
And this again is C++:
To end this section, introduce everything in the dealii library into the namespace into which the contents of this program will go:
Here we define the flux function for this particular system of conservation laws, as well as pretty much everything else that's specific to the Euler equations for gas dynamics, for reasons discussed in the introduction. We group all this into a structure that defines everything that has to do with the flux. All members of this structure are static, i.e. the structure has no actual state specified by instance member variables. The better way to do this, rather than a structure with all static members would be to use a namespace – but namespaces can't be templatized and we want some of the member variables of the structure to depend on the space dimension, which we in our usual way introduce using a template parameter.
First a few variables that describe the various components of our solution vector in a generic way. This includes the number of components in the system (Euler's equations have one entry for momenta in each spatial direction, plus the energy and density components, for a total of dim+2 components), as well as functions that describe the index within the solution vector of the first momentum component, the density component, and the energy density component. Note that all these numbers depend on the space dimension; defining them in a generic way (rather than by implicit convention) makes our code more flexible and makes it easier to later extend it, for example by adding more components to the equations.
When generating graphical output way down in this program, we need to specify the names of the solution variables as well as how the various components group into vector and scalar fields. We could describe this there, but in order to keep things that have to do with the Euler equation localized here and the rest of the program as generic as possible, we provide this sort of information in the following two functions:
Next, we define the gas constant. We will set it to 1.4 in its definition immediately following the declaration of this class (unlike integer variables, like the ones above, static const floating point member variables cannot be initialized within the class declaration in C++). This value of 1.4 is representative of a gas that consists of molecules composed of two atoms, such as air which consists up to small traces almost entirely of \(N_2\) and \(O_2\).
In the following, we will need to compute the kinetic energy and the pressure from a vector of conserved variables. This we can do based on the energy density and the kinetic energy \(\frac 12 \rho |\mathbf v|^2 = \frac{|\rho \mathbf v|^2}{2\rho}\) (note that the independent variables contain the momentum components \(\rho v_i\), not the velocities \(v_i\)).
We define the flux function \(F(W)\) as one large matrix. Each row of this matrix represents a scalar conservation law for the component in that row. The exact form of this matrix is given in the introduction. Note that we know the size of the matrix: it has as many rows as the system has components, and dim columns; rather than using a FullMatrix object for such a matrix (which has a variable number of rows and columns and must therefore allocate memory on the heap each time such a matrix is created), we use a rectangular array of numbers right away.
We templatize the numerical type of the flux function so that we may use the automatic differentiation type here. Similarly, we will call the function with different input vector data types, so we templatize on it as well:
First compute the pressure that appears in the flux matrix, and then compute the first dim columns of the matrix that correspond to the momentum terms:
Then the terms for the density (i.e. mass conservation), and, lastly, conservation of energy:
On the boundaries of the domain and across hanging nodes we use a numerical flux function to enforce boundary conditions. This routine is the basic Lax-Friedrich's flux with a stabilization parameter \(\alpha\). It's form has also been given already in the introduction:
In the same way as describing the flux function \(\mathbf F(\mathbf w)\), we also need to have a way to describe the right hand side forcing term. As mentioned in the introduction, we consider only gravity here, which leads to the specific form \(\mathbf G(\mathbf w) = \left( g_1\rho, g_2\rho, g_3\rho, 0, \rho \mathbf g \cdot \mathbf v \right)^T\), shown here for the 3d case. More specifically, we will consider only \(\mathbf g=(0,0,-1)^T\) in 3d, or \(\mathbf g=(0,-1)^T\) in 2d. This naturally leads to the following function:
Another thing we have to deal with is boundary conditions. To this end, let us first define the kinds of boundary conditions we currently know how to deal with:
The next part is to actually decide what to do at each kind of boundary. To this end, remember from the introduction that boundary conditions are specified by choosing a value \(\mathbf w^-\) on the outside of a boundary given an inhomogeneity \(\mathbf j\) and possibly the solution's value \(\mathbf w^+\) on the inside. Both are then passed to the numerical flux \(\mathbf H(\mathbf{w}^+, \mathbf{w}^-, \mathbf{n})\) to define boundary contributions to the bilinear form.
Boundary conditions can in some cases be specified for each component of the solution vector independently. For example, if component \(c\) is marked for inflow, then \(w^-_c = j_c\). If it is an outflow, then \(w^-_c = w^+_c\). These two simple cases are handled first in the function below.
There is a little snag that makes this function unpleasant from a C++ language viewpoint: The output vector Wminus will of course be modified, so it shouldn't be a const argument. Yet it is in the implementation below, and needs to be in order to allow the code to compile. The reason is that we call this function at a place where Wminus is of type Table<2,Sacado::Fad::DFad<double> >, this being 2d table with indices representing the quadrature point and the vector component, respectively. We call this function with Wminus[q] as last argument; subscripting a 2d table yields a temporary accessor object representing a 1d vector, just what we want here. The problem is that a temporary accessor object can't be bound to a non-const reference argument of a function, as we would like here, according to the C++ 1998 and 2003 standards (something that will be fixed with the next standard in the form of rvalue references). We get away with making the output argument here a constant because it is the accessor object that's constant, not the table it points to: that one can still be written to. The hack is unpleasant nevertheless because it restricts the kind of data types that may be used as template argument to this function: a regular vector isn't going to do because that one can not be written to when marked const. With no good solution around at the moment, we'll go with the pragmatic, even if not pretty, solution shown here:
Prescribed pressure boundary conditions are a bit more complicated by the fact that even though the pressure is prescribed, we really are setting the energy component here, which will depend on velocity and pressure. So even though this seems like a Dirichlet type boundary condition, we get sensitivities of energy to velocity and density (unless these are also prescribed):
We prescribe the velocity (we are dealing with a particular component here so that the average of the velocities is orthogonal to the surface normal. This creates sensitivities of across the velocity components.
In this class, we also want to specify how to refine the mesh. The class ConservationLaw that will use all the information we provide here in the EulerEquation class is pretty agnostic about the particular conservation law it solves: as doesn't even really care how many components a solution vector has. Consequently, it can't know what a reasonable refinement indicator would be. On the other hand, here we do, or at least we can come up with a reasonable choice: we simply look at the gradient of the density, and compute \(\eta_K=\log\left(1+|\nabla\rho(x_K)|\right)\), where \(x_K\) is the center of cell \(K\).
There are certainly a number of equally reasonable refinement indicators, but this one does, and it is easy to compute:
Finally, we declare a class that implements a postprocessing of data components. The problem this class solves is that the variables in the formulation of the Euler equations we use are in conservative rather than physical form: they are momentum densities \(\mathbf m=\rho\mathbf v\), density \(\rho\), and energy density \(E\). What we would like to also put into our output file are velocities \(\mathbf v=\frac{\mathbf m}{\rho}\) and pressure \(p=(\gamma-1)(E-\frac{1}{2} \rho |\mathbf v|^2)\).
In addition, we would like to add the possibility to generate schlieren plots. Schlieren plots are a way to visualize shocks and other sharp interfaces. The word "schlieren" is a German word that may be translated as "striae" – it may be simpler to explain it by an example, however: schlieren is what you see when you, for example, pour highly concentrated alcohol, or a transparent saline solution, into water; the two have the same color, but they have different refractive indices and so before they are fully mixed light goes through the mixture along bent rays that lead to brightness variations if you look at it. That's "schlieren". A similar effect happens in compressible flow because the refractive index depends on the pressure (and therefore the density) of the gas.
The origin of the word refers to two-dimensional projections of a three-dimensional volume (we see a 2d picture of the 3d fluid). In computational fluid dynamics, we can get an idea of this effect by considering what causes it: density variations. Schlieren plots are therefore produced by plotting \(s=|\nabla \rho|^2\); obviously, \(s\) is large in shocks and at other highly dynamic places. If so desired by the user (by specifying this in the input file), we would like to generate these schlieren plots in addition to the other derived quantities listed above.
The implementation of the algorithms to compute derived quantities from the ones that solve our problem, and to output them into data file, rests on the DataPostprocessor class. It has extensive documentation, and other uses of the class can also be found in step-29. We therefore refrain from extensive comments.
This is the only function worth commenting on. When generating graphical output, the DataOut and related classes will call this function on each cell, with access to values, gradients, Hessians, and normal vectors (in case we're working on faces) at each quadrature point. Note that the data at each quadrature point is itself vector-valued, namely the conserved variables. What we're going to do here is to compute the quantities we're interested in at each quadrature point. Note that for this we can ignore the Hessians ("inputs.solution_hessians") and normal vectors ("inputs.normals").
At the beginning of the function, let us make sure that all variables have the correct sizes, so that we can access individual vector elements without having to wonder whether we might read or write invalid elements; we also check that the solution_gradients vector only contains data if we really need it (the system knows about this because we say so in the get_needed_update_flags() function below). For the inner vectors, we check that at least the first element of the outer vector has the correct inner size:
Then loop over all quadrature points and do our work there. The code should be pretty self-explanatory. The order of output variables is first dim velocities, then the pressure, and if so desired the schlieren plot. Note that we try to be generic about the order of variables in the input vector, using the first_momentum_component and density_component information:
Our next job is to define a few classes that will contain run-time parameters (for example solver tolerances, number of iterations, stabilization parameter, and the like). One could do this in the main class, but we separate it from that one to make the program more modular and easier to read: Everything that has to do with run-time parameters will be in the following namespace, whereas the program logic is in the main class.
We will split the run-time parameters into a few separate structures, which we will all put into a namespace Parameters. Of these classes, there are a few that group the parameters for individual groups, such as for solvers, mesh refinement, or output. Each of these classes have functions declare_parameters() and parse_parameters() that declare parameter subsections and entries in a ParameterHandler object, and retrieve actual parameter values from such an object, respectively. These classes declare all their parameters in subsections of the ParameterHandler.
The final class of the following namespace combines all the previous classes by deriving from them and taking care of a few more entries at the top level of the input file, as well as a few odd other entries in subsections that are too short to warrant a structure by themselves.
It is worth pointing out one thing here: None of the classes below have a constructor that would initialize the various member variables. This isn't a problem, however, since we will read all variables declared in these classes from the input file (or indirectly: a ParameterHandler object will read it from there, and we will get the values from this object), and they will be initialized this way. In case a certain variable is not specified at all in the input file, this isn't a problem either: The ParameterHandler class will in this case simply take the default value that was specified when declaring an entry in the declare_parameters() functions of the classes below.
The first of these classes deals with parameters for the linear inner solver. It offers parameters that indicate which solver to use (GMRES as a solver for general non-symmetric indefinite systems, or a sparse direct solver), the amount of output to be produced, as well as various parameters that tweak the thresholded incomplete LU decomposition (ILUT) that we use as a preconditioner for GMRES.
In particular, the ILUT takes the following parameters:
The meaning of each parameter is also briefly described in the third argument of the ParameterHandler::declare_entry call in declare_parameters().
Similarly, here are a few parameters that determine how the mesh is to be refined (and if it is to be refined at all). For what exactly the shock parameters do, see the mesh refinement functions further down.
Next a section on flux modifications to make it more stable. In particular, two options are offered to stabilize the Lax-Friedrichs flux: either choose \(\mathbf{H}(\mathbf{a},\mathbf{b},\mathbf{n}) = \frac{1}{2}(\mathbf{F}(\mathbf{a})\cdot \mathbf{n} + \mathbf{F}(\mathbf{b})\cdot \mathbf{n} + \alpha (\mathbf{a} - \mathbf{b}))\) where \(\alpha\) is either a fixed number specified in the input file, or where \(\alpha\) is a mesh dependent value. In the latter case, it is chosen as \(\frac{h}{2\delta T}\) with \(h\) the diameter of the face to which the flux is applied, and \(\delta T\) the current time step.
Then a section on output parameters. We offer to produce Schlieren plots (the squared gradient of the density, a tool to visualize shock fronts), and a time interval between graphical output in case we don't want an output file every time step.
Finally the class that brings it all together. It declares a number of parameters itself, mostly ones at the top level of the parameter file as well as several in section too small to warrant their own classes. It also contains everything that is actually space dimension dependent, like initial or boundary conditions.
Since this class is derived from all the ones above, the declare_parameters() and parse_parameters() functions call the respective functions of the base classes as well.
Note that this class also handles the declaration of initial and boundary conditions specified in the input file. To this end, in both cases, there are entries like "w_0 value" which represent an expression in terms of \(x,y,z\) that describe the initial or boundary condition as a formula that will later be parsed by the FunctionParser class. Similar expressions exist for "w_1", "w_2", etc, denoting the dim+2 conserved variables of the Euler system. Similarly, we allow up to max_n_boundaries boundary indicators to be used in the input file, and each of these boundary indicators can be associated with an inflow, outflow, or pressure boundary condition, with homogeneous boundary conditions being specified for each component and each boundary indicator separately.
The data structure used to store the boundary indicators is a bit complicated. It is an array of max_n_boundaries elements indicating the range of boundary indicators that will be accepted. For each entry in this array, we store a pair of data in the BoundaryCondition structure: first, an array of size n_components that for each component of the solution vector indicates whether it is an inflow, outflow, or other kind of boundary, and second a FunctionParser object that describes all components of the solution vector for this boundary id at once.
The BoundaryCondition structure requires a constructor since we need to tell the function parser object at construction time how many vector components it is to describe. This initialization can therefore not wait till we actually set the formulas the FunctionParser object represents later in AllParameters::parse_parameters()
For the same reason of having to tell Function objects their vector size at construction time, we have to have a constructor of the AllParameters class that at least initializes the other FunctionParser object, i.e. the one describing initial conditions.
Here finally comes the class that actually does something with all the Euler equation and parameter specifics we've defined above. The public interface is pretty much the same as always (the constructor now takes the name of a file from which to read parameters, which is passed on the command line). The private function interface is also pretty similar to the usual arrangement, with the assemble_system function split into three parts: one that contains the main loop over all cells and that then calls the other two for integrals over cells and faces, respectively.
The first few member variables are also rather standard. Note that we define a mapping object to be used throughout the program when assembling terms (we will hand it to every FEValues and FEFaceValues object); the mapping we use is just the standard \(Q_1\) mapping – nothing fancy, in other words – but declaring one here and using it throughout the program will make it simpler later on to change it if that should become necessary. This is, in fact, rather pertinent: it is known that for transsonic simulations with the Euler equations, computations do not converge even as \(h\rightarrow 0\) if the boundary approximation is not of sufficiently high order.
Next come a number of data vectors that correspond to the solution of the previous time step (old_solution), the best guess of the current solution (current_solution; we say guess because the Newton iteration to compute it may not have converged yet, whereas old_solution refers to the fully converged final result of the previous time step), and a predictor for the solution at the next time step, computed by extrapolating the current and previous solution one time step into the future:
This final set of member variables (except for the object holding all run-time parameters at the very bottom and a screen output stream that only prints something if verbose output has been requested) deals with the interface we have in this program to the Trilinos library that provides us with linear solvers. Similarly to including PETSc matrices in step-17 and step-18, all we need to do is to create a Trilinos sparse matrix instead of the standard deal.II class. The system matrix is used for the Jacobian in each Newton step. Since we do not intend to run this program in parallel (which wouldn't be too hard with Trilinos data structures, though), we don't have to think about anything else like distributing the degrees of freedom.
There is nothing much to say about the constructor. Essentially, it reads the input file and fills the parameter object with the parsed values:
The following (easy) function is called each time the mesh is changed. All it does is to resize the Trilinos matrix according to a sparsity pattern that we generate as in all the previous tutorial programs.
This and the following two functions are the meat of this program: They assemble the linear system that results from applying Newton's method to the nonlinear system of conservation equations.
This first function puts all of the assembly pieces together in a routine that dispatches the correct piece for each cell/face. The actual implementation of the assembly on these objects is done in the following functions.
At the top of the function we do the usual housekeeping: allocate FEValues, FEFaceValues, and FESubfaceValues objects necessary to do the integrations on cells, faces, and subfaces (in case of adjoining cells on different refinement levels). Note that we don't need all information (like values, gradients, or real locations of quadrature points) for all of these objects, so we only let the FEValues classes whatever is actually necessary by specifying the minimal set of UpdateFlags. For example, when using a FEFaceValues object for the neighboring cell we only need the shape values: Given a specific face, the quadrature points and JxW values are the same as for the current cells, and the normal vectors are known to be the negative of the normal vectors of the current cell.
Then loop over all cells, initialize the FEValues object for the current cell and call the function that assembles the problem on this cell.
Then loop over all the faces of this cell. If a face is part of the external boundary, then assemble boundary conditions there (the fifth argument to assemble_face_terms indicates whether we are working on an external or internal face; if it is an external face, the fourth argument denoting the degrees of freedom indices of the neighbor is ignored, so we pass an empty vector):
The alternative is that we are dealing with an internal face. There are two cases that we need to distinguish: that this is a normal face between two cells at the same refinement level, and that it is a face between two cells of the different refinement levels.
In the first case, there is nothing we need to do: we are using a continuous finite element, and face terms do not appear in the bilinear form in this case. The second case usually does not lead to face terms either if we enforce hanging node constraints strongly (as in all previous tutorial programs so far whenever we used continuous finite elements – this enforcement is done by the AffineConstraints class together with DoFTools::make_hanging_node_constraints). In the current program, however, we opt to enforce continuity weakly at faces between cells of different refinement level, for two reasons: (i) because we can, and more importantly (ii) because we would have to thread the automatic differentiation we use to compute the elements of the Newton matrix from the residual through the operations of the AffineConstraints class. This would be possible, but is not trivial, and so we choose this alternative approach.
What needs to be decided is which side of an interface between two cells of different refinement level we are sitting on.
Let's take the case where the neighbor is more refined first. We then have to loop over the children of the face of the current cell and integrate on each of them. We sprinkle a couple of assertions into the code to ensure that our reasoning trying to figure out which of the neighbor's children's faces coincides with a given subface of the current cell's faces is correct – a bit of defensive programming never hurts.
We then call the function that integrates over faces; since this is an internal face, the fifth argument is false, and the sixth one is ignored so we pass an invalid value again:
The other possibility we have to care for is if the neighbor is coarser than the current cell (in particular, because of the usual restriction of only one hanging node per face, the neighbor must be exactly one level coarser than the current cell, something that we check with an assertion). Again, we then integrate over this interface:
This function assembles the cell term by computing the cell part of the residual, adding its negative to the right hand side vector, and adding its derivative with respect to the local variables to the Jacobian (i.e. the Newton matrix). Recall that the cell contributions to the residual read \(R_i = \left(\frac{\mathbf{w}^{k}_{n+1} - \mathbf{w}_n}{\delta t} , \mathbf{z}_i \right)_K \) \( + \theta \mathbf{B}(\mathbf{w}^{k}_{n+1})(\mathbf{z}_i)_K \) \( + (1-\theta) \mathbf{B}(\mathbf{w}_{n}) (\mathbf{z}_i)_K \) where \(\mathbf{B}(\mathbf{w})(\mathbf{z}_i)_K = - \left(\mathbf{F}(\mathbf{w}),\nabla\mathbf{z}_i\right)_K \) \( + h^{\eta}(\nabla \mathbf{w} , \nabla \mathbf{z}_i)_K \) \( - (\mathbf{G}(\mathbf {w}), \mathbf{z}_i)_K \) for both \(\mathbf{w} = \mathbf{w}^k_{n+1}\) and \(\mathbf{w} = \mathbf{w}_{n}\) , \(\mathbf{z}_i\) is the \(i\)th vector valued test function. Furthermore, the scalar product \(\left(\mathbf{F}(\mathbf{w}), \nabla\mathbf{z}_i\right)_K\) is understood as \(\int_K \sum_{c=1}^{\text{n\_components}} \sum_{d=1}^{\text{dim}} \mathbf{F}(\mathbf{w})_{cd} \frac{\partial z^c_i}{x_d}\) where \(z^c_i\) is the \(c\)th component of the \(i\)th test function.
At the top of this function, we do the usual housekeeping in terms of allocating some local variables that we will need later. In particular, we will allocate variables that will hold the values of the current solution \(W_{n+1}^k\) after the \(k\)th Newton iteration (variable W) and the previous time step's solution \(W_{n}\) (variable W_old).
In addition to these, we need the gradients of the current variables. It is a bit of a shame that we have to compute these; we almost don't. The nice thing about a simple conservation law is that the flux doesn't generally involve any gradients. We do need these, however, for the diffusion stabilization.
The actual format in which we store these variables requires some explanation. First, we need values at each quadrature point for each of the EulerEquations::n_components components of the solution vector. This makes for a two-dimensional table for which we use deal.II's Table class (this is more efficient than std::vector<std::vector<T> > because it only needs to allocate memory once, rather than once for each element of the outer vector). Similarly, the gradient is a three-dimensional table, which the Table class also supports.
Secondly, we want to use automatic differentiation. To this end, we use the Sacado::Fad::DFad template for everything that is computed from the variables with respect to which we would like to compute derivatives. This includes the current solution and gradient at the quadrature points (which are linear combinations of the degrees of freedom) as well as everything that is computed from them such as the residual, but not the previous time step's solution. These variables are all found in the first part of the function, along with a variable that we will use to store the derivatives of a single component of the residual:
Next, we have to define the independent variables that we will try to determine by solving a Newton step. These independent variables are the values of the local degrees of freedom which we extract here:
The next step incorporates all the magic: we declare a subset of the autodifferentiation variables as independent degrees of freedom, whereas all the other ones remain dependent functions. These are precisely the local degrees of freedom just extracted. All calculations that reference them (either directly or indirectly) will accumulate sensitivities with respect to these variables.
In order to mark the variables as independent, the following does the trick, marking independent_local_dof_values[i] as the \(i\)th independent variable out of a total of dofs_per_cell:
After all these declarations, let us actually compute something. First, the values of W, W_old, grad_W and grad_W_old, which we can compute from the local DoF values by using the formula \(W(x_q)=\sum_i \mathbf W_i \Phi_i(x_q)\), where \(\mathbf W_i\) is the \(i\)th entry of the (local part of the) solution vector, and \(\Phi_i(x_q)\) the value of the \(i\)th vector-valued shape function evaluated at quadrature point \(x_q\). The gradient can be computed in a similar way.
Ideally, we could compute this information using a call into something like FEValues::get_function_values and FEValues::get_function_gradients, but since (i) we would have to extend the FEValues class for this, and (ii) we don't want to make the entire old_solution vector fad types, only the local cell variables, we explicitly code the loop above. Before this, we add another loop that initializes all the fad variables to zero:
Next, in order to compute the cell contributions, we need to evaluate \(\mathbf{F}({\mathbf w}^k_{n+1})\), \(\mathbf{G}({\mathbf w}^k_{n+1})\) and \(\mathbf{F}({\mathbf w}_n)\), \(\mathbf{G}({\mathbf w}_n)\) at all quadrature points. To store these, we also need to allocate a bit of memory. Note that we compute the flux matrices and right hand sides in terms of autodifferentiation variables, so that the Jacobian contributions can later easily be computed from it:
We now have all of the pieces in place, so perform the assembly. We have an outer loop through the components of the system, and an inner loop over the quadrature points, where we accumulate contributions to the \(i\)th residual \(R_i\). The general formula for this residual is given in the introduction and at the top of this function. We can, however, simplify it a bit taking into account that the \(i\)th (vector-valued) test function \(\mathbf{z}_i\) has in reality only a single nonzero component (more on this topic can be found in the Handling vector valued problems module). It will be represented by the variable component_i below. With this, the residual term can be re-written as
\begin{eqnarray*} R_i &=& \left(\frac{(\mathbf{w}_{n+1} - \mathbf{w}_n)_{\text{component\_i}}}{\delta t},(\mathbf{z}_i)_{\text{component\_i}}\right)_K \\ &-& \sum_{d=1}^{\text{dim}} \left( \theta \mathbf{F} ({\mathbf{w}^k_{n+1}})_{\text{component\_i},d} + (1-\theta) \mathbf{F} ({\mathbf{w}_{n}})_{\text{component\_i},d} , \frac{\partial(\mathbf{z}_i)_{\text{component\_i}}} {\partial x_d}\right)_K \\ &+& \sum_{d=1}^{\text{dim}} h^{\eta} \left( \theta \frac{\partial (\mathbf{w}^k_{n+1})_{\text{component\_i}}}{\partial x_d} + (1-\theta) \frac{\partial (\mathbf{w}_n)_{\text{component\_i}}}{\partial x_d} , \frac{\partial (\mathbf{z}_i)_{\text{component\_i}}}{\partial x_d} \right)_K \\ &-& \left( \theta\mathbf{G}({\mathbf{w}^k_n+1} )_{\text{component\_i}} + (1-\theta)\mathbf{G}({\mathbf{w}_n})_{\text{component\_i}} , (\mathbf{z}_i)_{\text{component\_i}} \right)_K , \end{eqnarray*}
where integrals are understood to be evaluated through summation over quadrature points.
We initially sum all contributions of the residual in the positive sense, so that we don't need to negative the Jacobian entries. Then, when we sum into the right_hand_side vector, we negate this residual.
The residual for each row (i) will be accumulating into this fad variable. At the end of the assembly for this row, we will query for the sensitivities to this variable and add them into the Jacobian.
At the end of the loop, we have to add the sensitivities to the matrix and subtract the residual from the right hand side. Trilinos FAD data type gives us access to the derivatives using R_i.fastAccessDx(k), so we store the data in a temporary array. This information about the whole row of local dofs is then added to the Trilinos matrix at once (which supports the data types we have chosen).
Here, we do essentially the same as in the previous function. At the top, we introduce the independent variables. Because the current function is also used if we are working on an internal face between two cells, the independent variables are not only the degrees of freedom on the current cell but in the case of an interior face also the ones on the neighbor.
Next, we need to define the values of the conservative variables \({\mathbf W}\) on this side of the face ( \( {\mathbf W}^+\)) and on the opposite side ( \({\mathbf W}^-\)), for both \({\mathbf W} = {\mathbf W}^k_{n+1}\) and \({\mathbf W} = {\mathbf W}_n\). The "this side" values can be computed in exactly the same way as in the previous function, but note that the fe_v variable now is of type FEFaceValues or FESubfaceValues:
Computing "opposite side" is a bit more complicated. If this is an internal face, we can compute it as above by simply using the independent variables from the neighbor:
On the other hand, if this is an external boundary face, then the values of \(\mathbf{W}^-\) will be either functions of \(\mathbf{W}^+\), or they will be prescribed, depending on the kind of boundary condition imposed here.
To start the evaluation, let us ensure that the boundary id specified for this boundary is one for which we actually have data in the parameters object. Next, we evaluate the function object for the inhomogeneity. This is a bit tricky: a given boundary might have both prescribed and implicit values. If a particular component is not prescribed, the values evaluate to zero and are ignored below.
The rest is done by a function that actually knows the specifics of Euler equation boundary conditions. Note that since we are using fad variables here, sensitivities will be updated appropriately, a process that would otherwise be tremendously complicated.
Here we assume that boundary type, boundary normal vector and boundary data values maintain the same during time advancing.
Now that we have \(\mathbf w^+\) and \(\mathbf w^-\), we can go about computing the numerical flux function \(\mathbf H(\mathbf w^+,\mathbf w^-, \mathbf n)\) for each quadrature point. Before calling the function that does so, we also need to determine the Lax-Friedrich's stability parameter:
Now assemble the face term in exactly the same way as for the cell contributions in the previous function. The only difference is that if this is an internal face, we also have to take into account the sensitivities of the residual contributions to the degrees of freedom on the neighboring cell:
Here, we actually solve the linear system, using either of Trilinos' Aztec or Amesos linear solvers. The result of the computation will be written into the argument vector passed to this function. The result is a pair of number of iterations and the final linear residual.
If the parameter file specified that a direct solver shall be used, then we'll get here. The process is straightforward, since deal.II provides a wrapper class to the Amesos direct solver within Trilinos. All we have to do is to create a solver control object (which is just a dummy object here, since we won't perform any iterations), and then create the direct solver object. When actually doing the solve, note that we don't pass a preconditioner. That wouldn't make much sense for a direct solver anyway. At the end we return the solver control statistics — which will tell that no iterations have been performed and that the final linear residual is zero, absent any better information that may be provided here:
Likewise, if we are to use an iterative solver, we use Aztec's GMRES solver. We could use the Trilinos wrapper classes for iterative solvers and preconditioners here as well, but we choose to use an Aztec solver directly. For the given problem, Aztec's internal preconditioner implementations are superior over the ones deal.II has wrapper classes to, so we use ILU-T preconditioning within the AztecOO solver and set a bunch of options that can be changed from the parameter file.
There are two more practicalities: Since we have built our right hand side and solution vector as deal.II Vector objects (as opposed to the matrix, which is a Trilinos object), we must hand the solvers Trilinos Epetra vectors. Luckily, they support the concept of a 'view', so we just send in a pointer to our deal.II vectors. We have to provide an Epetra_Map for the vector that sets the parallel distribution, which is just a dummy object in serial. The easiest way is to ask the matrix for its map, and we're going to be ready for matrix-vector products with it.
Secondly, the Aztec solver wants us to pass a Trilinos Epetra_CrsMatrix in, not the deal.II wrapper class itself. So we access to the actual Trilinos matrix in the Trilinos wrapper class by the command trilinos_matrix(). Trilinos wants the matrix to be non-constant, so we have to manually remove the constantness using a const_cast.
This function is real simple: We don't pretend that we know here what a good refinement indicator would be. Rather, we assume that the EulerEquation class would know about this, and so we simply defer to the respective function we've implemented there:
Here, we use the refinement indicators computed before and refine the mesh. At the beginning, we loop over all cells and mark those that we think should be refined:
Then we need to transfer the various solution vectors from the old to the new grid while we do the refinement. The SolutionTransfer class is our friend here; it has a fairly extensive documentation, including examples, so we won't comment much on the following code. The last three lines simply re-set the sizes of some other vectors to the now correct size:
This function now is rather straightforward. All the magic, including transforming data from conservative variables to physical ones has been abstracted and moved into the EulerEquations class so that it can be replaced in case we want to solve some other hyperbolic conservation law.
Note that the number of the output file is determined by keeping a counter in the form of a static variable that is set to zero the first time we come to this function and is incremented by one at the end of each invocation.
This function contains the top-level logic of this program: initialization, the time loop, and the inner Newton iteration.
At the beginning, we read the mesh file specified by the parameter file, setup the DoFHandler and various vectors, and then interpolate the given initial conditions on this mesh. We then perform a number of mesh refinements, based on the initial conditions, to obtain a mesh that is already well adapted to the starting solution. At the end of this process, we output the initial solution.
Size all of the fields.
We then enter into the main time stepping loop. At the top we simply output some status information so one can keep track of where a computation is, as well as the header for a table that indicates progress of the nonlinear inner iteration:
Then comes the inner Newton iteration to solve the nonlinear problem in each time step. The way it works is to reset matrix and right hand side to zero, then assemble the linear system. If the norm of the right hand side is small enough, then we declare that the Newton iteration has converged. Otherwise, we solve the linear system, update the current solution with the Newton increment, and output convergence information. At the end, we check that the number of Newton iterations is not beyond a limit of 10 – if it is, it appears likely that iterations are diverging and further iterations would do no good. If that happens, we throw an exception that will be caught in main() with status information being displayed before the program aborts.
Note that the way we write the AssertThrow macro below is by and large equivalent to writing something like if (!(nonlin_iter <= 10)) throw ExcMessage ("No convergence in nonlinear
solver");. The only significant difference is that AssertThrow also makes sure that the exception being thrown carries with it information about the location (file name and line number) where it was generated. This is not overly critical here, because there is only a single place where this sort of exception can happen; however, it is generally a very useful tool when one wants to find out where an error occurred.
We only get to this point if the Newton iteration has converged, so do various post convergence tasks here:
First, we update the time and produce graphical output if so desired. Then we update a predictor for the solution at the next time step by approximating \(\mathbf w^{n+1}\approx \mathbf w^n + \delta t \frac{\partial \mathbf w}{\partial t} \approx \mathbf w^n + \delta t \; \frac{\mathbf w^n-\mathbf w^{n-1}}{\delta t} = 2 \mathbf w^n - \mathbf w^{n-1}\) to try and make adaptivity work better. The idea is to try and refine ahead of a front, rather than stepping into a coarse set of elements and smearing the old_solution. This simple time extrapolator does the job. With this, we then refine the mesh if so desired by the user, and finally continue on with the next time step:
The following `‘main’' function is similar to previous examples and need not to be commented on. Note that the program aborts if no input file name is given on the command line.
We run the problem with the mesh slide.inp (this file is in the same directory as the source code for this program) and the following input deck (available as input.prm in the same directory):
# Listing of Parameters # --------------------- # The input grid set mesh = slide.inp # Stabilization parameter set diffusion power = 2.0 # -------------------------------------------------- # Boundary conditions # We may specify boundary conditions for up to MAX_BD boundaries. # Your .inp file should have these boundaries designated. subsection boundary_1 set no penetration = true # reflective boundary condition end subsection boundary_2 # outflow boundary # set w_2 = pressure # set w_2 value = 1.5 - y end subsection boundary_3 set no penetration = true # reflective # set w_3 = pressure # set w_3 value = 1.0 end subsection boundary_4 set no penetration = true #reflective end # -------------------------------------------------- # Initial Conditions # We set the initial conditions of the conservative variables. These lines # are passed to the expression parsing function. You should use x,y,z for # the coordinate variables. subsection initial condition set w_0 value = 0 set w_1 value = 0 set w_2 value = 10*(x<-0.7)*(y> 0.3)*(y< 0.45) + (1-(x<-0.7)*(y> 0.3)*(y< 0.45))*1.0 set w_3 value = (1.5-(1.0*1.0*y))/0.4 end # -------------------------------------------------- # Time stepping control subsection time stepping set final time = 10.0 # simulation end time set time step = 0.02 # simulation time step set theta scheme value = 0.5 end subsection linear solver set output = quiet set method = gmres set ilut fill = 1.5 set ilut drop tolerance = 1e-6 set ilut absolute tolerance = 1e-6 set ilut relative tolerance = 1.0 end # -------------------------------------------------- # Output frequency and kind subsection output set step = 0.01 set schlieren plot = true end # -------------------------------------------------- # Refinement control subsection refinement set refinement = true # none only other option set shock value = 1.5 set shock levels = 1 # how many levels of refinement to allow end # -------------------------------------------------- # Flux parameters subsection flux set stab = constant #set stab value = 1.0 end
When we run the program, we get the following kind of output:
... T=0.14 Number of active cells: 1807 Number of degrees of freedom: 7696 NonLin Res Lin Iter Lin Res _____________________________________ 7.015e-03 0008 3.39e-13 2.150e-05 0008 1.56e-15 2.628e-09 0008 5.09e-20 5.243e-16 (converged) T=0.16 Number of active cells: 1807 Number of degrees of freedom: 7696 NonLin Res Lin Iter Lin Res _____________________________________ 7.145e-03 0008 3.80e-13 2.548e-05 0008 7.20e-16 4.063e-09 0008 2.49e-19 5.970e-16 (converged) T=0.18 Number of active cells: 1807 Number of degrees of freedom: 7696 NonLin Res Lin Iter Lin Res _____________________________________ 7.395e-03 0008 6.69e-13 2.867e-05 0008 1.33e-15 4.091e-09 0008 3.35e-19 5.617e-16 (converged) ...
This output reports the progress of the Newton iterations and the time stepping. Note that our implementation of the Newton iteration indeed shows the expected quadratic convergence order: the norm of the nonlinear residual in each step is roughly the norm of the previous step squared. This leads to the very rapid convergence we can see here. This holds until times up to \(t=1.9\) at which time the nonlinear iteration reports a lack of convergence:
...
T=1.88
Number of active cells: 2119
Number of degrees of freedom: 9096
NonLin Res Lin Iter Lin Res
_____________________________________
2.251e-01 0012 9.78e-12
5.698e-03 0012 2.04e-13
3.896e-05 0012 1.48e-15
3.915e-09 0012 1.94e-19
8.800e-16 (converged)
T=1.9
Number of active cells: 2140
Number of degrees of freedom: 9184
NonLin Res Lin Iter Lin Res
_____________________________________
2.320e-01 0013 3.94e-12
1.235e-01 0016 6.62e-12
8.494e-02 0016 6.05e-12
1.199e+01 0026 5.72e-10
1.198e+03 0002 1.20e+03
7.030e+03 0001 nan
7.030e+03 0001 nan
7.030e+03 0001 nan
7.030e+03 0001 nan
7.030e+03 0001 nan
7.030e+03 0001 nan
----------------------------------------------------
Exception on processing:
--------------------------------------------------------
An error occurred in line <2476> of file <step-33.cc> in function
void Step33::ConservationLaw<dim>::run() [with int dim = 2]
The violated condition was:
nonlin_iter <= 10
The name and call sequence of the exception was:
ExcMessage ("No convergence in nonlinear solver")
Additional Information:
No convergence in nonlinear solver
--------------------------------------------------------
Aborting!
----------------------------------------------------
We may find out the cause and possible remedies by looking at the animation of the solution.
The result of running these computations is a bunch of output files that we can pass to our visualization program of choice. When we collate them into a movie, the results of last several time steps looks like this:
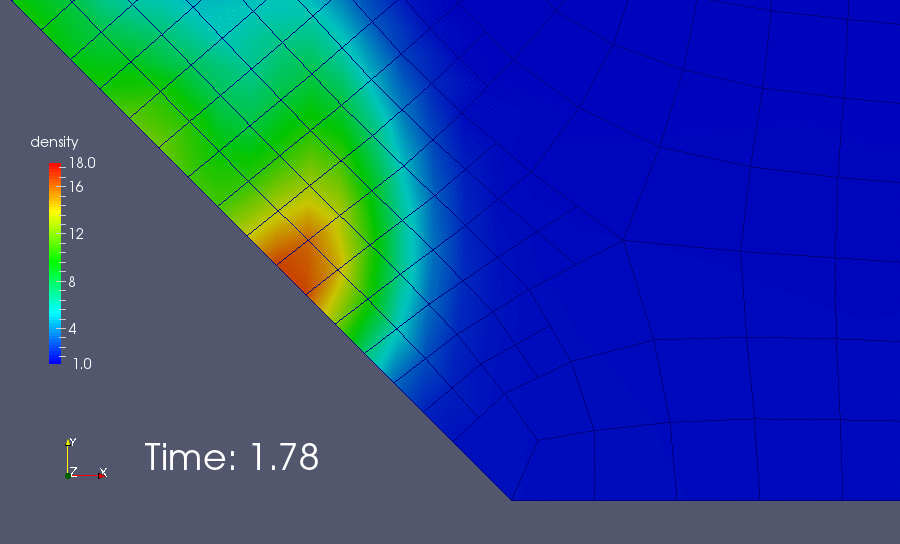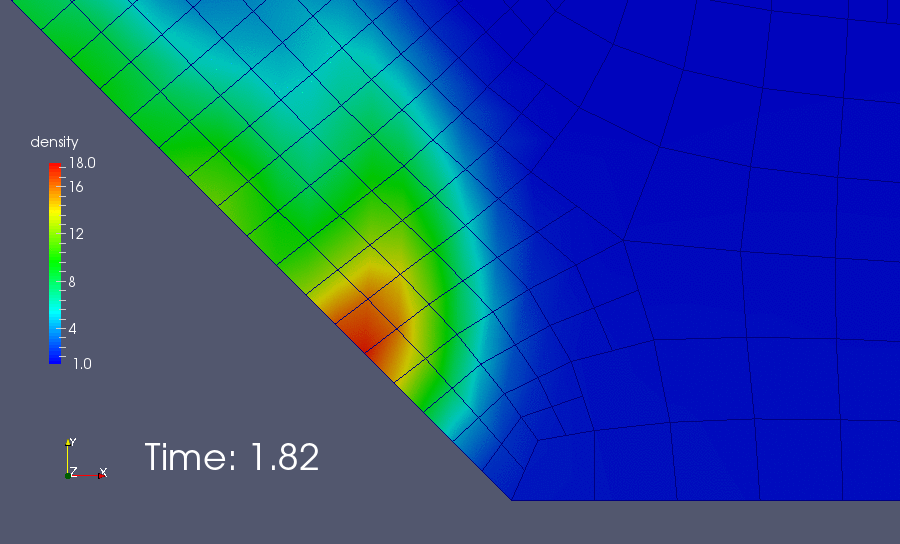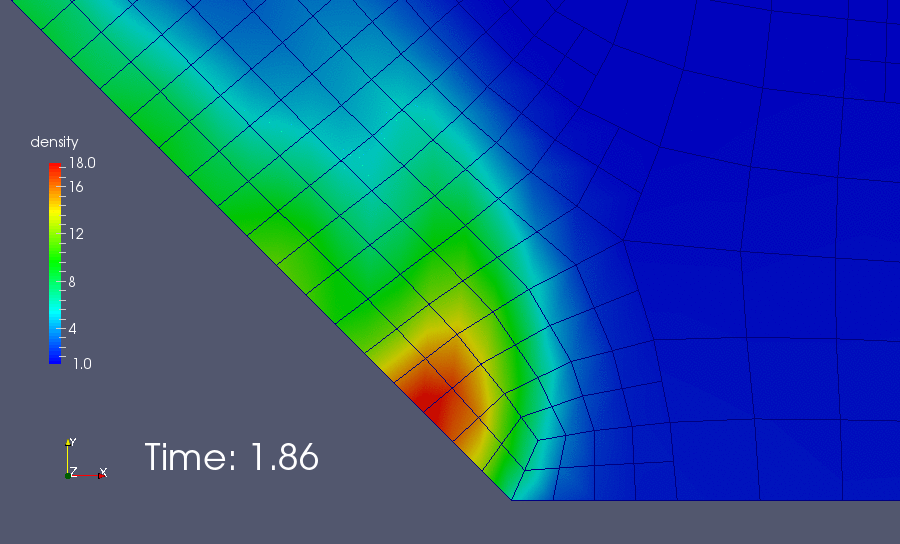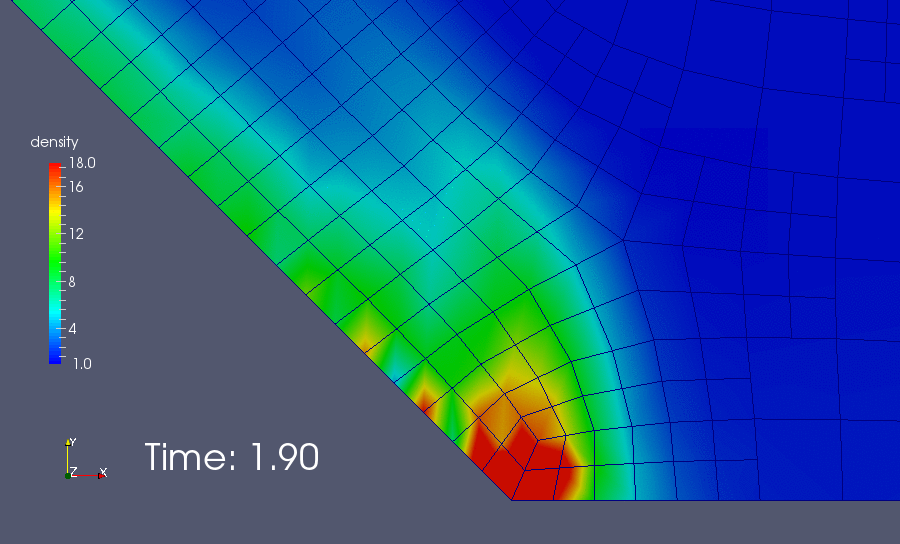
As we see, when the heavy mass of fluid hits the left bottom corner, some oscillation occurs and lead to the divergence of the iteration. A lazy solution to this issue is add more viscosity. If we set the diffusion power \(\eta = 1.5\) instead of \(2.0\), the simulation would be able to survive this crisis. Then, the result looks like this:

The heavy mass of fluid is drawn down the slope by gravity, where it collides with the ski lodge and is flung into the air! Hopefully everyone escapes! And also, we can see the boundary between heavy mass and light mass blur quickly due to the artificial viscosity.
We can also visualize the evolution of the adaptively refined grid:

The adaptivity follows and precedes the flow pattern, based on the heuristic refinement scheme discussed above.
The numerical scheme we have chosen is not particularly stable when the artificial viscosity is small while is too diffusive when the artificial viscosity is large. Furthermore, it is known there are more advanced techniques to stabilize the solution, for example streamline diffusion, least-squares stabilization terms, entropy viscosity.
While the Newton method as a nonlinear solver appears to work very well if the time step is small enough, the linear solver can be improved. For example, in the current scheme whenever we use an iterative solver, an ILU is computed anew for each Newton step; likewise, for the direct solver, an LU decomposition of the Newton matrix is computed in each step. This is obviously wasteful: from one Newton step to another, and probably also between time steps, the Newton matrix does not radically change: an ILU or a sparse LU decomposition for one Newton step is probably still a very good preconditioner for the next Newton or time step. Avoiding the recomputation would therefore be a good way to reduce the amount of compute time.
One could drive this a step further: since close to convergence the Newton matrix changes only a little bit, one may be able to define a quasi-Newton scheme where we only re-compute the residual (i.e. the right hand side vector) in each Newton iteration, and re-use the Newton matrix. The resulting scheme will likely not be of quadratic convergence order, and we have to expect to do a few more nonlinear iterations; however, given that we don't have to spend the time to build the Newton matrix each time, the resulting scheme may well be faster.
The residual calculated in ConservationLaw::assemble_cell_term function reads \(R_i = \left(\frac{\mathbf{w}^{k}_{n+1} - \mathbf{w}_n}{\delta t} , \mathbf{z}_i \right)_K + \theta \mathbf{B}({\mathbf{w}^{k}_{n+1}})(\mathbf{z}_i)_K + (1-\theta) \mathbf{B}({\mathbf{w}_{n}}) (\mathbf{z}_i)_K \) This means that we calculate the spatial residual twice at one Newton iteration step: once respect to the current solution \(\mathbf{w}^{k}_{n+1}\) and once more respect to the last time step solution \(\mathbf{w}_{n}\) which remains the same during all Newton iterations through one timestep. Cache up the explicit part of residual \( \mathbf{B}({\mathbf{w}_{n}}) (\mathbf{z}_i)_K\) during Newton iteration will save lots of labor.
Finally, as a direction beyond the immediate solution of the Euler equations, this program tries very hard to separate the implementation of everything that is specific to the Euler equations into one class (the EulerEquation class), and everything that is specific to assembling the matrices and vectors, nonlinear and linear solvers, and the general top-level logic into another (the ConservationLaw class).
By replacing the definitions of flux matrices and numerical fluxes in this class, as well as the various other parts defined there, it should be possible to apply the ConservationLaw class to other hyperbolic conservation laws as well.
 1.8.17
1.8.17