 |
Reference documentation for deal.II version 9.2.0
|
 |
Reference documentation for deal.II version 9.2.0
|
#include <deal.II/fe/fe_q.h>
Public Member Functions | |
| FE_Q (const unsigned int p) | |
| FE_Q (const Quadrature< 1 > &points) | |
| virtual std::string | get_name () const override |
| virtual std::unique_ptr< FiniteElement< dim, spacedim > > | clone () const override |
| virtual void | convert_generalized_support_point_values_to_dof_values (const std::vector< Vector< double >> &support_point_values, std::vector< double > &nodal_values) const override |
| virtual FiniteElementDomination::Domination | compare_for_domination (const FiniteElement< dim, spacedim > &fe_other, const unsigned int codim=0) const override final |
 Public Member Functions inherited from FE_Q_Base< TensorProductPolynomials< dim >, dim, dim > Public Member Functions inherited from FE_Q_Base< TensorProductPolynomials< dim >, dim, dim > | |
| FE_Q_Base (const TensorProductPolynomials< dim > &poly_space, const FiniteElementData< dim > &fe_data, const std::vector< bool > &restriction_is_additive_flags) | |
| virtual void | get_interpolation_matrix (const FiniteElement< dim, spacedim > &source, FullMatrix< double > &matrix) const override |
| virtual void | get_face_interpolation_matrix (const FiniteElement< dim, spacedim > &source, FullMatrix< double > &matrix) const override |
| virtual void | get_subface_interpolation_matrix (const FiniteElement< dim, spacedim > &source, const unsigned int subface, FullMatrix< double > &matrix) const override |
| virtual bool | has_support_on_face (const unsigned int shape_index, const unsigned int face_index) const override |
| virtual const FullMatrix< double > & | get_restriction_matrix (const unsigned int child, const RefinementCase< dim > &refinement_case=RefinementCase< dim >::isotropic_refinement) const override |
| virtual const FullMatrix< double > & | get_prolongation_matrix (const unsigned int child, const RefinementCase< dim > &refinement_case=RefinementCase< dim >::isotropic_refinement) const override |
| virtual unsigned int | face_to_cell_index (const unsigned int face_dof_index, const unsigned int face, const bool face_orientation=true, const bool face_flip=false, const bool face_rotation=false) const override |
| virtual std::pair< Table< 2, bool >, std::vector< unsigned int > > | get_constant_modes () const override |
| virtual bool | hp_constraints_are_implemented () const override |
| virtual std::vector< std::pair< unsigned int, unsigned int > > | hp_vertex_dof_identities (const FiniteElement< dim, spacedim > &fe_other) const override |
| virtual std::vector< std::pair< unsigned int, unsigned int > > | hp_line_dof_identities (const FiniteElement< dim, spacedim > &fe_other) const override |
| virtual std::vector< std::pair< unsigned int, unsigned int > > | hp_quad_dof_identities (const FiniteElement< dim, spacedim > &fe_other) const override |
 Public Member Functions inherited from FE_Poly< TensorProductPolynomials< dim >, dim, spacedim > Public Member Functions inherited from FE_Poly< TensorProductPolynomials< dim >, dim, spacedim > | |
| FE_Poly (const TensorProductPolynomials< dim > &poly_space, const FiniteElementData< dim > &fe_data, const std::vector< bool > &restriction_is_additive_flags, const std::vector< ComponentMask > &nonzero_components) | |
| unsigned int | get_degree () const |
| virtual UpdateFlags | requires_update_flags (const UpdateFlags update_flags) const override |
| std::vector< unsigned int > | get_poly_space_numbering () const |
| std::vector< unsigned int > | get_poly_space_numbering_inverse () const |
| virtual double | shape_value (const unsigned int i, const Point< dim > &p) const override |
| virtual double | shape_value_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const override |
| virtual Tensor< 1, dim > | shape_grad (const unsigned int i, const Point< dim > &p) const override |
| virtual Tensor< 1, dim > | shape_grad_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const override |
| virtual Tensor< 2, dim > | shape_grad_grad (const unsigned int i, const Point< dim > &p) const override |
| virtual Tensor< 2, dim > | shape_grad_grad_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const override |
| virtual Tensor< 3, dim > | shape_3rd_derivative (const unsigned int i, const Point< dim > &p) const override |
| virtual Tensor< 3, dim > | shape_3rd_derivative_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const override |
| virtual Tensor< 4, dim > | shape_4th_derivative (const unsigned int i, const Point< dim > &p) const override |
| virtual Tensor< 4, dim > | shape_4th_derivative_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const override |
| virtual std::size_t | memory_consumption () const override |
 Public Member Functions inherited from FiniteElement< dim, spacedim > Public Member Functions inherited from FiniteElement< dim, spacedim > | |
| FiniteElement (const FiniteElementData< dim > &fe_data, const std::vector< bool > &restriction_is_additive_flags, const std::vector< ComponentMask > &nonzero_components) | |
| FiniteElement (FiniteElement< dim, spacedim > &&)=default | |
| FiniteElement (const FiniteElement< dim, spacedim > &)=default | |
| virtual | ~FiniteElement () override=default |
| std::pair< std::unique_ptr< FiniteElement< dim, spacedim > >, unsigned int > | operator^ (const unsigned int multiplicity) const |
| const FiniteElement< dim, spacedim > & | operator[] (const unsigned int fe_index) const |
| bool | prolongation_is_implemented () const |
| bool | isotropic_prolongation_is_implemented () const |
| bool | restriction_is_implemented () const |
| bool | isotropic_restriction_is_implemented () const |
| bool | restriction_is_additive (const unsigned int index) const |
| const FullMatrix< double > & | constraints (const ::internal::SubfaceCase< dim > &subface_case=::internal::SubfaceCase< dim >::case_isotropic) const |
| bool | constraints_are_implemented (const ::internal::SubfaceCase< dim > &subface_case=::internal::SubfaceCase< dim >::case_isotropic) const |
| virtual bool | hp_constraints_are_implemented () const |
| virtual FiniteElementDomination::Domination | compare_for_face_domination (const FiniteElement< dim, spacedim > &fe_other) const final |
| virtual bool | operator== (const FiniteElement< dim, spacedim > &fe) const |
| bool | operator!= (const FiniteElement< dim, spacedim > &) const |
| std::pair< unsigned int, unsigned int > | system_to_component_index (const unsigned int index) const |
| unsigned int | component_to_system_index (const unsigned int component, const unsigned int index) const |
| std::pair< unsigned int, unsigned int > | face_system_to_component_index (const unsigned int index) const |
| unsigned int | adjust_quad_dof_index_for_face_orientation (const unsigned int index, const bool face_orientation, const bool face_flip, const bool face_rotation) const |
| unsigned int | adjust_line_dof_index_for_line_orientation (const unsigned int index, const bool line_orientation) const |
| const ComponentMask & | get_nonzero_components (const unsigned int i) const |
| unsigned int | n_nonzero_components (const unsigned int i) const |
| bool | is_primitive () const |
| bool | is_primitive (const unsigned int i) const |
| unsigned int | n_base_elements () const |
| virtual const FiniteElement< dim, spacedim > & | base_element (const unsigned int index) const |
| unsigned int | element_multiplicity (const unsigned int index) const |
| const FiniteElement< dim, spacedim > & | get_sub_fe (const ComponentMask &mask) const |
| virtual const FiniteElement< dim, spacedim > & | get_sub_fe (const unsigned int first_component, const unsigned int n_selected_components) const |
| std::pair< std::pair< unsigned int, unsigned int >, unsigned int > | system_to_base_index (const unsigned int index) const |
| std::pair< std::pair< unsigned int, unsigned int >, unsigned int > | face_system_to_base_index (const unsigned int index) const |
| types::global_dof_index | first_block_of_base (const unsigned int b) const |
| std::pair< unsigned int, unsigned int > | component_to_base_index (const unsigned int component) const |
| std::pair< unsigned int, unsigned int > | block_to_base_index (const unsigned int block) const |
| std::pair< unsigned int, types::global_dof_index > | system_to_block_index (const unsigned int component) const |
| unsigned int | component_to_block_index (const unsigned int component) const |
| ComponentMask | component_mask (const FEValuesExtractors::Scalar &scalar) const |
| ComponentMask | component_mask (const FEValuesExtractors::Vector &vector) const |
| ComponentMask | component_mask (const FEValuesExtractors::SymmetricTensor< 2 > &sym_tensor) const |
| ComponentMask | component_mask (const BlockMask &block_mask) const |
| BlockMask | block_mask (const FEValuesExtractors::Scalar &scalar) const |
| BlockMask | block_mask (const FEValuesExtractors::Vector &vector) const |
| BlockMask | block_mask (const FEValuesExtractors::SymmetricTensor< 2 > &sym_tensor) const |
| BlockMask | block_mask (const ComponentMask &component_mask) const |
| virtual std::pair< Table< 2, bool >, std::vector< unsigned int > > | get_constant_modes () const |
| const std::vector< Point< dim > > & | get_unit_support_points () const |
| bool | has_support_points () const |
| virtual Point< dim > | unit_support_point (const unsigned int index) const |
| const std::vector< Point< dim - 1 > > & | get_unit_face_support_points () const |
| bool | has_face_support_points () const |
| virtual Point< dim - 1 > | unit_face_support_point (const unsigned int index) const |
| const std::vector< Point< dim > > & | get_generalized_support_points () const |
| bool | has_generalized_support_points () const |
| GeometryPrimitive | get_associated_geometry_primitive (const unsigned int cell_dof_index) const |
| virtual std::size_t | memory_consumption () const |
 Public Member Functions inherited from Subscriptor Public Member Functions inherited from Subscriptor | |
| Subscriptor () | |
| Subscriptor (const Subscriptor &) | |
| Subscriptor (Subscriptor &&) noexcept | |
| virtual | ~Subscriptor () |
| Subscriptor & | operator= (const Subscriptor &) |
| Subscriptor & | operator= (Subscriptor &&) noexcept |
| void | subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const |
| void | unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const |
| unsigned int | n_subscriptions () const |
| template<typename StreamType > | |
| void | list_subscribers (StreamType &stream) const |
| void | list_subscribers () const |
| template<class Archive > | |
| void | serialize (Archive &ar, const unsigned int version) |
 Public Member Functions inherited from FiniteElementData< dim > Public Member Functions inherited from FiniteElementData< dim > | |
| FiniteElementData (const std::vector< unsigned int > &dofs_per_object, const unsigned int n_components, const unsigned int degree, const Conformity conformity=unknown, const BlockIndices &block_indices=BlockIndices()) | |
| unsigned int | n_dofs_per_vertex () const |
| unsigned int | n_dofs_per_line () const |
| unsigned int | n_dofs_per_quad () const |
| unsigned int | n_dofs_per_hex () const |
| unsigned int | n_dofs_per_face () const |
| unsigned int | n_dofs_per_cell () const |
| template<int structdim> | |
| unsigned int | n_dofs_per_object () const |
| unsigned int | n_components () const |
| unsigned int | n_blocks () const |
| const BlockIndices & | block_indices () const |
| unsigned int | tensor_degree () const |
| bool | conforms (const Conformity) const |
| bool | operator== (const FiniteElementData &) const |
Additional Inherited Members | |
 Public Types inherited from FiniteElementData< dim > Public Types inherited from FiniteElementData< dim > | |
| enum | Conformity { unknown = 0x00, L2 = 0x01, Hcurl = 0x02, Hdiv = 0x04, H1 = Hcurl | Hdiv, H2 = 0x0e } |
 Static Public Member Functions inherited from FE_Q_Base< TensorProductPolynomials< dim >, dim, dim > Static Public Member Functions inherited from FE_Q_Base< TensorProductPolynomials< dim >, dim, dim > | |
| static ::ExceptionBase & | ExcFEQCannotHaveDegree0 () |
 Static Public Member Functions inherited from FiniteElement< dim, spacedim > Static Public Member Functions inherited from FiniteElement< dim, spacedim > | |
| static ::ExceptionBase & | ExcShapeFunctionNotPrimitive (int arg1) |
| static ::ExceptionBase & | ExcFENotPrimitive () |
| static ::ExceptionBase & | ExcUnitShapeValuesDoNotExist () |
| static ::ExceptionBase & | ExcFEHasNoSupportPoints () |
| static ::ExceptionBase & | ExcEmbeddingVoid () |
| static ::ExceptionBase & | ExcProjectionVoid () |
| static ::ExceptionBase & | ExcWrongInterfaceMatrixSize (int arg1, int arg2) |
| static ::ExceptionBase & | ExcInterpolationNotImplemented () |
 Static Public Member Functions inherited from Subscriptor Static Public Member Functions inherited from Subscriptor | |
| static ::ExceptionBase & | ExcInUse (int arg1, std::string arg2, std::string arg3) |
| static ::ExceptionBase & | ExcNoSubscriber (std::string arg1, std::string arg2) |
 Public Attributes inherited from FiniteElementData< dim > Public Attributes inherited from FiniteElementData< dim > | |
| const unsigned int | dofs_per_vertex |
| const unsigned int | dofs_per_line |
| const unsigned int | dofs_per_quad |
| const unsigned int | dofs_per_hex |
| const unsigned int | first_line_index |
| const unsigned int | first_quad_index |
| const unsigned int | first_hex_index |
| const unsigned int | first_face_line_index |
| const unsigned int | first_face_quad_index |
| const unsigned int | dofs_per_face |
| const unsigned int | dofs_per_cell |
| const unsigned int | components |
| const unsigned int | degree |
| const Conformity | conforming_space |
| const BlockIndices | block_indices_data |
 Static Public Attributes inherited from FiniteElement< dim, spacedim > Static Public Attributes inherited from FiniteElement< dim, spacedim > | |
| static const unsigned int | space_dimension = spacedim |
 Static Public Attributes inherited from FiniteElementData< dim > Static Public Attributes inherited from FiniteElementData< dim > | |
| static const unsigned int | dimension = dim |
 Protected Member Functions inherited from FE_Q_Base< TensorProductPolynomials< dim >, dim, dim > Protected Member Functions inherited from FE_Q_Base< TensorProductPolynomials< dim >, dim, dim > | |
| void | initialize (const std::vector< Point< 1 >> &support_points_1d) |
| void | initialize_constraints (const std::vector< Point< 1 >> &points) |
| void | initialize_unit_support_points (const std::vector< Point< 1 >> &points) |
| void | initialize_unit_face_support_points (const std::vector< Point< 1 >> &points) |
| void | initialize_quad_dof_index_permutation () |
 Protected Member Functions inherited from FE_Poly< TensorProductPolynomials< dim >, dim, spacedim > Protected Member Functions inherited from FE_Poly< TensorProductPolynomials< dim >, dim, spacedim > | |
| virtual std::unique_ptr< typename FiniteElement< dim, spacedim >::InternalDataBase > | get_data (const UpdateFlags update_flags, const Mapping< dim, spacedim > &, const Quadrature< dim > &quadrature, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const override |
| virtual void | fill_fe_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const CellSimilarity::Similarity cell_similarity, const Quadrature< dim > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const typename FiniteElement< dim, spacedim >::InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const override |
| void | fill_fe_values (const Triangulation< 1, 2 >::cell_iterator &, const CellSimilarity::Similarity cell_similarity, const Quadrature< 1 > &quadrature, const Mapping< 1, 2 > &mapping, const Mapping< 1, 2 >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< 1, 2 > &mapping_data, const FiniteElement< 1, 2 >::InternalDataBase &fe_internal,::internal::FEValuesImplementation::FiniteElementRelatedData< 1, 2 > &output_data) const |
| void | fill_fe_values (const Triangulation< 2, 3 >::cell_iterator &, const CellSimilarity::Similarity cell_similarity, const Quadrature< 2 > &quadrature, const Mapping< 2, 3 > &mapping, const Mapping< 2, 3 >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< 2, 3 > &mapping_data, const FiniteElement< 2, 3 >::InternalDataBase &fe_internal,::internal::FEValuesImplementation::FiniteElementRelatedData< 2, 3 > &output_data) const |
| virtual void | fill_fe_face_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const Quadrature< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const typename FiniteElement< dim, spacedim >::InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const override |
| virtual void | fill_fe_subface_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const unsigned int sub_no, const Quadrature< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const typename FiniteElement< dim, spacedim >::InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const override |
| void | correct_hessians (internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data, const internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const unsigned int n_q_points) const |
| void | correct_third_derivatives (internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data, const internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const unsigned int n_q_points) const |
 Protected Member Functions inherited from FiniteElement< dim, spacedim > Protected Member Functions inherited from FiniteElement< dim, spacedim > | |
| void | reinit_restriction_and_prolongation_matrices (const bool isotropic_restriction_only=false, const bool isotropic_prolongation_only=false) |
| TableIndices< 2 > | interface_constraints_size () const |
| virtual std::unique_ptr< InternalDataBase > | get_face_data (const UpdateFlags update_flags, const Mapping< dim, spacedim > &mapping, const Quadrature< dim - 1 > &quadrature, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const |
| virtual std::unique_ptr< InternalDataBase > | get_subface_data (const UpdateFlags update_flags, const Mapping< dim, spacedim > &mapping, const Quadrature< dim - 1 > &quadrature, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const |
| virtual void | fill_fe_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const CellSimilarity::Similarity cell_similarity, const Quadrature< dim > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const =0 |
| virtual void | fill_fe_face_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const Quadrature< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const =0 |
| virtual void | fill_fe_subface_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const unsigned int sub_no, const Quadrature< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const =0 |
 Static Protected Member Functions inherited from FE_Q_Base< TensorProductPolynomials< dim >, dim, dim > Static Protected Member Functions inherited from FE_Q_Base< TensorProductPolynomials< dim >, dim, dim > | |
| static std::vector< unsigned int > | get_dpo_vector (const unsigned int degree) |
 Static Protected Member Functions inherited from FiniteElement< dim, spacedim > Static Protected Member Functions inherited from FiniteElement< dim, spacedim > | |
| static std::vector< unsigned int > | compute_n_nonzero_components (const std::vector< ComponentMask > &nonzero_components) |
 Protected Attributes inherited from FE_Poly< TensorProductPolynomials< dim >, dim, spacedim > Protected Attributes inherited from FE_Poly< TensorProductPolynomials< dim >, dim, spacedim > | |
| TensorProductPolynomials< dim > | poly_space |
 Protected Attributes inherited from FiniteElement< dim, spacedim > Protected Attributes inherited from FiniteElement< dim, spacedim > | |
| std::vector< std::vector< FullMatrix< double > > > | restriction |
| std::vector< std::vector< FullMatrix< double > > > | prolongation |
| FullMatrix< double > | interface_constraints |
| std::vector< Point< dim > > | unit_support_points |
| std::vector< Point< dim - 1 > > | unit_face_support_points |
| std::vector< Point< dim > > | generalized_support_points |
| std::vector< Point< dim - 1 > > | generalized_face_support_points |
| Table< 2, int > | adjust_quad_dof_index_for_face_orientation_table |
| std::vector< int > | adjust_line_dof_index_for_line_orientation_table |
| std::vector< std::pair< unsigned int, unsigned int > > | system_to_component_table |
| std::vector< std::pair< unsigned int, unsigned int > > | face_system_to_component_table |
| std::vector< std::pair< std::pair< unsigned int, unsigned int >, unsigned int > > | system_to_base_table |
| std::vector< std::pair< std::pair< unsigned int, unsigned int >, unsigned int > > | face_system_to_base_table |
| BlockIndices | base_to_block_indices |
| std::vector< std::pair< std::pair< unsigned int, unsigned int >, unsigned int > > | component_to_base_table |
| const std::vector< bool > | restriction_is_additive_flags |
| const std::vector< ComponentMask > | nonzero_components |
| const std::vector< unsigned int > | n_nonzero_components_table |
| const bool | cached_primitivity |
Implementation of a scalar Lagrange finite element Qp that yields the finite element space of continuous, piecewise polynomials of degree p in each coordinate direction. This class is realized using tensor product polynomials based on 1D Lagrange polynomials with equidistant (degree up to 2), Gauss-Lobatto (starting from degree 3), or given support points.
The standard constructor of this class takes the degree p of this finite element. Alternatively, it can take a quadrature formula points defining the support points of the Lagrange interpolation in one coordinate direction.
For more information about the spacedim template parameter check the documentation of FiniteElement or the one of Triangulation.
The constructor creates a TensorProductPolynomials object that includes the tensor product of LagrangeEquidistant polynomials of degree p. This TensorProductPolynomials object provides all values and derivatives of the shape functions. In case a quadrature rule is given, the constructor creates a TensorProductPolynomials object that includes the tensor product of Lagrange polynomials with the support points from points.
Furthermore the constructor fills the interface_constraints, the prolongation (embedding) and the restriction matrices. These are implemented only up to a certain degree and may not be available for very high polynomial degree.
When constructing an FE_Q element at polynomial degrees one or two, equidistant support points at 0 and 1 (linear case) or 0, 0.5, and 1 (quadratic case) are used. The unit support or nodal points xi are those points where the jth Lagrange polynomial satisfies the \delta_{ij} property, i.e., where one polynomial is one and all the others are zero. For higher polynomial degrees, the support points are non-equidistant by default, and chosen to be the support points of the (degree+1)-order Gauss-Lobatto quadrature rule. This point distribution yields well-conditioned Lagrange interpolation at arbitrary polynomial degrees. By contrast, polynomials based on equidistant points get increasingly ill-conditioned as the polynomial degree increases. In interpolation, this effect is known as the Runge phenomenon. For Galerkin methods, the Runge phenomenon is typically not visible in the solution quality but rather in the condition number of the associated system matrices. For example, the elemental mass matrix of equidistant points at degree 10 has condition number 2.6e6, whereas the condition number for Gauss-Lobatto points is around 400.
The Gauss-Lobatto points in 1D include the end points 0 and +1 of the unit interval. The interior points are shifted towards the end points, which gives a denser point distribution close to the element boundary.
If combined with Gauss-Lobatto quadrature, FE_Q based on the default support points gives diagonal mass matrices. This case is demonstrated in step-48. However, this element can be combined with arbitrary quadrature rules through the usual FEValues approach, including full Gauss quadrature. In the general case, the mass matrix is non-diagonal.
The original ordering of the shape functions represented by the TensorProductPolynomials is a tensor product numbering. However, the shape functions on a cell are renumbered beginning with the shape functions whose support points are at the vertices, then on the line, on the quads, and finally (for 3d) on the hexes. To be explicit, these numberings are listed in the following:
1D case:
* 0-------1 *
2D case:
* 2-------3 * | | * | | * | | * 0-------1 *
3D case:
* 6-------7 6-------7 * /| | / /| * / | | / / | * / | | / / | * 4 | | 4-------5 | * | 2-------3 | | 3 * | / / | | / * | / / | | / * |/ / | |/ * 0-------1 0-------1 *
The respective coordinate values of the support points of the shape functions are as follows:
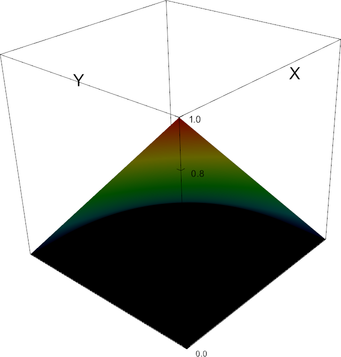
[0, 0, 0]; [1, 0, 0]; [0, 1, 0]; [1, 1, 0]; [0, 0, 1]; [1, 0, 1]; [0, 1, 1]; [1, 1, 1]; In 2d, these shape functions look as follows:
| 
|
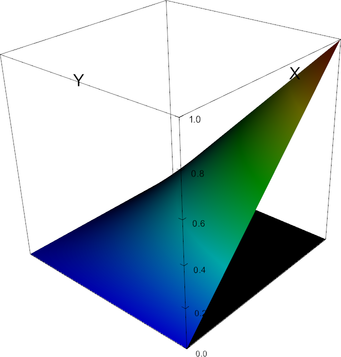
Q_1 element, shape function 0 | Q_1 element, shape function 1 |
| 
|
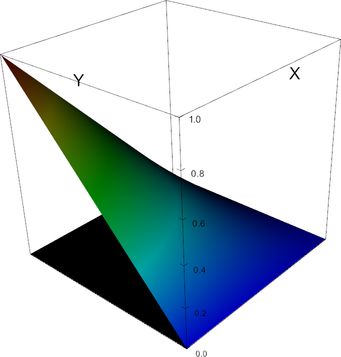
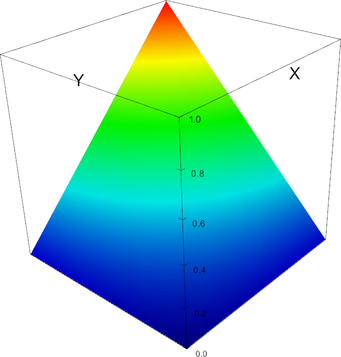
Q_1 element, shape function 2 | Q_1 element, shape function 3 |
1D case:
* 0---2---1 *
2D case:
* 2---7---3 * | | * 4 8 5 * | | * 0---6---1 *
3D case:
* 6--15---7 6--15---7 * /| | / /| * 12 | 19 12 1319 * / 18 | / / | * 4 | | 4---14--5 | * | 2---11--3 | | 3 * | / / | 17 / * 16 8 9 16 | 9 * |/ / | |/ * 0---10--1 0---10--1 * * *-------* *-------* * /| | / /| * / | 23 | / 25 / | * / | | / / | * * | | *-------* | * |20 *-------* | |21 * * | / / | 22 | / * | / 24 / | | / * |/ / | |/ * *-------* *-------* *
The center vertex has number 26.
The respective coordinate values of the support points of the shape functions are as follows:
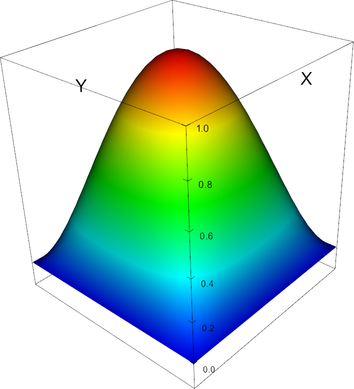
[0, 0, 0]; [1, 0, 0]; [0, 1, 0]; [1, 1, 0]; [0, 0, 1]; [1, 0, 1]; [0, 1, 1]; [1, 1, 1]; [0, 1/2, 0]; [1, 1/2, 0]; [1/2, 0, 0]; [1/2, 1, 0]; [0, 1/2, 1]; [1, 1/2, 1]; [1/2, 0, 1]; [1/2, 1, 1]; [0, 0, 1/2]; [1, 0, 1/2]; [0, 1, 1/2]; [1, 1, 1/2]; [0, 1/2, 1/2]; [1, 1/2, 1/2]; [1/2, 0, 1/2]; [1/2, 1, 1/2]; [1/2, 1/2, 0]; [1/2, 1/2, 1]; [1/2, 1/2, 1/2]; In 2d, these shape functions look as follows (the black plane corresponds to zero; negative shape function values may not be visible):
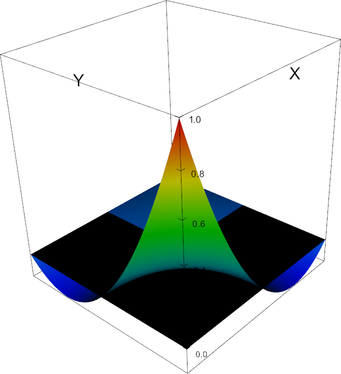
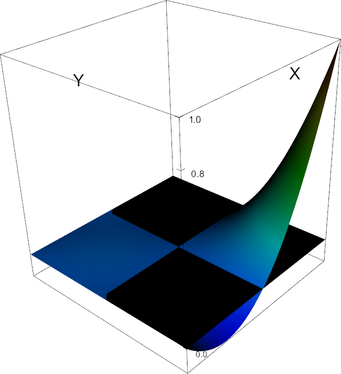
| 
|
Q_2 element, shape function 0 | Q_2 element, shape function 1 |
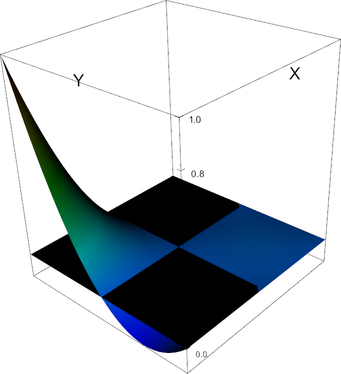
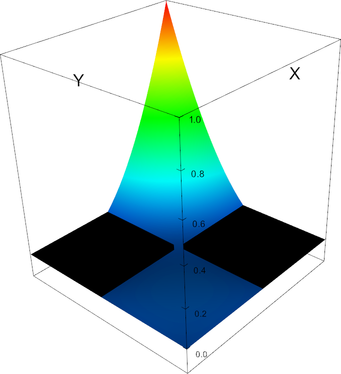
| 
|
Q_2 element, shape function 2 | Q_2 element, shape function 3 |
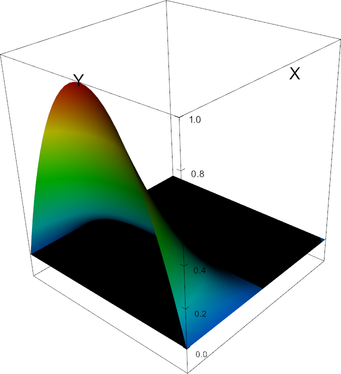
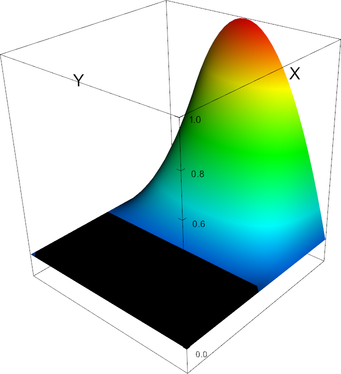
| 
|
Q_2 element, shape function 4 | Q_2 element, shape function 5 |
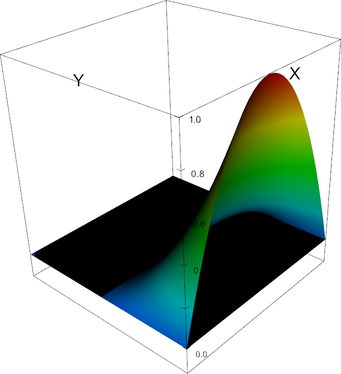
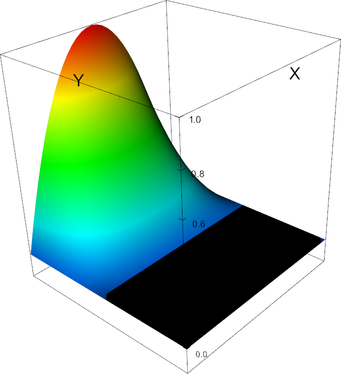
| 
|
Q_2 element, shape function 6 | Q_2 element, shape function 7 |
| |
Q_2 element, shape function 8 |
1D case:
* 0--2--3--1 *
* 2--10-11-3 * | | * 5 14 15 7 * | | * 4 12 13 6 * | | * 0--8--9--1 *
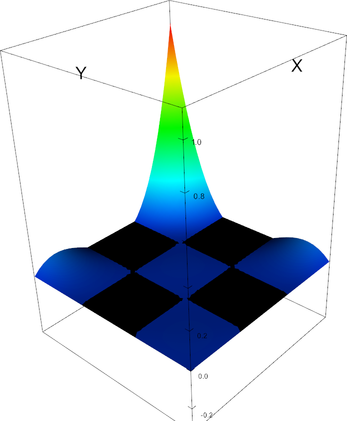
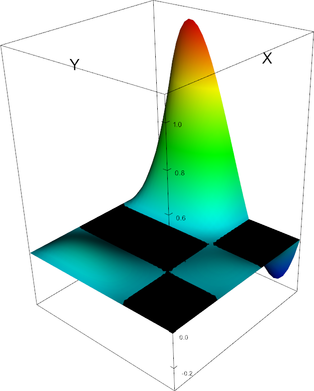
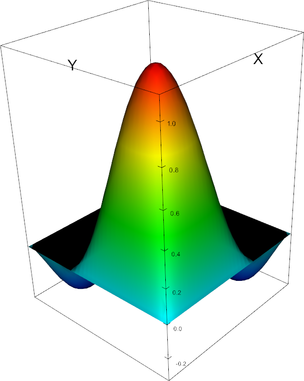
In 2d, these shape functions look as follows (the black plane corresponds to zero; negative shape function values may not be visible):
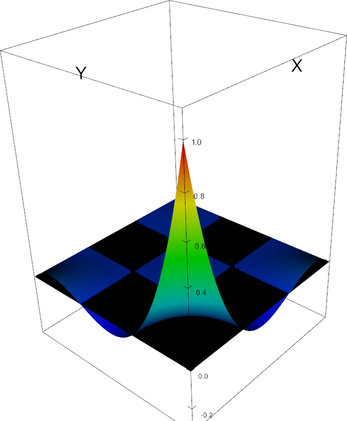
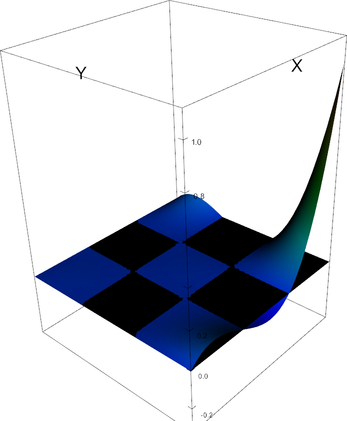
| 
|
Q_3 element, shape function 0 | Q_3 element, shape function 1 |
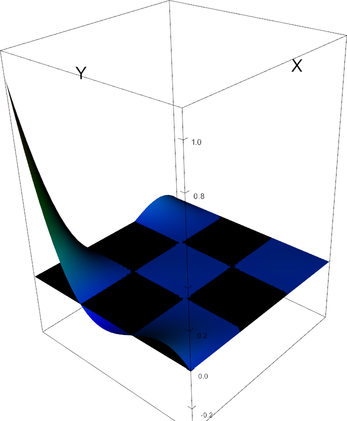
| 
|
Q_3 element, shape function 2 | Q_3 element, shape function 3 |
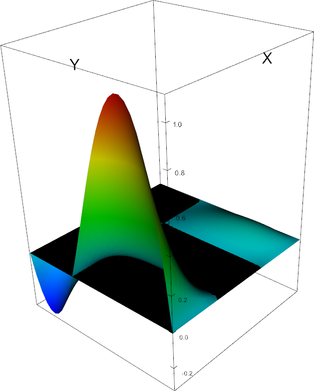
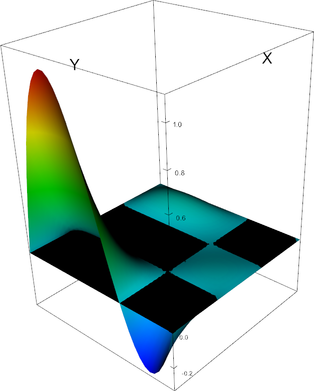
| 
|
Q_3 element, shape function 4 | Q_3 element, shape function 5 |
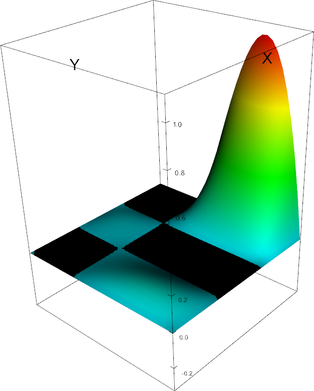
| 
|
Q_3 element, shape function 6 | Q_3 element, shape function 7 |
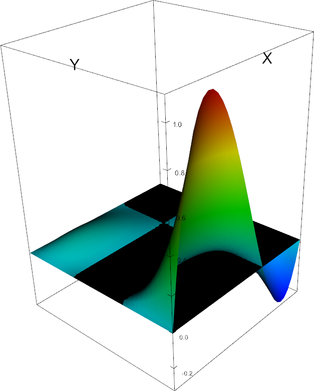
| 
|
Q_3 element, shape function 8 | Q_3 element, shape function 9 |
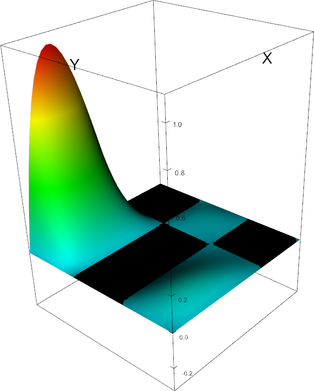
| 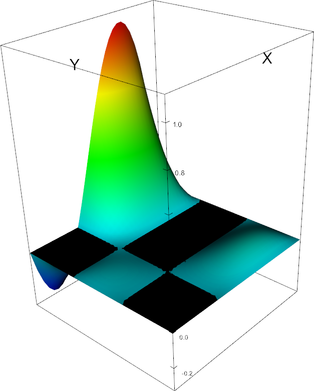
|
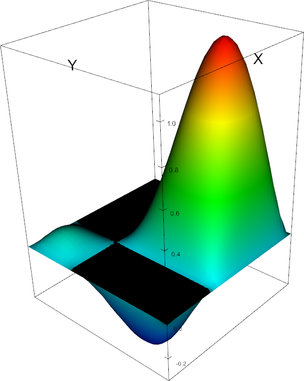
Q_3 element, shape function 10 | Q_3 element, shape function 11 |
| 
|
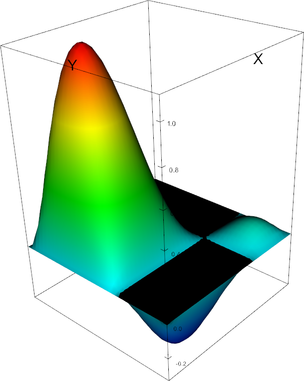
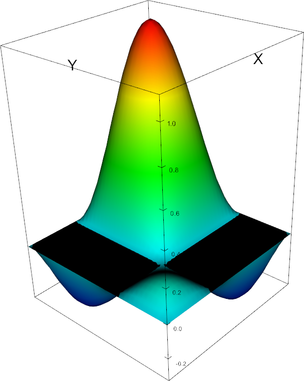
Q_3 element, shape function 12 | Q_3 element, shape function 13 |
| 
|
Q_3 element, shape function 14 | Q_3 element, shape function 15 |
1D case:
* 0--2--3--4--1 *
* 2--13-14-15-3 * | | * 6 22 23 24 9 * | | * 5 19 20 21 8 * | | * 4 16 17 18 7 * | | * 0--10-11-12-1 *
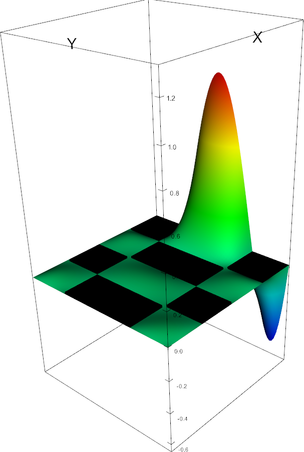
In 2d, these shape functions look as follows (the black plane corresponds to zero; negative shape function values may not be visible):
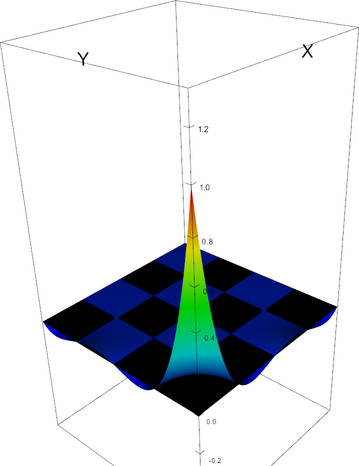
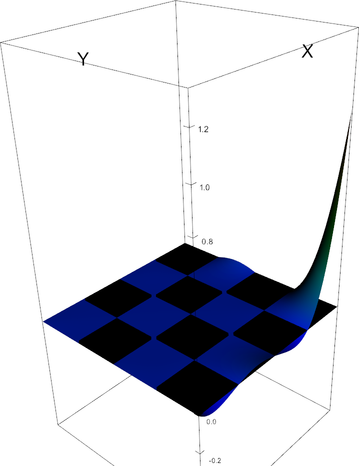
| 
|
Q_4 element, shape function 0 | Q_4 element, shape function 1 |
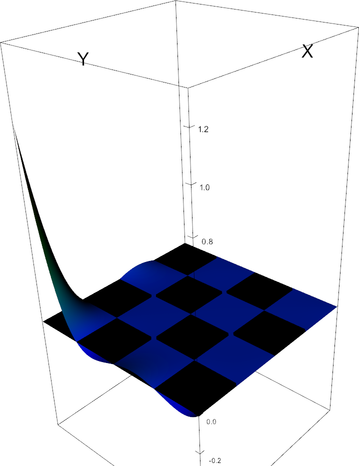
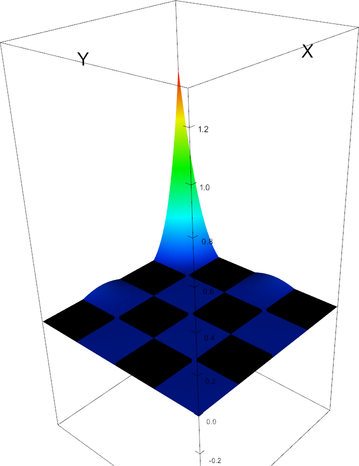
| 
|
Q_4 element, shape function 2 | Q_4 element, shape function 3 |
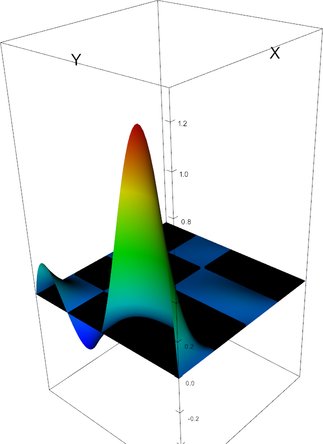
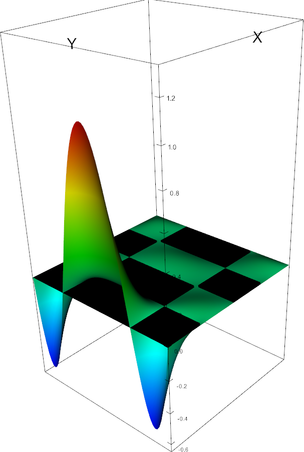
| 
|
Q_4 element, shape function 4 | Q_4 element, shape function 5 |
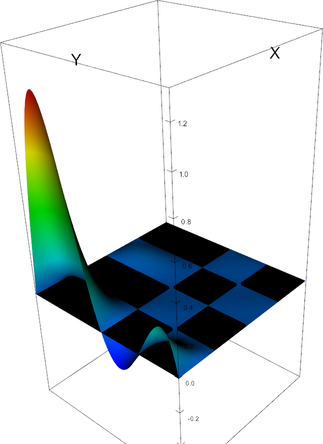
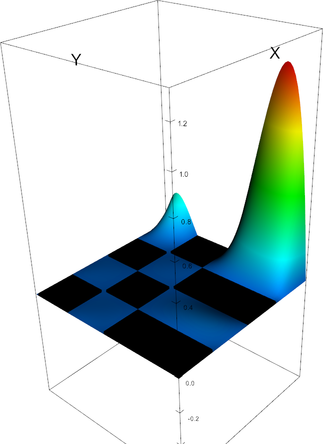
| 
|
Q_4 element, shape function 6 | Q_4 element, shape function 7 |
| 
|
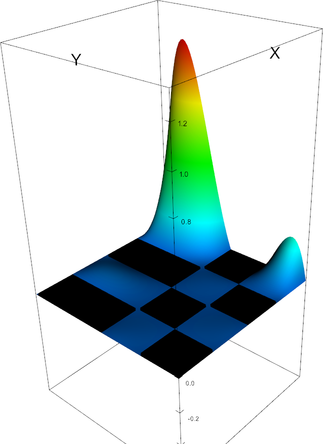
Q_4 element, shape function 8 | Q_4 element, shape function 9 |
| 
|
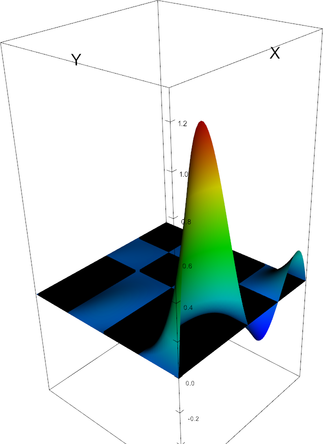
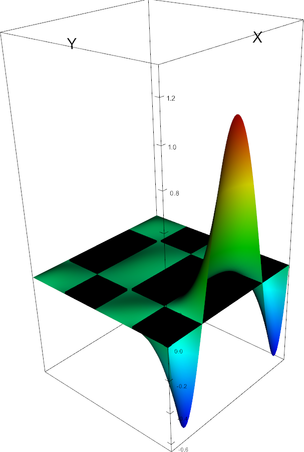
Q_4 element, shape function 10 | Q_4 element, shape function 11 |
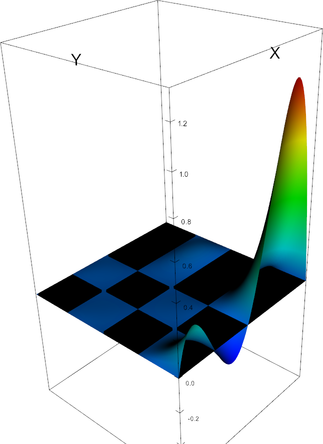
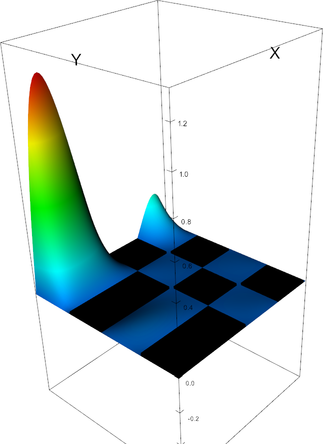
| 
|
Q_4 element, shape function 12 | Q_4 element, shape function 13 |
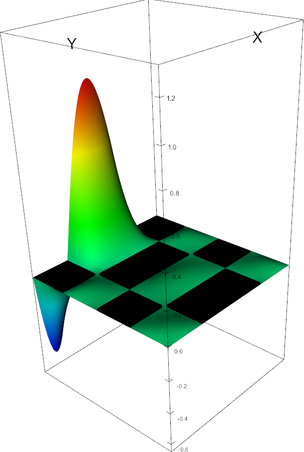
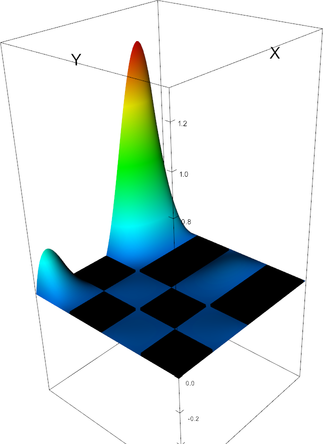
| 
|
Q_4 element, shape function 14 | Q_4 element, shape function 15 |
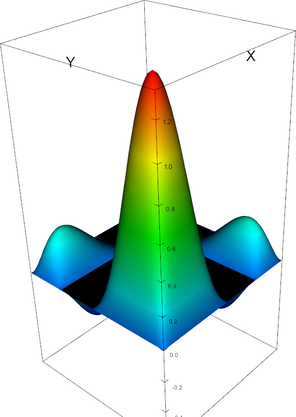
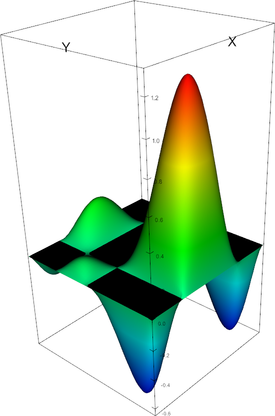
| 
|
Q_4 element, shape function 16 | Q_4 element, shape function 17 |
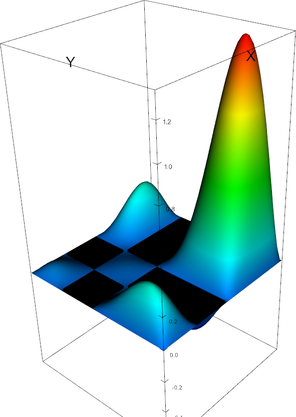
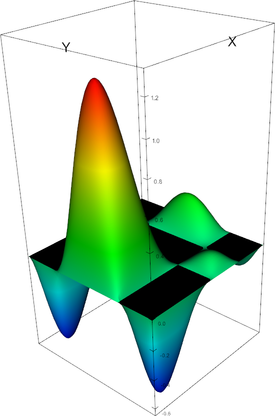
| 
|
Q_4 element, shape function 18 | Q_4 element, shape function 19 |
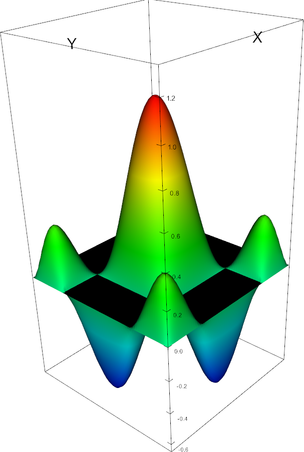
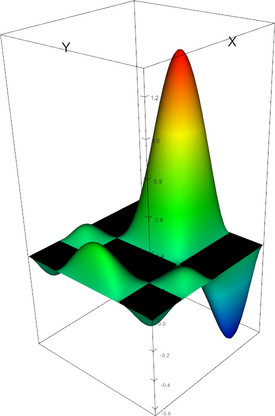
| 
|
Q_4 element, shape function 20 | Q_4 element, shape function 21 |
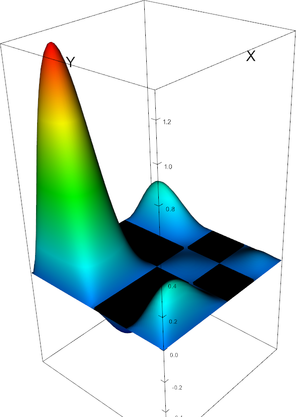
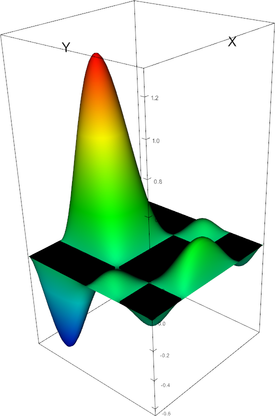
| 
|
Q_4 element, shape function 22 | Q_4 element, shape function 23 |
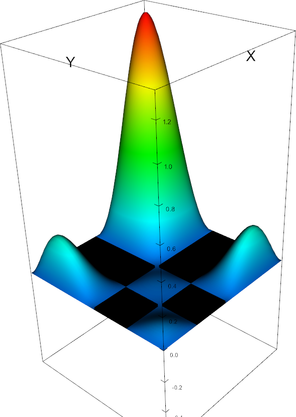
| |
Q_4 element, shape function 24 |
| FE_Q< dim, spacedim >::FE_Q | ( | const Quadrature< 1 > & | points | ) |
Constructor for tensor product polynomials with support points points based on a one-dimensional quadrature formula. The degree of the finite element is points.size()-1. Note that the first point has to be 0 and the last one 1. Constructing FE_Q<dim>(QGaussLobatto<1>(fe_degree+1)) is equivalent to the constructor that specifies the polynomial degree only. For selecting equidistant nodes at fe_degree > 2, construct FE_Q<dim>(QIterated<1>(QTrapez<1>(),fe_degree)).
|
overridevirtual |
Return a string that uniquely identifies a finite element. This class returns FE_Q<dim>(degree), with dim and degree replaced by appropriate values.
Implements FiniteElement< dim, spacedim >.
|
overridevirtual |
A sort of virtual copy constructor, this function returns a copy of the finite element object. Derived classes need to override the function here in this base class and return an object of the same type as the derived class.
Some places in the library, for example the constructors of FESystem as well as the hp::FECollection class, need to make copies of finite elements without knowing their exact type. They do so through this function.
Implements FiniteElement< dim, spacedim >.
|
overridevirtual |
Implementation of the corresponding function in the FiniteElement class. Since the current element is interpolatory, the nodal values are exactly the support point values. Furthermore, since the current element is scalar, the support point values need to be vectors of length 1.
Reimplemented from FiniteElement< dim, spacedim >.
|
finaloverridevirtual |
Return whether this element dominates another one given as argument fe_other, whether it is the other way around, whether neither dominates, or if either could dominate. The codim parameter describes the codimension of the investigated subspace and specifies that it is subject to this comparison. For example, if codim==0 then this function compares which element dominates at the cell level. If codim==1, then the elements are compared at faces, i.e., the comparison happens between the function spaces of the two finite elements as restricted to a face. Larger values of codim work correspondingly.
For a definition of domination, see FiniteElementDomination::Domination and in particular the hp paper.
Reimplemented from FiniteElement< dim, spacedim >.
 1.8.17
1.8.17