This program was contributed by Jean-Paul Pelteret <jppelteret@gmail.com>.
This program is part of the deal.II code gallery and consists of the following files (click to inspect):
Pictures from this code gallery program
Annotated version of README.md
Overview
Many rubber-like materials are not only near-incompressible in nature, but also exhibit a viscoelastic response (within the tested load and time scales). In this example, we extend the near-incompressible rate-independent constitutive used in step-44 (which implements three-field quasi-static quasi-incompressible finite elasticity) to one that displays rate-dependent behavior. It may seem that there is a contradiction of terms here, so lets clarify by saying the the problem remains "quasi-static" in the sense that inertial terms remain insignificant, even though the material response itself is rate-dependent. This implies that, for these fictitious material parameters, it is assumed that the timescale for material relaxation is much longer than that of elastic wave propagation.
We've also taken the opportunity to extend the code first shown in step-44 to parallel (the primary reason for this contribution), using Metis as a grid partitioner and Trilinos for linear algebra. As a motivation as to why one might still choose to use Metis (also associated with parallel::shared::Triangulation in step-18 , although this triangulation is not used in this instance) over p4est (also associated with parallel::distributed::Triangulation ) as a grid partitioner, at this point in time it is not possible to use the hp finite-element in conjunction with the distributed grid, meaning that this code could not, for example, be readily extended to the application shown in
J-P. V. Pelteret, D. Davydov, A. McBride, D. Vu, P. Steinmann, Computational electro-elasticity and magneto-elasticity for quasi-incompressible media immersed in free space. International Journal for Numerical Methods in Engineering, 2016, 108, 1307-1342. DOI: 10.1002/nme.5254
The discerning reader will observe that we've chosen to employ deal.II's built in solvers as opposed to using Trilinos solvers. This is because the system matrices K_Jp and K_pJ, although block diagonal and well conditioned, and for some reason (perhaps pertaining to the negative definite nature of these blocks, or that the entries are very small in magnitude) Trilinos solvers are not sufficiently robust to compute inverse matrix-vector multiplication with. We do stress, however, that to date no great attempt has been made by the author to overcome this issue other than by making an entirely different choice of solver.
Finite deformation of a thin strip with a hole.
Various permutations of the problem of an elastomeric strip with a centered cut-out can be found in the literature for solid mechanics, in particular (but not limited to) that pertaining to
incompressible elasticity elasto-plasticity electro-elasticity thermo-elasticity.
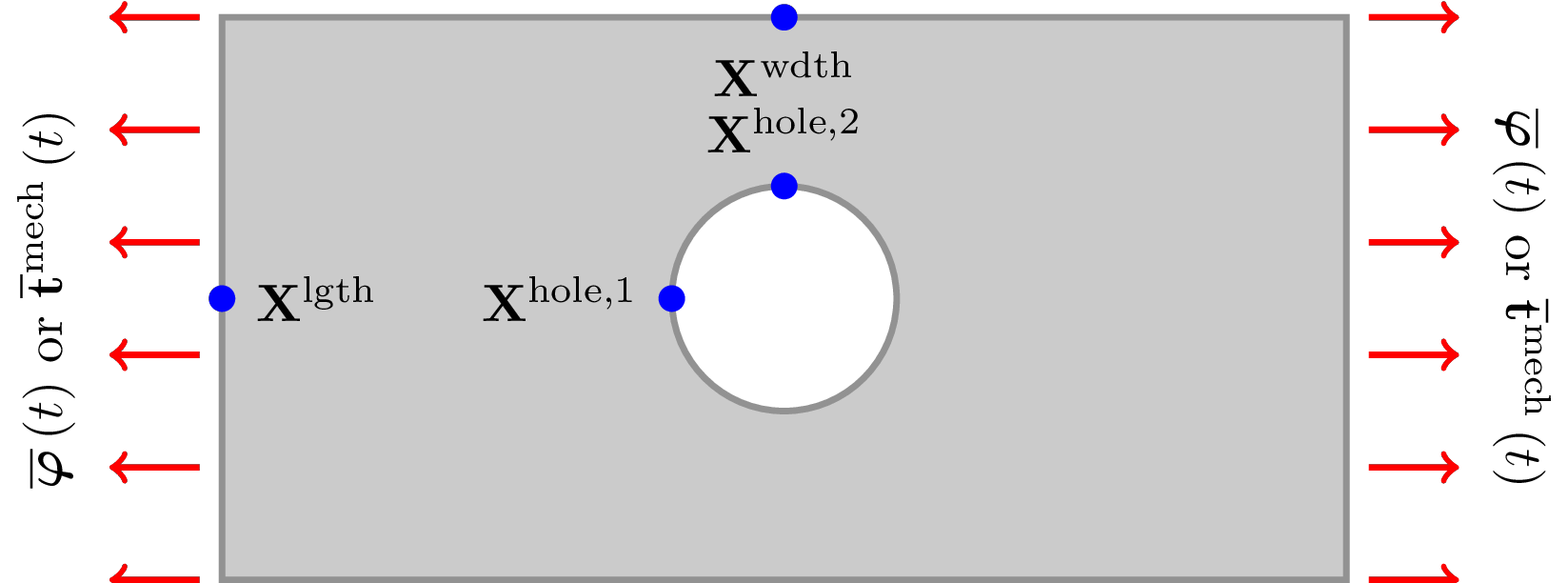
Here we implement another permutation (one that is not necessarily benchmarked elsewhere), simply for demonstration purposes. The basic problem configuration is summarized in the following image.
A thin strip of material with a circular hole is (in 3d) constrained in the Z direction and loaded in the direction of its long edge. In our implementation, this load is applied to the +Y surface and may either be displacement control (a Dirichlet condition) or a traction load (a Neumann boundary condition). Due to the symmetry of both the geometry and load, the problem can be simplified by modeling only an eighth of the geometry in 3d or a quarter in 2d. By doing so, it it necessary to then implement symmetry conditions on the surfaces coincident with the X-Z and Y-Z planes (and the X-Y plane in 3d). The +X surface, and that of the hole itself, remain traction-free.
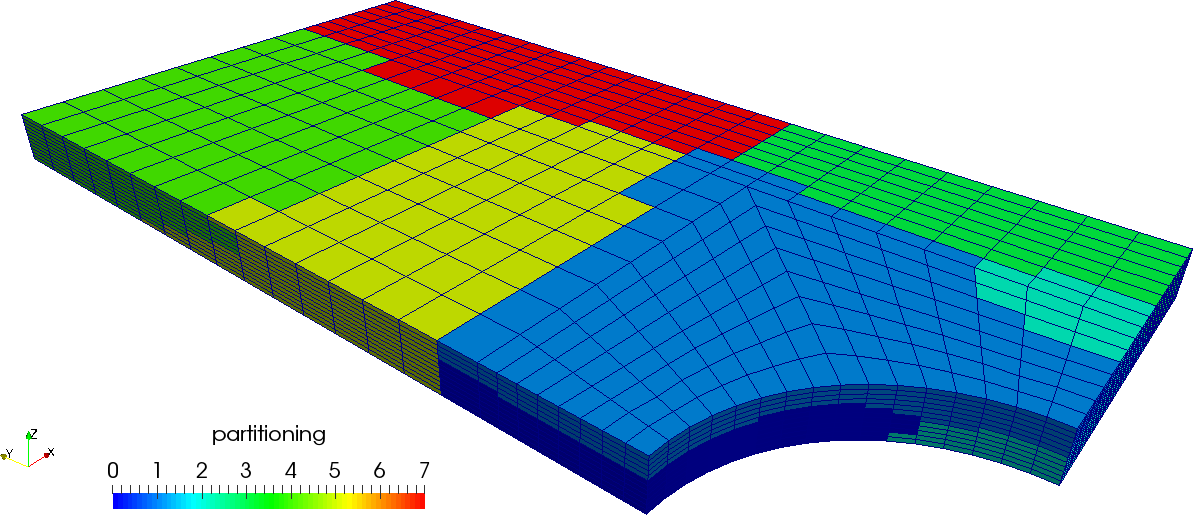
In three dimensions, the geometry (and a potential partitioning over 8 processors) looks as follows:
Note that, for this particular formulation, the two-dimensional case corresponds to neither plane-strain nor plane-stress conditions.
Requirements
Version 8.5.0 or greater of deal.II C++11 and MPI must be enabled The following packages must also be enabled: Metis Trilinos
Compiling and running
Similar to the example programs, run
cmake -DDEAL_II_DIR=/path/to/deal.II .
in this directory to configure the problem.
or
The problem may then be run in serial mode with
and in parallel (in this case, on 4 processors) with
mpirun -np 4 ./viscoelastic_strip_with_hole
This program can be run in 2d or 3d; this choice can be made by making the appropriate changes in the main() function.
Reference for this work
If you use this program as a basis for your own work, please consider citing it in your list of references. The initial version of this work was contributed to the deal.II project by the authors listed in the following citation: J-P. V. Pelteret, The deal.II code gallery: Quasi-static Finite-Strain Quasi-incompressible Visco-elasticity, 2017. DOI: 10.5281/zenodo.437604
Acknowledgements
The support of this work by the European Research Council (ERC) through the Advanced Grant 289049 MOCOPOLY is gratefully acknowledged by the author.
Recommended Literature
C. Miehe (1994), Aspects of the formulation and finite element implementation of large strain isotropic elasticity. International Journal for Numerical Methods in Engineering 37 , 12, 1981-2004. DOI: 10.1002/nme.1620371202 ; G.A. Holzapfel (2001), Nonlinear Solid Mechanics. A Continuum Approach for Engineering, John Wiley & Sons. ISBN: 978-0-471-82319-3 ; P. Wriggers (2008), Nonlinear finite element methods, Springer. DOI: 10.1007/978-3-540-71001-1 ; T.J.R. Hughes (2000), The Finite Element Method: Linear Static and Dynamic Finite Element Analysis, Dover. ISBN: 978-0486411811
The derivation of the finite-element problem, namely the definition and linearization of the residual and their subsequent discretization are quite lengthy and involved. However, this is already detailed in step-44 , some of the aforementioned literature, as well as J-P. V. Pelteret, A computational neuromuscular model of the human upper airway with application to the study of obstructive sleep apnoea. PhD Thesis, University of Cape Town, 2013. http://hdl.handle.net/11427/9519
and need not be repeated here. As for the viscoelastic constitutive law (which satisfies the dissipation inequality through the definition of an internal variable that we denote as Q in the code), this is derived and presented in detail in C. Linder, M. Tkachuk & C. Miehe, A micromechanically motivated diffusion-based transient network model and its incorporation into finite rubber viscoelasticity. Journal of the Mechanics and Physics of Solids, 2011, 59, 2134-2156. DOI: 10.1016/j.jmps.2011.05.005
In particular, the relevant equations from Linder et al.'s work that are implemented in this work are equations 47, 54 and 56. Note that the time discretization for the rate-dependent internal variable for this single dissipative mechanism is only first-order accurate.
Results
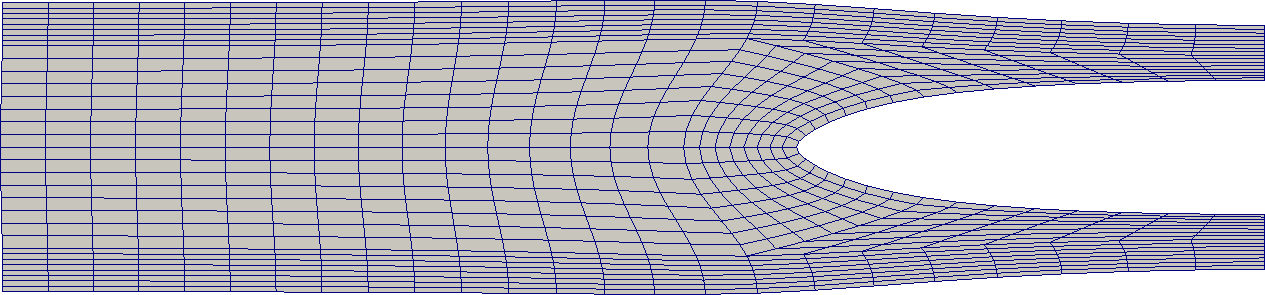
To begin, here is a comparison of the initial grid for the 2d version of the problem (mirrored about the x-axis and rotated 90 degrees anti-clockwise)
and of the final, displaced grid after the load has been applied and the material is in a (near-completely) relaxed state.
These results, as well as those that follow, were produced using the following material properties: The Poisson ratio is 0.4995 The elastic shear modulus is 80MPa The viscoelastic shear modulus is 160MPa The viscoelastic relaxation time is 2.5s
while the boundary conditions were configured in the following manner: The "driving" boundary condition on the short-side (+Y face) is of the Neumann variety The applied hydrostatic pressure is -150Pa (i.e. a tensile load) The load ramp time is 1s
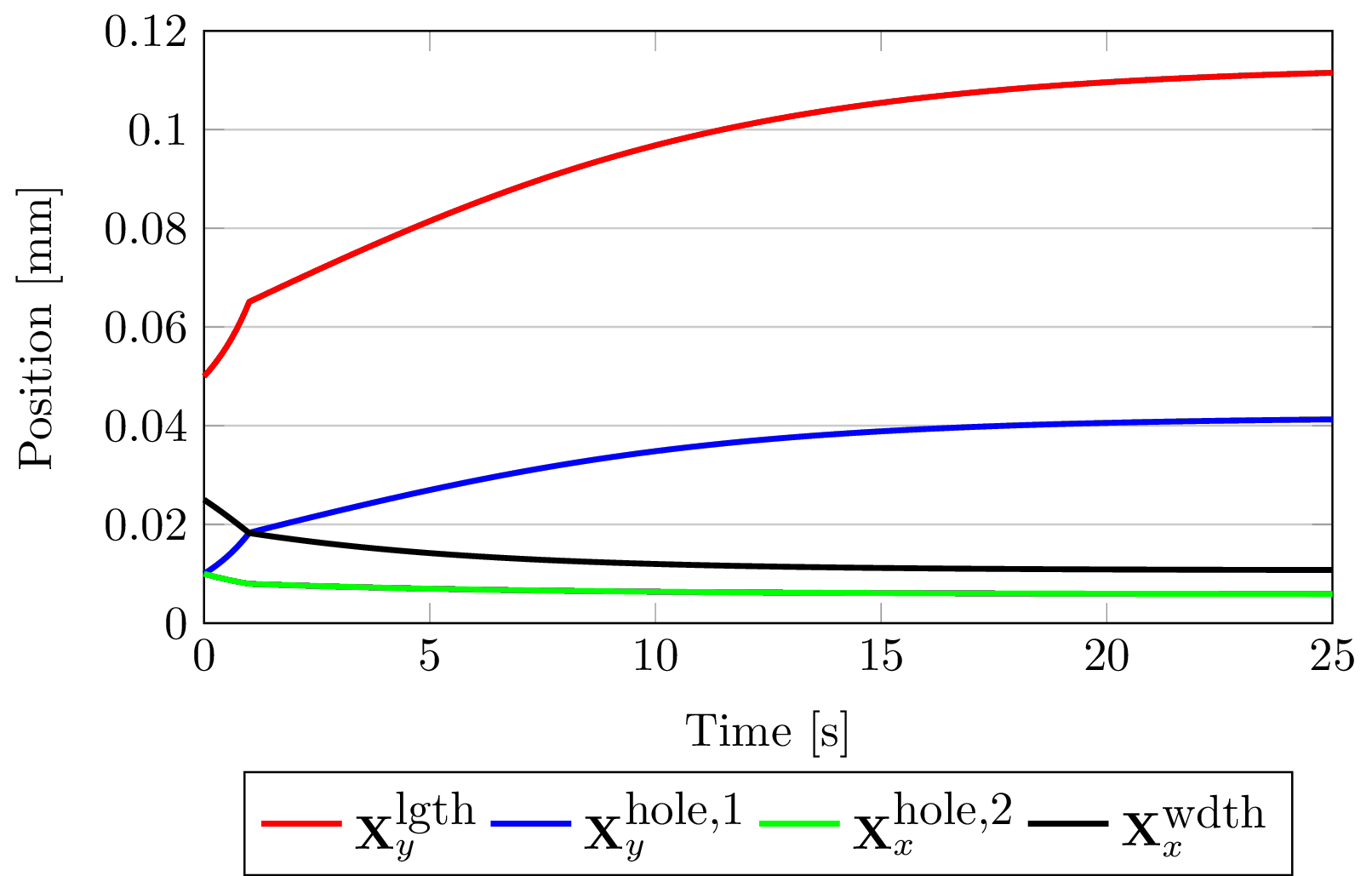
The following chart highlights the displacement of several vertices and clearly illustrates the viscoelastic nature of the material.
During the initial phase, the load is applied over a period of time much shorter than the material's characteristic relaxation time. The material therefore exhibits a very stiff response, and relaxes as the load remains constant for the remainder of the simulation. This deformation that occurs under constant load is commonly known as creep.
We've been lazy and stopped the simulation slightly prematurely, but it is clear that the material's displacement is moving asymptotically towards a equilibrium solution. You can also check what the true resting load state is by removing the dissipative mechanism (setting its shear modulus to zero) and rerunning the simulation with the material then exhibiting rate-independent behavior. Note that in this case, the number of time step over which the load is applied must likely be increased in order to ensure stability of the nonlinear problem.
Animations
Just in case you found the presented chart a little dry and undigestible, below are a couple of animations that demonstrate the viscoelastic nature of the material in a more visually appealing manner.
Animation of the evolution of the displacement field**
Animation of the evolution of the pressure field**
Annotated version of viscoelastic_strip_with_hole.cc
/ * ---------------------------------------------------------------------
* Copyright (C) 2017 by the deal.II authors and
* Jean-Paul Pelteret
*
* This file is part of the deal.II library.
*
* The deal.II library is
free software; you can use it, redistribute
* it, and/or modify it under the terms of the GNU Lesser General
* Public License as published by the Free Software Foundation; either
* version 2.1 of the License, or (at your option) any later version.
* The full text of the license can be found in the file LICENSE at
* the top level of the deal.II distribution.
*
* ---------------------------------------------------------------------
* /
/ *
* Authors: Jean-Paul Pelteret, University of Erlangen-Nuremberg, 2017
* /
#include <deal.II/base/mpi.h>
#include <deal.II/base/function.h>
#include <deal.II/base/parameter_handler.h>
#include <deal.II/base/point.h>
#include <deal.II/base/quadrature_lib.h>
#include <deal.II/base/tensor.h>
#include <deal.II/base/timer.h>
#include <deal.II/base/work_stream.h>
#include <deal.II/dofs/dof_renumbering.h>
#include <deal.II/dofs/dof_tools.h>
#include <deal.II/base/quadrature_point_data.h>
#include <deal.II/grid/filtered_iterator.h>
#include <deal.II/grid/grid_generator.h>
#include <deal.II/grid/grid_tools.h>
#include <deal.II/grid/grid_in.h>
#include <deal.II/grid/manifold_lib.h>
#include <deal.II/grid/tria.h>
#include <deal.II/grid/tria_boundary_lib.h>
#include <deal.II/fe/fe_dgp_monomial.h>
#include <deal.II/fe/fe_q.h>
#include <deal.II/fe/fe_system.h>
#include <deal.II/fe/fe_tools.h>
#include <deal.II/fe/fe_values.h>
#include <deal.II/fe/mapping_q_eulerian.h>
#include <deal.II/lac/block_sparsity_pattern.h>
#include <deal.II/lac/dynamic_sparsity_pattern.h>
#include <deal.II/lac/full_matrix.h>
#include <deal.II/lac/constraint_matrix.h>
#include <deal.II/lac/solver_selector.h>
#include <deal.II/lac/trilinos_block_sparse_matrix.h>
#include <deal.II/lac/trilinos_precondition.h>
#include <deal.II/lac/trilinos_sparsity_pattern.h>
#include <deal.II/lac/trilinos_sparse_matrix.h>
#include <deal.II/lac/trilinos_vector.h>
#include <deal.II/lac/linear_operator.h>
#include <deal.II/lac/packaged_operation.h>
#include <deal.II/lac/trilinos_linear_operator.h>
#include <deal.II/numerics/data_out.h>
#include <deal.II/numerics/vector_tools.h>
#include <deal.II/physics/transformations.h>
#include <deal.II/physics/elasticity/kinematics.h>
#include <deal.II/physics/elasticity/standard_tensors.h>
#include <iostream>
#include <fstream>
#include <numeric>
#include <deal.II/grid/grid_out.h>
namespace ViscoElasStripHole
{
namespace Parameters
{
struct BoundaryConditions
{
BoundaryConditions();
std::string driver;
double stretch;
double pressure;
double load_time;
static void
void
};
BoundaryConditions::BoundaryConditions()
:
driver ("Neumann" ),
stretch (2.0),
pressure(0.0),
load_time(2.5),
boundary_id_minus_X (1),
boundary_id_plus_X (2),
boundary_id_minus_Y (3),
boundary_id_plus_Y (4),
boundary_id_minus_Z (5),
boundary_id_plus_Z (6),
boundary_id_hole (10),
manifold_id_hole (10)
{ }
{
{
"Driver boundary condition for the problem" );
"Positive stretch applied length-ways to the strip" );
"Hydrostatic pressure applied (in the referential configuration) to the interior surface of the hole" );
"Total time over which the stretch/pressure is ramped up" );
}
}
{
{
driver = prm.
get (
"Driver" );
}
}
{
unsigned int poly_degree;
unsigned int quad_order;
static void
void
};
{
{
"Displacement system polynomial order" );
"Gauss quadrature order" );
}
}
{
{
}
}
struct Geometry
{
double length;
double width;
double thickness;
double hole_diameter;
double hole_division_fraction;
unsigned int n_repetitions_xy;
unsigned int n_repetitions_z;
unsigned int global_refinement;
static void
void
};
{
{
"Total sample length" );
"Total sample width" );
"Total sample thickness" );
"Hole diameter" );
"A geometric factor affecting the discretisation near the hole" );
prm.
declare_entry (
"Number of subdivisions in cross-section" ,
"2" ,
"A factor defining the number of initial grid subdivisions in the cross-section" );
"A factor defining the number of initial grid subdivisions through the thickness" );
"Global refinement level" );
"Global grid scaling factor" );
}
}
{
{
hole_division_fraction = prm.
get_double (
"Hole division fraction" );
n_repetitions_xy = prm.
get_integer (
"Number of subdivisions in cross-section" );
n_repetitions_z = prm.
get_integer (
"Number of subdivisions thickness" );
global_refinement = prm.
get_integer (
"Global refinement" );
}
}
struct Materials
{
double nu_e;
double mu_e;
double mu_v;
double tau_v;
static void
void
};
{
{
"Poisson's ratio" );
"Elastic shear modulus" );
"Viscous shear modulus" );
"Viscous relaxation time" );
}
}
{
{
tau_v = prm.
get_double (
"Viscous relaxation time" );
}
}
struct LinearSolver
{
std::string type_lin;
double tol_lin;
double max_iterations_lin;
static void
void
};
{
{
"Type of solver used to solve the linear system" );
"Linear solver residual (scaled by residual norm)" );
"Linear solver iterations (multiples of the system matrix size)" );
}
}
{
{
type_lin = prm.
get (
"Solver type" );
max_iterations_lin = prm.
get_double (
"Max iteration multiplier" );
}
}
struct NonlinearSolver
{
unsigned int max_iterations_NR;
double tol_f;
double tol_u;
static void
void
};
{
{
"Number of Newton-Raphson iterations allowed" );
"Displacement error tolerance" );
"Force residual tolerance" );
}
}
{
{
max_iterations_NR = prm.
get_integer (
"Max iterations Newton-Raphson" );
}
}
struct Time
{
double delta_t;
double end_time;
static void
void
};
{
{
"End time" );
"Time step size" );
}
}
{
{
}
}
struct AllParameters
: public BoundaryConditions,
public Geometry,
public Materials,
public LinearSolver,
public NonlinearSolver,
public Time
{
AllParameters(const std::string &input_file);
static void
void
};
AllParameters::AllParameters(const std::string &input_file)
{
declare_parameters(prm);
parse_parameters(prm);
}
{
BoundaryConditions::declare_parameters(prm);
FESystem::declare_parameters(prm);
Geometry::declare_parameters(prm);
Materials::declare_parameters(prm);
LinearSolver::declare_parameters(prm);
NonlinearSolver::declare_parameters(prm);
Time::declare_parameters(prm);
}
{
BoundaryConditions::parse_parameters(prm);
FESystem::parse_parameters(prm);
Geometry::parse_parameters(prm);
Materials::parse_parameters(prm);
LinearSolver::parse_parameters(prm);
NonlinearSolver::parse_parameters(prm);
Time::parse_parameters(prm);
}
}
class Time
{
public :
Time (const double time_end,
const double delta_t)
:
timestep(0),
time_current(0.0),
time_end(time_end),
delta_t(delta_t)
{}
virtual ~Time()
{}
double current() const
{
return time_current;
}
double end() const
{
return time_end;
}
double get_delta_t() const
{
return delta_t;
}
unsigned int get_timestep() const
{
return timestep;
}
void increment()
{
time_current += delta_t;
++timestep;
}
private :
unsigned int timestep;
double time_current;
const double time_end;
const double delta_t;
};
template <int dim>
class Material_Compressible_Three_Field_Linear_Viscoelastic
{
public :
Material_Compressible_Three_Field_Linear_Viscoelastic(const double mu_e,
const double nu_e,
const double mu_v,
const double tau_v,
const Time &time)
:
kappa((2.0 * mu_e * (1.0 + nu_e)) / (3.0 * (1.0 - 2.0 * nu_e))),
mu_e(mu_e),
mu_v(mu_v),
tau_v(tau_v),
time(time),
Q_n_t(
Physics ::Elasticity::StandardTensors<dim>::I),
Q_t1(
Physics ::Elasticity::StandardTensors<dim>::I)
{
}
~Material_Compressible_Three_Field_Linear_Viscoelastic()
{}
const double &p_tilde) const
{
return get_tau_iso(F) + get_tau_vol(F,p_tilde);
}
const double &p_tilde) const
{
return get_Jc_iso(F) + get_Jc_vol(F,p_tilde);
}
double
get_dPsi_vol_dJ(const double &J_tilde) const
{
return (kappa / 2.0) * (J_tilde - 1.0 / J_tilde);
}
double
get_d2Psi_vol_dJ2(const double &J_tilde) const
{
return ( (kappa / 2.0) * (1.0 + 1.0 / (J_tilde * J_tilde)));
}
void
const double &/ *p_tilde* /,
const double &/ *J_tilde* /)
{
Linder2011 eq 54 Assumes first-oder backward Euler time discretisation
Q_n_t = (1.0/(1.0 + time.get_delta_t()/tau_v))*(Q_t1 + (time.get_delta_t()/tau_v)*
invert (C_bar));
}
void
update_end_timestep()
{
Q_t1 = Q_n_t;
}
protected :
const double kappa;
const double mu_e;
const double mu_v;
const double tau_v;
const Time &time;
const double &p_tilde) const
{
}
{
}
{
Elastic Neo-Hookean + Linder2011 eq 47
return mu_e * b_bar
}
const double &p_tilde) const
return p_tilde * det_F
}
tau_iso);
return (2.0 / dim) *
trace (tau_bar)
- (2.0 / dim) * (tau_iso_x_I + I_x_tau_iso)
}
Elastic Neo-Hookean + Linder2011 eq 56
}
};
template <int dim>
class PointHistory
{
public :
PointHistory()
{}
virtual ~PointHistory()
{}
void
setup_lqp (const Parameters::AllParameters ¶meters,
const Time &time)
{
material.reset(new Material_Compressible_Three_Field_Linear_Viscoelastic<dim>(
parameters.mu_e, parameters.nu_e,
parameters.mu_v, parameters.tau_v,
time));
}
const double &p_tilde) const
{
return material->get_tau(F, p_tilde);
}
const double &p_tilde) const
{
return material->get_Jc(F, p_tilde);
}
double
get_dPsi_vol_dJ(const double &J_tilde) const
{
return material->get_dPsi_vol_dJ(J_tilde);
}
double
get_d2Psi_vol_dJ2(const double &J_tilde) const
{
return material->get_d2Psi_vol_dJ2(J_tilde);
}
void
const double &p_tilde,
const double &J_tilde)
{
material->update_internal_equilibrium(F,p_tilde,J_tilde);
}
void
update_end_timestep()
{
material->update_end_timestep();
}
private :
std::shared_ptr< Material_Compressible_Three_Field_Linear_Viscoelastic<dim> > material;
};
template <int dim>
class Solid
{
public :
Solid(const std::string &input_file);
virtual
~Solid();
void
private :
struct PerTaskData_ASM;
struct ScratchData_ASM;
void
make_grid();
void
const double half_length,
const double half_width,
const double hole_radius,
const unsigned int n_repetitions_xy = 1,
const double hole_division_fraction = 0.25);
void
void
determine_component_extractors();
void
void
ScratchData_ASM &scratch,
PerTaskData_ASM &data) const ;
void
copy_local_to_global_system(const PerTaskData_ASM &data);
void
make_constraints(const int &it_nr);
void
setup_qph();
void
std::pair<unsigned int, double>
void
update_end_timestep();
void
output_results(const unsigned int timestep,
const double current_time) const ;
void
compute_vertex_positions(std::vector<double> &real_time,
std::vector<std::vector<
Point<dim> > > &tracked_vertices,
Parallel communication
MPI_Comm mpi_communicator;
Parameters::AllParameters parameters;
Time time;
PointHistory<dim> > quadrature_point_history;
const unsigned int degree;
const unsigned int dofs_per_cell;
static const unsigned int n_blocks = 3;
static const unsigned int first_u_component = 0;
static const unsigned int p_component = dim;
static const unsigned int J_component = dim + 1;
enum
{
u_block = 0,
p_block = 1,
J_block = 2
};
Block data
std::vector<unsigned int> block_component;
DoF index data
std::vector<IndexSet> all_locally_owned_dofs;
std::vector<IndexSet> locally_owned_partitioning;
std::vector<IndexSet> locally_relevant_partitioning;
std::vector<types::global_dof_index> dofs_per_block;
std::vector<types::global_dof_index> element_indices_u;
std::vector<types::global_dof_index> element_indices_p;
std::vector<types::global_dof_index> element_indices_J;
const QGauss <dim - 1> qf_face;
const unsigned int n_q_points;
const unsigned int n_q_points_f;
LA::BlockSparseMatrix tangent_matrix;
struct Errors
{
Errors()
:
norm (1.0), u(1.0), p(1.0), J(1.0)
{}
void reset()
{
u = 1.0;
p = 1.0;
J = 1.0;
}
void normalise(const Errors &rhs)
{
if (rhs.norm != 0.0)
if (rhs.u != 0.0)
u /= rhs.u;
if (rhs.p != 0.0)
p /= rhs.p;
if (rhs.J != 0.0)
J /= rhs.J;
}
};
Errors error_residual, error_residual_0, error_residual_norm, error_update,
error_update_0, error_update_norm;
void
get_error_residual(Errors &error_residual);
void
Errors &error_update);
std::pair<double, std::pair<double,double> >
void
print_conv_header();
void
};
template <int dim>
Solid<dim>::Solid(const std::string &input_file)
:
mpi_communicator(MPI_COMM_WORLD),
parameters(input_file),
time(parameters.end_time, parameters.delta_t),
timer(mpi_communicator,
pcout,
degree(parameters.poly_degree),
fe(
FE_Q <dim>(parameters.poly_degree), dim,
dof_handler(triangulation),
dofs_per_cell (fe.dofs_per_cell),
u_fe(first_u_component),
p_fe(p_component),
J_fe(J_component),
dofs_per_block(n_blocks),
qf_cell(parameters.quad_order),
qf_face(parameters.quad_order),
n_q_points (qf_cell.size()),
n_q_points_f (qf_face.size())
{
Assert (dim==2 || dim==3,
ExcMessage (
"This problem only works in 2 or 3 space dimensions." ));
determine_component_extractors();
}
template <int dim>
Solid<dim>::~Solid()
{
}
template <int dim>
void Solid<dim>::run()
{
make_grid();
setup_system(solution_delta);
{
J_mask (J_component, n_components);
constraints,
J_mask,
solution_n);
}
output_results(time.get_timestep(), time.current());
time.increment();
Some points for post-processing
std::vector<double> real_time;
real_time.push_back(0);
std::vector<std::vector<Point<dim> > > tracked_vertices (4);
{
p[1] = parameters.length/2.0;
tracked_vertices[0].push_back(p*parameters.scale);
}
{
p[1] = parameters.hole_diameter/2.0;
tracked_vertices[1].push_back(p*parameters.scale);
}
{
p[0] = parameters.hole_diameter/2.0;
tracked_vertices[2].push_back(p*parameters.scale);
}
{
p[0] = parameters.width/2.0;
tracked_vertices[3].push_back(p*parameters.scale);
}
while (time.current() < time.end()+0.01*time.get_delta_t())
{
solve_nonlinear_timestep(solution_delta);
solution_n += solution_delta;
solution_delta = 0.0;
output_results(time.get_timestep(), time.current());
compute_vertex_positions(real_time,
tracked_vertices,
get_solution_total(solution_delta));
update_end_timestep();
time.increment();
}
pcout << "\n\n*** Spatial position history for tracked vertices ***" << std::endl;
for (unsigned int t=0; t<real_time.size(); ++t)
{
if (t == 0)
{
pcout << "Time," ;
for (unsigned int p=0; p<tracked_vertices.size(); ++p)
{
for (
unsigned int d=0;
d <dim; ++
d )
{
pcout <<
"Point " << p <<
" [" <<
d <<
"]" ;
if (!(p == tracked_vertices.size()-1 &&
d == dim-1))
pcout << "," ;
}
}
pcout << std::endl;
}
pcout << std::setprecision(6);
pcout << real_time[t] << "," ;
for (unsigned int p=0; p<tracked_vertices.size(); ++p)
{
Assert (tracked_vertices[p].size() == real_time.size(),
ExcMessage (
"Vertex not tracked at each timestep" ));
for (
unsigned int d=0;
d <dim; ++
d )
{
pcout << tracked_vertices[p][t][
d ];
if (!(p == tracked_vertices.size()-1 &&
d == dim-1))
pcout << "," ;
}
}
pcout << std::endl;
}
}
template <int dim>
struct Solid<dim>::PerTaskData_ASM
{
std::vector<types::global_dof_index> local_dof_indices;
PerTaskData_ASM(const unsigned int dofs_per_cell)
:
cell_rhs(dofs_per_cell),
local_dof_indices(dofs_per_cell)
{}
void reset()
{
cell_rhs = 0.0;
}
};
template <int dim>
struct Solid<dim>::ScratchData_ASM
{
Integration helper
Quadrature point solution
std::vector<Tensor<2, dim> > solution_grads_u_total;
std::vector<double> solution_values_p_total;
std::vector<double> solution_values_J_total;
Shape function values and gradients
std::vector<std::vector<double> > Nx;
std::vector<std::vector<Tensor<2, dim> > > grad_Nx;
std::vector<std::vector<SymmetricTensor<2, dim> > > symm_grad_Nx;
:
solution_total (solution_total),
fe_values_ref(fe_cell, qf_cell, uf_cell),
fe_face_values_ref(fe_cell, qf_face, uf_face),
solution_grads_u_total(qf_cell.size()),
solution_values_p_total(qf_cell.size()),
solution_values_J_total(qf_cell.size()),
Nx(qf_cell.size(),
std ::vector<double>(fe_cell.dofs_per_cell)),
grad_Nx(qf_cell.size(),
std ::vector<
Tensor <2, dim> >(fe_cell.dofs_per_cell)),
symm_grad_Nx(qf_cell.size(),
(fe_cell.dofs_per_cell))
{}
ScratchData_ASM(const ScratchData_ASM &rhs)
:
solution_total (rhs.solution_total),
fe_values_ref(rhs.fe_values_ref.get_fe(),
rhs.fe_values_ref.get_quadrature(),
rhs.fe_values_ref.get_update_flags()),
fe_face_values_ref(rhs.fe_face_values_ref.get_fe(),
rhs.fe_face_values_ref.get_quadrature(),
rhs.fe_face_values_ref.get_update_flags()),
solution_grads_u_total(rhs.solution_grads_u_total),
solution_values_p_total(rhs.solution_values_p_total),
solution_values_J_total(rhs.solution_values_J_total),
Nx(rhs.Nx),
grad_Nx(rhs.grad_Nx),
symm_grad_Nx(rhs.symm_grad_Nx)
{}
void reset()
{
const unsigned int n_q_points = solution_grads_u_total.size();
const unsigned int n_dofs_per_cell = Nx[0].size();
Assert (solution_grads_u_total.size() == n_q_points,
Assert (solution_values_p_total.size() == n_q_points,
Assert (solution_values_J_total.size() == n_q_points,
Assert (Nx.size() == n_q_points,
Assert (grad_Nx.size() == n_q_points,
Assert (symm_grad_Nx.size() == n_q_points,
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
{
Assert ( grad_Nx[q_point].size() == n_dofs_per_cell,
Assert ( symm_grad_Nx[q_point].size() == n_dofs_per_cell,
solution_grads_u_total[q_point] = 0.0;
solution_values_p_total[q_point] = 0.0;
solution_values_J_total[q_point] = 0.0;
for (unsigned int k = 0; k < n_dofs_per_cell; ++k)
{
Nx[q_point][k] = 0.0;
grad_Nx[q_point][k] = 0.0;
symm_grad_Nx[q_point][k] = 0.0;
}
}
}
};
template <>
void Solid<2>::make_grid()
{
const int dim = 2;
const double tol = 1
e -12;
make_2d_quarter_plate_with_hole(triangulation,
parameters.length/2.0,
parameters.width/2.0,
parameters.hole_diameter/2.0,
parameters.n_repetitions_xy,
parameters.hole_division_fraction);
Clear boundary ID's
cell = triangulation.begin_active();
cell != triangulation.end(); ++cell)
{
for (unsigned int face=0; face<GeometryInfo<dim>::faces_per_cell; ++face)
if (cell->face(face)->at_boundary())
{
cell->face(face)->set_all_boundary_ids(0);
}
}
Set boundary IDs and and manifolds
cell = triangulation.begin_active();
cell != triangulation.end(); ++cell)
{
for (unsigned int face=0; face<GeometryInfo<dim>::faces_per_cell; ++face)
if (cell->face(face)->at_boundary())
{
Set boundary IDs
if (std::abs(cell->face(face)->center()[0] - 0.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_minus_X);
}
else if (std::abs(cell->face(face)->center()[0] - parameters.width/2.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_plus_X);
}
else if (std::abs(cell->face(face)->center()[1] - 0.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_minus_Y);
}
else if (std::abs(cell->face(face)->center()[1] - parameters.length/2.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_plus_Y);
}
else
{
for (unsigned int vertex=0; vertex<GeometryInfo<dim>::vertices_per_face; ++vertex)
if (std::abs(cell->vertex(vertex).distance(centre) - parameters.hole_diameter/2.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_hole);
break ;
}
}
Set manifold IDs
for (unsigned int vertex=0; vertex<GeometryInfo<dim>::vertices_per_face; ++vertex)
if (std::abs(cell->vertex(vertex).distance(centre) - parameters.hole_diameter/2.0) < tol)
{
cell->face(face)->set_manifold_id(parameters.manifold_id_hole);
break ;
}
}
}
triangulation.set_manifold(parameters.manifold_id_hole,spherical_manifold);
triangulation.refine_global(parameters.global_refinement);
}
template <>
void Solid<3>::make_grid()
{
const int dim = 3;
const double tol = 1
e -12;
make_2d_quarter_plate_with_hole(tria_2d,
parameters.length/2.0,
parameters.width/2.0,
parameters.hole_diameter/2.0,
parameters.n_repetitions_xy,
parameters.hole_division_fraction);
parameters.n_repetitions_z+1,
parameters.thickness/2.0,
triangulation);
Clear boundary ID's
cell = triangulation.begin_active();
cell != triangulation.end(); ++cell)
{
for (unsigned int face=0; face<GeometryInfo<dim>::faces_per_cell; ++face)
if (cell->face(face)->at_boundary())
{
cell->face(face)->set_all_boundary_ids(0);
}
}
Set boundary IDs and and manifolds
cell = triangulation.begin_active();
cell != triangulation.end(); ++cell)
{
for (unsigned int face=0; face<GeometryInfo<dim>::faces_per_cell; ++face)
if (cell->face(face)->at_boundary())
{
Set boundary IDs
if (std::abs(cell->face(face)->center()[0] - 0.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_minus_X);
}
else if (std::abs(cell->face(face)->center()[0] - parameters.width/2.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_plus_X);
}
else if (std::abs(cell->face(face)->center()[1] - 0.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_minus_Y);
}
else if (std::abs(cell->face(face)->center()[1] - parameters.length/2.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_plus_Y);
}
else if (std::abs(cell->face(face)->center()[2] - 0.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_minus_Z);
}
else if (std::abs(cell->face(face)->center()[2] - parameters.thickness/2.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_plus_Z);
}
else
{
for (unsigned int vertex=0; vertex<GeometryInfo<dim>::vertices_per_face; ++vertex)
{
Project the cell vertex to the XY plane and test the distance from the cylinder axis
vertex_proj[2] = 0.0;
if (std::abs(vertex_proj.
distance (centre) - parameters.hole_diameter/2.0) < tol)
{
cell->face(face)->set_boundary_id(parameters.boundary_id_hole);
break ;
}
}
}
Set manifold IDs
for (unsigned int vertex=0; vertex<GeometryInfo<dim>::vertices_per_face; ++vertex)
{
Project the cell vertex to the XY plane and test the distance from the cylinder axis
vertex_proj[2] = 0.0;
if (std::abs(vertex_proj.
distance (centre) - parameters.hole_diameter/2.0) < 1
e -12)
{
Set manifold ID on face and edges
cell->face(face)->set_all_manifold_ids(parameters.manifold_id_hole);
break ;
}
}
}
}
triangulation.set_manifold(parameters.manifold_id_hole,cylindrical_manifold);
triangulation.refine_global(parameters.global_refinement);
}
template <int dim>
const double half_length,
const double half_width,
const double hole_radius,
const unsigned int n_repetitions_xy,
const double hole_division_fraction)
{
const double length = 2.0*half_length;
const double width = 2.0*half_width;
const double hole_diameter = 2.0*hole_radius;
const double internal_width = hole_diameter + hole_division_fraction*(width - hole_diameter);
{
hole_diameter/2.0,
internal_width/2.0);
std::set<typename Triangulation<2>::active_cell_iterator > cells_to_remove;
cell != tria_plate_hole.
end (); ++cell)
{
Remove all cells that are not in the first quadrant
if (cell->center()[0] < 0.0 || cell->center()[1] < 0.0)
cells_to_remove.insert(cell);
}
}
{
Subdivide the plate so that we're left one cell to remove (we'll replace this with the plate with the hole) and then make the rest of the subdivisions so that we're left with cells with a decent aspect ratio
std::vector<std::vector<double> > step_sizes;
{
std::vector<double> subdivision_width;
subdivision_width.push_back(internal_width/2.0);
const double width_remaining = (width - internal_width)/2.0;
const unsigned int n_subs = std::max(1.0,std::ceil(width_remaining/(internal_width/2.0)));
for (unsigned int s=0; s<n_subs; ++s)
subdivision_width.push_back(width_remaining/n_subs);
step_sizes.push_back(subdivision_width);
const double sum_half_width = std::accumulate(subdivision_width.begin(), subdivision_width.end(), 0.0);
}
{
std::vector<double> subdivision_length;
subdivision_length.push_back(internal_width/2.0);
const double length_remaining = (length - internal_width)/2.0;
const unsigned int n_subs = std::max(1.0,std::ceil(length_remaining/(internal_width/2.0)));
for (unsigned int s=0; s<n_subs; ++s)
subdivision_length.push_back(length_remaining/n_subs);
step_sizes.push_back(subdivision_length);
const double sum_half_length = std::accumulate(subdivision_length.begin(), subdivision_length.end(), 0.0);
}
step_sizes,
std::set<typename Triangulation<2>::active_cell_iterator > cells_to_remove;
cell != tria_plate.
end (); ++cell)
{
Remove all cells that are in the first quadrant
if (cell->center()[0] < internal_width/2.0 && cell->center()[1] < internal_width/2.0)
cells_to_remove.insert(cell);
}
}
tria_cut_plate,
tria_2d_not_flat);
Attach a manifold to the curved boundary and refine Note: We can only guarentee that the vertices sit on the curve, so we must test with their position instead of the cell centre.
cell != tria_2d_not_flat.
end (); ++cell)
{
for (unsigned int face=0; face<GeometryInfo<2>::faces_per_cell; ++face)
if (cell->face(face)->at_boundary())
for (unsigned int vertex=0; vertex<GeometryInfo<2>::vertices_per_face; ++vertex)
if (std::abs(cell->vertex(vertex).distance(centre_2d) - hole_diameter/2.0) < 1
e -12)
{
cell->face(face)->set_manifold_id(10);
break ;
}
}
}
template <int dim>
{
pcout << "Setting up linear system..." << std::endl;
Partition triangulation
triangulation);
block_component = std::vector<unsigned int> (
n_components , u_block);
block_component[p_component] = p_block;
block_component[J_component] = J_block;
Count DoFs in each block
dofs_per_block.clear();
dofs_per_block.resize(n_blocks);
block_component);
std::vector<IndexSet> all_locally_relevant_dofs
locally_owned_dofs.
clear ();
locally_owned_partitioning.clear();
locally_relevant_dofs.
clear ();
locally_relevant_partitioning.clear();
locally_owned_partitioning.reserve(n_blocks);
locally_relevant_partitioning.reserve(n_blocks);
for (
unsigned int b=0;
b <n_blocks; ++
b )
{
= std::accumulate(dofs_per_block.begin(),
std::next(dofs_per_block.begin(),
b ), 0);
= std::accumulate(dofs_per_block.begin(),
std::next(dofs_per_block.begin(),
b +1), 0);
locally_owned_partitioning.push_back(locally_owned_dofs.get_view(idx_begin, idx_end));
locally_relevant_partitioning.push_back(locally_relevant_dofs.get_view(idx_begin, idx_end));
}
pcout
<< " Number of active cells: " << triangulation.n_active_cells()
<< " (by partition:" ;
pcout
<< (p==0 ? ' ' : '+' )
pcout << ")" << std::endl;
pcout
<<
" Number of degrees of freedom: " << dof_handler.
n_dofs ()
<< " (by partition:" ;
pcout
<< (p==0 ? ' ' : '+' )
pcout << ")" << std::endl;
pcout
<< " Number of degrees of freedom per block: "
<< "[n_u, n_p, n_J] = ["
<< dofs_per_block[u_block] << ", "
<< dofs_per_block[p_block] << ", "
<< dofs_per_block[J_block] << "]"
<< std::endl;
if (((ii < p_component) && (jj == J_component))
|| ((ii == J_component) && (jj < p_component))
|| ((ii == p_component) && (jj == p_component)))
else
locally_owned_partitioning,
locally_relevant_partitioning,
mpi_communicator);
constraints, false ,
this_mpi_process);
bsp.compress();
tangent_matrix.reinit (bsp);
We then set up storage vectors
system_rhs.reinit(locally_owned_partitioning,
mpi_communicator);
solution_n.reinit(locally_owned_partitioning,
mpi_communicator);
solution_delta.reinit(locally_owned_partitioning,
mpi_communicator);
setup_qph();
}
template <int dim>
void
Solid<dim>::determine_component_extractors()
{
element_indices_u.clear();
element_indices_p.clear();
element_indices_J.clear();
{
if (k_group == u_block)
element_indices_u.push_back(k);
else if (k_group == p_block)
element_indices_p.push_back(k);
else if (k_group == J_block)
element_indices_J.push_back(k);
else
{
}
}
}
template <int dim>
void Solid<dim>::setup_qph()
{
pcout << "Setting up quadrature point data..." << std::endl;
quadrature_point_history.
initialize (triangulation.begin_active(),
triangulation.end(),
n_q_points);
for (; cell!=endc; ++cell)
{
const std::vector<std::shared_ptr<PointHistory<dim> > > lqph =
quadrature_point_history.
get_data (cell);
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
lqph[q_point]->setup_lqp(parameters, time);
}
}
template <int dim>
void
{
pcout << std::endl
<< "Timestep " << time.get_timestep() << " @ "
<< time.current() << "s of "
<< time.end() << "s" << std::endl;
mpi_communicator);
error_residual.reset();
error_residual_0.reset();
error_residual_norm.reset();
error_update.reset();
error_update_0.reset();
error_update_norm.reset();
print_conv_header();
unsigned int newton_iteration = 0;
for (; newton_iteration < parameters.max_iterations_NR;
++newton_iteration)
{
pcout << " " << std::setw(2) << newton_iteration << " " << std::flush;
make_constraints(newton_iteration);
assemble_system(solution_delta);
get_error_residual(error_residual);
if (newton_iteration == 0)
error_residual_0 = error_residual;
error_residual_norm = error_residual;
error_residual_norm.normalise(error_residual_0);
if (newton_iteration > 0 &&
(error_update_norm.u <= parameters.tol_u &&
error_residual_norm.u <= parameters.tol_f) )
{
pcout << " CONVERGED! " << std::endl;
print_conv_footer(solution_delta);
break ;
}
const std::pair<unsigned int, double>
lin_solver_output = solve_linear_system(newton_update);
get_error_update(newton_update, error_update);
if (newton_iteration == 0)
error_update_0 = error_update;
error_update_norm = error_update;
error_update_norm.normalise(error_update_0);
solution_delta += newton_update;
newton_update = 0.0;
pcout << " | " << std::fixed << std::setprecision(3) << std::setw(7)
<< std::scientific << lin_solver_output.first << " "
<< lin_solver_output.second << " " << error_residual_norm.norm
<< " " << error_residual_norm.u << " "
<< error_residual_norm.p << " " << error_residual_norm.J
<< " " << error_update_norm.norm << " " << error_update_norm.u
<< " " << error_update_norm.p << " " << error_update_norm.J
<< " " << std::endl;
}
AssertThrow (newton_iteration <= parameters.max_iterations_NR,
ExcMessage (
"No convergence in nonlinear solver!" ));
}
template <int dim>
void Solid<dim>::print_conv_header()
{
pcout << std::string(132,'_' ) << std::endl;
pcout << " SOLVER STEP "
<< " | LIN_IT LIN_RES RES_NORM "
<< " RES_U RES_P RES_J NU_NORM "
<< " NU_U NU_P NU_J " << std::endl;
pcout << std::string(132,'_' ) << std::endl;
}
template <int dim>
{
pcout << std::string(132,'_' ) << std::endl;
const std::pair<double,std::pair<double,double> > error_dil = get_error_dilation(get_solution_total(solution_delta));
pcout << "Relative errors:" << std::endl
<< "Displacement:\t" << error_update.u / error_update_0.u << std::endl
<< "Force: \t\t" << error_residual.u / error_residual_0.u << std::endl
<< "Dilatation:\t" << error_dil.first << std::endl
<< "v / V_0:\t" << error_dil.second.second << " / " << error_dil.second.first
<< " = " << (error_dil.second.second/error_dil.second.first) << std::endl;
}
template <int dim>
std::pair<double,std::pair<double,double> >
double vol_reference = 0.0;
double vol_current = 0.0;
double dil_L2_error = 0.0;
std::vector<Tensor<2, dim> > solution_grads_u_total (qf_cell.
size ());
std::vector<double> solution_values_J_total (qf_cell.
size ());
for (; cell != endc; ++cell)
{
solution_grads_u_total);
solution_values_J_total);
const std::vector<std::shared_ptr<const PointHistory<dim> > > lqph =
quadrature_point_history.
get_data (cell);
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
{
const double J_tilde_qp = solution_values_J_total[q_point];
const double the_error_qp_squared = std::pow((det_F_qp - J_tilde_qp),
2);
const double JxW = fe_values_ref.
JxW (q_point);
dil_L2_error += the_error_qp_squared * JxW;
vol_reference += JxW;
vol_current += det_F_qp * JxW;
}
}
Sum across all porcessors
return std::make_pair(std::sqrt(dil_L2_error),
std::make_pair(vol_reference,vol_current));
}
template <int dim>
void Solid<dim>::get_error_residual(Errors &error_residual)
{
Construct a residual vector that has the values for all of its constrained DoFs set to zero.
error_residual.norm = error_res.l2_norm();
error_residual.u = error_res.block(u_block).l2_norm();
error_residual.p = error_res.block(p_block).l2_norm();
error_residual.J = error_res.block(J_block).l2_norm();
}
template <int dim>
Errors &error_update)
{
Construct a update vector that has the values for all of its constrained DoFs set to zero.
error_update.norm = error_ud.l2_norm();
error_update.u = error_ud.block(u_block).l2_norm();
error_update.p = error_ud.block(p_block).l2_norm();
error_update.J = error_ud.block(J_block).l2_norm();
}
template <int dim>
Cell interpolation -> Ghosted vector
locally_relevant_partitioning,
mpi_communicator,
/ *vector_writable = * / false );
solution_total = solution_n;
tmp = solution_delta;
solution_total += tmp;
return solution_total;
}
template <int dim>
{
pcout << " ASM_SYS " << std::flush;
tangent_matrix = 0.0;
system_rhs = 0.0;
PerTaskData_ASM per_task_data(dofs_per_cell);
ScratchData_ASM scratch_data(fe, qf_cell, uf_cell, qf_face, uf_face, solution_total);
for (; cell != endc; ++cell)
{
assemble_system_one_cell(cell, scratch_data, per_task_data);
copy_local_to_global_system(per_task_data);
}
}
template <int dim>
void Solid<dim>::copy_local_to_global_system(const PerTaskData_ASM &data)
{
data.local_dof_indices,
tangent_matrix, system_rhs);
}
template <int dim>
void
ScratchData_ASM &scratch,
PerTaskData_ASM &data) const
data.reset();
scratch.reset();
scratch.fe_values_ref.reinit(cell);
cell->get_dof_indices(data.local_dof_indices);
const std::vector<std::shared_ptr<const PointHistory<dim> > > lqph =
quadrature_point_history.
get_data (cell);
Update quadrature point solution
scratch.fe_values_ref[u_fe].get_function_gradients(scratch.solution_total,
scratch.solution_grads_u_total);
scratch.fe_values_ref[p_fe].get_function_values(scratch.solution_total,
scratch.solution_values_p_total);
scratch.fe_values_ref[J_fe].get_function_values(scratch.solution_total,
scratch.solution_values_J_total);
Update shape functions and their gradients (push-forward)
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
{
for (unsigned int k = 0; k < dofs_per_cell; ++k)
{
if (k_group == u_block)
{
scratch.grad_Nx[q_point][k] = scratch.fe_values_ref[u_fe].gradient(k, q_point)
* F_inv;
scratch.symm_grad_Nx[q_point][k] =
symmetrize (scratch.grad_Nx[q_point][k]);
}
else if (k_group == p_block)
scratch.Nx[q_point][k] = scratch.fe_values_ref[p_fe].value(k,
q_point);
else if (k_group == J_block)
scratch.Nx[q_point][k] = scratch.fe_values_ref[J_fe].value(k,
q_point);
else
}
}
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
{
const double &p_tilde = scratch.solution_values_p_total[q_point];
const double &J_tilde = scratch.solution_values_J_total[q_point];
{
PointHistory<dim> *lqph_q_point_nc = const_cast< PointHistory<dim>*> (lqph[q_point].get());
lqph_q_point_nc->update_internal_equilibrium(F,p_tilde,J_tilde);
}
const double dPsi_vol_dJ = lqph[q_point]->get_dPsi_vol_dJ(J_tilde);
const double d2Psi_vol_dJ2 = lqph[q_point]->get_d2Psi_vol_dJ2(J_tilde);
const std::vector<double> &Nx = scratch.Nx[q_point];
const std::vector<Tensor<2, dim> > &grad_Nx = scratch.grad_Nx[q_point];
const std::vector<SymmetricTensor<2, dim> > &symm_grad_Nx = scratch.symm_grad_Nx[q_point];
const double JxW = scratch.fe_values_ref.JxW(q_point);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
if (i_group == u_block)
data.cell_rhs(i) -= (symm_grad_Nx[i] * tau) * JxW;
else if (i_group == p_block)
data.cell_rhs(i) -= Nx[i] * (det_F - J_tilde) * JxW;
else if (i_group == J_block)
data.cell_rhs(i) -= Nx[i] * (dPsi_vol_dJ - p_tilde) * JxW;
else
for (unsigned int j = 0; j <= i; ++j)
{
if ((i_group == u_block) && (j_group == u_block))
{
data.cell_matrix(i, j) += symm_grad_Nx[i] * Jc
* symm_grad_Nx[j] * JxW;
if (component_i == component_j)
data.cell_matrix(i, j) += grad_Nx[i][component_i] * tau_ns
* grad_Nx[j][component_j] * JxW;
}
else if ((i_group == u_block) && (j_group == p_block))
{
data.cell_matrix(i, j) += (symm_grad_Nx[i] * I)
* Nx[j] * det_F
* JxW;
}
else if ((i_group == p_block) && (j_group == u_block))
{
data.cell_matrix(i, j) += Nx[i] * det_F
* (symm_grad_Nx[j] * I)
* JxW;
}
else if ((i_group == p_block) && (j_group == J_block))
data.cell_matrix(i, j) -= Nx[i] * Nx[j] * JxW;
else if ((i_group == J_block) && (j_group == p_block))
data.cell_matrix(i, j) -= Nx[i] * Nx[j] * JxW;
else if ((i_group == J_block) && (j_group == J_block))
data.cell_matrix(i, j) += Nx[i] * d2Psi_vol_dJ2 * Nx[j] * JxW;
else
Assert ((i_group <= J_block) && (j_group <= J_block),
}
}
}
for (unsigned int i = 0; i < dofs_per_cell; ++i)
for (unsigned int j = i + 1; j < dofs_per_cell; ++j)
data.cell_matrix(i, j) = data.cell_matrix(j, i);
if (parameters.driver == "Neumann" )
for (unsigned int face = 0; face < GeometryInfo<dim>::faces_per_cell;
++face)
if (cell->face(face)->at_boundary() == true
&& cell->face(face)->boundary_id() == parameters.boundary_id_plus_Y)
{
scratch.fe_face_values_ref.reinit(cell, face);
for (unsigned int f_q_point = 0; f_q_point < n_q_points_f;
++f_q_point)
{
scratch.fe_face_values_ref.normal_vector(f_q_point);
static const double pressure_nom = parameters.pressure
/ (parameters.scale * parameters.scale);
const double time_ramp = (time.current() < parameters.load_time ?
time.current() / parameters.load_time : 1.0);
const double pressure = -pressure_nom * time_ramp;
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
const unsigned int i_group =
if (i_group == u_block)
{
const unsigned int component_i =
const double Ni =
scratch.fe_face_values_ref.shape_value(i,
f_q_point);
const double JxW = scratch.fe_face_values_ref.JxW(
f_q_point);
data.cell_rhs(i) += (Ni * traction[component_i])
* JxW;
}
}
}
}
}
template <int dim>
void Solid<dim>::make_constraints(const int &it_nr)
{
pcout << " CST " << std::flush;
if (it_nr > 1)
return ;
const bool apply_dirichlet_bc = (it_nr == 0);
{
const int boundary_id = parameters.boundary_id_minus_X;
if (apply_dirichlet_bc == true )
boundary_id,
constraints,
else
boundary_id,
constraints,
}
{
const int boundary_id = parameters.boundary_id_minus_Y;
if (apply_dirichlet_bc == true )
boundary_id,
constraints,
else
boundary_id,
constraints,
}
if (dim==3)
{
{
const int boundary_id = parameters.boundary_id_minus_Z;
if (apply_dirichlet_bc == true )
boundary_id,
constraints,
else
boundary_id,
constraints,
}
{
if (apply_dirichlet_bc == true )
boundary_id,
constraints,
else
boundary_id,
constraints,
}
}
if (parameters.driver == "Dirichlet" )
{
if (apply_dirichlet_bc == true )
{
if (time.current() < parameters.load_time+0.01*time.get_delta_t())
{
const double delta_length = parameters.length*(parameters.stretch - 1.0)*parameters.scale;
const unsigned int n_stretch_steps = parameters.load_time/time.get_delta_t();
const double delta_u_y = delta_length/2.0/n_stretch_steps;
boundary_id,
constraints,
}
else
boundary_id,
constraints,
}
else
boundary_id,
constraints,
}
}
template <int dim>
std::pair<unsigned int, double>
{
unsigned int lin_it = 0;
double lin_res = 0.0;
pcout << " SLV " << std::flush;
const auto K_uu = linear_operator<LA::MPI::Vector>(tangent_matrix.block(u_block, u_block));
const auto K_up = linear_operator<LA::MPI::Vector>(tangent_matrix.block(u_block, p_block));
const auto K_pu = linear_operator<LA::MPI::Vector>(tangent_matrix.block(p_block, u_block));
const auto K_Jp = linear_operator<LA::MPI::Vector>(tangent_matrix.block(J_block, p_block));
const auto K_JJ = linear_operator<LA::MPI::Vector>(tangent_matrix.block(J_block, J_block));
LA::PreconditionJacobi preconditioner_K_Jp_inv;
preconditioner_K_Jp_inv.initialize(
tangent_matrix.block(J_block, p_block),
LA::PreconditionJacobi::AdditionalData());
tangent_matrix.block(J_block, p_block).m() * parameters.max_iterations_lin,
solver_K_Jp_inv,
preconditioner_K_Jp_inv);
const auto K_pp_bar = K_Jp_inv * K_JJ * K_pJ_inv;
const auto K_uu_bar_bar = K_up * K_pp_bar * K_pu;
const auto K_uu_con = K_uu + K_uu_bar_bar;
LA::PreconditionAMG preconditioner_K_con_inv;
preconditioner_K_con_inv.initialize(
tangent_matrix.block(u_block, u_block),
LA::PreconditionAMG::AdditionalData(
true / *elliptic* /,
(parameters.poly_degree > 1 / *higher_order_elements* /)) );
tangent_matrix.block(u_block, u_block).m() * parameters.max_iterations_lin,
1.0e-30, parameters.tol_lin);
solver_K_con_inv.
select (parameters.type_lin);
solver_K_con_inv.set_control(solver_control_K_con_inv);
solver_K_con_inv,
preconditioner_K_con_inv);
d_u = K_uu_con_inv*(f_u - K_up*(K_Jp_inv*f_J - K_pp_bar*f_p));
lin_it = solver_control_K_con_inv.last_step();
lin_res = solver_control_K_con_inv.last_value();
d_J = K_pJ_inv*(f_p - K_pu*d_u);
d_p = K_Jp_inv*(f_J - K_JJ*d_J);
return std::make_pair(lin_it, lin_res);
}
template <int dim>
void
Solid<dim>::update_end_timestep ()
{
for (; cell != endc; ++cell)
{
const std::vector<std::shared_ptr<PointHistory<dim> > > lqph =
quadrature_point_history.
get_data (cell);
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
lqph[q_point]->update_end_timestep();
}
}
template <int dim, class DH=DoFHandler<dim> >
class FilteredDataOut :
public DataOut <dim, DH>
{
public :
FilteredDataOut (const unsigned int subdomain_id)
:
{}
virtual ~FilteredDataOut() {}
{
typename DataOut<dim, DH>::active_cell_iterator
while ((cell != this->dofs->end()) &&
++cell;
return cell;
}
{
if (old_cell != this->dofs->end())
{
return
<typename DataOut<dim, DH>::active_cell_iterator>
(predicate,old_cell));
}
else
return old_cell;
}
private :
};
template <int dim>
void Solid<dim>::output_results(const unsigned int timestep,
const double current_time) const
Output -> Ghosted vector
locally_relevant_partitioning,
mpi_communicator,
/ *vector_writable = * / false );
locally_relevant_partitioning,
mpi_communicator,
/ *vector_writable = * / false );
solution_total = solution_n;
residual = system_rhs;
residual *= -1.0;
— Additional data —
polynomial_order.
reinit (triangulation.n_active_cells());
std::vector<types::subdomain_id> partition_int (triangulation.n_active_cells());
FilteredDataOut<dim> data_out(this_mpi_process);
std::vector<DataComponentInterpretation::DataComponentInterpretation>
data_component_interpretation(dim,
Can't use filtered iterators here because the cell count "c" is incorrect for the parallel case
unsigned int c = 0;
endc = dof_handler.
end ();
for (; cell!=endc; ++cell, ++c)
{
material_id (c) =
static_cast< int > (cell->material_id());
}
std::vector<std::string> solution_name(
n_components ,
"solution_" );
std::vector<std::string> residual_name(
n_components ,
"residual_" );
{
if (block_component[c] == u_block)
{
solution_name[c] += "u" ;
residual_name[c] += "u" ;
}
else if (block_component[c] == p_block)
{
solution_name[c] += "p" ;
residual_name[c] += "p" ;
}
else if (block_component[c] == J_block)
{
solution_name[c] += "J" ;
residual_name[c] += "J" ;
}
else
{
}
}
solution_name,
data_component_interpretation);
residual_name,
data_component_interpretation);
partition_int.end());
struct Filename
{
static std::string get_filename_vtu (unsigned int process,
unsigned int timestep,
const unsigned int n_digits = 4)
{
std::ostringstream filename_vtu;
filename_vtu
<< "solution-"
<< (std::to_string(dim) + "d" )
<< "."
<< "."
<< ".vtu" ;
return filename_vtu.str();
}
static std::string get_filename_pvtu (unsigned int timestep,
const unsigned int n_digits = 4)
{
std::ostringstream filename_vtu;
filename_vtu
<< "solution-"
<< (std::to_string(dim) + "d" )
<< "."
<< ".pvtu" ;
return filename_vtu.str();
}
static std::string get_filename_pvd (void )
{
std::ostringstream filename_vtu;
filename_vtu
<< "solution-"
<< (std::to_string(dim) + "d" )
<< ".pvd" ;
return filename_vtu.str();
}
};
Write out main data file
const std::string filename_vtu = Filename::get_filename_vtu(this_mpi_process, timestep);
std::ofstream output(filename_vtu.c_str());
Collection of files written in parallel This next set of steps should only be performed by master process
if (this_mpi_process == 0)
{
List of all files written out at this timestep by all processors
std::vector<std::string> parallel_filenames_vtu;
{
parallel_filenames_vtu.push_back(Filename::get_filename_vtu(p, timestep));
}
const std::string filename_pvtu (Filename::get_filename_pvtu(timestep));
std::ofstream pvtu_master(filename_pvtu.c_str());
parallel_filenames_vtu);
Time dependent data master file
static std::vector<std::pair<double,std::string> > time_and_name_history;
time_and_name_history.push_back (std::make_pair (current_time,
filename_pvtu));
const std::string filename_pvd (Filename::get_filename_pvd());
std::ofstream pvd_output (filename_pvd.c_str());
}
}
template <int dim>
void Solid<dim>::compute_vertex_positions(std::vector<double> &real_time,
std::vector<std::vector<
Point<dim> > > &tracked_vertices,
{
real_time.push_back(time.current());
std::vector<bool> vertex_found (tracked_vertices.size(), false );
std::vector<Tensor<1,dim> > vertex_update (tracked_vertices.size());
for (; cell != endc; ++cell)
{
for (unsigned int v=0; v<GeometryInfo<dim>::vertices_per_cell; ++v)
{
for (unsigned int p=0; p<tracked_vertices.size(); ++p)
{
if (vertex_found[p] == true ) continue ;
if (cell->vertex(v).distance(pt_ref) < 1
e -6*parameters.scale)
{
for (
unsigned int d=0;
d <dim; ++
d )
vertex_update[p][d] = solution_total(cell->vertex_dof_index(v,u_block+d));
vertex_found[p] = true ;
}
}
}
}
for (unsigned int p=0; p<tracked_vertices.size(); ++p)
{
Assert (found_on_n_processes>0,
ExcMessage (
"Vertex not found on any processor" ));
for (
unsigned int d=0;
d <dim; ++
d )
update /= found_on_n_processes;
tracked_vertices[p].push_back(tracked_vertices[p][0] + update);
}
}
}
int main (int argc, char *argv[])
{
using namespace ViscoElasStripHole;
try
{
const unsigned int dim = 2;
Solid<dim> solid("parameters.prm" );
solid.run();
}
catch (std::exception &exc)
{
{
std::cerr << std::endl << std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl << exc.what()
<< std::endl << "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
}
catch (...)
{
{
std::cerr << std::endl << std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl << "Aborting!"
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
}
return 0;
}












 1.8.14
1.8.14