#include <deal.II/fe/fe_dgp_monomial.h>

Inheritance diagram for FE_DGPMonomial< dim >:

Public Member Functions
	FE_DGPMonomial (const unsigned int p)

virtual std::string	get_name () const override

virtual void	get_interpolation_matrix (const FiniteElement< dim > &source, FullMatrix< double > &matrix) const override

virtual void	get_face_interpolation_matrix (const FiniteElement< dim > &source, FullMatrix< double > &matrix) const override

virtual void	get_subface_interpolation_matrix (const FiniteElement< dim > &source, const unsigned int subface, FullMatrix< double > &matrix) const override

virtual bool	has_support_on_face (const unsigned int shape_index, const unsigned int face_index) const override

virtual std::size_t	memory_consumption () const override

virtual std::unique_ptr< FiniteElement< dim, dim > >	clone () const override

template<>
bool	has_support_on_face (const unsigned int, const unsigned int face_index) const

template<>
bool	has_support_on_face (const unsigned int shape_index, const unsigned int face_index) const

template<>
bool	has_support_on_face (const unsigned int shape_index, const unsigned int face_index) const

Functions to support hp
virtual std::vector< std::pair< unsigned int, unsigned int > >	hp_vertex_dof_identities (const FiniteElement< dim > &fe_other) const override

virtual std::vector< std::pair< unsigned int, unsigned int > >	hp_line_dof_identities (const FiniteElement< dim > &fe_other) const override

virtual std::vector< std::pair< unsigned int, unsigned int > >	hp_quad_dof_identities (const FiniteElement< dim > &fe_other) const override

virtual bool	hp_constraints_are_implemented () const override

virtual FiniteElementDomination::Domination	compare_for_domination (const FiniteElement< dim > &fe_other, const unsigned int codim=0) const override final

Public Member Functions inherited from FE_Poly< PolynomialsP< dim >, dim >
	FE_Poly (const PolynomialsP< dim > &poly_space, const FiniteElementData< dim > &fe_data, const std::vector< bool > &restriction_is_additive_flags, const std::vector< ComponentMask > &nonzero_components)

unsigned int	get_degree () const

std::vector< unsigned int >	get_poly_space_numbering () const

std::vector< unsigned int >	get_poly_space_numbering_inverse () const

virtual double	shape_value (const unsigned int i, const Point< dim > &p) const override

virtual double	shape_value_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const override

virtual Tensor< 1, dim >	shape_grad (const unsigned int i, const Point< dim > &p) const override

virtual Tensor< 1, dim >	shape_grad_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const override

virtual Tensor< 2, dim >	shape_grad_grad (const unsigned int i, const Point< dim > &p) const override

virtual Tensor< 2, dim >	shape_grad_grad_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const override

virtual Tensor< 3, dim >	shape_3rd_derivative (const unsigned int i, const Point< dim > &p) const override

virtual Tensor< 3, dim >	shape_3rd_derivative_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const override

virtual Tensor< 4, dim >	shape_4th_derivative (const unsigned int i, const Point< dim > &p) const override

virtual Tensor< 4, dim >	shape_4th_derivative_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const override

Public Member Functions inherited from FiniteElement< dim, dim >
	FiniteElement (const FiniteElementData< dim > &fe_data, const std::vector< bool > &restriction_is_additive_flags, const std::vector< ComponentMask > &nonzero_components)

	FiniteElement (FiniteElement< dim, spacedim > &&)=default

	FiniteElement (const FiniteElement< dim, spacedim > &)=default

virtual	~FiniteElement () override=default

std::pair< std::unique_ptr< FiniteElement< dim, spacedim > >, unsigned int >	operator^ (const unsigned int multiplicity) const

const FiniteElement< dim, spacedim > &	operator[] (const unsigned int fe_index) const

virtual bool	operator== (const FiniteElement< dim, spacedim > &fe) const

bool	operator!= (const FiniteElement< dim, spacedim > &) const

virtual const FullMatrix< double > &	get_restriction_matrix (const unsigned int child, const RefinementCase< dim > &refinement_case=RefinementCase< dim >::isotropic_refinement) const

virtual const FullMatrix< double > &	get_prolongation_matrix (const unsigned int child, const RefinementCase< dim > &refinement_case=RefinementCase< dim >::isotropic_refinement) const

bool	prolongation_is_implemented () const

bool	isotropic_prolongation_is_implemented () const

bool	restriction_is_implemented () const

bool	isotropic_restriction_is_implemented () const

bool	restriction_is_additive (const unsigned int index) const

const FullMatrix< double > &	constraints (const ::internal::SubfaceCase< dim > &subface_case=::internal::SubfaceCase< dim >::case_isotropic) const

bool	constraints_are_implemented (const ::internal::SubfaceCase< dim > &subface_case=::internal::SubfaceCase< dim >::case_isotropic) const

virtual void	get_interpolation_matrix (const FiniteElement< dim, spacedim > &source, FullMatrix< double > &matrix) const

virtual void	get_face_interpolation_matrix (const FiniteElement< dim, spacedim > &source, FullMatrix< double > &matrix) const

virtual void	get_subface_interpolation_matrix (const FiniteElement< dim, spacedim > &source, const unsigned int subface, FullMatrix< double > &matrix) const

virtual std::vector< std::pair< unsigned int, unsigned int > >	hp_vertex_dof_identities (const FiniteElement< dim, spacedim > &fe_other) const

virtual std::vector< std::pair< unsigned int, unsigned int > >	hp_line_dof_identities (const FiniteElement< dim, spacedim > &fe_other) const

virtual std::vector< std::pair< unsigned int, unsigned int > >	hp_quad_dof_identities (const FiniteElement< dim, spacedim > &fe_other) const

virtual FiniteElementDomination::Domination	compare_for_face_domination (const FiniteElement< dim, spacedim > &fe_other) const final

virtual FiniteElementDomination::Domination	compare_for_domination (const FiniteElement< dim, spacedim > &fe_other, const unsigned int codim=0) const

std::pair< unsigned int, unsigned int >	system_to_component_index (const unsigned int index) const

unsigned int	component_to_system_index (const unsigned int component, const unsigned int index) const

std::pair< unsigned int, unsigned int >	face_system_to_component_index (const unsigned int index) const

unsigned int	adjust_quad_dof_index_for_face_orientation (const unsigned int index, const bool face_orientation, const bool face_flip, const bool face_rotation) const

virtual unsigned int	face_to_cell_index (const unsigned int face_dof_index, const unsigned int face, const bool face_orientation=true, const bool face_flip=false, const bool face_rotation=false) const

unsigned int	adjust_line_dof_index_for_line_orientation (const unsigned int index, const bool line_orientation) const

const ComponentMask &	get_nonzero_components (const unsigned int i) const

unsigned int	n_nonzero_components (const unsigned int i) const

bool	is_primitive () const

bool	is_primitive (const unsigned int i) const

unsigned int	n_base_elements () const

virtual const FiniteElement< dim, spacedim > &	base_element (const unsigned int index) const

unsigned int	element_multiplicity (const unsigned int index) const

const FiniteElement< dim, spacedim > &	get_sub_fe (const ComponentMask &mask) const

virtual const FiniteElement< dim, spacedim > &	get_sub_fe (const unsigned int first_component, const unsigned int n_selected_components) const

std::pair< std::pair< unsigned int, unsigned int >, unsigned int >	system_to_base_index (const unsigned int index) const

std::pair< std::pair< unsigned int, unsigned int >, unsigned int >	face_system_to_base_index (const unsigned int index) const

types::global_dof_index	first_block_of_base (const unsigned int b) const

std::pair< unsigned int, unsigned int >	component_to_base_index (const unsigned int component) const

std::pair< unsigned int, unsigned int >	block_to_base_index (const unsigned int block) const

std::pair< unsigned int, types::global_dof_index >	system_to_block_index (const unsigned int component) const

unsigned int	component_to_block_index (const unsigned int component) const

ComponentMask	component_mask (const FEValuesExtractors::Scalar &scalar) const

ComponentMask	component_mask (const FEValuesExtractors::Vector &vector) const

ComponentMask	component_mask (const FEValuesExtractors::SymmetricTensor< 2 > &sym_tensor) const

ComponentMask	component_mask (const BlockMask &block_mask) const

BlockMask	block_mask (const FEValuesExtractors::Scalar &scalar) const

BlockMask	block_mask (const FEValuesExtractors::Vector &vector) const

BlockMask	block_mask (const FEValuesExtractors::SymmetricTensor< 2 > &sym_tensor) const

BlockMask	block_mask (const ComponentMask &component_mask) const

virtual std::pair< Table< 2, bool >, std::vector< unsigned int > >	get_constant_modes () const

const std::vector< Point< dim > > &	get_unit_support_points () const

bool	has_support_points () const

virtual Point< dim >	unit_support_point (const unsigned int index) const

const std::vector< Point< dim - 1 > > &	get_unit_face_support_points () const

bool	has_face_support_points () const

virtual Point< dim - 1 >	unit_face_support_point (const unsigned int index) const

const std::vector< Point< dim > > &	get_generalized_support_points () const

bool	has_generalized_support_points () const

const std::vector< Point< dim - 1 > > &	get_generalized_face_support_points () const

bool	has_generalized_face_support_points () const

GeometryPrimitive	get_associated_geometry_primitive (const unsigned int cell_dof_index) const

virtual void	convert_generalized_support_point_values_to_dof_values (const std::vector< Vector< double >> &support_point_values, std::vector< double > &nodal_values) const

Public Member Functions inherited from Subscriptor
	Subscriptor ()

	Subscriptor (const Subscriptor &)

	Subscriptor (Subscriptor &&) noexcept

virtual	~Subscriptor ()

Subscriptor &	operator= (const Subscriptor &)

Subscriptor &	operator= (Subscriptor &&) noexcept

void	subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

void	unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

unsigned int	n_subscriptions () const

template<typename StreamType >
void	list_subscribers (StreamType &stream) const

void	list_subscribers () const

template<class Archive >
void	serialize (Archive &ar, const unsigned int version)

Public Member Functions inherited from FiniteElementData< dim >
	FiniteElementData (const std::vector< unsigned int > &dofs_per_object, const unsigned int n_components, const unsigned int degree, const Conformity conformity=unknown, const BlockIndices &block_indices=BlockIndices())

unsigned int	n_dofs_per_vertex () const

unsigned int	n_dofs_per_line () const

unsigned int	n_dofs_per_quad () const

unsigned int	n_dofs_per_hex () const

unsigned int	n_dofs_per_face () const

unsigned int	n_dofs_per_cell () const

template<int structdim>
unsigned int	n_dofs_per_object () const

unsigned int	n_components () const

unsigned int	n_blocks () const

const BlockIndices &	block_indices () const

unsigned int	tensor_degree () const

bool	conforms (const Conformity) const

bool	operator== (const FiniteElementData &) const

Private Member Functions
void	initialize_restriction ()

Static Private Member Functions
static std::vector< unsigned int >	get_dpo_vector (const unsigned int degree)

Additional Inherited Members
Public Types inherited from FiniteElementData< dim >
enum	Conformity { unknown = 0x00, L2 = 0x01, Hcurl = 0x02, Hdiv = 0x04, H1 = Hcurl \| Hdiv, H2 = 0x0e }

Static Public Member Functions inherited from FiniteElement< dim, dim >
static ::ExceptionBase &	ExcShapeFunctionNotPrimitive (int arg1)

static ::ExceptionBase &	ExcFENotPrimitive ()

static ::ExceptionBase &	ExcUnitShapeValuesDoNotExist ()

static ::ExceptionBase &	ExcFEHasNoSupportPoints ()

static ::ExceptionBase &	ExcEmbeddingVoid ()

static ::ExceptionBase &	ExcProjectionVoid ()

static ::ExceptionBase &	ExcWrongInterfaceMatrixSize (int arg1, int arg2)

static ::ExceptionBase &	ExcInterpolationNotImplemented ()

Static Public Member Functions inherited from Subscriptor
static ::ExceptionBase &	ExcInUse (int arg1, std::string arg2, std::string arg3)

static ::ExceptionBase &	ExcNoSubscriber (std::string arg1, std::string arg2)

Public Attributes inherited from FiniteElementData< dim >
const unsigned int	dofs_per_vertex

const unsigned int	dofs_per_line

const unsigned int	dofs_per_quad

const unsigned int	dofs_per_hex

const unsigned int	first_line_index

const unsigned int	first_quad_index

const unsigned int	first_hex_index

const unsigned int	first_face_line_index

const unsigned int	first_face_quad_index

const unsigned int	dofs_per_face

const unsigned int	dofs_per_cell

const unsigned int	components

const unsigned int	degree

const Conformity	conforming_space

const BlockIndices	block_indices_data

Static Public Attributes inherited from FiniteElement< dim, dim >
static const unsigned int	space_dimension

Static Public Attributes inherited from FiniteElementData< dim >
static const unsigned int	dimension = dim

Protected Member Functions inherited from FE_Poly< PolynomialsP< dim >, dim >
void	correct_third_derivatives (internal::FEValuesImplementation::FiniteElementRelatedData< dim, dim > &output_data, const internal::FEValuesImplementation::MappingRelatedData< dim, dim > &mapping_data, const unsigned int n_q_points, const unsigned int dof) const

Protected Member Functions inherited from FiniteElement< dim, dim >
void	reinit_restriction_and_prolongation_matrices (const bool isotropic_restriction_only=false, const bool isotropic_prolongation_only=false)

TableIndices< 2 >	interface_constraints_size () const

virtual std::unique_ptr< InternalDataBase >	get_data (const UpdateFlags update_flags, const Mapping< dim, spacedim > &mapping, const Quadrature< dim > &quadrature, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const=0

virtual std::unique_ptr< InternalDataBase >	get_face_data (const UpdateFlags update_flags, const Mapping< dim, spacedim > &mapping, const Quadrature< dim - 1 > &quadrature, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const

virtual std::unique_ptr< InternalDataBase >	get_subface_data (const UpdateFlags update_flags, const Mapping< dim, spacedim > &mapping, const Quadrature< dim - 1 > &quadrature, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const

virtual void	fill_fe_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const CellSimilarity::Similarity cell_similarity, const Quadrature< dim > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const=0

virtual void	fill_fe_face_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const Quadrature< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const=0

virtual void	fill_fe_subface_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const unsigned int sub_no, const Quadrature< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const=0

Static Protected Member Functions inherited from FiniteElement< dim, dim >
static std::vector< unsigned int >	compute_n_nonzero_components (const std::vector< ComponentMask > &nonzero_components)

Protected Attributes inherited from FE_Poly< PolynomialsP< dim >, dim >
PolynomialsP< dim >	poly_space

Protected Attributes inherited from FiniteElement< dim, dim >
std::vector< std::vector< FullMatrix< double > > >	restriction

std::vector< std::vector< FullMatrix< double > > >	prolongation

FullMatrix< double >	interface_constraints

std::vector< Point< dim > >	unit_support_points

std::vector< Point< dim - 1 > >	unit_face_support_points

std::vector< Point< dim > >	generalized_support_points

std::vector< Point< dim - 1 > >	generalized_face_support_points

Table< 2, int >	adjust_quad_dof_index_for_face_orientation_table

std::vector< int >	adjust_line_dof_index_for_line_orientation_table

std::vector< std::pair< unsigned int, unsigned int > >	system_to_component_table

std::vector< std::pair< unsigned int, unsigned int > >	face_system_to_component_table

std::vector< std::pair< std::pair< unsigned int, unsigned int >, unsigned int > >	system_to_base_table

std::vector< std::pair< std::pair< unsigned int, unsigned int >, unsigned int > >	face_system_to_base_table

BlockIndices	base_to_block_indices

std::vector< std::pair< std::pair< unsigned int, unsigned int >, unsigned int > >	component_to_base_table

const std::vector< bool >	restriction_is_additive_flags

const std::vector< ComponentMask >	nonzero_components

const std::vector< unsigned int >	n_nonzero_components_table

const bool	cached_primitivity

Detailed Description

template<int dim>
class FE_DGPMonomial< dim >

Discontinuous finite elements based on monomials.

This finite element implements complete polynomial spaces, that is, dim- dimensional polynomials of degree p. For example, in 2d the element FE_DGP(1) would represent the span of the functions \(\{1,\hat x,\hat y\}\), which is in contrast to the element FE_DGQ(1) that is formed by the span of \(\{1,\hat x,\hat y,\hat x\hat y\}\). Since the DGP space has only three unknowns for each quadrilateral, it is immediately clear that this element can not be continuous.

The basis functions for this element are chosen to be the monomials listed above. Note that this is the main difference to the FE_DGP class that uses a set of polynomials of complete degree p that form a Legendre basis on the unit square. Thus, there, the mass matrix is diagonal, if the grid cells are parallelograms. The basis here does not have this property; however, it is simpler to compute. On the other hand, this element has the additional disadvantage that the local cell matrices usually have a worse condition number than the ones originating from the FE_DGP element.

This class is not implemented for the codimension one case (spacedim != dim).

Transformation properties

It is worth noting that under a (bi-, tri-)linear mapping, the space described by this element does not contain \(P(k)\), even if we use a basis of polynomials of degree \(k\). Consequently, for example, on meshes with non-affine cells, a linear function can not be exactly represented by elements of type FE_DGP(1) or FE_DGPMonomial(1).

This can be understood by the following 2-d example: consider the cell with vertices at \((0,0),(1,0),(0,1),(s,s)\):

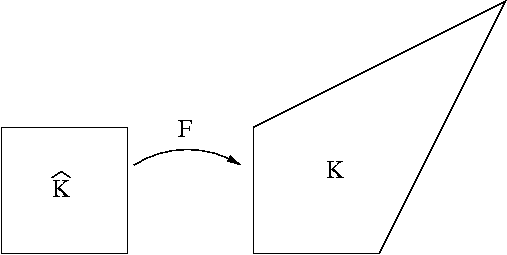
For this cell, a bilinear transformation \(F\) produces the relations \(x=\hat x+\hat x\hat y\) and \(y=\hat y+\hat x\hat y\) that correlate reference coordinates \(\hat x,\hat y\) and coordinates in real space \(x,y\). Under this mapping, the constant function is clearly mapped onto itself, but the two other shape functions of the \(P_1\) space, namely \(\phi_1(\hat x,\hat y)=\hat x\) and \(\phi_2(\hat x,\hat y)=\hat y\) are mapped onto \(\phi_1(x,y)=\frac{x-t}{t(s-1)},\phi_2(x,y)=t\) where \(t=\frac{y}{s-x+sx+y-sy}\).

For the simple case that \(s=1\), i.e. if the real cell is the unit square, the expressions can be simplified to \(t=y\) and \(\phi_1(x,y)=x,\phi_2(x,y)=y\). However, for all other cases, the functions \(\phi_1(x,y),\phi_2(x,y)\) are not linear any more, and neither is any linear combination of them. Consequently, the linear functions are not within the range of the mapped \(P_1\) polynomials.

Visualization of shape functions

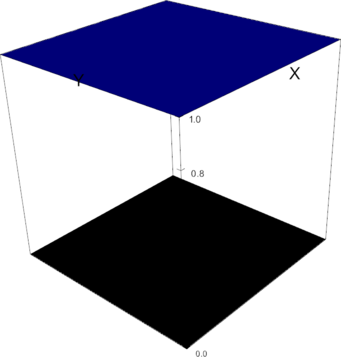
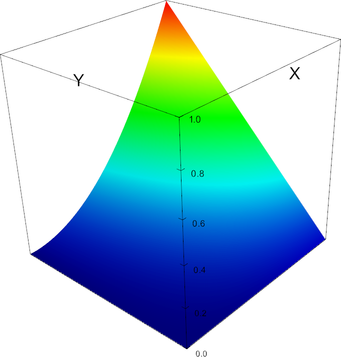
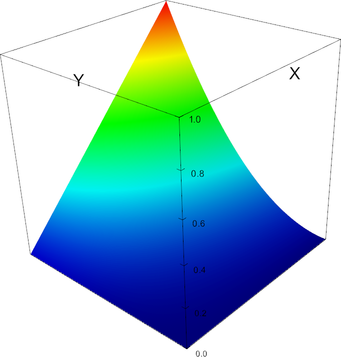
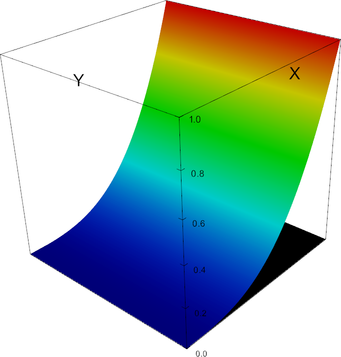
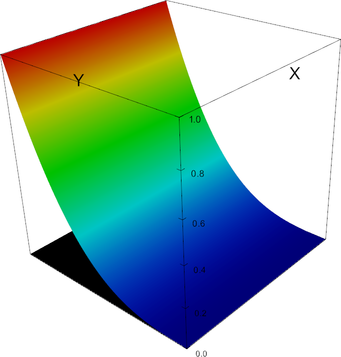
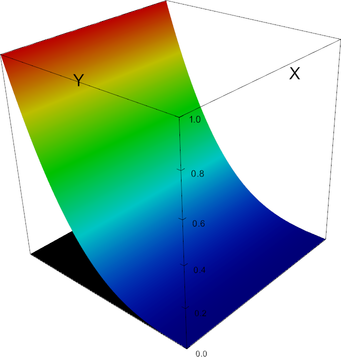
In 2d, the shape functions of this element look as follows.

\(P_0\) element

\(P_0\) element, shape function 0

\(P_1\) element


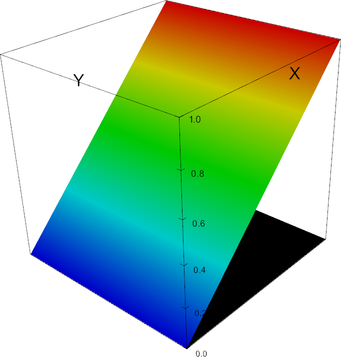
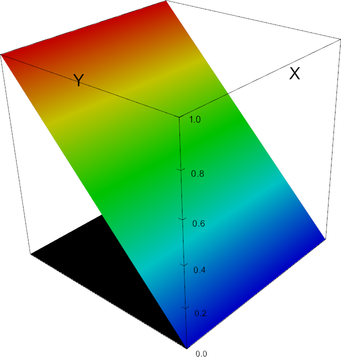
\(P_1\) element, shape function 0	\(P_1\) element, shape function 1

\(P_1\) element, shape function 2

\(P_2\) element


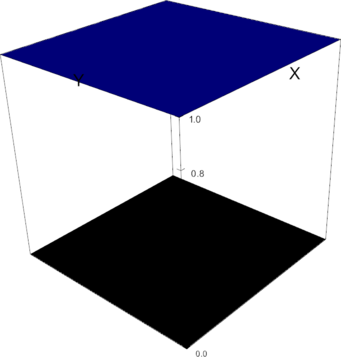
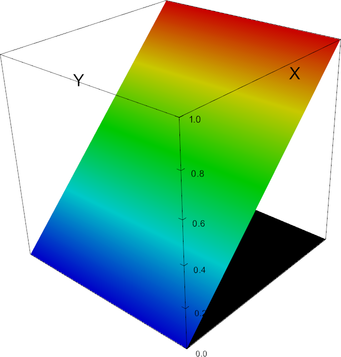
\(P_2\) element, shape function 0	\(P_2\) element, shape function 1

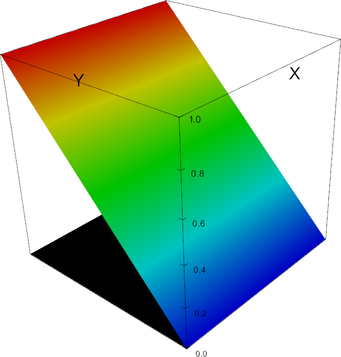
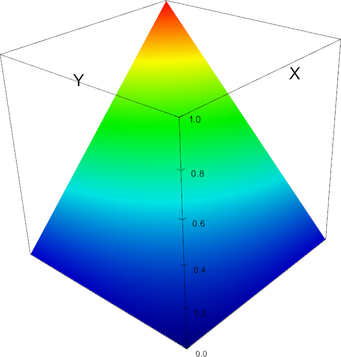
\(P_2\) element, shape function 2	\(P_2\) element, shape function 3

\(P_2\) element, shape function 4	\(P_2\) element, shape function 5

\(P_3\) element


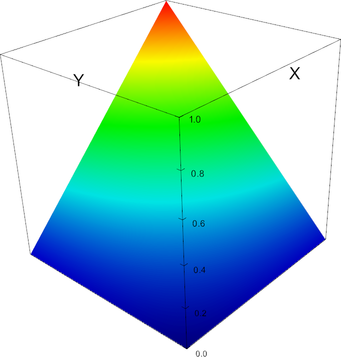
\(P_3\) element, shape function 0	\(P_3\) element, shape function 1

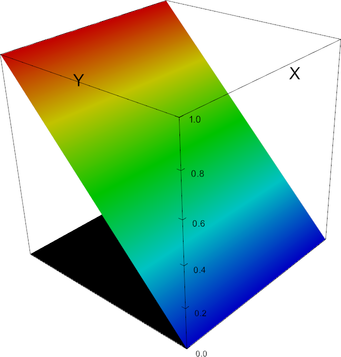
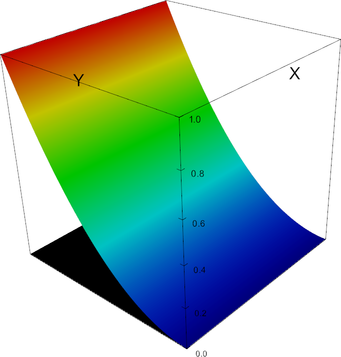
\(P_3\) element, shape function 2	\(P_3\) element, shape function 3

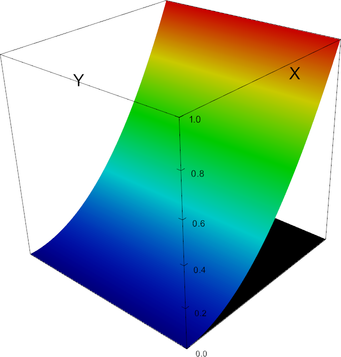
\(P_3\) element, shape function 4	\(P_3\) element, shape function 5

\(P_3\) element, shape function 6	\(P_3\) element, shape function 7

\(P_3\) element, shape function 8	\(P_3\) element, shape function 9

\(P_4\) element


\(P_4\) element, shape function 0	\(P_4\) element, shape function 1

\(P_4\) element, shape function 2	\(P_4\) element, shape function 3

\(P_4\) element, shape function 4	\(P_4\) element, shape function 5

\(P_4\) element, shape function 6	\(P_4\) element, shape function 7

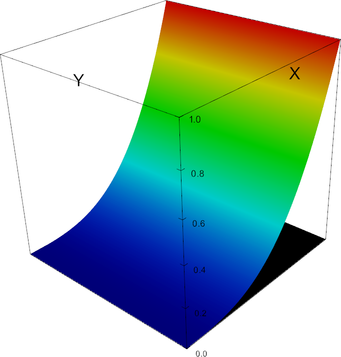
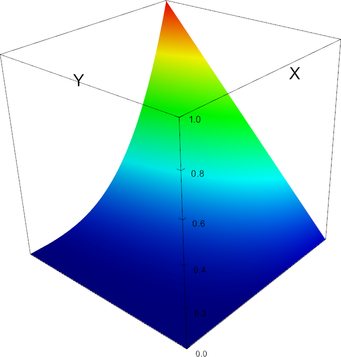
\(P_4\) element, shape function 8	\(P_4\) element, shape function 9

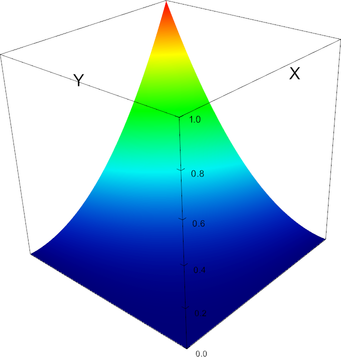
\(P_4\) element, shape function 10	\(P_4\) element, shape function 11

\(P_4\) element, shape function 12	\(P_4\) element, shape function 13

\(P_4\) element, shape function 14

Author: Ralf Hartmann, 2004

Definition at line 286 of file fe_dgp_monomial.h.

Constructor & Destructor Documentation

◆ FE_DGPMonomial()

template<int dim>

FE_DGPMonomial< dim >::FE_DGPMonomial ( const unsigned int p )

Constructor for the polynomial space of degree p.

Definition at line 132 of file fe_dgp_monomial.cc.

Member Function Documentation

◆ get_name()

template<int dim>

std::string FE_DGPMonomial< dim >::get_name ( ) const

overridevirtual

Return a string that uniquely identifies a finite element. This class returns FE_DGPMonomial<dim>(degree), with dim and p replaced by appropriate values.

Implements FiniteElement< dim, dim >.

Definition at line 166 of file fe_dgp_monomial.cc.

◆ hp_vertex_dof_identities()

template<int dim>

std::vector< std::pair< unsigned int, unsigned int > > FE_DGPMonomial< dim >::hp_vertex_dof_identities ( const FiniteElement< dim > & fe_other ) const

overridevirtual

If, on a vertex, several finite elements are active, the hp code first assigns the degrees of freedom of each of these FEs different global indices. It then calls this function to find out which of them should get identical values, and consequently can receive the same global DoF index. This function therefore returns a list of identities between DoFs of the present finite element object with the DoFs of fe_other, which is a reference to a finite element object representing one of the other finite elements active on this particular vertex. The function computes which of the degrees of freedom of the two finite element objects are equivalent, both numbered between zero and the corresponding value of dofs_per_vertex of the two finite elements. The first index of each pair denotes one of the vertex dofs of the present element, whereas the second is the corresponding index of the other finite element.

This being a discontinuous element, the set of such constraints is of course empty.

Definition at line 340 of file fe_dgp_monomial.cc.

◆ hp_line_dof_identities()

template<int dim>

std::vector< std::pair< unsigned int, unsigned int > > FE_DGPMonomial< dim >::hp_line_dof_identities ( const FiniteElement< dim > & fe_other ) const

overridevirtual

Same as hp_vertex_dof_indices(), except that the function treats degrees of freedom on lines.

This being a discontinuous element, the set of such constraints is of course empty.

Definition at line 358 of file fe_dgp_monomial.cc.

◆ hp_quad_dof_identities()

template<int dim>

std::vector< std::pair< unsigned int, unsigned int > > FE_DGPMonomial< dim >::hp_quad_dof_identities ( const FiniteElement< dim > & fe_other ) const

overridevirtual

Same as hp_vertex_dof_indices(), except that the function treats degrees of freedom on quads.

This being a discontinuous element, the set of such constraints is of course empty.

Definition at line 376 of file fe_dgp_monomial.cc.

◆ hp_constraints_are_implemented()

template<int dim>

bool FE_DGPMonomial< dim >::hp_constraints_are_implemented ( ) const

overridevirtual

Return whether this element implements its hanging node constraints in the new way, which has to be used to make elements "hp compatible".

For the FE_DGPMonomial class the result is always true (independent of the degree of the element), as it has no hanging nodes (being a discontinuous element).

Reimplemented from FiniteElement< dim, dim >.

Definition at line 331 of file fe_dgp_monomial.cc.

◆ compare_for_domination()

template<int dim>

FiniteElementDomination::Domination FE_DGPMonomial< dim >::compare_for_domination	(	const FiniteElement< dim > &	fe_other,
		const unsigned int	codim = `0`
	)		const

finaloverridevirtual

Return whether this element dominates another one given as argument fe_other, whether it is the other way around, whether neither dominates, or if either could dominate. The codim parameter describes the codimension of the investigated subspace and specifies that it is subject to this comparison. For example, if codim==0 then this function compares which element dominates at the cell level. If codim==1, then the elements are compared at faces, i.e., the comparison happens between the function spaces of the two finite elements as restricted to a face. Larger values of codim work correspondingly.

For a definition of domination, see FiniteElementDomination::Domination and in particular the hp paper.

Definition at line 394 of file fe_dgp_monomial.cc.

◆ get_interpolation_matrix()

template<int dim>

void FE_DGPMonomial< dim >::get_interpolation_matrix	(	const FiniteElement< dim > &	source,
		FullMatrix< double > &	matrix
	)		const

overridevirtual

Return the matrix interpolating from the given finite element to the present one. The size of the matrix is then dofs_per_cell times source.dofs_per_cell.

These matrices are only available if the source element is also a FE_Q element. Otherwise, an exception of type FiniteElement<dim>::ExcInterpolationNotImplemented is thrown.

Definition at line 195 of file fe_dgp_monomial.cc.

◆ get_face_interpolation_matrix()

template<int dim>

void FE_DGPMonomial< dim >::get_face_interpolation_matrix	(	const FiniteElement< dim > &	source,
		FullMatrix< double > &	matrix
	)		const

overridevirtual

Return the matrix interpolating from a face of one element to the face of the neighboring element. The size of the matrix is then dofs_per_face times source.dofs_per_face.

Derived elements will have to implement this function. They may only provide interpolation matrices for certain source finite elements, for example those from the same family. If they don't implement interpolation from a given element, then they must throw an exception of type FiniteElement<dim>::ExcInterpolationNotImplemented.

Definition at line 278 of file fe_dgp_monomial.cc.

◆ get_subface_interpolation_matrix()

template<int dim>

void FE_DGPMonomial< dim >::get_subface_interpolation_matrix	(	const FiniteElement< dim > &	source,
		const unsigned int	subface,
		FullMatrix< double > &	matrix
	)		const

overridevirtual

Return the matrix interpolating from a face of one element to the face of the neighboring element. The size of the matrix is then dofs_per_face times source.dofs_per_face.

Derived elements will have to implement this function. They may only provide interpolation matrices for certain source finite elements, for example those from the same family. If they don't implement interpolation from a given element, then they must throw an exception of type FiniteElement<dim>::ExcInterpolationNotImplemented.

Definition at line 304 of file fe_dgp_monomial.cc.

◆ has_support_on_face() [1/4]

template<int dim>

virtual bool FE_DGPMonomial< dim >::has_support_on_face	(	const unsigned int	shape_index,
		const unsigned int	face_index
	)		const

overridevirtual

This function returns true, if the shape function shape_index has non-zero function values somewhere on the face face_index.

Reimplemented from FiniteElement< dim, dim >.

◆ memory_consumption()

template<int dim>

std::size_t FE_DGPMonomial< dim >::memory_consumption ( ) const

overridevirtual

Determine an estimate for the memory consumption (in bytes) of this object.

This function is made virtual, since finite element objects are usually accessed through pointers to their base class, rather than the class itself.

Reimplemented from FiniteElement< dim, dim >.

Definition at line 494 of file fe_dgp_monomial.cc.

◆ clone()

template<int dim>

std::unique_ptr< FiniteElement< dim, dim > > FE_DGPMonomial< dim >::clone ( ) const

overridevirtual

A sort of virtual copy constructor, this function returns a copy of the finite element object. Derived classes need to override the function here in this base class and return an object of the same type as the derived class.

Some places in the library, for example the constructors of FESystem as well as the hp::FECollection class, need to make copies of finite elements without knowing their exact type. They do so through this function.

Implements FiniteElement< dim, dim >.

Definition at line 185 of file fe_dgp_monomial.cc.

◆ get_dpo_vector()

template<int dim>

std::vector< unsigned int > FE_DGPMonomial< dim >::get_dpo_vector ( const unsigned int degree )

staticprivate

Only for internal use. Its full name is get_dofs_per_object_vector function and it creates the dofs_per_object vector that is needed within the constructor to be passed to the constructor of FiniteElementData.

Definition at line 263 of file fe_dgp_monomial.cc.

◆ initialize_restriction()

template<int dim>

void FE_DGPMonomial< dim >::initialize_restriction ( )

private

Initialize the restriction matrices. Called from the constructor.

Definition at line 250 of file fe_dgp_monomial.cc.

◆ has_support_on_face() [2/4]

template<>

bool FE_DGPMonomial< 1 >::has_support_on_face	(	const unsigned int	shape_index,
		const unsigned int	face_index
	)		const

virtual

This function returns true, if the shape function shape_index has non-zero function values somewhere on the face face_index. The function is typically used to determine whether some matrix elements resulting from face integrals can be assumed to be zero and may therefore be omitted from integration.

A default implementation is provided in this base class which always returns true. This is the safe way to go.

Reimplemented from FiniteElement< dim, dim >.

Definition at line 439 of file fe_dgp_monomial.cc.

◆ has_support_on_face() [3/4]

template<>

bool FE_DGPMonomial< 2 >::has_support_on_face	(	const unsigned int	shape_index,
		const unsigned int	face_index
	)		const

virtual

This function returns true, if the shape function shape_index has non-zero function values somewhere on the face face_index. The function is typically used to determine whether some matrix elements resulting from face integrals can be assumed to be zero and may therefore be omitted from integration.

A default implementation is provided in this base class which always returns true. This is the safe way to go.

Reimplemented from FiniteElement< dim, dim >.

Definition at line 449 of file fe_dgp_monomial.cc.

◆ has_support_on_face() [4/4]

template<>

bool FE_DGPMonomial< 3 >::has_support_on_face	(	const unsigned int	shape_index,
		const unsigned int	face_index
	)		const

virtual

This function returns true, if the shape function shape_index has non-zero function values somewhere on the face face_index. The function is typically used to determine whether some matrix elements resulting from face integrals can be assumed to be zero and may therefore be omitted from integration.

A default implementation is provided in this base class which always returns true. This is the safe way to go.

Reimplemented from FiniteElement< dim, dim >.

Definition at line 471 of file fe_dgp_monomial.cc.

The documentation for this class was generated from the following files:

deal.II/fe/fe_dgp_monomial.h
source/fe/fe_dgp_monomial.cc

Public Member Functions

Private Member Functions

Static Private Member Functions

Additional Inherited Members

Detailed Description

template<int dim> class FE_DGPMonomial< dim >

Transformation properties

Visualization of shape functions

\(P_0\) element

\(P_1\) element

\(P_2\) element

\(P_3\) element

\(P_4\) element

Constructor & Destructor Documentation

◆ FE_DGPMonomial()

Member Function Documentation

◆ get_name()

◆ hp_vertex_dof_identities()

◆ hp_line_dof_identities()

◆ hp_quad_dof_identities()

◆ hp_constraints_are_implemented()

◆ compare_for_domination()

◆ get_interpolation_matrix()

◆ get_face_interpolation_matrix()

◆ get_subface_interpolation_matrix()

◆ has_support_on_face() [1/4]

◆ memory_consumption()

◆ clone()

◆ get_dpo_vector()

◆ initialize_restriction()

◆ has_support_on_face() [2/4]

◆ has_support_on_face() [3/4]

◆ has_support_on_face() [4/4]

template<int dim>
class FE_DGPMonomial< dim >