This tutorial depends on step-6.
This program was contributed by Yaqi Wang and Wolfgang Bangerth. Results from this program are used and discussed in the publication "Three-dimensional h-adaptivity for the multigroup neutron diffusion
equations" by Yaqi Wang, Wolfgang Bangerth and Jean Ragusa. The paper's full bibliographic details are as follows:
@Article{WBR09,
author = {Yaqi Wang and Wolfgang Bangerth and Jean Ragusa},
title = {Three-dimensional h-adaptivity for the multigroup
neutron diffusion equations},
journal = {Progr. Nucl. Energy},
year = 2009,
pages = {543--555}
}
The paper is available here.
Introduction
In this example, we intend to solve the multigroup diffusion approximation of the neutron transport equation. Essentially, the way to view this is as follows: In a nuclear reactor, neutrons are speeding around at different energies, get absorbed or scattered, or start a new fission event. If viewed at long enough length scales, the movement of neutrons can be considered a diffusion process.
A mathematical description of this would group neutrons into energy bins, and consider the balance equations for the neutron fluxes in each of these bins, or energy groups. The scattering, absorption, and fission events would then be operators within the diffusion equation describing the neutron fluxes. Assume we have energy groups g=1,\ldots,G, where by convention we assume that the neutrons with the highest energy are in group 1 and those with the lowest energy in group G. Then the neutron flux of each group satisfies the following equations:
\begin{eqnarray*}
\frac 1{v_g}\frac{\partial \phi_g(x,t)}{\partial t}
&=&
\nabla \cdot(D_g(x) \nabla \phi_g(x,t))
-
\Sigma_{r,g}(x)\phi_g(x,t)
\\
&& \qquad
+
\chi_g\sum_{g'=1}^G\nu\Sigma_{f,g'}(x)\phi_{g'}(x,t)
+
\sum_{g'\ne g}\Sigma_{s,g'\to g}(x)\phi_{g'}(x,t)
+
s_{\mathrm{ext},g}(x,t)
\end{eqnarray*}
augmented by appropriate boundary conditions. Here, v_g is the velocity of neutrons within group g. In other words, the change in time in flux of neutrons in group g is governed by the following processes:
-
Diffusion \nabla \cdot(D_g(x) \nabla \phi_g(x,t)). Here, D_g is the (spatially variable) diffusion coefficient.
-
Absorption \Sigma_{r,g}(x)\phi_g(x,t) (note the negative sign). The coefficient \Sigma_{r,g} is called the removal cross section.
-
Nuclear fission \chi_g\sum_{g'=1}^G\nu\Sigma_{f,g'}(x)\phi_{g'}(x,t). The production of neutrons of energy g is proportional to the flux of neutrons of energy g' times the probability \Sigma_{f,g'} that neutrons of energy g' cause a fission event times the number \nu of neutrons produced in each fission event times the probability that a neutron produced in this event has energy g. \nu\Sigma_{f,g'} is called the fission cross section and \chi_g the fission spectrum. We will denote the term \chi_g\nu\Sigma_{f,g'} as the fission distribution cross section in the program.
-
Scattering \sum_{g'\ne g}\Sigma_{s,g'\to g}(x)\phi_{g'}(x,t) of neutrons of energy g' producing neutrons of energy g. \Sigma_{s,g'\to g} is called the scattering cross section. The case of elastic, in-group scattering g'=g exists, too, but we subsume this into the removal cross section. The case g'<g is called down-scattering, since a neutron loses energy in such an event. On the other hand, g'>g corresponds to up-scattering: a neutron gains energy in a scattering event from the thermal motion of the atoms surrounding it; up-scattering is therefore only an important process for neutrons with kinetic energies that are already on the same order as the thermal kinetic energy (i.e. in the sub eV range).
-
An extraneous source s_{\mathrm{ext},g}.
For realistic simulations in reactor analysis, one may want to split the continuous spectrum of neutron energies into many energy groups, often up to 100. However, if neutron energy spectra are known well enough for some type of reactor (for example Pressurized Water Reactors, PWR), it is possible to obtain satisfactory results with only 2 energy groups.
In the program shown in this tutorial program, we provide the structure to compute with as many energy groups as desired. However, to keep computing times moderate and in order to avoid tabulating hundreds of coefficients, we only provide the coefficients for above equations for a two-group simulation, i.e. g=1,2. We do, however, consider a realistic situation by assuming that the coefficients are not constant, but rather depend on the materials that are assembled into reactor fuel assemblies in rather complicated ways (see below).
The eigenvalue problem
If we consider all energy groups at once, we may write above equations in the following operator form:
\begin{eqnarray*}
\frac 1v \frac{\partial \phi}{\partial t}
=
-L\phi
+
F\phi
+
X\phi
+
s_{\mathrm{ext}},
\end{eqnarray*}
where L,F,X are sinking, fission, and scattering operators, respectively. L here includes both the diffusion and removal terms. Note that L is symmetric, whereas F and X are not.
It is well known that this equation admits a stable solution if all eigenvalues of the operator -L+F+X are negative. This can be readily seen by multiplying the equation by \phi and integrating over the domain, leading to
\begin{eqnarray*}
\frac 1{2v} \frac{\partial}{\partial t} \|\phi\|^2 = ((-L+F+X)\phi,\phi).
\end{eqnarray*}
Stability means that the solution does not grow, i.e. we want the left hand side to be less than zero, which is the case if the eigenvalues of the operator on the right are all negative. For obvious reasons, it is not very desirable if a nuclear reactor produces neutron fluxes that grow exponentially, so eigenvalue analyses are the bread-and-butter of nuclear engineers. The main point of the program is therefore to consider the eigenvalue problem
\begin{eqnarray*}
(L-F-X) \phi = \lambda \phi,
\end{eqnarray*}
where we want to make sure that all eigenvalues are positive. Note that L, being the diffusion operator plus the absorption (removal), is positive definite; the condition that all eigenvalues are positive therefore means that we want to make sure that fission and inter-group scattering are weak enough to not shift the spectrum into the negative.
In nuclear engineering, one typically looks at a slightly different formulation of the eigenvalue problem. To this end, we do not just multiply with \phi and integrate, but rather multiply with \phi(L-X)^{-1}. We then get the following evolution equation:
\begin{eqnarray*}
\frac 1{2v} \frac{\partial}{\partial t} \|\phi\|^2_{(L-X)^{-1}} = ((L-X)^{-1}(-L+F+X)\phi,\phi).
\end{eqnarray*}
Stability is then guaranteed if the eigenvalues of the following problem are all negative:
\begin{eqnarray*}
(L-X)^{-1}(-L+F+X)\phi = \lambda_F \phi,
\end{eqnarray*}
which is equivalent to the eigenvalue problem
\begin{eqnarray*}
(L-X)\phi = \frac 1{\lambda_F+1} F \phi.
\end{eqnarray*}
The typical formulation in nuclear engineering is to write this as
\begin{eqnarray*}
(L-X) \phi = \frac 1{k_{\mathrm{eff}}} F \phi,
\end{eqnarray*}
where k_{\mathrm{eff}}=\frac 1{\lambda^F+1}. Intuitively, k_{\mathrm{eff}} is something like the multiplication factor for neutrons per typical time scale and should be less than or equal to one for stable operation of a reactor: if it is less than one, the chain reaction will die down, whereas nuclear bombs for example have a k-eigenvalue larger than one. A stable reactor should have k_{\mathrm{eff}}=1.
For those who wonder how this can be achieved in practice without inadvertently getting slightly larger than one and triggering a nuclear bomb: first, fission processes happen on different time scales. While most neutrons are released very quickly after a fission event, a small number of neutrons are only released by daughter nuclei after several further decays, up to 10-60 seconds after the fission was initiated. If one is therefore slightly beyond k_{\mathrm{eff}}=1, one therefore has many seconds to react until all the neutrons created in fission re-enter the fission cycle. Nevertheless, control rods in nuclear reactors absorbing neutrons – and therefore reducing k_{\mathrm{eff}} – are designed in such a way that they are all the way in the reactor in at most 2 seconds.
One therefore has on the order of 10-60 seconds to regulate the nuclear reaction if k_{\mathrm{eff}} should be larger than one for some time, as indicated by a growing neutron flux. Regulation can be achieved by continuously monitoring the neutron flux, and if necessary increase or reduce neutron flux by moving neutron-absorbing control rods a few millimeters into or out of the reactor. On a longer scale, the water cooling the reactor contains boron, a good neutron absorber. Every few hours, boron concentrations are adjusted by adding boron or diluting the coolant.
Finally, some of the absorption and scattering reactions have some stability built in; for example, higher neutron fluxes result in locally higher temperatures, which lowers the density of water and therefore reduces the number of scatterers that are necessary to moderate neutrons from high to low energies before they can start fission events themselves.
In this tutorial program, we solve above k-eigenvalue problem for two energy groups, and we are looking for the largest multiplication factor k_{\mathrm{eff}}, which is proportional to the inverse of the minimum eigenvalue plus one. To solve the eigenvalue problem, we generally use a modified version of the inverse power method. The algorithm looks like this:
-
Initialize \phi_g and k_{\mathrm{eff}} with \phi_g^{(0)} and k_{\mathrm{eff}}^{(0)} and let n=1.
-
Define the so-called fission source by
\begin{eqnarray*}
s_f^{(n-1)}(x)
=
\frac{1}{k_{\mathrm{eff}}^{(n-1)}}
\sum_{g'=1}^G\nu\Sigma_{f,g'}(x)\phi_{g'}^{(n-1)}(x).
\end{eqnarray*}
-
Solve for all group fluxes \phi_g,g=1,\ldots,G using
\begin{eqnarray*}
-\nabla \cdot D_g\nabla \phi_g^{(n)}
+
\Sigma_{r,g}\phi_g^{(n)}
=
\chi_g s_f^{(n-1)}
+
\sum_{g'< g} \Sigma_{s,g'\to g} \phi_{g'}^{(n)}
+
\sum_{g'> g}\Sigma_{s,g'\to g}\phi_{g'}^{(n-1)}.
\end{eqnarray*}
-
Update
\begin{eqnarray*}
k_{\mathrm{eff}}^{(n)}
=
\sum_{g'=1}^G
\int_{\Omega}\nu\Sigma_{f,g'}(x)
\phi_{g'}^{(n)}(x)dx.
\end{eqnarray*}
-
Compare k_{\mathrm{eff}}^{(n)} with k_{\mathrm{eff}}^{(n-1)}. If the change greater than a prescribed tolerance then set n=n+1 repeat the iteration starting at step 2, otherwise end the iteration.
Note that in this scheme, we do not solve group fluxes exactly in each power iteration, but rather consider previously compute \phi_{g'}^{(n)} only for down-scattering events g'<g. Up-scattering is only treated by using old iterators \phi_{g'}^{(n-1)}, in essence assuming that the scattering operator is triangular. This is physically motivated since up-scattering does not play a too important role in neutron scattering. In addition, practices shows that the inverse power iteration is stable even using this simplification.
Note also that one can use lots of extrapolation techniques to accelerate the power iteration laid out above. However, none of these are implemented in this example.
Meshes and mesh refinement
One may wonder whether it is appropriate to solve for the solutions of the individual energy group equations on the same meshes. The question boils down to this: will \phi_g and \phi_{g'} have similar smoothness properties? If this is the case, then it is appropriate to use the same mesh for the two; a typical application could be chemical combustion, where typically the concentrations of all or most chemical species change rapidly within the flame front. As it turns out, and as will be apparent by looking at the graphs shown in the results section of this tutorial program, this isn't the case here, however: since the diffusion coefficient is different for different energy groups, fast neutrons (in bins with a small group number g) have a very smooth flux function, whereas slow neutrons (in bins with a large group number) are much more affected by the local material properties and have a correspondingly rough solution if the coefficient are rough as in the case we compute here. Consequently, we will want to use different meshes to compute each energy group.
This has two implications that we will have to consider: First, we need to find a way to refine the meshes individually. Second, assembling the source terms for the inverse power iteration, where we have to integrate solution \phi_{g'}^{(n)} defined on mesh g' against the shape functions defined on mesh g, becomes a much more complicated task.
Mesh refinement
We use the usual paradigm: solve on a given mesh, then evaluate an error indicator for each cell of each mesh we have. Because it is so convenient, we again use the a posteriori error estimator by Kelly, Gago, Zienkiewicz and Babuska which approximates the error per cell by integrating the jump of the gradient of the solution along the faces of each cell. Using this, we obtain indicators
\begin{eqnarray*}
\eta_{g,K}, \qquad g=1,2,\ldots,G,\qquad K\in{\cal T}_g,
\end{eqnarray*}
where {\cal T}_g is the triangulation used in the solution of \phi_g. The question is what to do with this. For one, it is clear that refining only those cells with the highest error indicators might lead to bad results. To understand this, it is important to realize that \eta_{g,K} scales with the second derivative of \phi_g. In other words, if we have two energy groups g=1,2 whose solutions are equally smooth but where one is larger by a factor of 10,000, for example, then only the cells of that mesh will be refined, whereas the mesh for the solution of small magnitude will remain coarse. This is probably not what one wants, since we can consider both components of the solution equally important.
In essence, we would therefore have to scale \eta_{g,K} by an importance factor z_g that says how important it is to resolve \phi_g to any given accuracy. Such important factors can be computed using duality techniques (see, for example, the step-14 tutorial program, and the reference to the book by Bangerth and Rannacher cited there). We won't go there, however, and simply assume that all energy groups are equally important, and will therefore normalize the error indicators \eta_{g,K} for group g by the maximum of the solution \phi_g. We then refine the cells whose errors satisfy
\begin{eqnarray*}
\frac{\eta_{g,K}}{\|\phi_g\|_\infty}
>
\alpha_1
\displaystyle{\max_{\begin{matrix}1\le g\le G \\ K\in {\cal T}_g\end{matrix}}
\frac{\eta_{g,K}}{\|\phi_g\|_\infty}}
\end{eqnarray*}
and coarsen the cells where
\begin{eqnarray*}
\frac{\eta_{g,K}}{\|\phi_g\|_\infty}
<
\alpha_2
\displaystyle{\max_{\begin{matrix}1\le g\le G \\ K\in {\cal T}_g\end{matrix}}
\frac{\eta_{g,K}}{\|\phi_g\|_\infty}}.
\end{eqnarray*}
We chose \alpha_1=0.3 and \alpha_2=0.01 in the code. Note that this will, of course, lead to different meshes for the different energy groups.
The strategy above essentially means the following: If for energy group g there are many cells K\in {\cal T}_g on which the error is large, for example because the solution is globally very rough, then many cells will be above the threshold. On the other hand, if there are a few cells with large and many with small errors, for example because the solution is overall rather smooth except at a few places, then only the few cells with large errors will be refined. Consequently, the strategy allows for meshes that track the global smoothness properties of the corresponding solutions rather well.
Assembling terms on different meshes
As pointed out above, the multigroup refinement strategy results in different meshes for the different solutions \phi_g. So what's the problem? In essence it goes like this: in step 3 of the eigenvalue iteration, we have form the weak form for the equation to compute \phi_g^{(n)} as usual by multiplication with test functions \varphi_g^i defined on the mesh for energy group g; in the process, we have to compute the right hand side vector that contains terms of the following form:
\begin{eqnarray*}
F_i = \int_\Omega f(x) \varphi_g^i(x) \phi_{g'}(x) \ dx,
\end{eqnarray*}
where f(x) is one of the coefficient functions \Sigma_{s,g'\to g} or \nu\chi_g\Sigma_{f,g'} used in the right hand side of eigenvalue equation. The difficulty now is that \phi_{g'} is defined on the mesh for energy group g', i.e. it can be expanded as \phi_{g'}(x)=\sum_j\phi_{g'}^j \varphi_{g'}^j(x), with basis functions \varphi_{g'}^j(x) defined on mesh g'. The contribution to the right hand side can therefore be written as
\begin{eqnarray*}
F_i = \sum_j \left\{\int_\Omega f(x) \varphi_g^i(x) \varphi_{g'}^j(x)
\ dx \right\} \phi_{g'}^j ,
\end{eqnarray*}
On the other hand, the test functions \varphi_g^i(x) are defined on mesh g. This means that we can't just split the integral \Omega into integrals over the cells of either mesh g or g', since the respectively other basis functions may not be defined on these cells.
The solution to this problem lies in the fact that both the meshes for g and g' are derived by adaptive refinement from a common coarse mesh. We can therefore always find a set of cells, which we denote by {\cal T}_g \cap
{\cal T}_{g'}, that satisfy the following conditions:
-
the union of the cells covers the entire domain, and
-
a cell K \in {\cal T}_g \cap {\cal T}_{g'} is active on at least one of the two meshes.
A way to construct this set is to take each cell of coarse mesh and do the following steps: (i) if the cell is active on either {\cal T}_g or {\cal T}_{g'}, then add this cell to the set; (ii) otherwise, i.e. if this cell has children on both meshes, then do step (i) for each of the children of this cell. In fact, deal.II has a function GridTools::get_finest_common_cells that computes exactly this set of cells that are active on at least one of two meshes.
With this, we can write above integral as follows:
\begin{eqnarray*}
F_i
=
\sum_{K \in {\cal T}_g \cap {\cal T}_{g'}}
\sum_j \left\{\int_K f(x) \varphi_g^i(x) \varphi_{g'}^j(x)
\ dx \right\} \phi_{g'}^j.
\end{eqnarray*}
In the code, we compute the right hand side in the function NeutronDiffusionProblem::assemble_rhs, where (among other things) we loop over the set of common most refined cells, calling the function NeutronDiffusionProblem::assemble_common_cell on each pair of these cells.
By construction, there are now three cases to be considered:
-
The cell K is active on both meshes, i.e. both the basis functions \varphi_g^i as well as \varphi_{g'}^j are defined on K.
-
The cell K is active on mesh g, but not g', i.e. the \varphi_g^i are defined on K, whereas the \varphi_{g'}^j are defined on children of K.
-
The cell K is active on mesh g', but not g, with opposite conclusions than in (ii).
To compute the right hand side above, we then need to have different code for these three cases, as follows:
-
If the cell K is active on both meshes, then we can directly evaluate the integral. In fact, we don't even have to bother with the basis functions \varphi_{g'}, since all we need is the values of \phi_{g'} at the quadrature points. We can do this using the FEValues::get_function_values function. This is done directly in the NeutronDiffusionProblem::assemble_common_cell function.
-
If the cell K is active on mesh g, but not g', then the basis functions \varphi_{g'}^j are only defined either on the children K_c,0\le c<2^{\texttt{dim}}, or on children of these children if cell K is refined more than once on mesh g'.
Let us assume for a second that K is only once more refined on mesh g' than on mesh g. Using the fact that we use embedded finite element spaces where each basis function on one mesh can be written as a linear combination of basis functions on the next refined mesh, we can expand the restriction of \phi_g^i to child cell K_c into the basis functions defined on that child cell (i.e. on cells on which the basis functions \varphi_{g'}^l are defined):
\begin{eqnarray*}
\phi_g^i|_{K_c} = B_c^{il} \varphi_{g'}^l|_{K_c}.
\end{eqnarray*}
Here, and in the following, summation over indices appearing twice is implied. The matrix B_c is the matrix that interpolated data from a cell to its c-th child.
Then we can write the contribution of cell K to the right hand side component F_i as
\begin{eqnarray*}
F_i|_K
&=&
\left\{ \int_K f(x) \varphi_g^i(x) \varphi_{g'}^j(x)
\ dx \right\} \phi_{g'}^j
\\
&=&
\left\{
\sum_{0\le c<2^{\texttt{dim}}}
B_c^{il} \int_{K_c} f(x) \varphi_{g'}^l(x) \varphi_{g'}^j(x)
\ dx \right\} \phi_{g'}^j.
\end{eqnarray*}
In matrix notation, this can be written as
\begin{eqnarray*}
F_i|_K
=
\sum_{0\le c<2^{\texttt{dim}}}
F_i|_{K_c},
\qquad
\qquad
F_i|_{K_c} = B_c^{il} M_{K_c}^{lj} \phi_{g'}^j
= (B_c M_{K_c})^{ij} \phi_{g'}^j,
\end{eqnarray*}
where M_{K_c}^{lj}=\int_{K_c} f(x) \varphi_{g'}^l(x) \varphi_{g'}^j(x) is the weighted mass matrix on child c of cell K.
The next question is what happens if a child K_c of K is not active. Then, we have to apply the process recursively, i.e. we have to interpolate the basis functions \varphi_g^i onto child K_c of K, then onto child K_{cc'} of that cell, onto child K_{cc'c''} of that one, etc, until we find an active cell. We then have to sum up all the contributions from all the children, grandchildren, etc, of cell K, with contributions of the form
\begin{eqnarray*}
F_i|_{K_{cc'}} = (B_cB_{c'} M_{K_{cc'}})^{ij} \phi_{g'}^j,
\end{eqnarray*}
or
\begin{eqnarray*}
F_i|_{K_{cc'c''}} = (B_c B_{c'} B_{c''}M_{K_{cc'c''}})^{ij}
\phi_{g'}^j,
\end{eqnarray*}
etc. We do this process recursively, i.e. if we sit on cell K and see that it has children on grid g', then we call a function assemble_case_2 with an identity matrix; the function will multiply it's argument from the left with the prolongation matrix; if the cell has further children, it will call itself with this new matrix, otherwise it will perform the integration.
-
The last case is where K is active on mesh g' but not mesh g. In that case, we have to express basis function \varphi_{g'}^j in terms of the basis functions defined on the children of cell K, rather than \varphi_g^i as before. This of course works in exactly the same way. If the children of K are active on mesh g, then leading to the expression
\begin{eqnarray*}
F_i|_K
&=&
\left\{ \int_K f(x) \varphi_g^i(x) \varphi_{g'}^j(x)
\ dx \right\} \phi_{g'}^j
\\
&=&
\left\{
\sum_{0\le c<2^{\texttt{dim}}}
\int_{K_c} f(x) \varphi_g^i(x) B_c^{jl} \varphi_{g}^l(x)
\ dx \right\} \phi_{g'}^j.
\end{eqnarray*}
In matrix notation, this expression now reads as
\begin{eqnarray*}
F_i|_K
=
\sum_{0\le c<2^{\texttt{dim}}}
F_i|_{K_c},
\qquad
\qquad
F_i|_{K_c} = M_{K_c}^{il} B_c^{jl} \phi_{g'}^j
=
(M_{K_c} B_c^T)^{ij} \phi_{g'}^j,
\end{eqnarray*}
and correspondingly for cases where cell K is refined more than once on mesh g:
\begin{eqnarray*}
F_i|_{K_{cc'}} = (M_{K_{cc'}} B_{c'}^T B_c^T)^{ij} \phi_{g'}^j,
\end{eqnarray*}
or
\begin{eqnarray*}
F_i|_{K_{cc'c''}} = (M_{K_{cc'c''}} B_{c''}^T B_{c'}^T B_c^T)^{ij}
\phi_{g'}^j,
\end{eqnarray*}
etc. In other words, the process works in exactly the same way as before, except that we have to take the transpose of the prolongation matrices and need to multiply it to the mass matrix from the other side.
The expressions for cases (ii) and (iii) can be understood as repeatedly interpolating either the left or right basis functions in the scalar product (f \varphi_g^i, \varphi_{g'}^j)_K onto child cells, and then finally forming the inner product (the mass matrix) on the final cell. To make the symmetry in these cases more obvious, we can write them like this: for case (ii), we have
\begin{eqnarray*}
F_i|_{K_{cc'\cdots c^{(k)}}}
= [B_c B_{c'} \cdots B_{c^{(k)}} M_{K_{cc'\cdots c^{(k)}}}]^{ij}
\phi_{g'}^j,
\end{eqnarray*}
whereas for case (iii) we get
\begin{eqnarray*}
F_i|_{K_{cc'\cdots c^{(k)}}}
= [(B_c B_{c'} \cdots B_{c^{(k)}} M_{K_{cc'\cdots c^{(k)}}})^T]^{ij}
\phi_{g'}^j,
\end{eqnarray*}
Description of the test case
A nuclear reactor core is composed of different types of assemblies. An assembly is essentially the smallest unit that can be moved in and out of a reactor, and is usually rectangular or square. However, assemblies are not fixed units, as they are assembled from a complex lattice of different fuel rods, control rods, and instrumentation elements that are held in place relative to each other by spacers that are permanently attached to the rods. To make things more complicated, there are different kinds of assemblies that are used at the same time in a reactor, where assemblies differ in the type and arrangement of rods they are made up of.
Obviously, the arrangement of assemblies as well as the arrangement of rods inside them affect the distribution of neutron fluxes in the reactor (a fact that will be obvious by looking at the solution shown below in the results sections of this program). Fuel rods, for example, differ from each other in the enrichment of U-235 or Pu-239. Control rods, on the other hand, have zero fission, but nonzero scattering and absorption cross sections.
This whole arrangement would make the description or spatially dependent material parameters very complicated. It will not become much simpler, but we will make one approximation: we merge the volume inhabited by each cylindrical rod and the surrounding water into volumes of quadratic cross section into so-called ‘pin cells’ for which homogenized material data are obtained with nuclear database and knowledge of neutron spectrum. The homogenization makes all material data piecewise constant on the solution domain for a reactor with fresh fuel. Spatially dependent material parameters are then looked up for the quadratic assembly in which a point is located, and then for the quadratic pin cell within this assembly.
In this tutorial program, we simulate a quarter of a reactor consisting of 4
\times 4 assemblies. We use symmetry (Neumann) boundary conditions to reduce the problem to one quarter of the domain, and consequently only simulate a 2\times 2 set of assemblies. Two of them will be UO {}_2 fuel, the other two of them MOX fuel. Each of these assemblies consists of 17\times 17 rods of different compositions. In total, we therefore create a 34\times 34 lattice of rods. To make things simpler later on, we reflect this fact by creating a coarse mesh of 34\times 34 cells (even though the domain is a square, for which we would usually use a single cell). In deal.II, each cell has a material_id which one may use to associated each cell with a particular number identifying the material from which this cell's volume is made of; we will use this material ID to identify which of the 8 different kinds of rods that are used in this testcase make up a particular cell. Note that upon mesh refinement, the children of a cell inherit the material ID, making it simple to track the material even after mesh refinement.
The arrangement of the rods will be clearly visible in the images shown in the results section. The cross sections for materials and for both energy groups are taken from a OECD/NEA benchmark problem. The detailed configuration and material data is given in the code.
What the program does (and how it does that)
As a coarse overview of what exactly the program does, here is the basic layout: starting on a coarse mesh that is the same for each energy group, we compute inverse eigenvalue iterations to compute the k-eigenvalue on a given set of meshes. We stop these iterations when the change in the eigenvalue drops below a certain tolerance, and then write out the meshes and solutions for each energy group for inspection by a graphics program. Because the meshes for the solutions are different, we have to generate a separate output file for each energy group, rather than being able to add all energy group solutions into the same file.
After this, we evaluate the error indicators as explained in one of the sections above for each of the meshes, and refine and coarsen the cells of each mesh independently. Since the eigenvalue iterations are fairly expensive, we don't want to start all over on the new mesh; rather, we use the SolutionTransfer class to interpolate the solution on the previous mesh to the next one upon mesh refinement. A simple experiment will convince you that this is a lot cheaper than if we omitted this step. After doing so, we resume our eigenvalue iterations on the next set of meshes.
The program is controlled by a parameter file, using the ParameterHandler class. We will show a parameter file in the results section of this tutorial. For the moment suffice it to say that it controls the polynomial degree of the finite elements used, the number of energy groups (even though all that is presently implemented are the coefficients for a 2-group problem), the tolerance where to stop the inverse eigenvalue iteration, and the number of refinement cycles we will do.
The commented program
Include files
We start with a bunch of include files that have already been explained in previous tutorial programs. One new one is timer.h: This is the first example program that uses the Timer class. The Timer keeps track of both the elapsed wall clock time (that is, the amount of time that a clock mounted on the wall would measure) and CPU clock time (the amount of time that the current process uses on the CPUs). We will use a Timer below to measure how much CPU time each grid refinement cycle takes.
#include <deal.II/base/timer.h>
#include <deal.II/base/quadrature_lib.h>
#include <deal.II/base/function.h>
#include <deal.II/base/parameter_handler.h>
#include <deal.II/base/thread_management.h>
#include <deal.II/base/utilities.h>
#include <deal.II/lac/vector.h>
#include <deal.II/lac/full_matrix.h>
#include <deal.II/lac/sparsity_pattern.h>
#include <deal.II/lac/dynamic_sparsity_pattern.h>
#include <deal.II/lac/sparse_matrix.h>
#include <deal.II/lac/solver_cg.h>
#include <deal.II/lac/precondition.h>
#include <deal.II/lac/affine_constraints.h>
#include <deal.II/grid/tria.h>
#include <deal.II/grid/grid_refinement.h>
#include <deal.II/grid/grid_out.h>
#include <deal.II/grid/grid_generator.h>
#include <deal.II/dofs/dof_handler.h>
#include <deal.II/dofs/dof_tools.h>
#include <deal.II/fe/fe_q.h>
#include <deal.II/fe/fe_values.h>
#include <deal.II/numerics/vector_tools.h>
#include <deal.II/numerics/matrix_tools.h>
#include <deal.II/numerics/data_out.h>
#include <deal.II/numerics/error_estimator.h>
#include <fstream>
#include <iostream>
We use the next include file to access block vectors which provide us a convenient way to manage solution and right hand side vectors of all energy groups:
#include <deal.II/lac/block_vector.h>
This include file is for transferring solutions from one mesh to another different mesh. We use it when we are initializing solutions after each mesh iteration:
#include <deal.II/numerics/solution_transfer.h>
When integrating functions defined on one mesh against shape functions defined on a different mesh, we need a function get_finest_common_cells (as discussed in the introduction) which is defined in the following header file :
#include <deal.II/grid/grid_tools.h>
We use a little utility class from boost to save the state of an output stream (see the run function below):
#include <
boost/io/ios_state.hpp>
Here are two more C++ standard headers that we use to define list data types as well as to fine-tune the output we generate:
#include <list>
#include <iomanip>
The last step is as in all previous programs:
Material data
First up, we need to define a class that provides material data (including diffusion coefficients, removal cross sections, scattering cross sections, fission cross sections and fission spectra) to the main class.
The parameter to the constructor determines for how many energy groups we set up the relevant tables. At present, this program only includes data for 2 energy groups, but a more sophisticated program may be able to initialize the data structures for more groups as well, depending on how many energy groups are selected in the parameter file.
For each of the different coefficient types, there is one function that returns the value of this coefficient for a particular energy group (or combination of energy groups, as for the distribution cross section \chi_g\nu\Sigma_{f,g'} or scattering cross section \Sigma_{s,g'\to
g}). In addition to the energy group or groups, these coefficients depend on the type of fuel or control rod, as explained in the introduction. The functions therefore take an additional parameter, material_id, that identifies the particular kind of rod. Within this program, we use n_materials=8 different kinds of rods.
Except for the scattering cross section, each of the coefficients therefore can be represented as an entry in a two-dimensional array of floating point values indexed by the energy group number as well as the material ID. The Table class template is the ideal way to store such data. Finally, the scattering coefficient depends on both two energy group indices and therefore needs to be stored in a three-dimensional array, for which we again use the Table class, where this time the first template argument (denoting the dimensionality of the array) of course needs to be three:
class MaterialData
{
public:
MaterialData(const unsigned int n_groups);
double get_diffusion_coefficient(const unsigned int group,
const unsigned int material_id) const;
double get_removal_XS(const unsigned int group,
const unsigned int material_id) const;
double get_fission_XS(const unsigned int group,
const unsigned int material_id) const;
double get_fission_dist_XS(const unsigned int group_1,
const unsigned int group_2,
const unsigned int material_id) const;
double get_scattering_XS(const unsigned int group_1,
const unsigned int group_2,
const unsigned int material_id) const;
double get_fission_spectrum(const unsigned int group,
const unsigned int material_id) const;
private:
const unsigned int n_groups;
const unsigned int n_materials;
};
The constructor of the class is used to initialize all the material data arrays. It takes the number of energy groups as an argument (an throws an error if that value is not equal to two, since at presently only data for two energy groups is implemented; however, using this, the function remains flexible and extendable into the future). In the member initialization part at the beginning, it also resizes the arrays to their correct sizes.
At present, material data is stored for 8 different types of material. This, as well, may easily be extended in the future.
MaterialData::MaterialData(const unsigned int n_groups)
: n_groups(n_groups)
, n_materials(8)
, diffusion(n_materials, n_groups)
, sigma_r(n_materials, n_groups)
, nu_sigma_f(n_materials, n_groups)
, sigma_s(n_materials, n_groups, n_groups)
, chi(n_materials, n_groups)
{
switch (this->n_groups)
{
case 2:
{
for (unsigned
int m = 0; m < n_materials; ++m)
{
diffusion[m][0] = 1.2;
diffusion[m][1] = 0.4;
chi[m][0] = 1.0;
chi[m][1] = 0.0;
sigma_r[m][0] = 0.03;
for (unsigned int group_1 = 0; group_1 < n_groups; ++group_1)
for (unsigned int group_2 = 0; group_2 < n_groups; ++group_2)
sigma_s[m][group_1][group_2] = 0.0;
}
diffusion[5][1] = 0.2;
sigma_r[4][0] = 0.026;
sigma_r[5][0] = 0.051;
sigma_r[6][0] = 0.026;
sigma_r[7][0] = 0.050;
sigma_r[0][1] = 0.100;
sigma_r[1][1] = 0.200;
sigma_r[2][1] = 0.250;
sigma_r[3][1] = 0.300;
sigma_r[4][1] = 0.020;
sigma_r[5][1] = 0.040;
sigma_r[6][1] = 0.020;
sigma_r[7][1] = 0.800;
nu_sigma_f[0][0] = 0.0050;
nu_sigma_f[1][0] = 0.0075;
nu_sigma_f[2][0] = 0.0075;
nu_sigma_f[3][0] = 0.0075;
nu_sigma_f[4][0] = 0.000;
nu_sigma_f[5][0] = 0.000;
nu_sigma_f[6][0] = 1e-7;
nu_sigma_f[7][0] = 0.00;
nu_sigma_f[0][1] = 0.125;
nu_sigma_f[1][1] = 0.300;
nu_sigma_f[2][1] = 0.375;
nu_sigma_f[3][1] = 0.450;
nu_sigma_f[4][1] = 0.000;
nu_sigma_f[5][1] = 0.000;
nu_sigma_f[6][1] = 3e-6;
nu_sigma_f[7][1] = 0.00;
sigma_s[0][0][1] = 0.020;
sigma_s[1][0][1] = 0.015;
sigma_s[2][0][1] = 0.015;
sigma_s[3][0][1] = 0.015;
sigma_s[4][0][1] = 0.025;
sigma_s[5][0][1] = 0.050;
sigma_s[6][0][1] = 0.025;
sigma_s[7][0][1] = 0.010;
break;
}
default:
ExcMessage(
"Presently, only data for 2 groups is implemented"));
}
}
#define Assert(cond, exc)
Next are the functions that return the coefficient values for given materials and energy groups. All they do is to make sure that the given arguments are within the allowed ranges, and then look the respective value up in the corresponding tables:
double
MaterialData::get_diffusion_coefficient(const unsigned int group,
const unsigned int material_id) const
{
Assert(group < n_groups, ExcIndexRange(group, 0, n_groups));
Assert(material_id < n_materials,
ExcIndexRange(material_id, 0, n_materials));
return diffusion[material_id][group];
}
double MaterialData::get_removal_XS(const unsigned int group,
const unsigned int material_id) const
{
Assert(group < n_groups, ExcIndexRange(group, 0, n_groups));
Assert(material_id < n_materials,
ExcIndexRange(material_id, 0, n_materials));
return sigma_r[material_id][group];
}
double MaterialData::get_fission_XS(const unsigned int group,
const unsigned int material_id) const
{
Assert(group < n_groups, ExcIndexRange(group, 0, n_groups));
Assert(material_id < n_materials,
ExcIndexRange(material_id, 0, n_materials));
}
double MaterialData::get_scattering_XS(const unsigned int group_1,
const unsigned int group_2,
const unsigned int material_id) const
{
Assert(group_1 < n_groups, ExcIndexRange(group_1, 0, n_groups));
Assert(group_2 < n_groups, ExcIndexRange(group_2, 0, n_groups));
Assert(material_id < n_materials,
ExcIndexRange(material_id, 0, n_materials));
}
double
MaterialData::get_fission_spectrum(const unsigned int group,
const unsigned int material_id) const
{
Assert(group < n_groups, ExcIndexRange(group, 0, n_groups));
Assert(material_id < n_materials,
ExcIndexRange(material_id, 0, n_materials));
}
The function computing the fission distribution cross section is slightly different, since it computes its value as the product of two other coefficients. We don't need to check arguments here, since this already happens when we call the two other functions involved, even though it would probably not hurt either:
double MaterialData::get_fission_dist_XS(const unsigned int group_1,
const unsigned int group_2,
const unsigned int material_id) const
{
return (get_fission_spectrum(group_1, material_id) *
get_fission_XS(group_2, material_id));
}
The EnergyGroup class
The first interesting class is the one that contains everything that is specific to a single energy group. To group things that belong together into individual objects, we declare a structure that holds the Triangulation and DoFHandler objects for the mesh used for a single energy group, and a number of other objects and member functions that we will discuss in the following sections.
The main reason for this class is as follows: for both the forward problem (with a specified right hand side) as well as for the eigenvalue problem, one typically solves a sequence of problems for a single energy group each, rather than the fully coupled problem. This becomes understandable once one realizes that the system matrix for a single energy group is symmetric and positive definite (it is simply a diffusion operator), whereas the matrix for the fully coupled problem is generally nonsymmetric and not definite. It is also very large and quite full if more than a few energy groups are involved.
Let us first look at the equation to solve in the case of an external right hand side (for the time independent case):
\begin{eqnarray*} -\nabla
\cdot(D_g(x) \nabla \phi_g(x)) + \Sigma_{r,g}(x)\phi_g(x) =
\chi_g\sum_{g'=1}^G\nu\Sigma_{f,g'}(x)\phi_{g'}(x) + \sum_{g'\ne
g}\Sigma_{s,g'\to g}(x)\phi_{g'}(x) + s_{\mathrm{ext},g}(x) \end{eqnarray*}
We would typically solve this equation by moving all the terms on the right hand side with g'=g to the left hand side, and solving for \phi_g. Of course, we don't know \phi_{g'} yet, since the equations for those variables include right hand side terms involving \phi_g. What one typically does in such situations is to iterate: compute
\begin{eqnarray*} -\nabla \cdot(D_g(x) \nabla \phi^{(n)}_g(x)) &+&
\Sigma_{r,g}(x)\phi^{(n)}_g(x) \\ &=&
\chi_g\sum_{g'=1}^{g-1}\nu\Sigma_{f,g'}(x)\phi^{(n)}_{g'}(x) +
\chi_g\sum_{g'=g}^G\nu\Sigma_{f,g'}(x)\phi^{(n-1)}_{g'}(x) + \sum_{g'\ne
g, g'<g}\Sigma_{s,g'\to g}(x)\phi^{(n)}_{g'}(x) + \sum_{g'\ne g,
g'>g}\Sigma_{s,g'\to g}(x)\phi^{(n-1)}_{g'}(x) + s_{\mathrm{ext},g}(x)
\end{eqnarray*}
In other words, we solve the equation one by one, using values for \phi_{g'} from the previous iteration n-1 if g'\ge g and already computed values for \phi_{g'} from the present iteration if g'<g.
When computing the eigenvalue, we do a very similar iteration, except that we have no external right hand side and that the solution is scaled after each iteration as explained in the introduction.
In either case, these two cases can be treated jointly if all we do is to equip the following class with these abilities: (i) form the left hand side matrix, (ii) form the in-group right hand side contribution, i.e. involving the extraneous source, and (iii) form that contribution to the right hand side that stems from group g'. This class does exactly these tasks (as well as some book-keeping, such as mesh refinement, setting up matrices and vectors, etc). On the other hand, the class itself has no idea how many energy groups there are, and in particular how they interact, i.e. the decision of how the outer iteration looks (and consequently whether we solve an eigenvalue or a direct problem) is left to the NeutronDiffusionProblem class further down below in this program.
So let us go through the class and its interface:
template <int dim>
class EnergyGroup
{
public:
EnergyGroup public member functions
The class has a good number of public member functions, since its the way it operates is controlled from the outside, and therefore all functions that do something significant need to be called from another class. Let's start off with book-keeping: the class obviously needs to know which energy group it represents, which material data to use, and from what coarse grid to start. The constructor takes this information and initializes the relevant member variables with that (see below).
Then we also need functions that set up the linear system, i.e. correctly size the matrix and its sparsity pattern, etc, given a finite element object to use. The setup_linear_system function does that. Finally, for this initial block, there are two functions that return the number of active cells and degrees of freedom used in this object – using this, we can make the triangulation and DoF handler member variables private, and do not have to grant external use to it, enhancing encapsulation:
EnergyGroup(const unsigned int group,
const MaterialData &material_data,
void setup_linear_system();
unsigned int n_active_cells() const;
unsigned int n_dofs() const;
Then there are functions that assemble the linear system for each iteration and the present energy group. Note that the matrix is independent of the iteration number, so only has to be computed once for each refinement cycle. The situation is a bit more involved for the right hand side that has to be updated in each inverse power iteration, and that is further complicated by the fact that computing it may involve several different meshes as explained in the introduction. To make things more flexible with regard to solving the forward or the eigenvalue problem, we split the computation of the right hand side into a function that assembles the extraneous source and in-group contributions (which we will call with a zero function as source terms for the eigenvalue problem) and one that computes contributions to the right hand side from another energy group:
void assemble_system_matrix();
void assemble_ingroup_rhs(
const Function<dim> &extraneous_source);
void assemble_cross_group_rhs(const EnergyGroup<dim> &g_prime);
Next we need a set of functions that actually compute the solution of a linear system, and do something with it (such as computing the fission source contribution mentioned in the introduction, writing graphical information to an output file, computing error indicators, or actually refining the grid based on these criteria and thresholds for refinement and coarsening). All these functions will later be called from the driver class NeutronDiffusionProblem, or any other class you may want to implement to solve a problem involving the neutron flux equations:
void solve();
double get_fission_source() const;
void output_results(const unsigned int cycle) const;
const double refine_threshold,
const double coarsen_threshold);
EnergyGroup public data members
As is good practice in object oriented programming, we hide most data members by making them private. However, we have to grant the class that drives the process access to the solution vector as well as the solution of the previous iteration, since in the power iteration, the solution vector is scaled in every iteration by the present guess of the eigenvalue we are looking for:
EnergyGroup private data members
The rest of the data members are private. Compared to all the previous tutorial programs, the only new data members are an integer storing which energy group this object represents, and a reference to the material data object that this object's constructor gets passed from the driver class. Likewise, the constructor gets a reference to the finite element object we are to use.
Finally, we have to apply boundary values to the linear system in each iteration, i.e. quite frequently. Rather than interpolating them every time, we interpolate them once on each new mesh and then store them along with all the other data of this class:
private:
const unsigned int group;
const MaterialData &material_data;
std::map<types::global_dof_index, double> boundary_values;
const ::parallel::distributed::Triangulation< dim, spacedim > * triangulation
EnergyGroup private member functions
There is one private member function in this class. It recursively walks over cells of two meshes to compute the cross-group right hand side terms. The algorithm for this is explained in the introduction to this program. The arguments to this function are a reference to an object representing the energy group against which we want to integrate a right hand side term, an iterator to a cell of the mesh used for the present energy group, an iterator to a corresponding cell on the other mesh, and the matrix that interpolates the degrees of freedom from the coarser of the two cells to the finer one:
private:
void assemble_cross_group_rhs_recursive(
const EnergyGroup<dim> &g_prime,
};
typename ActiveSelector::cell_iterator cell_iterator
Implementation of the EnergyGroup class
The first few functions of this class are mostly self-explanatory. The constructor only sets a few data members and creates a copy of the given triangulation as the base for the triangulation used for this energy group. The next two functions simply return data from private data members, thereby enabling us to make these data members private.
template <int dim>
EnergyGroup<dim>::EnergyGroup(const unsigned int group,
const MaterialData &material_data,
: group(group)
, material_data(material_data)
, fe(fe)
{
dof_handler.distribute_dofs(fe);
}
template <int dim>
unsigned int EnergyGroup<dim>::n_active_cells() const
{
}
template <int dim>
unsigned int EnergyGroup<dim>::n_dofs() const
{
return dof_handler.n_dofs();
}
EnergyGroup::setup_linear_system
The first "real" function is the one that sets up the mesh, matrices, etc, on the new mesh or after mesh refinement. We use this function to initialize sparse system matrices, and the right hand side vector. If the solution vector has never been set before (as indicated by a zero size), we also initialize it and set it to a default value. We don't do that if it already has a non-zero size (i.e. this function is called after mesh refinement) since in that case we want to preserve the solution across mesh refinement (something we do in the EnergyGroup::refine_grid function).
template <int dim>
void EnergyGroup<dim>::setup_linear_system()
{
const unsigned int n_dofs = dof_handler.n_dofs();
hanging_node_constraints.clear();
hanging_node_constraints);
hanging_node_constraints.close();
system_matrix.clear();
hanging_node_constraints.condense(dsp);
sparsity_pattern.copy_from(dsp);
system_matrix.reinit(sparsity_pattern);
system_rhs.reinit(n_dofs);
if (solution.empty())
{
solution.reinit(n_dofs);
solution_old.reinit(n_dofs);
solution_old = 1.0;
solution = solution_old;
}
void make_hanging_node_constraints(const DoFHandler< dim, spacedim > &dof_handler, AffineConstraints< number > &constraints)
void make_sparsity_pattern(const DoFHandler< dim, spacedim > &dof_handler, SparsityPatternBase &sparsity_pattern, const AffineConstraints< number > &constraints={}, const bool keep_constrained_dofs=true, const types::subdomain_id subdomain_id=numbers::invalid_subdomain_id)
At the end of this function, we update the list of boundary nodes and their values, by first clearing this list and the re-interpolating boundary values (remember that this function is called after first setting up the mesh, and each time after mesh refinement).
To understand the code, it is necessary to realize that we create the mesh using the GridGenerator::subdivided_hyper_rectangle function (in NeutronDiffusionProblem::initialize_problem) where we set the last parameter to true. This means that boundaries of the domain are "colored", i.e. the four (or six, in 3d) sides of the domain are assigned different boundary indicators. As it turns out, the bottom boundary gets indicator zero, the top one boundary indicator one, and left and right boundaries get indicators two and three, respectively.
In this program, we simulate only one, namely the top right, quarter of a reactor. That is, we want to interpolate boundary conditions only on the top and right boundaries, while do nothing on the bottom and left boundaries (i.e. impose natural, no-flux Neumann boundary conditions). This is most easily generalized to arbitrary dimension by saying that we want to interpolate on those boundaries with indicators 1, 3, ..., which we do in the following loop (note that calls to VectorTools::interpolate_boundary_values are additive, i.e. they do not first clear the boundary value map):
boundary_values.clear();
for (unsigned int i = 0; i < dim; ++i)
2 * i + 1,
boundary_values);
}
EnergyGroup::assemble_system_matrix
Next we need functions assembling the system matrix and right hand sides. Assembling the matrix is straightforward given the equations outlined in the introduction as well as what we've seen in previous example programs. Note the use of cell->material_id() to get at the kind of material from which a cell is made up of. Note also how we set the order of the quadrature formula so that it is always appropriate for the finite element in use.
Finally, note that since we only assemble the system matrix here, we can't yet eliminate boundary values (we need the right hand side vector for this). We defer this to the EnergyGroup::solve function, at which point all the information is available.
template <int dim>
void EnergyGroup<dim>::assemble_system_matrix()
{
quadrature_formula,
const unsigned int dofs_per_cell = fe.n_dofs_per_cell();
const unsigned int n_q_points = quadrature_formula.size();
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
for (const auto &cell : dof_handler.active_cell_iterators())
{
cell_matrix = 0;
fe_values.reinit(cell);
const double diffusion_coefficient =
material_data.get_diffusion_coefficient(group, cell->material_id());
const double removal_XS =
material_data.get_removal_XS(group, cell->material_id());
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
for (unsigned int i = 0; i < dofs_per_cell; ++i)
for (unsigned int j = 0; j < dofs_per_cell; ++j)
cell_matrix(i, j) +=
((diffusion_coefficient * fe_values.shape_grad(i, q_point) *
fe_values.shape_grad(j, q_point) +
removal_XS * fe_values.shape_value(i, q_point) *
fe_values.shape_value(j, q_point)) *
fe_values.JxW(q_point));
cell->get_dof_indices(local_dof_indices);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
for (unsigned int j = 0; j < dofs_per_cell; ++j)
system_matrix.add(local_dof_indices[i],
local_dof_indices[j],
cell_matrix(i, j));
}
hanging_node_constraints.condense(system_matrix);
}
@ update_values
Shape function values.
@ update_JxW_values
Transformed quadrature weights.
@ update_gradients
Shape function gradients.
EnergyGroup::assemble_ingroup_rhs
As explained in the documentation of the EnergyGroup class, we split assembling the right hand side into two parts: the ingroup and the cross-group couplings. First, we need a function to assemble the right hand side of one specific group here, i.e. including an extraneous source (that we will set to zero for the eigenvalue problem) as well as the ingroup fission contributions. (In-group scattering has already been accounted for with the definition of removal cross section.) The function's workings are pretty standard as far as assembling right hand sides go, and therefore does not require more comments except that we mention that the right hand side vector is set to zero at the beginning of the function – something we are not going to do for the cross-group terms that simply add to the right hand side vector.
template <int dim>
void
EnergyGroup<dim>::assemble_ingroup_rhs(
const Function<dim> &extraneous_source)
{
system_rhs.reinit(dof_handler.n_dofs());
const unsigned int dofs_per_cell = fe.n_dofs_per_cell();
const unsigned int n_q_points = quadrature_formula.size();
quadrature_formula,
std::vector<double> extraneous_source_values(n_q_points);
std::vector<double> solution_old_values(n_q_points);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
for (const auto &cell : dof_handler.active_cell_iterators())
{
cell_rhs = 0;
fe_values.reinit(cell);
const double fission_dist_XS =
material_data.get_fission_dist_XS(group, group, cell->material_id());
extraneous_source.
value_list(fe_values.get_quadrature_points(),
extraneous_source_values);
fe_values.get_function_values(solution_old, solution_old_values);
cell->get_dof_indices(local_dof_indices);
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
for (unsigned int i = 0; i < dofs_per_cell; ++i)
cell_rhs(i) +=
((extraneous_source_values[q_point] +
fission_dist_XS * solution_old_values[q_point]) *
fe_values.shape_value(i, q_point) * fe_values.JxW(q_point));
for (unsigned int i = 0; i < dofs_per_cell; ++i)
system_rhs(local_dof_indices[i]) += cell_rhs(i);
}
}
virtual void value_list(const std::vector< Point< dim > > &points, std::vector< RangeNumberType > &values, const unsigned int component=0) const
@ update_quadrature_points
Transformed quadrature points.
EnergyGroup::assemble_cross_group_rhs
The more interesting function for assembling the right hand side vector for the equation of a single energy group is the one that couples energy group g and g'. As explained in the introduction, we first have to find the set of cells common to the meshes of the two energy groups. First we call get_finest_common_cells to obtain this list of pairs of common cells from both meshes. Both cells in a pair may not be active but at least one of them is. We then hand each of these cell pairs off to a function that computes the right hand side terms recursively.
Note that ingroup coupling is handled already before, so we exit the function early if g=g'.
template <int dim>
void
EnergyGroup<dim>::assemble_cross_group_rhs(const EnergyGroup<dim> &g_prime)
{
if (group == g_prime.group)
return;
const std::list<std::pair<typename DoFHandler<dim>::cell_iterator,
cell_list =
for (const auto &cell_pair : cell_list)
{
FullMatrix<double> unit_matrix(fe.n_dofs_per_cell());
for (unsigned int i = 0; i < unit_matrix.m(); ++i)
unit_matrix(i, i) = 1;
assemble_cross_group_rhs_recursive(g_prime,
cell_pair.first,
cell_pair.second,
unit_matrix);
}
}
EnergyGroup::assemble_cross_group_rhs_recursive
This is finally the function that handles assembling right hand side terms on potentially different meshes recursively, using the algorithm described in the introduction. The function takes a reference to the object representing energy group g', as well as iterators to corresponding cells in the meshes for energy groups g and g'. At first, i.e. when this function is called from the one above, these two cells will be matching cells on two meshes; however, one of the two may be further refined, and we will call the function recursively with one of the two iterators replaced by one of the children of the original cell.
The last argument is the matrix product matrix B_{c^{(k)}}^T \cdots
B_{c'}^T B_c^T from the introduction that interpolates from the coarser of the two cells to the finer one. If the two cells match, then this is the identity matrix – exactly what we pass to this function initially.
The function has to consider two cases: that both of the two cells are not further refined, i.e. have no children, in which case we can finally assemble the right hand side contributions of this pair of cells; and that one of the two cells is further refined, in which case we have to keep recursing by looping over the children of the one cell that is not active. These two cases will be discussed below:
template <int dim>
void EnergyGroup<dim>::assemble_cross_group_rhs_recursive(
const EnergyGroup<dim> &g_prime,
{
The first case is that both cells are no further refined. In that case, we can assemble the relevant terms (see the introduction). This involves assembling the mass matrix on the finer of the two cells (in fact there are two mass matrices with different coefficients, one for the fission distribution cross section \chi_g\nu\Sigma_{f,g'} and one for the scattering cross section \Sigma_{s,g'\to g}). This is straight forward, but note how we determine which of the two cells is the finer one by looking at the refinement level of the two cells:
if (!cell_g->has_children() && !cell_g_prime->has_children())
{
const unsigned int n_q_points = quadrature_formula.size();
quadrature_formula,
if (cell_g->level() > cell_g_prime->level())
fe_values.reinit(cell_g);
else
fe_values.reinit(cell_g_prime);
const double fission_dist_XS =
material_data.get_fission_dist_XS(group,
g_prime.group,
cell_g_prime->material_id());
const double scattering_XS =
material_data.get_scattering_XS(g_prime.group,
group,
cell_g_prime->material_id());
fe.n_dofs_per_cell());
fe.n_dofs_per_cell());
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
for (unsigned int i = 0; i < fe.n_dofs_per_cell(); ++i)
for (unsigned int j = 0; j < fe.n_dofs_per_cell(); ++j)
{
local_mass_matrix_f(i, j) +=
(fission_dist_XS * fe_values.shape_value(i, q_point) *
fe_values.shape_value(j, q_point) * fe_values.JxW(q_point));
local_mass_matrix_g(i, j) +=
(scattering_XS * fe_values.shape_value(i, q_point) *
fe_values.shape_value(j, q_point) * fe_values.JxW(q_point));
}
Now we have all the interpolation (prolongation) matrices as well as local mass matrices, so we only have to form the product
F_i|_{K_{cc'\cdots c^{(k)}}} = [B_c B_{c'} \cdots B_{c^{(k)}}
M_{K_{cc'\cdots c^{(k)}}}]^{ij} \phi_{g'}^j,
or
F_i|_{K_{cc'\cdots c^{(k)}}} = [(B_c B_{c'} \cdots B_{c^{(k)}}
M_{K_{cc'\cdots c^{(k)}}})^T]^{ij} \phi_{g'}^j,
depending on which of the two cells is the finer. We do this using either the matrix-vector product provided by the vmult function, or the product with the transpose matrix using Tvmult. After doing so, we transfer the result into the global right hand side vector of energy group g.
cell_g_prime->get_dof_values(g_prime.solution_old, g_prime_old_values);
cell_g_prime->get_dof_values(g_prime.solution, g_prime_new_values);
if (cell_g->level() > cell_g_prime->level())
{
prolongation_matrix.vmult(tmp, g_prime_old_values);
local_mass_matrix_f.vmult(cell_rhs, tmp);
prolongation_matrix.vmult(tmp, g_prime_new_values);
local_mass_matrix_g.vmult_add(cell_rhs, tmp);
}
else
{
local_mass_matrix_f.vmult(tmp, g_prime_old_values);
prolongation_matrix.Tvmult(cell_rhs, tmp);
local_mass_matrix_g.vmult(tmp, g_prime_new_values);
prolongation_matrix.Tvmult_add(cell_rhs, tmp);
}
std::vector<types::global_dof_index> local_dof_indices(
fe.n_dofs_per_cell());
cell_g->get_dof_indices(local_dof_indices);
for (unsigned int i = 0; i < fe.n_dofs_per_cell(); ++i)
system_rhs(local_dof_indices[i]) += cell_rhs(i);
}
The alternative is that one of the two cells is further refined. In that case, we have to loop over all the children, multiply the existing interpolation (prolongation) product of matrices from the left with the interpolation from the present cell to its child (using the matrix-matrix multiplication function mmult), and then hand the result off to this very same function again, but with the cell that has children replaced by one of its children:
else
for (unsigned int child = 0;
child < GeometryInfo<dim>::max_children_per_cell;
++child)
{
fe.n_dofs_per_cell());
fe.get_prolongation_matrix(child).mmult(new_matrix,
prolongation_matrix);
if (cell_g->has_children())
assemble_cross_group_rhs_recursive(g_prime,
cell_g->child(child),
cell_g_prime,
new_matrix);
else
assemble_cross_group_rhs_recursive(g_prime,
cell_g,
cell_g_prime->child(child),
new_matrix);
}
}
EnergyGroup::get_fission_source
In the (inverse) power iteration, we use the integrated fission source to update the k-eigenvalue. Given its definition, the following function is essentially self-explanatory:
template <int dim>
double EnergyGroup<dim>::get_fission_source() const
{
const unsigned int n_q_points = quadrature_formula.size();
quadrature_formula,
std::vector<double> solution_values(n_q_points);
double fission_source = 0;
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
const double fission_XS =
material_data.get_fission_XS(group, cell->material_id());
fe_values.get_function_values(solution, solution_values);
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
fission_source +=
(fission_XS * solution_values[q_point] * fe_values.JxW(q_point));
}
return fission_source;
}
EnergyGroup::solve
Next a function that solves the linear system assembled before. Things are pretty much standard, except that we delayed applying boundary values until we get here, since in all the previous functions we were still adding up contributions the right hand side vector.
template <int dim>
void EnergyGroup<dim>::solve()
{
hanging_node_constraints.condense(system_rhs);
system_matrix,
solution,
system_rhs);
1e-12 * system_rhs.l2_norm());
cg.solve(system_matrix, solution, system_rhs, preconditioner);
hanging_node_constraints.distribute(solution);
}
void initialize(const MatrixType &A, const AdditionalData ¶meters=AdditionalData())
EnergyGroup::estimate_errors
Mesh refinement is split into two functions. The first estimates the error for each cell, normalizes it by the magnitude of the solution, and returns it in the vector given as an argument. The calling function collects all error indicators from all energy groups, and computes thresholds for refining and coarsening cells.
template <int dim>
void EnergyGroup<dim>::estimate_errors(
Vector<float> &error_indicators)
const
{
dof_handler,
solution,
error_indicators);
error_indicators /= solution.linfty_norm();
}
static void estimate(const Mapping< dim, spacedim > &mapping, const DoFHandler< dim, spacedim > &dof, const Quadrature< dim - 1 > &quadrature, const std::map< types::boundary_id, const Function< spacedim, Number > * > &neumann_bc, const ReadVector< Number > &solution, Vector< float > &error, const ComponentMask &component_mask={}, const Function< spacedim > *coefficients=nullptr, const unsigned int n_threads=numbers::invalid_unsigned_int, const types::subdomain_id subdomain_id=numbers::invalid_subdomain_id, const types::material_id material_id=numbers::invalid_material_id, const Strategy strategy=cell_diameter_over_24)
EnergyGroup::refine_grid
The second part is to refine the grid given the error indicators compute in the previous function and error thresholds above which cells shall be refined or below which cells shall be coarsened. Note that we do not use any of the functions in GridRefinement here, but rather set refinement flags ourselves.
After setting these flags, we use the SolutionTransfer class to move the solution vector from the old to the new mesh. The procedure used here is described in detail in the documentation of that class:
template <int dim>
void EnergyGroup<dim>::refine_grid(
const Vector<float> &error_indicators,
const double refine_threshold,
const double coarsen_threshold)
{
if (error_indicators(cell->active_cell_index()) > refine_threshold)
cell->set_refine_flag();
else if (error_indicators(cell->active_cell_index()) < coarsen_threshold)
cell->set_coarsen_flag();
soltrans.prepare_for_coarsening_and_refinement(solution);
dof_handler.distribute_dofs(fe);
setup_linear_system();
solution.reinit(dof_handler.n_dofs());
soltrans.interpolate(solution);
enforce constraints to make the interpolated solution conforming on the new mesh:
hanging_node_constraints.distribute(solution);
solution_old.reinit(dof_handler.n_dofs());
solution_old = solution;
}
EnergyGroup::output_results
The last function of this class outputs meshes and solutions after each mesh iteration. This has been shown many times before. The only thing worth pointing out is the use of the Utilities::int_to_string function to convert an integer into its string representation. The second argument of that function denotes how many digits we shall use – if this value was larger than one, then the number would be padded by leading zeros.
template <int dim>
void EnergyGroup<dim>::output_results(const unsigned int cycle) const
{
const std::string filename = "solution-" +
data_out.add_data_vector(solution, "solution");
data_out.build_patches();
std::ofstream output(filename);
data_out.write_vtu(output);
}
void attach_dof_handler(const DoFHandler< dim, spacedim > &)
std::string int_to_string(const unsigned int value, const unsigned int digits=numbers::invalid_unsigned_int)
The NeutronDiffusionProblem class template
This is the main class of the program, not because it implements all the functionality (in fact, most of it is implemented in the EnergyGroup class) but because it contains the driving algorithm that determines what to compute and when. It is mostly as shown in many of the other tutorial programs in that it has a public run function and private functions doing all the rest. In several places, we have to do something for all energy groups, in which case we will start tasks for each group to let these things run in parallel if deal.II was configured for multithreading. For strategies of parallelization, take a look at the Parallel computing with multiple processors accessing shared memory topic.
The biggest difference to previous example programs is that we also declare a nested class that has member variables for all the run-time parameters that can be passed to the program in an input file. Right now, these are the number of energy groups, the number of refinement cycles, the polynomial degree of the finite element to be used, and the tolerance used to determine when convergence of the inverse power iteration has occurred. In addition, we have a constructor of this class that sets all these values to their default values, a function declare_parameters that describes to the ParameterHandler class what parameters are accepted in the input file, and a function get_parameters that can extract the values of these parameters from a ParameterHandler object. See also step-29 for another example of using ParameterHandler.
template <int dim>
class NeutronDiffusionProblem
{
public:
class Parameters
{
public:
Parameters();
unsigned int n_groups;
unsigned int n_refinement_cycles;
unsigned int fe_degree;
double convergence_tolerance;
};
NeutronDiffusionProblem(const Parameters ¶meters);
void run();
private:
NeutronDiffusionProblem private member functions
There are not that many member functions in this class since most of the functionality has been moved into the EnergyGroup class and is simply called from the run() member function of this class. The ones that remain have self-explanatory names:
void initialize_problem();
void refine_grid();
double get_total_fission_source() const;
NeutronDiffusionProblem private member variables
Next, we have a few member variables. In particular, these are (i) a reference to the parameter object (owned by the main function of this program, and passed to the constructor of this class), (ii) an object describing the material parameters for the number of energy groups requested in the input file, and (iii) the finite element to be used by all energy groups:
const Parameters ¶meters;
const MaterialData material_data;
Furthermore, we have (iv) the value of the computed eigenvalue at the present iteration. This is, in fact, the only part of the solution that is shared between all energy groups – all other parts of the solution, such as neutron fluxes are particular to one or the other energy group, and are therefore stored in objects that describe a single energy group:
The last computational object (v) is an array of pointers to the energy group objects. The length of this array is, of course, equal to the number of energy groups specified in the parameter file.
std::vector<std::unique_ptr<EnergyGroup<dim>>> energy_groups;
Finally (vi) we have a file stream to which we will save summarized output.
std::ofstream convergence_table_stream;
};
Implementation of the Parameters class
Before going on to the implementation of the outer class, we have to implement the functions of the parameters structure. This is pretty straightforward and, in fact, looks pretty much the same for all such parameters classes using the ParameterHandler capabilities. We will therefore not comment further on this:
template <int dim>
NeutronDiffusionProblem<dim>::Parameters::Parameters()
: n_groups(2)
, n_refinement_cycles(5)
, fe_degree(2)
, convergence_tolerance(1e-12)
{}
template <int dim>
void NeutronDiffusionProblem<dim>::Parameters::declare_parameters(
{
prm.declare_entry("Number of energy groups",
"2",
"The number of energy different groups considered");
prm.declare_entry("Refinement cycles",
"5",
"Number of refinement cycles to be performed");
prm.declare_entry("Finite element degree",
"2",
"Polynomial degree of the finite element to be used");
prm.declare_entry(
"Power iteration tolerance",
"1e-12",
"Inner power iterations are stopped when the change in k_eff falls "
"below this tolerance");
}
template <int dim>
void NeutronDiffusionProblem<dim>::Parameters::get_parameters(
{
n_groups = prm.get_integer("Number of energy groups");
n_refinement_cycles = prm.get_integer("Refinement cycles");
fe_degree = prm.get_integer("Finite element degree");
convergence_tolerance = prm.get_double("Power iteration tolerance");
}
Implementation of the NeutronDiffusionProblem class
Now for the NeutronDiffusionProblem class. The constructor and destructor have nothing of much interest:
template <int dim>
NeutronDiffusionProblem<dim>::NeutronDiffusionProblem(
const Parameters ¶meters)
: parameters(parameters)
, material_data(parameters.n_groups)
, fe(parameters.fe_degree)
, k_eff(
std::numeric_limits<double>::quiet_NaN())
{}
NeutronDiffusionProblem::initialize_problem
The first function of interest is the one that sets up the geometry of the reactor core. This is described in more detail in the introduction.
The first part of the function defines geometry data, and then creates a coarse mesh that has as many cells as there are fuel rods (or pin cells, for that matter) in that part of the reactor core that we simulate. As mentioned when interpolating boundary values above, the last parameter to the GridGenerator::subdivided_hyper_rectangle function specifies that sides of the domain shall have unique boundary indicators that will later allow us to determine in a simple way which of the boundaries have Neumann and which have Dirichlet conditions attached to them.
template <int dim>
void NeutronDiffusionProblem<dim>::initialize_problem()
{
const unsigned int rods_per_assembly_x = 17, rods_per_assembly_y = 17;
const double pin_pitch_x = 1.26, pin_pitch_y = 1.26;
const double assembly_height = 200;
const unsigned int assemblies_x = 2, assemblies_y = 2, assemblies_z = 1;
(dim == 2 ?
Point<dim>(assemblies_x * rods_per_assembly_x * pin_pitch_x,
assemblies_y * rods_per_assembly_y * pin_pitch_y) :
Point<dim>(assemblies_x * rods_per_assembly_x * pin_pitch_x,
assemblies_y * rods_per_assembly_y * pin_pitch_y,
assemblies_z * assembly_height));
std::vector<unsigned int> n_subdivisions;
n_subdivisions.push_back(assemblies_x * rods_per_assembly_x);
if (dim >= 2)
n_subdivisions.push_back(assemblies_y * rods_per_assembly_y);
if (dim >= 3)
n_subdivisions.push_back(assemblies_z);
coarse_grid, n_subdivisions, bottom_left, upper_right, true);
void subdivided_hyper_rectangle(Triangulation< dim, spacedim > &tria, const std::vector< unsigned int > &repetitions, const Point< dim > &p1, const Point< dim > &p2, const bool colorize=false)
The second part of the function deals with material numbers of pin cells of each type of assembly. Here, we define four different types of assembly, for which we describe the arrangement of fuel rods in the following tables.
The assemblies described here are taken from the benchmark mentioned in the introduction and are (in this order):
-
'UX' Assembly: UO2 fuel assembly with 24 guide tubes and a central Moveable Fission Chamber
-
'UA' Assembly: UO2 fuel assembly with 24 AIC and a central Moveable Fission Chamber
-
'PX' Assembly: MOX fuel assembly with 24 guide tubes and a central Moveable Fission Chamber
-
'R' Assembly: a reflector.
Note that the numbers listed here and taken from the benchmark description are, in good old Fortran fashion, one-based. We will later subtract one from each number when assigning materials to individual cells to convert things into the C-style zero-based indexing.
const unsigned int n_assemblies = 4;
const unsigned int assembly_materials
[n_assemblies][rods_per_assembly_x][rods_per_assembly_y] = {
{{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 1, 1, 1},
{1, 1, 1, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 5, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 5, 1, 1, 5, 1, 1, 7, 1, 1, 5, 1, 1, 5, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 5, 1, 1, 1},
{1, 1, 1, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}},
{{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 1, 1, 1},
{1, 1, 1, 8, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 8, 1, 1, 8, 1, 1, 7, 1, 1, 8, 1, 1, 8, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 8, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 1, 1, 1},
{1, 1, 1, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}},
{{2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2},
{2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2},
{2, 3, 3, 3, 3, 5, 3, 3, 5, 3, 3, 5, 3, 3, 3, 3, 2},
{2, 3, 3, 5, 3, 4, 4, 4, 4, 4, 4, 4, 3, 5, 3, 3, 2},
{2, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 3, 2},
{2, 3, 5, 4, 4, 5, 4, 4, 5, 4, 4, 5, 4, 4, 5, 3, 2},
{2, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 2},
{2, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 2},
{2, 3, 5, 4, 4, 5, 4, 4, 7, 4, 4, 5, 4, 4, 5, 3, 2},
{2, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 2},
{2, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 2},
{2, 3, 5, 4, 4, 5, 4, 4, 5, 4, 4, 5, 4, 4, 5, 3, 2},
{2, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 3, 2},
{2, 3, 3, 5, 3, 4, 4, 4, 4, 4, 4, 4, 3, 5, 3, 3, 2},
{2, 3, 3, 3, 3, 5, 3, 3, 5, 3, 3, 5, 3, 3, 3, 3, 2},
{2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2},
{2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2}},
{{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6}}};
After the description of the materials that make up an assembly, we have to specify the arrangement of assemblies within the core. We use a symmetric pattern that in fact only uses the 'UX' and 'PX' assemblies:
const unsigned int core[assemblies_x][assemblies_y][assemblies_z] = {
{{0}, {2}}, {{2}, {0}}};
We are now in a position to actually set material IDs for each cell. To this end, we loop over all cells, look at the location of the cell's center, and determine which assembly and fuel rod this would be in. (We add a few checks to see that the locations we compute are within the bounds of the arrays in which we have to look up materials.) At the end of the loop, we set material identifiers accordingly:
for (auto &cell : coarse_grid.active_cell_iterators())
{
const
Point<dim> cell_center = cell->center();
const unsigned int tmp_x =
int(cell_center[0] / pin_pitch_x);
const unsigned int ax = tmp_x / rods_per_assembly_x;
const unsigned int cx = tmp_x - ax * rods_per_assembly_x;
const unsigned tmp_y =
int(cell_center[1] / pin_pitch_y);
const unsigned int ay = tmp_y / rods_per_assembly_y;
const unsigned int cy = tmp_y - ay * rods_per_assembly_y;
const unsigned int az =
(dim == 2 ? 0 :
int(cell_center[dim - 1] / assembly_height));
Assert(ax < assemblies_x, ExcInternalError());
Assert(ay < assemblies_y, ExcInternalError());
Assert(az < assemblies_z, ExcInternalError());
Assert(core[ax][ay][az] < n_assemblies, ExcInternalError());
Assert(cx < rods_per_assembly_x, ExcInternalError());
Assert(cy < rods_per_assembly_y, ExcInternalError());
cell->set_material_id(assembly_materials[core[ax][ay][az]][cx][cy] - 1);
}
With the coarse mesh so initialized, we create the appropriate number of energy group objects and let them initialize their individual meshes with the coarse mesh generated above:
for (unsigned int group = 0; group < parameters.n_groups; ++group)
energy_groups.emplace_back(std::make_unique<EnergyGroup<dim>>(
group, material_data, coarse_grid, fe));
convergence_table_stream.open("convergence_table");
convergence_table_stream.precision(12);
}
NeutronDiffusionProblem::get_total_fission_source
In the eigenvalue computation, we need to calculate total fission neutron source after each power iteration. The total power then is used to renew k-effective.
Since the total fission source is a sum over all the energy groups, and since each of these sums can be computed independently, we actually do this in parallel. One of the problems is that the function in the EnergyGroup class that computes the fission source returns a value. We would like to add these values together in the loop itself: ideally, each task would compute its value and then immediately add it to the total. Concurrently summing values in this way requires two features:
-
We need a way of storing a value such that multiple threads can read and write into concurrently in a way that prevents data races (i.e., thread-safe reading and writing).
-
We need a way to increment such a value that is also thread-safe.
The first feature is available through the template class std::atomic. However, the second feature, implemented by std::atomic<double>::fetch_add(), is only available in C++20 and later: since deal.II supports older versions of the C++ language standard we cannot use this feature yet. Hence, instead, we simply write each group's value out to an entry in a vector and sum the values at the end of the function.
template <int dim>
double NeutronDiffusionProblem<dim>::get_total_fission_source() const
{
std::vector<double> fission_sources(parameters.n_groups);
for (unsigned int group = 0; group < parameters.n_groups; ++group)
tasks += Threads::new_task<>([&, group]() {
fission_sources[group] = energy_groups[group]->get_fission_source();
});
return std::accumulate(fission_sources.begin(), fission_sources.end(), 0.0);
}
NeutronDiffusionProblem::refine_grid
The next function lets the individual energy group objects refine their meshes. Much of this, again, is a task that can be done independently in parallel: first, let all the energy group objects calculate their error indicators in parallel, then compute the maximum error indicator over all energy groups and determine thresholds for refinement and coarsening of cells, and then ask all the energy groups to refine their meshes accordingly, again in parallel.
template <int dim>
void NeutronDiffusionProblem<dim>::refine_grid()
{
std::vector<types::global_dof_index> n_cells(parameters.n_groups);
for (unsigned int group = 0; group < parameters.n_groups; ++group)
n_cells[group] = energy_groups[group]->n_active_cells();
{
for (unsigned int group = 0; group < parameters.n_groups; ++group)
energy_groups[group]->estimate_errors(
group_error_indicators.block(group));
});
}
Task< RT > new_task(const std::function< RT()> &function)
The destructor of Threads::TaskGroup joins all threads so we know that the computation is done by the time we exit the scope.
const float max_error = group_error_indicators.linfty_norm();
const float refine_threshold = 0.3 * max_error;
const float coarsen_threshold = 0.01 * max_error;
{
for (unsigned int group = 0; group < parameters.n_groups; ++group)
energy_groups[group]->refine_grid(group_error_indicators.block(group),
refine_threshold,
coarsen_threshold);
});
}
}
NeutronDiffusionProblem::run
Finally, this is the function where the meat is: iterate on a sequence of meshes, and on each of them do a power iteration to compute the eigenvalue.
Given the description of the algorithm in the introduction, there is actually not much to comment on:
template <int dim>
void NeutronDiffusionProblem<dim>::run()
{
We would like to change the output precision for just this function and restore the state of std::cout when this function returns. Hence, we need a way to undo the output format change. Boost provides a convenient way to save the state of an output stream and restore it at the end of the current block (when the destructor of restore_flags is called) with the ios_flags_saver class, which we use here.
boost::io::ios_flags_saver restore_flags(std::cout);
std::cout << std::setprecision(12) << std::fixed;
We calculate the error below by the change in k_eff (i.e., the difference between k_eff_old,
double k_eff_old = 0.0;
for (unsigned int cycle = 0; cycle < parameters.n_refinement_cycles;
++cycle)
{
We will measure the CPU time that each cycle takes below. The constructor for Timer calls Timer::start(), so once we create a timer we can query it for information. Since many parts of this loop are parallelized with tasks, the CPU time we measure (if we run with more than one thread) will be larger than the wall time.
std::cout << "Cycle " << cycle << ':' << std::endl;
if (cycle == 0)
{
initialize_problem();
for (unsigned int group = 0; group < parameters.n_groups; ++group)
energy_groups[group]->setup_linear_system();
}
else
{
refine_grid();
for (unsigned int group = 0; group < parameters.n_groups; ++group)
energy_groups[group]->solution *= k_eff;
}
std::cout << " Numbers of active cells: ";
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
std::cout << std::endl;
std::cout << " Numbers of degrees of freedom: ";
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
std::cout << energy_groups[group]->n_dofs() << ' ';
std::cout << std::endl << std::endl;
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
[&, group]() { energy_groups[
group]->assemble_system_matrix(); });
double error;
unsigned int iteration = 1;
do
{
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
{
energy_groups[
group]->assemble_ingroup_rhs(
for (unsigned int bgroup = 0; bgroup < parameters.n_groups;
++bgroup)
energy_groups[group]->assemble_cross_group_rhs(
*energy_groups[bgroup]);
energy_groups[
group]->solve();
}
k_eff = get_total_fission_source();
const double flux_ratio = energy_groups[0]->solution.linfty_norm() /
energy_groups[1]->solution.linfty_norm();
const double max_thermal = energy_groups[1]->solution.linfty_norm();
std::cout << "Iter number:" << std::setw(2) << std::right
<< iteration << " k_eff=" << k_eff
<< " flux_ratio=" << flux_ratio
<< " max_thermal=" << max_thermal << std::endl;
k_eff_old = k_eff;
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
{
energy_groups[
group]->solution_old =
energy_groups[
group]->solution;
energy_groups[
group]->solution_old /= k_eff;
}
++iteration;
}
while ((error > parameters.convergence_tolerance) && (iteration < 500));
convergence_table_stream << cycle << ' ' << energy_groups[0]->n_dofs()
<< ' ' << energy_groups[1]->n_dofs() << ' '
<< k_eff << ' '
<< energy_groups[0]->solution.linfty_norm() /
energy_groups[1]->solution.linfty_norm()
<< '\n';
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
energy_groups[group]->output_results(cycle);
unsigned int n_active_cells(const internal::TriangulationImplementation::NumberCache< 1 > &c)
::VectorizedArray< Number, width > abs(const ::VectorizedArray< Number, width > &)
Print out information about the simulation as well as the elapsed CPU time. We can call Timer::cpu_time() without first calling Timer::stop() to get the elapsed CPU time at the point of calling the function.
std::cout << std::endl;
std::cout << " Cycle=" << cycle << ", n_dofs="
<< energy_groups[0]->n_dofs() + energy_groups[1]->n_dofs()
<< ", k_eff=" << k_eff << ", time=" << timer.cpu_time()
<< std::endl;
std::cout << std::endl << std::endl;
}
}
}
The main() function
The last thing in the program in the main() function. The structure is as in most other tutorial programs, with the only exception that we here handle a parameter file. To this end, we first look at the command line arguments passed to this function: if no input file is specified on the command line, then use "project.prm", otherwise take the filename given as the first argument on the command line.
With this, we create a ParameterHandler object, let the NeutronDiffusionProblem::Parameters class declare all the parameters it wants to see in the input file (or, take the default values, if nothing is listed in the parameter file), then read the input file, ask the parameters object to extract the values, and finally hand everything off to an object of type NeutronDiffusionProblem for computation of the eigenvalue:
int main(int argc, char **argv)
{
try
{
using namespace Step28;
std::string filename;
if (argc < 2)
filename = "project.prm";
else
filename = argv[1];
const unsigned int dim = 2;
NeutronDiffusionProblem<dim>::Parameters parameters;
parameters.declare_parameters(parameter_handler);
parameters.get_parameters(parameter_handler);
NeutronDiffusionProblem<dim> neutron_diffusion_problem(parameters);
neutron_diffusion_problem.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
virtual void parse_input(std::istream &input, const std::string &filename="input file", const std::string &last_line="", const bool skip_undefined=false)
Results
We can run the program with the following input file :
# Listing of Parameters
# ---------------------
# Polynomial degree of the finite element to be used
set Finite element degree = 2
# The number of energy different groups considered
set Number of energy groups = 2
# Inner power iterations are stopped when the change in k_eff falls below this
# tolerance
set Power iteration tolerance = 1e-12
# Number of refinement cycles to be performed
set Refinement cycles = 12
The output of this program then consists of the console output, a file named ‘convergence_table’ to record main results of mesh iteration, and the graphical output in vtu format.
The console output looks like this:
Cycle 0:
Numbers of active cells: 1156 1156
Numbers of degrees of freedom: 4761 4761
Iter number: 1 k_eff=319.375676634310 flux_ratio=6.836246075630 max_thermal=1.433899030144
Iter number: 2 k_eff=0.834072546055 flux_ratio=5.204601882144 max_thermal=0.004630925876
Iter number: 3 k_eff=0.862826188043 flux_ratio=4.645051765984 max_thermal=0.005380396338
...
Iter number:69 k_eff=0.906841960370 flux_ratio=4.384056022578 max_thermal=0.008466414246
Iter number:70 k_eff=0.906841960371 flux_ratio=4.384056022583 max_thermal=0.008466414246
Cycle=0, n_dofs=9522, k_eff=0.906841960371, time=7.623425000000
Cycle 1:
Numbers of active cells: 1156 2380
Numbers of degrees of freedom: 4761 10667
Iter number: 1 k_eff=0.906838267472 flux_ratio=4.385474405125 max_thermal=0.008463675976
...
Cycle 11:
Numbers of active cells: 11749 47074
Numbers of degrees of freedom: 50261 204523
Iter number: 1 k_eff=0.906798057750 flux_ratio=4.384878772166 max_thermal=0.008464822382
Iter number: 2 k_eff=0.906833008185 flux_ratio=4.384868138638 max_thermal=0.008465057191
...
Iter number:32 k_eff=0.906834736550 flux_ratio=4.384846081793 max_thermal=0.008465019607
Iter number:33 k_eff=0.906834736551 flux_ratio=4.384846081798 max_thermal=0.008465019607
Cycle=11, n_dofs=254784, k_eff=0.906834736551, time=238.593762000000
We see that power iteration does converge faster after cycle 0 due to the initialization with solution from last mesh iteration. The contents of ‘convergence_table’ are,
0 4761 4761 0.906841960371 4.38405602258
1 4761 10667 0.906837901031 4.38548908776
2 4761 18805 0.906836075928 4.3854666475
3 6629 27301 0.90683550011 4.38540458087
4 12263 48095 0.906835001796 4.38538179873
5 17501 69297 0.906834858174 4.38485382341
6 19933 78605 0.90683482406 4.38485065879
7 23979 93275 0.906834787555 4.38484837926
8 30285 117017 0.906834761604 4.38484654495
9 40087 154355 0.906834746215 4.38484608319
10 45467 179469 0.906834740155 4.38484600505
11 50261 204523 0.906834736551 4.3848460818
The meanings of columns are: number of mesh iteration, numbers of degrees of freedom of fast energy group, numbers of DoFs of thermal group, converged k-effective and the ratio between maximum of fast flux and maximum of thermal one.
The grids of fast and thermal energy groups at mesh iteration #9 look as follows:


We see that the grid of thermal group is much finer than the one of fast group. The solutions on these grids are, (Note: flux are normalized with total fission source equal to 1)

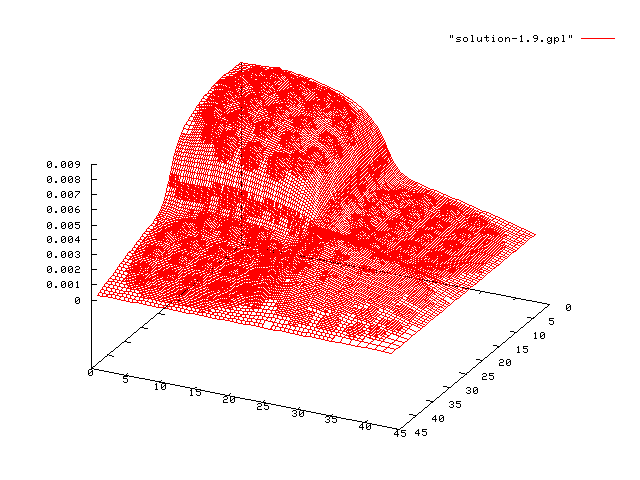
Then we plot the convergence data with polynomial order being equal to 1,2 and 3.
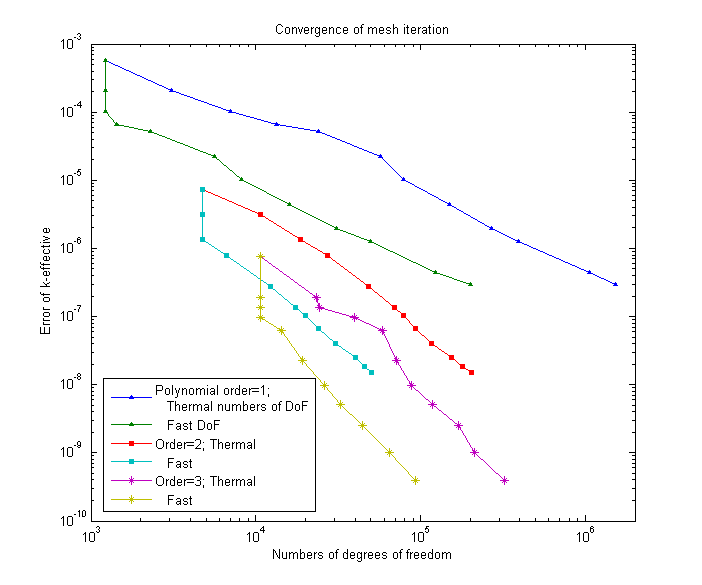
The estimated ‘exact’ k-effective = 0.906834721253 which is simply from last mesh iteration of polynomial order 3 minus 2e-10. We see that h-adaptive calculations deliver an algebraic convergence. And the higher polynomial order is, the faster mesh iteration converges. In our problem, we need smaller number of DoFs to achieve same accuracy with higher polynomial order.
The plain program
#include <fstream>
#include <iostream>
#include <boost/io/ios_state.hpp>
#include <list>
#include <iomanip>
namespace Step28
{
class MaterialData
{
public:
MaterialData(const unsigned int n_groups);
double get_diffusion_coefficient(const unsigned int group,
const unsigned int material_id) const;
double get_removal_XS(const unsigned int group,
const unsigned int material_id) const;
double get_fission_XS(const unsigned int group,
const unsigned int material_id) const;
double get_fission_dist_XS(const unsigned int group_1,
const unsigned int group_2,
const unsigned int material_id) const;
double get_scattering_XS(const unsigned int group_1,
const unsigned int group_2,
const unsigned int material_id) const;
double get_fission_spectrum(const unsigned int group,
const unsigned int material_id) const;
private:
const unsigned int n_groups;
const unsigned int n_materials;
};
MaterialData::MaterialData(const unsigned int n_groups)
: n_groups(n_groups)
, n_materials(8)
, diffusion(n_materials, n_groups)
, sigma_r(n_materials, n_groups)
, nu_sigma_f(n_materials, n_groups)
, sigma_s(n_materials, n_groups, n_groups)
, chi(n_materials, n_groups)
{
switch (this->n_groups)
{
case 2:
{
for (unsigned int m = 0; m < n_materials; ++m)
{
diffusion[m][0] = 1.2;
diffusion[m][1] = 0.4;
chi[m][0] = 1.0;
chi[m][1] = 0.0;
sigma_r[m][0] = 0.03;
for (unsigned int group_1 = 0; group_1 < n_groups; ++group_1)
for (unsigned int group_2 = 0; group_2 < n_groups; ++group_2)
sigma_s[m][group_1][group_2] = 0.0;
}
diffusion[5][1] = 0.2;
sigma_r[4][0] = 0.026;
sigma_r[5][0] = 0.051;
sigma_r[6][0] = 0.026;
sigma_r[7][0] = 0.050;
sigma_r[0][1] = 0.100;
sigma_r[1][1] = 0.200;
sigma_r[2][1] = 0.250;
sigma_r[3][1] = 0.300;
sigma_r[4][1] = 0.020;
sigma_r[5][1] = 0.040;
sigma_r[6][1] = 0.020;
sigma_r[7][1] = 0.800;
nu_sigma_f[0][0] = 0.0050;
nu_sigma_f[1][0] = 0.0075;
nu_sigma_f[2][0] = 0.0075;
nu_sigma_f[3][0] = 0.0075;
nu_sigma_f[4][0] = 0.000;
nu_sigma_f[5][0] = 0.000;
nu_sigma_f[7][0] = 0.00;
nu_sigma_f[0][1] = 0.125;
nu_sigma_f[1][1] = 0.300;
nu_sigma_f[2][1] = 0.375;
nu_sigma_f[3][1] = 0.450;
nu_sigma_f[4][1] = 0.000;
nu_sigma_f[5][1] = 0.000;
nu_sigma_f[7][1] = 0.00;
sigma_s[0][0][1] = 0.020;
sigma_s[1][0][1] = 0.015;
sigma_s[2][0][1] = 0.015;
sigma_s[3][0][1] = 0.015;
sigma_s[4][0][1] = 0.025;
sigma_s[5][0][1] = 0.050;
sigma_s[6][0][1] = 0.025;
sigma_s[7][0][1] = 0.010;
break;
}
default:
ExcMessage(
"Presently, only data for 2 groups is implemented"));
}
}
double
MaterialData::get_diffusion_coefficient(const unsigned int group,
const unsigned int material_id) const
{
Assert(group < n_groups, ExcIndexRange(group, 0, n_groups));
Assert(material_id < n_materials,
ExcIndexRange(material_id, 0, n_materials));
}
double MaterialData::get_removal_XS(const unsigned int group,
const unsigned int material_id) const
{
Assert(group < n_groups, ExcIndexRange(group, 0, n_groups));
Assert(material_id < n_materials,
ExcIndexRange(material_id, 0, n_materials));
}
double MaterialData::get_fission_XS(const unsigned int group,
const unsigned int material_id) const
{
Assert(group < n_groups, ExcIndexRange(group, 0, n_groups));
Assert(material_id < n_materials,
ExcIndexRange(material_id, 0, n_materials));
}
double MaterialData::get_scattering_XS(const unsigned int group_1,
const unsigned int group_2,
const unsigned int material_id) const
{
Assert(group_1 < n_groups, ExcIndexRange(group_1, 0, n_groups));
Assert(group_2 < n_groups, ExcIndexRange(group_2, 0, n_groups));
Assert(material_id < n_materials,
ExcIndexRange(material_id, 0, n_materials));
}
double
MaterialData::get_fission_spectrum(const unsigned int group,
const unsigned int material_id) const
{
Assert(group < n_groups, ExcIndexRange(group, 0, n_groups));
Assert(material_id < n_materials,
ExcIndexRange(material_id, 0, n_materials));
}
double MaterialData::get_fission_dist_XS(const unsigned int group_1,
const unsigned int group_2,
const unsigned int material_id) const
{
return (get_fission_spectrum(group_1, material_id) *
get_fission_XS(group_2, material_id));
}
template <int dim>
class EnergyGroup
{
public:
EnergyGroup(const unsigned int group,
const MaterialData &material_data,
void setup_linear_system();
unsigned int n_dofs() const;
void assemble_system_matrix();
void assemble_ingroup_rhs(
const Function<dim> &extraneous_source);
void assemble_cross_group_rhs(const EnergyGroup<dim> &g_prime);
void solve();
double get_fission_source() const;
void output_results(const unsigned int cycle) const;
const double refine_threshold,
const double coarsen_threshold);
public:
private:
const unsigned int group;
const MaterialData &material_data;
std::map<types::global_dof_index, double> boundary_values;
private:
void assemble_cross_group_rhs_recursive(
const EnergyGroup<dim> &g_prime,
};
template <int dim>
EnergyGroup<dim>::EnergyGroup(const unsigned int group,
const MaterialData &material_data,
, material_data(material_data)
, fe(fe)
{
dof_handler.distribute_dofs(fe);
}
template <int dim>
unsigned int EnergyGroup<dim>::n_active_cells() const
{
}
template <int dim>
unsigned int EnergyGroup<dim>::n_dofs() const
{
return dof_handler.n_dofs();
}
template <int dim>
void EnergyGroup<dim>::setup_linear_system()
{
const unsigned int n_dofs = dof_handler.n_dofs();
hanging_node_constraints.clear();
hanging_node_constraints);
hanging_node_constraints.close();
system_matrix.clear();
hanging_node_constraints.condense(dsp);
sparsity_pattern.copy_from(dsp);
system_matrix.reinit(sparsity_pattern);
system_rhs.reinit(n_dofs);
if (solution.empty())
{
solution.reinit(n_dofs);
solution_old.reinit(n_dofs);
solution_old = 1.0;
solution = solution_old;
}
boundary_values.clear();
for (unsigned int i = 0; i < dim; ++i)
2 * i + 1,
boundary_values);
}
template <int dim>
void EnergyGroup<dim>::assemble_system_matrix()
{
quadrature_formula,
const unsigned int n_q_points = quadrature_formula.size();
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
const double diffusion_coefficient =
material_data.get_diffusion_coefficient(group, cell->material_id());
const double removal_XS =
material_data.get_removal_XS(group, cell->material_id());
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
for (unsigned int i = 0; i < dofs_per_cell; ++i)
for (unsigned int j = 0; j < dofs_per_cell; ++j)
((diffusion_coefficient * fe_values.shape_grad(i, q_point) *
fe_values.shape_grad(j, q_point) +
removal_XS * fe_values.shape_value(i, q_point) *
fe_values.shape_value(j, q_point)) *
fe_values.JxW(q_point));
cell->get_dof_indices(local_dof_indices);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
for (unsigned int j = 0; j < dofs_per_cell; ++j)
system_matrix.add(local_dof_indices[i],
local_dof_indices[j],
}
hanging_node_constraints.condense(system_matrix);
}
template <int dim>
void
EnergyGroup<dim>::assemble_ingroup_rhs(
const Function<dim> &extraneous_source)
{
system_rhs.reinit(dof_handler.n_dofs());
const unsigned int n_q_points = quadrature_formula.size();
quadrature_formula,
std::vector<double> extraneous_source_values(n_q_points);
std::vector<double> solution_old_values(n_q_points);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
for (const auto &cell : dof_handler.active_cell_iterators())
{
cell_rhs = 0;
fe_values.reinit(cell);
const double fission_dist_XS =
material_data.get_fission_dist_XS(group, group, cell->material_id());
extraneous_source.
value_list(fe_values.get_quadrature_points(),
extraneous_source_values);
fe_values.get_function_values(solution_old, solution_old_values);
cell->get_dof_indices(local_dof_indices);
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
for (unsigned int i = 0; i < dofs_per_cell; ++i)
cell_rhs(i) +=
((extraneous_source_values[q_point] +
fission_dist_XS * solution_old_values[q_point]) *
fe_values.shape_value(i, q_point) * fe_values.JxW(q_point));
for (unsigned int i = 0; i < dofs_per_cell; ++i)
system_rhs(local_dof_indices[i]) += cell_rhs(i);
}
}
template <int dim>
void
EnergyGroup<dim>::assemble_cross_group_rhs(const EnergyGroup<dim> &g_prime)
{
if (group == g_prime.group)
return;
const std::list<std::pair<typename DoFHandler<dim>::cell_iterator,
cell_list =
for (const auto &cell_pair : cell_list)
{
for (unsigned int i = 0; i < unit_matrix.m(); ++i)
unit_matrix(i, i) = 1;
assemble_cross_group_rhs_recursive(g_prime,
cell_pair.first,
cell_pair.second,
unit_matrix);
}
}
template <int dim>
void EnergyGroup<dim>::assemble_cross_group_rhs_recursive(
const EnergyGroup<dim> &g_prime,
{
if (!cell_g->has_children() && !cell_g_prime->has_children())
{
const unsigned int n_q_points = quadrature_formula.size();
quadrature_formula,
if (cell_g->level() > cell_g_prime->level())
fe_values.reinit(cell_g);
else
fe_values.reinit(cell_g_prime);
const double fission_dist_XS =
material_data.get_fission_dist_XS(group,
g_prime.group,
cell_g_prime->material_id());
const double scattering_XS =
material_data.get_scattering_XS(g_prime.group,
group,
cell_g_prime->material_id());
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
{
local_mass_matrix_f(i, j) +=
(fission_dist_XS * fe_values.shape_value(i, q_point) *
fe_values.shape_value(j, q_point) * fe_values.JxW(q_point));
local_mass_matrix_g(i, j) +=
(scattering_XS * fe_values.shape_value(i, q_point) *
fe_values.shape_value(j, q_point) * fe_values.JxW(q_point));
}
cell_g_prime->get_dof_values(g_prime.solution_old, g_prime_old_values);
cell_g_prime->get_dof_values(g_prime.solution, g_prime_new_values);
if (cell_g->level() > cell_g_prime->level())
{
prolongation_matrix.
vmult(tmp, g_prime_old_values);
local_mass_matrix_f.vmult(cell_rhs, tmp);
prolongation_matrix.
vmult(tmp, g_prime_new_values);
local_mass_matrix_g.vmult_add(cell_rhs, tmp);
}
else
{
local_mass_matrix_f.vmult(tmp, g_prime_old_values);
prolongation_matrix.
Tvmult(cell_rhs, tmp);
local_mass_matrix_g.vmult(tmp, g_prime_new_values);
}
std::vector<types::global_dof_index> local_dof_indices(
cell_g->get_dof_indices(local_dof_indices);
system_rhs(local_dof_indices[i]) += cell_rhs(i);
}
else
for (unsigned int child = 0;
child < GeometryInfo<dim>::max_children_per_cell;
++child)
{
prolongation_matrix);
if (cell_g->has_children())
assemble_cross_group_rhs_recursive(g_prime,
cell_g->child(child),
cell_g_prime,
new_matrix);
else
assemble_cross_group_rhs_recursive(g_prime,
cell_g,
cell_g_prime->child(child),
new_matrix);
}
}
template <int dim>
double EnergyGroup<dim>::get_fission_source() const
{
const unsigned int n_q_points = quadrature_formula.size();
quadrature_formula,
std::vector<double> solution_values(n_q_points);
double fission_source = 0;
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
const double fission_XS =
material_data.get_fission_XS(group, cell->material_id());
fe_values.get_function_values(solution, solution_values);
for (unsigned int q_point = 0; q_point < n_q_points; ++q_point)
fission_source +=
(fission_XS * solution_values[q_point] * fe_values.JxW(q_point));
}
return fission_source;
}
template <int dim>
void EnergyGroup<dim>::solve()
{
hanging_node_constraints.condense(system_rhs);
system_matrix,
solution,
system_rhs);
1e-12 * system_rhs.l2_norm());
cg.solve(system_matrix, solution, system_rhs, preconditioner);
hanging_node_constraints.distribute(solution);
}
template <int dim>
void EnergyGroup<dim>::estimate_errors(
Vector<float> &error_indicators)
const
{
dof_handler,
solution,
error_indicators);
}
template <int dim>
void EnergyGroup<dim>::refine_grid(
const Vector<float> &error_indicators,
const double refine_threshold,
const double coarsen_threshold)
{
if (error_indicators(cell->active_cell_index()) > refine_threshold)
cell->set_refine_flag();
else if (error_indicators(cell->active_cell_index()) < coarsen_threshold)
cell->set_coarsen_flag();
soltrans.prepare_for_coarsening_and_refinement(solution);
dof_handler.distribute_dofs(fe);
setup_linear_system();
solution.reinit(dof_handler.n_dofs());
soltrans.interpolate(solution);
hanging_node_constraints.distribute(solution);
solution_old.reinit(dof_handler.n_dofs());
solution_old = solution;
}
template <int dim>
void EnergyGroup<dim>::output_results(const unsigned int cycle) const
{
const std::string filename = "solution-" +
std::ofstream output(filename);
}
template <int dim>
class NeutronDiffusionProblem
{
public:
class Parameters
{
public:
Parameters();
unsigned int n_groups;
unsigned int n_refinement_cycles;
unsigned int fe_degree;
double convergence_tolerance;
};
NeutronDiffusionProblem(const Parameters ¶meters);
private:
void initialize_problem();
void refine_grid();
double get_total_fission_source() const;
const Parameters ¶meters;
const MaterialData material_data;
double k_eff;
std::vector<std::unique_ptr<EnergyGroup<dim>>> energy_groups;
std::ofstream convergence_table_stream;
};
template <int dim>
NeutronDiffusionProblem<dim>::Parameters::Parameters()
: n_groups(2)
, n_refinement_cycles(5)
, fe_degree(2)
, convergence_tolerance(1
e-12)
{}
template <int dim>
void NeutronDiffusionProblem<dim>::Parameters::declare_parameters(
{
"2",
"The number of energy different groups considered");
"5",
"Number of refinement cycles to be performed");
"2",
"Polynomial degree of the finite element to be used");
"Power iteration tolerance",
"1e-12",
"Inner power iterations are stopped when the change in k_eff falls "
"below this tolerance");
}
template <int dim>
void NeutronDiffusionProblem<dim>::Parameters::get_parameters(
{
n_refinement_cycles = prm.
get_integer(
"Refinement cycles");
convergence_tolerance = prm.
get_double(
"Power iteration tolerance");
}
template <int dim>
NeutronDiffusionProblem<dim>::NeutronDiffusionProblem(
const Parameters ¶meters)
: parameters(parameters)
, material_data(parameters.n_groups)
, fe(parameters.fe_degree)
, k_eff(
std::numeric_limits<double>::quiet_NaN())
{}
template <int dim>
void NeutronDiffusionProblem<dim>::initialize_problem()
{
const unsigned int rods_per_assembly_x = 17, rods_per_assembly_y = 17;
const double pin_pitch_x = 1.26, pin_pitch_y = 1.26;
const double assembly_height = 200;
const unsigned int assemblies_x = 2, assemblies_y = 2, assemblies_z = 1;
(dim == 2 ?
Point<dim>(assemblies_x * rods_per_assembly_x * pin_pitch_x,
assemblies_y * rods_per_assembly_y * pin_pitch_y) :
Point<dim>(assemblies_x * rods_per_assembly_x * pin_pitch_x,
assemblies_y * rods_per_assembly_y * pin_pitch_y,
assemblies_z * assembly_height));
std::vector<unsigned int> n_subdivisions;
n_subdivisions.push_back(assemblies_x * rods_per_assembly_x);
if (dim >= 2)
n_subdivisions.push_back(assemblies_y * rods_per_assembly_y);
if (dim >= 3)
n_subdivisions.push_back(assemblies_z);
coarse_grid, n_subdivisions, bottom_left, upper_right, true);
const unsigned int n_assemblies = 4;
const unsigned int assembly_materials
[n_assemblies][rods_per_assembly_x][rods_per_assembly_y] = {
{{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 1, 1, 1},
{1, 1, 1, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 5, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 5, 1, 1, 5, 1, 1, 7, 1, 1, 5, 1, 1, 5, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 5, 1, 1, 1, 1, 1, 1, 1, 1, 1, 5, 1, 1, 1},
{1, 1, 1, 1, 1, 5, 1, 1, 5, 1, 1, 5, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}},
{{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 1, 1, 1},
{1, 1, 1, 8, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 8, 1, 1, 8, 1, 1, 7, 1, 1, 8, 1, 1, 8, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 8, 1, 1, 1, 1, 1, 1, 1, 1, 1, 8, 1, 1, 1},
{1, 1, 1, 1, 1, 8, 1, 1, 8, 1, 1, 8, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}},
{{2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2},
{2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2},
{2, 3, 3, 3, 3, 5, 3, 3, 5, 3, 3, 5, 3, 3, 3, 3, 2},
{2, 3, 3, 5, 3, 4, 4, 4, 4, 4, 4, 4, 3, 5, 3, 3, 2},
{2, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 3, 2},
{2, 3, 5, 4, 4, 5, 4, 4, 5, 4, 4, 5, 4, 4, 5, 3, 2},
{2, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 2},
{2, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 2},
{2, 3, 5, 4, 4, 5, 4, 4, 7, 4, 4, 5, 4, 4, 5, 3, 2},
{2, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 2},
{2, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 2},
{2, 3, 5, 4, 4, 5, 4, 4, 5, 4, 4, 5, 4, 4, 5, 3, 2},
{2, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 3, 2},
{2, 3, 3, 5, 3, 4, 4, 4, 4, 4, 4, 4, 3, 5, 3, 3, 2},
{2, 3, 3, 3, 3, 5, 3, 3, 5, 3, 3, 5, 3, 3, 3, 3, 2},
{2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2},
{2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2}},
{{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6}}};
const unsigned int core[assemblies_x][assemblies_y][assemblies_z] = {
{{0}, {2}}, {{2}, {0}}};
for (auto &cell : coarse_grid.active_cell_iterators())
{
const unsigned int tmp_x =
int(cell_center[0] / pin_pitch_x);
const unsigned int ax = tmp_x / rods_per_assembly_x;
const unsigned int cx = tmp_x - ax * rods_per_assembly_x;
const unsigned tmp_y =
int(cell_center[1] / pin_pitch_y);
const unsigned int ay = tmp_y / rods_per_assembly_y;
const unsigned int cy = tmp_y - ay * rods_per_assembly_y;
const unsigned int az =
(dim == 2 ? 0 :
int(cell_center[dim - 1] / assembly_height));
Assert(ax < assemblies_x, ExcInternalError());
Assert(ay < assemblies_y, ExcInternalError());
Assert(az < assemblies_z, ExcInternalError());
Assert(core[ax][ay][az] < n_assemblies, ExcInternalError());
Assert(cx < rods_per_assembly_x, ExcInternalError());
Assert(cy < rods_per_assembly_y, ExcInternalError());
cell->set_material_id(assembly_materials[core[ax][ay][az]][cx][cy] - 1);
}
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
energy_groups.emplace_back(std::make_unique<EnergyGroup<dim>>(
group, material_data, coarse_grid, fe));
convergence_table_stream.open("convergence_table");
convergence_table_stream.precision(12);
}
template <int dim>
double NeutronDiffusionProblem<dim>::get_total_fission_source() const
{
std::vector<double> fission_sources(parameters.n_groups);
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
tasks += Threads::new_task<>([&, group]() {
fission_sources[
group] = energy_groups[
group]->get_fission_source();
});
return std::accumulate(fission_sources.begin(), fission_sources.end(), 0.0);
}
template <int dim>
void NeutronDiffusionProblem<dim>::refine_grid()
{
std::vector<types::global_dof_index>
n_cells(parameters.n_groups);
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
{
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
energy_groups[
group]->estimate_errors(
group_error_indicators.block(group));
});
}
const float max_error = group_error_indicators.linfty_norm();
const float refine_threshold = 0.3 * max_error;
const float coarsen_threshold = 0.01 * max_error;
{
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
energy_groups[
group]->refine_grid(group_error_indicators.block(group),
refine_threshold,
coarsen_threshold);
});
}
}
template <int dim>
void NeutronDiffusionProblem<dim>::run()
{
boost::io::ios_flags_saver restore_flags(std::cout);
std::cout << std::setprecision(12) << std::fixed;
double k_eff_old = 0.0;
for (unsigned int cycle = 0; cycle < parameters.n_refinement_cycles;
++cycle)
{
std::cout << "Cycle " << cycle << ':' << std::endl;
if (cycle == 0)
{
initialize_problem();
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
energy_groups[group]->setup_linear_system();
}
else
{
refine_grid();
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
energy_groups[group]->solution *= k_eff;
}
std::cout << " Numbers of active cells: ";
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
std::cout << std::endl;
std::cout << " Numbers of degrees of freedom: ";
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
std::cout << energy_groups[group]->n_dofs() << ' ';
std::cout << std::endl << std::endl;
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
[&, group]() { energy_groups[
group]->assemble_system_matrix(); });
double error;
unsigned int iteration = 1;
do
{
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
{
energy_groups[
group]->assemble_ingroup_rhs(
for (unsigned int bgroup = 0; bgroup < parameters.n_groups;
++bgroup)
energy_groups[group]->assemble_cross_group_rhs(
*energy_groups[bgroup]);
energy_groups[
group]->solve();
}
k_eff = get_total_fission_source();
const double flux_ratio = energy_groups[0]->solution.linfty_norm() /
energy_groups[1]->solution.linfty_norm();
const double max_thermal = energy_groups[1]->solution.linfty_norm();
std::cout << "Iter number:" << std::setw(2) << std::right
<< iteration << " k_eff=" << k_eff
<< " flux_ratio=" << flux_ratio
<< " max_thermal=" << max_thermal << std::endl;
k_eff_old = k_eff;
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
{
energy_groups[
group]->solution_old =
energy_groups[
group]->solution;
energy_groups[
group]->solution_old /= k_eff;
}
++iteration;
}
while ((error > parameters.convergence_tolerance) && (iteration < 500));
convergence_table_stream << cycle << ' ' << energy_groups[0]->n_dofs()
<< ' ' << energy_groups[1]->n_dofs() << ' '
<< k_eff << ' '
<< energy_groups[0]->solution.linfty_norm() /
energy_groups[1]->solution.linfty_norm()
<< '\n';
for (
unsigned int group = 0;
group < parameters.n_groups; ++
group)
energy_groups[group]->output_results(cycle);
std::cout << std::endl;
std::cout << " Cycle=" << cycle << ", n_dofs="
<< energy_groups[0]->n_dofs() + energy_groups[1]->n_dofs()
<<
", k_eff=" << k_eff <<
", time=" << timer.
cpu_time()
<< std::endl;
std::cout << std::endl << std::endl;
}
}
}
int main(int argc, char **argv)
{
try
{
using namespace Step28;
std::string filename;
if (argc < 2)
filename = "project.prm";
else
filename = argv[1];
const unsigned int dim = 2;
NeutronDiffusionProblem<dim>::Parameters parameters;
parameters.declare_parameters(parameter_handler);
parameters.get_parameters(parameter_handler);
NeutronDiffusionProblem<dim> neutron_diffusion_problem(parameters);
neutron_diffusion_problem.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
void write_vtu(std::ostream &out) const
void add_data_vector(const VectorType &data, const std::vector< std::string > &names, const DataVectorType type=type_automatic, const std::vector< DataComponentInterpretation::DataComponentInterpretation > &data_component_interpretation={})
virtual void build_patches(const unsigned int n_subdivisions=0)
const unsigned int degree
unsigned int n_dofs_per_cell() const
virtual const FullMatrix< double > & get_prolongation_matrix(const unsigned int child, const RefinementCase< dim > &refinement_case=RefinementCase< dim >::isotropic_refinement) const
void mmult(FullMatrix< number2 > &C, const FullMatrix< number2 > &B, const bool adding=false) const
void vmult(Vector< number2 > &w, const Vector< number2 > &v, const bool adding=false) const
void Tvmult(Vector< number2 > &w, const Vector< number2 > &v, const bool adding=false) const
void Tvmult_add(Vector< number2 > &w, const Vector< number2 > &v) const
long int get_integer(const std::string &entry_string) const
void declare_entry(const std::string &entry, const std::string &default_value, const Patterns::PatternBase &pattern=Patterns::Anything(), const std::string &documentation="", const bool has_to_be_set=false)
double get_double(const std::string &entry_name) const
real_type linfty_norm() const
void cell_matrix(FullMatrix< double > &M, const FEValuesBase< dim > &fe, const FEValuesBase< dim > &fetest, const ArrayView< const std::vector< double > > &velocity, const double factor=1.)
SymmetricTensor< 2, dim, Number > e(const Tensor< 2, dim, Number > &F)
void run(const Iterator &begin, const std_cxx20::type_identity_t< Iterator > &end, Worker worker, Copier copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const unsigned int queue_length, const unsigned int chunk_size)
unsigned int n_cells(const internal::TriangulationImplementation::NumberCache< 1 > &c)






