This tutorial depends on step-8 , step-18 , step-20 , step-40 .
This program was contributed by Daniel Garcia-Sanchez.
Note As a prerequisite of this program, you need to have HDF5 , complex PETSc, and the p4est libraries installed. The installation of deal.II together with these additional libraries is described in the README file.
Introduction
A phononic crystal is a periodic nanostructure that modifies the motion of mechanical vibrations or phonons . Phononic structures can be used to disperse, route and confine mechanical vibrations. These structures have potential applications in quantum information and have been used to study macroscopic quantum phenomena . Phononic crystals are usually fabricated in cleanrooms .
In this tutorial we show how to a design a phononic superlattice cavity which is a particular type of phononic crystal that can be used to confine mechanical vibrations. A phononic superlattice cavity is formed by two Distributed Bragg Reflector , mirrors and a \(\lambda/2\) cavity where \(\lambda\) is the acoustic wavelength. Acoustic DBRs are periodic structures where a set of bilayer stacks with contrasting physical properties (sound velocity index) is repeated \(N\) times. Superlattice cavities are usually grown on a Gallium Arsenide wafer by Molecular Beam Epitaxy . The bilayers correspond to GaAs/AlAs mirror pairs. As shown below, the thickness of the mirror layers (brown and green) is \(\lambda/4\) and the thickness of the cavity (blue) is \(\lambda/2\).
In this tutorial we calculate the band gap and the mechanical resonance of a phononic superlattice cavity but the code presented here can be easily used to design and calculate other types of phononic crystals .
The device is a waveguide in which the wave goes from left to right. The simulations of this tutorial are done in 2D, but the code is dimension independent and can be easily used with 3D simulations. The waveguide width is equal to the \(y\) dimension of the domain and the waveguide length is equal to the \(x\) dimension of the domain. There are two regimes that depend on the waveguide width:
Single mode: In this case the width of the structure is much smaller than the wavelength. This case can be solved either with FEM (the approach that we take here) or with a simple semi-analytical 1D transfer matrix formalism .
Multimode: In this case the width of the structure is larger than the wavelength. This case can be solved using FEM or with a scattering matrix formalism . Although we do not study this case in this tutorial, it is very easy to reach the multimode regime by increasing the parameter waveguide width (dimension_y in the jupyter notebook).
The simulations of this tutorial are performed in the frequency domain. To calculate the transmission spectrum, we use a procedure that is commonly used in time domain FDTD simulations. A pulse at a certain frequency is generated on the left side of the structure and the transmitted energy is measured on the right side of the structure. The simulation is run twice. First, we run the simulation with the phononic structure and measure the transmitted energy:
Then, we run the simulation without the phononic structure and measure the transmitted energy. We use the simulation without the structure for the calibration:
The transmission coefficient corresponds to the energy of the first simulation divided by the calibration energy. We repeat this procedure for each frequency step.
Elastic equations
What we want to simulate here is the transmission of elastic waves. Consequently, the right description of the problem uses the elastic equations, which in the time domain are given by
\[ \rho\partial_{tt} u_i - \partial_j (c_{ijkl} \varepsilon_{kl}) = f_i, \qquad i=0,1,2 \]
where the stiffness tensor \(c_{ijkl}\) depends on the spatial coordinates and the strain is the symmetrized gradient of the displacement, given by
\[ \varepsilon_{kl} =\frac{1}{2}(\partial_k u_l + \partial_l u_k) \]
A perfectly matched layer (PML) can be used to truncate the solution at the boundaries. A PML is a transformation that results in a complex coordinate stretching.
Instead of a time domain approach, this tutorial program converts the equations above into the frequency domain by performing a Fourier transform with regard to the time variable. The elastic equations in the frequency domain then read as follows
\begin{eqnarray*} \nabla\cdot(\boldsymbol{\bar\sigma} \xi \boldsymbol{\Lambda})&=&-\omega^2\rho\xi\mathbf{\bar u}\\ \boldsymbol{\bar \sigma} &=&\mathbf{C}\boldsymbol{\bar\varepsilon}\\ \boldsymbol{\bar\varepsilon}&=&\frac{1}{2}[(\nabla\mathbf{\bar{u}}\boldsymbol{\Lambda}+\boldsymbol{\Lambda}^\mathrm{T}(\nabla\mathbf{\bar{u}})^\mathrm{T})]\\ \xi &=&\prod_i^\textrm{dim}s_i\\ \boldsymbol{\Lambda} &=& \operatorname{diag}(1/s_0,1/s_1,1/s_2)\qquad\textrm{for 3D}\\ \boldsymbol{\Lambda} &=& \operatorname{diag}(1/s_0,1/s_1)\qquad\textrm{for 2D} \end{eqnarray*}
where the coefficients \(s_i = 1+is_i'(x,y,z)\) account for the absorption. There are 3 \(s_i\) coefficients in 3D and 2 in 2D. The imaginary par of \(s_i\) is equal to zero outside the PML. The PMLs are reflectionless only for the exact wave equations. When the set of equations is discretized the PML is no longer reflectionless. The reflections can be made arbitrarily small as long as the medium is slowly varying, see the adiabatic theorem . In the code a quadratic turn-on of the PML has been used. A linear and cubic turn-on is also known to work . These equations can be expanded into
\[ -\omega^2\rho \xi u_m - \partial_n \left(\frac{\xi}{s_n}c_{mnkl} \varepsilon_{kl}\right) = f_m \]
\[ \varepsilon_{kl} =\frac{1}{2}\left(\frac{1}{s_k}\partial_k u_l + \frac{1}{s_l}\partial_l u_k\right) \]
where summation over repeated indices (here \(n\), as well as \(k\) and \(l\)) is as always implied. Note that the strain is no longer symmetric after applying the complex coordinate stretching of the PML. This set of equations can be written as
\[ -\omega^2\rho \xi u_m - \partial_n \left(\frac{\xi c_{mnkl}}{2s_n s_k} \partial_k u_l + \frac{\xi c_{mnkl}}{2s_n s_l} \partial_l u_k\right) = f_m \]
The same as the strain, the stress tensor is not symmetric inside the PML ( \(s_j\neq 0\)). Indeed the fields inside the PML are not physical. It is useful to introduce the tensors \(\alpha_{mnkl}\) and \(\beta_{mnkl}\).
\[ -\omega^2\rho \xi u_m - \partial_n \left(\alpha_{mnkl}\partial_k u_l + \beta_{mnkl}\partial_l u_k\right) = f_m \]
We can multiply by \(\varphi_m\) and integrate over the domain \(\Omega\) and integrate by parts.
\begin{eqnarray*} -\omega^2\int_\Omega\rho\xi\varphi_m u_m + \int_\Omega\partial_n\varphi_m \left(\frac{\xi c_{mnkl}}{2s_n s_k} \partial_k u_l + \frac{\xi c_{mnkl}}{2s_n s_l} \partial_l u_k\right) = \int_\Omega\varphi_m f_m \end{eqnarray*}
It is this set of equations we want to solve for a set of frequencies \(\omega\) in order to compute the transmission coefficient as function of frequency. The linear system becomes
\begin{eqnarray*} AU&=&F\\ A_{ij} &=& -\omega^2\int_\Omega\rho \xi\varphi_m^i \varphi_m^j + \int_\Omega\partial_n\varphi_m^i \left(\frac{\xi c_{mnkl}}{2s_n s_k} \partial_k \varphi_l^j + \frac{\xi c_{mnkl}}{2s_n s_l} \partial_l \varphi_k^j\right)\\ F_i &=& \int_\Omega\varphi_m^i f_m \end{eqnarray*}
Simulation parameters
In this tutorial we use a python jupyter notebook to set up the parameters and run the simulation. First we create a HDF5 file where we store the parameters and the results of the simulation.
Each of the simulations (displacement and calibration) is stored in a separate HDF5 group:
import numpy as np
import h5py
import matplotlib.pyplot as plt
import subprocess
import scipy.constants as constants
import scipy.optimize
plt.rcParams['svg.fonttype' ] = 'none'
h5_file = h5py.File('results.h5' , 'w' )
data = h5_file.create_group('data' )
displacement = data.create_group('displacement' )
calibration = data.create_group('calibration' )
for group in [displacement, calibration]:
group.attrs['dimension_x' ] = 2e-5
group.attrs['dimension_y' ] = 2e-8
group.attrs['probe_pos_x' ] = 8e-6
group.attrs['probe_pos_y' ] = 0
group.attrs['probe_width_y' ] = 2e-08
group.attrs['nb_probe_points' ] = 5
group.attrs['grid_level' ] = 1
group.attrs['cavity_resonance_frequency' ] = 20e9
group.attrs['nb_mirror_pairs' ] = 15
group.attrs['poissons_ratio' ] = 0.27
group.attrs['youngs_modulus' ] = 270000000000.0
group.attrs['material_a_rho' ] = 3200
if group == displacement:
group.attrs['material_b_rho' ] = 2000
else :
group.attrs['material_b_rho' ] = 3200
group.attrs['lambda' ] = (group.attrs['youngs_modulus' ] * group.attrs['poissons_ratio' ] /
((1 + group.attrs['poissons_ratio' ]) *
(1 - 2 * group.attrs['poissons_ratio' ])))
group.attrs['mu' ]= (group.attrs['youngs_modulus' ] / (2 * (1 + group.attrs['poissons_ratio' ])))
group.attrs['max_force_amplitude' ] = 1e26
group.attrs['force_sigma_x' ] = 1e-7
group.attrs['force_sigma_y' ] = 1
group.attrs['max_force_width_x' ] = 3e-7
group.attrs['max_force_width_y' ] = 2e-8
group.attrs['force_x_pos' ] = -8e-6
group.attrs['force_y_pos' ] = 0
group.attrs['pml_x' ] = True
group.attrs['pml_y' ] = False
group.attrs['pml_width_x' ] = 1.8e-6
group.attrs['pml_width_y' ] = 5e-7
group.attrs['pml_coeff' ] = 1.6
group.attrs['pml_coeff_degree' ] = 2
group.attrs['center_frequency' ] = 20e9
group.attrs['frequency_range' ] = 0.5e9
group.attrs['start_frequency' ] = group.attrs['center_frequency' ] - group.attrs['frequency_range' ] / 2
group.attrs['stop_frequency' ] = group.attrs['center_frequency' ] + group.attrs['frequency_range' ] / 2
group.attrs['nb_frequency_points' ] = 400
if group == displacement:
group.attrs['simulation_name' ] = 'phononic_cavity_displacement'
else :
group.attrs['simulation_name' ] = 'phononic_cavity_calibration'
group.attrs['save_vtu_files' ] = False
h5_file.close()
The commented program
Include files
Most of the include files we need for this program have already been discussed in previous programs, in particular in step-40 .
#include <deal.II/base/conditional_ostream.h>
#include <deal.II/base/function.h>
#include <deal.II/base/index_set.h>
#include <deal.II/base/quadrature_lib.h>
#include <deal.II/base/timer.h>
#include <deal.II/base/utilities.h>
#include <deal.II/dofs/dof_accessor.h>
#include <deal.II/dofs/dof_handler.h>
#include <deal.II/dofs/dof_tools.h>
#include <deal.II/fe/fe_q.h>
#include <deal.II/fe/fe_system.h>
#include <deal.II/fe/fe_values.h>
#include <deal.II/grid/grid_generator.h>
#include <deal.II/grid/grid_refinement.h>
#include <deal.II/lac/affine_constraints.h>
#include <deal.II/lac/dynamic_sparsity_pattern.h>
#include <deal.II/lac/full_matrix.h>
#include <deal.II/lac/generic_linear_algebra.h>
#include <deal.II/lac/petsc_solver.h>
#include <deal.II/lac/vector.h>
#include <deal.II/numerics/data_out.h>
#include <deal.II/numerics/error_estimator.h>
#include <fstream>
#include <iostream>
The following header provides the Tensor class that we use to represent the material properties.
#include <deal.II/base/tensor.h>
The following header is necessary for the HDF5 interface of deal.II.
#include <deal.II/base/hdf5.h>
This header is required for the function VectorTools::point_value that we use to evaluate the result of the simulation.
#include <deal.II/numerics/vector_tools.h>
We need this header for the function GridTools::find_active_cell_around_point that we use in the function ElasticWave<dim>::store_frequency_step_data()
#include <deal.II/grid/grid_tools.h>
namespace step62
{
Auxiliary classes and functions
The following classes are used to store the parameters of the simulation.
The RightHandSide class
This class is used to define the force pulse on the left side of the structure:
template <int dim>
class RightHandSide :
public Function <dim>
{
public :
const unsigned int component) const override ;
private :
The variable data is the HDF5::Group in which all the simulation results will be stored. Note that the variables RightHandSide::data, PML::data, Rho::data and Parameters::data point to the same group of the HDF5 file. When a HDF5::Group is copied, it will point to the same group of the HDF5 file.
The simulation parameters are stored in data as HDF5 attributes. The following attributes are defined in the jupyter notebook, stored in data as HDF5 attributes and then read by the constructor.
const double max_force_amplitude;
const double force_sigma_x;
const double force_sigma_y;
const double max_force_width_x;
const double max_force_width_y;
public :
In this particular simulation the force has only a \(x\) component, \(F_y=0\).
const unsigned int force_component = 0;
};
The PML class
This class is used to define the shape of the Perfectly Matches Layer (PML) to absorb waves traveling towards the boundary:
template <int dim>
class PML :
public Function <dim, std::complex<double>>
{
public :
virtual std::complex<double>
private :
HDF5::Group in which all the simulation results will be stored.
The same as before, the following attributes are defined in the jupyter notebook, stored in data as HDF5 attributes and then read by the constructor.
const double pml_coeff;
const int pml_coeff_degree;
const double dimension_x;
const double dimension_y;
const bool pml_x;
const bool pml_y;
const double pml_width_x;
const double pml_width_y;
const double a_coeff_x;
const double a_coeff_y;
};
The Rho class
This class is used to define the mass density.
template <int dim>
{
public :
const unsigned int component = 0) const override ;
private :
HDF5::Group in which all the simulation results will be stored.
The same as before, the following attributes are defined in the jupyter notebook, stored in data as HDF5 attributes and then read by the constructor.
const double lambda;
const double material_a_rho;
const double material_b_rho;
const double cavity_resonance_frequency;
const unsigned int nb_mirror_pairs;
const double dimension_y;
const unsigned int grid_level;
double average_rho_width;
};
The Parameters class
This class contains all the parameters that will be used in the simulation.
template <int dim>
class Parameters
{
public :
HDF5::Group in which all the simulation results will be stored.
The same as before, the following attributes are defined in the jupyter notebook, stored in data as HDF5 attributes and then read by the constructor.
const std::string simulation_name;
const bool save_vtu_files;
const double start_frequency;
const double stop_frequency;
const unsigned int nb_frequency_points;
const double lambda;
const double dimension_x;
const double dimension_y;
const unsigned int nb_probe_points;
const unsigned int grid_level;
const RightHandSide<dim> right_hand_side;
const PML<dim> pml;
const Rho<dim> rho;
private :
const double comparison_float_constant = 1
e -12;
};
The QuadratureCache class
The calculation of the mass and stiffness matrices is very expensive. These matrices are the same for all the frequency steps. The right hand side vector is also the same for all the frequency steps. We use this class to store these objects and re-use them at each frequency step. Note that here we don't store the assembled mass and stiffness matrices and right hand sides, but instead the data for a single cell. QuadratureCache class is very similar to the PointHistory class that has been used in step-18 .
template <int dim>
class QuadratureCache
{
public :
QuadratureCache(const unsigned int dofs_per_cell);
private :
unsigned int dofs_per_cell;
public :
We store the mass and stiffness matrices in the variables mass_coefficient and stiffness_coefficient. We store as well the right_hand_side and JxW values which are going to be the same for all the frequency steps.
std::vector<std::complex<double>> right_hand_side;
double JxW;
};
The get_stiffness_tensor() function
This function returns the stiffness tensor of the material. For the sake of simplicity we consider the stiffness to be isotropic and homogeneous; only the density \(\rho\) depends on the position. As we have previously shown in step-8 , if the stiffness is isotropic and homogeneous, the stiffness coefficients \(c_{ijkl}\) can be expressed as a function of the two coefficients \(\lambda\) and \(\mu\). The coefficient tensor reduces to
\[ c_{ijkl} = \lambda \delta_{ij} \delta_{kl} + \mu (\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk}). \]
template <int dim>
{
for (unsigned int i = 0; i < dim; ++i)
for (unsigned int j = 0; j < dim; ++j)
for (unsigned int k = 0; k < dim; ++k)
for (
unsigned int l = 0;
l < dim; ++
l )
stiffness_tensor[i][j][k][l] =
(((i == k) && (j == l) ?
mu : 0.0) +
((i == l) && (j == k) ?
mu : 0.0) +
((i == j) && (k == l) ? lambda : 0.0));
return stiffness_tensor;
}
The ElasticWave class
Next let's declare the main class of this program. Its structure is very similar to the step-40 tutorial program. The main differences are:
The sweep over the frequency values.
We save the stiffness and mass matrices in quadrature_cache and use them for each frequency step.
We store the measured energy by the probe for each frequency step in the HDF5 file.
template <int dim>
class ElasticWave
{
public :
ElasticWave(const Parameters<dim> ¶meters);
private :
void setup_system();
void assemble_system(const double omega,
const bool calculate_quadrature_data);
void solve();
void initialize_probe_positions_vector();
void store_frequency_step_data(const unsigned int frequency_idx);
void output_results();
This is called before every frequency step to set up a pristine state for the cache variables.
void setup_quadrature_cache();
This function loops over the frequency vector and runs the simulation for each frequency step.
The parameters are stored in this variable.
Parameters<dim> parameters;
MPI_Comm mpi_communicator;
We store the mass and stiffness matrices for each cell this vector.
std::vector<QuadratureCache<dim>> quadrature_cache;
This vector contains the range of frequencies that we are going to simulate.
std::vector<double> frequency;
This vector contains the coordinates \((x,y)\) of the points of the measurement probe.
HDF5 datasets to store the frequency and probe_positions vectors.
HDF5 dataset that stores the values of the energy measured by the proble.
Implementation of the auxiliary classes
The RightHandSide class
The constructor reads all the parameters from the HDF5::Group data using the HDF5::Group::get_attribute() function.
template <int dim>
, data(data)
, max_force_amplitude(data.get_attribute<double>("max_force_amplitude" ))
, force_sigma_x(data.get_attribute<double>("force_sigma_x" ))
, force_sigma_y(data.get_attribute<double>("force_sigma_y" ))
, max_force_width_x(data.get_attribute<double>("max_force_width_x" ))
, max_force_width_y(data.get_attribute<double>("max_force_width_y" ))
, force_center(
Point <dim>(data.get_attribute<double>(
"force_x_pos" ),
data.get_attribute<double>("force_y_pos" )))
{}
This function defines the spatial shape of the force vector pulse which takes the form of a Gaussian function
\begin{align*} F_x &= \left\{ \begin{array}{ll} a \exp(- (\frac{(x-b_x)^2 }{ 2 \sigma_x^2}+\frac{(y-b_y)^2 }{ 2 \sigma_y^2})) & \text{if}\, x_\textrm{min} <x<x_\textrm{max}\, \text{and}\, y_\textrm{min} <y<y_\textrm{max} \\ 0 & \text{otherwise}, \end{array} \right.\\ F_y &= 0 \end{align*}
where \(a\) is the maximum amplitude that takes the force and \(\sigma_x\) and \(\sigma_y\) are the standard deviations for the \(x\) and \(y\) components. Note that the pulse has been cropped to \(x_\textrm{min}<x<x_\textrm{max}\) and \(y_\textrm{min} <y<y_\textrm{max}\).
template <int dim>
double RightHandSide<dim>::value(
const Point<dim> & p,
const unsigned int component) const
if (component == force_component)
{
if (std::abs(p[0] - force_center[0]) < max_force_width_x / 2 &&
std::abs(p[1] - force_center[1]) < max_force_width_y / 2)
{
return max_force_amplitude *
std::exp(-(std::pow(p[0] - force_center[0], 2) /
(2 * std::pow(force_sigma_x, 2)) +
std::pow(p[1] - force_center[1], 2) /
(2 * std::pow(force_sigma_y, 2))));
}
else
{
return 0;
}
}
else
{
return 0;
}
}
The PML class
As before, the constructor reads all the parameters from the HDF5::Group data using the HDF5::Group::get_attribute() function. As we have discussed, a quadratic turn-on of the PML has been defined in the jupyter notebook. It is possible to use a linear, cubic or another power degree by changing the parameter pml_coeff_degree. The parameters pml_x and pml_y can be used to turn on and off the x and y PMLs.
template <int dim>
, data(data)
, pml_coeff(data.get_attribute<double>("pml_coeff" ))
, pml_coeff_degree(data.get_attribute<int>("pml_coeff_degree" ))
, dimension_x(data.get_attribute<double>("dimension_x" ))
, dimension_y(data.get_attribute<double>("dimension_y" ))
, pml_x(data.get_attribute<bool>("pml_x" ))
, pml_y(data.get_attribute<bool>("pml_y" ))
, pml_width_x(data.get_attribute<double>("pml_width_x" ))
, pml_width_y(data.get_attribute<double>("pml_width_y" ))
, a_coeff_x(pml_coeff /
std ::
pow (pml_width_x, pml_coeff_degree))
, a_coeff_y(pml_coeff /
std ::
pow (pml_width_y, pml_coeff_degree))
{}
The PML coefficient for the x component takes the form \(s'_x = a_x x^{\textrm{degree}}\)
template <int dim>
std::complex<double> PML<dim>::value(
const Point<dim> & p,
const unsigned int component) const
double calculated_pml_x_coeff = 0;
double calculated_pml_y_coeff = 0;
if ((component == 0) && pml_x)
{
const double pml_x_start_position = dimension_x / 2 - pml_width_x;
if (std::abs(p[0]) > pml_x_start_position)
{
const double x_prime = std::abs(p[0]) - pml_x_start_position;
calculated_pml_x_coeff =
a_coeff_x * std::pow(x_prime, pml_coeff_degree);
}
}
if ((component == 1) && pml_y)
{
const double pml_y_start_position = dimension_y / 2 - pml_width_y;
if (std::abs(p[1]) > pml_y_start_position)
{
const double y_prime = std::abs(p[1]) - pml_y_start_position;
calculated_pml_y_coeff =
a_coeff_y * std::pow(y_prime, pml_coeff_degree);
}
}
return 1. + std::max(calculated_pml_x_coeff, calculated_pml_y_coeff) *
std::complex<double>(0., 1.);
}
The Rho class
This class is used to define the mass density. As we have explaine before, a phononic superlattice cavity is formed by two Distributed Reflector , mirrors and a \(\lambda/2\) cavity where \(\lambda\) is the acoustic wavelength. Acoustic DBRs are periodic structures where a set of bilayer stacks with contrasting physical properties (sound velocity index) is repeated \(N\) times. The change of in the wave velocity is generated by alternating layers with different density.
template <int dim>
, data(data)
, lambda(data.get_attribute<double>("lambda" ))
,
mu (data.get_attribute<double>(
"mu" ))
, material_a_rho(data.get_attribute<double>("material_a_rho" ))
, material_b_rho(data.get_attribute<double>("material_b_rho" ))
, cavity_resonance_frequency(
data.get_attribute<double>("cavity_resonance_frequency" ))
, nb_mirror_pairs(data.get_attribute<int>("nb_mirror_pairs" ))
, dimension_y(data.get_attribute<double>("dimension_y" ))
, grid_level(data.get_attribute<int>("grid_level" ))
{
In order to increase the precision we use subpixel smoothing .
average_rho_width = dimension_y / (std::pow(2.0, grid_level));
}
template <int dim>
const unsigned int / *component* /) const
The speed of sound is defined by
\[ c = \frac{K_e}{\rho} \]
where \(K_e\) is the effective elastic constant and \(\rho\) the density. Here we consider the case in which the waveguide width is much smaller than the wavelength. In this case it can be shown that for the two dimensional case
\[ K_e = 4\mu\frac{\lambda +\mu}{\lambda+2\mu} \]
and for the three dimensional case \(K_e\) is equal to the Young's modulus.
\[ K_e = \mu\frac{3\lambda +2\mu}{\lambda+\mu} \]
double elastic_constant;
if (dim == 2)
{
elastic_constant = 4 *
mu * (lambda +
mu ) / (lambda + 2 *
mu );
}
else if (dim == 3)
{
elastic_constant =
mu * (3 * lambda + 2 *
mu ) / (lambda +
mu );
}
else
{
}
const double material_a_speed_of_sound =
std::sqrt(elastic_constant / material_a_rho);
const double material_a_wavelength =
material_a_speed_of_sound / cavity_resonance_frequency;
const double material_b_speed_of_sound =
std::sqrt(elastic_constant / material_b_rho);
const double material_b_wavelength =
material_b_speed_of_sound / cavity_resonance_frequency;
The density \(\rho\) takes the following form
where the brown color represents material_a and the green color represents material_b.
for (unsigned int idx = 0; idx < nb_mirror_pairs; idx++)
{
const double layer_transition_center =
material_a_wavelength / 2 +
idx * (material_b_wavelength / 4 + material_a_wavelength / 4);
if (std::abs(p[0]) >=
(layer_transition_center - average_rho_width / 2) &&
std::abs(p[0]) <= (layer_transition_center + average_rho_width / 2))
{
const double coefficient =
(std::abs(p[0]) -
(layer_transition_center - average_rho_width / 2)) /
average_rho_width;
return (1 - coefficient) * material_a_rho +
coefficient * material_b_rho;
}
}
Here we define the subpixel smoothing which improves the precision of the simulation.
for (unsigned int idx = 0; idx < nb_mirror_pairs; idx++)
{
const double layer_transition_center =
material_a_wavelength / 2 +
idx * (material_b_wavelength / 4 + material_a_wavelength / 4) +
material_b_wavelength / 4;
if (std::abs(p[0]) >=
(layer_transition_center - average_rho_width / 2) &&
std::abs(p[0]) <= (layer_transition_center + average_rho_width / 2))
{
const double coefficient =
(std::abs(p[0]) -
(layer_transition_center - average_rho_width / 2)) /
average_rho_width;
return (1 - coefficient) * material_b_rho +
coefficient * material_a_rho;
}
}
then the cavity
if (std::abs(p[0]) <= material_a_wavelength / 2)
{
return material_a_rho;
}
the material_a layers
for (unsigned int idx = 0; idx < nb_mirror_pairs; idx++)
{
const double layer_center =
material_a_wavelength / 2 +
idx * (material_b_wavelength / 4 + material_a_wavelength / 4) +
material_b_wavelength / 4 + material_a_wavelength / 8;
const double layer_width = material_a_wavelength / 4;
if (std::abs(p[0]) >= (layer_center - layer_width / 2) &&
std::abs(p[0]) <= (layer_center + layer_width / 2))
{
return material_a_rho;
}
}
the material_b layers
for (unsigned int idx = 0; idx < nb_mirror_pairs; idx++)
{
const double layer_center =
material_a_wavelength / 2 +
idx * (material_b_wavelength / 4 + material_a_wavelength / 4) +
material_b_wavelength / 8;
const double layer_width = material_b_wavelength / 4;
if (std::abs(p[0]) >= (layer_center - layer_width / 2) &&
std::abs(p[0]) <= (layer_center + layer_width / 2))
{
return material_b_rho;
}
}
and finally the default is material_a.
The Parameters class
The constructor reads all the parameters from the HDF5::Group data using the HDF5::Group::get_attribute() function.
template <int dim>
: data(data)
, simulation_name(data.get_attribute<
std ::string>(
"simulation_name" ))
, save_vtu_files(data.get_attribute<bool>("save_vtu_files" ))
, start_frequency(data.get_attribute<double>("start_frequency" ))
, stop_frequency(data.get_attribute<double>("stop_frequency" ))
, nb_frequency_points(data.get_attribute<int>("nb_frequency_points" ))
, lambda(data.get_attribute<double>("lambda" ))
,
mu (data.get_attribute<double>(
"mu" ))
, dimension_x(data.get_attribute<double>("dimension_x" ))
, dimension_y(data.get_attribute<double>("dimension_y" ))
, nb_probe_points(data.get_attribute<int>("nb_probe_points" ))
, grid_level(data.get_attribute<int>("grid_level" ))
, probe_start_point(data.get_attribute<double>("probe_pos_x" ),
data.get_attribute<double>("probe_pos_y" ) -
data.get_attribute<double>("probe_width_y" ) / 2)
, probe_stop_point(data.get_attribute<double>("probe_pos_x" ),
data.get_attribute<double>("probe_pos_y" ) +
data.get_attribute<double>("probe_width_y" ) / 2)
, right_hand_side(data)
, pml(data)
, rho(data)
{}
The QuadratureCache class
We need to reserve enough space for the mass and stiffness matrices and the right hand side vector.
template <int dim>
QuadratureCache<dim>::QuadratureCache(const unsigned int dofs_per_cell)
: dofs_per_cell(dofs_per_cell)
, mass_coefficient(dofs_per_cell, dofs_per_cell)
, stiffness_coefficient(dofs_per_cell, dofs_per_cell)
, right_hand_side(dofs_per_cell)
{}
Implementation of the ElasticWave class
Constructor
This is very similar to the constructor of step-40 . In addition we create the HDF5 datasets frequency_dataset, position_dataset and displacement. Note the use of the template keyword for the creation of the HDF5 datasets. It is a C++ requirement to use the template keyword in order to treat create_dataset as a dependent template name.
template <int dim>
ElasticWave<dim>::ElasticWave(const Parameters<dim> ¶meters)
: parameters(parameters)
, mpi_communicator(MPI_COMM_WORLD)
, triangulation(mpi_communicator,
, quadrature_formula(2)
, dof_handler(triangulation)
, frequency(parameters.nb_frequency_points)
, probe_positions(parameters.nb_probe_points, dim)
, frequency_dataset(parameters.data.template create_dataset<double>(
"frequency" ,
std ::vector<hsize_t>{parameters.nb_frequency_points}))
, probe_positions_dataset(parameters.data.template create_dataset<double>(
"position" ,
std::vector<hsize_t>{parameters.nb_probe_points, dim}))
, displacement(
parameters.data.template create_dataset<std::complex<double>>(
"displacement" ,
std::vector<hsize_t>{parameters.nb_probe_points,
parameters.nb_frequency_points}))
, pcout(std::cout,
, computing_timer(mpi_communicator,
pcout,
{}
ElasticWave::setup_system
There is nothing new in this function, the only difference with step-40 is that we don't have to apply boundary conditions because we use the PMLs to truncate the domain.
template <int dim>
void ElasticWave<dim>::setup_system()
{
locally_relevant_solution.reinit(locally_owned_dofs,
locally_relevant_dofs,
mpi_communicator);
system_rhs.
reinit (locally_owned_dofs, mpi_communicator);
constraints.clear();
constraints.reinit(locally_relevant_dofs);
constraints.close();
dsp,
mpi_communicator,
locally_relevant_dofs);
system_matrix.reinit(locally_owned_dofs,
locally_owned_dofs,
dsp,
mpi_communicator);
}
ElasticWave::assemble_system
This function is also very similar to step-40 , though there are notable differences. We assemble the system for each frequency/omega step. In the first step we set calculate_quadrature_data = True and we calculate the mass and stiffness matrices and the right hand side vector. In the subsequent steps we will use that data to accelerate the calculation.
template <int dim>
void ElasticWave<dim>::assemble_system(const double omega,
const bool calculate_quadrature_data)
{
quadrature_formula,
const unsigned int n_q_points = quadrature_formula.
size ();
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
Here we store the value of the right hand side, rho and the PML.
std::vector<Vector<double>> rhs_values(n_q_points,
Vector<double> (dim));
std::vector<double> rho_values(n_q_points);
std::vector<Vector<std::complex<double>>> pml_values(
n_q_points,
Vector <std::complex<double>>(dim));
We calculate the stiffness tensor for the \(\lambda\) and \(\mu\) that have been defined in the jupyter notebook. Note that contrary to \(\rho\) the stiffness is constant among for the whole domain.
get_stiffness_tensor<dim>(parameters.lambda, parameters.mu);
We use the same method of step-20 for vector-valued problems.
if (cell->is_locally_owned())
{
cell_rhs = 0;
We have to calculate the values of the right hand side, rho and the PML only if we are going to calculate the mass and the stiffness matrices. Otherwise we can skip this calculation which considerably reduces the total calculation time.
if (calculate_quadrature_data)
{
parameters.right_hand_side.vector_value_list(
rho_values);
parameters.pml.vector_value_list(
}
We have done this in step-18 . Get a pointer to the quadrature cache data local to the present cell, and, as a defensive measure, make sure that this pointer is within the bounds of the global array:
QuadratureCache<dim> *local_quadrature_points_data =
reinterpret_cast< QuadratureCache<dim> *> (cell->user_pointer());
Assert (local_quadrature_points_data >= &quadrature_cache.front(),
Assert (local_quadrature_points_data <= &quadrature_cache.back(),
for (unsigned int q = 0; q < n_q_points; ++q)
{
The quadrature_data variable is used to store the mass and stiffness matrices, the right hand side vector and the value of JxW.
QuadratureCache<dim> &quadrature_data =
local_quadrature_points_data[q];
Below we declare the force vector and the parameters of the PML \(s\) and \(\xi\).
std::complex<double> xi(1, 0);
The following block is calculated only in the first frequency step.
if (calculate_quadrature_data)
{
Store the value of JxW.
quadrature_data.JxW = fe_values.
JxW (q);
for (unsigned int component = 0; component < dim; ++component)
{
Convert vectors to tensors and calculate xi
force[component] = rhs_values[q][component];
s[component] = pml_values[q][component];
xi *= s[component];
}
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
fe_values[displacement].value(i, q);
fe_values[displacement].gradient(i, q);
for (unsigned int j = 0; j < dofs_per_cell; ++j)
{
fe_values[displacement].value(j, q);
fe_values[displacement].gradient(j, q);
calculate the values of the mass matrix.
quadrature_data.mass_coefficient[i][j] =
rho_values[q] * xi * phi_i * phi_j;
Loop over the \(mnkl\) indices of the stiffness tensor.
std::complex<double> stiffness_coefficient = 0;
for (unsigned int m = 0; m < dim; ++m)
for (unsigned int n = 0; n < dim; ++n)
for (unsigned int k = 0; k < dim; ++k)
for (
unsigned int l = 0;
l < dim; ++
l )
{
Here we calculate the tensors \(\alpha_{mnkl}\) and \(\beta_{mnkl}\)
const std::complex<double> alpha =
xi * stiffness_tensor[m][n][k][
l ] /
(2.0 * s[n] * s[k]);
const std::complex<double> beta =
xi * stiffness_tensor[m][n][k][
l ] /
Here we calculate the stiffness matrix. Note that the stiffness matrix is not symmetric because of the PMLs. We use the gradient function (see the documentation ) which is a Tensor <2,dim>
\[ G_{ij}= \frac{\partial\phi_i}{\partial x_j} =\partial_j \phi_i \]
Note the position of the indices \(i\) and \(j\) and the notation that we use in this tutorial: \(\partial_j\phi_i\). As the stiffness tensor is not symmetric, it is very easy to make a mistake.
stiffness_coefficient +=
grad_phi_i[m][n] *
(alpha * grad_phi_j[
l ][k] +
beta * grad_phi_j[k][
l ]);
}
We save the value of the stiffness matrix in quadrature_data
quadrature_data.stiffness_coefficient[i][j] =
stiffness_coefficient;
}
and the value of the right hand side in quadrature_data.
quadrature_data.right_hand_side[i] =
phi_i * force * fe_values.
JxW (q);
}
}
We loop again over the degrees of freedom of the cells to calculate the system matrix. These loops are really quick because we have already calculated the stiffness and mass matrices, only the value of \(\omega\) changes.
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
for (unsigned int j = 0; j < dofs_per_cell; ++j)
{
std::complex<double> matrix_sum = 0;
matrix_sum += -std::pow(omega, 2) *
quadrature_data.mass_coefficient[i][j];
matrix_sum += quadrature_data.stiffness_coefficient[i][j];
}
cell_rhs(i) += quadrature_data.right_hand_side[i];
}
}
cell->get_dof_indices(local_dof_indices);
constraints.distribute_local_to_global(cell_matrix,
cell_rhs,
local_dof_indices,
system_matrix,
system_rhs);
}
}
ElasticWave::solve
This is even more simple than in step-40 . We use the parallel direct solver MUMPS which requires less options than an iterative solver. The drawback is that it does not scale very well. It is not straightforward to solve the Helmholtz equation with an iterative solver. The shifted Laplacian multigrid method is a well known approach to precondition this system, but this is beyond the scope of this tutorial.
template <int dim>
void ElasticWave<dim>::solve()
{
locally_owned_dofs, mpi_communicator);
solver.solve(system_matrix, completely_distributed_solution, system_rhs);
pcout <<
" Solved in " << solver_control.
last_step () <<
" iterations." << std::endl;
constraints.distribute(completely_distributed_solution);
locally_relevant_solution = completely_distributed_solution;
}
ElasticWave::initialize_position_vector
We use this function to calculate the values of the position vector.
template <int dim>
void ElasticWave<dim>::initialize_probe_positions_vector()
{
for (unsigned int position_idx = 0;
position_idx < parameters.nb_probe_points;
++position_idx)
{
Because of the way the operator + and - are overloaded to subtract two points, the following has to be done: Point_b<dim> + (-Point_a<dim>)
(position_idx / ((double)(parameters.nb_probe_points - 1))) *
(parameters.probe_stop_point + (-parameters.probe_start_point)) +
parameters.probe_start_point;
probe_positions[position_idx][0] = p[0];
probe_positions[position_idx][1] = p[1];
if (dim == 3)
{
probe_positions[position_idx][2] = p[2];
}
}
}
ElasticWave::store_frequency_step_data
This function stores in the HDF5 file the measured energy by the probe.
template <int dim>
void
ElasticWave<dim>::store_frequency_step_data(const unsigned int frequency_idx)
{
We store the displacement in the \(x\) direction; the displacement in the \(y\) direction is negligible.
const unsigned int probe_displacement_component = 0;
The vector coordinates contains the coordinates in the HDF5 file of the points of the probe that are located in locally owned cells. The vector displacement_data contains the value of the displacement at these points.
std::vector<hsize_t> coordinates;
std::vector<std::complex<double>> displacement_data;
for (unsigned int position_idx = 0;
position_idx < parameters.nb_probe_points;
++position_idx)
{
for (unsigned int dim_idx = 0; dim_idx < dim; ++dim_idx)
{
point [dim_idx] = probe_positions[position_idx][dim_idx];
}
bool point_in_locally_owned_cell;
{
First we have to find out if the point is in a locally owned cell.
const std::pair<typename DoFHandler<dim>::active_cell_iterator,
dof_handler,
point);
point_in_locally_owned_cell = cell_point.first->is_locally_owned();
}
if (point_in_locally_owned_cell)
{
Then we can store the values of the displacement in the points of the probe in displacement_data.
locally_relevant_solution,
point,
tmp_vector);
coordinates.emplace_back(position_idx);
coordinates.emplace_back(frequency_idx);
displacement_data.emplace_back(
tmp_vector(probe_displacement_component));
}
}
We write the displacement data in the HDF5 file. The call HDF5::DataSet::write_selection() is MPI collective which means that all the processes have to participate.
if (coordinates.size() > 0)
{
displacement.write_selection(displacement_data, coordinates);
}
Therefore even if the process has no data to write it has to participate in the collective call. For this we can use HDF5::DataSet::write_none() . Note that we have to specify the data type, in this case std::complex<double>.
else
{
displacement.write_none<std::complex<double>>();
}
If the variable save_vtu_files in the input file equals True then all the data will be saved as vtu. The procedure to write vtu files has been described in step-40 .
if (parameters.save_vtu_files)
{
std::vector<std::string> solution_names(1, "displacement_x" );
if (dim >= 2)
{
solution_names.emplace_back("displacement_y" );
}
if (dim == 3)
{
solution_names.emplace_back("displacement_z" );
}
std::vector<DataComponentInterpretation::DataComponentInterpretation>
locally_relevant_solution,
solution_names,
interpretation);
for (unsigned int i = 0; i < subdomain.size(); ++i)
subdomain(i) = triangulation.locally_owned_subdomain();
std::vector<Vector<double>> force(
std::vector<Vector<double>> pml(
for (auto &cell : triangulation.active_cell_iterators())
{
if (cell->is_locally_owned())
{
for (unsigned int dim_idx = 0; dim_idx < dim; ++dim_idx)
{
force[dim_idx](cell->active_cell_index()) =
parameters.right_hand_side.value(cell->center(), dim_idx);
pml[dim_idx](cell->active_cell_index()) =
parameters.pml.value(cell->center(), dim_idx).imag();
}
rho(cell->active_cell_index()) =
parameters.rho.value(cell->center());
}
And on the cells that we are not interested in, set the respective value to a bogus value in order to make sure that if we were somehow wrong about our assumption we would find out by looking at the graphical output:
else
{
for (unsigned int dim_idx = 0; dim_idx < dim; ++dim_idx)
{
force[dim_idx](cell->active_cell_index()) = -1e+20;
pml[dim_idx](cell->active_cell_index()) = -1e+20;
}
rho(cell->active_cell_index()) = -1e+20;
}
}
for (unsigned int dim_idx = 0; dim_idx < dim; ++dim_idx)
{
"force_" + std::to_string(dim_idx));
"pml_" + std::to_string(dim_idx));
}
std::stringstream frequency_idx_stream;
const unsigned int nb_number_positions =
((unsigned int)std::log10(parameters.nb_frequency_points)) + 1;
frequency_idx_stream << std::setw(nb_number_positions)
<< std::setfill('0' ) << frequency_idx;
std::string filename = (parameters.simulation_name + "_" +
frequency_idx_stream.str() + ".vtu" );
}
}
ElasticWave::output_results
This function writes the datasets that have not already been written.
template <int dim>
void ElasticWave<dim>::output_results()
{
The vectors frequency and position are the same for all the processes. Therefore any of the processes can write the corresponding datasets. Because the call HDF5::DataSet::write is MPI collective, the rest of the processes will have to call HDF5::DataSet::write_none .
{
frequency_dataset.write(frequency);
probe_positions_dataset.write(probe_positions);
}
else
{
frequency_dataset.write_none<double >();
probe_positions_dataset.write_none<double >();
}
}
ElasticWave::setup_quadrature_cache
We use this function at the beginning of our computations to set up initial values of the cache variables. This function has been described in step-18 . There are no differences with the function of step-18 .
template <int dim>
void ElasticWave<dim>::setup_quadrature_cache()
{
triangulation.clear_user_data();
{
std::vector<QuadratureCache<dim>> tmp;
quadrature_cache.swap(tmp);
}
quadrature_cache.resize(triangulation.n_locally_owned_active_cells() *
quadrature_formula.
size (),
unsigned int cache_index = 0;
for (const auto &cell : triangulation.active_cell_iterators())
if (cell->is_locally_owned())
{
cell->set_user_pointer(&quadrature_cache[cache_index]);
cache_index += quadrature_formula.
size ();
}
}
ElasticWave::frequency_sweep
For clarity we divide the function run of step-40 into the functions run and frequency_sweep. In the function frequency_sweep we place the iteration over the frequency vector.
template <int dim>
void ElasticWave<dim>::frequency_sweep()
{
for (unsigned int frequency_idx = 0;
frequency_idx < parameters.nb_frequency_points;
++frequency_idx)
{
pcout << parameters.simulation_name + " frequency idx: "
<< frequency_idx << '/' << parameters.nb_frequency_points - 1
<< std::endl;
setup_system();
if (frequency_idx == 0)
{
pcout << " Number of active cells : "
<< triangulation.n_active_cells() << std::endl;
pcout << " Number of degrees of freedom : "
<< dof_handler.
n_dofs () << std::endl;
}
if (frequency_idx == 0)
{
Write the simulation parameters only once
parameters.data.set_attribute("active_cells" ,
triangulation.n_active_cells());
parameters.data.set_attribute("degrees_of_freedom" ,
}
We calculate the frequency and omega values for this particular step.
const double current_loop_frequency =
(parameters.start_frequency +
frequency_idx *
(parameters.stop_frequency - parameters.start_frequency) /
(parameters.nb_frequency_points - 1));
const double current_loop_omega =
In the first frequency step we calculate the mass and stiffness matrices and the right hand side. In the subsequent frequency steps we will use those values. This improves considerably the calculation time.
assemble_system(current_loop_omega,
(frequency_idx == 0) ? true : false );
solve();
frequency[frequency_idx] = current_loop_frequency;
store_frequency_step_data(frequency_idx);
computing_timer.print_summary();
computing_timer.reset();
pcout << std::endl;
}
}
ElasticWave::run
This function is very similar to the one in step-40 .
template <int dim>
void ElasticWave<dim>::run()
{
#ifdef DEBUG
pcout << "Debug mode" << std::endl;
#else
pcout << "Release mode" << std::endl;
#endif
{
p1(0) = -parameters.dimension_x / 2;
p1(1) = -parameters.dimension_y / 2;
if (dim == 3)
{
p1(2) = -parameters.dimension_y / 2;
}
p2(0) = parameters.dimension_x / 2;
p2(1) = parameters.dimension_y / 2;
if (dim == 3)
{
p2(2) = parameters.dimension_y / 2;
}
std::vector<unsigned int> divisions(dim);
divisions[0] = int(parameters.dimension_x / parameters.dimension_y);
divisions[1] = 1;
if (dim == 3)
{
divisions[2] = 1;
}
divisions,
p1,
p2);
}
triangulation.refine_global(parameters.grid_level);
setup_quadrature_cache();
initialize_probe_positions_vector();
frequency_sweep();
output_results();
}
}
The main function
The main function is very similar to the one in step-40 .
int main(int argc, char *argv[])
{
try
{
const unsigned int dim = 2;
MPI_COMM_WORLD);
{
Displacement simulation. The parameters are read from the displacement HDF5 group and the results are saved in the same HDF5 group.
auto displacement = data.
open_group (
"displacement" );
step62::Parameters<dim> parameters(displacement);
step62::ElasticWave<dim> elastic_problem(parameters);
elastic_problem.run();
}
{
Calibration simulation. The parameters are read from the calibration HDF5 group and the results are saved in the same HDF5 group.
auto calibration = data.
open_group (
"calibration" );
step62::Parameters<dim> parameters(calibration);
step62::ElasticWave<dim> elastic_problem(parameters);
elastic_problem.run();
}
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
Results
Resonance frequency and bandgap
The results are analyzed in the jupyter notebook with the following code
h5_file = h5py.File('results.h5' , 'r')
data = h5_file['data' ]
def resonance_f(freq, freq_m, quality_factor, max_amplitude):
omega = 2 * constants.pi * freq
omega_m = 2 * constants.pi * freq_m
gamma = omega_m / quality_factor
return max_amplitude * omega_m**2 * gamma**2 / (((omega_m**2 - omega**2)**2 + gamma**2 * omega**2))
frequency = data['displacement' ]['frequency' ][...]
displacement = np.mean(data['displacement' ]['displacement' ], axis=0)
calibration_displacement = np.mean(data['calibration' ]['displacement' ], axis=0)
reflection_coefficient = displacement / calibration_displacement
reflectivity = (np.abs(np.mean(data['displacement' ]['displacement' ][...]**2, axis=0))/
np.abs(np.mean(data['calibration' ]['displacement' ][...]**2, axis=0)))
try :
x_data = frequency
y_data = reflectivity
quality_factor_guess = 1e3
freq_guess = x_data[np.argmax(y_data)]
amplitude_guess = np.max(y_data)
fit_result, covariance = scipy.optimize.curve_fit(resonance_f, x_data, y_data,
[freq_guess, quality_factor_guess, amplitude_guess])
freq_m = fit_result[0]
quality_factor = np.abs(fit_result[1])
max_amplitude = fit_result[2]
y_data_fit = resonance_f(x_data, freq_m, quality_factor, max_amplitude)
fig = plt.figure()
plt.plot(frequency / 1e9, reflectivity, frequency / 1e9, y_data_fit)
plt.xlabel('frequency (GHz)' )
plt.ylabel('amplitude^2 (a.u.)' )
plt.title('Transmission\n' + 'freq = ' + "%.7g" % (freq_guess / 1e9) + 'GHz Q = ' + "%.6g" % quality_factor)
except :
fig = plt.figure()
plt.plot(frequency / 1e9, reflectivity)
plt.xlabel('frequency (GHz)' )
plt.ylabel('amplitude^2 (a.u.)' )
plt.title('Transmission' )
fig = plt.figure()
plt.plot(frequency / 1e9, np.angle(reflection_coefficient))
plt.xlabel('frequency (GHz)' )
plt.ylabel('phase (rad)' )
plt.title('Phase (transmission coefficient)\n' )
plt.show()
h5_file.close()
A phononic cavity is characterized by the resonance frequency and the the quality factor . The quality factor is equal to the ratio between the stored energy in the resonator and the energy dissipated energy per cycle, which is approximately equivalent to the ratio between the resonance frequency and the full width at half maximum (FWHM) . The FWHM is equal to the bandwidth over which the power of vibration is greater than half the power at the resonant frequency.
\[ Q = \frac{f_r}{\Delta f} = \frac{\omega_r}{\Delta \omega} = 2 \pi \times \frac{\text{energy stored}}{\text{energy dissipated per cycle}} \]
The square of the amplitude of the mechanical resonance \(a^2\) as a function of the frequency has a gaussian shape
\[ a^2 = a_\textrm{max}^2\frac{\omega^2\Gamma^2}{(\omega_r^2-\omega^2)^2+\Gamma^2\omega^2} \]
where \(f_r = \frac{\omega_r}{2\pi}\) is the resonance frequency and \(\Gamma=\frac{\omega_r}{Q}\) is the dissipation rate. We used the previous equation in the jupyter notebook to fit the mechanical resonance.
Given the values we have chosen for the parameters, one could estimate the resonance frequency analytically. Indeed, this is then confirmed by what we get in this program: the phononic superlattice cavity exhibits a mechanical resonance at 20GHz and a quality factor of 5046. The following images show the transmission amplitude and phase as a function of frequency in the vicinity of the resonance frequency:
The images above suggest that the periodic structure has its intended effect: It really only lets waves of a very specific frequency pass through, whereas all other waves are reflected. This is of course precisely what one builds these sorts of devices for. But it is not quite this easy. In practice, there is really only a "band gap", i.e., the device blocks waves other than the desired one at 20GHz only within a certain frequency range. Indeed, to find out how large this "gap" is within which waves are blocked, we can extend the frequency range to 16 GHz through the appropriate parameters in the input file. We then obtain the following image:
What this image suggests is that in the range of around 18 to around 22 GHz, really only the waves with a frequency of 20 GHz are allowed to pass through, but beyond this range, there are plenty of other frequencies that can pass through the device.
Mode profile
We can inspect the mode profile with Paraview or Visit. As we have discussed, at resonance all the mechanical energy is transmitted and the amplitude of motion is amplified inside the cavity. It can be observed that the PMLs are quite effective to truncate the solution. The following image shows the mode profile at resonance:
On the other hand, out of resonance all the mechanical energy is reflected. The following image shows the profile at 19.75 GHz. Note the interference between the force pulse and the reflected wave at the position \(x=-8\mu\textrm{m}\).
Experimental applications
Phononic superlattice cavities find application in quantum optomechanics . Here we have presented the simulation of a 2D superlattice cavity, but this code can be used as well to simulate "real world" 3D devices such as micropillar superlattice cavities , which are promising candidates to study macroscopic quantum phenomena. The 20GHz mode of a micropillar superlattice cavity is essentially a mechanical harmonic oscillator that is very well isolated from the environment. If the device is cooled down to 20mK in a dilution fridge, the mode would then become a macroscopic quantum harmonic oscillator.
The plain program
#include <deal.II/base/conditional_ostream.h>
#include <deal.II/base/function.h>
#include <deal.II/base/index_set.h>
#include <deal.II/base/quadrature_lib.h>
#include <deal.II/base/timer.h>
#include <deal.II/base/utilities.h>
#include <deal.II/dofs/dof_accessor.h>
#include <deal.II/dofs/dof_handler.h>
#include <deal.II/dofs/dof_tools.h>
#include <deal.II/fe/fe_q.h>
#include <deal.II/fe/fe_system.h>
#include <deal.II/fe/fe_values.h>
#include <deal.II/grid/grid_generator.h>
#include <deal.II/grid/grid_refinement.h>
#include <deal.II/lac/affine_constraints.h>
#include <deal.II/lac/dynamic_sparsity_pattern.h>
#include <deal.II/lac/full_matrix.h>
#include <deal.II/lac/generic_linear_algebra.h>
#include <deal.II/lac/petsc_solver.h>
#include <deal.II/lac/vector.h>
#include <deal.II/numerics/data_out.h>
#include <deal.II/numerics/error_estimator.h>
#include <fstream>
#include <iostream>
#include <deal.II/base/tensor.h>
#include <deal.II/base/hdf5.h>
#include <deal.II/numerics/vector_tools.h>
#include <deal.II/grid/grid_tools.h>
namespace step62
{
template <int dim>
class RightHandSide :
public Function <dim>
{
public :
const unsigned int component) const override ;
private :
const double max_force_amplitude;
const double force_sigma_x;
const double force_sigma_y;
const double max_force_width_x;
const double max_force_width_y;
public :
const unsigned int force_component = 0;
};
template <int dim>
class PML :
public Function <dim, std::complex<double>>
{
public :
virtual std::complex<double>
value(
const Point<dim> &p,
const unsigned int component)
const override ;
private :
const double pml_coeff;
const int pml_coeff_degree;
const double dimension_x;
const double dimension_y;
const bool pml_x;
const bool pml_y;
const double pml_width_x;
const double pml_width_y;
const double a_coeff_x;
const double a_coeff_y;
};
template <int dim>
{
public :
const unsigned int component = 0) const override ;
private :
const double lambda;
const double material_a_rho;
const double material_b_rho;
const double cavity_resonance_frequency;
const unsigned int nb_mirror_pairs;
const double dimension_y;
const unsigned int grid_level;
double average_rho_width;
};
template <int dim>
class Parameters
{
public :
const std::string simulation_name;
const bool save_vtu_files;
const double start_frequency;
const double stop_frequency;
const unsigned int nb_frequency_points;
const double lambda;
const double dimension_x;
const double dimension_y;
const unsigned int nb_probe_points;
const unsigned int grid_level;
const RightHandSide<dim> right_hand_side;
const PML<dim> pml;
const Rho<dim> rho;
private :
const double comparison_float_constant = 1
e -12;
};
template <int dim>
class QuadratureCache
{
public :
QuadratureCache(const unsigned int dofs_per_cell);
private :
unsigned int dofs_per_cell;
public :
std::vector<std::complex<double>> right_hand_side;
double JxW;
};
template <int dim>
{
for (unsigned int i = 0; i < dim; ++i)
for (unsigned int j = 0; j < dim; ++j)
for (unsigned int k = 0; k < dim; ++k)
for (
unsigned int l = 0;
l < dim; ++
l )
stiffness_tensor[i][j][k][l] =
(((i == k) && (j == l) ?
mu : 0.0) +
((i == l) && (j == k) ?
mu : 0.0) +
((i == j) && (k == l) ? lambda : 0.0));
return stiffness_tensor;
}
template <int dim>
class ElasticWave
{
public :
ElasticWave(const Parameters<dim> ¶meters);
private :
void setup_system();
void assemble_system(const double omega,
const bool calculate_quadrature_data);
void solve();
void initialize_probe_positions_vector();
void store_frequency_step_data(const unsigned int frequency_idx);
void output_results();
void setup_quadrature_cache();
void frequency_sweep();
Parameters<dim> parameters;
MPI_Comm mpi_communicator;
std::vector<QuadratureCache<dim>> quadrature_cache;
std::vector<double> frequency;
};
template <int dim>
, data(data)
, max_force_amplitude(data.get_attribute<double>("max_force_amplitude" ))
, force_sigma_x(data.get_attribute<double>("force_sigma_x" ))
, force_sigma_y(data.get_attribute<double>("force_sigma_y" ))
, max_force_width_x(data.get_attribute<double>("max_force_width_x" ))
, max_force_width_y(data.get_attribute<double>("max_force_width_y" ))
, force_center(
Point <dim>(data.get_attribute<double>(
"force_x_pos" ),
data.get_attribute<double>("force_y_pos" )))
{}
template <int dim>
double RightHandSide<dim>::value(
const Point<dim> & p,
const unsigned int component) const
{
if (component == force_component)
{
if (std::abs(p[0] - force_center[0]) < max_force_width_x / 2 &&
std::abs(p[1] - force_center[1]) < max_force_width_y / 2)
{
return max_force_amplitude *
std::exp(-(std::pow(p[0] - force_center[0], 2) /
(2 * std::pow(force_sigma_x, 2)) +
std::pow(p[1] - force_center[1], 2) /
(2 * std::pow(force_sigma_y, 2))));
}
else
{
return 0;
}
}
else
{
return 0;
}
}
template <int dim>
, data(data)
, pml_coeff(data.get_attribute<double>("pml_coeff" ))
, pml_coeff_degree(data.get_attribute<int>("pml_coeff_degree" ))
, dimension_x(data.get_attribute<double>("dimension_x" ))
, dimension_y(data.get_attribute<double>("dimension_y" ))
, pml_x(data.get_attribute<bool>("pml_x" ))
, pml_y(data.get_attribute<bool>("pml_y" ))
, pml_width_x(data.get_attribute<double>("pml_width_x" ))
, pml_width_y(data.get_attribute<double>("pml_width_y" ))
, a_coeff_x(pml_coeff /
std ::pow(pml_width_x, pml_coeff_degree))
, a_coeff_y(pml_coeff /
std ::pow(pml_width_y, pml_coeff_degree))
{}
template <int dim>
std::complex<double> PML<dim>::value(
const Point<dim> & p,
const unsigned int component) const
{
double calculated_pml_x_coeff = 0;
double calculated_pml_y_coeff = 0;
if ((component == 0) && pml_x)
{
const double pml_x_start_position = dimension_x / 2 - pml_width_x;
if (std::abs(p[0]) > pml_x_start_position)
{
const double x_prime = std::abs(p[0]) - pml_x_start_position;
calculated_pml_x_coeff =
a_coeff_x * std::pow(x_prime, pml_coeff_degree);
}
}
if ((component == 1) && pml_y)
{
const double pml_y_start_position = dimension_y / 2 - pml_width_y;
if (std::abs(p[1]) > pml_y_start_position)
{
const double y_prime = std::abs(p[1]) - pml_y_start_position;
calculated_pml_y_coeff =
a_coeff_y * std::pow(y_prime, pml_coeff_degree);
}
}
return 1. + std::max(calculated_pml_x_coeff, calculated_pml_y_coeff) *
std::complex<double>(0., 1.);
}
template <int dim>
, data(data)
, lambda(data.get_attribute<double>("lambda" ))
,
mu (data.get_attribute<double>(
"mu" ))
, material_a_rho(data.get_attribute<double>("material_a_rho" ))
, material_b_rho(data.get_attribute<double>("material_b_rho" ))
, cavity_resonance_frequency(
data.get_attribute<double>("cavity_resonance_frequency" ))
, nb_mirror_pairs(data.get_attribute<int>("nb_mirror_pairs" ))
, dimension_y(data.get_attribute<double>("dimension_y" ))
, grid_level(data.get_attribute<int>("grid_level" ))
{
average_rho_width = dimension_y / (std::pow(2.0, grid_level));
data .set_attribute(
"average_rho_width" , average_rho_width);
}
template <int dim>
const unsigned int ) const
{
double elastic_constant;
if (dim == 2)
{
elastic_constant = 4 *
mu * (lambda +
mu ) / (lambda + 2 *
mu );
}
else if (dim == 3)
{
elastic_constant =
mu * (3 * lambda + 2 *
mu ) / (lambda +
mu );
}
else
{
}
const double material_a_speed_of_sound =
std::sqrt(elastic_constant / material_a_rho);
const double material_a_wavelength =
material_a_speed_of_sound / cavity_resonance_frequency;
const double material_b_speed_of_sound =
std::sqrt(elastic_constant / material_b_rho);
const double material_b_wavelength =
material_b_speed_of_sound / cavity_resonance_frequency;
for (unsigned int idx = 0; idx < nb_mirror_pairs; idx++)
{
const double layer_transition_center =
material_a_wavelength / 2 +
idx * (material_b_wavelength / 4 + material_a_wavelength / 4);
if (std::abs(p[0]) >=
(layer_transition_center - average_rho_width / 2) &&
std::abs(p[0]) <= (layer_transition_center + average_rho_width / 2))
{
const double coefficient =
(std::abs(p[0]) -
(layer_transition_center - average_rho_width / 2)) /
average_rho_width;
return (1 - coefficient) * material_a_rho +
coefficient * material_b_rho;
}
}
for (unsigned int idx = 0; idx < nb_mirror_pairs; idx++)
{
const double layer_transition_center =
material_a_wavelength / 2 +
idx * (material_b_wavelength / 4 + material_a_wavelength / 4) +
material_b_wavelength / 4;
if (std::abs(p[0]) >=
(layer_transition_center - average_rho_width / 2) &&
std::abs(p[0]) <= (layer_transition_center + average_rho_width / 2))
{
const double coefficient =
(std::abs(p[0]) -
(layer_transition_center - average_rho_width / 2)) /
average_rho_width;
return (1 - coefficient) * material_b_rho +
coefficient * material_a_rho;
}
}
if (std::abs(p[0]) <= material_a_wavelength / 2)
{
return material_a_rho;
}
for (unsigned int idx = 0; idx < nb_mirror_pairs; idx++)
{
const double layer_center =
material_a_wavelength / 2 +
idx * (material_b_wavelength / 4 + material_a_wavelength / 4) +
material_b_wavelength / 4 + material_a_wavelength / 8;
const double layer_width = material_a_wavelength / 4;
if (std::abs(p[0]) >= (layer_center - layer_width / 2) &&
std::abs(p[0]) <= (layer_center + layer_width / 2))
{
return material_a_rho;
}
}
for (unsigned int idx = 0; idx < nb_mirror_pairs; idx++)
{
const double layer_center =
material_a_wavelength / 2 +
idx * (material_b_wavelength / 4 + material_a_wavelength / 4) +
material_b_wavelength / 8;
const double layer_width = material_b_wavelength / 4;
if (std::abs(p[0]) >= (layer_center - layer_width / 2) &&
std::abs(p[0]) <= (layer_center + layer_width / 2))
{
return material_b_rho;
}
}
return material_a_rho;
}
template <int dim>
: data(data)
, simulation_name(data.get_attribute<
std ::string>(
"simulation_name" ))
, save_vtu_files(data.get_attribute<bool>("save_vtu_files" ))
, start_frequency(data.get_attribute<double>("start_frequency" ))
, stop_frequency(data.get_attribute<double>("stop_frequency" ))
, nb_frequency_points(data.get_attribute<int>("nb_frequency_points" ))
, lambda(data.get_attribute<double>("lambda" ))
,
mu (data.get_attribute<double>(
"mu" ))
, dimension_x(data.get_attribute<double>("dimension_x" ))
, dimension_y(data.get_attribute<double>("dimension_y" ))
, nb_probe_points(data.get_attribute<int>("nb_probe_points" ))
, grid_level(data.get_attribute<int>("grid_level" ))
, probe_start_point(data.get_attribute<double>("probe_pos_x" ),
data.get_attribute<double>("probe_pos_y" ) -
data.get_attribute<double>("probe_width_y" ) / 2)
, probe_stop_point(data.get_attribute<double>("probe_pos_x" ),
data.get_attribute<double>("probe_pos_y" ) +
data.get_attribute<double>("probe_width_y" ) / 2)
, right_hand_side(data)
, pml(data)
, rho(data)
{}
template <int dim>
QuadratureCache<dim>::QuadratureCache(const unsigned int dofs_per_cell)
: dofs_per_cell(dofs_per_cell)
, mass_coefficient(dofs_per_cell, dofs_per_cell)
, stiffness_coefficient(dofs_per_cell, dofs_per_cell)
, right_hand_side(dofs_per_cell)
{}
template <int dim>
ElasticWave<dim>::ElasticWave(const Parameters<dim> ¶meters)
: parameters(parameters)
, mpi_communicator(MPI_COMM_WORLD)
, triangulation(mpi_communicator,
, quadrature_formula(2)
, dof_handler(triangulation)
, frequency(parameters.nb_frequency_points)
, probe_positions(parameters.nb_probe_points, dim)
, frequency_dataset(parameters.data.template create_dataset<double>(
"frequency" ,
std ::vector<hsize_t>{parameters.nb_frequency_points}))
, probe_positions_dataset(parameters.data.template create_dataset<double>(
"position" ,
std::vector<hsize_t>{parameters.nb_probe_points, dim}))
, displacement(
parameters.data.template create_dataset<std::complex<double>>(
"displacement" ,
std::vector<hsize_t>{parameters.nb_probe_points,
parameters.nb_frequency_points}))
, pcout(std::cout,
, computing_timer(mpi_communicator,
pcout,
{}
template <int dim>
void ElasticWave<dim>::setup_system()
{
locally_relevant_solution.reinit(locally_owned_dofs,
locally_relevant_dofs,
mpi_communicator);
system_rhs.
reinit (locally_owned_dofs, mpi_communicator);
constraints.clear();
constraints.reinit(locally_relevant_dofs);
constraints.close();
dsp,
mpi_communicator,
locally_relevant_dofs);
system_matrix.reinit(locally_owned_dofs,
locally_owned_dofs,
dsp,
mpi_communicator);
}
template <int dim>
void ElasticWave<dim>::assemble_system(const double omega,
const bool calculate_quadrature_data)
{
quadrature_formula,
const unsigned int n_q_points = quadrature_formula.
size ();
Vector<std::complex<double>> cell_rhs(dofs_per_cell);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
std::vector<Vector<double>> rhs_values(n_q_points,
Vector<double> (dim));
std::vector<double> rho_values(n_q_points);
std::vector<Vector<std::complex<double>>> pml_values(
n_q_points,
Vector <std::complex<double>>(dim));
get_stiffness_tensor<dim>(parameters.lambda, parameters.mu);
if (cell->is_locally_owned())
{
cell_rhs = 0;
if (calculate_quadrature_data)
{
parameters.right_hand_side.vector_value_list(
rho_values);
parameters.pml.vector_value_list(
}
QuadratureCache<dim> *local_quadrature_points_data =
reinterpret_cast< QuadratureCache<dim> *> (cell->user_pointer());
Assert (local_quadrature_points_data >= &quadrature_cache.front(),
Assert (local_quadrature_points_data <= &quadrature_cache.back(),
for (unsigned int q = 0; q < n_q_points; ++q)
{
QuadratureCache<dim> &quadrature_data =
local_quadrature_points_data[q];
std::complex<double> xi(1, 0);
if (calculate_quadrature_data)
{
quadrature_data.JxW = fe_values.
JxW (q);
for (unsigned int component = 0; component < dim; ++component)
{
force[component] = rhs_values[q][component];
s[component] = pml_values[q][component];
xi *= s[component];
}
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
fe_values[displacement].value(i, q);
fe_values[displacement].gradient(i, q);
for (unsigned int j = 0; j < dofs_per_cell; ++j)
{
fe_values[displacement].value(j, q);
fe_values[displacement].gradient(j, q);
quadrature_data.mass_coefficient[i][j] =
rho_values[q] * xi * phi_i * phi_j;
std::complex<double> stiffness_coefficient = 0;
for (unsigned int m = 0; m < dim; ++m)
for (unsigned int n = 0; n < dim; ++n)
for (unsigned int k = 0; k < dim; ++k)
for (
unsigned int l = 0;
l < dim; ++
l )
{
const std::complex<double> alpha =
xi * stiffness_tensor[m][n][k][
l ] /
(2.0 * s[n] * s[k]);
const std::complex<double> beta =
xi * stiffness_tensor[m][n][k][
l ] /
stiffness_coefficient +=
grad_phi_i[m][n] *
(alpha * grad_phi_j[
l ][k] +
beta * grad_phi_j[k][
l ]);
}
quadrature_data.stiffness_coefficient[i][j] =
stiffness_coefficient;
}
quadrature_data.right_hand_side[i] =
phi_i * force * fe_values.
JxW (q);
}
}
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
for (unsigned int j = 0; j < dofs_per_cell; ++j)
{
std::complex<double> matrix_sum = 0;
matrix_sum += -std::pow(omega, 2) *
quadrature_data.mass_coefficient[i][j];
matrix_sum += quadrature_data.stiffness_coefficient[i][j];
}
cell_rhs(i) += quadrature_data.right_hand_side[i];
}
}
cell->get_dof_indices(local_dof_indices);
constraints.distribute_local_to_global(cell_matrix,
cell_rhs,
local_dof_indices,
system_matrix,
system_rhs);
}
}
template <int dim>
void ElasticWave<dim>::solve()
{
locally_owned_dofs, mpi_communicator);
solver.solve(system_matrix, completely_distributed_solution, system_rhs);
pcout <<
" Solved in " << solver_control.
last_step () <<
" iterations." << std::endl;
constraints.distribute(completely_distributed_solution);
locally_relevant_solution = completely_distributed_solution;
}
template <int dim>
void ElasticWave<dim>::initialize_probe_positions_vector()
{
for (unsigned int position_idx = 0;
position_idx < parameters.nb_probe_points;
++position_idx)
{
(position_idx / ((double)(parameters.nb_probe_points - 1))) *
(parameters.probe_stop_point + (-parameters.probe_start_point)) +
parameters.probe_start_point;
probe_positions[position_idx][0] = p[0];
probe_positions[position_idx][1] = p[1];
if (dim == 3)
{
probe_positions[position_idx][2] = p[2];
}
}
}
template <int dim>
void
ElasticWave<dim>::store_frequency_step_data(const unsigned int frequency_idx)
{
const unsigned int probe_displacement_component = 0;
std::vector<hsize_t> coordinates;
std::vector<std::complex<double>> displacement_data;
for (unsigned int position_idx = 0;
position_idx < parameters.nb_probe_points;
++position_idx)
{
for (unsigned int dim_idx = 0; dim_idx < dim; ++dim_idx)
{
point [dim_idx] = probe_positions[position_idx][dim_idx];
}
bool point_in_locally_owned_cell;
{
const std::pair<typename DoFHandler<dim>::active_cell_iterator,
dof_handler,
point);
point_in_locally_owned_cell = cell_point.first->is_locally_owned();
}
if (point_in_locally_owned_cell)
{
Vector<std::complex<double>> tmp_vector(dim);
locally_relevant_solution,
point,
tmp_vector);
coordinates.emplace_back(position_idx);
coordinates.emplace_back(frequency_idx);
displacement_data.emplace_back(
tmp_vector(probe_displacement_component));
}
}
if (coordinates.size() > 0)
{
displacement.write_selection(displacement_data, coordinates);
}
else
{
displacement.write_none<std::complex<double>>();
}
if (parameters.save_vtu_files)
{
std::vector<std::string> solution_names(1, "displacement_x" );
if (dim >= 2)
{
solution_names.emplace_back("displacement_y" );
}
if (dim == 3)
{
solution_names.emplace_back("displacement_z" );
}
std::vector<DataComponentInterpretation::DataComponentInterpretation>
locally_relevant_solution,
solution_names,
interpretation);
Vector<float> subdomain(triangulation.n_active_cells());
for (unsigned int i = 0; i < subdomain.size(); ++i)
subdomain(i) = triangulation.locally_owned_subdomain();
std::vector<Vector<double>> force(
std::vector<Vector<double>> pml(
for (auto &cell : triangulation.active_cell_iterators())
{
if (cell->is_locally_owned())
{
for (unsigned int dim_idx = 0; dim_idx < dim; ++dim_idx)
{
force[dim_idx](cell->active_cell_index()) =
parameters.right_hand_side.value(cell->center(), dim_idx);
pml[dim_idx](cell->active_cell_index()) =
parameters.pml.value(cell->center(), dim_idx).imag();
}
rho(cell->active_cell_index()) =
parameters.rho.value(cell->center());
}
else
{
for (unsigned int dim_idx = 0; dim_idx < dim; ++dim_idx)
{
force[dim_idx](cell->active_cell_index()) = -1e+20;
pml[dim_idx](cell->active_cell_index()) = -1e+20;
}
rho(cell->active_cell_index()) = -1e+20;
}
}
for (unsigned int dim_idx = 0; dim_idx < dim; ++dim_idx)
{
"force_" + std::to_string(dim_idx));
"pml_" + std::to_string(dim_idx));
}
std::stringstream frequency_idx_stream;
const unsigned int nb_number_positions =
((unsigned int)std::log10(parameters.nb_frequency_points)) + 1;
frequency_idx_stream << std::setw(nb_number_positions)
<< std::setfill('0' ) << frequency_idx;
std::string filename = (parameters.simulation_name + "_" +
frequency_idx_stream.str() + ".vtu" );
}
}
template <int dim>
void ElasticWave<dim>::output_results()
{
{
frequency_dataset.write(frequency);
probe_positions_dataset.write(probe_positions);
}
else
{
frequency_dataset.write_none<double >();
probe_positions_dataset.write_none<double >();
}
}
template <int dim>
void ElasticWave<dim>::setup_quadrature_cache()
{
triangulation.clear_user_data();
{
std::vector<QuadratureCache<dim>> tmp;
quadrature_cache.swap(tmp);
}
quadrature_cache.resize(triangulation.n_locally_owned_active_cells() *
quadrature_formula.
size (),
unsigned int cache_index = 0;
for (const auto &cell : triangulation.active_cell_iterators())
if (cell->is_locally_owned())
{
cell->set_user_pointer(&quadrature_cache[cache_index]);
cache_index += quadrature_formula.
size ();
}
}
template <int dim>
void ElasticWave<dim>::frequency_sweep()
{
for (unsigned int frequency_idx = 0;
frequency_idx < parameters.nb_frequency_points;
++frequency_idx)
{
pcout << parameters.simulation_name + " frequency idx: "
<< frequency_idx << '/' << parameters.nb_frequency_points - 1
<< std::endl;
setup_system();
if (frequency_idx == 0)
{
pcout << " Number of active cells : "
<< triangulation.n_active_cells() << std::endl;
pcout << " Number of degrees of freedom : "
<< dof_handler.
n_dofs () << std::endl;
}
if (frequency_idx == 0)
{
parameters.data.set_attribute("active_cells" ,
triangulation.n_active_cells());
parameters.data.set_attribute("degrees_of_freedom" ,
}
const double current_loop_frequency =
(parameters.start_frequency +
frequency_idx *
(parameters.stop_frequency - parameters.start_frequency) /
(parameters.nb_frequency_points - 1));
const double current_loop_omega =
assemble_system(current_loop_omega,
(frequency_idx == 0) ? true : false );
solve();
frequency[frequency_idx] = current_loop_frequency;
store_frequency_step_data(frequency_idx);
computing_timer.print_summary();
computing_timer.reset();
pcout << std::endl;
}
}
template <int dim>
void ElasticWave<dim>::run()
{
#ifdef DEBUG
pcout << "Debug mode" << std::endl;
#else
pcout << "Release mode" << std::endl;
#endif
{
p1(0) = -parameters.dimension_x / 2;
p1(1) = -parameters.dimension_y / 2;
if (dim == 3)
{
p1(2) = -parameters.dimension_y / 2;
}
p2(0) = parameters.dimension_x / 2;
p2(1) = parameters.dimension_y / 2;
if (dim == 3)
{
p2(2) = parameters.dimension_y / 2;
}
std::vector<unsigned int> divisions(dim);
divisions[0] = int(parameters.dimension_x / parameters.dimension_y);
divisions[1] = 1;
if (dim == 3)
{
divisions[2] = 1;
}
divisions,
p1,
p2);
}
triangulation.refine_global(parameters.grid_level);
setup_quadrature_cache();
initialize_probe_positions_vector();
frequency_sweep();
output_results();
}
}
int main(int argc, char *argv[])
{
try
{
const unsigned int dim = 2;
MPI_COMM_WORLD);
{
auto displacement = data.
open_group (
"displacement" );
step62::Parameters<dim> parameters(displacement);
step62::ElasticWave<dim> elastic_problem(parameters);
elastic_problem.run();
}
{
auto calibration = data.
open_group (
"calibration" );
step62::Parameters<dim> parameters(calibration);
step62::ElasticWave<dim> elastic_problem(parameters);
elastic_problem.run();
}
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}


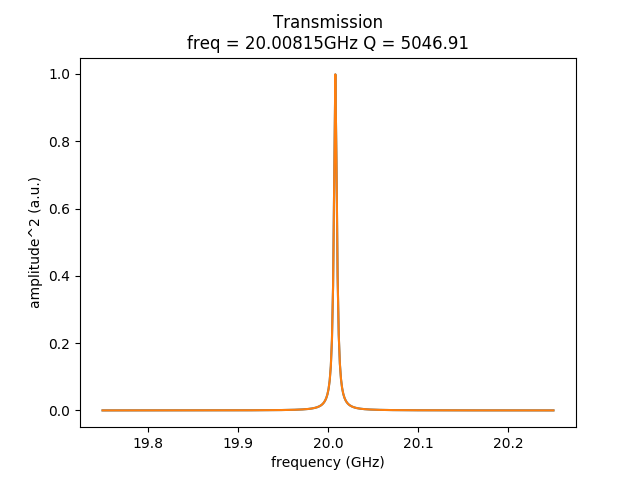
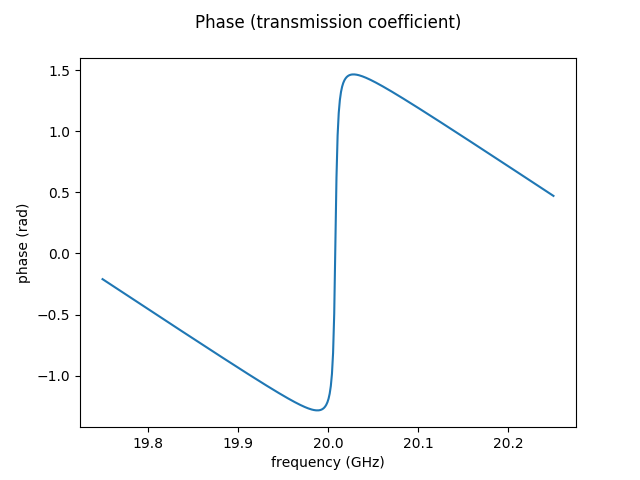
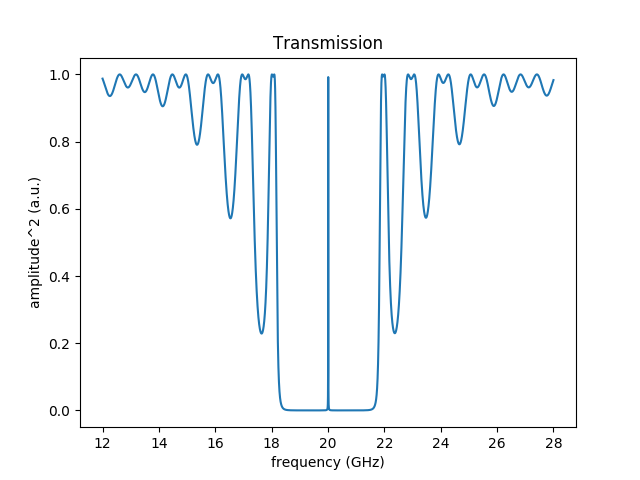
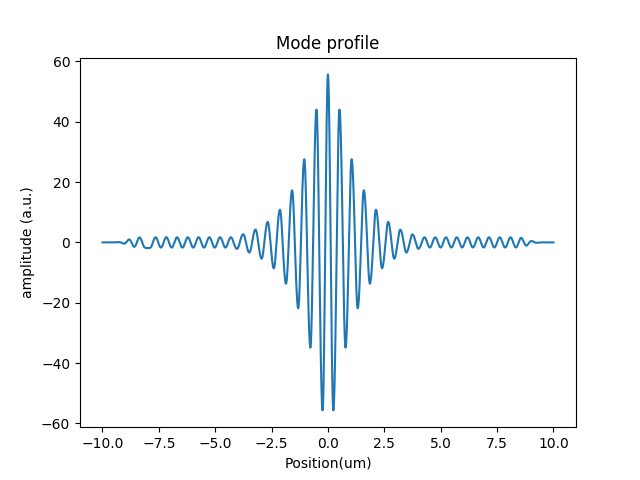
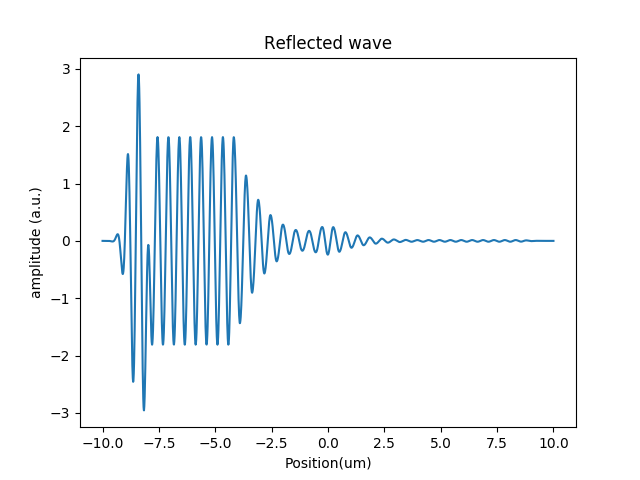
 1.8.14
1.8.14