245#include "allheaders.h"
246#include "nonlinear_heat.h"
261 const QGauss<1> face_quadrature_formula(fe.degree+1);
270 const unsigned int dofs_per_cell = fe.dofs_per_cell;
271 const unsigned int n_q_points = quadrature_formula.size();
272 const unsigned int n_q_f_points = face_quadrature_formula.size();
280should be fairly straightforward. The variable `cell_rhs` holds the local (
for an element or a cell) residual. Note that we use the `
FEFaceValues<2>` as we will need to
apply the Neuman boundary conditions on the right hand side of the domain.
282The lines below define the *Number type* we want to use to define our variables so that they are suitable
for automatic differentiation. Here, we are
using variables that will allow /automatic differentiation/. (The other option is symbolic differentiation
using SYMENGINE package. Here we are
using the automatic differentiation
using SACADO.)
286 using ADNumberType =
typename ADHelper::ad_type;
290The following lines are once again straightforward to understand.
294 std::vector<types::global_dof_index> local_dof_indices(
300 std::vector<double> consol(n_q_points);
303We only comment that the variable `consol` holds the
values of the variable `converged_solution` at the gauss points of the current, active cell. Similarly, the variable `consol_grad` holds the
values of the
gradients of the `converged_solution` at the gauss points. The variable `converged_solution` refers is solution at the previous time step (time step @f$s@f$).
306In following lines the variables `old_solution` and `old_solution_grad` are
307crucial. They define the variables of the appropriate number type
using which we will define our residual, so that it is suitable
for the automatic differentiation. `old_solution` is a solution variable of the appropriate number type with respect to which we need to define the residual and then
differentiate it to get the Jacobian. For ease of understanding,
one may consider
this variable to be a special variable, that will look like
this
309 \text{old_solution} =
311 \psi_i (\zeta_1,\eta_1) d_i\\
312 \psi_i (\zeta_2,\eta_2) d_i\\
313 \psi_i (\zeta_3,\eta_3) d_i\\
314 \psi_i (\zeta_4,\eta_4) d_i
317where @f$\psi_i@f$ are the shape
functions and @f$d_i@f$ is some way of representing the primary variable in the problem (in
this case the temperature). Could be viewed as something like a symbol, which could be used to define
functions and then differentiated later. `old_solution` holds the
values in the corresponding gauss points and the repeated indices in the previous equation indicate summation over the nodes. Similarly, the variable `old_solution_grad` holds the corresponding
gradients.
319 std::vector<ADNumberType> old_solution(
324 std::vector<Tensor<1, 2>> consol_grad(
326 std::vector<Tensor<1, 2,ADNumberType>> old_solution_grad(
341are straightforward to understand. The vector `residual` will hold the *numerical*
value of the residual and is hence initialized to be
zero.
345 for (
const auto &cell: dof_handler.active_cell_iterators())
348 fe_values.reinit(cell);
349 cell->get_dof_indices(local_dof_indices);
350 const unsigned int n_independent_variables = local_dof_indices.size();
351 const unsigned int n_dependent_variables = dofs_per_cell;
354should be clear. In the following line we inform how many
independent and dependent variables we will have.
356 ADHelper ad_helper(n_independent_variables, n_dependent_variables);
359then, in the following line we tell the system, at which
point it should numerically evaluate the residual. This is the
point given by `evaluation_point`, which will contain the solution that is getting iterated to find the actual solution
for each time step.
361 ad_helper.register_dof_values(evaluation_point,local_dof_indices);
367 const std::vector<ADNumberType> &dof_values_ad = ad_helper.get_sensitive_dof_values();
368 fe_values[t].get_function_values_from_local_dof_values(dof_values_ad,
370 fe_values[t].get_function_gradients_from_local_dof_values(dof_values_ad,
374the actual storage of the
values of the shape
functions and its derivatives at the gauss points is taking place in the variables `old_solution` and `old_solution_grad`.
378 fe_values[t].get_function_values(converged_solution, consol);
379 fe_values[t].get_function_gradients(converged_solution, consol_grad);
382the
values of the `converged_solution` and its
gradients get stored in the variables `consol` and `con_sol_grad`.
386 for (
unsigned int q_index = 0; q_index < n_q_points; ++q_index)
388 for (
unsigned int i = 0; i < dofs_per_cell; ++i)
393 ADNumberType MijTjcurr = Cp*rho*fe_values[t].value(i,q_index)*old_solution[q_index];
394 ADNumberType MijTjprev = Cp*rho*fe_values[t].value(i,q_index)*consol[q_index];
395 ADNumberType k_curr = a +
b*old_solution[q_index] + c*
std::pow(old_solution[q_index],2);
396 ADNumberType k_prev = a +
b*consol[q_index] + c*
std::pow(consol[q_index],2);
397 ADNumberType Licurr = alpha * delta_t * (fe_values[t].gradient(i,q_index)*k_curr*old_solution_grad[q_index]);
398 ADNumberType Liprev = (1-alpha) * delta_t * (fe_values[t].
gradient(i,q_index)*k_prev*consol_grad[q_index]);
399 residual_ad[i] += (MijTjcurr+Licurr-MijTjprev+Liprev)*fe_values.JxW(q_index);
432 residual_ad[i]+= -delta_t*(-10)*fe_face_values[t].
value(i,q_point)*fe_face_values.JxW(q_point);
442 ad_helper.register_residual_vector(residual_ad);
445actually tells the `ad_helper` that
this is the residual it should use, and the line
447 ad_helper.compute_residual(cell_rhs);
450evaluates the residual at the appropriate
point, which is the `evaluation_point`. Then
452 cell->get_dof_indices(local_dof_indices);
454 for (
unsigned int i =0;i < dofs_per_cell; ++i)
455 residual(local_dof_indices[i])+= cell_rhs(i);
460are used to calculate the global `residual` from the local `cell_rhs`. Now `residual` is numerical and not of the special number type. Finally, lines
465 std::cout <<
" The Norm is :: = " << residual.l2_norm() << std::endl;
469are routine, in particular, it makes the global degrees of freedom, where the
dirichlet boundary conditions are applied to be
zero.
472#### The compute_jacobian() function
474The `compute_jacobian()` only takes in the `evaluation_point` as an input and is identical to the
475`compute_residual()` except for some minor modification. In particular the line
477 ad_helper.compute_linearization(cell_matrix);
480computes the actual jacobian by performing the automatic differentiation and evaluates it at the `evaluation_point`. The remaining lines are routine and should be straightforward.
483### General ideas involved in solving coupled nonlinear equations using Newton Raphson's technique
484Consider that we have the equations
486 f_i^1(p_j^{{s+1}}, T_j^{{s+1}})=0 \\
487 f_i^2(p_j^{{s+1}}, T_j^{{s+1}})=0
489are coupled non-linear algebraic equations in the variables @f$p_j@f$ and @f$T_j@f$. In the problem we are trying to solve, we only have
one unknown, but
this set of derivation clarifies what
one should
do for coupled problems as well.
491We need to solve the set equations immediately above
using Newton-Raphson
's technique. Now suppose we have 4 noded linear element, with values as @f$p_1^{{s+1}},p_2^{{s+1}},p_3^{{s+1}},p_4^{{s+1}}@f$ and @f$T_1^{{s+1}},T_2^{{s+1}},T_3^{{s+1}},T_4^{{s+1}}@f$, then actually @f$f_i^1@f$ and @f$f_i^2@f$ are
493 f_i^1(p_1^{{s+1}},p_2^{{s+1}},p_3^{{s+1}},p_4^{{s+1}},T_1^{{s+1}},T_2^{{s+1}},T_3^{{s+1}},T_4^{{s+1}})=0 \\
494 f_i^2(p_1^{{s+1}},p_2^{{s+1}},p_3^{{s+1}},p_4^{{s+1}},T_1^{{s+1}},T_2^{{s+1}},T_3^{{s+1}},T_4^{{s+1}})=0
496Also, note that @f$i@f$ goes from 1 to 4 for @f$f^1@f$ and from 1 to 4 for @f$f^2@f$. For the Newton Raphson's technique, we have to find the Jacobian. This is written explicitly below
for clear understanding.
500 \frac{\partial f^1_1}{\partial p^{s+1}_1} & \frac{\partial f^1_1}{\partial p^{s+1}_2} & \frac{\partial f^1_1}{\partial p^{s+1}_3} & \frac{\partial f^1_1}{\partial p^{s+1}_4} & \frac{\partial f^1_1}{\partial
T^{s+1}_1} & \frac{\partial f^1_1}{\partial
T^{s+1}_2}&\frac{\partial f^1_1}{\partial
T^{s+1}_3}&\frac{\partial f^1_1}{\partial
T^{s+1}_4}\\
502 \frac{\partial f^1_2}{\partial p^{s+1}_1} & \frac{\partial f^1_2}{\partial p^{s+1}_2} & \frac{\partial f^1_2}{\partial p^{s+1}_3} & \frac{\partial f^1_2}{\partial p^{s+1}_4} & \frac{\partial f^1_2}{\partial
T^{s+1}_1} & \frac{\partial f^1_2}{\partial
T^{s+1}_2}&\frac{\partial f^1_2}{\partial
T^{s+1}_3}&\frac{\partial f^1_2}{\partial
T^{s+1}_4}\\
504 \frac{\partial f^1_3}{\partial p^{s+1}_1} & \frac{\partial f^1_3}{\partial p^{s+1}_2} & \frac{\partial f^1_3}{\partial p^{s+1}_3} & \frac{\partial f^1_3}{\partial p^{s+1}_4} & \frac{\partial f^1_3}{\partial
T^{s+1}_1} & \frac{\partial f^1_3}{\partial
T^{s+1}_2}&\frac{\partial f^1_3}{\partial
T^{s+1}_3}&\frac{\partial f^1_3}{\partial
T^{s+1}_4}\\
506 \frac{\partial f^1_4}{\partial p^{s+1}_1} & \frac{\partial f^1_4}{\partial p^{s+1}_2} & \frac{\partial f^1_4}{\partial p^{s+1}_3} & \frac{\partial f^1_4}{\partial p^{s+1}_4} & \frac{\partial f^1_4}{\partial
T^{s+1}_1} & \frac{\partial f^1_4}{\partial
T^{s+1}_2}&\frac{\partial f^1_4}{\partial
T^{s+1}_3}&\frac{\partial f^1_4}{\partial
T^{s+1}_4}\\
507 %================================================================
508 \frac{\partial f^2_1}{\partial p^{s+1}_1} & \frac{\partial f^2_1}{\partial p^{s+1}_2} & \frac{\partial f^2_1}{\partial p^{s+1}_3} & \frac{\partial f^2_1}{\partial p^{s+1}_4} & \frac{\partial f^2_1}{\partial
T^{s+1}_1} & \frac{\partial f^2_1}{\partial
T^{s+1}_2}&\frac{\partial f^2_1}{\partial
T^{s+1}_3}&\frac{\partial f^2_1}{\partial
T^{s+1}_4}\\
510 \frac{\partial f^2_2}{\partial p^{s+1}_1} & \frac{\partial f^2_2}{\partial p^{s+1}_2} & \frac{\partial f^2_2}{\partial p^{s+1}_3} & \frac{\partial f^2_2}{\partial p^{s+1}_4} & \frac{\partial f^2_2}{\partial
T^{s+1}_1} & \frac{\partial f^2_2}{\partial
T^{s+1}_2}&\frac{\partial f^2_2}{\partial
T^{s+1}_3}&\frac{\partial f^2_2}{\partial
T^{s+1}_4}\\
512 \frac{\partial f^2_3}{\partial p^{s+1}_1} & \frac{\partial f^2_3}{\partial p^{s+1}_2} & \frac{\partial f^2_3}{\partial p^{s+1}_3} & \frac{\partial f^2_3}{\partial p^{s+1}_4} & \frac{\partial f^2_3}{\partial
T^{s+1}_1} & \frac{\partial f^2_3}{\partial
T^{s+1}_2}&\frac{\partial f^2_3}{\partial
T^{s+1}_3}&\frac{\partial f^2_3}{\partial
T^{s+1}_4}\\
514 \frac{\partial f^2_4}{\partial p^{s+1}_1} & \frac{\partial f^2_4}{\partial p^{s+1}_2} & \frac{\partial f^2_4}{\partial p^{s+1}_3} & \frac{\partial f^2_4}{\partial p^{s+1}_4} & \frac{\partial f^2_4}{\partial
T^{s+1}_1} & \frac{\partial f^2_4}{\partial
T^{s+1}_2}&\frac{\partial f^2_4}{\partial
T^{s+1}_3}&\frac{\partial f^2_4}{\partial
T^{s+1}_4}
517We use the Jacobian evaluated at the
values of the variables (@f$p_j^{{s+1}}@f$, @f$T_j^{{s+1}}@f$) at the /previous iteration/ (denoted by the variable `present_solution` in the code) to obtain a
new value of the required vector. That is
541 \frac{\partial f^1_1}{\partial p^{s+1}_1} & \frac{\partial f^1_1}{\partial p^{s+1}_2} & \frac{\partial f^1_1}{\partial p^{s+1}_3} & \frac{\partial f^1_1}{\partial p^{s+1}_4} & \frac{\partial f^1_1}{\partial
T^{s+1}_1} & \frac{\partial f^1_1}{\partial
T^{s+1}_2}&\frac{\partial f^1_1}{\partial
T^{s+1}_3}&\frac{\partial f^1_1}{\partial
T^{s+1}_4}\\
543 \frac{\partial f^1_2}{\partial p^{s+1}_1} & \frac{\partial f^1_2}{\partial p^{s+1}_2} & \frac{\partial f^1_2}{\partial p^{s+1}_3} & \frac{\partial f^1_2}{\partial p^{s+1}_4} & \frac{\partial f^1_2}{\partial
T^{s+1}_1} & \frac{\partial f^1_2}{\partial
T^{s+1}_2}&\frac{\partial f^1_2}{\partial
T^{s+1}_3}&\frac{\partial f^1_2}{\partial
T^{s+1}_4}\\
545 \frac{\partial f^1_3}{\partial p^{s+1}_1} & \frac{\partial f^1_3}{\partial p^{s+1}_2} & \frac{\partial f^1_3}{\partial p^{s+1}_3} & \frac{\partial f^1_3}{\partial p^{s+1}_4} & \frac{\partial f^1_3}{\partial
T^{s+1}_1} & \frac{\partial f^1_3}{\partial
T^{s+1}_2}&\frac{\partial f^1_3}{\partial
T^{s+1}_3}&\frac{\partial f^1_3}{\partial
T^{s+1}_4}\\
547 \frac{\partial f^1_4}{\partial p^{s+1}_1} & \frac{\partial f^1_4}{\partial p^{s+1}_2} & \frac{\partial f^1_4}{\partial p^{s+1}_3} & \frac{\partial f^1_4}{\partial p^{s+1}_4} & \frac{\partial f^1_4}{\partial
T^{s+1}_1} & \frac{\partial f^1_4}{\partial
T^{s+1}_2}&\frac{\partial f^1_4}{\partial
T^{s+1}_3}&\frac{\partial f^1_4}{\partial
T^{s+1}_4}\\
548 %================================================================
549 \frac{\partial f^2_1}{\partial p^{s+1}_1} & \frac{\partial f^2_1}{\partial p^{s+1}_2} & \frac{\partial f^2_1}{\partial p^{s+1}_3} & \frac{\partial f^2_1}{\partial p^{s+1}_4} & \frac{\partial f^2_1}{\partial
T^{s+1}_1} & \frac{\partial f^2_1}{\partial
T^{s+1}_2}&\frac{\partial f^2_1}{\partial
T^{s+1}_3}&\frac{\partial f^2_1}{\partial
T^{s+1}_4}\\
551 \frac{\partial f^2_2}{\partial p^{s+1}_1} & \frac{\partial f^2_2}{\partial p^{s+1}_2} & \frac{\partial f^2_2}{\partial p^{s+1}_3} & \frac{\partial f^2_2}{\partial p^{s+1}_4} & \frac{\partial f^2_2}{\partial
T^{s+1}_1} & \frac{\partial f^2_2}{\partial
T^{s+1}_2}&\frac{\partial f^2_2}{\partial
T^{s+1}_3}&\frac{\partial f^2_2}{\partial
T^{s+1}_4}\\
553 \frac{\partial f^2_3}{\partial p^{s+1}_1} & \frac{\partial f^2_3}{\partial p^{s+1}_2} & \frac{\partial f^2_3}{\partial p^{s+1}_3} & \frac{\partial f^2_3}{\partial p^{s+1}_4} & \frac{\partial f^2_3}{\partial
T^{s+1}_1} & \frac{\partial f^2_3}{\partial
T^{s+1}_2}&\frac{\partial f^2_3}{\partial
T^{s+1}_3}&\frac{\partial f^2_3}{\partial
T^{s+1}_4}\\
555 \frac{\partial f^2_4}{\partial p^{s+1}_1} & \frac{\partial f^2_4}{\partial p^{s+1}_2} & \frac{\partial f^2_4}{\partial p^{s+1}_3} & \frac{\partial f^2_4}{\partial p^{s+1}_4} & \frac{\partial f^2_4}{\partial
T^{s+1}_1} & \frac{\partial f^2_4}{\partial
T^{s+1}_2}&\frac{\partial f^2_4}{\partial
T^{s+1}_3}&\frac{\partial f^2_4}{\partial
T^{s+1}_4}
568The @f$J_{pq}@f$ is evaluated with
values obtained at the @f$k^{th}@f$ iteration. To avoid taking the inverse, we solve the following,
for the changes @f$\Delta p@f$ and @f$\Delta
T@f$.
571 \frac{\partial f^1_1}{\partial p^{s+1}_1} & \frac{\partial f^1_1}{\partial p^{s+1}_2} & \frac{\partial f^1_1}{\partial p^{s+1}_3} & \frac{\partial f^1_1}{\partial p^{s+1}_4} & \frac{\partial f^1_1}{\partial
T^{s+1}_1} & \frac{\partial f^1_1}{\partial
T^{s+1}_2}&\frac{\partial f^1_1}{\partial
T^{s+1}_3}&\frac{\partial f^1_1}{\partial
T^{s+1}_4}\\
573 \frac{\partial f^1_2}{\partial p^{s+1}_1} & \frac{\partial f^1_2}{\partial p^{s+1}_2} & \frac{\partial f^1_2}{\partial p^{s+1}_3} & \frac{\partial f^1_2}{\partial p^{s+1}_4} & \frac{\partial f^1_2}{\partial
T^{s+1}_1} & \frac{\partial f^1_2}{\partial
T^{s+1}_2}&\frac{\partial f^1_2}{\partial
T^{s+1}_3}&\frac{\partial f^1_2}{\partial
T^{s+1}_4}\\
575 \frac{\partial f^1_3}{\partial p^{s+1}_1} & \frac{\partial f^1_3}{\partial p^{s+1}_2} & \frac{\partial f^1_3}{\partial p^{s+1}_3} & \frac{\partial f^1_3}{\partial p^{s+1}_4} & \frac{\partial f^1_3}{\partial
T^{s+1}_1} & \frac{\partial f^1_3}{\partial
T^{s+1}_2}&\frac{\partial f^1_3}{\partial
T^{s+1}_3}&\frac{\partial f^1_3}{\partial
T^{s+1}_4}\\
577 \frac{\partial f^1_4}{\partial p^{s+1}_1} & \frac{\partial f^1_4}{\partial p^{s+1}_2} & \frac{\partial f^1_4}{\partial p^{s+1}_3} & \frac{\partial f^1_4}{\partial p^{s+1}_4} & \frac{\partial f^1_4}{\partial
T^{s+1}_1} & \frac{\partial f^1_4}{\partial
T^{s+1}_2}&\frac{\partial f^1_4}{\partial
T^{s+1}_3}&\frac{\partial f^1_4}{\partial
T^{s+1}_4}\\
578 %================================================================
579 \frac{\partial f^2_1}{\partial p^{s+1}_1} & \frac{\partial f^2_1}{\partial p^{s+1}_2} & \frac{\partial f^2_1}{\partial p^{s+1}_3} & \frac{\partial f^2_1}{\partial p^{s+1}_4} & \frac{\partial f^2_1}{\partial
T^{s+1}_1} & \frac{\partial f^2_1}{\partial
T^{s+1}_2}&\frac{\partial f^2_1}{\partial
T^{s+1}_3}&\frac{\partial f^2_1}{\partial
T^{s+1}_4}\\
581 \frac{\partial f^2_2}{\partial p^{s+1}_1} & \frac{\partial f^2_2}{\partial p^{s+1}_2} & \frac{\partial f^2_2}{\partial p^{s+1}_3} & \frac{\partial f^2_2}{\partial p^{s+1}_4} & \frac{\partial f^2_2}{\partial
T^{s+1}_1} & \frac{\partial f^2_2}{\partial
T^{s+1}_2}&\frac{\partial f^2_2}{\partial
T^{s+1}_3}&\frac{\partial f^2_2}{\partial
T^{s+1}_4}\\
583 \frac{\partial f^2_3}{\partial p^{s+1}_1} & \frac{\partial f^2_3}{\partial p^{s+1}_2} & \frac{\partial f^2_3}{\partial p^{s+1}_3} & \frac{\partial f^2_3}{\partial p^{s+1}_4} & \frac{\partial f^2_3}{\partial
T^{s+1}_1} & \frac{\partial f^2_3}{\partial
T^{s+1}_2}&\frac{\partial f^2_3}{\partial
T^{s+1}_3}&\frac{\partial f^2_3}{\partial
T^{s+1}_4}\\
585 \frac{\partial f^2_4}{\partial p^{s+1}_1} & \frac{\partial f^2_4}{\partial p^{s+1}_2} & \frac{\partial f^2_4}{\partial p^{s+1}_3} & \frac{\partial f^2_4}{\partial p^{s+1}_4} & \frac{\partial f^2_4}{\partial
T^{s+1}_1} & \frac{\partial f^2_4}{\partial
T^{s+1}_2}&\frac{\partial f^2_4}{\partial
T^{s+1}_3}&\frac{\partial f^2_4}{\partial
T^{s+1}_4}
610 J_{pq}\{\Delta solution\}^{k+1}=\{function\}^{k}
612Then add
this to the
value of
625We keep doing
this, until the @f$L_2@f$-error of the vector is small. Determining whether the
norm is small can be done
using either
627 ||(function)^k||<\delta^0 ||function^0||
633where @f$tol@f$ is some small number. In the code, we use the
second of these two choices. The
final converged solution in the
one that satisfies the set of equations and is called by the variable `converged_solution` in the code. This iterative process is carried out
for every time step. The variable `present_solution` is given the
value of `converged_solution` at the beginning of the iteration of a given time step, so that it serves as a better
initial guess
for the nonlinear set of equations
for the next time step.
636#### The
run() function
638The function which implements the nonlinear solver is the `run()` function for every time step. In particular the lines
641 additional_data.abs_tol = target_tolerance;
642 additional_data.max_iter = 100;
649 nonlinear_solver.residual =
652 compute_residual(evaluation_point, residual);
659 nonlinear_solver.setup_jacobian =
661 compute_jacobian(current_u);
667 nonlinear_solver.solve_with_jacobian = [&](
const Vector<double> &rhs,
669 const double tolerance) {
670 solve(rhs, dst, tolerance);
676 nonlinear_solver.solve(present_solution);
680Here,
one needs to give how the residual is to be calculated and at what
point, how the jacobian is to be calculated and at what
point and
finally, how to solve the linear system occurring during each iteration. These are given as `
lambda`
functions.
685 additional_data.abs_tol = target_tolerance;
686 additional_data.max_iter = 100;
691setup the solver and give any basic
data needed, such as the tolerance to converge or the maximum number of iterations it can
try.
695 nonlinear_solver.residual =
698 compute_residual(evaluation_point, residual);
702essentially, defines the function from where the residual will be calculated. Notice here that the `compute_residual()` function is called with `evaluation_point` and `residual`.
706 nonlinear_solver.setup_jacobian =
708 compute_jacobian(current_u);
712define the function from where the jacobian will be calculated. Note that it takes in a variable `current_u` which will be the `evaluation_point`
for the computing the jacobian. Thus, the actual points
for evaluating the jacobian and the residual need not be the same.
716 nonlinear_solver.solve_with_jacobian = [&](
const Vector<double> &rhs,
718 const double tolerance) {
719 solve(rhs, dst, tolerance);
723tells the solution needs to be done with the jacobian
using the function `solve()`.
727 nonlinear_solver.solve_with_jacobian = [&](
const Vector<double> &rhs,
729 const double tolerance) {
730 solve(rhs, dst, tolerance);
734actually calls the nonlinear solver.
736For details as to how these
lambda functions work together, please see @ref step_77
"step-77" and also the file `tests/trilinos/step-77-with-nox.cc`. Overall, the variable `present_solution` is presented as an
initial guess to the non-linear solver, which performs the iteration and gives the
final converged solution in the same variable. Hence,
this will be the converged solution
for the current step and
this assignment happens in the following line
738 converged_solution = present_solution;
741The variable `present_solution` is assigned the
value of `converged_solution` from the previous time step to serve as an
initial guess. This is done in line 45.
743 present_solution = converged_solution;
750The results are essentially the time evolution of the temperature throughout the domain. The
first of the pictures below shows the temperature distribution at the
final step, i.e. at time @f$t=5@f$. This should be very similar to the figure at the bottom on the page [here](https:
752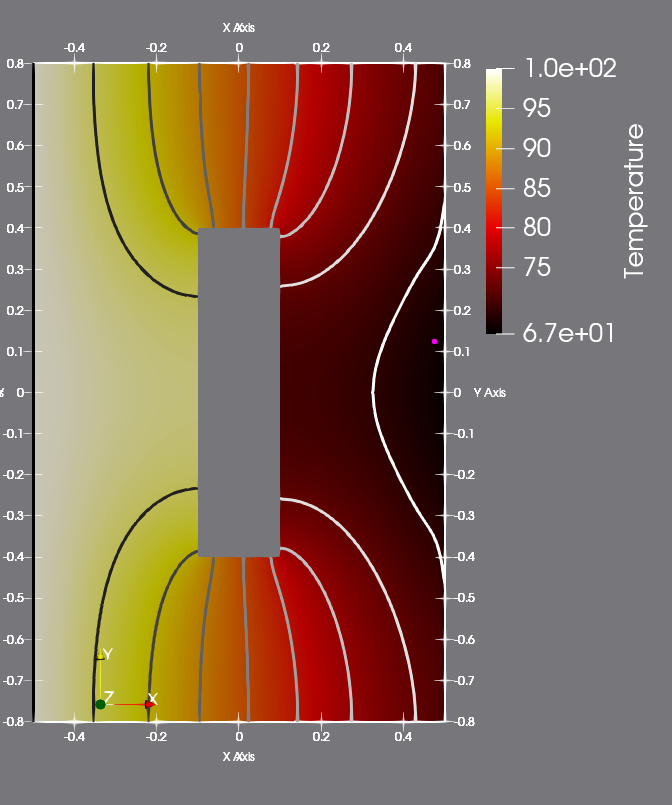
754Contour plot of the temperature at the
final step
756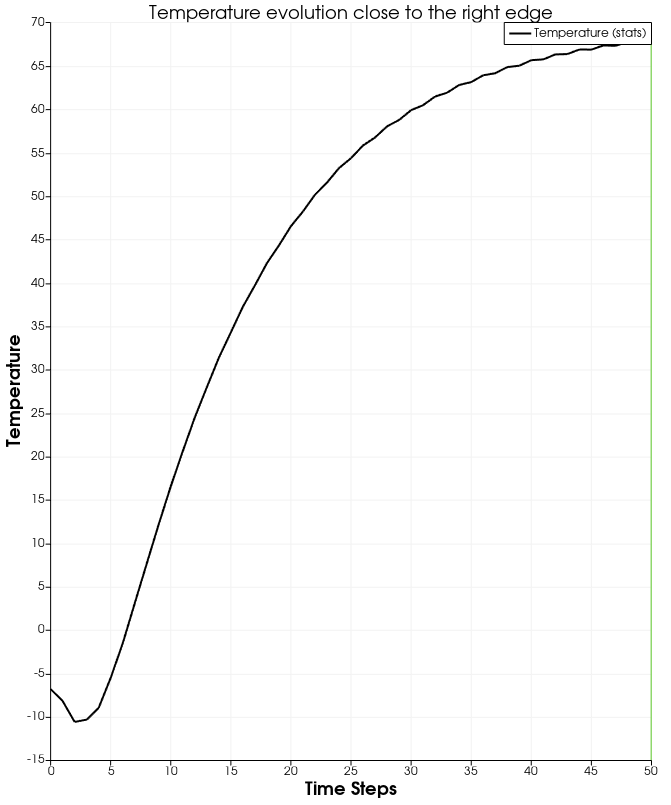
758Evolution of temperature at a
point close to the right edge @f$\approx (0.49, 0.12)@f$
760In closing, we give some ideas as to how the residuals and the jacobians are actually calculated in a finite element setting.
763### Evaluating the function at previous iterations
765For solving the linear equation every iteration, we have to evaluate the right hand side
functions (@f$f_i^1@f$ and @f$f_i^2@f$) at the
values @f$p@f$ and @f$T@f$ had at their previous iteration. For instance, in the current problem consider the
final equation above (we only have only one function @f$f_I@f$ in
this case), which is
767 M_{IJ}T_{J}^{s+1} + \alpha \Delta t L_I^{s+1} - M_{IJ}T_{J}^s + \Delta t \left( 1-\alpha \right) L_I^s - \Delta t Q_I = R_I^{s+1}
769Each term is written in the following manner. We write it
for only
one term to illustrate the details.
770Consider @f$\alpha \Delta t L_I^{s+1} @f$
772\alpha \Delta t \int_{\Omega_e} \left( \psi_{I,i} \left( k (\psi_PT_P) \psi_{J,i}T_J \right) - \psi_I f \right)
dx dy = L_I^{s+1}
776 \alpha \Delta t \int_{\Omega_e} \left( \psi_{I,i} \left( k (\psi_PT_P^{s+1}) \psi_{J,i}T_J^{s+1} \right) - \psi_I f \right)
dx dy = L_I^{s+1}
778again, the term @f$\psi_{J,i} T_J^{{s+1}}@f$ is
nothing but the
value of
gradient of @f$T^{{s+1}}@f$ at whatever
point the
gradient of @f$\psi_{J}@f$ is evaluated in. We write
this gradient as @f$\nabla
T^{{s+1}}(x,y)@f$. Similarly, @f$\psi_PT_P^{{s+1}}@f$ is the
value of the temperature at the
point where @f$\psi_P@f$ is evaluated and we call it @f$T^{{s+1}}@f$. While evaluating these terms to calculate the residual, we will use Gauss quadrature and
this evaluation of
this integral would become something like
780L_I^{{s+1}} = \Delta t \alpha \sum_{h} \nabla \psi_I (\xi_h,\eta_h) \cdot k(T^{{s+1}}) \nabla T^{{s+1}}(\xi_h,\eta_h) w_hJ_h
782where @f$h@f$ runs over the total number of quadrature points in the finite element and @f$w_hJ_h@f$ takes care of appropriate weights needed and other corrections needed to due to transforming the finite element onto a master element (See any finite element book
for details). All other terms can also be calculated in a similar manner to obtain the per-element residual from the
first equation in
this section. This has to assembled over all finite elements to get the global residual.
784Similar evaluations have to be done to obtain the Jacobian as well. In the current
case, the per element Jacobian is given by
786 J^e_{IQ} = \frac{\partial R_I^{s+1}}{\partial T_{Q}^{s+1}} = M_{IQ} + \alpha \Delta t \frac{\partial L_I^{s+1}}{\partial T_Q}
790 J_{IQ}^
e = \int_{\Omega_e}\rho C_p \psi_I \psi_J
dx dy +
791 \alpha \Delta t \int_{\Omega_e} \left( \psi_{I,i} (\psi_{J,i}T_J) (b\psi_Q + 2c (\psi_Y T_Y) \psi_Q) + \psi_{I,i}\psi_{Q,i}(a +
b (\psi_R T_R) + c \left( \psi_Y T_Y) \right)^2 \right)
dx dy
793which are evaluated
using gauss quadrature by summing the
functions after evaluation at the gauss points. Once again, the terms @f$\psi_{J,i}T_J@f$ and @f$\psi_R T_R@f$ are the
values of the
gradients of the temperature and the temperature itself at the Gauss points.
799To understand
this application, @ref step_71
"step-71", @ref step_72
"step-72" and @ref step_77
"step-77" are needed.
802<a name=
"ann-mesh/README.md"></a>
803<h1>Annotated version of mesh/README.md</h1>
804The following copyright notice applies to the mesh files in
this directory:
817<a name=
"ann-include/allheaders.h"></a>
818<h1>Annotated version of include/allheaders.h</h1>
834 * #ifndef __ALLHEADERS_H_INCLUDED__
835 * #define __ALLHEADERS_H_INCLUDED__
838 * These are some of the header files
for this programme. Most of them
839 * are common from previous steps.
842 * #include <deal.II/base/quadrature_lib.h>
843 * #include <deal.II/base/function_lib.h>
844 * #include <deal.II/lac/generic_linear_algebra.h>
845 * #include <deal.II/base/function.h>
847 * #include <deal.II/dofs/dof_handler.h>
848 * #include <deal.II/dofs/dof_tools.h>
850 * #include <deal.II/fe/fe_values.h>
851 * #include <deal.II/fe/fe.h>
853 * #include <deal.II/grid/tria.h>
854 * #include <deal.II/grid/grid_generator.h>
856 * #include <deal.II/lac/dynamic_sparsity_pattern.h>
857 * #include <deal.II/lac/full_matrix.h>
858 * #include <deal.II/lac/precondition.h>
859 * #include <deal.II/lac/solver_cg.h>
860 * #include <deal.II/lac/sparse_matrix.h>
861 * #include <deal.II/lac/vector.h>
862 * #include <deal.II/grid/grid_tools.h>
864 * #include <deal.II/numerics/data_out.h>
865 * #include <deal.II/numerics/vector_tools.h>
866 * #include <deal.II/fe/fe_q.h>
867 * #include <deal.II/grid/grid_out.h>
868 * #include <deal.II/grid/grid_in.h>
870 * #include <deal.II/fe/fe_system.h>
872 * #include <deal.II/grid/tria_accessor.h>
873 * #include <deal.II/grid/tria_iterator.h>
874 * #include <deal.II/dofs/dof_handler.h>
875 * #include <deal.II/dofs/dof_accessor.h>
876 * #include <deal.II/dofs/dof_tools.h>
877 * #include <deal.II/fe/fe_values.h>
878 * #include <deal.II/fe/fe.h>
879 * #include <deal.II/numerics/matrix_tools.h>
880 * #include <deal.II/numerics/vector_tools.h>
881 * #include <deal.II/lac/vector.h>
882 * #include <deal.II/base/quadrature.h>
883 * #include <deal.II/distributed/tria.h>
884 * #include <deal.II/distributed/grid_refinement.h>
886 * #include <deal.II/lac/sparse_direct.h>
887 * #include <deal.II/base/timer.h>
888 * #include <deal.II/base/utilities.h>
890 * #include <deal.II/base/exceptions.h>
891 * #include <deal.II/base/geometric_utilities.h>
892 * #include <deal.II/base/conditional_ostream.h>
893 * #include <deal.II/base/mpi.h>
895 * #include <deal.II/grid/grid_tools.h>
896 * #include <deal.II/dofs/dof_renumbering.h>
897 * #include <deal.II/numerics/solution_transfer.h>
898 * #include <deal.II/base/index_set.h>
899 * #include <deal.II/lac/sparsity_tools.h>
900 * #include <deal.II/fe/fe_values_extractors.h>
903 * Automatic differentiation is carried out with TRILINOS Automatic differentiation scheme/
904 * This is invoked with the following include.
907 * #include <deal.II/differentiation/ad.h>
910 * We use Trilinos wrappers based NOX to solve the non-linear equations.
913 * #include <deal.II/trilinos/nox.h>
917 * #include <iostream>
924<a name=
"ann-include/nonlinear_heat.h"></a>
925<h1>Annotated version of include/nonlinear_heat.h</h1>
941 * #ifndef __MAIN_ALL_HEADER_H_INCLUDED__
942 * #define __MAIN_ALL_HEADER_H_INCLUDED__
943 * #include
"allheaders.h"
947 *
class nonlinear_heat
962 *
const double delta_t;
966 *
const double alpha;
970 *
const double tot_time;
1007 *
void setup_system(
unsigned int time_step);
1019 *
void output_results(
unsigned int prn)
const;
1024 *
void set_boundary_conditions(
double time);
1035 * std::unique_ptr<SparseDirectUMFPACK> matrix_factorization;
1052 *
class Initialcondition :
public Function<2>
1055 * Initialcondition():
Function<2>(1)
1063 * const unsigned
int component =0) const override;
1070 *
class Boundary_values_left:
public Function<2>
1073 * Boundary_values_left():
Function<2>(1)
1075 * virtual double
value(const
Point<2> & p,const unsigned
int component = 0) const override;
1081<a name=
"ann-nonlinear_heat.cc"></a>
1082<h1>Annotated version of nonlinear_heat.cc</h1>
1098 * #include
"allheaders.h"
1099 * #include
"nonlinear_heat.h"
1104 * nonlinear_heat nlheat;
1107 *
catch (std::exception &exc)
1109 * std::cerr << std::endl
1111 * <<
"----------------------------------------------------"
1113 * std::cerr <<
"Exception on processing: " << std::endl
1114 * << exc.what() << std::endl
1115 * <<
"Aborting!" << std::endl
1116 * <<
"----------------------------------------------------"
1123 * std::cerr << std::endl
1125 * <<
"----------------------------------------------------"
1127 * std::cerr <<
"Unknown exception!" << std::endl
1128 * <<
"Aborting!" << std::endl
1129 * <<
"----------------------------------------------------"
1139<a name=
"ann-source/boundary_values.cc"></a>
1140<h1>Annotated version of source/boundary_values.cc</h1>
1156 * #include
"nonlinear_heat.h"
1163 *
double Boundary_values_left::value(
const Point<2> & ,
const unsigned int )
const
1174 * nonlinear_heat nlheat;
1175 *
double total_time = nlheat.tot_time;
1176 *
return this->
get_time() * 100.0/total_time;
1183<a name=
"ann-source/compute_jacobian.cc"></a>
1184<h1>Annotated version of source/compute_jacobian.cc</h1>
1200 * #include
"allheaders.h"
1201 * #include
"nonlinear_heat.h"
1208 *
void nonlinear_heat::compute_jacobian(
const Vector<double> &evaluation_point)
1213 *
const QGauss<1> face_quadrature_formula(fe.degree+1);
1216 * quadrature_formula,
1225 *
const unsigned int dofs_per_cell = fe.dofs_per_cell;
1226 *
const unsigned int n_q_points = quadrature_formula.size();
1227 *
const unsigned int n_q_f_points = face_quadrature_formula.size();
1231 *
using ADNumberType =
typename ADHelper::ad_type;
1236 * system_matrix = 0.0;
1237 * std::vector<types::global_dof_index> local_dof_indices(
1240 * std::vector<double> consol(n_q_points);
1241 * std::vector<ADNumberType> old_solution(
1244 * std::vector<Tensor<1, 2>> consol_grad(
1246 * std::vector<Tensor<1, 2,ADNumberType>> old_solution_grad(
1249 *
for (
const auto &cell: dof_handler.active_cell_iterators())
1253 * fe_values.reinit(cell);
1254 * cell->get_dof_indices(local_dof_indices);
1255 *
const unsigned int n_independent_variables = local_dof_indices.size();
1256 *
const unsigned int n_dependent_variables = dofs_per_cell;
1257 * ADHelper ad_helper(n_independent_variables, n_dependent_variables);
1258 * ad_helper.register_dof_values(evaluation_point,local_dof_indices);
1259 *
const std::vector<ADNumberType> &dof_values_ad = ad_helper.get_sensitive_dof_values();
1260 * fe_values[t].get_function_values_from_local_dof_values(dof_values_ad,
1262 * fe_values[t].get_function_gradients_from_local_dof_values(dof_values_ad,
1263 * old_solution_grad);
1265 * fe_values[t].get_function_values(converged_solution, consol);
1266 * fe_values[t].get_function_gradients(converged_solution, consol_grad);
1267 * std::vector<ADNumberType> residual_ad(n_dependent_variables,
1268 * ADNumberType(0.0));
1269 *
for (
unsigned int q_index = 0; q_index < n_q_points; ++q_index)
1271 *
for (
unsigned int i = 0; i < dofs_per_cell; ++i)
1274 * ADNumberType MijTjcurr = Cp*rho*fe_values[t].value(i,q_index)*old_solution[q_index];
1275 * ADNumberType MijTjprev = Cp*rho*fe_values[t].value(i,q_index)*consol[q_index];
1276 * ADNumberType k_curr = a +
b*old_solution[q_index] + c*
std::pow(old_solution[q_index],2);
1277 * ADNumberType k_prev = a +
b*consol[q_index] + c*
std::pow(consol[q_index],2);
1278 * ADNumberType Licurr = alpha * delta_t * (fe_values[t].gradient(i,q_index)*k_curr*old_solution_grad[q_index]);
1279 * ADNumberType Liprev = (1-alpha) * delta_t * (fe_values[t].
gradient(i,q_index)*k_prev*consol_grad[q_index]);
1280 * residual_ad[i] += (MijTjcurr+Licurr-MijTjprev+Liprev)*fe_values.JxW(q_index);
1285 *
for (
unsigned int face_number = 0;face_number<GeometryInfo<2>::faces_per_cell; ++face_number)
1288 *
if (cell->face(face_number)->boundary_id() == 3)
1290 * fe_face_values.reinit(cell, face_number);
1291 *
for (
unsigned int q_point=0;q_point<n_q_f_points;++q_point)
1293 *
for (
unsigned int i =0;i<dofs_per_cell;++i)
1294 * residual_ad[i]+= -delta_t*(-10)*fe_face_values[t].value(i,q_point)*fe_face_values.JxW(q_point);
1300 * ad_helper.register_residual_vector(residual_ad);
1301 * ad_helper.compute_residual(cell_rhs);
1305 * ad_helper.compute_linearization(cell_matrix);
1306 * cell->get_dof_indices(local_dof_indices);
1311 *
for (
unsigned int i =0;i < dofs_per_cell; ++i){
1312 *
for(
unsigned int j = 0;j < dofs_per_cell;++j){
1313 * system_matrix.add(local_dof_indices[i],local_dof_indices[j],
cell_matrix(i,j));
1321 * std::map<types::global_dof_index, double> boundary_values;
1335 * std::cout <<
" Factorizing Jacobian matrix" << std::endl;
1336 * matrix_factorization = std::make_unique<SparseDirectUMFPACK>();
1337 * matrix_factorization->factorize(system_matrix);
1343<a name=
"ann-source/compute_residual.cc"></a>
1344<h1>Annotated version of source/compute_residual.cc</h1>
1360 * #include
"allheaders.h"
1361 * #include
"nonlinear_heat.h"
1376 *
const QGauss<1> face_quadrature_formula(fe.degree+1);
1378 * quadrature_formula,
1385 *
const unsigned int dofs_per_cell = fe.dofs_per_cell;
1386 *
const unsigned int n_q_points = quadrature_formula.size();
1387 *
const unsigned int n_q_f_points = face_quadrature_formula.size();
1399 *
using ADNumberType =
typename ADHelper::ad_type;
1408 * std::vector<types::global_dof_index> local_dof_indices(
1414 * std::vector<double> consol(n_q_points);
1415 * std::vector<ADNumberType> old_solution(
1420 * std::vector<Tensor<1, 2>> consol_grad(
1422 * std::vector<Tensor<1, 2,ADNumberType>> old_solution_grad(
1430 *
for (
const auto &cell: dof_handler.active_cell_iterators())
1433 * fe_values.reinit(cell);
1434 * cell->get_dof_indices(local_dof_indices);
1435 *
const unsigned int n_independent_variables = local_dof_indices.size();
1436 *
const unsigned int n_dependent_variables = dofs_per_cell;
1437 * ADHelper ad_helper(n_independent_variables, n_dependent_variables);
1442 * ad_helper.register_dof_values(evaluation_point,local_dof_indices);
1444 *
const std::vector<ADNumberType> &dof_values_ad = ad_helper.get_sensitive_dof_values();
1445 * fe_values[t].get_function_values_from_local_dof_values(dof_values_ad,
1447 * fe_values[t].get_function_gradients_from_local_dof_values(dof_values_ad,
1448 * old_solution_grad);
1453 * fe_values[t].get_function_values(converged_solution, consol);
1454 * fe_values[t].get_function_gradients(converged_solution, consol_grad);
1458 * std::vector<ADNumberType> residual_ad(n_dependent_variables,
1459 * ADNumberType(0.0));
1460 *
for (
unsigned int q_index = 0; q_index < n_q_points; ++q_index)
1462 *
for (
unsigned int i = 0; i < dofs_per_cell; ++i)
1467 * ADNumberType MijTjcurr = Cp*rho*fe_values[t].value(i,q_index)*old_solution[q_index];
1468 * ADNumberType MijTjprev = Cp*rho*fe_values[t].value(i,q_index)*consol[q_index];
1469 * ADNumberType k_curr = a +
b*old_solution[q_index] + c*
std::pow(old_solution[q_index],2);
1470 * ADNumberType k_prev = a +
b*consol[q_index] + c*
std::pow(consol[q_index],2);
1471 * ADNumberType Licurr = alpha * delta_t * (fe_values[t].gradient(i,q_index)*k_curr*old_solution_grad[q_index]);
1472 * ADNumberType Liprev = (1-alpha) * delta_t * (fe_values[t].
gradient(i,q_index)*k_prev*consol_grad[q_index]);
1473 * residual_ad[i] += (MijTjcurr+Licurr-MijTjprev+Liprev)*fe_values.JxW(q_index);
1480 *
for (
unsigned int face_number = 0;face_number<GeometryInfo<2>::faces_per_cell; ++face_number)
1483 *
if (cell->face(face_number)->boundary_id() == 3)
1485 * fe_face_values.reinit(cell, face_number);
1486 *
for (
unsigned int q_point=0;q_point<n_q_f_points;++q_point)
1488 *
for (
unsigned int i =0;i<dofs_per_cell;++i)
1492 * residual_ad[i]+= -delta_t*(-10)*fe_face_values[t].value(i,q_point)*fe_face_values.JxW(q_point);
1500 * ad_helper.register_residual_vector(residual_ad);
1506 * ad_helper.compute_residual(cell_rhs);
1507 * cell->get_dof_indices(local_dof_indices);
1509 *
for (
unsigned int i =0;i < dofs_per_cell; ++i)
1510 * residual(local_dof_indices[i])+= cell_rhs(i);
1517 * std::cout <<
" The Norm is :: = " << residual.l2_norm() << std::endl;
1522<a name=
"ann-source/initial_conditions.cc"></a>
1523<h1>Annotated version of source/initial_conditions.cc</h1>
1539 * #include
"nonlinear_heat.h"
1547 *
double Initialcondition::value(
const Point<2> & ,
const unsigned int )
const
1557<a name=
"ann-source/nonlinear_heat_cons_des.cc"></a>
1558<h1>Annotated version of source/nonlinear_heat_cons_des.cc</h1>
1574 * #include
"nonlinear_heat.h"
1580 * nonlinear_heat::nonlinear_heat ()
1596 * nonlinear_heat::~nonlinear_heat()
1598 * dof_handler.clear();
1605<a name=
"ann-source/output_results.cc"></a>
1606<h1>Annotated version of source/output_results.cc</h1>
1622 * #include
"nonlinear_heat.h"
1628 *
void nonlinear_heat::output_results(
unsigned int prn)
const
1632 * std::vector<std::string> solution_names;
1633 * solution_names.emplace_back (
"Temperature");
1634 * data_out.add_data_vector(converged_solution, solution_names);
1635 * data_out.build_patches();
1636 *
const std::string filename =
1638 * std::ofstream output(filename);
1639 * data_out.write_vtu(output);
1644<a name=
"ann-source/set_boundary_conditions.cc"></a>
1645<h1>Annotated version of source/set_boundary_conditions.cc</h1>
1661 * #include
"nonlinear_heat.h"
1662 * #include
"allheaders.h"
1668 *
void nonlinear_heat::set_boundary_conditions(
double time)
1670 * Boundary_values_left bl_left;
1671 * bl_left.set_time(time);
1672 * std::map<types::global_dof_index,double> boundary_values;
1678 *
for (
auto &boundary_value: boundary_values)
1679 * present_solution(boundary_value.
first) = boundary_value.
second;
1684<a name=
"ann-source/setup_system.cc"></a>
1685<h1>Annotated version of source/setup_system.cc</h1>
1701 * #include
"allheaders.h"
1702 * #include
"nonlinear_heat.h"
1708 *
void nonlinear_heat::setup_system(
unsigned int time_step)
1710 *
if (time_step ==0) {
1711 * dof_handler.distribute_dofs(fe);
1712 * converged_solution.reinit(dof_handler.n_dofs());
1713 * present_solution.reinit(dof_handler.n_dofs());
1718 * sparsity_pattern.copy_from(dsp);
1719 * system_matrix.reinit(sparsity_pattern);
1720 * matrix_factorization.reset();
1725<a name=
"ann-source/solve_and_run.cc"></a>
1726<h1>Annotated version of source/solve_and_run.cc</h1>
1742 * #include
"nonlinear_heat.h"
1751 * std::cout <<
" Solving linear system" << std::endl;
1752 * matrix_factorization->vmult(solution, rhs);
1755 *
void nonlinear_heat::run()
1759 * std::ifstream f(
"mesh/mesh.msh");
1760 * gridin.read_msh(f);
1764 *
unsigned int timestep_number = 0;
1765 *
unsigned int prn =0;
1768 *
while (time <=tot_time)
1772 * setup_system(timestep_number);
1775 * Initialcondition(),
1776 * present_solution);
1779 * Initialcondition(),
1780 * converged_solution);
1787 * present_solution = converged_solution;
1789 * std::cout<<
">>>>> Time now is: "<<time <<std::endl;
1790 * std::cout<<
">>>>> Time step is:"<<timestep_number<<std::endl;
1791 * set_boundary_conditions(time);
1794 *
const double target_tolerance = 1
e-3;
1800 * additional_data.abs_tol = target_tolerance;
1801 * additional_data.max_iter = 100;
1808 * nonlinear_solver.residual =
1811 * compute_residual(evaluation_point, residual);
1818 * nonlinear_solver.setup_jacobian =
1820 * compute_jacobian(current_u);
1826 * nonlinear_solver.solve_with_jacobian = [&](
const Vector<double> &rhs,
1828 *
const double tolerance) {
1829 * solve(rhs, dst, tolerance);
1835 * nonlinear_solver.solve(present_solution);
1840 * converged_solution = present_solution;
1842 *
if(timestep_number % 1 == 0) {
1844 * output_results(prn);
1847 * timestep_number++;
1848 * time=time+delta_t;
std::vector< bool > component_mask
void attach_dof_handler(const DoFHandler< dim, spacedim > &)
void attach_triangulation(Triangulation< dim, spacedim > &tria)
void make_sparsity_pattern(const DoFHandler< dim, spacedim > &dof_handler, SparsityPatternBase &sparsity_pattern, const AffineConstraints< number > &constraints={}, const bool keep_constrained_dofs=true, const types::subdomain_id subdomain_id=numbers::invalid_subdomain_id)
@ update_values
Shape function values.
@ update_normal_vectors
Normal vectors.
@ update_JxW_values
Transformed quadrature weights.
@ update_gradients
Shape function gradients.
@ update_quadrature_points
Transformed quadrature points.
std::vector< index_type > data
Expression differentiate(const Expression &f, const Expression &x)
constexpr types::blas_int zero
constexpr types::blas_int one
void cell_matrix(FullMatrix< double > &M, const FEValuesBase< dim > &fe, const FEValuesBase< dim > &fetest, const ArrayView< const std::vector< double > > &velocity, const double factor=1.)
double norm(const FEValuesBase< dim > &fe, const ArrayView< const std::vector< Tensor< 1, dim > > > &Du)
Point< spacedim > point(const gp_Pnt &p, const double tolerance=1e-10)
SymmetricTensor< 2, dim, Number > e(const Tensor< 2, dim, Number > &F)
SymmetricTensor< 2, dim, Number > b(const Tensor< 2, dim, Number > &F)
void apply(const Kokkos::TeamPolicy< MemorySpace::Default::kokkos_space::execution_space >::member_type &team_member, const Kokkos::View< Number *, MemorySpace::Default::kokkos_space > shape_data, const ViewTypeIn in, ViewTypeOut out)
VectorType::value_type * end(VectorType &V)
VectorType::value_type * begin(VectorType &V)
std::string int_to_string(const unsigned int value, const unsigned int digits=numbers::invalid_unsigned_int)
void run(const Iterator &begin, const std_cxx20::type_identity_t< Iterator > &end, Worker worker, Copier copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const unsigned int queue_length, const unsigned int chunk_size)
int(&) functions(const void *v1, const void *v2)
::VectorizedArray< Number, width > pow(const ::VectorizedArray< Number, width > &, const Number p)
const ::parallel::distributed::Triangulation< dim, spacedim > * triangulation

