 |
Reference documentation for deal.II version 9.1.1
|
 |
Reference documentation for deal.II version 9.1.1
|
This tutorial depends on step-6.
| Table of contents | |
|---|---|
This program was contributed by Daniel Arndt and Matthias Maier.
In this example we present how to use periodic boundary conditions in deal.II. Periodic boundary conditions are algebraic constraints that typically occur in computations on representative regions of a larger domain that repeat in one or more directions.
An example is the simulation of the electronic structure of photonic crystals, because they have a lattice-like structure and, thus, it often suffices to do the actual computation on only one box of the lattice. To be able to proceed this way one has to assume that the model can be periodically extended to the other boxes; this requires the solution to have a periodic structure.
deal.II provides a number of high level entry points to impose periodic boundary conditions. The general approach to apply periodic boundary conditions consists of three steps (see also the Glossary entry on periodic boundary conditions):
The second and third step are necessary for parallel meshes using the parallel::distributed::Triangulation class to ensure that cells on opposite sides of the domain but connected by periodic faces are part of the ghost layer if one of them is stored on the local processor. If the Triangulation is not a parallel::distributed::Triangulation, these steps are not necessary.
The first step consists of collecting matching periodic faces and storing them in a std::vector of GridTools::PeriodicFacePair. This is done with the function GridTools::collect_periodic_faces() that can be invoked for example like this:
This call loops over all faces of the container dof_handler on the periodic boundaries with boundary indicator b_id1 and b_id2, respectively. (You can assign these boundary indicators by hand after creating the coarse mesh, see Boundary indicator. Alternatively, you can also let many of the functions in namespace GridGenerator do this for if you specify the "colorize" flag; in that case, these functions will assign different boundary indicators to different parts of the boundary, with the details typically spelled out in the documentation of these functions.)
Concretely, if \text{vertices}_{1/2} are the vertices of two faces \text{face}_{1/2}, then the function call above will match pairs of faces (and dofs) such that the difference between \text{vertices}_2 and matrix\cdot \text{vertices}_1+\text{offset} vanishes in every component apart from direction and stores the resulting pairs with associated data in matched_pairs. (See GridTools::orthogonal_equality() for detailed information about the matching process.)
Consider, for example, the colored unit square \Omega=[0,1]^2 with boundary indicator 0 on the left, 1 on the right, 2 on the bottom and 3 on the top faces. (See the documentation of GridGenerator::hyper_cube() for this convention on how boundary indicators are assigned.) Then,
would yield periodicity constraints such that u(0,y)=u(1,y) for all y\in[0,1].
If we instead consider the parallelogram given by the convex hull of (0,0), (1,1), (1,2), (0,1) we can achieve the constraints u(0,y)=u(1,y+1) by specifying an offset:
or
Here, again, the assignment of boundary indicators 0 and 1 stems from what GridGenerator::parallelogram() documents.
The resulting matched_pairs can be used in DoFTools::make_periodicity_constraints for populating an AffineConstraints object with periodicity constraints:
Apart from this high level interface there are also variants of DoFTools::make_periodicity_constraints available that combine those two steps (see the variants of DofTools::make_periodicity_constraints).
There is also a low level interface to DoFTools::make_periodicity_constraints if more flexibility is needed. The low level variant allows to directly specify two faces that shall be constrained:
Here, we need to specify the orientation of the two faces using face_orientation, face_flip and face_orientation. For a closer description have a look at the documentation of DoFTools::make_periodicity_constraints. The remaining parameters are the same as for the high level interface apart from the self-explaining component_mask and affine_constraints.
In the following, we show how to use the above functions in a more involved example. The task is to enforce rotated periodicity constraints for the velocity component of a Stokes flow.
On a quarter-circle defined by \Omega=\{{\bf x}\in(0,1)^2:\|{\bf x}\|\in (0.5,1)\} we are going to solve the Stokes problem
\begin{eqnarray*} -\Delta \; \textbf{u} + \nabla p &=& (\exp(-100\|{\bf x}-(.75,0.1)^T\|^2),0)^T, \\ -\textrm{div}\; \textbf{u}&=&0,\\ \textbf{u}|_{\Gamma_1}&=&{\bf 0}, \end{eqnarray*}
where the boundary \Gamma_1 is defined as \Gamma_1 \dealcoloneq \{x\in \partial\Omega: \|x\|\in\{0.5,1\}\}. For the remaining parts of the boundary we are going to use periodic boundary conditions, i.e.
\begin{align*} u_x(0,\nu)&=-u_y(\nu,0)&\nu&\in[0,1]\\ u_y(0,\nu)&=u_x(\nu,0)&\nu&\in[0,1]. \end{align*}
The mesh will be generated by GridGenerator::quarter_hyper_shell(), which also documents how it assigns boundary indicators to its various boundaries if its colorize argument is set to true.
This example program is a slight modification of step-22 running in parallel using Trilinos to demonstrate the usage of periodic boundary conditions in deal.II. We thus omit to discuss the majority of the source code and only comment on the parts that deal with periodicity constraints. For the rest have a look at step-22 and the full source code at the bottom.
In order to implement periodic boundary conditions only two functions have to be modified:
StokesProblem<dim>::setup_dofs(): To populate an AffineConstraints object with periodicity constraintsStokesProblem<dim>::run(): To supply a distributed triangulation with periodicity information.The rest of the program is identical to step-22, so let us skip this part and only show these two functions in the following. (The full program can be found in the "Plain program" section below, though.)
Before we can prescribe periodicity constraints, we need to ensure that cells on opposite sides of the domain but connected by periodic faces are part of the ghost layer if one of them is stored on the local processor. At this point we need to think about how we want to prescribe periodicity. The vertices \text{vertices}_2 of a face on the left boundary should be matched to the vertices \text{vertices}_1 of a face on the lower boundary given by \text{vertices}_2=R\cdot \text{vertices}_1+b where the rotation matrix R and the offset b are given by
\begin{align*} R=\begin{pmatrix} 0&1\\-1&0 \end{pmatrix}, \quad b=\begin{pmatrix}0&0\end{pmatrix}. \end{align*}
The data structure we are saving the resulting information into is here based on the Triangulation.
Now telling the triangulation about the desired periodicity is particularly easy by just calling parallel::distributed::Triangulation::add_periodicity.
After we provided the mesh with the necessary information for the periodicity constraints, we are now able to actual create them. For describing the matching we are using the same approach as before, i.e., the \text{vertices}_2 of a face on the left boundary should be matched to the vertices \text{vertices}_1 of a face on the lower boundary given by \text{vertices}_2=R\cdot \text{vertices}_1+b where the rotation matrix R and the offset b are given by
\begin{align*} R=\begin{pmatrix} 0&1\\-1&0 \end{pmatrix}, \quad b=\begin{pmatrix}0&0\end{pmatrix}. \end{align*}
These two objects not only describe how faces should be matched but also in which sense the solution should be transformed from \text{face}_2 to \text{face}_1.
For setting up the constraints, we first store the periodicity information in an auxiliary object of type std::vector<GridTools::PeriodicFacePair<typename DoFHandler<dim>::cell_iterator> . The periodic boundaries have the boundary indicators 2 (x=0) and 3 (y=0). All the other parameters we have set up before. In this case the direction does not matter. Due to \text{vertices}_2=R\cdot \text{vertices}_1+b this is exactly what we want.
Next, we need to provide information on which vector valued components of the solution should be rotated. Since we choose here to just constraint the velocity and this starts at the first component of the solution vector, we simply insert a 0:
After setting up all the information in periodicity_vector all we have to do is to tell make_periodicity_constraints to create the desired constraints.
The rest of the program is then again identical to step-22. We will omit it here now, but as before, you can find these parts in the "Plain program" section below.
The created output is not very surprising. We simply see that the solution is periodic with respect to the left and lower boundary:
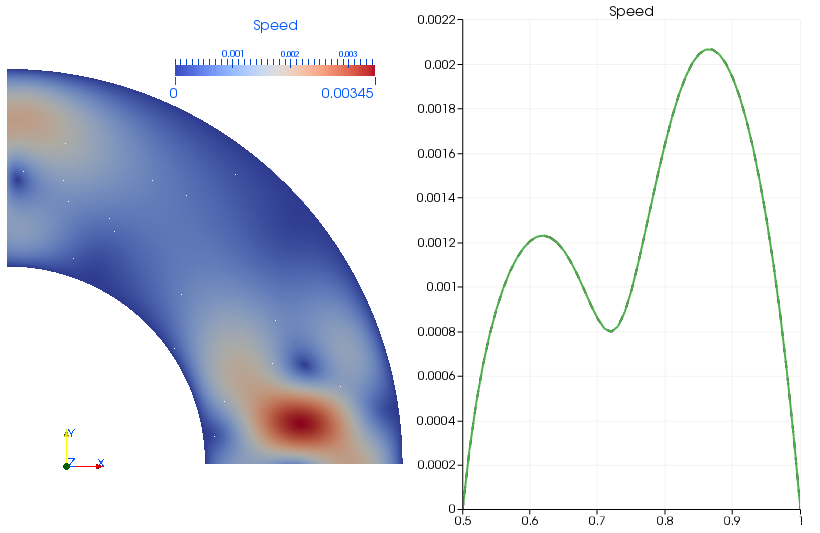
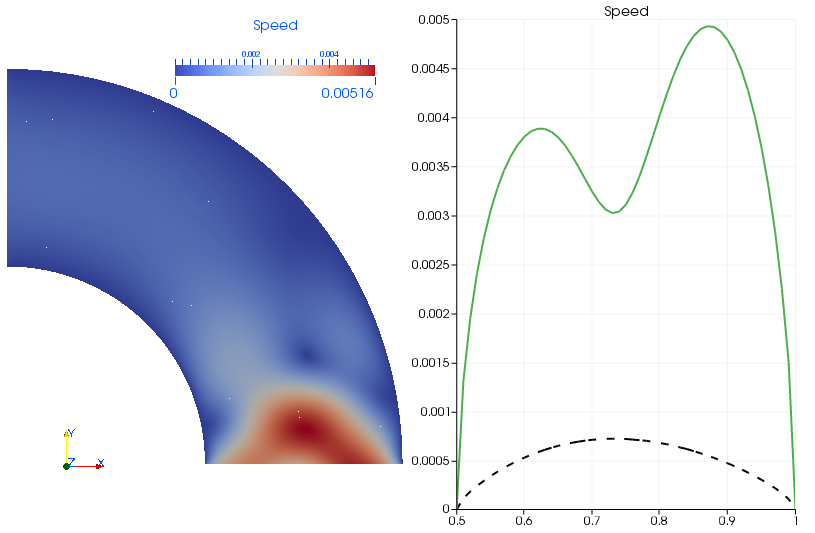
Without the periodicity constraints we would have ended up with the following solution:
 1.8.14
1.8.14