SolutionTransfer< dim, VectorType, DoFHandlerType > Class Template Reference

#include <deal.II/numerics/solution_transfer.h>

Classes
struct	Pointerstruct

Public Member Functions
	SolutionTransfer (const DoFHandlerType &dof)
	~SolutionTransfer ()
void	clear ()
void	prepare_for_pure_refinement ()
void	prepare_for_coarsening_and_refinement (const std::vector< VectorType > &all_in)
void	prepare_for_coarsening_and_refinement (const VectorType &in)
void	refine_interpolate (const VectorType &in, VectorType &out) const
void	interpolate (const std::vector< VectorType > &all_in, std::vector< VectorType > &all_out) const
void	interpolate (const VectorType &in, VectorType &out) const
std::size_t	memory_consumption () const

Static Public Member Functions
static ::ExceptionBase &	ExcNotPrepared ()
static ::ExceptionBase &	ExcAlreadyPrepForRef ()
static ::ExceptionBase &	ExcAlreadyPrepForCoarseAndRef ()

Private Types
enum	PreparationState { none, pure_refinement, coarsening_and_refinement }

Private Attributes
SmartPointer< const DoFHandlerType, SolutionTransfer< dim, VectorType, DoFHandlerType > >	dof_handler
types::global_dof_index	n_dofs_old
PreparationState	prepared_for
std::vector< std::vector< types::global_dof_index > >	indices_on_cell
std::map< std::pair< unsigned int, unsigned int >, Pointerstruct >	cell_map
std::vector< std::vector< Vector< typename VectorType::value_type > > >	dof_values_on_cell

Detailed Description

template<int dim, typename VectorType = Vector<double>, typename DoFHandlerType = DoFHandler<dim>>
class SolutionTransfer< dim, VectorType, DoFHandlerType >

This class implements the transfer of a discrete FE function (e.g. a solution vector) from one mesh to another that is obtained from the first by a single refinement and/or coarsening step. During interpolation the vector is reinitialized to the new size and filled with the interpolated values. This class is used in the step-15, step-26, step-31, and step-33 tutorial programs. A version of this class that works on parallel triangulations is available as parallel::distributed::SolutionTransfer.

Usage

This class implements the algorithms in two different ways:

• If the grid will only be refined (i.e. no cells are coarsened) then use SolutionTransfer as follows:

  SolutionTransfer<dim, double> soltrans(*dof_handler);
  
  // flag some cells for refinement, e.g.
  GridRefinement::refine_and_coarsen_fixed_fraction(*tria,
                                                    error_indicators,
                                                    0.3,
                                                    0);
  // prepare the triangulation for refinement,
  tria->prepare_coarsening_and_refinement();
  
  // tell the SolutionTransfer object that we intend to do pure refinement,
  soltrans.prepare_for_pure_refinement();
  
  // actually execute the refinement,
  tria->execute_coarsening_and_refinement();
  
  // and redistribute dofs.
  dof_handler->distribute_dofs (fe);

  Then to proceed do

  // take a copy of the solution vector
  Vector<double> solution_old(solution);
  
  // resize solution vector to the correct size, as the @p refine_interpolate
  // function requires the vectors to be of right sizes
  solution.reinit(dof_handler->n_dofs());
  
  // and finally interpolate
  soltrans.refine_interpolate(solution_old, solution);

  Although the refine_interpolate functions are allowed to be called multiple times, e.g. for interpolating several solution vectors, there is the following possibility of interpolating several functions simultaneously.

  std::vector<Vector<double> > solutions_old(n_vectors, Vector<double> (n));
  ...
  std::vector<Vector<double> > solutions(n_vectors, Vector<double> (n));
  soltrans.refine_interpolate(solutions_old, solutions);

  This is used in several of the tutorial programs, for example step-31.

• If the grid has cells that will be coarsened, then use SolutionTransfer as follows:

  SolutionTransfer<dim, Vector<double> > soltrans(*dof_handler);
  
  // flag some cells for refinement and coarsening, e.g.
  GridRefinement::refine_and_coarsen_fixed_fraction(*tria,
                                                    error_indicators,
                                                    0.3,
                                                    0.05);
  
  // prepare the triangulation,
  tria->prepare_coarsening_and_refinement();
  
  // prepare the SolutionTransfer object for coarsening and refinement and give
  // the solution vector that we intend to interpolate later,
  soltrans.prepare_for_coarsening_and_refinement(solution);
  
  // actually execute the refinement,
  tria->execute_coarsening_and_refinement ();
  
  // redistribute dofs,
  dof_handler->distribute_dofs (fe);
  
  // and interpolate the solution
  Vector<double> interpolate_solution(dof_handler->n_dofs());
  soltrans.interpolate(solution, interpolated_solution);

  If the grid is partitioned across several MPI processes, then it is important to note that the old solution(s) must be copied to one that also provides access to the locally relevant DoF values (these values required for the interpolation process):

  // Create initial indexsets pertaining to the grid before refinement
  IndexSet locally_owned_dofs, locally_relevant_dofs;
  locally_owned_dofs = dof_handler.locally_owned_dofs();
  DoFTools::extract_locally_relevant_dofs(dof_handler, locally_relevant_dofs);
  
  // The solution vector only knows about locally owned DoFs
  TrilinosWrappers::MPI::Vector solution;
  solution.reinit(locally_owned_dofs,
                  mpi_communicator);
  ...
  // Transfer solution to vector that provides access to locally relevant DoFs
  TrilinosWrappers::MPI::Vector old_solution;
  old_solution.reinit(locally_owned_dofs,
                      locally_relevant_dofs,
                      mpi_communicator);
  old_solution = solution;
  ...
  // Refine grid
  // Recreate locally_owned_dofs and locally_relevant_dofs index sets
  ...
  solution.reinit(locally_owned_dofs, mpi_communicator);
  soltrans.refine_interpolate(old_solution, solution);

  Multiple calls to the function interpolate (const Vector<number> &in, Vector<number> &out) are NOT allowed. Interpolating several functions can be performed in one step by using void interpolate (const vector<Vector<number> >&all_in, vector<Vector<number> >&all_out) const, and using the respective prepare_for_coarsening_and_refinement function taking several vectors as input before actually refining and coarsening the triangulation (see there).

For deleting all stored data in SolutionTransfer and reinitializing it use the clear() function.

The template argument number denotes the data type of the vectors you want to transfer.

Interpolating in the presence of hanging nodes and boundary values

The interpolation onto the new mesh is a local operation, i.e., it interpolates onto the new mesh only. If that new mesh has hanging nodes, you will therefore get a solution that does not satisfy hanging node constraints. The same is true with boundary values: the interpolated solution will just be the interpolation of the old solution at the boundary, and this may or may not satisfy boundary values at newly introduced boundary nodes.

Consequently, you may have to apply hanging node or boundary value constraints after interpolation. step-15 and step-26 have examples of dealing with this.

Implementation

• Solution transfer with only refinement. Assume that we have got a solution vector on the current (original) grid. Each entry of this vector belongs to one of the DoFs of the discretization. If we now refine the grid then the calling of DoFHandler::distribute_dofs() will change at least some of the DoF indices. Hence we need to store the DoF indices of all active cells before the refinement. A pointer for each active cell is used to point to the vector of these DoF indices of that cell. This is done by prepare_for_pure_refinement().

  In the function refine_interpolate(in,out) and on each cell where the pointer is set (i.e. the cells that were active in the original grid) we can now access the local values of the solution vector in on that cell by using the stored DoF indices. These local values are interpolated and set into the vector out that is at the end the discrete function in interpolated on the refined mesh.

  The refine_interpolate(in,out) function can be called multiple times for arbitrary many discrete functions (solution vectors) on the original grid.

• Solution transfer with coarsening and refinement. After calling Triangulation::prepare_coarsening_and_refinement the coarsen flags of either all or none of the children of a (father-)cell are set. While coarsening (Triangulation::execute_coarsening_and_refinement) the cells that are not needed any more will be deleted from the Triangulation.

  For the interpolation from the (to be coarsenend) children to their father the children cells are needed. Hence this interpolation and the storing of the interpolated values of each of the discrete functions that we want to interpolate needs to take place before these children cells are coarsened (and deleted!!). Again a pointers for the relevant cells is set to point to these values (see below). Additionally the DoF indices of the cells that will not be coarsened need to be stored according to the solution transfer while pure refinement (cf there). All this is performed by prepare_for_coarsening_and_refinement(all_in) where the vector<Vector<number> >vector all_in includes all discrete functions to be interpolated onto the new grid.

  As we need two different kinds of pointers (vector<unsigned int> * for the Dof indices and vector<Vector<number> > * for the interpolated DoF values) we use the Pointerstruct that includes both of these pointers and the pointer for each cell points to these Pointerstructs. On each cell only one of the two different pointers is used at one time hence we could use a void * pointer as vector<unsigned int> * at one time and as vector<Vector<number> > * at the other but using this Pointerstruct in between makes the use of these pointers more safe and gives better possibility to expand their usage.

  In interpolate(all_in, all_out) the refined cells are treated according to the solution transfer while pure refinement. Additionally, on each cell that is coarsened (hence previously was a father cell), the values of the discrete functions in all_out are set to the stored local interpolated values that are accessible due to the 'vector<Vector<number> > *' pointer in Pointerstruct that is pointed to by the pointer of that cell. It is clear that interpolate(all_in, all_out) only can be called with the vector<Vector<number> > all_in that previously was the parameter of the prepare_for_coarsening_and_refinement(all_in) function. Hence interpolate(all_in, all_out) can (in contrast to refine_interpolate(in, out)) only be called once.

Interaction with hanging nodes

This class does its best to represent on the new mesh the finite element function that existed on the old mesh, but this may lead to situations where the function on the new mesh is no longer conforming at hanging nodes. To this end, consider a situation of a twice refined mesh that started with a single square cell (i.e., we now have 16 cells). Consider also that we coarsen 4 of the cells back to the first refinement level. In this case, we end up with a mesh that will look as follows if we were to use a \(Q_1\) element:

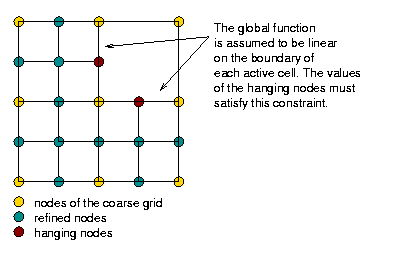
The process of interpolating from the old to the new mesh would imply that the values of the finite element function will not change on all of the cells that remained as they are (i.e., the fine cells) but that on the coarse cell at the top right, the four values at the vertices are obtained by interpolating down from its former children. If the original function was not linear, this implies that the marked hanging nodes will retain their old values which, in general, will not lead to a continuous function along the corresponding edges. In other words, the solution vector obtained after SolutionTransfer::interpolate() does not satisfy hanging node constraints: it corresponds to the pointwise interpolation, but not to the interpolation onto the new finite element space that contains constraints from hanging nodes.

Whether this is a problem you need to worry about or not depends on your application. The situation is easily corrected, of course, by applying AffineConstraints::distribute() to your solution vector after transfer, using a constraints object computed on the new DoFHandler object (you probably need to create this object anyway if you have hanging nodes). This is also what is done, for example, in step-15.

Note

This situation can only happen if you do coarsening. If all cells remain as they are or are refined, then SolutionTransfer::interpolate() computes a new vector of nodal values, but the function represented is of course exactly the same because the old finite element space is a subspace of the new one. Thus, if the old function was conforming (i.e., satisfied hanging node constraints), then so does the new one, and it is not necessary to call AffineConstraints::distribute().

Implementation in the context of hp finite elements

In the case of hp::DoFHandlers, nothing defines which of the finite elements that are part of the hp::FECollection associated with the DoF handler, should be considered on cells that are not active (i.e., that have children). This is because degrees of freedom are only allocated for active cells and, in fact, it is not allowed to set an active_fe_index on non- active cells using DoFAccessor::set_active_fe_index().

It is, thus, not entirely natural what should happen if, for example, a few cells are coarsened away. This class then implements the following algorithm: - If a cell is refined, then the values of the solution vector(s) are saved before refinement on the to-be-refined cell and in the space associated with this cell. These values are then interpolated to the finite element spaces of the children post-refinement. This may lose information if, for example, the old cell used a Q2 space and the children use Q1 spaces, or the information may be prolonged if the mother cell used a Q1 space and the children are Q2s. - If cells are to be coarsened, then the values from the child cells are interpolated to the mother cell using the largest of the child cell spaces. For example, if the children of a cell use Q1, Q2 and Q3 spaces, then the values from the children are interpolated into a Q3 space on the mother cell. After refinement, this Q3 function on the mother cell is then interpolated into the space the user has selected for this cell (which may be different from Q3, in this example, if the user has set the active_fe_index for a different space post-refinement and before calling hp::DoFHandler::distribute_dofs()).

Note

In the context of hp refinement, if cells are coarsened or the polynomial degree is lowered on some cells, then the old finite element space is not a subspace of the new space and you may run into the same situation as discussed above with hanging nodes. You may want to consider calling AffineConstraints::distribute() on the vector obtained by transferring the solution.

Author

Ralf Hartmann, 1999, Oliver Kayser-Herold and Wolfgang Bangerth, 2006, Wolfgang Bangerth 2014

Definition at line 335 of file solution_transfer.h.

Member Enumeration Documentation

PreparationState

template<int dim, typename VectorType = Vector<double>, typename DoFHandlerType = DoFHandler<dim>>

enum SolutionTransfer::PreparationState

private

Declaration of PreparationState that denotes the three possible states of the SolutionTransfer: being prepared for 'pure refinement', prepared for 'coarsening and refinement' or not prepared.

Enumerator
none	The SolutionTransfer is not yet prepared.
pure_refinement	The SolutionTransfer is prepared for purely refinement.
coarsening_and_refinement	The SolutionTransfer is prepared for coarsening and refinement.

Definition at line 490 of file solution_transfer.h.

Constructor & Destructor Documentation

SolutionTransfer()

template<int dim, typename VectorType , typename DoFHandlerType >

SolutionTransfer< dim, VectorType, DoFHandlerType >::SolutionTransfer

(

const DoFHandlerType &

dof

)

Constructor, takes the current DoFHandler as argument.

Definition at line 45 of file solution_transfer.cc.

~SolutionTransfer()

template<int dim, typename VectorType , typename DoFHandlerType >

SolutionTransfer< dim, VectorType, DoFHandlerType >::~SolutionTransfer

(

)

Destructor

Definition at line 65 of file solution_transfer.cc.

Member Function Documentation

clear()

template<int dim, typename VectorType , typename DoFHandlerType >

void SolutionTransfer< dim, VectorType, DoFHandlerType >::clear

(

)

Reinit this class to the state that it has directly after calling the Constructor

Definition at line 74 of file solution_transfer.cc.

prepare_for_pure_refinement()

template<int dim, typename VectorType , typename DoFHandlerType >

void SolutionTransfer< dim, VectorType, DoFHandlerType >::prepare_for_pure_refinement

(

)

Prepares the SolutionTransfer for pure refinement. It stores the dof indices of each cell. After calling this function only calling the refine_interpolate functions is allowed.

Definition at line 87 of file solution_transfer.cc.

prepare_for_coarsening_and_refinement() [1/2]

template<int dim, typename VectorType , typename DoFHandlerType >

void SolutionTransfer< dim, VectorType, DoFHandlerType >::prepare_for_coarsening_and_refinement

(

const std::vector< VectorType > &

all_in

)

Prepares the SolutionTransfer for coarsening and refinement. It stores the dof indices of each cell and stores the dof values of the vectors in all_in in each cell that'll be coarsened. all_in includes all vectors that are to be interpolated onto the new (refined and/or coarsenend) grid.

Definition at line 265 of file solution_transfer.cc.

prepare_for_coarsening_and_refinement() [2/2]

template<int dim, typename VectorType , typename DoFHandlerType >

void SolutionTransfer< dim, VectorType, DoFHandlerType >::prepare_for_coarsening_and_refinement

(

const VectorType &

in

)

Same as previous function but for only one discrete function to be interpolated.

Definition at line 428 of file solution_transfer.cc.

refine_interpolate()

template<int dim, typename VectorType , typename DoFHandlerType >

void SolutionTransfer< dim, VectorType, DoFHandlerType >::refine_interpolate	(	const VectorType &	in,
		VectorType &	out
	)		const

This function interpolates the discrete function in, which is a vector on the grid before the refinement, to the function out which then is a vector on the refined grid. It assumes the vectors having the right sizes (i.e. in.size()==n_dofs_old, out.size()==n_dofs_refined)

Calling this function is allowed only if prepare_for_pure_refinement is called and the refinement is executed before. Multiple calling of this function is allowed. e.g. for interpolating several functions.

Definition at line 127 of file solution_transfer.cc.

interpolate() [1/2]

template<int dim, typename VectorType , typename DoFHandlerType >

void SolutionTransfer< dim, VectorType, DoFHandlerType >::interpolate	(	const std::vector< VectorType > &	all_in,
		std::vector< VectorType > &	all_out
	)		const

This function interpolates the discrete functions that are stored in all_in onto the refined and/or coarsenend grid. It assumes the vectors in all_in denote the same vectors as in all_in as parameter of prepare_for_refinement_and_coarsening(all_in). However, there is no way of verifying this internally, so be careful here.

Calling this function is allowed only if first Triangulation::prepare_coarsening_and_refinement, second SolutionTransfer::prepare_for_coarsening_and_refinement, an then third Triangulation::execute_coarsening_and_refinement are called before. Multiple calling of this function is NOT allowed. Interpolating several functions can be performed in one step.

The number of output vectors is assumed to be the same as the number of input vectors. Also, the sizes of the output vectors are assumed to be of the right size (n_dofs_refined). Otherwise an assertion will be thrown.

Definition at line 438 of file solution_transfer.cc.

interpolate() [2/2]

template<int dim, typename VectorType , typename DoFHandlerType >

void SolutionTransfer< dim, VectorType, DoFHandlerType >::interpolate	(	const VectorType &	in,
		VectorType &	out
	)		const

Same as the previous function. It interpolates only one function. It assumes the vectors having the right sizes (i.e. in.size()==n_dofs_old, out.size()==n_dofs_refined)

Multiple calling of this function is NOT allowed. Interpolating several functions can be performed in one step by using interpolate (all_in, all_out)

Definition at line 576 of file solution_transfer.cc.

memory_consumption()

template<int dim, typename VectorType , typename DoFHandlerType >

std::size_t SolutionTransfer< dim, VectorType, DoFHandlerType >::memory_consumption

(

)

const

Determine an estimate for the memory consumption (in bytes) of this object.

Definition at line 596 of file solution_transfer.cc.

Member Data Documentation

dof_handler

template<int dim, typename VectorType = Vector<double>, typename DoFHandlerType = DoFHandler<dim>>

SmartPointer<const DoFHandlerType, SolutionTransfer<dim, VectorType, DoFHandlerType> > SolutionTransfer< dim, VectorType, DoFHandlerType >::dof_handler

private

Pointer to the degree of freedom handler to work with.

Definition at line 478 of file solution_transfer.h.

n_dofs_old

template<int dim, typename VectorType = Vector<double>, typename DoFHandlerType = DoFHandler<dim>>

types::global_dof_index SolutionTransfer< dim, VectorType, DoFHandlerType >::n_dofs_old

private

Stores the number of DoFs before the refinement and/or coarsening.

Definition at line 483 of file solution_transfer.h.

prepared_for

template<int dim, typename VectorType = Vector<double>, typename DoFHandlerType = DoFHandler<dim>>

PreparationState SolutionTransfer< dim, VectorType, DoFHandlerType >::prepared_for

private

Definition of the respective variable.

Definition at line 509 of file solution_transfer.h.

indices_on_cell

template<int dim, typename VectorType = Vector<double>, typename DoFHandlerType = DoFHandler<dim>>

std::vector<std::vector<types::global_dof_index> > SolutionTransfer< dim, VectorType, DoFHandlerType >::indices_on_cell

private

Is used for prepare_for_refining (of course also for repare_for_refining_and_coarsening) and stores all dof indices of the cells that'll be refined

Definition at line 517 of file solution_transfer.h.

cell_map

template<int dim, typename VectorType = Vector<double>, typename DoFHandlerType = DoFHandler<dim>>

std::map<std::pair<unsigned int, unsigned int>, Pointerstruct> SolutionTransfer< dim, VectorType, DoFHandlerType >::cell_map

private

Map mapping from level and index of cell to the Pointerstructs (cf. there). This map makes it possible to keep all the information needed to transfer the solution inside this object rather than using user pointers of the Triangulation for this purpose.

Definition at line 564 of file solution_transfer.h.

dof_values_on_cell

template<int dim, typename VectorType = Vector<double>, typename DoFHandlerType = DoFHandler<dim>>

std::vector<std::vector<Vector<typename VectorType::value_type> > > SolutionTransfer< dim, VectorType, DoFHandlerType >::dof_values_on_cell

private

Is used for prepare_for_refining_and_coarsening The interpolated dof values of all cells that'll be coarsened will be stored in this vector.

Definition at line 571 of file solution_transfer.h.

---

The documentation for this class was generated from the following files:

• deal.II/numerics/solution_transfer.h
• source/numerics/solution_transfer.cc