 |
Reference documentation for deal.II version 9.1.1
|
 |
Reference documentation for deal.II version 9.1.1
|
#include <deal.II/grid/tria_accessor.h>
Public Types | |
| using | AccessorData = typename TriaAccessor< dim, dim, spacedim >::AccessorData |
| using | Container = Triangulation< dim, spacedim > |
 Public Types inherited from TriaAccessor< dim, dim, spacedim > Public Types inherited from TriaAccessor< dim, dim, spacedim > | |
| using | AccessorData = typename TriaAccessorBase< structdim, dim, spacedim >::AccessorData |
 Public Types inherited from TriaAccessorBase< structdim, dim, spacedim > Public Types inherited from TriaAccessorBase< structdim, dim, spacedim > | |
| using | LocalData = void * |
Public Member Functions | |
Constructors | |
| CellAccessor (const Triangulation< dim, spacedim > *parent=nullptr, const int level=-1, const int index=-1, const AccessorData *local_data=nullptr) | |
| CellAccessor (const TriaAccessor< dim, dim, spacedim > &cell_accessor) | |
| template<int structdim2, int dim2, int spacedim2> | |
| CellAccessor (const InvalidAccessor< structdim2, dim2, spacedim2 > &) | |
| template<int structdim2, int dim2, int spacedim2> | |
| CellAccessor (const TriaAccessor< structdim2, dim2, spacedim2 > &) | |
| void | operator= (const CellAccessor< dim, spacedim > &)=delete |
Dealing with periodic neighbors | |
| bool | has_periodic_neighbor (const unsigned int i) const |
| TriaIterator< CellAccessor< dim, spacedim > > | periodic_neighbor (const unsigned int i) const |
| TriaIterator< CellAccessor< dim, spacedim > > | neighbor_or_periodic_neighbor (const unsigned int i) const |
| TriaIterator< CellAccessor< dim, spacedim > > | periodic_neighbor_child_on_subface (const unsigned int face_no, const unsigned int subface_no) const |
| std::pair< unsigned int, unsigned int > | periodic_neighbor_of_coarser_periodic_neighbor (const unsigned face_no) const |
| int | periodic_neighbor_index (const unsigned int i) const |
| int | periodic_neighbor_level (const unsigned int i) const |
| unsigned int | periodic_neighbor_of_periodic_neighbor (const unsigned int i) const |
| unsigned int | periodic_neighbor_face_no (const unsigned int i) const |
| bool | periodic_neighbor_is_coarser (const unsigned int i) const |
Dealing with boundary indicators | |
| bool | at_boundary (const unsigned int i) const |
| bool | at_boundary () const |
| bool | has_boundary_lines () const |
Dealing with refinement indicators | |
| RefinementCase< dim > | refine_flag_set () const |
| void | set_refine_flag (const RefinementCase< dim > ref_case=RefinementCase< dim >::isotropic_refinement) const |
| void | clear_refine_flag () const |
| bool | flag_for_face_refinement (const unsigned int face_no, const RefinementCase< dim - 1 > &face_refinement_case=RefinementCase< dim - 1 >::isotropic_refinement) const |
| bool | flag_for_line_refinement (const unsigned int line_no) const |
| ::internal::SubfaceCase< dim > | subface_case (const unsigned int face_no) const |
| bool | coarsen_flag_set () const |
| void | set_coarsen_flag () const |
| void | clear_coarsen_flag () const |
Dealing with material indicators | |
| types::material_id | material_id () const |
| void | set_material_id (const types::material_id new_material_id) const |
| void | recursively_set_material_id (const types::material_id new_material_id) const |
Dealing with subdomain indicators | |
| types::subdomain_id | subdomain_id () const |
| void | set_subdomain_id (const types::subdomain_id new_subdomain_id) const |
| types::subdomain_id | level_subdomain_id () const |
| void | set_level_subdomain_id (const types::subdomain_id new_level_subdomain_id) const |
| void | recursively_set_subdomain_id (const types::subdomain_id new_subdomain_id) const |
Dealing with codim 1 cell orientation | |
| bool | direction_flag () const |
| unsigned int | active_cell_index () const |
| int | parent_index () const |
| TriaIterator< CellAccessor< dim, spacedim > > | parent () const |
Other functions | |
| bool | active () const |
| bool | is_locally_owned () const |
| bool | is_locally_owned_on_level () const |
| bool | is_ghost () const |
| bool | is_artificial () const |
| bool | point_inside (const Point< spacedim > &p) const |
| void | set_neighbor (const unsigned int i, const TriaIterator< CellAccessor< dim, spacedim >> &pointer) const |
| CellId | id () const |
 Public Member Functions inherited from TriaAccessor< dim, dim, spacedim > Public Member Functions inherited from TriaAccessor< dim, dim, spacedim > | |
| TriaAccessor (const Triangulation< dim, spacedim > *parent=nullptr, const int level=-1, const int index=-1, const AccessorData *local_data=nullptr) | |
| TriaAccessor (const InvalidAccessor< structdim2, dim2, spacedim2 > &) | |
| TriaAccessor (const TriaAccessor< structdim2, dim2, spacedim2 > &) | |
| void | operator= (const TriaAccessor &)=delete |
| bool | used () const |
| double | extent_in_direction (const unsigned int axis) const |
| double | extent_in_direction (const unsigned int axis) const |
| double | extent_in_direction (const unsigned int axis) const |
| TriaIterator< TriaAccessor< 0, dim, spacedim > > | vertex_iterator (const unsigned int i) const |
| unsigned int | vertex_index (const unsigned int i) const |
| Point< spacedim > & | vertex (const unsigned int i) const |
| typename ::internal::TriangulationImplementation::Iterators< dim, spacedim >::line_iterator | line (const unsigned int i) const |
| unsigned int | line_index (const unsigned int i) const |
| typename ::internal::TriangulationImplementation::Iterators< dim, spacedim >::quad_iterator | quad (const unsigned int i) const |
| unsigned int | quad_index (const unsigned int i) const |
| bool | face_orientation (const unsigned int face) const |
| bool | face_flip (const unsigned int face) const |
| bool | face_rotation (const unsigned int face) const |
| bool | line_orientation (const unsigned int line) const |
| bool | has_children () const |
| unsigned int | n_children () const |
| unsigned int | number_of_children () const |
| unsigned int | max_refinement_depth () const |
| TriaIterator< TriaAccessor< structdim, dim, spacedim > > | child (const unsigned int i) const |
| TriaIterator< TriaAccessor< structdim, dim, spacedim > > | isotropic_child (const unsigned int i) const |
| RefinementCase< structdim > | refinement_case () const |
| int | child_index (const unsigned int i) const |
| int | isotropic_child_index (const unsigned int i) const |
| types::boundary_id | boundary_id () const |
| void | set_boundary_id (const types::boundary_id) const |
| void | set_all_boundary_ids (const types::boundary_id) const |
| bool | at_boundary () const |
| const Manifold< dim, spacedim > & | get_manifold () const |
| types::manifold_id | manifold_id () const |
| void | set_manifold_id (const types::manifold_id) const |
| void | set_all_manifold_ids (const types::manifold_id) const |
| bool | user_flag_set () const |
| void | set_user_flag () const |
| void | clear_user_flag () const |
| void | recursively_set_user_flag () const |
| void | recursively_clear_user_flag () const |
| void | clear_user_data () const |
| void | set_user_pointer (void *p) const |
| void | clear_user_pointer () const |
| void * | user_pointer () const |
| void | recursively_set_user_pointer (void *p) const |
| void | recursively_clear_user_pointer () const |
| void | set_user_index (const unsigned int p) const |
| void | clear_user_index () const |
| unsigned int | user_index () const |
| void | recursively_set_user_index (const unsigned int p) const |
| void | recursively_clear_user_index () const |
| double | diameter () const |
| std::pair< Point< spacedim >, double > | enclosing_ball () const |
| BoundingBox< spacedim > | bounding_box () const |
| double | extent_in_direction (const unsigned int axis) const |
| double | minimum_vertex_distance () const |
| Point< spacedim > | intermediate_point (const Point< structdim > &coordinates) const |
| Point< structdim > | real_to_unit_cell_affine_approximation (const Point< spacedim > &point) const |
| Point< spacedim > | center (const bool respect_manifold=false, const bool interpolate_from_surrounding=false) const |
| Point< spacedim > | barycenter () const |
| double | measure () const |
| bool | is_translation_of (const TriaIterator< TriaAccessor< structdim, dim, spacedim >> &o) const |
 Public Member Functions inherited from TriaAccessorBase< structdim, dim, spacedim > Public Member Functions inherited from TriaAccessorBase< structdim, dim, spacedim > | |
| void | operator= (const TriaAccessorBase *)=delete |
| int | level () const |
| int | index () const |
| IteratorState::IteratorStates | state () const |
| const Triangulation< dim, spacedim > & | get_triangulation () const |
Static Public Member Functions | |
| static ::ExceptionBase & | ExcRefineCellNotActive () |
| static ::ExceptionBase & | ExcCellFlaggedForRefinement () |
| static ::ExceptionBase & | ExcCellFlaggedForCoarsening () |
Protected Member Functions | |
| unsigned int | neighbor_of_neighbor_internal (const unsigned int neighbor) const |
| template<int dim_, int spacedim_> | |
| bool | point_inside_codim (const Point< spacedim_ > &p) const |
 Protected Member Functions inherited from TriaAccessorBase< structdim, dim, spacedim > Protected Member Functions inherited from TriaAccessorBase< structdim, dim, spacedim > | |
| TriaAccessorBase (const Triangulation< dim, spacedim > *parent=nullptr, const int level=-1, const int index=-1, const AccessorData *=nullptr) | |
| TriaAccessorBase (const TriaAccessorBase &) | |
| void | copy_from (const TriaAccessorBase &) |
| TriaAccessorBase & | operator= (const TriaAccessorBase &) |
| bool | operator< (const TriaAccessorBase &other) const |
| bool | operator== (const TriaAccessorBase &) const |
| bool | operator!= (const TriaAccessorBase &) const |
| ::internal::TriangulationImplementation::TriaObjects< ::internal::TriangulationImplementation::TriaObject< structdim > > & | objects () const |
| void | operator++ () |
| void | operator-- () |
Private Member Functions | |
| void | set_active_cell_index (const unsigned int active_cell_index) |
| void | set_parent (const unsigned int parent_index) |
| void | set_direction_flag (const bool new_direction_flag) const |
Friends | |
| template<int , int > | |
| class | Triangulation |
Accessing sub-objects and neighbors | |
| TriaIterator< CellAccessor< dim, spacedim > > | child (const unsigned int i) const |
| TriaIterator< TriaAccessor< dim - 1, dim, spacedim > > | face (const unsigned int i) const |
| unsigned int | face_index (const unsigned int i) const |
| TriaIterator< CellAccessor< dim, spacedim > > | neighbor_child_on_subface (const unsigned int face_no, const unsigned int subface_no) const |
| TriaIterator< CellAccessor< dim, spacedim > > | neighbor (const unsigned int i) const |
| int | neighbor_index (const unsigned int i) const |
| int | neighbor_level (const unsigned int i) const |
| unsigned int | neighbor_of_neighbor (const unsigned int neighbor) const |
| bool | neighbor_is_coarser (const unsigned int neighbor) const |
| std::pair< unsigned int, unsigned int > | neighbor_of_coarser_neighbor (const unsigned int neighbor) const |
| unsigned int | neighbor_face_no (const unsigned int neighbor) const |
| static bool | is_level_cell () |
Additional Inherited Members | |
 Static Public Attributes inherited from TriaAccessorBase< structdim, dim, spacedim > Static Public Attributes inherited from TriaAccessorBase< structdim, dim, spacedim > | |
| static const unsigned int | space_dimension = spacedim |
| static const unsigned int | dimension = dim |
| static const unsigned int | structure_dimension = structdim |
 Protected Types inherited from TriaAccessorBase< structdim, dim, spacedim > Protected Types inherited from TriaAccessorBase< structdim, dim, spacedim > | |
| using | AccessorData = void |
 Protected Attributes inherited from TriaAccessorBase< structdim, dim, spacedim > Protected Attributes inherited from TriaAccessorBase< structdim, dim, spacedim > | |
| typename ::internal::TriaAccessorImplementation::PresentLevelType< structdim, dim >::type | present_level |
| int | present_index |
| const Triangulation< dim, spacedim > * | tria |
This class allows access to a cell: a line in one dimension, a quad in two dimension, etc.
The following refers to any dimension:
This class allows access to a cell, which is a line in 1D and a quad in 2D. Cells have more functionality than lines or quads by themselves, for example they can be flagged for refinement, they have neighbors, they have the possibility to check whether they are at the boundary etc. This class offers access to all this data.
Definition at line 2645 of file tria_accessor.h.
| using CellAccessor< dim, spacedim >::AccessorData = typename TriaAccessor<dim, dim, spacedim>::AccessorData |
Propagate the AccessorData type into the present class.
Definition at line 2651 of file tria_accessor.h.
| using CellAccessor< dim, spacedim >::Container = Triangulation<dim, spacedim> |
Define the type of the container this is part of.
Definition at line 2656 of file tria_accessor.h.
| CellAccessor< dim, spacedim >::CellAccessor | ( | const Triangulation< dim, spacedim > * | parent = nullptr, |
| const int | level = -1, |
||
| const int | index = -1, |
||
| const AccessorData * | local_data = nullptr |
||
| ) |
Constructor.
| CellAccessor< dim, spacedim >::CellAccessor | ( | const TriaAccessor< dim, dim, spacedim > & | cell_accessor | ) |
Copy constructor.
| CellAccessor< dim, spacedim >::CellAccessor | ( | const InvalidAccessor< structdim2, dim2, spacedim2 > & | ) |
Conversion constructor. This constructor exists to make certain constructs simpler to write in dimension independent code. For example, it allows assigning a face iterator to a line iterator, an operation that is useful in 2d but doesn't make any sense in 3d. The constructor here exists for the purpose of making the code conform to C++ but it will unconditionally abort; in other words, assigning a face iterator to a line iterator is better put into an if-statement that checks that the dimension is two, and assign to a quad iterator in 3d (an operator that, without this constructor would be illegal if we happen to compile for 2d).
Definition at line 3625 of file tria_accessor.h.
| CellAccessor< dim, spacedim >::CellAccessor | ( | const TriaAccessor< structdim2, dim2, spacedim2 > & | ) |
Another conversion operator between objects that don't make sense, just like the previous one.
Definition at line 3655 of file tria_accessor.h.
|
delete |
Copy operator. These operators are usually used in a context like iterator a,b; *a=*b;. Presumably, the intent here is to copy the object pointed to by b to the object pointed to by a. However, the result of dereferencing an iterator is not an object but an accessor; consequently, this operation is not useful for iterators on triangulations. Consequently, this operator is declared as deleted and can not be used.
| TriaIterator<CellAccessor<dim, spacedim> > CellAccessor< dim, spacedim >::child | ( | const unsigned int | i | ) | const |
Return a pointer to the ith child. Overloaded version which returns a more reasonable iterator class.
| TriaIterator<TriaAccessor<dim - 1, dim, spacedim> > CellAccessor< dim, spacedim >::face | ( | const unsigned int | i | ) | const |
Return an iterator to the ith face of this cell.
| unsigned int CellAccessor< dim, spacedim >::face_index | ( | const unsigned int | i | ) | const |
Return the (global) index of the ith face of this cell.
| TriaIterator< CellAccessor< dim, spacedim > > CellAccessor< dim, spacedim >::neighbor_child_on_subface | ( | const unsigned int | face_no, |
| const unsigned int | subface_no | ||
| ) | const |
Return an iterator to that cell that neighbors the present cell on the given face and subface number.
To succeed, the present cell must not be further refined, and the neighbor on the given face must be further refined exactly once; the returned cell is then a child of that neighbor.
The function may not be called in 1d, since there we have no subfaces. The implementation of this function is rather straightforward in 2d, by first determining which face of the neighbor cell the present cell is bordering on (this is what the neighbor_of_neighbor function does), and then asking GeometryInfo::child_cell_on_subface for the index of the child.
However, the situation is more complicated in 3d, since there faces may have more than one orientation, and we have to use face_orientation, face_flip and face_rotation for both this and the neighbor cell to figure out which cell we want to have.
This can lead to surprising results: if we are sitting on a cell and are asking for a cell behind subface sf, then this means that we are considering the subface for the face in the natural direction for the present cell. However, if the face as seen from this cell has face_orientation()==false, then the child of the face that separates the present cell from the neighboring cell's child is not necessarily the sf-th child of the face of this cell. This is so because the subface_no on a cell corresponds to the subface with respect to the intrinsic ordering of the present cell, whereas children of face iterators are computed with respect to the intrinsic ordering of faces; these two orderings are only identical if the face orientation is true, and reversed otherwise.
Similarly, effects of face_flip()==true and face_rotation()==true(), both of which indicate a non-standard face have to be considered.
Fortunately, this is only very rarely of concern, since usually one simply wishes to loop over all finer neighbors at a given face of an active cell. Only in the process of refinement of a Triangulation we want to set neighbor information for both our child cells and the neighbor's children. Since we can respect orientation of faces from our current cell in that case, we do NOT respect face_orientation, face_flip and face_rotation of the present cell within this function, i.e. the returned neighbor's child is behind subface subface concerning the intrinsic ordering of the given face.
Definition at line 2857 of file tria_accessor.cc.
| TriaIterator<CellAccessor<dim, spacedim> > CellAccessor< dim, spacedim >::neighbor | ( | const unsigned int | i | ) | const |
Return a pointer to the ith neighbor. If the neighbor does not exist, i.e., if the ith face of the current object is at the boundary, then an invalid iterator is returned.
The neighbor of a cell has at most the same level as this cell. For example, consider the following situation:
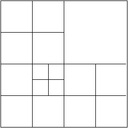
Here, if you are on the top right cell and you ask for its left neighbor (which is, according to the conventions spelled out in the GeometryInfo class, its zeroth neighbor), then you will get the mother cell of the four small cells at the top left. In other words, the cell you get as neighbor has the same refinement level as the one you're on right now (the top right one) and it may have children.
On the other hand, if you were at the top right cell of the four small cells at the top left, and you asked for the right neighbor (which is associated with index i=1), then you would get the large cell at the top right which in this case has a lower refinement level and no children of its own.
| int CellAccessor< dim, spacedim >::neighbor_index | ( | const unsigned int | i | ) | const |
Return the index of the ith neighbor. If the neighbor does not exist, its index is -1.
| int CellAccessor< dim, spacedim >::neighbor_level | ( | const unsigned int | i | ) | const |
Return the level of the ith neighbor. If the neighbor does not exist, its level is -1.
| unsigned int CellAccessor< dim, spacedim >::neighbor_of_neighbor | ( | const unsigned int | neighbor | ) | const |
Return the how-many'th neighbor this cell is of cell->neighbor(neighbor), i.e. return the face_no such that cell->neighbor(neighbor)->neighbor(face_no)==cell. This function is the right one if you want to know how to get back from a neighbor to the present cell.
Note that this operation is only useful if the neighbor is not coarser than the present cell. If the neighbor is coarser this function throws an exception. Use the neighbor_of_coarser_neighbor function in that case.
Definition at line 2295 of file tria_accessor.cc.
| bool CellAccessor< dim, spacedim >::neighbor_is_coarser | ( | const unsigned int | neighbor | ) | const |
Return, whether the neighbor is coarser then the present cell. This is important in case of ansiotropic refinement where this information does not depend on the levels of the cells.
Note, that in an anisotropic setting, a cell can only be coarser than another one at a given face, not on a general basis. The face of the finer cell is contained in the corresponding face of the coarser cell, the finer face is either a child or a grandchild of the coarser face.
Definition at line 2309 of file tria_accessor.cc.
| std::pair< unsigned int, unsigned int > CellAccessor< dim, spacedim >::neighbor_of_coarser_neighbor | ( | const unsigned int | neighbor | ) | const |
This function is a generalization of the neighbor_of_neighbor function for the case of a coarser neighbor. It returns a pair of numbers, face_no and subface_no, with the following property, if the neighbor is not refined: cell->neighbor(neighbor)->neighbor_child_on_subface(face_no, subface_no)==cell. In 3D, a coarser neighbor can still be refined. In that case subface_no denotes the child index of the neighbors face that relates to our face: cell->neighbor(neighbor)->face(face_no)->child(subface_no)==cell->face(neighbor). This case in 3d and how it can happen is discussed in the introduction of the step-30 tutorial program.
This function is impossible for dim==1.
Definition at line 2320 of file tria_accessor.cc.
| unsigned int CellAccessor< dim, spacedim >::neighbor_face_no | ( | const unsigned int | neighbor | ) | const |
This function is a generalization of the neighbor_of_neighbor and the neighbor_of_coarser_neighbor functions. It checks whether the neighbor is coarser or not and calls the respective function. In both cases, only the face_no is returned.
|
static |
Compatibility interface with DoFCellAccessor. Always returns false.
| bool CellAccessor< dim, spacedim >::has_periodic_neighbor | ( | const unsigned int | i | ) | const |
If the cell has a periodic neighbor at its ith face, this function returns true, otherwise, the returned value is false.
Definition at line 2500 of file tria_accessor.cc.
| TriaIterator< CellAccessor< dim, spacedim > > CellAccessor< dim, spacedim >::periodic_neighbor | ( | const unsigned int | i | ) | const |
For a cell with its ith face at a periodic boundary, see the entry for periodic boundaries, this function returns an iterator to the cell on the other side of the periodic boundary. If there is no periodic boundary at the ith face, an exception will be thrown. In order to avoid running into an exception, check the result of has_periodic_neighbor() for the ith face prior to using this function. The behavior of periodic_neighbor() is similar to neighbor(), in the sense that the returned cell has at most the same level of refinement as the current cell. On distributed meshes, by calling Triangulation::add_periodicity(), we can make sure that the element on the other side of the periodic boundary exists in this rank as a ghost cell or a locally owned cell.
Definition at line 2540 of file tria_accessor.cc.
| TriaIterator< CellAccessor< dim, spacedim > > CellAccessor< dim, spacedim >::neighbor_or_periodic_neighbor | ( | const unsigned int | i | ) | const |
For a cell whose ith face is not at a boundary, this function returns the same result as neighbor(). If the ith face is at a periodic boundary this function returns the same result as periodic_neighbor(). If neither of the aforementioned conditions are met, i.e. the ith face is on a nonperiodic boundary, an exception will be thrown.
Definition at line 2569 of file tria_accessor.cc.
| TriaIterator< CellAccessor< dim, spacedim > > CellAccessor< dim, spacedim >::periodic_neighbor_child_on_subface | ( | const unsigned int | face_no, |
| const unsigned int | subface_no | ||
| ) | const |
Return an iterator to the periodic neighbor of the cell at a given face and subface number. The general guidelines for using this function is similar to the function neighbor_child_on_subface(). The implementation of this function is consistent with periodic_neighbor_of_coarser_periodic_neighbor(). For instance, assume that we are sitting on a cell named cell1, whose neighbor behind the ith face is one level coarser. Let us name this coarser neighbor cell2. Then, by calling periodic_neighbor_of_coarser_periodic_neighbor(), from cell1, we get a face_num and a subface_num. Now, if we call periodic_neighbor_child_on_subface() from cell2, with the above face_num and subface_num, we get an iterator to cell1.
Definition at line 2586 of file tria_accessor.cc.
| std::pair< unsigned int, unsigned int > CellAccessor< dim, spacedim >::periodic_neighbor_of_coarser_periodic_neighbor | ( | const unsigned | face_no | ) | const |
This function is a generalization of periodic_neighbor_of_periodic_neighbor() for those cells which have a coarser periodic neighbor. The returned pair of numbers can be used in periodic_neighbor_child_on_subface() to get back to the current cell. In other words, the following assertion should be true, for a cell with coarser periodic neighbor: cell->periodic_neighbor(i)->periodic_neighbor_child_on_subface(face_no, subface_no)==cell
Definition at line 2640 of file tria_accessor.cc.
| int CellAccessor< dim, spacedim >::periodic_neighbor_index | ( | const unsigned int | i | ) | const |
This function returns the index of the periodic neighbor at the ith face of the current cell. If there is no periodic neighbor at the given face, the returned value is -1.
Definition at line 2705 of file tria_accessor.cc.
| int CellAccessor< dim, spacedim >::periodic_neighbor_level | ( | const unsigned int | i | ) | const |
This function returns the level of the periodic neighbor at the ith face of the current cell. If there is no periodic neighbor at the given face, the returned value is -1.
Definition at line 2715 of file tria_accessor.cc.
| unsigned int CellAccessor< dim, spacedim >::periodic_neighbor_of_periodic_neighbor | ( | const unsigned int | i | ) | const |
For a cell with a periodic neighbor at its ith face, this function returns the face number of that periodic neighbor such that the current cell is the periodic neighbor of that neighbor. In other words the following assertion holds for those cells which have a periodic neighbor with the same or a higher level of refinement as the current cell: {cell->periodic_neighbor(i)-> periodic_neighbor(cell->periodic_neighbor_of_periodic_neighbor(i))==cell} For the cells with a coarser periodic neighbor, one should use periodic_neighbor_of_coarser_periodic_neighbor() and periodic_neighbor_child_on_subface() to get back to the current cell.
Definition at line 2725 of file tria_accessor.cc.
| unsigned int CellAccessor< dim, spacedim >::periodic_neighbor_face_no | ( | const unsigned int | i | ) | const |
If a cell has a periodic neighbor at its ith face, this function returns the face number of the periodic neighbor, which is connected to the ith face of this cell.
Definition at line 2735 of file tria_accessor.cc.
| bool CellAccessor< dim, spacedim >::periodic_neighbor_is_coarser | ( | const unsigned int | i | ) | const |
This function returns true if the element on the other side of the periodic boundary is coarser and returns false otherwise. The implementation allows this function to work in the case of anisotropic refinement.
Definition at line 2768 of file tria_accessor.cc.
| bool CellAccessor< dim, spacedim >::at_boundary | ( | const unsigned int | i | ) | const |
Return whether the ith vertex or face (depending on the dimension) is part of the boundary. This is true, if the ith neighbor does not exist.
Definition at line 2826 of file tria_accessor.cc.
| bool CellAccessor< dim, spacedim >::at_boundary | ( | ) | const |
Return whether the cell is at the boundary. Being at the boundary is defined by one face being on the boundary. Note that this does not catch cases where only one vertex of a quad or of a hex is at the boundary, or where only one line of a hex is at the boundary while the interiors of all faces are in the interior of the domain. For the latter case, the has_boundary_lines function is the right one to ask.
Definition at line 1950 of file tria_accessor.cc.
| bool CellAccessor< dim, spacedim >::has_boundary_lines | ( | ) | const |
This is a slight variation to the at_boundary function: for 1 and 2 dimensions, it is equivalent, for three dimensions it returns whether at least one of the 12 lines of the hexahedron is at a boundary. This, of course, includes the case where a whole face is at the boundary, but also some other cases.
Definition at line 2839 of file tria_accessor.cc.
| RefinementCase<dim> CellAccessor< dim, spacedim >::refine_flag_set | ( | ) | const |
Return the RefinementCase<dim> this cell was flagged to be refined with. The return value of this function can be compared to a bool to check if this cell is flagged for any kind of refinement. For example, if you have previously called cell->set_refine_flag() for a cell, then you will enter the 'if' block in the following snippet:
| void CellAccessor< dim, spacedim >::set_refine_flag | ( | const RefinementCase< dim > | ref_case = RefinementCase< dim >::isotropic_refinement | ) | const |
Flag the cell pointed to for refinement. This function is only allowed for active cells. Keeping the default value for ref_case will mark this cell for isotropic refinement.
If you choose anisotropic refinement, for example by passing as argument one of the flags RefinementCase::cut_x, RefinementCase::cut_y, RefinementCase::cut_z, or a combination of these, then keep in mind that refining in x-, y-, or z-direction happens with regard to the local coordinate system of the cell. In other words, these flags determine which edges and faces of the cell will be cut into new edges and faces. On the other hand, this process is independent of how the cell is oriented within the global coordinate system, and you should not assume any particular orientation of the cell's local coordinate system within the global coordinate system of the space it lives in.
| void CellAccessor< dim, spacedim >::clear_refine_flag | ( | ) | const |
Clear the refinement flag.
| bool CellAccessor< dim, spacedim >::flag_for_face_refinement | ( | const unsigned int | face_no, |
| const RefinementCase< dim - 1 > & | face_refinement_case = RefinementCase< dim - 1 >::isotropic_refinement |
||
| ) | const |
Modify the refinement flag of the cell to ensure (at least) the given refinement case face_refinement_case at face face_no, taking into account orientation, flip and rotation of the face. Return, whether the refinement flag had to be modified. This function is only allowed for active cells.
| bool CellAccessor< dim, spacedim >::flag_for_line_refinement | ( | const unsigned int | line_no | ) | const |
Modify the refinement flag of the cell to ensure that line face_no will be refined. Return, whether the refinement flag had to be modified. This function is only allowed for active cells.
| ::internal::SubfaceCase<dim> CellAccessor< dim, spacedim >::subface_case | ( | const unsigned int | face_no | ) | const |
Return the SubfaceCase of face face_no. Note that this is not identical to asking cell->face(face_no)->refinement_case() since the latter returns a RefinementCase<dim-1> and thus only considers one (anisotropic) refinement, whereas this function considers the complete refinement situation including possible refinement of the face's children. This function may only be called for active cells in 2d and 3d.
| bool CellAccessor< dim, spacedim >::coarsen_flag_set | ( | ) | const |
Return whether the coarsen flag is set or not.
| void CellAccessor< dim, spacedim >::set_coarsen_flag | ( | ) | const |
Flag the cell pointed to for coarsening. This function is only allowed for active cells.
| void CellAccessor< dim, spacedim >::clear_coarsen_flag | ( | ) | const |
Clear the coarsen flag.
| types::material_id CellAccessor< dim, spacedim >::material_id | ( | ) | const |
Return the material id of this cell.
For a typical use of this function, see the step-28 tutorial program.
See the glossary for more information.
Definition at line 1972 of file tria_accessor.cc.
| void CellAccessor< dim, spacedim >::set_material_id | ( | const types::material_id | new_material_id | ) | const |
Set the material id of this cell.
For a typical use of this function, see the step-28 tutorial program.
See the glossary for more information.
Definition at line 1984 of file tria_accessor.cc.
| void CellAccessor< dim, spacedim >::recursively_set_material_id | ( | const types::material_id | new_material_id | ) | const |
Set the material id of this cell and all its children (and grand- children, and so on) to the given value.
See the glossary for more information.
Definition at line 1999 of file tria_accessor.cc.
| types::subdomain_id CellAccessor< dim, spacedim >::subdomain_id | ( | ) | const |
Return the subdomain id of this cell.
See the glossary for more information.
| void CellAccessor< dim, spacedim >::set_subdomain_id | ( | const types::subdomain_id | new_subdomain_id | ) | const |
Set the subdomain id of this cell.
See the glossary for more information. This function should not be called if you use a parallel::distributed::Triangulation object.
Definition at line 2013 of file tria_accessor.cc.
| types::subdomain_id CellAccessor< dim, spacedim >::level_subdomain_id | ( | ) | const |
Get the level subdomain id of this cell. This is used for parallel multigrid.
Definition at line 2026 of file tria_accessor.cc.
| void CellAccessor< dim, spacedim >::set_level_subdomain_id | ( | const types::subdomain_id | new_level_subdomain_id | ) | const |
Set the level subdomain id of this cell. This is used for parallel multigrid.
Definition at line 2037 of file tria_accessor.cc.
| void CellAccessor< dim, spacedim >::recursively_set_subdomain_id | ( | const types::subdomain_id | new_subdomain_id | ) | const |
Set the subdomain id of this cell (if it is active) or all its terminal children (and grand-children, and so on, as long as they have no children of their own) to the given value. Since the subdomain id is a concept that is only defined for cells that are active (i.e., have no children of their own), this function only sets the subdomain ids for all children and grand children of this cell that are actually active, skipping intermediate child cells.
See the glossary for more information. This function should not be called if you use a parallel::distributed::Triangulation object since there the subdomain id is implicitly defined by which processor you're on.
Definition at line 2145 of file tria_accessor.cc.
| bool CellAccessor< dim, spacedim >::direction_flag | ( | ) | const |
Return the orientation of this cell.
For the meaning of this flag, see GlossDirectionFlag.
Definition at line 2048 of file tria_accessor.cc.
| unsigned int CellAccessor< dim, spacedim >::active_cell_index | ( | ) | const |
Return the how many-th active cell the current cell is (assuming the current cell is indeed active). This is useful, for example, if you are accessing the elements of a vector with as many entries as there are active cells. Such vectors are used for estimating the error on each cell of a triangulation, for specifying refinement criteria passed to the functions in GridRefinement, and for generating cell-wise output.
The function throws an exception if the current cell is not active.
Definition at line 2119 of file tria_accessor.cc.
| int CellAccessor< dim, spacedim >::parent_index | ( | ) | const |
Return the index of the parent of this cell within the level of the triangulation to which the parent cell belongs. The level of the parent is of course one lower than that of the present cell. If the parent does not exist (i.e., if the object is at the coarsest level of the mesh hierarchy), an exception is generated.
Definition at line 2104 of file tria_accessor.cc.
| TriaIterator< CellAccessor< dim, spacedim > > CellAccessor< dim, spacedim >::parent | ( | ) | const |
Return an iterator to the parent. If the parent does not exist (i.e., if the object is at the coarsest level of the mesh hierarchy), an exception is generated.
Definition at line 2131 of file tria_accessor.cc.
| bool CellAccessor< dim, spacedim >::active | ( | ) | const |
Test whether the cell has children (this is the criterion for activity of a cell).
See the glossary for more information.
| bool CellAccessor< dim, spacedim >::is_locally_owned | ( | ) | const |
Return whether this cell is owned by the current processor or is owned by another processor. The function always returns true if applied to an object of type Triangulation, but may yield false if the triangulation is of type parallel::distributed::Triangulation.
See the glossary and the Parallel computing with multiple processors using distributed memory module for more information.
!is_ghost() && !is_artificial().| bool CellAccessor< dim, spacedim >::is_locally_owned_on_level | ( | ) | const |
Return true if either the Triangulation is not distributed or if level_subdomain_id() is equal to the id of the current processor.
| bool CellAccessor< dim, spacedim >::is_ghost | ( | ) | const |
Return whether this cell exists in the global mesh but (i) is owned by another processor, i.e. has a subdomain_id different from the one the current processor owns and (ii) is adjacent to a cell owned by the current processor.
This function only makes sense if the triangulation used is of kind parallel::distributed::Triangulation. In all other cases, the returned value is always false.
See the glossary and the Parallel computing with multiple processors using distributed memory module for more information.
!is_locally_owned() && !is_artificial().| bool CellAccessor< dim, spacedim >::is_artificial | ( | ) | const |
Return whether this cell is artificial, i.e. it isn't one of the cells owned by the current processor, and it also doesn't border on one. As a consequence, it exists in the mesh to ensure that each processor has all coarse mesh cells and that the 2:1 ratio of neighboring cells is maintained, but it is not one of the cells we should work on on the current processor. In particular, there is no guarantee that this cell isn't, in fact, further refined on one of the other processors.
This function only makes sense if the triangulation used is of kind parallel::distributed::Triangulation. In all other cases, the returned value is always false.
See the glossary and the Parallel computing with multiple processors using distributed memory module for more information.
!is_ghost() && !is_locally_owned().| bool CellAccessor< dim, spacedim >::point_inside | ( | const Point< spacedim > & | p | ) | const |
Test whether the point p is inside this cell. Points on the boundary are counted as being inside the cell.
Note that this function assumes that the mapping between unit cell and real cell is (bi-, tri-)linear, i.e. that faces in 2d and edges in 3d are straight lines. If you have higher order transformations, results may be different as to whether a point is in- or outside the cell in real space.
In case of codim>0, the point is first projected to the manifold where the cell is embedded and then check if this projection is inside the cell.
| void CellAccessor< dim, spacedim >::set_neighbor | ( | const unsigned int | i, |
| const TriaIterator< CellAccessor< dim, spacedim >> & | pointer | ||
| ) | const |
Set the neighbor i of this cell to the cell pointed to by pointer.
This function shouldn't really be public (but needs to for various reasons in order not to make a long list of functions friends): it modifies internal data structures and may leave things. Do not use it from application codes.
Definition at line 2159 of file tria_accessor.cc.
| CellId CellAccessor< dim, spacedim >::id | ( | ) | const |
Return a unique ID for the current cell. This ID is constructed from the path in the hierarchy from the coarse father cell and works correctly in parallel computations using objects of type parallel::distributed::Triangulation. This function is therefore useful in providing a unique identifier for cells (active or not) that also works for parallel triangulations. See the documentation of the CellId class for more information.
Definition at line 2189 of file tria_accessor.cc.
|
protected |
This function assumes that the neighbor is not coarser than the current cell. In this case it returns the neighbor_of_neighbor() value. If, however, the neighbor is coarser this function returns an invalid_unsigned_int.
This function is not for public use. Use the function neighbor_of_neighbor() instead which throws an exception if called for a coarser neighbor. If neighbor is indeed coarser (you get to know this by e.g. the neighbor_is_coarser() function) then the neighbor_of_coarser_neighbor() function should be call. If you'd like to know only the face_no which is required to get back from the neighbor to the present cell then simply use the neighbor_face_no() function which can be used for coarser as well as non-coarser neighbors.
Definition at line 2228 of file tria_accessor.cc.
|
protected |
As for any codim>0 we can use a similar code and c++ does not allow partial templates. we use this auxiliary function that is then called from point_inside.
Definition at line 1911 of file tria_accessor.cc.
|
private |
Set the active cell index of a cell. This is done at the end of refinement.
Definition at line 2079 of file tria_accessor.cc.
|
private |
Set the parent of a cell.
Definition at line 2092 of file tria_accessor.cc.
|
private |
Set the orientation of this cell.
For the meaning of this flag, see GlossDirectionFlag.
Definition at line 2062 of file tria_accessor.cc.
 1.8.14
1.8.14