This program was contributed by Marco Feder <marco.feder@sissa.it>.
It comes without any warranty or support by its authors or the authors of deal.II.
This program is part of the deal.II code gallery and consists of the following files (click to inspect):
Pictures from this code gallery program
Annotated version of README.md
A posteriori error estimator for first order hyperbolic problems
Running the code:
As in the tutorial programs, type
cmake -DDEAL_II_DIR=/path/to/deal.II .
on the command line to configure the program. After that you can compile with make and run with either make run or using
./DG_advection_reaction
on the command line.
Parameter file :
If you run ./DG_advection_reaction parameters.prm, an error message will tell you that a parameter file has been created for you. You can open it and change some useful parameters like the number of refinement cycles, the advection coefficient, and others. If you don't specify anything, then the default values used for the test case (see paragraph below) will be used.
The problem:
This program solves the problem, for \(\Omega \in \mathbb{R^2}\)
\[
\begin{cases} b \cdot \nabla u + c u = f \qquad \text{in } \Omega \\
\qquad \qquad u=g \qquad \text{on } \partial_{-}\Omega \end{cases}
\]
where \(g \in L^2(\partial_{-}\Omega)\) and \(\partial_{-}\Omega=\{ x \in
\partial \Omega: b(x)\cdot n(x) <0\}\) is the inflow part of the boundary, with \(b=(b_1,b_2) \in \mathbb{R^2}\). As we know from classical DG theory, we need to ensure that
\[
c(x) - \frac{1}{2}\nabla \cdot b \geq \gamma_0 >0
\]
for some positive \(\gamma_0\) so that we have coercivity in \(L^2\) at the continuous level. Discrete coercivity is achieved by using a stronger norm which takes care of jumps, see Di Pietro and Ern [2] for details.
The weak formulation:
As trial space we choose \(V_h = \{ v_h \in L^2(\Omega): v_h \in P^1(\mathbb{T_h})\} \notin H^1(\Omega)\). If we integrate by parts and sum over all cells
\[
\sum_{T \in \mathbb{T}_h} \Bigl( (-u,\beta \cdot \nabla v_h) _T + (c
u,v_h)_T + \bigl<(b \cdot n) u ,v_h \bigr>_{\partial T} \Bigr) =
(f,v_h)_{\Omega}
\]
and use the so-called DG magic formula and exploit the property \([bu]_{\mathbb{F}^i} = 0\) where \(\mathbb{F}^i\) are set of internal faces we obtain the (unstable!) formulation:
Find \(u_h \in V_h\):
\[
a_h(u_h,v_h) + b_h(u_h,v_h)=l(v_h) \qquad \forall v_h \in V_h
\]
where
\[
a_h(u,v_h)=\sum_{T \in \mathbb{T}_h} \Bigl( (-u,b \cdot \nabla v_h) _T + (c u,v_h)_T \Bigr)
\]
\[
b_h(u,v_h)= \sum_{F \not \in \partial_{-}\Omega} \bigl< \{ bu\}, [v_h]\bigr>_F
\]
\[
l(v_h)= (f,v_h)_{\Omega} - \sum_{F \in \partial_{-}\Omega} \bigl< (b \cdot n) g,v_h \bigr>_F
\]
It's well known this formulation is coercive only in \(L^2\), hence the formulation is unstable as we don't "see" the derivatives. To stabilize this, we can use a jump-penalty term, i.e. our \(b_h\) is replaced by:
\[
b_h^s(u_h,v_h)=b_h(u_h,v_h)+ \sum_{F \in \mathbb{F}^i} \bigl< c_F
[u_h],[v_h] \bigr>
\]
where \(c_F>0\) is a function on each edge such that \(c_F \geq \theta |b \cdot n|\) for some positive \(\theta\). In this program, \(\theta=\frac{1}{2}\) and \(c_F = \frac{1}{2} |b \cdot n|\), which corresponds to an upwind formulation. Notice that consistency is trivially achieved, as \([u]_{\mathbb{F}^i} =0\). This formulation is stable in the energy norm
\[
|||\cdot ||| = \Bigl(||\cdot||_{0,\Omega}^2 + \sum_{F \in
\mathbb{F}}||c_F^{\frac{1}{2}}[\cdot] ||_{0,F}^2
\Bigr)^{\frac{1}{2}}
\]
(well defined on \(H^1(\Omega) + V_h\)) and moreover we have the a-priori bound:
\[
|||u-u_h||| \leq C h^{k+\frac{1}{2}}||u||_{k+1,\Omega}
\]
valid for \(u \in H^{k+1}(\Omega)\).
See Brezzi-Marini-Süli [3] for more details.
A-posteriori error estimator:
The estimator is the one proposed by Georgoulis, Edward Hall and Charalambos Makridakis in [3]. This approach is quite different with respect to other works in the field, as the authors are trying to develop an estimator for the original hyperbolic problem, rather than taking the hyperbolic regime as the vanishing diffusivity limit.
The reliability is:
\[
|||u-u_h|||^2 \leq C || \sqrt{b \cdot n}[u_h]||_{\Gamma^{-}}^2 + C
\sum_{T \in \mathbb{T}_h}\Bigl( ||\beta (g-u_h^+)||_{\partial_{-}T
\cap \partial_{-} \Omega}^2 +||f-c u_h - \Pi(f- cu_h)||_T^2 \Bigr)
\]
where:
- \(\Pi\) is the (local) \(L^2\) orthogonal projection onto \(V_h\)
- \(\Gamma\) is the skeleton of the mesh
- \(c\) is constant
- \(\beta = |b \cdot n|\)
- \(u_h^+\) is the interior trace from the current cell \(T\) of a the finite element function \(u_h\).
Test case:
The following test case has been taken from [3]. Consider:
- \(c=1\)
- \(b=(1,1)\)
- \(f\) to be such that the exact solution is \(u(x,y)=\tanh(100(x+y-\frac{1}{2}))\) This solution has an internal layer along the line \(y=\frac{1}{2} -x\), hence we would like to see that part of the domain to be much more refined than the rest.
The next image is the 3D view of the numerical solution:

More interestingly, we see that the estimator has been able to capture the layer. Here a bulk-chasing criterion is used, with bottom fraction ´0.5´ and no coarsening. This mesh is obtained after 12 refinement cycles. 
If we look at the decrease of the energy norm of the error in the globally refined case and in the adaptively case, with respect to the DoFs, we obtain:
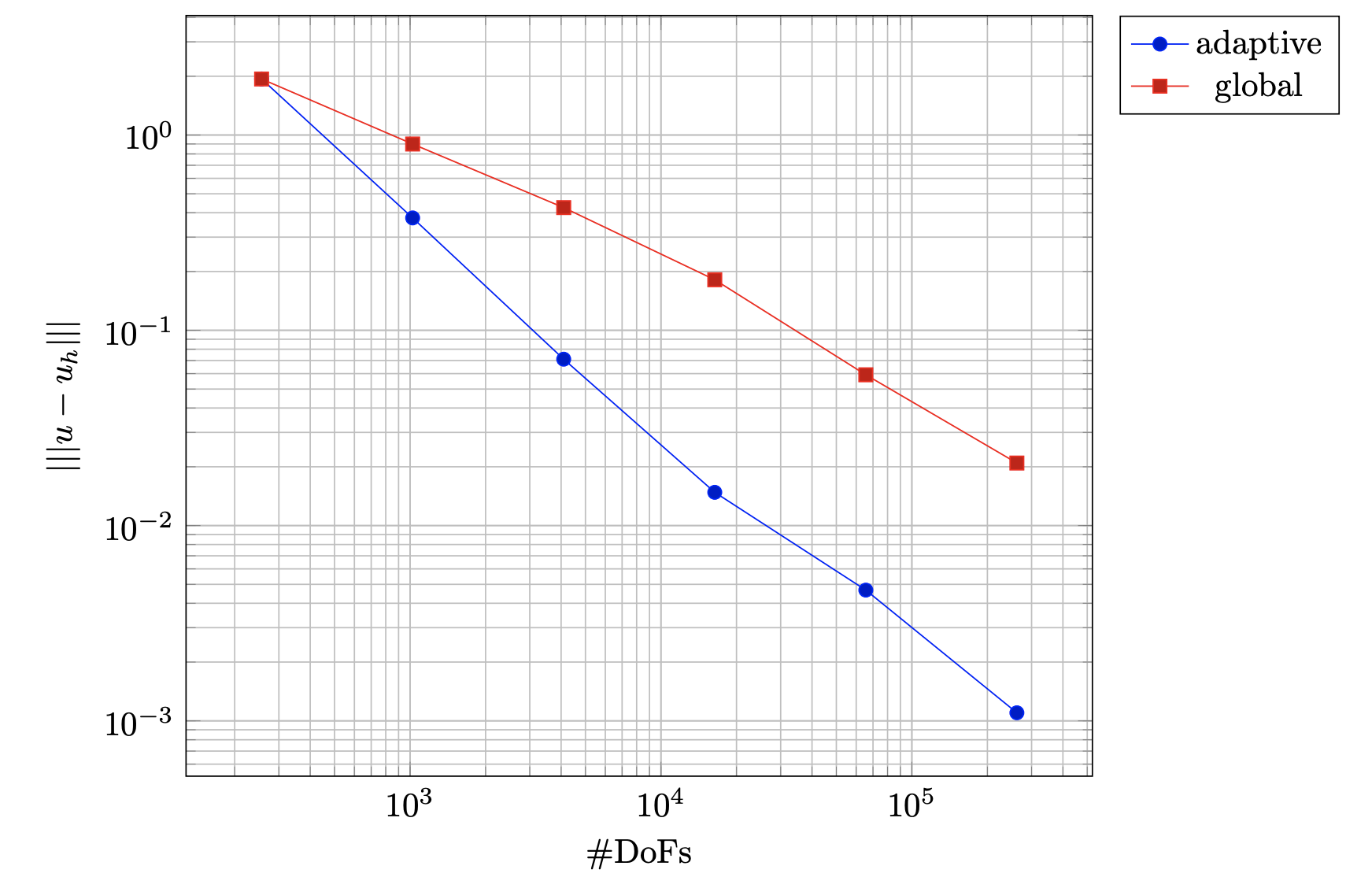
References
[1] Emmanuil H. Georgoulis, Edward Hall and Charalambos Makridakis (2013), Error Control for Discontinuous Galerkin Methods for First Order Hyperbolic Problems. DOI: 10.1007/978-3-319-01818-8_8 [2] Di Pietro, Daniele Antonio and Ern, Alexandre (2012), Mathematical Aspects of Discontinuous Galerkin Methods. ISBN: 978-3-642-22980-0 [3] Franco Brezzi, Luisa Donatella Marini and Endre Süli (2004) Discontinuous Galerkin Methods for First-Order Hyperbolic Problems. DOI: 10.1142/S0218202504003866
Annotated version of include/DG_advection_reaction.h
#ifndef INCLUDE_DG_UPWIND_H_
#define INCLUDE_DG_UPWIND_H_
This header is needed for FEInterfaceValues to compute integrals on interfaces:
Solver
We are going to use gradients as refinement indicator.
Using using the mesh_loop from the MeshWorker framework
To enable parameter handling
#include <fstream>
#include <iostream>
This is a struct used only for throwing an exception when theta parameter is not okay.
struct theta_exc
{
std::string message;
theta_exc(std::string &&s)
: message{
std::move(s)} {};
const char *
what() const
{
return message.c_str();
}
};
template <int dim>
{
public:
AdvectionReaction();
void
initialize_params(const std::string &filename);
void
private:
void
parse_string(const std::string ¶meters);
void
setup_system();
void
assemble_system();
void
solve();
void
refine_grid();
void
output_results(const unsigned int cycle) const;
void
compute_error();
double
compute_energy_norm();
void
compute_local_projection_and_estimate();
typename ActiveSelector::active_cell_iterator active_cell_iterator
void run(const Iterator &begin, const typename identity< Iterator >::type &end, Worker worker, Copier copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const unsigned int queue_length, const unsigned int chunk_size)
const ::parallel::distributed::Triangulation< dim, spacedim > * triangulation
Furthermore we want to use DG elements.
std::unique_ptr<FE_DGQ<dim>> fe;
So far we declared the usual objects. Hereafter we declare FunctionParser<dim> objects
unsigned int fe_degree = 1;
and then we define default values that will be parsed from the following strings
std::string exact_solution_expression =
"tanh(100*(x+y-0.5))";
std::string rhs_expression =
"-200*tanh(100*x + 100*y - 50.0)^2 + tanh(100*x + 100*y - 50.0) + 200";
std::string advection_coefficient_expression = "1.0";
std::string boundary_conditions_expression = "tanh(100*x + 100*y - 50.0)";
std::string refinement = "residual";
std::string output_filename = "DG_advection_reaction_estimator";
std::map<std::string, double> constants;
bool use_direct_solver = true;
unsigned int n_refinement_cycles = 8;
unsigned int n_global_refinements = 3;
double theta = 0.5;
};
#endif
The ParsedConvergenceTable class.
Annotated version of main.cc
#include "include/DG_advection_reaction.h"
int
main(int argc, char **argv)
{
try
{
std::string par_name = "";
if (argc > 1)
{
par_name = argv[1];
}
else
{
par_name = "parameters.prm";
}
AdvectionReaction<2> problem;
problem.initialize_params(par_name);
problem.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (const theta_exc &theta_range)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< theta_range.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
unsigned int depth_console(const unsigned int n)
Annotated version of source/DG_advection_reaction.cc
#include "../include/DG_advection_reaction.h"
Compute and returns the wind field b
template <int dim>
{
Assert(dim > 1, ExcNotImplemented());
(void)p;
wind_field[0] = 1.0;
wind_field[1] = 1.0;
return wind_field;
}
#define Assert(cond, exc)
The ScratchData and CopyData classes
The following objects are the scratch and copy objects we use in the call to MeshWorker::mesh_loop(). The new object is the FEInterfaceValues object, that works similar to FEValues or FEFacesValues, except that it acts on an interface between two cells and allows us to assemble the interface terms in our weak form.
template <int dim>
struct ScratchData
{
: fe_values(mapping, fe, quadrature, update_flags)
, fe_interface_values(mapping, fe, quadrature_face, interface_update_flags)
{}
ScratchData(const ScratchData<dim> &scratch_data)
: fe_values(scratch_data.fe_values.get_mapping(),
scratch_data.fe_values.get_fe(),
scratch_data.fe_values.get_quadrature(),
scratch_data.fe_values.get_update_flags())
, fe_interface_values(scratch_data.fe_interface_values.get_mapping(),
scratch_data.fe_interface_values.get_fe(),
scratch_data.fe_interface_values.get_quadrature(),
scratch_data.fe_interface_values.get_update_flags())
{}
};
struct CopyDataFace
{
std::vector<types::global_dof_index> joint_dof_indices;
std::array<unsigned int, 2> cell_indices;
};
struct CopyData
{
std::vector<types::global_dof_index> local_dof_indices;
std::vector<CopyDataFace> face_data;
double value_estimator;
template <class Iterator>
void
reinit(
const Iterator &cell,
unsigned int dofs_per_cell)
{
cell_mass_matrix.reinit(dofs_per_cell, dofs_per_cell);
cell_rhs.
reinit(dofs_per_cell);
cell_mass_rhs.
reinit(dofs_per_cell);
local_dof_indices.resize(dofs_per_cell);
cell->get_dof_indices(local_dof_indices);
}
};
Abstract base class for mapping classes.
@ update_values
Shape function values.
@ update_normal_vectors
Normal vectors.
@ update_JxW_values
Transformed quadrature weights.
@ update_gradients
Shape function gradients.
@ update_quadrature_points
Transformed quadrature points.
virtual void reinit(const size_type N, const bool omit_zeroing_entries=false)
void cell_matrix(FullMatrix< double > &M, const FEValuesBase< dim > &fe, const FEValuesBase< dim > &fetest, const ArrayView< const std::vector< double > > &velocity, const double factor=1.)
void reinit(MatrixBlock< MatrixType > &v, const BlockSparsityPattern &p)
Auxiliary function
This auxiliary function is taken from step-74 and it's used to compute the jump of the finite element function \(u_h\) on a face.
template <int dim>
void
std::vector<double> &jump)
{
std::array<std::vector<double>, 2> face_values;
jump.resize(n_q);
for (unsigned int i = 0; i < 2; ++i)
{
face_values[i].resize(n_q);
}
for (unsigned int q = 0; q < n_q; ++q)
jump[q] = face_values[0][q] - face_values[1][q];
}
template <int dim>
AdvectionReaction<dim>::AdvectionReaction()
: mapping()
{
Assert(dim > 1, ExcMessage(
"Not implemented in 1D."));
add_parameter("Finite element degree", fe_degree);
add_parameter("Problem constants", constants);
add_parameter("Output filename", output_filename);
add_parameter("Use direct solver", use_direct_solver);
add_parameter("Number of refinement cycles", n_refinement_cycles);
add_parameter("Number of global refinement", n_global_refinements);
add_parameter("Refinement", refinement);
add_parameter("Exact solution expression", exact_solution_expression);
add_parameter("Boundary conditions expression",
boundary_conditions_expression);
add_parameter("Theta", theta);
add_parameter("Advection coefficient expression",
advection_coefficient_expression);
add_parameter("Right hand side expression", rhs_expression);
this->prm.enter_subsection("Error table");
error_table.add_parameters(this->prm);
this->prm.leave_subsection();
}
template <int dim>
void
AdvectionReaction<dim>::initialize_params(const std::string &filename)
{
"last_used_parameters.prm",
if (theta < 0.0 || theta > 10.0 ||
std::abs(theta) < 1e-12)
{
throw(
theta_exc("Theta parameter is not in a suitable range: see paper by "
"Brezzi, Marini, Suli for an extended discussion"));
}
}
template <int dim>
void
AdvectionReaction<dim>::parse_string(const std::string ¶meters)
{
}
template <int dim>
void
AdvectionReaction<dim>::setup_system()
{
const unsigned int n_quadrature_points
const FEFaceValuesBase< dim, spacedim > & get_fe_face_values(const unsigned int cell_index) const
void get_function_values(const InputVector &fe_function, std::vector< typename InputVector::value_type > &values) const
static void initialize(const std::string &filename="", const std::string &output_filename="", const ParameterHandler::OutputStyle output_style_for_output_filename=ParameterHandler::Short, ParameterHandler &prm=ParameterAcceptor::prm, const ParameterHandler::OutputStyle output_style_for_filename=ParameterHandler::DefaultStyle)
static ParameterHandler prm
static void parse_all_parameters(ParameterHandler &prm=ParameterAcceptor::prm)
virtual void parse_input_from_string(const std::string &s, const std::string &last_line="", const bool skip_undefined=false)
::VectorizedArray< Number, width > abs(const ::VectorizedArray< Number, width > &)
first need to distribute the DoFs.
if (!fe)
{
fe = std::make_unique<FE_DGQ<dim>>(fe_degree);
const auto vars = dim == 2 ? "x,y" : "x,y,z";
exact_solution.initialize(vars, exact_solution_expression, constants);
rhs.initialize(vars, rhs_expression, constants);
advection_coeff.initialize(vars,
advection_coefficient_expression,
constants);
boundary_conditions.initialize(vars,
boundary_conditions_expression,
constants);
}
dof_handler.distribute_dofs(*fe);
To build the sparsity pattern for DG discretizations, we can call the function analogue to DoFTools::make_sparsity_pattern, which is called DoFTools::make_flux_sparsity_pattern:
dsp);
sparsity_pattern.copy_from(dsp);
void make_flux_sparsity_pattern(const DoFHandler< dim, spacedim > &dof_handler, SparsityPatternType &sparsity_pattern)
Finally, we set up the structure of all components of the linear system.
system_matrix.reinit(sparsity_pattern);
solution.
reinit(dof_handler.n_dofs());
right_hand_side.reinit(dof_handler.n_dofs());
}
in the call to MeshWorker::mesh_loop() we only need to specify what should happen on each cell, each boundary face, and each interior face. These three tasks are handled by the lambda functions inside the function below.
template <int dim>
void
AdvectionReaction<dim>::assemble_system()
{
const QGauss<dim> quadrature = fe->tensor_degree() + 1;
const QGauss<dim - 1> quadrature_face = fe->tensor_degree() + 1;
This is the function that will be executed for each cell.
const auto cell_worker = [&](const Iterator &cell,
ScratchData<dim> &scratch_data,
CopyData ©_data) {
quadrature,
const unsigned int n_dofs =
scratch_data.fe_values.get_fe().n_dofs_per_cell();
copy_data.reinit(cell, n_dofs);
scratch_data.fe_values.reinit(cell);
const auto &q_points = scratch_data.fe_values.get_quadrature_points();
{
auto beta_q = beta(q_points[point]);
for (unsigned int i = 0; i < n_dofs; ++i)
{
for (unsigned int j = 0; j < n_dofs; ++j)
{
copy_data.cell_matrix(i, j) +=
(-beta_q
+ advection_coeff.value(q_points[point]) *
) *
JxW[point];
}
copy_data.cell_rhs(i) += rhs.value(q_points[point])
* JxW[point];
}
}
};
const std::vector< double > & get_JxW_values() const
const unsigned int n_quadrature_points
const Tensor< 1, spacedim > & shape_grad(const unsigned int function_no, const unsigned int quadrature_point) const
const double & shape_value(const unsigned int function_no, const unsigned int point_no) const
This is the function called for boundary faces and consists of a normal integration using FEFaceValues. New is the logic to decide if the term goes into the system matrix (outflow) or the right-hand side (inflow).
const auto boundary_worker = [&](const Iterator &cell,
const unsigned int &face_no,
ScratchData<dim> &scratch_data,
CopyData ©_data) {
scratch_data.fe_interface_values.reinit(cell, face_no);
scratch_data.fe_interface_values.get_fe_face_values(0);
std::vector<double> g(q_points.size());
exact_solution.value_list(q_points, g);
for (unsigned int point = 0; point < q_points.size(); ++point)
{
const double beta_dot_n = beta(q_points[point]) * normals[point];
if (beta_dot_n > 0)
{
for (unsigned int i = 0; i < n_facet_dofs; ++i)
for (unsigned int j = 0; j < n_facet_dofs; ++j)
copy_data.cell_matrix(i, j) +=
point)
* beta_dot_n
* JxW[point];
}
else
for (unsigned int i = 0; i < n_facet_dofs; ++i)
copy_data.cell_rhs(i) += -fe_face.
shape_value(i, point)
* g[point]
* beta_dot_n
* JxW[point];
}
};
const std::vector< Point< spacedim > > & get_quadrature_points() const
const std::vector< Tensor< 1, spacedim > > & get_normal_vectors() const
const FiniteElement< dim, spacedim > & get_fe() const
unsigned int n_dofs_per_cell() const
This is the function called on interior faces. The arguments specify cells, face and subface indices (for adaptive refinement). We just pass them along to the reinit() function of FEInterfaceValues.
const auto face_worker = [&](const Iterator &cell,
const unsigned int &f,
const unsigned int &sf,
const Iterator &ncell,
const unsigned int &nf,
const unsigned int &nsf,
ScratchData<dim> &scratch_data,
CopyData ©_data) {
fe_iv.
reinit(cell, f, sf, ncell, nf, nsf);
copy_data.face_data.emplace_back();
CopyDataFace ©_data_face = copy_data.face_data.back();
copy_data_face.cell_matrix.reinit(n_dofs, n_dofs);
for (unsigned int qpoint = 0; qpoint < q_points.size(); ++qpoint)
{
const double beta_dot_n = beta(q_points[qpoint]) * normals[qpoint];
for (unsigned int i = 0; i < n_dofs; ++i)
{
for (unsigned int j = 0; j < n_dofs; ++j)
{
copy_data_face.cell_matrix(i, j) +=
(beta(q_points[qpoint]) * normals[qpoint] *
JxW[qpoint];
}
}
}
};
const std::vector< double > & get_JxW_values() const
unsigned n_current_interface_dofs() const
const std::vector< Tensor< 1, spacedim > > & get_normal_vectors() const
double average_of_shape_values(const unsigned int interface_dof_index, const unsigned int q_point, const unsigned int component=0) const
const std::vector< Point< spacedim > > & get_quadrature_points() const
void reinit(const CellIteratorType &cell, const unsigned int face_no, const unsigned int sub_face_no, const CellNeighborIteratorType &cell_neighbor, const unsigned int face_no_neighbor, const unsigned int sub_face_no_neighbor)
double jump_in_shape_values(const unsigned int interface_dof_index, const unsigned int q_point, const unsigned int component=0) const
std::vector< types::global_dof_index > get_interface_dof_indices() const
The following lambda function will handle copying the data from the cell and face assembly into the global matrix and right-hand side.
While we would not need an AffineConstraints object, because there are no hanging node constraints in DG discretizations, we use an empty object here as this allows us to use its copy_local_to_global functionality.
const auto copier = [&](const CopyData &c) {
c.cell_rhs,
c.local_dof_indices,
system_matrix,
right_hand_side);
for (auto &cdf : c.face_data)
{
cdf.joint_dof_indices,
system_matrix);
}
};
ScratchData<dim> scratch_data(mapping, *fe, quadrature, quadrature_face);
CopyData copy_data;
void distribute_local_to_global(const InVector &local_vector, const std::vector< size_type > &local_dof_indices, OutVector &global_vector) const
Here, we finally handle the assembly. We pass in ScratchData and CopyData objects, the lambda functions from above, an specify that we want to assemble interior faces once.
dof_handler.end(),
cell_worker,
copier,
scratch_data,
copy_data,
boundary_worker,
face_worker);
}
template <int dim>
void
AdvectionReaction<dim>::solve()
{
if (use_direct_solver)
{
system_matrix_inverse.
vmult(solution, right_hand_side);
}
else
{
void initialize(const SparsityPattern &sparsity_pattern)
void vmult(Vector< double > &dst, const Vector< double > &src) const
void mesh_loop(const CellIteratorType &begin, const CellIteratorType &end, const CellWorkerFunctionType &cell_worker, const CopierType &copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const AssembleFlags flags=assemble_own_cells, const BoundaryWorkerFunctionType &boundary_worker=BoundaryWorkerFunctionType(), const FaceWorkerFunctionType &face_worker=FaceWorkerFunctionType(), const unsigned int queue_length=2 *MultithreadInfo::n_threads(), const unsigned int chunk_size=8)
@ assemble_boundary_faces
@ assemble_own_interior_faces_once
Here we have a classic iterative solver, as done in many tutorials:
preconditioner.
initialize(system_matrix, fe->n_dofs_per_cell());
solver.solve(system_matrix, solution, right_hand_side, preconditioner);
std::cout << " Solver converged in " << solver_control.last_step()
<< " iterations." << std::endl;
}
}
void initialize(const MatrixType &A, const AdditionalData parameters)
Mesh refinement
We refine the grid according the proposed estimator or with an approximation to the gradient of the solution. The first option is the default one (you can see it in the header file)
template <int dim>
void
AdvectionReaction<dim>::refine_grid()
{
if (refinement == "residual")
{
If the refinement string is "residual", then we first compute the local projection
compute_local_projection_and_estimate();
We then set the refinement fraction and as usual we execute the refinement.
const double refinement_fraction = 0.6;
triangulation, error_indicator_per_cell, refinement_fraction, 0.0);
}
else if (refinement == "gradient")
{
void refine_and_coarsen_fixed_fraction(Triangulation< dim, spacedim > &tria, const Vector< Number > &criteria, const double top_fraction, const double bottom_fraction, const unsigned int max_n_cells=std::numeric_limits< unsigned int >::max(), const VectorTools::NormType norm_type=VectorTools::NormType::L1_norm)
Now the approximate gradients are computed
dof_handler,
solution,
gradient_indicator);
void approximate_gradient(const Mapping< dim, spacedim > &mapping, const DoFHandler< dim, spacedim > &dof, const InputVector &solution, Vector< float > &derivative_norm, const unsigned int component=0)
and they are cell-wise scaled by the factor \(h^{1+d/2}\)
unsigned int cell_no = 0;
for (const auto &cell : dof_handler.active_cell_iterators())
gradient_indicator(cell_no++) *=
std::pow(cell->diameter(), 1 + 1.0 * dim / 2);
::VectorizedArray< Number, width > pow(const ::VectorizedArray< Number, width > &, const Number p)
Finally they serve as refinement indicator.
gradient_indicator,
0.25,
0.0);
std::cout << gradient_indicator.l2_norm() << '\n';
}
else if (refinement == "global")
{
1);
}
else
{
Assert(
false, ExcInternalError());
}
}
The output of this program consists of a vtk file of the adaptively refined grids and the numerical solutions.
template <int dim>
void
AdvectionReaction<dim>::output_results(const unsigned int cycle) const
{
const std::string filename = "solution-" + std::to_string(cycle) + ".vtk";
std::cout << " Writing solution to <" << filename << ">" << std::endl;
std::ofstream output(filename);
}
template <int dim>
void
AdvectionReaction<dim>::compute_error()
{
error_table.error_from_exact(
mapping,
dof_handler,
solution,
exact_solution);
void attach_dof_handler(const DoFHandler< dim, spacedim > &)
void add_data_vector(const VectorType &data, const std::vector< std::string > &names, const DataVectorType type=type_automatic, const std::vector< DataComponentInterpretation::DataComponentInterpretation > &data_component_interpretation={})
virtual void build_patches(const unsigned int n_subdivisions=0)
void write_vtk(std::ostream &out) const
to compute the H^1 norm if Solution<dim> doesn't implements the Gradient function
Compute the energy norm
The energy norm is defined as \( |||\cdot ||| = \Bigl(||\cdot||_{0,\Omega}^2 +
\sum_{F \in \mathbb{F}}||c_F^{\frac{1}{2}}[\cdot] ||_{0,F}^2
\Bigr)^{\frac{1}{2}}\) Notice that in the current case we have \(c_f = \frac{|b
\cdot n|}{2}\) Like in the assembly, all the contributions are handled separately by using ScratchData and CopyData objects.
template <int dim>
double
AdvectionReaction<dim>::compute_energy_norm()
{
energy_norm_square_per_cell.reinit(
triangulation.n_active_cells());
We start off by adding cell contributions
const auto cell_worker = [&](const Iterator &cell,
ScratchData<dim> &scratch_data,
CopyData ©_data) {
const unsigned int n_dofs =
scratch_data.fe_values.get_fe().n_dofs_per_cell();
copy_data.reinit(cell, n_dofs);
scratch_data.fe_values.reinit(cell);
copy_data.cell_index = cell->active_cell_index();
const auto &q_points = scratch_data.fe_values.get_quadrature_points();
double error_square_norm{0.0};
{
const double diff =
(sol_u[point] - exact_solution.value(q_points[point]));
error_square_norm += diff * diff * JxW[point];
}
copy_data.value = error_square_norm;
};
Here we add contributions coming from the internal faces
const auto face_worker = [&](const Iterator &cell,
const unsigned int &f,
const unsigned int &sf,
const Iterator &ncell,
const unsigned int &nf,
const unsigned int &nsf,
ScratchData<dim> &scratch_data,
CopyData ©_data) {
fe_iv.
reinit(cell, f, sf, ncell, nf, nsf);
copy_data.face_data.emplace_back();
CopyDataFace ©_data_face = copy_data.face_data.back();
copy_data_face.cell_indices[0] = cell->active_cell_index();
copy_data_face.cell_indices[1] = ncell->active_cell_index();
const unsigned n_q_points = q_points.size();
std::vector<double> g(n_q_points);
std::vector<double> jump(n_q_points);
get_function_jump(fe_iv, solution, jump);
double error_jump_square{0.0};
for (unsigned int point = 0; point < n_q_points; ++point)
{
const double beta_dot_n =
theta *
std::abs(beta(q_points[point]) * normals[point]);
error_jump_square +=
beta_dot_n * jump[point] * jump[point] * JxW[point];
}
copy_data.value = error_jump_square;
};
Finally, we add the boundary contributions
const auto boundary_worker = [&](const Iterator &cell,
const unsigned int &face_no,
ScratchData<dim> &scratch_data,
CopyData ©_data) {
scratch_data.fe_interface_values.reinit(cell, face_no);
scratch_data.fe_interface_values.get_fe_face_values(0);
const unsigned n_q_points = q_points.size();
std::vector<double> g(n_q_points);
std::vector<double> sol_u(n_q_points);
double difference_norm_square = 0.;
for (unsigned int point = 0; point < q_points.size(); ++point)
{
const double beta_dot_n =
theta *
std::abs(beta(q_points[point]) * normals[point]);
const double diff =
(boundary_conditions.value(q_points[point]) - sol_u[point]);
difference_norm_square += beta_dot_n * diff * diff * JxW[point];
}
copy_data.value = difference_norm_square;
};
const auto copier = [&](const auto ©_data) {
{
energy_norm_square_per_cell[copy_data.cell_index] += copy_data.value;
}
for (auto &cdf : copy_data.face_data)
for (unsigned int j = 0; j < 2; ++j)
energy_norm_square_per_cell[cdf.cell_indices[j]] += cdf.values[j];
};
ScratchData<dim> scratch_data(mapping,
*fe,
QGauss<dim - 1>{fe->tensor_degree() + 1});
CopyData copy_data;
dof_handler.end(),
cell_worker,
copier,
scratch_data,
copy_data,
boundary_worker,
face_worker);
const double energy_error =
std::sqrt(energy_norm_square_per_cell.l1_norm());
return energy_error;
}
static const unsigned int invalid_unsigned_int
::VectorizedArray< Number, width > sqrt(const ::VectorizedArray< Number, width > &)
Computing the estimator
In the estimator, we have to compute the term \(||f- c u_h - \Pi(f- c
u_h)||_{T}^{2}\) over a generic cell \(T\). To achieve this, we first need to compute the projection involving the finite element function \(u_h\). Using the definition of orthogonal projection, we're required to solve cellwise \((v_h,f-c u_h)_T = (v_h,\Pi)_T \qquad \forall v_h \in V_h\) for \(\Pi\), which means that we have to build a mass-matrix on each cell. Once we have the projection, which is a finite element function, we can add its contribution in the cell_worker lambda. As done in step-74, the square of the error indicator is computed.
template <int dim>
void
AdvectionReaction<dim>::compute_local_projection_and_estimate()
{
Compute the term \(||f-c u_h - \Pi(f- cu_h)||_T^2\)
const auto cell_worker = [&](const Iterator &cell,
ScratchData<dim> &scratch_data,
CopyData ©_data) {
const unsigned int n_dofs =
scratch_data.fe_values.get_fe().n_dofs_per_cell();
copy_data.reinit(cell, n_dofs);
scratch_data.fe_values.reinit(cell);
copy_data.cell_index = cell->active_cell_index();
const auto &q_points = scratch_data.fe_values.get_quadrature_points();
const unsigned n_q_points = q_points.size();
Compute local L^2 projection of \(f- c u_h\) over the local finite element space
for (unsigned int point = 0; point < n_q_points; ++point)
{
for (unsigned int i = 0; i < n_dofs; ++i)
{
for (unsigned int j = 0; j < n_dofs; ++j)
{
copy_data.cell_mass_matrix(i, j) +=
JxW[point];
}
copy_data.cell_mass_rhs(i) +=
(rhs.value(q_points[point]) *
- advection_coeff.value(q_points[point]) *
sol_u_at_quadrature_points[point]) *
JxW[point];
}
}
inverse.invert(copy_data.cell_mass_matrix);
the local fe_space
inverse.vmult(proj, copy_data.cell_mass_rhs);
double square_norm_over_cell = 0.0;
for (unsigned int point = 0; point < n_q_points; ++point)
{
const double diff = rhs.value(q_points[point]) -
sol_u_at_quadrature_points[point] - proj[point];
square_norm_over_cell += diff * diff * JxW[point];
}
copy_data.value_estimator = square_norm_over_cell;
};
Finally we have the boundary term with \(||\beta (g-u_h^+)||^2\)
const auto boundary_worker = [&](const Iterator &cell,
const unsigned int &face_no,
ScratchData<dim> &scratch_data,
CopyData ©_data) {
scratch_data.fe_interface_values.reinit(cell, face_no);
scratch_data.fe_interface_values.get_fe_face_values(0);
const unsigned n_q_points = q_points.size();
std::vector<double> g(n_q_points);
exact_solution.value_list(q_points, g);
std::vector<double> sol_u(n_q_points);
double square_norm_over_bdary_face = 0.;
for (unsigned int point = 0; point < q_points.size(); ++point)
{
const double beta_dot_n = beta(q_points[point]) * normals[point];
if (beta_dot_n < 0)
{
const double diff =
std::abs(beta_dot_n) * (g[point] - sol_u[point]);
square_norm_over_bdary_face += diff * diff * JxW[point];
}
}
copy_data.value_estimator += square_norm_over_bdary_face;
};
Then compute the interior face terms with \(|| \sqrt{b \cdot n}[u_h]||^2\)
const auto face_worker = [&](const Iterator &cell,
const unsigned int &f,
const unsigned int &sf,
const Iterator &ncell,
const unsigned int &nf,
const unsigned int &nsf,
ScratchData<dim> &scratch_data,
CopyData ©_data) {
fe_iv.
reinit(cell, f, sf, ncell, nf, nsf);
copy_data.face_data.emplace_back();
CopyDataFace ©_data_face = copy_data.face_data.back();
copy_data_face.cell_indices[0] = cell->active_cell_index();
copy_data_face.cell_indices[1] = ncell->active_cell_index();
const unsigned n_q_points = q_points.size();
std::vector<double> g(n_q_points);
std::vector<double> jump(n_q_points);
get_function_jump(fe_iv, solution, jump);
double error_jump_square{0.0};
for (unsigned int point = 0; point < n_q_points; ++point)
{
const double beta_dot_n = beta(q_points[point]) * normals[point];
if (beta_dot_n < 0)
{
error_jump_square +=
std::abs(beta_dot_n) * jump[point] * jump[point] * JxW[point];
}
}
copy_data_face.values[0] = error_jump_square;
copy_data_face.values[1] = copy_data_face.values[0];
};
ScratchData<dim> scratch_data(mapping,
*fe,
QGauss<dim - 1>{fe->tensor_degree() + 1});
const auto copier = [&](const auto ©_data) {
{
error_indicator_per_cell[copy_data.cell_index] +=
copy_data.value_estimator;
}
for (auto &cdf : copy_data.face_data)
{
for (unsigned int j = 0; j < 2; ++j)
{
error_indicator_per_cell[cdf.cell_indices[j]] += cdf.values[j];
}
}
};
Here, we finally handle the assembly of the Mass matrix (M)_{ij} = (\phi_j, \phi_i)_T. We pass in ScratchData and CopyData objects
CopyData copy_data;
dof_handler.end(),
cell_worker,
copier,
scratch_data,
copy_data,
boundary_worker,
face_worker);
}
Usual run function, which runs over several refinement cycles
template <int dim>
void
AdvectionReaction<dim>::run()
{
std::vector<double> energy_errors;
std::vector<int> dofs_hist;
for (unsigned int cycle = 0; cycle < n_refinement_cycles; ++cycle)
{
std::cout << "Cycle " << cycle << std::endl;
if (cycle == 0)
{
}
else
{
refine_grid();
}
std::cout << " Number of active cells: "
std::cout << " Number of degrees of freedom: " << dof_handler.n_dofs()
<< std::endl;
setup_system();
assemble_system();
solve();
compute_error();
output_results(cycle);
energy_errors.emplace_back(compute_energy_norm());
}
error_table.output_table(std::cout);
for (unsigned int i = 0; i < n_refinement_cycles; ++i)
std::cout << "Cycle " << i << "\t" << energy_errors[i] << std::endl;
}
void hyper_cube(Triangulation< dim, spacedim > &tria, const double left=0., const double right=1., const bool colorize=false)
Explicit instantiation
template class AdvectionReaction<1>;
template class AdvectionReaction<2>;
template class AdvectionReaction<3>;







