This program was contributed by Giuseppe Orlando <giuseppe.orlando@polimi.it>.
It comes without any warranty or support by its authors or the authors of deal.II.
This program is part of the deal.II code gallery and consists of the following files (click to inspect):
Pictures from this code gallery program
Annotated version of README.md
TRBDF2-DG projection solver for the incompressible Navier-Stokes equations
Compiling and Running
To generate a makefile for this code using CMake, type the following command into the terminal from the main directory:
cmake . -DDEAL_II_DIR=/path/to/deal.II
To compile the code in release mode use:
make release
This command will create the executable, NS_TRBDF2_DG.
To run the code on N processors type the following command into the terminal from the main directory,
mpirun -np N ./NS_TRBDF2_DG
The output of the code will be in .vtu format and be written to disk in parallel. The results can be viewed using ParaView. A parameter file called parameter-file.prm has to be present in the same folder of the executable, following the same structure employed in step-35. Two extra fields are present: saving_directory with the name of the folder where the results should be saved (which has therefore to be created before launching the program) and refinement_iterations that specifies how often the remeshing procedure has to be performed.
The Navier-Stokes equations and the time discretization strategy
In this section, we briefly describe the problem and the approach employed. A detailed explanation of the numerical scheme is reported in [1]. We consider the classical unsteady incompressible Navier-Stokes equations, written in non-dimensional form as:
\begin{align*}
\frac{\partial \mathbf{u}}{\partial t} + \nabla\cdot\left(\mathbf{u} \otimes\mathbf{u}\right) + \nabla p &= \frac{1}{Re}\Delta\mathbf{u} + \mathbf{f} \\
\nabla\cdot\mathbf{u} &= 0,
\end{align*}
where \(Re\) denotes the Reynolds number. In the case of projection methods, difficulties arise in choosing the boundary conditions to be imposed for the Poisson equation which is to be solved at each time step to compute the pressure. An alternative that allows to avoid or reduce some of these problems is the so-called artificial compressibility formulation. In this formulation, the incompressibility constraint is relaxed and a time evolution equation for the pressure is introduced, which is characterized by an artificial sound speed \(c\), so as to obtain:
\begin{align*}
\frac{\partial\mathbf{u}}{\partial t} + \nabla\cdot\left(\mathbf{u}\otimes\mathbf{u}\right) + \nabla p &= \frac{1}{Re}\Delta\mathbf{u} + \mathbf{f} \\
\frac{1}{c^2}\frac{\partial p}{\partial t} + \nabla\cdot\mathbf{u} &= 0.
\end{align*}
For the sake of simplicity, we shall only consider \(\mathbf{f} =
\mathbf{0}\). The numerical scheme is an extension of the projection method introduced in [2] based on the TR-BDF2 method. For a generic time-dependent problem \(\mathbf{u}' = \mathcal{N}(\mathbf{u})\), the TR-BDF2 method can be described in terms of two stages as follows:
\begin{align*}
\frac{\mathbf{u}^{n+\gamma} - \mathbf{u}^{n}}{\gamma\Delta t} &= \frac{1}{2}\mathcal{N}\left(\mathbf{u}^{n+\gamma}\right) + \frac{1}{2}\mathcal{N}\left(\mathbf{u}^{n}\right) \\
\frac{\mathbf{u}^{n+1} - \mathbf{u}^{n + \gamma}}{\left(1 - \gamma\right)\Delta t} &= \frac{1}{2 - \gamma}\mathcal{N}\left(\mathbf{u}^{n+1}\right) + \frac{1 - \gamma}{2\left(2 - \gamma\right)}\mathcal{N}\left(\mathbf{u}^{n+\gamma}\right) + \frac{1 - \gamma}{2\left(2 - \gamma\right)}\mathcal{N}\left(\mathbf{u}^{n}\right).
\end{align*}
Following then the projection approach described in [2], the momentum predictor equation for the first stage reads:
\begin{align*}
&&\frac{\mathbf{u}^{n+\gamma,\ast} - \mathbf{u}^{n}}{\gamma\Delta t} - \frac{1}{2Re}\Delta\mathbf{u}^{n+\gamma,\ast} + \frac{1}{2}\nabla\cdot\left(\mathbf{u}^{n+\gamma,\ast}\otimes\mathbf{u}^{n+\frac{\gamma}{2}}\right) = \nonumber \\
&&\frac{1}{2Re}\Delta\mathbf{u}^{n} - \frac{1}{2}\nabla\cdot\left(\mathbf{u}^{n}\otimes\mathbf{u}^{n+\frac{\gamma}{2}}\right) - \nabla p^n \nonumber \\
&&\mathbf{u}^{n+\gamma,\ast}\rvert_{\partial\Omega} = \mathbf{u}_D^{n+\gamma}. \nonumber
\end{align*}
Notice that, in order to avoid solving a nonlinear system at each time step, an approximation is introduced in the nonlinear momentum advection term, so that \(\mathbf{u}^{n + \frac{\gamma}{2}}\) is defined by extrapolation as
\begin{align*}
\mathbf{u}^{n + \frac{\gamma}{2}} = \left(1 + \frac{\gamma}{2\left(1-\gamma\right)}\right)\mathbf{u}^{n} - \frac{\gamma}{2\left(1-\gamma\right)}\mathbf{u}^{n-1}.
\end{align*}
For what concerns the pressure, we introduce the intermediate update \(\mathbf{u}^{n+\gamma,\ast\ast} = \mathbf{u}^{n+\gamma,\ast} + \gamma\Delta t\nabla p^{n}\), and we solve the following Helmholtz equation
\begin{align*}
\frac{1}{c^2}\frac{p^{n+\gamma}}{\gamma^2\Delta t^2} -\Delta p^{n+\gamma} = - \frac{1}{\gamma\Delta t} \nabla\cdot\mathbf{u}^{n+\gamma,\ast\ast} + \frac{1}{c^2}\frac{p^{n }}{\gamma^2\Delta t^2}
\end{align*}
and, finally, we set \(\mathbf{u}^{n+\gamma} = \mathbf{u}^{n+\gamma,\ast\ast} - \gamma\Delta t\nabla p^{n+\gamma}\). The second stage of the TR-BDF2 scheme is performed in a similar manner (see [1] for all the details).
Some implementation details
A matrix-free approach was employed like for step-37 or step-50. Another feature of the library which it is possible to employ during the numerical simulations is the mesh adaptation capability. On each element \(K\) we define the quantity
\[
\eta_K = \text{diam}(K)^2\left\|\nabla \times \mathbf{u}\right\|^2_K
\]
that acts as local refinement indicator. The preconditioned conjugate gradient method implemented in the function SolverCG was employed to solve the Helmholtz equations, whereas, for the momentum equations, the GMRES solver implemented in the function SolverGMRES was used. A Jacobi preconditioner is used for the two momentum predictors, whereas a Geometric Multigrid preconditioner is employed for the Helmholtz equations (see step-37).
Test case
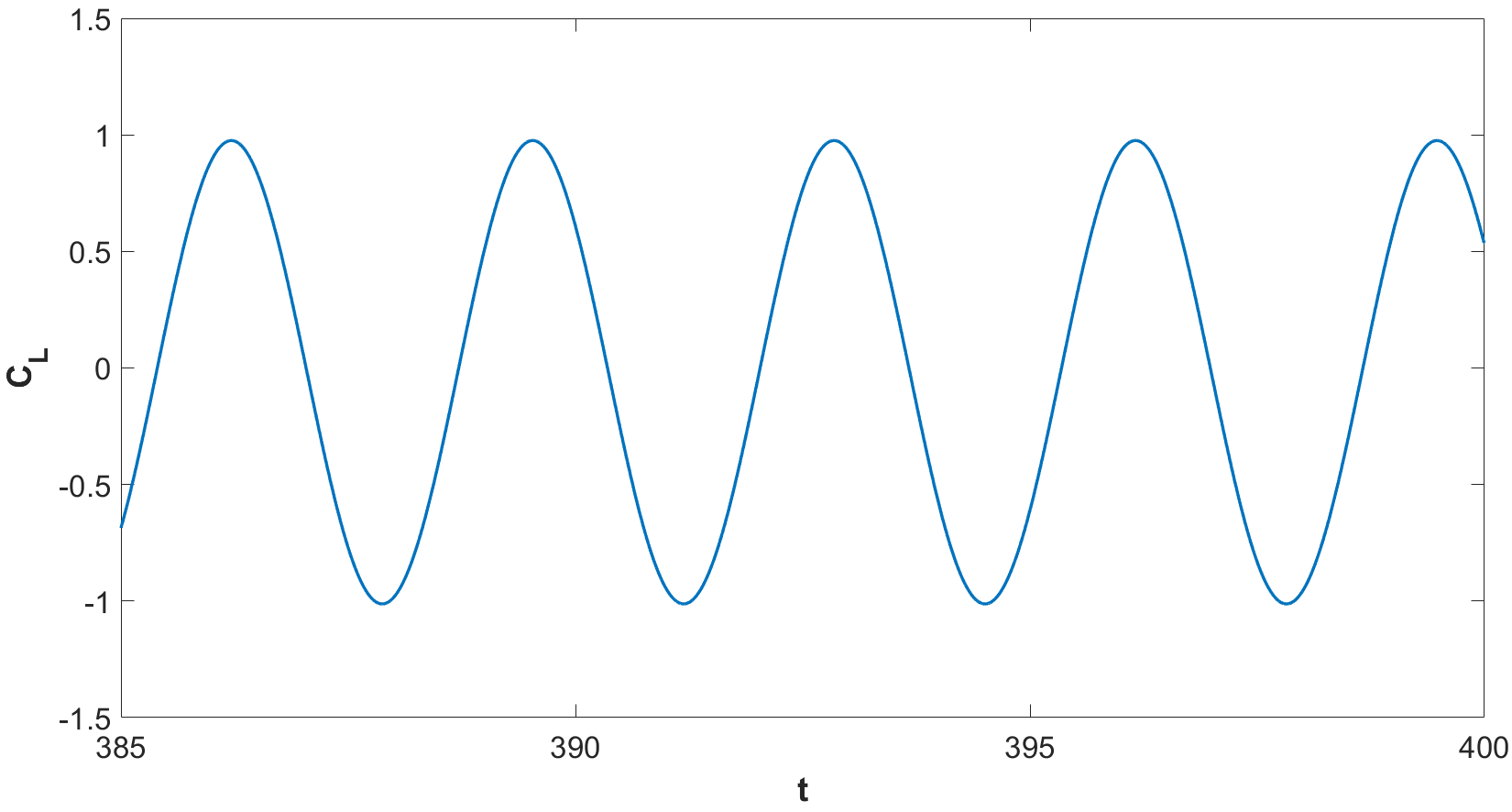
We test the code with a classical benchmark case, namely the flow past a cylinder in 2D at \(Re = 100\) (see [1] for all the details). The image shows the contour plot of the velocity magnitude at \(t = T_{f} = 400\). The evolution of the lift and drag coefficients from \(t = 385\) to \(t = T_{f}\) are also reported and the expected periodic behaviour is retrieved.



References
[1] G. Orlando, A. Della Rocca, P.F. Barbante, L. Bonaventura, and N. Parolini. An efficient and accurate implicit DG solver for the incompressible Navier-Stokes equations. International Journal for Numerical Methods in Fluids, 2022. DOI: 10.1002/FLD.5098
[2] A. Della Rocca. Large-Eddy Simulations of Turbulent Reacting Flows with Industrial Applications. PhD thesis. Politecnico di Milano, 2018. http://hdl.handle.net/10589/137775
Annotated version of equation_data.h
We start by including all the necessary deal.II header files.
@sect{Equation data}
In the next namespace, we declare and implement suitable functions that may be used for the initial and boundary conditions
namespace EquationData {
static const unsigned int degree_p = 1;
We declare class that describes the boundary conditions and initial one for velocity:
template<int dim>
public:
Velocity(const double initial_time = 0.0);
const unsigned int component = 0) const override;
};
template<int dim>
Velocity<dim>::Velocity(
const double initial_time):
Function<dim>(dim, initial_time) {}
template<int dim>
double Velocity<dim>::value(
const Point<dim>& p,
const unsigned int component)
const {
if(component == 0) {
const double Um = 1.5;
const double H = 4.1;
return 4.0*Um*p(1)*(H - p(1))/(H*H);
}
else
return 0.0;
}
template<int dim>
for(unsigned int i = 0; i < dim; ++i)
}
virtual RangeNumberType value(const Point< dim > &p, const unsigned int component=0) const
virtual void vector_value(const Point< dim > &p, Vector< RangeNumberType > &values) const
#define Assert(cond, exc)
#define AssertIndexRange(index, range)
We do the same for the pressure
template<int dim>
public:
Pressure(const double initial_time = 0.0);
const unsigned int component = 0) const override;
};
template<int dim>
Pressure<dim>::Pressure(
const double initial_time):
Function<dim>(1, initial_time) {}
template<int dim>
double Pressure<dim>::value(
const Point<dim>& p,
const unsigned int component)
const {
(void)component;
return 22.0 - p(0);
}
}
Annotated version of navier_stokes_TRBDF2_DG.cc
We start by including all the necessary deal.II header files and some C++ related ones.
#include <fstream>
#include <cmath>
#include <iostream>
#include "runtime_parameters.h"
#include "equation_data.h"
template<int dim, typename Number, typename VectorizedArrayType>
const unsigned int&,
const std::pair<unsigned int, unsigned int>&)>& cell_operation,
const unsigned int&,
const std::pair<unsigned int, unsigned int>&)>& face_operation,
const unsigned int&,
const std::pair<unsigned int, unsigned int>&)>& boundary_operation,
const unsigned int dof_no = 0) {
initialize vector
const unsigned int dummy = 0;
matrix_free.
loop(cell_operation, face_operation, boundary_operation,
diagonal_global, dummy, false,
}
}
void loop(const std::function< void(const MatrixFree< dim, Number, VectorizedArrayType > &, OutVector &, const InVector &, const std::pair< unsigned int, unsigned int > &)> &cell_operation, const std::function< void(const MatrixFree< dim, Number, VectorizedArrayType > &, OutVector &, const InVector &, const std::pair< unsigned int, unsigned int > &)> &face_operation, const std::function< void(const MatrixFree< dim, Number, VectorizedArrayType > &, OutVector &, const InVector &, const std::pair< unsigned int, unsigned int > &)> &boundary_operation, OutVector &dst, const InVector &src, const bool zero_dst_vector=false, const DataAccessOnFaces dst_vector_face_access=DataAccessOnFaces::unspecified, const DataAccessOnFaces src_vector_face_access=DataAccessOnFaces::unspecified) const
void initialize_dof_vector(VectorType &vec, const unsigned int dof_handler_index=0) const
We include the code in a suitable namespace:
The following class is an auxiliary one for post-processing of the vorticity
template<int dim>
public:
virtual std::vector<std::string>
get_names()
const override;
virtual std::vector<DataComponentInterpretation::DataComponentInterpretation>
};
virtual UpdateFlags get_needed_update_flags() const =0
virtual void evaluate_vector_field(const DataPostprocessorInputs::Vector< dim > &input_data, std::vector< Vector< double > > &computed_quantities) const
virtual std::vector< std::string > get_names() const =0
virtual std::vector< DataComponentInterpretation::DataComponentInterpretation > get_data_component_interpretation() const
This function evaluates the vorticty in both 2D and 3D cases
template <int dim>
Assert(computed_quantities.size() == n_quadrature_points, ExcInternalError());
if(dim == 2) {
Assert(computed_quantities[0].size() == 1, ExcInternalError());
}
else {
Assert(computed_quantities[0].size() == dim, ExcInternalError());
}
if(dim == 2) {
for(unsigned int q = 0; q < n_quadrature_points; ++q)
}
else {
for(unsigned int q = 0; q < n_quadrature_points; ++q) {
}
}
}
std::vector<::Vector< double > > solution_values
std::vector< std::vector< Tensor< 1, spacedim > > > solution_gradients
This auxiliary function is required by the base class DataProcessor and simply sets the name for the output file
template<int dim>
std::vector<std::string> PostprocessorVorticity<dim>::get_names() const {
std::vector<std::string> names;
names.emplace_back("vorticity");
if(dim == 3) {
names.emplace_back("vorticity");
names.emplace_back("vorticity");
}
return names;
}
This auxiliary function is required by the base class DataProcessor and simply specifies if the vorticity is a scalar (2D) or a vector (3D)
template<int dim>
std::vector<DataComponentInterpretation::DataComponentInterpretation>
PostprocessorVorticity<dim>::get_data_component_interpretation() const {
std::vector<DataComponentInterpretation::DataComponentInterpretation> interpretation;
if(dim == 2)
else {
}
return interpretation;
}
@ component_is_part_of_vector
This auxiliary function is required by the base class DataProcessor and simply sets which variables have to updated (only the gradients)
template<int dim>
UpdateFlags PostprocessorVorticity<dim>::get_needed_update_flags()
const {
}
@ update_gradients
Shape function gradients.
The following structs are auxiliary objects for mesh refinement. ScratchData simply sets the FEValues object
template <int dim>
struct ScratchData {
const unsigned int quadrature_degree,
const UpdateFlags update_flags): fe_values(fe,
QGauss<dim>(quadrature_degree), update_flags) {}
ScratchData(const ScratchData<dim>& scratch_data): fe_values(scratch_data.fe_values.get_fe(),
scratch_data.fe_values.get_quadrature(),
scratch_data.fe_values.get_update_flags()) {}
};
CopyData simply sets the cell index
struct CopyData {
CopyData(const CopyData &) = default;
double value;
};
@sect{ NavierStokesProjectionOperator::NavierStokesProjectionOperator }
The following class sets effecively the weak formulation of the problems for the different stages and for both velocity and pressure. The template parameters are the dimnesion of the problem, the polynomial degree for the pressure, the polynomial degree for the velocity, the number of quadrature points for integrals for the pressure step, the number of quadrature points for integrals for the velocity step, the type of vector for storage and the type of floating point data (in general double or float for preconditioners structures if desired).
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
public:
using Number = typename Vec::value_type;
NavierStokesProjectionOperator();
NavierStokesProjectionOperator(RunTimeParameters::Data_Storage& data);
void set_dt(const double time_step);
void set_TR_BDF2_stage(const unsigned int stage);
void set_NS_stage(const unsigned int stage);
void set_u_extr(const Vec& src);
void vmult_rhs_velocity(Vec& dst, const std::vector<Vec>& src) const;
void vmult_rhs_pressure(Vec& dst, const std::vector<Vec>& src) const;
void vmult_grad_p_projection(Vec& dst, const Vec& src) const;
protected:
double Re;
double dt;
double gamma;
double a31;
double a32;
double a33;
unsigned int TR_BDF2_stage;
unsigned int NS_stage;
virtual void apply_add(Vec& dst,
const Vec& src)
const override;
private:
const double a21 = 0.5;
const double a22 = 0.5;
const double theta_v = 1.0;
const double theta_p = 1.0;
const double C_p = 1.0*(fe_degree_p + 1)*(fe_degree_p + 1);
const double C_u = 1.0*(fe_degree_v + 1)*(fe_degree_v + 1);
Vec u_extr;
EquationData::Velocity<dim> vel_boundary_inflow;
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& cell_range) const;
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& cell_range) const;
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& cell_range) const;
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& cell_range) const;
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& cell_range) const;
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& cell_range) const;
Vec& dst,
const unsigned int& src,
const std::pair<unsigned int, unsigned int>& cell_range) const;
Vec& dst,
const unsigned int& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const unsigned int& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const unsigned int& src,
const std::pair<unsigned int, unsigned int>& cell_range) const;
Vec& dst,
const unsigned int& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
Vec& dst,
const unsigned int& src,
const std::pair<unsigned int, unsigned int>& face_range) const;
};
virtual void compute_diagonal()=0
virtual void apply_add(VectorType &dst, const VectorType &src) const =0
We start with the default constructor. It is important for MultiGrid, so it is fundamental to properly set the parameters of the time scheme.
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
NavierStokesProjectionOperator():
MatrixFreeOperators::Base<dim, Vec>(), Re(), dt(), gamma(2.0 -
std::sqrt(2.0)), a31((1.0 - gamma)/(2.0*(2.0 - gamma))),
a32(a31), a33(1.0/(2.0 - gamma)), TR_BDF2_stage(1), NS_stage(1), u_extr() {}
We focus now on the constructor with runtime parameters storage
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
NavierStokesProjectionOperator(RunTimeParameters::Data_Storage& data):
gamma(2.0 -
std::sqrt(2.0)), a31((1.0 - gamma)/(2.0*(2.0 - gamma))),
a32(a31), a33(1.0/(2.0 - gamma)), TR_BDF2_stage(1), NS_stage(1), u_extr(),
vel_boundary_inflow(data.initial_time) {}
Setter of time-step (called by Multigrid and in case a smaller time-step towards the end is needed)
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
set_dt(const double time_step) {
dt = time_step;
}
Setter of TR-BDF2 stage (this can be known only during the effective execution and so it has to be demanded to the class that really solves the problem)
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
set_TR_BDF2_stage(const unsigned int stage) {
Assert(stage > 0, ExcInternalError());
TR_BDF2_stage = stage;
}
Setter of NS stage (this can be known only during the effective execution and so it has to be demanded to the class that really solves the problem)
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
set_NS_stage(const unsigned int stage) {
Assert(stage > 0, ExcInternalError());
NS_stage = stage;
}
Setter of extrapolated velocity for different stages
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
set_u_extr(const Vec& src) {
u_extr = src;
u_extr.update_ghost_values();
}
We are in a DG-MatrixFree framework, so it is convenient to compute separately cell contribution, internal faces contributions and boundary faces contributions. We start by assembling the rhs cell term for the velocity.
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& cell_range) const {
if(TR_BDF2_stage == 1) {
phi_old(data, 0),
phi_old_extr(data, 0);
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi_old.reinit(cell);
phi_old_extr.reinit(cell);
phi_old_press.reinit(cell);
phi.reinit(cell);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& u_n = phi_old.get_value(q);
const auto& grad_u_n = phi_old.get_gradient(q);
const auto& u_n_gamma_ov_2 = phi_old_extr.get_value(q);
const auto& tensor_product_u_n =
outer_product(u_n, u_n_gamma_ov_2);
const auto& p_n = phi_old_press.get_value(q);
auto p_n_times_identity = tensor_product_u_n;
p_n_times_identity = 0;
for(unsigned int d = 0; d < dim; ++d)
p_n_times_identity[d][d] = p_n;
phi.submit_value(1.0/(gamma*dt)*u_n, q);
phi.submit_gradient(-a21/Re*grad_u_n + a21*tensor_product_u_n + p_n_times_identity, q);
}
}
}
else {
phi_old(data, 0),
phi_int(data, 0);
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi_old.reinit(cell);
phi_int.reinit(cell);
phi_old_press.reinit(cell);
phi.reinit(cell);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& u_n = phi_old.get_value(q);
const auto& grad_u_n = phi_old.get_gradient(q);
const auto& u_n_gamma = phi_int.get_value(q);
const auto& grad_u_n_gamma = phi_int.get_gradient(q);
const auto& tensor_product_u_n_gamma =
outer_product(u_n_gamma, u_n_gamma);
const auto& p_n = phi_old_press.get_value(q);
auto p_n_times_identity = tensor_product_u_n;
p_n_times_identity = 0;
for(
unsigned int d = 0;
d < dim; ++
d)
p_n_times_identity[d][d] = p_n;
phi.submit_value(1.0/((1.0 - gamma)*dt)*u_n_gamma, q);
phi.submit_gradient(a32*tensor_product_u_n_gamma + a31*tensor_product_u_n -
a32/Re*grad_u_n_gamma - a31/Re*grad_u_n + p_n_times_identity, q);
}
}
}
}
SymmetricTensor< 2, dim, Number > d(const Tensor< 2, dim, Number > &F, const Tensor< 2, dim, Number > &dF_dt)
constexpr SymmetricTensor< 4, dim, Number > outer_product(const SymmetricTensor< 2, dim, Number > &t1, const SymmetricTensor< 2, dim, Number > &t2)
The followinf function assembles rhs face term for the velocity
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& face_range) const {
if(TR_BDF2_stage == 1) {
phi_m(data, false, 0),
phi_old_p(data, true, 0),
phi_old_m(data, false, 0),
phi_old_extr_p(data, true, 0),
phi_old_extr_m(data, false, 0);
phi_old_press_m(data, false, 1);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_old_p.reinit(face);
phi_old_m.reinit(face);
phi_old_extr_p.reinit(face);
phi_old_extr_m.reinit(face);
phi_old_press_p.reinit(face);
phi_old_press_m.reinit(face);
phi_p.reinit(face);
phi_m.reinit(face);
for(unsigned int q = 0; q < phi_p.n_q_points; ++q) {
const auto& n_plus = phi_p.get_normal_vector(q);
const auto& avg_grad_u_old = 0.5*(phi_old_p.get_gradient(q) + phi_old_m.get_gradient(q));
const auto& avg_tensor_product_u_n = 0.5*(
outer_product(phi_old_p.get_value(q), phi_old_extr_p.get_value(q)) +
outer_product(phi_old_m.get_value(q), phi_old_extr_m.get_value(q)));
const auto& avg_p_old = 0.5*(phi_old_press_p.get_value(q) + phi_old_press_m.get_value(q));
phi_p.submit_value((a21/Re*avg_grad_u_old - a21*avg_tensor_product_u_n)*n_plus - avg_p_old*n_plus, q);
phi_m.submit_value(-(a21/Re*avg_grad_u_old - a21*avg_tensor_product_u_n)*n_plus + avg_p_old*n_plus, q);
}
}
}
else {
phi_m(data, false, 0),
phi_old_p(data, true, 0),
phi_old_m(data, false, 0),
phi_int_p(data, true, 0),
phi_int_m(data, false, 0);
phi_old_press_m(data, false, 1);
for(unsigned int face = face_range.first; face < face_range.second; ++ face) {
phi_old_p.reinit(face);
phi_old_m.reinit(face);
phi_int_p.reinit(face);
phi_int_m.reinit(face);
phi_old_press_p.reinit(face);
phi_old_press_m.reinit(face);
phi_p.reinit(face);
phi_m.reinit(face);
for(unsigned int q = 0; q < phi_p.n_q_points; ++q) {
const auto& n_plus = phi_p.get_normal_vector(q);
const auto& avg_grad_u_old = 0.5*(phi_old_p.get_gradient(q) + phi_old_m.get_gradient(q));
const auto& avg_grad_u_int = 0.5*(phi_int_p.get_gradient(q) + phi_int_m.get_gradient(q));
const auto& avg_tensor_product_u_n = 0.5*(
outer_product(phi_old_p.get_value(q), phi_old_p.get_value(q)) +
const auto& avg_tensor_product_u_n_gamma = 0.5*(
outer_product(phi_int_p.get_value(q), phi_int_p.get_value(q)) +
const auto& avg_p_old = 0.5*(phi_old_press_p.get_value(q) + phi_old_press_m.get_value(q));
phi_p.submit_value((a31/Re*avg_grad_u_old + a32/Re*avg_grad_u_int -
a31*avg_tensor_product_u_n - a32*avg_tensor_product_u_n_gamma)*n_plus - avg_p_old*n_plus, q);
phi_m.submit_value(-(a31/Re*avg_grad_u_old + a32/Re*avg_grad_u_int -
a31*avg_tensor_product_u_n - a32*avg_tensor_product_u_n_gamma)*n_plus + avg_p_old*n_plus, q);
}
}
}
}
The followinf function assembles rhs boundary term for the velocity
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& face_range) const {
if(TR_BDF2_stage == 1) {
phi_old(data, true, 0),
phi_old_extr(data, true, 0);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_old.reinit(face);
phi_old_extr.reinit(face);
phi_old_press.reinit(face);
phi.reinit(face);
const auto coef_jump = (boundary_id == 1) ? 0.0 : C_u*
std::abs((phi.get_normal_vector(0) * phi.inverse_jacobian(0))[dim - 1]);
const double aux_coeff = (boundary_id == 1) ? 0.0 : 1.0;
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_u_old = phi_old.get_gradient(q);
const auto& tensor_product_u_n =
outer_product(phi_old.get_value(q), phi_old_extr.get_value(q));
const auto& p_old = phi_old_press.get_value(q);
const auto& point_vectorized = phi.quadrature_point(q);
if(boundary_id == 0) {
for(unsigned int v = 0; v < VectorizedArray<Number>::size(); ++v) {
for(unsigned int d = 0; d < dim; ++d)
point[d] = point_vectorized[d][v];
for(unsigned int d = 0; d < dim; ++d)
u_int_m[d][v] = vel_boundary_inflow.value(point, d);
}
}
const auto tensor_product_u_int_m =
outer_product(u_int_m, phi_old_extr.get_value(q));
phi.submit_value((a21/Re*grad_u_old - a21*tensor_product_u_n)*n_plus - p_old*n_plus +
a22/Re*2.0*coef_jump*u_int_m -
aux_coeff*a22*tensor_product_u_int_m*n_plus + a22*
lambda*u_int_m, q);
phi.submit_normal_derivative(-aux_coeff*theta_v*a22/Re*u_int_m, q);
}
}
}
else {
phi_old(data, true, 0),
phi_int(data, true, 0),
phi_int_extr(data, true, 0);
for(unsigned int face = face_range.first; face < face_range.second; ++ face) {
phi_old.reinit(face);
phi_int.reinit(face);
phi_old_press.reinit(face);
phi_int_extr.reinit(face);
phi.reinit(face);
const auto coef_jump = (
boundary_id == 1) ? 0.0 : C_u*
std::abs((phi.get_normal_vector(0) * phi.inverse_jacobian(0))[dim - 1]);
const double aux_coeff = (
boundary_id == 1) ? 0.0 : 1.0;
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_u_old = phi_old.get_gradient(q);
const auto& grad_u_int = phi_int.get_gradient(q);
const auto& tensor_product_u_n =
outer_product(phi_old.get_value(q), phi_old.get_value(q));
const auto& tensor_product_u_n_gamma =
outer_product(phi_int.get_value(q), phi_int.get_value(q));
const auto& p_old = phi_old_press.get_value(q);
const auto& point_vectorized = phi.quadrature_point(q);
if(boundary_id == 0) {
for(unsigned int v = 0; v < VectorizedArray<Number>::size(); ++v) {
for(
unsigned int d = 0;
d < dim; ++
d)
point[d] = point_vectorized[d][v];
for(
unsigned int d = 0;
d < dim; ++
d)
u_m[d][v] = vel_boundary_inflow.value(point, d);
}
}
const auto tensor_product_u_m =
outer_product(u_m, phi_int_extr.get_value(q));
phi.submit_value((a31/Re*grad_u_old + a32/Re*grad_u_int -
a31*tensor_product_u_n - a32*tensor_product_u_n_gamma)*n_plus - p_old*n_plus +
a33/Re*2.0*coef_jump*u_m -
aux_coeff*a33*tensor_product_u_m*n_plus + a33*
lambda*u_m, q);
phi.submit_normal_derivative(-aux_coeff*theta_v*a33/Re*u_m, q);
}
}
}
}
types::boundary_id get_boundary_id(const unsigned int face_batch_index) const
Point< spacedim > point(const gp_Pnt &p, const double tolerance=1e-10)
::VectorizedArray< Number, width > abs(const ::VectorizedArray< Number, width > &)
constexpr ProductType< Number, OtherNumber >::type scalar_product(const SymmetricTensor< 2, dim, Number > &t1, const SymmetricTensor< 2, dim, OtherNumber > &t2)
Put together all the previous steps for velocity. This is done automatically by the loop function of 'MatrixFree' class
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
vmult_rhs_velocity(Vec& dst, const std::vector<Vec>& src) const {
for(auto& vec : src)
vec.update_ghost_values();
this->data->
loop(&NavierStokesProjectionOperator::assemble_rhs_cell_term_velocity,
&NavierStokesProjectionOperator::assemble_rhs_face_term_velocity,
&NavierStokesProjectionOperator::assemble_rhs_boundary_term_velocity,
this, dst, src, true,
}
Now we focus on computing the rhs for the projection step for the pressure with the same ratio. The following function assembles rhs cell term for the pressure
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& cell_range) const {
phi_old(data, 1, 1);
const double coeff = (TR_BDF2_stage == 1) ? 1.0e6*gamma*dt*gamma*dt : 1.0e6*(1.0 - gamma)*dt*(1.0 - gamma)*dt;
const double coeff_2 = (TR_BDF2_stage == 1) ? gamma*dt : (1.0 - gamma)*dt;
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi_proj.reinit(cell);
phi_old.reinit(cell);
phi.reinit(cell);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& u_star_star = phi_proj.get_value(q);
const auto& p_old = phi_old.get_value(q);
phi.submit_value(1.0/coeff*p_old, q);
phi.submit_gradient(1.0/coeff_2*u_star_star, q);
}
}
}
The following function assembles rhs face term for the pressure
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& face_range) const {
phi_m(data, false, 1, 1);
phi_proj_m(data, false, 0, 1);
const double coeff = (TR_BDF2_stage == 1) ? 1.0/(gamma*dt) : 1.0/((1.0 - gamma)*dt);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_proj_p.reinit(face);
phi_proj_m.reinit(face);
phi_p.reinit(face);
phi_m.reinit(face);
for(unsigned int q = 0; q < phi_p.n_q_points; ++q) {
const auto& n_plus = phi_p.get_normal_vector(q);
const auto& avg_u_star_star = 0.5*(phi_proj_p.get_value(q) + phi_proj_m.get_value(q));
phi_p.submit_value(-coeff*
scalar_product(avg_u_star_star, n_plus), q);
}
}
}
The following function assembles rhs boundary term for the pressure
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const std::vector<Vec>& src,
const std::pair<unsigned int, unsigned int>& face_range) const {
const double coeff = (TR_BDF2_stage == 1) ? 1.0/(gamma*dt) : 1.0/((1.0 - gamma)*dt);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_proj.reinit(face);
phi.reinit(face);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
phi.submit_value(-coeff*
scalar_product(phi_proj.get_value(q), n_plus), q);
}
}
}
Put together all the previous steps for pressure
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
vmult_rhs_pressure(Vec& dst, const std::vector<Vec>& src) const {
for(auto& vec : src)
vec.update_ghost_values();
this->data->
loop(&NavierStokesProjectionOperator::assemble_rhs_cell_term_pressure,
&NavierStokesProjectionOperator::assemble_rhs_face_term_pressure,
&NavierStokesProjectionOperator::assemble_rhs_boundary_term_pressure,
this, dst, src, true,
}
Now we need to build the 'matrices', i.e. the bilinear forms. We start by assembling the cell term for the velocity
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& cell_range) const {
if(TR_BDF2_stage == 1) {
phi_old_extr(data, 0);
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi.reinit(cell);
phi_old_extr.reinit(cell);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& u_int = phi.get_value(q);
const auto& grad_u_int = phi.get_gradient(q);
const auto& u_n_gamma_ov_2 = phi_old_extr.get_value(q);
const auto& tensor_product_u_int =
outer_product(u_int, u_n_gamma_ov_2);
phi.submit_value(1.0/(gamma*dt)*u_int, q);
phi.submit_gradient(-a22*tensor_product_u_int + a22/Re*grad_u_int, q);
}
}
}
else {
phi_int_extr(data, 0);
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi.reinit(cell);
phi_int_extr.reinit(cell);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& u_curr = phi.get_value(q);
const auto& grad_u_curr = phi.get_gradient(q);
const auto& u_n1_int = phi_int_extr.get_value(q);
const auto& tensor_product_u_curr =
outer_product(u_curr, u_n1_int);
phi.submit_value(1.0/((1.0 - gamma)*dt)*u_curr, q);
phi.submit_gradient(-a33*tensor_product_u_curr + a33/Re*grad_u_curr, q);
}
}
}
}
The following function assembles face term for the velocity
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& face_range) const {
if(TR_BDF2_stage == 1) {
phi_m(data, false, 0),
phi_old_extr_p(data, true, 0),
phi_old_extr_m(data, false, 0);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_p.reinit(face);
phi_m.reinit(face);
phi_old_extr_p.reinit(face);
phi_old_extr_m.reinit(face);
const auto coef_jump = C_u*0.5*(
std::abs((phi_p.get_normal_vector(0)*phi_p.inverse_jacobian(0))[dim - 1]) +
std::abs((phi_m.get_normal_vector(0)*phi_m.inverse_jacobian(0))[dim - 1]));
for(unsigned int q = 0; q < phi_p.n_q_points; ++q) {
const auto& n_plus = phi_p.get_normal_vector(q);
const auto& avg_grad_u_int = 0.5*(phi_p.get_gradient(q) + phi_m.get_gradient(q));
const auto& jump_u_int = phi_p.get_value(q) - phi_m.get_value(q);
const auto& avg_tensor_product_u_int = 0.5*(
outer_product(phi_p.get_value(q), phi_old_extr_p.get_value(q)) +
phi_p.submit_value(a22/Re*(-avg_grad_u_int*n_plus + coef_jump*jump_u_int) +
a22*avg_tensor_product_u_int*n_plus + 0.5*a22*lambda*jump_u_int, q);
phi_m.submit_value(-a22/Re*(-avg_grad_u_int*n_plus + coef_jump*jump_u_int) -
a22*avg_tensor_product_u_int*n_plus - 0.5*a22*lambda*jump_u_int, q);
phi_p.submit_normal_derivative(-theta_v*a22/Re*0.5*jump_u_int, q);
phi_m.submit_normal_derivative(-theta_v*a22/Re*0.5*jump_u_int, q);
}
}
}
else {
phi_m(data, false, 0),
phi_extr_p(data, true, 0),
phi_extr_m(data, false, 0);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_p.reinit(face);
phi_m.reinit(face);
phi_extr_p.reinit(face);
phi_extr_m.reinit(face);
const auto coef_jump = C_u*0.5*(
std::abs((phi_p.get_normal_vector(0)*phi_p.inverse_jacobian(0))[dim - 1]) +
std::abs((phi_m.get_normal_vector(0)*phi_m.inverse_jacobian(0))[dim - 1]));
for(unsigned int q = 0; q < phi_p.n_q_points; ++q) {
const auto& n_plus = phi_p.get_normal_vector(q);
const auto& avg_grad_u = 0.5*(phi_p.get_gradient(q) + phi_m.get_gradient(q));
const auto& jump_u = phi_p.get_value(q) - phi_m.get_value(q);
const auto& avg_tensor_product_u = 0.5*(
outer_product(phi_p.get_value(q), phi_extr_p.get_value(q)) +
phi_p.submit_value(a33/Re*(-avg_grad_u*n_plus + coef_jump*jump_u) +
a33*avg_tensor_product_u*n_plus + 0.5*a33*lambda*jump_u, q);
phi_m.submit_value(-a33/Re*(-avg_grad_u*n_plus + coef_jump*jump_u) -
a33*avg_tensor_product_u*n_plus - 0.5*a33*lambda*jump_u, q);
phi_p.submit_normal_derivative(-theta_v*a33/Re*0.5*jump_u, q);
phi_m.submit_normal_derivative(-theta_v*a33/Re*0.5*jump_u, q);
}
}
}
}
::VectorizedArray< Number, width > max(const ::VectorizedArray< Number, width > &, const ::VectorizedArray< Number, width > &)
The following function assembles boundary term for the velocity
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& face_range) const {
if(TR_BDF2_stage == 1) {
phi_old_extr(data, true, 0);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi.reinit(face);
phi_old_extr.reinit(face);
const auto coef_jump = C_u*
std::abs((phi.get_normal_vector(0) * phi.inverse_jacobian(0))[dim - 1]);
if(boundary_id != 1) {
const double coef_trasp = 0.0;
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_u_int = phi.get_gradient(q);
const auto& u_int = phi.get_value(q);
const auto& tensor_product_u_int =
outer_product(phi.get_value(q), phi_old_extr.get_value(q));
phi.submit_value(a22/Re*(-grad_u_int*n_plus + 2.0*coef_jump*u_int) +
a22*coef_trasp*tensor_product_u_int*n_plus + a22*lambda*u_int, q);
phi.submit_normal_derivative(-theta_v*a22/Re*u_int, q);
}
}
else {
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_u_int = phi.get_gradient(q);
const auto& u_int = phi.get_value(q);
const auto& point_vectorized = phi.quadrature_point(q);
auto u_int_m = u_int;
auto grad_u_int_m = grad_u_int;
for(unsigned int v = 0; v < VectorizedArray<Number>::size(); ++v) {
for(
unsigned int d = 0;
d < dim; ++
d)
point[d] = point_vectorized[d][v];
u_int_m[1][v] = -u_int_m[1][v];
grad_u_int_m[0][0][v] = -grad_u_int_m[0][0][v];
grad_u_int_m[0][1][v] = -grad_u_int_m[0][1][v];
}
phi.submit_value(a22/Re*(-(0.5*(grad_u_int + grad_u_int_m))*n_plus + coef_jump*(u_int - u_int_m)) +
a22*
outer_product(0.5*(u_int + u_int_m), phi_old_extr.get_value(q))*n_plus +
a22*0.5*
lambda*(u_int - u_int_m), q);
phi.submit_normal_derivative(-theta_v*a22/Re*(u_int - u_int_m), q);
}
}
}
}
else {
phi_extr(data, true, 0);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi.reinit(face);
phi_extr.reinit(face);
const auto coef_jump = C_u*
std::abs((phi.get_normal_vector(0) * phi.inverse_jacobian(0))[dim - 1]);
if(boundary_id != 1) {
const double coef_trasp = 0.0;
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_u = phi.get_gradient(q);
const auto& u = phi.get_value(q);
const auto& tensor_product_u =
outer_product(phi.get_value(q), phi_extr.get_value(q));
phi.submit_value(a33/Re*(-grad_u*n_plus + 2.0*coef_jump*u) +
a33*coef_trasp*tensor_product_u*n_plus + a33*lambda*u, q);
phi.submit_normal_derivative(-theta_v*a33/Re*u, q);
}
}
else {
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_u = phi.get_gradient(q);
const auto& u = phi.get_value(q);
const auto& point_vectorized = phi.quadrature_point(q);
auto u_m = u;
auto grad_u_m = grad_u;
for(unsigned int v = 0; v < VectorizedArray<Number>::size(); ++v) {
for(
unsigned int d = 0;
d < dim; ++
d)
point[d] = point_vectorized[d][v];
u_m[1][v] = -u_m[1][v];
grad_u_m[0][0][v] = -grad_u_m[0][0][v];
grad_u_m[0][1][v] = -grad_u_m[0][1][v];
}
phi.submit_value(a33/Re*(-(0.5*(grad_u + grad_u_m))*n_plus + coef_jump*(u - u_m)) +
phi.submit_normal_derivative(-theta_v*a33/Re*(u - u_m), q);
}
}
}
}
}
Next, we focus on 'matrices' to compute the pressure. We first assemble cell term for the pressure
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& cell_range) const {
const double coeff = (TR_BDF2_stage == 1) ? 1.0e6*gamma*dt*gamma*dt : 1.0e6*(1.0 - gamma)*dt*(1.0 - gamma)*dt;
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi.reinit(cell);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
phi.submit_gradient(phi.get_gradient(q), q);
phi.submit_value(1.0/coeff*phi.get_value(q), q);
}
}
}
The following function assembles face term for the pressure
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& face_range) const {
phi_m(data, false, 1, 1);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_p.reinit(face);
phi_m.reinit(face);
const auto coef_jump = C_p*0.5*(
std::abs((phi_p.get_normal_vector(0)*phi_p.inverse_jacobian(0))[dim - 1]) +
std::abs((phi_m.get_normal_vector(0)*phi_m.inverse_jacobian(0))[dim - 1]));
for(unsigned int q = 0; q < phi_p.n_q_points; ++q) {
const auto& n_plus = phi_p.get_normal_vector(q);
const auto& avg_grad_pres = 0.5*(phi_p.get_gradient(q) + phi_m.get_gradient(q));
const auto& jump_pres = phi_p.get_value(q) - phi_m.get_value(q);
phi_p.submit_value(-
scalar_product(avg_grad_pres, n_plus) + coef_jump*jump_pres, q);
phi_m.submit_value(
scalar_product(avg_grad_pres, n_plus) - coef_jump*jump_pres, q);
phi_p.submit_gradient(-theta_p*0.5*jump_pres*n_plus, q);
phi_m.submit_gradient(-theta_p*0.5*jump_pres*n_plus, q);
}
}
}
The following function assembles boundary term for the pressure
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& face_range) const {
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
if(boundary_id == 1) {
phi.reinit(face);
phi.gather_evaluate(src, true, true);
const auto coef_jump = C_p*
std::abs((phi.get_normal_vector(0)*phi.inverse_jacobian(0))[dim - 1]);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_pres = phi.get_gradient(q);
const auto& pres = phi.get_value(q);
phi.submit_value(-
scalar_product(grad_pres, n_plus) + coef_jump*pres , q);
phi.submit_normal_derivative(-theta_p*pres, q);
}
}
}
}
Before coding the 'apply_add' function, which is the one that will perform the loop, we focus on the linear system that arises to project the gradient of the pressure into the velocity space. The following function assembles rhs cell term for the projection of gradient of pressure. Since no integration by parts is performed, only a cell term contribution is present.
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& cell_range) const {
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi_pres.reinit(cell);
phi.reinit(cell);
for(unsigned int q = 0; q < phi.n_q_points; ++q)
phi.submit_value(phi_pres.get_gradient(q), q);
}
}
Put together all the previous steps for porjection of pressure gradient. Here we loop only over cells
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
vmult_grad_p_projection(Vec& dst, const Vec& src) const {
this->data->
cell_loop(&NavierStokesProjectionOperator::assemble_rhs_cell_term_projection_grad_p,
this, dst, src, true);
}
void cell_loop(const std::function< void(const MatrixFree< dim, Number, VectorizedArrayType > &, OutVector &, const InVector &, const std::pair< unsigned int, unsigned int > &)> &cell_operation, OutVector &dst, const InVector &src, const bool zero_dst_vector=false) const
Assemble now cell term for the projection of gradient of pressure. This is nothing but a mass matrix
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const Vec& src,
const std::pair<unsigned int, unsigned int>& cell_range) const {
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi.reinit(cell);
for(unsigned int q = 0; q < phi.n_q_points; ++q)
phi.submit_value(phi.get_value(q), q);
}
}
Put together all previous steps. This is the overriden function that effectively performs the matrix-vector multiplication.
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
apply_add(Vec& dst, const Vec& src) const {
if(NS_stage == 1) {
this->data->
loop(&NavierStokesProjectionOperator::assemble_cell_term_velocity,
&NavierStokesProjectionOperator::assemble_face_term_velocity,
&NavierStokesProjectionOperator::assemble_boundary_term_velocity,
this, dst, src, false,
}
else if(NS_stage == 2) {
this->data->
loop(&NavierStokesProjectionOperator::assemble_cell_term_pressure,
&NavierStokesProjectionOperator::assemble_face_term_pressure,
&NavierStokesProjectionOperator::assemble_boundary_term_pressure,
this, dst, src, false,
}
else if(NS_stage == 3) {
this->data->
cell_loop(&NavierStokesProjectionOperator::assemble_cell_term_projection_grad_p,
this, dst, src, false);
}
else
Assert(
false, ExcNotImplemented());
}
Finally, we focus on computing the diagonal for preconditioners and we start by assembling the diagonal cell term for the velocity. Since we do not have access to the entries of the matrix, in order to compute the element i, we test the matrix against a vector which is equal to 1 in position i and 0 elsewhere. This is why 'src' will result as unused.
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const unsigned int& ,
const std::pair<unsigned int, unsigned int>& cell_range) const {
if(TR_BDF2_stage == 1) {
phi_old_extr(data, 0);
for(unsigned int d = 0; d < dim; ++d)
tmp[d] = make_vectorized_array<Number>(1.0);
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi_old_extr.reinit(cell);
phi_old_extr.gather_evaluate(u_extr, true, false);
phi.reinit(cell);
for(unsigned int i = 0; i < phi.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi.dofs_per_component; ++j)
phi.submit_dof_value(tmp, i);
phi.evaluate(true, true);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& u_int = phi.get_value(q);
const auto& grad_u_int = phi.get_gradient(q);
const auto& u_n_gamma_ov_2 = phi_old_extr.get_value(q);
const auto& tensor_product_u_int =
outer_product(u_int, u_n_gamma_ov_2);
phi.submit_value(1.0/(gamma*dt)*u_int, q);
phi.submit_gradient(-a22*tensor_product_u_int + a22/Re*grad_u_int, q);
}
phi.integrate(true, true);
diagonal[i] = phi.get_dof_value(i);
}
for(unsigned int i = 0; i < phi.dofs_per_component; ++i)
phi.submit_dof_value(diagonal[i], i);
phi.distribute_local_to_global(dst);
}
}
else {
phi_int_extr(data, 0);
for(
unsigned int d = 0;
d < dim; ++
d)
tmp[d] = make_vectorized_array<Number>(1.0);
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi_int_extr.reinit(cell);
phi_int_extr.gather_evaluate(u_extr, true, false);
phi.reinit(cell);
for(unsigned int i = 0; i < phi.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi.dofs_per_component; ++j)
phi.submit_dof_value(tmp, i);
phi.evaluate(true, true);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& u_curr = phi.get_value(q);
const auto& grad_u_curr = phi.get_gradient(q);
const auto& u_n1_int = phi_int_extr.get_value(q);
const auto& tensor_product_u_curr =
outer_product(u_curr, u_n1_int);
phi.submit_value(1.0/((1.0 - gamma)*dt)*u_curr, q);
phi.submit_gradient(-a33*tensor_product_u_curr + a33/Re*grad_u_curr, q);
}
phi.integrate(true, true);
}
for(unsigned int i = 0; i < phi.dofs_per_component; ++i)
phi.submit_dof_value(diagonal[i], i);
phi.distribute_local_to_global(dst);
}
}
}
@ diagonal
Matrix is diagonal.
The following function assembles diagonal face term for the velocity
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const unsigned int& ,
const std::pair<unsigned int, unsigned int>& face_range) const {
if(TR_BDF2_stage == 1) {
phi_m(data, false, 0),
phi_old_extr_p(data, true, 0),
phi_old_extr_m(data, false, 0);
diagonal_m(phi_m.dofs_per_component);
for(unsigned int d = 0; d < dim; ++d)
tmp[d] = make_vectorized_array<Number>(1.0);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_old_extr_p.reinit(face);
phi_old_extr_p.gather_evaluate(u_extr, true, false);
phi_old_extr_m.reinit(face);
phi_old_extr_m.gather_evaluate(u_extr, true, false);
phi_p.reinit(face);
phi_m.reinit(face);
const auto coef_jump = C_u*0.5*(
std::abs((phi_p.get_normal_vector(0)*phi_p.inverse_jacobian(0))[dim - 1]) +
std::abs((phi_m.get_normal_vector(0)*phi_m.inverse_jacobian(0))[dim - 1]));
for(unsigned int i = 0; i < phi_p.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi_p.dofs_per_component; ++j) {
}
phi_p.submit_dof_value(tmp, i);
phi_p.evaluate(true, true);
phi_m.submit_dof_value(tmp, i);
phi_m.evaluate(true, true);
for(unsigned int q = 0; q < phi_p.n_q_points; ++q) {
const auto& n_plus = phi_p.get_normal_vector(q);
const auto& avg_grad_u_int = 0.5*(phi_p.get_gradient(q) + phi_m.get_gradient(q));
const auto& jump_u_int = phi_p.get_value(q) - phi_m.get_value(q);
const auto& avg_tensor_product_u_int = 0.5*(
outer_product(phi_p.get_value(q), phi_old_extr_p.get_value(q)) +
phi_p.submit_value(a22/Re*(-avg_grad_u_int*n_plus + coef_jump*jump_u_int) +
a22*avg_tensor_product_u_int*n_plus + 0.5*a22*lambda*jump_u_int , q);
phi_m.submit_value(-a22/Re*(-avg_grad_u_int*n_plus + coef_jump*jump_u_int) -
a22*avg_tensor_product_u_int*n_plus - 0.5*a22*lambda*jump_u_int, q);
phi_p.submit_normal_derivative(-theta_v*0.5*a22/Re*jump_u_int, q);
phi_m.submit_normal_derivative(-theta_v*0.5*a22/Re*jump_u_int, q);
}
phi_p.integrate(true, true);
diagonal_p[i] = phi_p.get_dof_value(i);
phi_m.integrate(true, true);
diagonal_m[i] = phi_m.get_dof_value(i);
}
for(unsigned int i = 0; i < phi_p.dofs_per_component; ++i) {
phi_p.submit_dof_value(diagonal_p[i], i);
phi_m.submit_dof_value(diagonal_m[i], i);
}
phi_p.distribute_local_to_global(dst);
phi_m.distribute_local_to_global(dst);
}
}
else {
phi_m(data, false, 0),
phi_extr_p(data, true, 0),
phi_extr_m(data, false, 0);
diagonal_m(phi_m.dofs_per_component);
for(
unsigned int d = 0;
d < dim; ++
d)
tmp[d] = make_vectorized_array<Number>(1.0);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_extr_p.reinit(face);
phi_extr_p.gather_evaluate(u_extr, true, false);
phi_extr_m.reinit(face);
phi_extr_m.gather_evaluate(u_extr, true, false);
phi_p.reinit(face);
phi_m.reinit(face);
const auto coef_jump = C_u*0.5*(
std::abs((phi_p.get_normal_vector(0)*phi_p.inverse_jacobian(0))[dim - 1]) +
std::abs((phi_m.get_normal_vector(0)*phi_m.inverse_jacobian(0))[dim - 1]));
for(unsigned int i = 0; i < phi_p.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi_p.dofs_per_component; ++j) {
}
phi_p.submit_dof_value(tmp, i);
phi_p.evaluate(true, true);
phi_m.submit_dof_value(tmp, i);
phi_m.evaluate(true, true);
for(unsigned int q = 0; q < phi_p.n_q_points; ++q) {
const auto& n_plus = phi_p.get_normal_vector(q);
const auto& avg_grad_u = 0.5*(phi_p.get_gradient(q) + phi_m.get_gradient(q));
const auto& jump_u = phi_p.get_value(q) - phi_m.get_value(q);
const auto& avg_tensor_product_u = 0.5*(
outer_product(phi_p.get_value(q), phi_extr_p.get_value(q)) +
phi_p.submit_value(a33/Re*(-avg_grad_u*n_plus + coef_jump*jump_u) +
a33*avg_tensor_product_u*n_plus + 0.5*a33*lambda*jump_u, q);
phi_m.submit_value(-a33/Re*(-avg_grad_u*n_plus + coef_jump*jump_u) -
a33*avg_tensor_product_u*n_plus - 0.5*a33*lambda*jump_u, q);
phi_p.submit_normal_derivative(-theta_v*0.5*a33/Re*jump_u, q);
phi_m.submit_normal_derivative(-theta_v*0.5*a33/Re*jump_u, q);
}
phi_p.integrate(true, true);
diagonal_p[i] = phi_p.get_dof_value(i);
phi_m.integrate(true, true);
diagonal_m[i] = phi_m.get_dof_value(i);
}
for(unsigned int i = 0; i < phi_p.dofs_per_component; ++i) {
phi_p.submit_dof_value(diagonal_p[i], i);
phi_m.submit_dof_value(diagonal_m[i], i);
}
phi_p.distribute_local_to_global(dst);
phi_m.distribute_local_to_global(dst);
}
}
}
#define AssertDimension(dim1, dim2)
The following function assembles boundary term for the velocity
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const unsigned int& ,
const std::pair<unsigned int, unsigned int>& face_range) const {
if(TR_BDF2_stage == 1) {
phi_old_extr(data, true, 0);
for(unsigned int d = 0; d < dim; ++d)
tmp[d] = make_vectorized_array<Number>(1.0);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_old_extr.reinit(face);
phi_old_extr.gather_evaluate(u_extr, true, false);
phi.reinit(face);
const auto coef_jump = C_u*
std::abs((phi.get_normal_vector(0) * phi.inverse_jacobian(0))[dim - 1]);
if(boundary_id != 1) {
const double coef_trasp = 0.0;
for(unsigned int i = 0; i < phi.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi.dofs_per_component; ++j)
phi.submit_dof_value(tmp, i);
phi.evaluate(true, true);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_u_int = phi.get_gradient(q);
const auto& u_int = phi.get_value(q);
const auto& tensor_product_u_int =
outer_product(phi.get_value(q), phi_old_extr.get_value(q));
phi.submit_value(a22/Re*(-grad_u_int*n_plus + 2.0*coef_jump*u_int) +
a22*coef_trasp*tensor_product_u_int*n_plus + a22*lambda*u_int, q);
phi.submit_normal_derivative(-theta_v*a22/Re*u_int, q);
}
phi.integrate(true, true);
diagonal[i] = phi.get_dof_value(i);
}
for(unsigned int i = 0; i < phi.dofs_per_component; ++i)
phi.submit_dof_value(diagonal[i], i);
phi.distribute_local_to_global(dst);
}
else {
for(unsigned int i = 0; i < phi.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi.dofs_per_component; ++j)
phi.submit_dof_value(tmp, i);
phi.evaluate(true, true);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_u_int = phi.get_gradient(q);
const auto& u_int = phi.get_value(q);
const auto& point_vectorized = phi.quadrature_point(q);
auto u_int_m = u_int;
auto grad_u_int_m = grad_u_int;
for(unsigned int v = 0; v < VectorizedArray<Number>::size(); ++v) {
for(
unsigned int d = 0;
d < dim; ++
d)
point[d] = point_vectorized[d][v];
u_int_m[1][v] = -u_int_m[1][v];
grad_u_int_m[0][0][v] = -grad_u_int_m[0][0][v];
grad_u_int_m[0][1][v] = -grad_u_int_m[0][1][v];
}
phi.submit_value(a22/Re*(-(0.5*(grad_u_int + grad_u_int_m))*n_plus + coef_jump*(u_int - u_int_m)) +
a22*
outer_product(0.5*(u_int + u_int_m), phi_old_extr.get_value(q))*n_plus +
a22*0.5*
lambda*(u_int - u_int_m), q);
phi.submit_normal_derivative(-theta_v*a22/Re*(u_int - u_int_m), q);
}
phi.integrate(true, true);
}
for(unsigned int i = 0; i < phi.dofs_per_component; ++i)
phi.submit_dof_value(diagonal[i], i);
phi.distribute_local_to_global(dst);
}
}
}
else {
phi_extr(data, true, 0);
for(
unsigned int d = 0;
d < dim; ++
d)
tmp[d] = make_vectorized_array<Number>(1.0);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_extr.reinit(face);
phi_extr.gather_evaluate(u_extr, true, false);
phi.reinit(face);
const auto coef_jump = C_u*
std::abs((phi.get_normal_vector(0) * phi.inverse_jacobian(0))[dim - 1]);
if(boundary_id != 1) {
const double coef_trasp = 0.0;
for(unsigned int i = 0; i < phi.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi.dofs_per_component; ++j)
phi.submit_dof_value(tmp, i);
phi.evaluate(true, true);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_u = phi.get_gradient(q);
const auto& u = phi.get_value(q);
const auto& tensor_product_u =
outer_product(phi.get_value(q), phi_extr.get_value(q));
phi.submit_value(a33/Re*(-grad_u*n_plus + 2.0*coef_jump*u) +
a33*coef_trasp*tensor_product_u*n_plus + a33*lambda*u, q);
phi.submit_normal_derivative(-theta_v*a33/Re*u, q);
}
phi.integrate(true, true);
}
for(unsigned int i = 0; i < phi.dofs_per_component; ++i)
phi.submit_dof_value(diagonal[i], i);
phi.distribute_local_to_global(dst);
}
else {
for(unsigned int i = 0; i < phi.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi.dofs_per_component; ++j)
phi.submit_dof_value(tmp, i);
phi.evaluate(true, true);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_u = phi.get_gradient(q);
const auto& u = phi.get_value(q);
const auto& point_vectorized = phi.quadrature_point(q);
auto u_m = u;
auto grad_u_m = grad_u;
for(unsigned int v = 0; v < VectorizedArray<Number>::size(); ++v) {
for(
unsigned int d = 0;
d < dim; ++
d)
point[d] = point_vectorized[d][v];
u_m[1][v] = -u_m[1][v];
grad_u_m[0][0][v] = -grad_u_m[0][0][v];
grad_u_m[0][1][v] = -grad_u_m[0][1][v];
}
phi.submit_value(a33/Re*(-(0.5*(grad_u + grad_u_m))*n_plus + coef_jump*(u - u_m)) +
phi.submit_normal_derivative(-theta_v*a33/Re*(u - u_m), q);
}
phi.integrate(true, true);
}
for(unsigned int i = 0; i < phi.dofs_per_component; ++i)
phi.submit_dof_value(diagonal[i], i);
phi.distribute_local_to_global(dst);
}
}
}
}
Now we consider the pressure related bilinear forms. We first assemble diagonal cell term for the pressure
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const unsigned int& ,
const std::pair<unsigned int, unsigned int>& cell_range) const {
const double coeff = (TR_BDF2_stage == 1) ? 1e6*gamma*dt*gamma*dt : 1e6*(1.0 - gamma)*dt*(1.0 - gamma)*dt;
for(unsigned int cell = cell_range.first; cell < cell_range.second; ++cell) {
phi.reinit(cell);
for(unsigned int i = 0; i < phi.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi.dofs_per_component; ++j)
phi.submit_dof_value(make_vectorized_array<Number>(1.0), i);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
phi.submit_value(1.0/coeff*phi.get_value(q), q);
phi.submit_gradient(phi.get_gradient(q), q);
}
diagonal[i] = phi.get_dof_value(i);
}
for(unsigned int i = 0; i < phi.dofs_per_component; ++i)
phi.submit_dof_value(diagonal[i], i);
phi.distribute_local_to_global(dst);
}
}
The following function assembles diagonal face term for the pressure
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const unsigned int& ,
const std::pair<unsigned int, unsigned int>& face_range) const {
phi_m(data, false, 1, 1);
diagonal_m(phi_m.dofs_per_component);
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
phi_p.reinit(face);
phi_m.reinit(face);
const auto coef_jump = C_p*0.5*(
std::abs((phi_p.get_normal_vector(0)*phi_p.inverse_jacobian(0))[dim - 1]) +
std::abs((phi_m.get_normal_vector(0)*phi_m.inverse_jacobian(0))[dim - 1]));
for(unsigned int i = 0; i < phi_p.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi_p.dofs_per_component; ++j) {
}
phi_p.submit_dof_value(make_vectorized_array<Number>(1.0), i);
phi_m.submit_dof_value(make_vectorized_array<Number>(1.0), i);
for(unsigned int q = 0; q < phi_p.n_q_points; ++q) {
const auto& n_plus = phi_p.get_normal_vector(q);
const auto& avg_grad_pres = 0.5*(phi_p.get_gradient(q) + phi_m.get_gradient(q));
const auto& jump_pres = phi_p.get_value(q) - phi_m.get_value(q);
phi_p.submit_value(-
scalar_product(avg_grad_pres, n_plus) + coef_jump*jump_pres, q);
phi_m.submit_value(
scalar_product(avg_grad_pres, n_plus) - coef_jump*jump_pres, q);
phi_p.submit_gradient(-theta_p*0.5*jump_pres*n_plus, q);
phi_m.submit_gradient(-theta_p*0.5*jump_pres*n_plus, q);
}
diagonal_p[i] = phi_p.get_dof_value(i);
diagonal_m[i] = phi_m.get_dof_value(i);
}
for(unsigned int i = 0; i < phi_p.dofs_per_component; ++i) {
phi_p.submit_dof_value(diagonal_p[i], i);
phi_m.submit_dof_value(diagonal_m[i], i);
}
phi_p.distribute_local_to_global(dst);
phi_m.distribute_local_to_global(dst);
}
}
Eventually, we assemble diagonal boundary term for the pressure
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
Vec& dst,
const unsigned int& ,
const std::pair<unsigned int, unsigned int>& face_range) const {
for(unsigned int face = face_range.first; face < face_range.second; ++face) {
if(boundary_id == 1) {
phi.reinit(face);
const auto coef_jump = C_p*
std::abs((phi.get_normal_vector(0)*phi.inverse_jacobian(0))[dim - 1]);
for(unsigned int i = 0; i < phi.dofs_per_component; ++i) {
for(unsigned int j = 0; j < phi.dofs_per_component; ++j)
phi.submit_dof_value(make_vectorized_array<Number>(1.0), i);
for(unsigned int q = 0; q < phi.n_q_points; ++q) {
const auto& n_plus = phi.get_normal_vector(q);
const auto& grad_pres = phi.get_gradient(q);
const auto& pres = phi.get_value(q);
phi.submit_value(-
scalar_product(grad_pres, n_plus) + 2.0*coef_jump*pres , q);
phi.submit_normal_derivative(-theta_p*pres, q);
}
diagonal[i] = phi.get_dof_value(i);
}
for(unsigned int i = 0; i < phi.dofs_per_component; ++i)
phi.submit_dof_value(diagonal[i], i);
phi.distribute_local_to_global(dst);
}
}
}
Put together all previous steps. We create a dummy auxliary vector that serves for the src input argument in the previous functions that as we have seen before is unused. Then everything is done by the 'loop' function and it is saved in the field 'inverse_diagonal_entries' already present in the base class. Anyway since there is only one field, we need to resize properly depending on whether we are considering the velocity or the pressure.
template<int dim, int fe_degree_p, int fe_degree_v, int n_q_points_1d_p, int n_q_points_1d_v, typename Vec>
void NavierStokesProjectionOperator<dim, fe_degree_p, fe_degree_v, n_q_points_1d_p, n_q_points_1d_v, Vec>::
compute_diagonal() {
Assert(NS_stage == 1 || NS_stage == 2, ExcInternalError());
auto& inverse_diagonal = this->inverse_diagonal_entries->get_vector();
if(NS_stage == 1) {
::MatrixFreeTools::compute_diagonal<dim, Number, VectorizedArray<Number>>
(*(this->data),
inverse_diagonal,
[&](const auto& data, auto& dst, const auto& src, const auto& cell_range) {
(this->assemble_diagonal_cell_term_velocity)(data, dst, src, cell_range);
},
[&](const auto& data, auto& dst, const auto& src, const auto& face_range) {
(this->assemble_diagonal_face_term_velocity)(data, dst, src, face_range);
},
[&](const auto& data, auto& dst, const auto& src, const auto& boundary_range) {
(this->assemble_diagonal_boundary_term_velocity)(data, dst, src, boundary_range);
},
0);
}
else if(NS_stage == 2) {
::MatrixFreeTools::compute_diagonal<dim, Number, VectorizedArray<Number>>
(*(this->data),
inverse_diagonal,
[&](const auto& data, auto& dst, const auto& src, const auto& cell_range) {
(this->assemble_diagonal_cell_term_pressure)(data, dst, src, cell_range);
},
[&](const auto& data, auto& dst, const auto& src, const auto& face_range) {
(this->assemble_diagonal_face_term_pressure)(data, dst, src, face_range);
},
[&](const auto& data, auto& dst, const auto& src, const auto& boundary_range) {
(this->assemble_diagonal_boundary_term_pressure)(data, dst, src, boundary_range);
},
1);
}
for(unsigned int i = 0; i < inverse_diagonal.locally_owned_size(); ++i) {
Assert(inverse_diagonal.local_element(i) != 0.0,
ExcMessage("No diagonal entry in a definite operator should be zero"));
inverse_diagonal.local_element(i) = 1.0/inverse_diagonal.local_element(i);
}
}
@sect{The NavierStokesProjection class}
Now we are ready for the main class of the program. It implements the calls to the various steps of the projection method for Navier-Stokes equations.
template<int dim>
class NavierStokesProjection {
public:
NavierStokesProjection(RunTimeParameters::Data_Storage& data);
void run(const bool verbose = false, const unsigned int output_interval = 10);
protected:
const double t_0;
const double T;
const double gamma;
unsigned int TR_BDF2_stage;
const double Re;
double dt;
EquationData::Velocity<dim> vel_init;
EquationData::Pressure<dim> pres_init;
double,
double,
<< " The time step " << arg1 << " is out of range."
<< std::endl
<< " The permitted range is (0," << arg2 << "]");
void create_triangulation(const unsigned int n_refines);
void setup_dofs();
void initialize();
void interpolate_velocity();
void diffusion_step();
void projection_step();
void project_grad(const unsigned int flag);
double get_maximal_velocity();
double get_maximal_difference_velocity();
void output_results(const unsigned int step);
void refine_mesh();
void interpolate_max_res(
const unsigned int level);
void save_max_res();
private:
void compute_lift_and_drag();
std::shared_ptr<MatrixFree<dim, double>> matrix_free_storage;
NavierStokesProjectionOperator<dim, EquationData::degree_p, EquationData::degree_p + 1,
EquationData::degree_p + 1, EquationData::degree_p + 2,
MGLevelObject<NavierStokesProjectionOperator<dim, EquationData::degree_p, EquationData::degree_p + 1,
EquationData::degree_p + 1, EquationData::degree_p + 2,
constraints_pressure;
unsigned int max_its;
double eps;
unsigned int max_loc_refinements;
unsigned int min_loc_refinements;
unsigned int refinement_iterations;
std::string saving_dir;
std::ofstream time_out;
std::ofstream output_n_dofs_velocity;
std::ofstream output_n_dofs_pressure;
std::ofstream output_lift;
std::ofstream output_drag;
};
#define DeclException2(Exception2, type1, type2, outsequence)
const ::parallel::distributed::Triangulation< dim, spacedim > * triangulation
In the constructor, we just read all the data from the Data_Storage object that is passed as an argument, verify that the data we read are reasonable and, finally, create the triangulation and load the initial data.
template<int dim>
NavierStokesProjection<dim>::NavierStokesProjection(RunTimeParameters::Data_Storage& data):
t_0(data.initial_time),
T(data.final_time),
gamma(2.0 -
std::sqrt(2.0)),
TR_BDF2_stage(1),
Re(data.Reynolds),
dt(data.dt),
vel_init(data.initial_time),
pres_init(data.initial_time),
fe_velocity(
FE_DGQ<dim>(EquationData::degree_p + 1), dim),
fe_pressure(
FE_DGQ<dim>(EquationData::degree_p), 1),
quadrature_pressure(EquationData::degree_p + 1),
quadrature_velocity(EquationData::degree_p + 2),
navier_stokes_matrix(data),
max_its(data.max_iterations),
eps(data.eps),
max_loc_refinements(data.max_loc_refinements),
min_loc_refinements(data.min_loc_refinements),
refinement_iterations(data.refinement_iterations),
saving_dir(data.dir),
pcout(
std::cout,
Utilities::MPI::this_mpi_process(MPI_COMM_WORLD) == 0),
time_out("./" + data.dir + "/time_analysis_" +
ptime_out(time_out,
Utilities::MPI::this_mpi_process(MPI_COMM_WORLD) == 0),
output_n_dofs_velocity(
"./" + data.dir +
"/n_dofs_velocity.dat",
std::ofstream::out),
output_n_dofs_pressure(
"./" + data.dir +
"/n_dofs_pressure.dat",
std::ofstream::out),
output_lift(
"./" + data.dir +
"/lift.dat",
std::ofstream::out),
output_drag(
"./" + data.dir +
"/drag.dat",
std::ofstream::out) {
if(EquationData::degree_p < 1) {
pcout
<< " WARNING: The chosen pair of finite element spaces is not stable."
<< std::endl
<< " The obtained results will be nonsense" << std::endl;
}
AssertThrow(!((dt <= 0.0) || (dt > 0.5*T)), ExcInvalidTimeStep(dt, 0.5*T));
matrix_free_storage = std::make_shared<MatrixFree<dim, double>>();
create_triangulation(data.n_refines);
setup_dofs();
initialize();
}
#define AssertThrow(cond, exc)
The method that creates the triangulation and refines it the needed number of times.
template<int dim>
void NavierStokesProjection<dim>::create_triangulation(const unsigned int n_refines) {
GridGenerator::plate_with_a_hole(
triangulation, 0.5, 1.0, 1.0, 1.1, 1.0, 19.0,
Point<2>(2.0, 2.0), 0, 1, 1.0, 2,
true);
pcout << "Number of refines = " << n_refines << std::endl;
}
void plate_with_a_hole(Triangulation< dim > &tria, const double inner_radius=0.4, const double outer_radius=1., const double pad_bottom=2., const double pad_top=2., const double pad_left=1., const double pad_right=1., const Point< dim > ¢er=Point< dim >(), const types::manifold_id polar_manifold_id=0, const types::manifold_id tfi_manifold_id=1, const double L=1., const unsigned int n_slices=2, const bool colorize=false)
Rectangular plate with an (offset) cylindrical hole.
After creating the triangulation, it creates the mesh dependent data, i.e. it distributes degrees of freedom, and initializes the vectors that we will use.
template<int dim>
void NavierStokesProjection<dim>::setup_dofs() {
pcout <<
"Number of active cells: " <<
triangulation.n_global_active_cells() << std::endl;
pcout <<
"Number of levels: " <<
triangulation.n_global_levels() << std::endl;
dof_handler_velocity.distribute_dofs(fe_velocity);
dof_handler_pressure.distribute_dofs(fe_pressure);
pcout << "dim (X_h) = " << dof_handler_velocity.n_dofs()
<< std::endl
<< "dim (M_h) = " << dof_handler_pressure.n_dofs()
<< std::endl
<< "Re = " << Re << std::endl
<< std::endl;
output_n_dofs_velocity << dof_handler_velocity.n_dofs() << std::endl;
output_n_dofs_pressure << dof_handler_pressure.n_dofs() << std::endl;
}
std::vector<const DoFHandler<dim>*> dof_handlers;
dof_handlers.push_back(&dof_handler_velocity);
dof_handlers.push_back(&dof_handler_pressure);
constraints_velocity.
clear();
constraints_velocity.close();
constraints_pressure.clear();
constraints_pressure.close();
std::vector<const AffineConstraints<double>*> constraints;
constraints.push_back(&constraints_velocity);
constraints.push_back(&constraints_pressure);
std::vector<QGauss<1>> quadratures;
quadratures.push_back(
QGauss<1>(EquationData::degree_p + 2));
quadratures.push_back(
QGauss<1>(EquationData::degree_p + 1));
matrix_free_storage->reinit(
MappingQ1<dim>(),dof_handlers, constraints, quadratures, additional_data);
matrix_free_storage->initialize_dof_vector(u_star, 0);
matrix_free_storage->initialize_dof_vector(rhs_u, 0);
matrix_free_storage->initialize_dof_vector(u_n, 0);
matrix_free_storage->initialize_dof_vector(u_extr, 0);
matrix_free_storage->initialize_dof_vector(u_n_minus_1, 0);
matrix_free_storage->initialize_dof_vector(u_n_gamma, 0);
matrix_free_storage->initialize_dof_vector(u_tmp, 0);
matrix_free_storage->initialize_dof_vector(grad_pres_int, 0);
matrix_free_storage->initialize_dof_vector(pres_int, 1);
matrix_free_storage->initialize_dof_vector(pres_n, 1);
matrix_free_storage->initialize_dof_vector(rhs_p, 1);
mg_matrices.clear_elements();
dof_handler_velocity.distribute_mg_dofs();
dof_handler_pressure.distribute_mg_dofs();
mg_matrices.resize(0, nlevels - 1);
std::vector<const DoFHandler<dim>*> dof_handlers_mg;
dof_handlers_mg.push_back(&dof_handler_velocity);
dof_handlers_mg.push_back(&dof_handler_pressure);
std::vector<const AffineConstraints<float>*> constraints_mg;
constraints_velocity_mg.
clear();
constraints_velocity_mg.
close();
constraints_mg.push_back(&constraints_velocity_mg);
constraints_pressure_mg.
clear();
constraints_pressure_mg.
close();
constraints_mg.push_back(&constraints_pressure_mg);
mg_mf_storage_level->reinit(
MappingQ1<dim>(),dof_handlers_mg, constraints_mg, quadratures, additional_data_mg);
const std::vector<unsigned int> tmp = {1};
mg_matrices[
level].initialize(mg_mf_storage_level, tmp, tmp);
mg_matrices[
level].set_dt(dt);
mg_matrices[
level].set_NS_stage(2);
}
Linfty_error_per_cell_vel.reinit(
triangulation.n_active_cells());
}
@ update_values
Shape function values.
@ update_normal_vectors
Normal vectors.
@ update_JxW_values
Transformed quadrature weights.
@ update_quadrature_points
Transformed quadrature points.
unsigned int this_mpi_process(const MPI_Comm &mpi_communicator)
TasksParallelScheme tasks_parallel_scheme
UpdateFlags mapping_update_flags_inner_faces
UpdateFlags mapping_update_flags_boundary_faces
UpdateFlags mapping_update_flags
This method loads the initial data. It simply uses the class Pressure instance for the pressure and the class Velocity instance for the velocity.
template<int dim>
void NavierStokesProjection<dim>::initialize() {
}
This function computes the extrapolated velocity to be used in the momentum predictor
template<int dim>
void NavierStokesProjection<dim>::interpolate_velocity() {
— TR-BDF2 first step
if(TR_BDF2_stage == 1) {
u_extr.equ(1.0 + gamma/(2.0*(1.0 - gamma)), u_n);
u_tmp.equ(gamma/(2.0*(1.0 - gamma)), u_n_minus_1);
u_extr -= u_tmp;
}
— TR-BDF2 second step
else {
u_extr.equ(1.0 + (1.0 - gamma)/gamma, u_n_gamma);
u_tmp.equ((1.0 - gamma)/gamma, u_n);
u_extr -= u_tmp;
}
}
We are finally ready to solve the diffusion step.
template<int dim>
void NavierStokesProjection<dim>::diffusion_step() {
const std::vector<unsigned int> tmp = {0};
navier_stokes_matrix.initialize(matrix_free_storage, tmp, tmp);
navier_stokes_matrix.set_NS_stage(1);
if(TR_BDF2_stage == 1) {
navier_stokes_matrix.vmult_rhs_velocity(rhs_u, {u_n, u_extr, pres_n});
navier_stokes_matrix.set_u_extr(u_extr);
u_star = u_extr;
}
else {
navier_stokes_matrix.vmult_rhs_velocity(rhs_u, {u_n, u_n_gamma, pres_int, u_extr});
navier_stokes_matrix.set_u_extr(u_extr);
u_star = u_extr;
}
EquationData::degree_p,
EquationData::degree_p + 1,
EquationData::degree_p + 1,
EquationData::degree_p + 2,
navier_stokes_matrix.compute_diagonal();
preconditioner.initialize(navier_stokes_matrix);
gmres.solve(navier_stokes_matrix, u_star, rhs_u, preconditioner);
}
Next, we solve the projection step.
template<int dim>
void NavierStokesProjection<dim>::projection_step() {
const std::vector<unsigned int> tmp = {1};
navier_stokes_matrix.initialize(matrix_free_storage, tmp, tmp);
navier_stokes_matrix.set_NS_stage(2);
if(TR_BDF2_stage == 1)
navier_stokes_matrix.vmult_rhs_pressure(rhs_p, {u_star, pres_n});
else
navier_stokes_matrix.vmult_rhs_pressure(rhs_p, {u_star, pres_int});
mg_transfer.
build(dof_handler_pressure);
EquationData::degree_p,
EquationData::degree_p + 1,
EquationData::degree_p + 1,
EquationData::degree_p + 2,
smoother_data[
level].smoothing_range = 15.0;
smoother_data[
level].degree = 3;
smoother_data[
level].eig_cg_n_iterations = 10;
}
else {
smoother_data[0].smoothing_range = 2
e-2;
smoother_data[0].eig_cg_n_iterations = mg_matrices[0].m();
}
mg_matrices[
level].compute_diagonal();
smoother_data[
level].preconditioner = mg_matrices[
level].get_matrix_diagonal_inverse();
}
mg_smoother.
initialize(mg_matrices, smoother_data);
NavierStokesProjectionOperator<dim,
EquationData::degree_p,
EquationData::degree_p + 1,
EquationData::degree_p + 1,
EquationData::degree_p + 2,
if(TR_BDF2_stage == 1) {
pres_int = pres_n;
cg.solve(navier_stokes_matrix, pres_int, rhs_p, preconditioner);
}
else {
pres_n = pres_int;
cg.solve(navier_stokes_matrix, pres_n, rhs_p, preconditioner);
}
}
void resize(const unsigned int new_minlevel, const unsigned int new_maxlevel, Args &&...args)
void build(const DoFHandler< dim, dim > &dof_handler, const std::vector< std::shared_ptr< const Utilities::MPI::Partitioner > > &external_partitioners=std::vector< std::shared_ptr< const Utilities::MPI::Partitioner > >())
void initialize(const MGLevelObject< MatrixType2 > &matrices, const typename RelaxationType::AdditionalData &additional_data=typename RelaxationType::AdditionalData())
SymmetricTensor< 2, dim, Number > e(const Tensor< 2, dim, Number > &F)
static const unsigned int invalid_unsigned_int
This implements the projection step for the gradient of pressure
template<int dim>
void NavierStokesProjection<dim>::project_grad(const unsigned int flag) {
Assert(flag > 0, ExcInternalError());
const std::vector<unsigned int> tmp = {0};
navier_stokes_matrix.initialize(matrix_free_storage, tmp, tmp);
if(flag == 1)
navier_stokes_matrix.vmult_grad_p_projection(rhs_u, pres_n);
else if(flag == 2)
navier_stokes_matrix.vmult_grad_p_projection(rhs_u, pres_int);
navier_stokes_matrix.set_NS_stage(3);
}
The following function is used in determining the maximal velocity in order to compute the Courant number.
template<int dim>
double NavierStokesProjection<dim>::get_maximal_velocity() {
return u_n.linfty_norm();
}
The following function is used in determining the maximal nodal difference between old and current velocity value in order to see if we have reched steady-state.
template<int dim>
double NavierStokesProjection<dim>::get_maximal_difference_velocity() {
u_tmp = u_n;
u_tmp -= u_n_minus_1;
return u_tmp.linfty_norm();
}
This method plots the current solution. The main difficulty is that we want to create a single output file that contains the data for all velocity components and the pressure. On the other hand, velocities and the pressure live on separate DoFHandler objects, so we need to pay attention when we use 'add_data_vector' to select the proper space.
template<int dim>
void NavierStokesProjection<dim>::output_results(const unsigned int step) {
std::vector<std::string> velocity_names(dim, "v");
std::vector<DataComponentInterpretation::DataComponentInterpretation>
u_n.update_ghost_values();
data_out.
add_data_vector(dof_handler_velocity, u_n, velocity_names, component_interpretation_velocity);
pres_n.update_ghost_values();
std::vector<std::string> velocity_names_old(dim, "v_old");
u_n_minus_1.update_ghost_values();
data_out.
add_data_vector(dof_handler_velocity, u_n_minus_1, velocity_names_old, component_interpretation_velocity);
PostprocessorVorticity<dim> postprocessor;
}
void add_data_vector(const VectorType &data, const std::vector< std::string > &names, const DataVectorType type=type_automatic, const std::vector< DataComponentInterpretation::DataComponentInterpretation > &data_component_interpretation={})
virtual void build_patches(const unsigned int n_subdivisions=0)
void write_vtu_in_parallel(const std::string &filename, const MPI_Comm &comm) const
std::string int_to_string(const unsigned int value, const unsigned int digits=numbers::invalid_unsigned_int)
@sect{NavierStokesProjection::compute_lift_and_drag}
This routine computes the lift and the drag forces in a non-dimensional framework (so basically for the classical coefficients, it is necessary to multiply by a factor 2).
template<int dim>
void NavierStokesProjection<dim>::compute_lift_and_drag() {
QGauss<dim - 1> face_quadrature_formula(EquationData::degree_p + 2);
const int n_q_points = face_quadrature_formula.size();
std::vector<double> pressure_values(n_q_points);
std::vector<std::vector<Tensor<1, dim>>> velocity_gradients(n_q_points, std::vector<
Tensor<1, dim>>(dim));
double local_drag = 0.0;
double local_lift = 0.0;
auto tmp_cell = dof_handler_pressure.begin_active();
for(const auto& cell : dof_handler_velocity.active_cell_iterators()) {
if(cell->is_locally_owned()) {
for(unsigned int face = 0; face < GeometryInfo<dim>::faces_per_cell; ++face) {
if(cell->face(face)->at_boundary() && cell->face(face)->boundary_id() == 4) {
fe_face_values_velocity.reinit(cell, face);
fe_face_values_pressure.reinit(tmp_cell, face);
fe_face_values_velocity.get_function_gradients(u_n, velocity_gradients);
fe_face_values_pressure.get_function_values(pres_n, pressure_values);
for(int q = 0; q < n_q_points; q++) {
normal_vector = -fe_face_values_velocity.normal_vector(q);
for(unsigned int d = 0; d < dim; ++ d) {
fluid_pressure[d][d] = pressure_values[q];
for(unsigned int k = 0; k < dim; ++k)
fluid_stress[d][k] = 1.0/Re*velocity_gradients[q][d][k];
}
fluid_stress = fluid_stress - fluid_pressure;
forces = fluid_stress*normal_vector*fe_face_values_velocity.JxW(q);
local_drag += forces[0];
local_lift += forces[1];
}
}
}
}
++tmp_cell;
}
output_lift << lift << std::endl;
output_drag << drag << std::endl;
}
}
T sum(const T &t, const MPI_Comm &mpi_communicator)
@sect{ NavierStokesProjection::refine_mesh}
After finding a good initial guess on the coarse mesh, we hope to decrease the error through refining the mesh. We also need to transfer the current solution to the next mesh using the SolutionTransfer class.
template <int dim>
void NavierStokesProjection<dim>::refine_mesh() {
tmp_velocity.
reinit(dof_handler_velocity.locally_owned_dofs(), locally_relevant_dofs, MPI_COMM_WORLD);
tmp_velocity = u_n;
const auto cell_worker = [&](const Iterator& cell,
ScratchData<dim>& scratch_data,
CopyData& copy_data) {
copy_data.cell_index = cell->active_cell_index();
double vorticity_norm_square = 0.0;
const double vorticity = gradients[k][1][0] - gradients[k][0][1];
vorticity_norm_square += vorticity*vorticity*fe_values.
JxW(k);
}
copy_data.value = cell->diameter()*cell->diameter()*vorticity_norm_square;
};
const auto copier = [&](const CopyData ©_data) {
estimated_error_per_cell[copy_data.cell_index] += copy_data.value;
};
ScratchData<dim> scratch_data(fe_velocity, EquationData::degree_p + 2, cell_flags);
CopyData copy_data;
dof_handler_velocity.end(),
cell_worker,
copier,
scratch_data,
copy_data,
if(cell->refine_flag_set() && static_cast<unsigned int>(cell->level()) == max_loc_refinements)
cell->clear_refine_flag();
if(cell->coarsen_flag_set() && static_cast<unsigned int>(cell->level()) == min_loc_refinements)
cell->clear_coarsen_flag();
}
std::vector<const LinearAlgebra::distributed::Vector<double>*> velocities;
velocities.push_back(&u_n);
velocities.push_back(&u_n_minus_1);
solution_transfer_velocity(dof_handler_velocity);
solution_transfer_velocity.prepare_for_coarsening_and_refinement(velocities);
solution_transfer_pressure(dof_handler_pressure);
solution_transfer_pressure.prepare_for_coarsening_and_refinement(pres_n);
setup_dofs();
transfer_velocity_minus_1,
transfer_pressure;
transfer_velocity.
reinit(u_n);
transfer_velocity_minus_1.
reinit(u_n_minus_1);
transfer_pressure.
reinit(pres_n);
std::vector<LinearAlgebra::distributed::Vector<double>*> transfer_velocities;
transfer_velocities.push_back(&transfer_velocity);
transfer_velocities.push_back(&transfer_velocity_minus_1);
solution_transfer_velocity.interpolate(transfer_velocities);
solution_transfer_pressure.interpolate(transfer_pressure);
u_n = transfer_velocity;
u_n_minus_1 = transfer_velocity_minus_1;
pres_n = transfer_pressure;
}
const unsigned int n_quadrature_points
void get_function_gradients(const InputVector &fe_function, std::vector< Tensor< 1, spacedim, typename InputVector::value_type > > &gradients) const
double JxW(const unsigned int quadrature_point) const
void reinit(const TriaIterator< DoFCellAccessor< dim, spacedim, level_dof_access > > &cell)
typename ActiveSelector::active_cell_iterator active_cell_iterator
void mesh_loop(const CellIteratorType &begin, const CellIteratorType &end, const CellWorkerFunctionType &cell_worker, const CopierType &copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const AssembleFlags flags=assemble_own_cells, const BoundaryWorkerFunctionType &boundary_worker=BoundaryWorkerFunctionType(), const FaceWorkerFunctionType &face_worker=FaceWorkerFunctionType(), const unsigned int queue_length=2 *MultithreadInfo::n_threads(), const unsigned int chunk_size=8)
void zero_out_ghost_values() const
void update_ghost_values() const
void reinit(const size_type size, const bool omit_zeroing_entries=false)
void refine_and_coarsen_fixed_number(parallel::distributed::Triangulation< dim, spacedim > &tria, const ::Vector< Number > &criteria, const double top_fraction_of_cells, const double bottom_fraction_of_cells, const types::global_cell_index max_n_cells=std::numeric_limits< types::global_cell_index >::max())
Interpolate the locally refined solution to a mesh with maximal resolution and transfer velocity and pressure.
template<int dim>
void NavierStokesProjection<dim>::interpolate_max_res(
const unsigned int level) {
solution_transfer_velocity(dof_handler_velocity);
std::vector<const LinearAlgebra::distributed::Vector<double>*> velocities;
velocities.push_back(&u_n);
velocities.push_back(&u_n_minus_1);
solution_transfer_velocity.prepare_for_coarsening_and_refinement(velocities);
solution_transfer_pressure(dof_handler_pressure);
solution_transfer_pressure.prepare_for_coarsening_and_refinement(pres_n);
if(cell->is_locally_owned())
cell->set_refine_flag();
}
setup_dofs();
transfer_pressure;
transfer_velocity.
reinit(u_n);
transfer_velocity_minus_1.
reinit(u_n_minus_1);
transfer_pressure.
reinit(pres_n);
std::vector<LinearAlgebra::distributed::Vector<double>*> transfer_velocities;
transfer_velocities.push_back(&transfer_velocity);
transfer_velocities.push_back(&transfer_velocity_minus_1);
solution_transfer_velocity.interpolate(transfer_velocities);
solution_transfer_pressure.interpolate(transfer_pressure);
u_n = transfer_velocity;
u_n_minus_1 = transfer_velocity_minus_1;
pres_n = transfer_pressure;
}
Save maximum resolution to a mesh adapted.
template<int dim>
void NavierStokesProjection<dim>::save_max_res() {
GridGenerator::plate_with_a_hole(triangulation_tmp, 0.5, 1.0, 1.0, 1.1, 1.0, 19.0,
Point<2>(2.0, 2.0), 0, 1, 1.0, 2,
true);
triangulation_tmp.refine_global(
triangulation.n_global_levels() - 1);
dof_handler_velocity_tmp.distribute_dofs(fe_velocity);
dof_handler_pressure_tmp.distribute_dofs(fe_pressure);
pres_n_tmp;
u_n_tmp.
reinit(dof_handler_velocity_tmp.n_dofs());
pres_n_tmp.
reinit(dof_handler_pressure_tmp.n_dofs());
std::vector<std::string> velocity_names(dim, "v");
std::vector<DataComponentInterpretation::DataComponentInterpretation>
data_out.
add_data_vector(dof_handler_velocity_tmp, u_n_tmp, velocity_names, component_interpretation_velocity);
PostprocessorVorticity<dim> postprocessor;
data_out.
add_data_vector(dof_handler_velocity_tmp, u_n_tmp, postprocessor);
const std::string output = "./" + saving_dir + "/solution_max_res_end.vtu";
}
@sect{ NavierStokesProjection::run }
This is the time marching function, which starting at t_0 advances in time using the projection method with time step dt until T.
Its second parameter, verbose indicates whether the function should output information what it is doing at any given moment: we use the ConditionalOStream class to do that for us.
template<int dim>
void NavierStokesProjection<dim>::run(const bool verbose, const unsigned int output_interval) {
output_results(1);
double time = t_0 + dt;
unsigned int n = 1;
time += dt;
n++;
pcout << "Step = " << n << " Time = " << time << std::endl;
TR_BDF2_stage = 1;
navier_stokes_matrix.set_TR_BDF2_stage(TR_BDF2_stage);
mg_matrices[
level].set_TR_BDF2_stage(TR_BDF2_stage);
verbose_cout << " Interpolating the velocity stage 1" << std::endl;
interpolate_velocity();
verbose_cout << " Diffusion Step stage 1 " << std::endl;
diffusion_step();
verbose_cout << " Projection Step stage 1" << std::endl;
project_grad(1);
u_tmp.equ(gamma*dt, u_tmp);
u_star += u_tmp;
projection_step();
verbose_cout << " Updating the Velocity stage 1" << std::endl;
u_n_gamma.equ(1.0, u_star);
project_grad(2);
grad_pres_int.equ(1.0, u_tmp);
u_tmp.equ(-gamma*dt, u_tmp);
u_n_gamma += u_tmp;
u_n_minus_1 = u_n;
TR_BDF2_stage = 2;
mg_matrices[
level].set_TR_BDF2_stage(TR_BDF2_stage);
navier_stokes_matrix.set_TR_BDF2_stage(TR_BDF2_stage);
verbose_cout << " Interpolating the velocity stage 2" << std::endl;
interpolate_velocity();
verbose_cout << " Diffusion Step stage 2 " << std::endl;
diffusion_step();
verbose_cout << " Projection Step stage 2" << std::endl;
u_tmp.equ((1.0 - gamma)*dt, grad_pres_int);
u_star += u_tmp;
projection_step();
verbose_cout << " Updating the Velocity stage 2" << std::endl;
u_n.equ(1.0, u_star);
project_grad(1);
u_tmp.equ((gamma - 1.0)*dt, u_tmp);
u_n += u_tmp;
const double max_vel = get_maximal_velocity();
pcout<< "Maximal velocity = " << max_vel << std::endl;
pcout << "CFL = " << dt*max_vel*(EquationData::degree_p + 1)*
compute_lift_and_drag();
if(n % output_interval == 0) {
verbose_cout << "Plotting Solution final" << std::endl;
output_results(n);
}
if(T - time < dt && T - time > 1e-10) {
dt = T - time;
navier_stokes_matrix.set_dt(dt);
mg_matrices[
level].set_dt(dt);
}
if(refinement_iterations > 0 && n % refinement_iterations == 0) {
verbose_cout << "Refining mesh" << std::endl;
refine_mesh();
}
}
if(n % output_interval != 0) {
verbose_cout << "Plotting Solution final" << std::endl;
output_results(n);
}
if(refinement_iterations > 0) {
for(
unsigned int lev = 0; lev <
triangulation.n_global_levels() - 1; ++ lev)
interpolate_max_res(lev);
save_max_res();
}
}
}
::VectorizedArray< Number, width > sqrt(const ::VectorizedArray< Number, width > &)
@sect{ The main function }
The main function looks very much like in all the other tutorial programs. We first initialize MPI, we initialize the class 'NavierStokesProjection' with the dimension as template parameter and then let the method 'run' do the job.
int main(int argc, char *argv[]) {
try {
using namespace NS_TRBDF2;
RunTimeParameters::Data_Storage data;
data.read_data("parameter-file.prm");
NavierStokesProjection<2> test(data);
test.run(data.verbose, data.output_interval);
if(curr_rank == 0)
std::cout << "----------------------------------------------------"
<< std::endl
<< "Apparently everything went fine!" << std::endl
<< "Don't forget to brush your teeth :-)" << std::endl
<< std::endl;
return 0;
}
catch(std::exception &exc) {
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch(...) {
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
}
unsigned int depth_console(const unsigned int n)
Annotated version of runtime_parameters.h
We start by including all the necessary deal.II header files
@sect{Run time parameters}
Since our method has several parameters that can be fine-tuned we put them into an external file, so that they can be determined at run-time.
namespace RunTimeParameters {
class Data_Storage {
public:
Data_Storage();
void read_data(const std::string& filename);
double initial_time;
double final_time;
double Reynolds;
double dt;
unsigned int n_refines;
unsigned int max_loc_refinements;
unsigned int min_loc_refinements;
unsigned int max_iterations;
double eps;
bool verbose;
unsigned int output_interval;
std::string dir;
unsigned int refinement_iterations;
protected:
};
In the constructor of this class we declare all the parameters in suitable (but arbitrary) subsections.
Data_Storage::Data_Storage(): initial_time(0.0),
final_time(1.0),
Reynolds(1.0),
dt(5e-4),
n_refines(0),
max_loc_refinements(0),
min_loc_refinements(0),
max_iterations(1000),
eps(1e-12),
verbose(true),
output_interval(15),
refinement_iterations(0) {
prm.enter_subsection("Physical data");
{
prm.declare_entry("initial_time",
"0.0",
" The initial time of the simulation. ");
prm.declare_entry("final_time",
"1.0",
" The final time of the simulation. ");
prm.declare_entry("Reynolds",
"1.0",
" The Reynolds number. ");
}
prm.leave_subsection();
prm.enter_subsection("Time step data");
{
prm.declare_entry("dt",
"5e-4",
" The time step size. ");
}
prm.leave_subsection();
prm.enter_subsection("Space discretization");
{
prm.declare_entry("n_of_refines",
"100",
" The number of cells we want on each direction of the mesh. ");
prm.declare_entry("max_loc_refinements",
"4",
" The number of maximum local refinements. ");
prm.declare_entry("min_loc_refinements",
"2",
" The number of minimum local refinements. ");
}
prm.leave_subsection();
prm.enter_subsection("Data solve");
{
prm.declare_entry("max_iterations",
"1000",
" The maximal number of iterations linear solvers must make. ");
prm.declare_entry("eps",
"1e-12",
" The stopping criterion. ");
}
prm.leave_subsection();
prm.declare_entry("refinement_iterations",
"0",
" This number indicates how often we need to "
"refine the mesh");
prm.declare_entry("saving directory", "SimTest");
prm.declare_entry("verbose",
"true",
" This indicates whether the output of the solution "
"process should be verbose. ");
prm.declare_entry("output_interval",
"1",
" This indicates between how many time steps we print "
"the solution. ");
}
We need now a routine to read all declared parameters in the constructor
void Data_Storage::read_data(const std::string& filename) {
std::ifstream file(filename);
prm.parse_input(file);
prm.enter_subsection("Physical data");
{
initial_time = prm.get_double("initial_time");
final_time = prm.get_double("final_time");
Reynolds = prm.get_double("Reynolds");
}
prm.leave_subsection();
prm.enter_subsection("Time step data");
{
dt = prm.get_double("dt");
}
prm.leave_subsection();
prm.enter_subsection("Space discretization");
{
n_refines = prm.get_integer("n_of_refines");
max_loc_refinements = prm.get_integer("max_loc_refinements");
min_loc_refinements = prm.get_integer("min_loc_refinements");
}
prm.leave_subsection();
prm.enter_subsection("Data solve");
{
max_iterations = prm.get_integer("max_iterations");
eps = prm.get_double(
"eps");
}
prm.leave_subsection();
dir = prm.get("saving directory");
refinement_iterations = prm.get_integer("refinement_iterations");
verbose = prm.get_bool("verbose");
output_interval = prm.get_integer("output_interval");
}
}









