This tutorial depends on step-12.
This program was contributed by Timo Heister and Jiaqi Zhang.
This material is based upon work partly supported by the National Science Foundation Award DMS-2028346, OAC-2015848, EAR-1925575, by the Computational Infrastructure in Geodynamics initiative (CIG), through the NSF under Award EAR-0949446 and EAR-1550901 and The University of California – Davis.
Symmetric interior penalty Galerkin (SIPG) method for Poisson's equation
Overview
In this tutorial, we display the usage of the FEInterfaceValues class, which is designed for assembling face terms arising from discontinuous Galerkin (DG) methods. The FEInterfaceValues class provides an easy way to obtain the jump and the average of shape functions and of the solution across cell faces. This tutorial includes the following topics.
-
The SIPG method for Poisson's equation, which has already been used in step-39 and step-59.
-
Assembling of face terms using FEInterfaceValues and the system matrix using MeshWorker::mesh_loop(), which is similar to step-12.
-
Adaptive mesh refinement using an error estimator.
-
Two test cases: convergence test for a smooth function and adaptive mesh refinement test for a singular solution.
The equation
In this example, we consider Poisson's equation
\[
- \nabla \cdot \left( \nu \nabla u\right) = f \qquad \mbox{in } \Omega,
\]
subject to the boundary condition
\[
u = g_D \qquad \mbox{on } \partial \Omega.
\]
For simplicity, we assume that the diffusion coefficient \(\nu\) is constant here. Note that if \(\nu\) is discontinuous, we need to take this into account when computing jump terms on cell faces.
We denote the mesh by \({\mathbb T}_h\), and \(K\in{\mathbb T}_h\) is a mesh cell. The sets of interior and boundary faces are denoted by \({\mathbb F}^i_h\) and \({\mathbb F}^b_h\) respectively. Let \(K^0\) and \(K^1\) be the two cells sharing a face \(f\in F_h^i\), and \(\mathbf n\) be the outer normal vector of \(K^0\). Then the jump operator is given by the "here minus there" formula,
\[
\jump{v} = v^0 - v^1
\]
and the averaging operator as
\[
\average{v} = \frac{v^0 + v^1}{2}
\]
respectively. Note that when \(f\subset \partial \Omega\), we define \(\jump{v} = v\) and \(\average{v}=v\). The discretization using the SIPG is given by the following weak formula (more details can be found in [37] and the references therein)
\begin{align*}
&\sum_{K\in {\mathbb T}_h} (\nabla v_h, \nu \nabla u_h)_K\\
&-\sum_{F \in F_h^i} \left\{
\left< \jump{v_h}, \nu\average{ \nabla u_h} \cdot \mathbf n \right>_F
+\left<\average{ \nabla v_h }\cdot \mathbf n,\nu\jump{u_h}\right>_F
-\left<\jump{v_h},\nu \sigma \jump{u_h} \right>_F
\right\}\\
&-\sum_{F \in F_h^b} \left\{
\left<v_h, \nu \nabla u_h\cdot \mathbf n \right>_F
+ \left< \nabla v_h \cdot \mathbf n , \nu u_h\right>_F
- \left< v_h,\nu \sigma u_h\right>_F
\right\}\\
&=(v_h, f)_\Omega
- \sum_{F \in F_h^b} \left\{
\left< \nabla v_h \cdot \mathbf n, \nu g_D\right>_F - \left<v_h,\nu \sigma g_D\right>_F
\right\}.
\end{align*}
The penalty parameter
The penalty parameter is defined as \(\sigma = \gamma/h_f\), where \(h_f\) a local length scale associated with the cell face; here we choose an approximation of the length of the cell in the direction normal to the face: \(\frac 1{h_f} = \frac 12 \left(\frac 1{h_K} + \frac 1{h_{K'}}\right)\), where \(K,K'\) are the two cells adjacent to the face \(f\) and we we compute \(h_K = \frac{|K|}{|f|}\).
In the formula above, \(\gamma\) is the penalization constant. To ensure the discrete coercivity, the penalization constant has to be large enough [3]. People do not really have consensus on which of the formulas proposed in the literature should be used. (This is similar to the situation discussed in the "Results" section of step-47.) One can just pick a large constant, while other options could be the multiples of \((p+1)^2\) or \(p(p+1)\). In this code, we follow step-39 and use \(\gamma = p(p+1)\).
A posteriori error estimator
In this example, with a slight modification, we use the error estimator by Karakashian and Pascal [73]
\[
\eta^2 = \sum_{K \in {\mathbb T}_h} \eta^2_{K} + \sum_{f_i \in {\mathbb F}^i_h} \eta^2_{f_i} + \sum_{f_b \in F^i_b}\eta^2_{f_b}
\]
where
\begin{align*}
\eta^2_{K} &= h_K^2 \left\| f + \nu \Delta u_h \right\|_K^2,
\\
\eta^2_{f_i} &= \sigma \left\| \jump{u_h} \right\|_f^2 + h_f \left\| \jump{\nu \nabla u_h} \cdot \mathbf n \right\|_f^2,
\\
\eta_{f_b}^2 &= \sigma \left\| u_h-g_D \right\|_f^2.
\end{align*}
Here we use \(\sigma = \gamma/h_f\) instead of \(\gamma^2/h_f\) for the jump terms of \(u_h\) (the first term in \(\eta^2_{f_i}\) and \(\eta_{f_b}^2\)).
In order to compute this estimator, in each cell \(K\) we compute
\begin{align*}
\eta_{c}^2 &= h_K^2 \left\| f + \nu \Delta u_h \right\|_K^2,
\\
\eta_{f}^2 &= \sum_{f\in \partial K}\lbrace \sigma \left\| \jump{u_h} \right\|_f^2 + h_f \left\| \jump{\nu \nabla u_h} \cdot \mathbf n \right\|_f^2 \rbrace,
\\
\eta_{b}^2 &= \sum_{f\in \partial K \cap \partial \Omega} \sigma \left\| (u_h -g_D) \right\|_f^2.
\end{align*}
Then the square of the error estimate per cell is
\[
\eta_\text{local}^2 =\eta_{c}^2+0.5\eta_{f}^2+\eta_{b}^2.
\]
The factor of \(0.5\) results from the fact that the overall error estimator includes each interior face only once, and so the estimators per cell count it with a factor of one half for each of the two adjacent cells. Note that we compute \(\eta_\text{local}^2\) instead of \(\eta_\text{local}\) to simplify the implementation. The error estimate square per cell is then stored in a global vector, whose \(l_1\) norm is equal to \(\eta^2\).
The test case
In the first test problem, we run a convergence test using a smooth manufactured solution with \(\nu =1\) in 2D
\begin{align*}
u&=\sin(2\pi x)\sin(2\pi y), &\qquad\qquad &(x,y)\in\Omega=(0,1)\times (0,1),
\\
u&=0, &\qquad\qquad &\text{on } \partial \Omega,
\end{align*}
and \(f= 8\pi^2 u\). We compute errors against the manufactured solution and evaluate the convergence rate.
In the second test, we choose Functions::LSingularityFunction on a L-shaped domain (GridGenerator::hyper_L) in 2D. The solution is given in the polar coordinates by \(u(r,\phi) = r^{\frac{2}{3}}\sin \left(\frac{2}{3}\phi \right)\), which has a singularity at the origin. An error estimator is constructed to detect the region with large errors, according to which the mesh is refined adaptively.
The commented program
The first few files have already been covered in previous examples and will thus not be further commented on:
Here the discontinuous finite elements and FEInterfaceValues are defined.
Equation data
Here we define two test cases: convergence_rate for a smooth function and l_singularity for the Functions::LSingularityFunction.
enum class TestCase
{
convergence_rate,
l_singularity
};
A smooth solution for the convergence test:
template <int dim>
class SmoothSolution :
public Function<dim>
{
public:
SmoothSolution()
{}
const unsigned int component = 0) const override;
const unsigned int component = 0) const override;
};
template <int dim>
void SmoothSolution<dim>::value_list(
const std::vector<
Point<dim>> &points,
const unsigned int ) const
{
for (
unsigned int i = 0; i <
values.size(); ++i)
}
template <int dim>
const unsigned int ) const
{
return_value[0] =
return_value[1] =
return return_value;
}
virtual Tensor< 1, dim, RangeNumberType > gradient(const Point< dim > &p, const unsigned int component=0) const
virtual void value_list(const std::vector< Point< dim > > &points, std::vector< RangeNumberType > &values, const unsigned int component=0) const
Point< spacedim > point(const gp_Pnt &p, const double tolerance=1e-10)
static constexpr double PI
::VectorizedArray< Number, width > cos(const ::VectorizedArray< Number, width > &)
::VectorizedArray< Number, width > sin(const ::VectorizedArray< Number, width > &)
The corresponding right-hand side of the smooth function:
template <int dim>
class SmoothRightHandSide :
public Function<dim>
{
public:
SmoothRightHandSide()
{}
const unsigned int ) const override;
};
template <int dim>
void
SmoothRightHandSide<dim>::value_list(
const std::vector<
Point<dim>> &points,
const unsigned int ) const
{
for (
unsigned int i = 0; i <
values.size(); ++i)
}
The right-hand side that corresponds to the function Functions::LSingularityFunction, where we assume that the diffusion coefficient \(\nu = 1\):
template <int dim>
class SingularRightHandSide :
public Function<dim>
{
public:
SingularRightHandSide()
{}
const unsigned int ) const override;
private:
};
template <int dim>
void
SingularRightHandSide<dim>::value_list(
const std::vector<
Point<dim>> &points,
const unsigned int ) const
{
for (
unsigned int i = 0; i <
values.size(); ++i)
values[i] = -ref.laplacian(points[i]);
}
Auxiliary functions
The following two auxiliary functions are used to compute jump terms for \(u_h\) and \(\nabla u_h\) on a face, respectively.
template <int dim>
std::vector<double> & jump)
{
std::array<std::vector<double>, 2> face_values;
jump.resize(n_q);
for (unsigned int i = 0; i < 2; ++i)
{
face_values[i].resize(n_q);
face_values[i]);
}
for (unsigned int q = 0; q < n_q; ++q)
jump[q] = face_values[0][q] - face_values[1][q];
}
template <int dim>
{
std::vector<Tensor<1, dim>> face_gradients[2];
gradient_jump.resize(n_q);
for (unsigned int i = 0; i < 2; ++i)
{
face_gradients[i].resize(n_q);
face_gradients[i]);
}
for (unsigned int q = 0; q < n_q; ++q)
gradient_jump[q] = face_gradients[0][q] - face_gradients[1][q];
}
const unsigned int n_quadrature_points
const FEFaceValuesBase< dim, spacedim > & get_fe_face_values(const unsigned int cell_index) const
void get_function_values(const InputVector &fe_function, std::vector< typename InputVector::value_type > &values) const
void get_function_gradients(const InputVector &fe_function, std::vector< Tensor< 1, spacedim, typename InputVector::value_type > > &gradients) const
This function computes the penalty \(\sigma\).
double get_penalty_factor(const unsigned int fe_degree,
const double cell_extent_left,
const double cell_extent_right)
{
const unsigned int degree =
std::max(1U, fe_degree);
return degree * (degree + 1.) * 0.5 *
(1. / cell_extent_left + 1. / cell_extent_right);
}
::VectorizedArray< Number, width > max(const ::VectorizedArray< Number, width > &, const ::VectorizedArray< Number, width > &)
The CopyData
In the following, we define "Copy" objects for the MeshWorker::mesh_loop(), which is essentially the same as step-12. Note that the "Scratch" object is not defined here because we use MeshWorker::ScratchData<dim> instead. (The use of "Copy" and "Scratch" objects is extensively explained in the WorkStream namespace documentation.
struct CopyDataFace
{
std::vector<types::global_dof_index> joint_dof_indices;
std::array<unsigned int, 2> cell_indices;
};
struct CopyData
{
std::vector<types::global_dof_index> local_dof_indices;
std::vector<CopyDataFace> face_data;
double value;
template <class Iterator>
void reinit(
const Iterator &cell,
const unsigned int dofs_per_cell)
{
cell_rhs.
reinit(dofs_per_cell);
local_dof_indices.resize(dofs_per_cell);
cell->get_dof_indices(local_dof_indices);
}
};
virtual void reinit(const size_type N, const bool omit_zeroing_entries=false)
void cell_matrix(FullMatrix< double > &M, const FEValuesBase< dim > &fe, const FEValuesBase< dim > &fetest, const ArrayView< const std::vector< double > > &velocity, const double factor=1.)
void reinit(MatrixBlock< MatrixType > &v, const BlockSparsityPattern &p)
The SIPGLaplace class
After these preparations, we proceed with the main class of this program, called SIPGLaplace. The overall structure of the class is as in many of the other tutorial programs. Major differences will only come up in the implementation of the assemble functions, since we use FEInterfaceValues to assemble face terms.
template <int dim>
class SIPGLaplace
{
public:
SIPGLaplace(const TestCase &test_case);
private:
void setup_system();
void assemble_system();
void solve();
void refine_grid();
void output_results(const unsigned int cycle) const;
void compute_errors();
void compute_error_estimate();
double compute_energy_norm_error();
const unsigned int degree;
const QGauss<dim - 1> face_quadrature;
const QGauss<dim - 1> face_quadrature_overintegration;
void run(const Iterator &begin, const typename identity< Iterator >::type &end, Worker worker, Copier copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const unsigned int queue_length, const unsigned int chunk_size)
const ::parallel::distributed::Triangulation< dim, spacedim > * triangulation
The remainder of the class's members are used for the following:
- Vectors to store error estimator square and energy norm square per cell.
- Print convergence rate and errors on the screen.
- The fiffusion coefficient \(\nu\) is set to 1.
- Members that store information about the test case to be computed.
const double diffusion_coefficient = 1.;
const TestCase test_case;
std::unique_ptr<const Function<dim>> exact_solution;
std::unique_ptr<const Function<dim>> rhs_function;
};
The constructor here takes the test case as input and then determines the correct solution and right-hand side classes. The remaining member variables are initialized in the obvious way.
template <int dim>
SIPGLaplace<dim>::SIPGLaplace(const TestCase &test_case)
: degree(3)
, quadrature(degree + 1)
, face_quadrature(degree + 1)
, quadrature_overintegration(degree + 2)
, face_quadrature_overintegration(degree + 2)
, mapping()
, fe(degree)
, test_case(test_case)
{
if (test_case == TestCase::convergence_rate)
{
exact_solution = std::make_unique<const SmoothSolution<dim>>();
rhs_function = std::make_unique<const SmoothRightHandSide<dim>>();
}
else if (test_case == TestCase::l_singularity)
{
exact_solution =
std::make_unique<const Functions::LSingularityFunction>();
rhs_function = std::make_unique<const SingularRightHandSide<dim>>();
}
else
}
template <int dim>
void SIPGLaplace<dim>::setup_system()
{
dof_handler.distribute_dofs(fe);
sparsity_pattern.copy_from(dsp);
system_matrix.reinit(sparsity_pattern);
solution.
reinit(dof_handler.n_dofs());
system_rhs.reinit(dof_handler.n_dofs());
}
static ::ExceptionBase & ExcNotImplemented()
#define AssertThrow(cond, exc)
void make_flux_sparsity_pattern(const DoFHandler< dim, spacedim > &dof_handler, SparsityPatternType &sparsity_pattern)
The assemble_system function
The assemble function here is similar to that in step-12 and step-47. Different from assembling by hand, we just need to focus on assembling on each cell, each boundary face, and each interior face. The loops over cells and faces are handled automatically by MeshWorker::mesh_loop().
The function starts by defining a local (lambda) function that is used to integrate the cell terms:
template <int dim>
void SIPGLaplace<dim>::assemble_system()
{
const auto cell_worker =
[&](const auto &cell, auto &scratch_data, auto ©_data) {
const unsigned int dofs_per_cell = fe_v.dofs_per_cell;
copy_data.reinit(cell, dofs_per_cell);
const auto & q_points = scratch_data.get_quadrature_points();
const unsigned int n_q_points = q_points.size();
const std::vector<double> &JxW = scratch_data.get_JxW_values();
std::vector<double> rhs(n_q_points);
rhs_function->value_list(q_points, rhs);
for (unsigned int i = 0; i < fe_v.dofs_per_cell; ++i)
{
for (unsigned int j = 0; j < fe_v.dofs_per_cell; ++j)
copy_data.cell_matrix(i, j) +=
diffusion_coefficient *
fe_v.shape_grad(i,
point) *
fe_v.shape_grad(j,
point) *
copy_data.cell_rhs(i) += fe_v.shape_value(i,
point) *
}
};
Next, we need a function that assembles face integrals on the boundary:
const auto boundary_worker = [&](const auto & cell,
const unsigned int &face_no,
auto & scratch_data,
auto & copy_data) {
const unsigned int n_q_points = q_points.size();
const std::vector<double> & JxW = scratch_data.get_JxW_values();
const std::vector<Tensor<1, dim>> &normals =
scratch_data.get_normal_vectors();
std::vector<double> g(n_q_points);
exact_solution->value_list(q_points, g);
const double extent1 = cell->measure() / cell->face(face_no)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent1);
{
for (unsigned int i = 0; i < dofs_per_cell; ++i)
for (unsigned int j = 0; j < dofs_per_cell; ++j)
copy_data.cell_matrix(i, j) +=
(-diffusion_coefficient *
- diffusion_coefficient *
+ diffusion_coefficient * penalty *
) *
for (unsigned int i = 0; i < dofs_per_cell; ++i)
copy_data.cell_rhs(i) +=
(-diffusion_coefficient *
+ diffusion_coefficient * penalty *
) *
}
};
const std::vector< Point< spacedim > > & get_quadrature_points() const
const unsigned int dofs_per_cell
const Tensor< 1, spacedim > & shape_grad(const unsigned int function_no, const unsigned int quadrature_point) const
const double & shape_value(const unsigned int function_no, const unsigned int point_no) const
Finally, a function that assembles face integrals on interior faces. To reinitialize FEInterfaceValues, we need to pass cells, face and subface indices (for adaptive refinement) to the reinit() function of FEInterfaceValues:
const auto face_worker = [&](const auto & cell,
const unsigned int &f,
const unsigned int &sf,
const auto & ncell,
const unsigned int &nf,
const unsigned int &nsf,
auto & scratch_data,
auto & copy_data) {
scratch_data.
reinit(cell, f, sf, ncell, nf, nsf);
const unsigned int n_q_points = q_points.size();
copy_data.face_data.emplace_back();
CopyDataFace & copy_data_face = copy_data.face_data.back();
copy_data_face.cell_matrix.reinit(n_dofs_face, n_dofs_face);
const double extent1 = cell->measure() / cell->face(f)->measure();
const double extent2 = ncell->measure() / ncell->face(nf)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent2);
{
for (unsigned int i = 0; i < n_dofs_face; ++i)
for (unsigned int j = 0; j < n_dofs_face; ++j)
copy_data_face.cell_matrix(i, j) +=
(-diffusion_coefficient *
- diffusion_coefficient *
+ diffusion_coefficient * penalty *
) *
}
};
const std::vector< double > & get_JxW_values() const
unsigned n_current_interface_dofs() const
const std::vector< Tensor< 1, spacedim > > & get_normal_vectors() const
const std::vector< Point< spacedim > > & get_quadrature_points() const
double jump(const unsigned int interface_dof_index, const unsigned int q_point, const unsigned int component=0) const
Tensor< 1, spacedim > average_gradient(const unsigned int interface_dof_index, const unsigned int q_point, const unsigned int component=0) const
std::vector< types::global_dof_index > get_interface_dof_indices() const
void reinit(const CellIteratorType &cell, const unsigned int face_no, const unsigned int sub_face_no, const typename identity< CellIteratorType >::type &cell_neighbor, const unsigned int face_no_neighbor, const unsigned int sub_face_no_neighbor)
The following lambda function will then copy data into the global matrix and right-hand side. Though there are no hanging node constraints in DG discretization, we define an empty AffineConstraints object that allows us to use the AffineConstraints::distribute_local_to_global() functionality.
const auto copier = [&](const auto &c) {
c.cell_rhs,
c.local_dof_indices,
system_matrix,
system_rhs);
void distribute_local_to_global(const InVector &local_vector, const std::vector< size_type > &local_dof_indices, OutVector &global_vector) const
Copy data from interior face assembly to the global matrix.
for (auto &cdf : c.face_data)
{
cdf.joint_dof_indices,
system_matrix);
}
};
With the assembly functions defined, we can now create ScratchData and CopyData objects, and pass them together with the lambda functions above to MeshWorker::mesh_loop(). In addition, we need to specify that we want to assemble on interior faces exactly once.
ScratchData scratch_data(
mapping, fe, quadrature, cell_flags, face_quadrature, face_flags);
CopyData copy_data;
dof_handler.end(),
cell_worker,
copier,
scratch_data,
copy_data,
boundary_worker,
face_worker);
}
@ update_values
Shape function values.
@ update_normal_vectors
Normal vectors.
@ update_JxW_values
Transformed quadrature weights.
@ update_gradients
Shape function gradients.
@ update_quadrature_points
Transformed quadrature points.
void mesh_loop(const CellIteratorType &begin, const CellIteratorType &end, const CellWorkerFunctionType &cell_worker, const CopierType &copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const AssembleFlags flags=assemble_own_cells, const BoundaryWorkerFunctionType &boundary_worker=BoundaryWorkerFunctionType(), const FaceWorkerFunctionType &face_worker=FaceWorkerFunctionType(), const unsigned int queue_length=2 *MultithreadInfo::n_threads(), const unsigned int chunk_size=8)
@ assemble_boundary_faces
@ assemble_own_interior_faces_once
The solve() and output_results() function
The following two functions are entirely standard and without difficulty.
template <int dim>
void SIPGLaplace<dim>::solve()
{
A_direct.
vmult(solution, system_rhs);
}
template <int dim>
void SIPGLaplace<dim>::output_results(const unsigned int cycle) const
{
".vtu";
std::ofstream output(filename);
}
void attach_dof_handler(const DoFHandlerType &)
void add_data_vector(const VectorType &data, const std::vector< std::string > &names, const DataVectorType type=type_automatic, const std::vector< DataComponentInterpretation::DataComponentInterpretation > &data_component_interpretation=std::vector< DataComponentInterpretation::DataComponentInterpretation >())
virtual void build_patches(const unsigned int n_subdivisions=0)
void initialize(const SparsityPattern &sparsity_pattern)
void vmult(Vector< double > &dst, const Vector< double > &src) const
void write_vtu(std::ostream &out) const
std::string int_to_string(const unsigned int value, const unsigned int digits=numbers::invalid_unsigned_int)
The compute_error_estimate() function
The assembly of the error estimator here is quite similar to that of the global matrix and right-had side and can be handled by the MeshWorker::mesh_loop() framework. To understand what each of the local (lambda) functions is doing, recall first that the local cell residual is defined as \(h_K^2 \left\| f + \nu \Delta u_h \right\|_K^2\):
template <int dim>
void SIPGLaplace<dim>::compute_error_estimate()
{
const auto cell_worker =
[&](const auto &cell, auto &scratch_data, auto ©_data) {
copy_data.cell_index = cell->active_cell_index();
const auto & q_points = fe_v.get_quadrature_points();
const unsigned int n_q_points = q_points.size();
const std::vector<double> &JxW = fe_v.get_JxW_values();
std::vector<Tensor<2, dim>>
hessians(n_q_points);
fe_v.get_function_hessians(solution,
hessians);
std::vector<double> rhs(n_q_points);
rhs_function->value_list(q_points, rhs);
const double hk = cell->diameter();
double residual_norm_square = 0;
{
const double residual =
residual_norm_square += residual * residual * JxW[
point];
}
copy_data.value = hk * hk * residual_norm_square;
};
constexpr Number trace(const SymmetricTensor< 2, dim, Number > &d)
Next compute boundary terms \(\sum_{f\in \partial K \cap \partial \Omega}
\sigma \left\| [ u_h-g_D ] \right\|_f^2 \):
const auto boundary_worker = [&](const auto & cell,
const unsigned int &face_no,
auto & scratch_data,
auto & copy_data) {
const unsigned n_q_points = q_points.size();
std::vector<double> g(n_q_points);
exact_solution->value_list(q_points, g);
std::vector<double> sol_u(n_q_points);
const double extent1 = cell->measure() / cell->face(face_no)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent1);
double difference_norm_square = 0.;
{
difference_norm_square += diff * diff * JxW[
point];
}
copy_data.value += penalty * difference_norm_square;
};
const std::vector< double > & get_JxW_values() const
And finally interior face terms \(\sum_{f\in \partial K}\lbrace \sigma
\left\| [u_h] \right\|_f^2 + h_f \left\| [\nu \nabla u_h \cdot
\mathbf n ] \right\|_f^2 \rbrace\):
const auto face_worker = [&](const auto & cell,
const unsigned int &f,
const unsigned int &sf,
const auto & ncell,
const unsigned int &nf,
const unsigned int &nsf,
auto & scratch_data,
auto & copy_data) {
scratch_data.
reinit(cell, f, sf, ncell, nf, nsf);
copy_data.face_data.emplace_back();
CopyDataFace ©_data_face = copy_data.face_data.back();
copy_data_face.cell_indices[0] = cell->active_cell_index();
copy_data_face.cell_indices[1] = ncell->active_cell_index();
const unsigned int n_q_points = q_points.size();
std::vector<double> jump(n_q_points);
get_function_jump(fe_iv, solution, jump);
std::vector<Tensor<1, dim>> grad_jump(n_q_points);
get_function_gradient_jump(fe_iv, solution, grad_jump);
const double h = cell->face(f)->diameter();
const double extent1 = cell->measure() / cell->face(f)->measure();
const double extent2 = ncell->measure() / ncell->face(nf)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent2);
double flux_jump_square = 0;
double u_jump_square = 0;
{
const double flux_jump = grad_jump[
point] * normals[
point];
flux_jump_square +=
diffusion_coefficient * flux_jump * flux_jump * JxW[
point];
}
copy_data_face.values[0] =
0.5 * h * (flux_jump_square + penalty * u_jump_square);
copy_data_face.values[1] = copy_data_face.values[0];
};
Having computed local contributions for each cell, we still need a way to copy these into the global vector that will hold the error estimators for all cells:
const auto copier = [&](const auto ©_data) {
estimated_error_square_per_cell[copy_data.cell_index] +=
copy_data.value;
for (auto &cdf : copy_data.face_data)
for (unsigned int j = 0; j < 2; ++j)
estimated_error_square_per_cell[cdf.cell_indices[j]] += cdf.values[j];
};
static const unsigned int invalid_unsigned_int
After all of this set-up, let's do the actual work: We resize the vector into which the results will be written, and then drive the whole process using the MeshWorker::mesh_loop() function.
estimated_error_square_per_cell.reinit(
triangulation.n_active_cells());
ScratchData scratch_data(
mapping, fe, quadrature, cell_flags, face_quadrature, face_flags);
CopyData copy_data;
dof_handler.end(),
cell_worker,
copier,
scratch_data,
copy_data,
boundary_worker,
face_worker);
}
@ update_hessians
Second derivatives of shape functions.
The compute_energy_norm_error() function
Next, we evaluate the accuracy in terms of the energy norm. This function is similar to the assembling of the error estimator above. Here we compute the square of the energy norm defined by
\[
\|u \|_{1,h}^2 = \sum_{K \in \Gamma_h} \nu\|\nabla u \|_K^2 +
\sum_{f \in F_i} \sigma \| [ u ] \|_f^2 +
\sum_{f \in F_b} \sigma \|u\|_f^2.
\]
Therefore the corresponding error is
\[
\|u -u_h \|_{1,h}^2 = \sum_{K \in \Gamma_h} \nu\|\nabla (u_h - u) \|_K^2
+ \sum_{f \in F_i} \sigma \|[ u_h ] \|_f^2 + \sum_{f \in F_b}\sigma
\|u_h-g_D\|_f^2.
\]
template <int dim>
double SIPGLaplace<dim>::compute_energy_norm_error()
{
energy_norm_square_per_cell.reinit(
triangulation.n_active_cells());
Assemble \(\sum_{K \in \Gamma_h} \nu\|\nabla (u_h - u) \|_K^2 \).
const auto cell_worker =
[&](const auto &cell, auto &scratch_data, auto ©_data) {
copy_data.cell_index = cell->active_cell_index();
const auto & q_points = fe_v.get_quadrature_points();
const unsigned int n_q_points = q_points.size();
const std::vector<double> &JxW = fe_v.get_JxW_values();
std::vector<Tensor<1, dim>> grad_u(n_q_points);
fe_v.get_function_gradients(solution, grad_u);
std::vector<Tensor<1, dim>> grad_exact(n_q_points);
exact_solution->gradient_list(q_points, grad_exact);
double norm_square = 0;
{
norm_square +=
}
copy_data.value = diffusion_coefficient * norm_square;
};
Assemble \(\sum_{f \in F_b}\sigma \|u_h-g_D\|_f^2\).
const auto boundary_worker = [&](const auto & cell,
const unsigned int &face_no,
auto & scratch_data,
auto & copy_data) {
const unsigned n_q_points = q_points.size();
std::vector<double> g(n_q_points);
exact_solution->value_list(q_points, g);
std::vector<double> sol_u(n_q_points);
const double extent1 = cell->measure() / cell->face(face_no)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent1);
double difference_norm_square = 0.;
{
difference_norm_square += diff * diff * JxW[
point];
}
copy_data.value += penalty * difference_norm_square;
};
Assemble \(\sum_{f \in F_i} \sigma \| [ u_h ] \|_f^2\).
const auto face_worker = [&](const auto & cell,
const unsigned int &f,
const unsigned int &sf,
const auto & ncell,
const unsigned int &nf,
const unsigned int &nsf,
auto & scratch_data,
auto & copy_data) {
scratch_data.
reinit(cell, f, sf, ncell, nf, nsf);
copy_data.face_data.emplace_back();
CopyDataFace ©_data_face = copy_data.face_data.back();
copy_data_face.cell_indices[0] = cell->active_cell_index();
copy_data_face.cell_indices[1] = ncell->active_cell_index();
const unsigned int n_q_points = q_points.size();
std::vector<double> jump(n_q_points);
get_function_jump(fe_iv, solution, jump);
const double extent1 = cell->measure() / cell->face(f)->measure();
const double extent2 = ncell->measure() / ncell->face(nf)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent2);
double u_jump_square = 0;
{
}
copy_data_face.values[0] = 0.5 * penalty * u_jump_square;
copy_data_face.values[1] = copy_data_face.values[0];
};
const auto copier = [&](const auto ©_data) {
energy_norm_square_per_cell[copy_data.cell_index] += copy_data.value;
for (auto &cdf : copy_data.face_data)
for (unsigned int j = 0; j < 2; ++j)
energy_norm_square_per_cell[cdf.cell_indices[j]] += cdf.values[j];
};
const ScratchData scratch_data(mapping,
fe,
quadrature_overintegration,
cell_flags,
face_quadrature_overintegration,
face_flags);
CopyData copy_data;
dof_handler.end(),
cell_worker,
copier,
scratch_data,
copy_data,
boundary_worker,
face_worker);
const double energy_error =
std::sqrt(energy_norm_square_per_cell.l1_norm());
return energy_error;
}
::VectorizedArray< Number, width > sqrt(const ::VectorizedArray< Number, width > &)
The refine_grid() function
template <int dim>
void SIPGLaplace<dim>::refine_grid()
{
const double refinement_fraction = 0.1;
triangulation, estimated_error_square_per_cell, refinement_fraction, 0.);
}
void refine_and_coarsen_fixed_number(Triangulation< dim, spacedim > &triangulation, const Vector< Number > &criteria, const double top_fraction_of_cells, const double bottom_fraction_of_cells, const unsigned int max_n_cells=std::numeric_limits< unsigned int >::max())
The compute_errors() function
We compute three errors in the \(L_2\) norm, \(H_1\) seminorm, and the energy norm, respectively. These are then printed to screen, but also stored in a table that records how these errors decay with mesh refinement and which can be output in one step at the end of the program.
template <int dim>
void SIPGLaplace<dim>::compute_errors()
{
double L2_error, H1_error, energy_error;
{
dof_handler,
solution,
*(exact_solution.get()),
difference_per_cell,
quadrature_overintegration,
difference_per_cell,
convergence_table.add_value("L2", L2_error);
}
{
dof_handler,
solution,
*(exact_solution.get()),
difference_per_cell,
quadrature_overintegration,
difference_per_cell,
convergence_table.add_value("H1", H1_error);
}
{
energy_error = compute_energy_norm_error();
convergence_table.add_value("Energy", energy_error);
}
std::cout << " Error in the L2 norm : " << L2_error << std::endl
<< " Error in the H1 seminorm : " << H1_error << std::endl
<< " Error in the energy norm : " << energy_error
<< std::endl;
}
The run() function
template <int dim>
{
const unsigned int max_cycle =
(test_case == TestCase::convergence_rate ? 6 : 20);
for (unsigned int cycle = 0; cycle < max_cycle; ++cycle)
{
std::cout << "Cycle " << cycle << std::endl;
switch (test_case)
{
case TestCase::convergence_rate:
{
if (cycle == 0)
{
}
else
{
}
break;
}
case TestCase::l_singularity:
{
if (cycle == 0)
{
}
else
{
refine_grid();
}
break;
}
default:
{
}
}
std::cout << " Number of active cells : "
setup_system();
std::cout << " Number of degrees of freedom : " << dof_handler.n_dofs()
<< std::endl;
assemble_system();
solve();
output_results(cycle);
{
convergence_table.add_value("cycle", cycle);
convergence_table.add_value(
"cells",
triangulation.n_active_cells());
convergence_table.add_value("dofs", dof_handler.n_dofs());
}
compute_errors();
if (test_case == TestCase::l_singularity)
{
compute_error_estimate();
std::cout << " Estimated error : "
<<
std::sqrt(estimated_error_square_per_cell.l1_norm())
<< std::endl;
convergence_table.add_value(
"Estimator",
std::sqrt(estimated_error_square_per_cell.l1_norm()));
}
std::cout << std::endl;
}
#define Assert(cond, exc)
void hyper_L(Triangulation< dim > &tria, const double left=-1., const double right=1., const bool colorize=false)
void hyper_cube(Triangulation< dim, spacedim > &tria, const double left=0., const double right=1., const bool colorize=false)
Having run all of our computations, let us tell the convergence table how to format its data and output it to screen:
convergence_table.set_precision("L2", 3);
convergence_table.set_precision("H1", 3);
convergence_table.set_precision("Energy", 3);
convergence_table.set_scientific("L2", true);
convergence_table.set_scientific("H1", true);
convergence_table.set_scientific("Energy", true);
if (test_case == TestCase::convergence_rate)
{
convergence_table.evaluate_convergence_rates(
convergence_table.evaluate_convergence_rates(
}
if (test_case == TestCase::l_singularity)
{
convergence_table.set_precision("Estimator", 3);
convergence_table.set_scientific("Estimator", true);
}
std::cout << "degree = " << degree << std::endl;
convergence_table.write_text(
std::cout, TableHandler::TextOutputFormat::org_mode_table);
}
}
The main() function
The following main function is similar to previous examples as well, and need not be commented on.
int main()
{
try
{
using namespace Step74;
const TestCase test_case = TestCase::l_singularity;
SIPGLaplace<2> problem(test_case);
problem.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
};
return 0;
}
Results
The output of this program consist of the console output and solutions in vtu format.
In the first test case, when you run the program, the screen output should look like the following:
Cycle 0
Number of active cells : 16
Number of degrees of freedom : 256
Error in the
L2 norm : 0.00193285
Error in the H1 seminorm : 0.106087
Error in the energy
norm : 0.150625
Cycle 1
Number of active cells : 64
Number of degrees of freedom : 1024
Error in the
L2 norm : 9.60497e-05
Error in the H1 seminorm : 0.0089954
Error in the energy
norm : 0.0113265
Cycle 2
.
.
.
double norm(const FEValuesBase< dim > &fe, const ArrayView< const std::vector< Tensor< 1, dim > > > &Du)
void L2(Vector< number > &result, const FEValuesBase< dim > &fe, const std::vector< double > &input, const double factor=1.)
When using the smooth case with polynomial degree 3, the convergence table will look like this:
| cycle | n_cellss | n_dofs | L2 | rate | H1 | rate | Energy |
| 0 | 16 | 256 | 1.933e-03 | | 1.061e-01 | | 1.506e-01 |
| 1 | 64 | 1024 | 9.605e-05 | 4.33 | 8.995e-03 | 3.56 | 1.133e-02 |
| 2 | 256 | 4096 | 5.606e-06 | 4.10 | 9.018e-04 | 3.32 | 9.736e-04 |
| 3 | 1024 | 16384 | 3.484e-07 | 4.01 | 1.071e-04 | 3.07 | 1.088e-04 |
| 4 | 4096 | 65536 | 2.179e-08 | 4.00 | 1.327e-05 | 3.01 | 1.331e-05 |
| 5 | 16384 | 262144 | 1.363e-09 | 4.00 | 1.656e-06 | 3.00 | 1.657e-06 |
Theoretically, for polynomial degree \(p\), the order of convergence in \(L_2\) norm and \(H^1\) seminorm should be \(p+1\) and \(p\), respectively. Our numerical results are in good agreement with theory.
In the second test case, when you run the program, the screen output should look like the following:
Cycle 0
Number of active cells : 192
Number of degrees of freedom : 3072
Error in the
L2 norm : 0.000323585
Error in the H1 seminorm : 0.0296202
Error in the energy
norm : 0.0420478
Estimated error : 0.136067
Cycle 1
Number of active cells : 249
Number of degrees of freedom : 3984
Error in the
L2 norm : 0.000114739
Error in the H1 seminorm : 0.0186571
Error in the energy
norm : 0.0264879
Estimated error : 0.0857186
Cycle 2
.
.
.
The following figure provides a log-log plot of the errors versus the number of degrees of freedom for this test case on the L-shaped domain. In order to interpret it, let \(n\) be the number of degrees of freedom, then on uniformly refined meshes, \(h\) is of order \(1/\sqrt{n}\) in 2D. Combining the theoretical results in the previous case, we see that if the solution is sufficiently smooth, we can expect the error in the \(L_2\) norm to be of order \(O(n^{-\frac{p+1}{2}})\) and in \(H^1\) seminorm to be \(O(n^{-\frac{p}{2}})\). It is not a priori clear that one would get the same kind of behavior as a function of \(n\) on adaptively refined meshes like the ones we use for this second test case, but one can certainly hope. Indeed, from the figure, we see that the SIPG with adaptive mesh refinement produces asymptotically the kinds of hoped-for results:
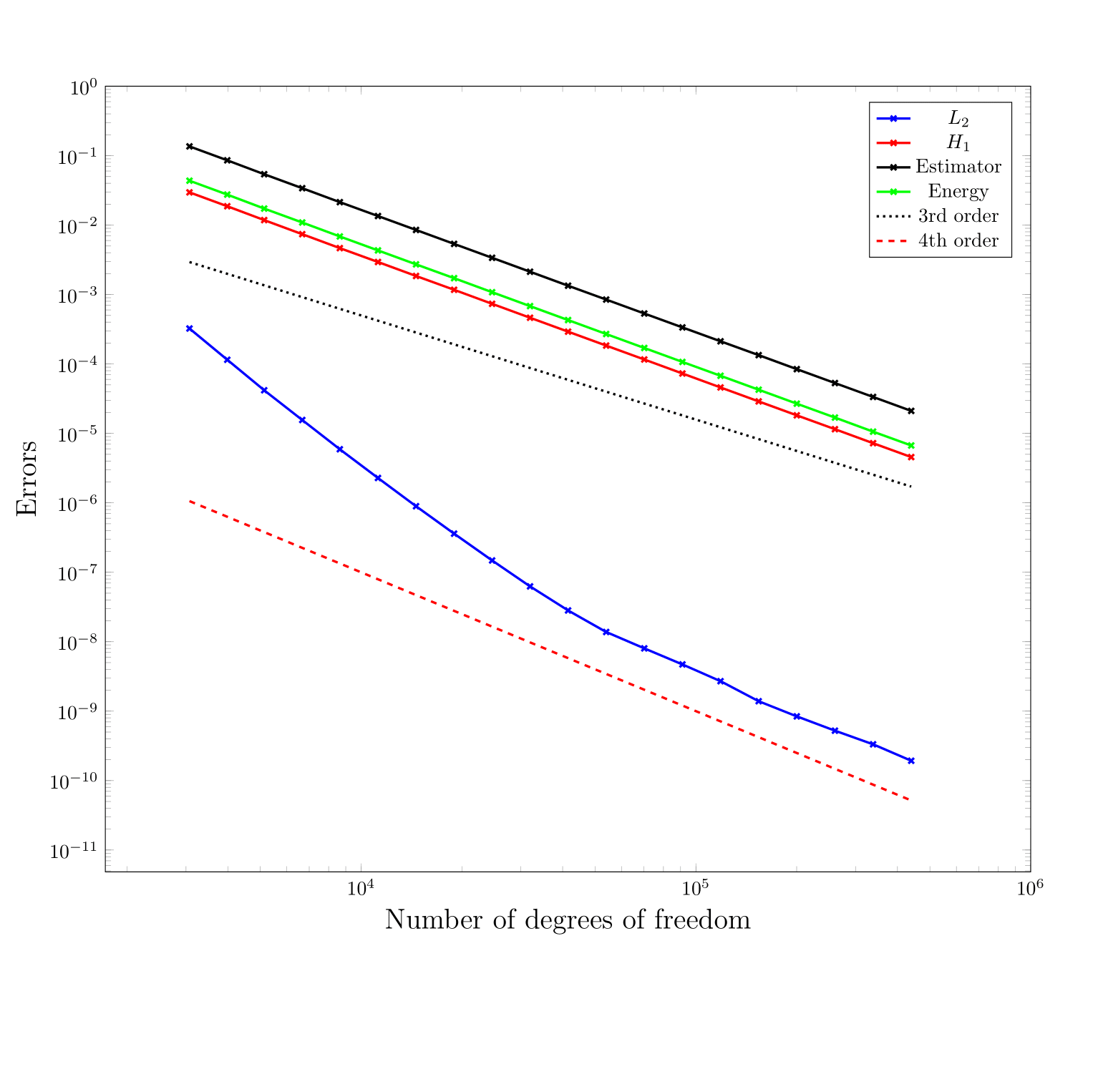
In addition, we observe that the error estimator decreases at almost the same rate as the errors in the energy norm and \(H^1\) seminorm, and one order lower than the \(L_2\) error. This suggests its ability to predict regions with large errors.
While this tutorial is focused on the implementation, the step-59 tutorial program achieves an efficient large-scale solver in terms of computing time with matrix-free solution techniques. Note that the step-59 tutorial does not work with meshes containing hanging nodes at this moment, because the multigrid interface matrices are not as easily determined, but that is merely the lack of some interfaces in deal.II, nothing fundamental.
The plain program
namespace Step74
{
enum class TestCase
{
convergence_rate,
l_singularity
};
template <int dim>
class SmoothSolution :
public Function<dim>
{
public:
SmoothSolution()
{}
virtual void value_list(
const std::vector<
Point<dim>> &points,
const unsigned int component = 0) const override;
const unsigned int component = 0) const override;
};
template <int dim>
void SmoothSolution<dim>::value_list(
const std::vector<
Point<dim>> &points,
const unsigned int ) const
{
for (
unsigned int i = 0; i <
values.size(); ++i)
}
template <int dim>
const unsigned int ) const
{
return_value[0] =
return_value[1] =
return return_value;
}
template <int dim>
class SmoothRightHandSide :
public Function<dim>
{
public:
SmoothRightHandSide()
{}
virtual void value_list(
const std::vector<
Point<dim>> &points,
const unsigned int ) const override;
};
template <int dim>
void
SmoothRightHandSide<dim>::value_list(
const std::vector<
Point<dim>> &points,
const unsigned int ) const
{
for (
unsigned int i = 0; i <
values.size(); ++i)
}
template <int dim>
class SingularRightHandSide :
public Function<dim>
{
public:
SingularRightHandSide()
{}
virtual void value_list(
const std::vector<
Point<dim>> &points,
const unsigned int ) const override;
private:
};
template <int dim>
void
SingularRightHandSide<dim>::value_list(
const std::vector<
Point<dim>> &points,
const unsigned int ) const
{
for (
unsigned int i = 0; i <
values.size(); ++i)
values[i] = -ref.laplacian(points[i]);
}
template <int dim>
std::vector<double> & jump)
{
std::array<std::vector<double>, 2> face_values;
jump.resize(n_q);
for (unsigned int i = 0; i < 2; ++i)
{
face_values[i].resize(n_q);
face_values[i]);
}
for (unsigned int q = 0; q < n_q; ++q)
jump[q] = face_values[0][q] - face_values[1][q];
}
template <int dim>
{
std::vector<Tensor<1, dim>> face_gradients[2];
gradient_jump.resize(n_q);
for (unsigned int i = 0; i < 2; ++i)
{
face_gradients[i].resize(n_q);
face_gradients[i]);
}
for (unsigned int q = 0; q < n_q; ++q)
gradient_jump[q] = face_gradients[0][q] - face_gradients[1][q];
}
double get_penalty_factor(const unsigned int fe_degree,
const double cell_extent_left,
const double cell_extent_right)
{
const unsigned int degree =
std::max(1U, fe_degree);
return degree * (degree + 1.) * 0.5 *
(1. / cell_extent_left + 1. / cell_extent_right);
}
struct CopyDataFace
{
std::vector<types::global_dof_index> joint_dof_indices;
std::array<unsigned int, 2> cell_indices;
};
struct CopyData
{
std::vector<types::global_dof_index> local_dof_indices;
std::vector<CopyDataFace> face_data;
template <class Iterator>
void reinit(
const Iterator &cell,
const unsigned int dofs_per_cell)
{
cell_rhs.
reinit(dofs_per_cell);
local_dof_indices.resize(dofs_per_cell);
cell->get_dof_indices(local_dof_indices);
}
};
template <int dim>
class SIPGLaplace
{
public:
SIPGLaplace(const TestCase &test_case);
private:
void setup_system();
void assemble_system();
void solve();
void refine_grid();
void output_results(const unsigned int cycle) const;
void compute_errors();
void compute_error_estimate();
double compute_energy_norm_error();
const unsigned int degree;
const QGauss<dim - 1> face_quadrature;
const QGauss<dim - 1> face_quadrature_overintegration;
const double diffusion_coefficient = 1.;
const TestCase test_case;
std::unique_ptr<const Function<dim>> exact_solution;
std::unique_ptr<const Function<dim>> rhs_function;
};
template <int dim>
SIPGLaplace<dim>::SIPGLaplace(const TestCase &test_case)
: degree(3)
, quadrature(degree + 1)
, face_quadrature(degree + 1)
, quadrature_overintegration(degree + 2)
, face_quadrature_overintegration(degree + 2)
, mapping()
, fe(degree)
, test_case(test_case)
{
if (test_case == TestCase::convergence_rate)
{
exact_solution = std::make_unique<const SmoothSolution<dim>>();
rhs_function = std::make_unique<const SmoothRightHandSide<dim>>();
}
else if (test_case == TestCase::l_singularity)
{
exact_solution =
std::make_unique<const Functions::LSingularityFunction>();
rhs_function = std::make_unique<const SingularRightHandSide<dim>>();
}
else
}
template <int dim>
void SIPGLaplace<dim>::setup_system()
{
dof_handler.distribute_dofs(fe);
sparsity_pattern.copy_from(dsp);
system_matrix.reinit(sparsity_pattern);
solution.
reinit(dof_handler.n_dofs());
system_rhs.reinit(dof_handler.n_dofs());
}
template <int dim>
void SIPGLaplace<dim>::assemble_system()
{
const auto cell_worker =
[&](const auto &cell, auto &scratch_data, auto ©_data) {
const unsigned int dofs_per_cell = fe_v.dofs_per_cell;
copy_data.reinit(cell, dofs_per_cell);
const auto & q_points = scratch_data.get_quadrature_points();
const unsigned int n_q_points = q_points.size();
const std::vector<double> &JxW = scratch_data.get_JxW_values();
std::vector<double> rhs(n_q_points);
rhs_function->value_list(q_points, rhs);
for (unsigned int i = 0; i < fe_v.dofs_per_cell; ++i)
{
for (unsigned int j = 0; j < fe_v.dofs_per_cell; ++j)
copy_data.cell_matrix(i, j) +=
diffusion_coefficient *
fe_v.shape_grad(i,
point) *
fe_v.shape_grad(j,
point) *
copy_data.cell_rhs(i) += fe_v.shape_value(i,
point) *
}
};
const auto boundary_worker = [&](const auto & cell,
const unsigned int &face_no,
auto & scratch_data,
auto & copy_data) {
const unsigned int n_q_points = q_points.size();
const std::vector<double> & JxW = scratch_data.get_JxW_values();
const std::vector<Tensor<1, dim>> &normals =
scratch_data.get_normal_vectors();
std::vector<double> g(n_q_points);
exact_solution->value_list(q_points, g);
const double extent1 = cell->measure() / cell->face(face_no)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent1);
{
for (unsigned int i = 0; i < dofs_per_cell; ++i)
for (unsigned int j = 0; j < dofs_per_cell; ++j)
copy_data.cell_matrix(i, j) +=
(-diffusion_coefficient *
- diffusion_coefficient *
+ diffusion_coefficient * penalty *
) *
for (unsigned int i = 0; i < dofs_per_cell; ++i)
copy_data.cell_rhs(i) +=
(-diffusion_coefficient *
+ diffusion_coefficient * penalty *
) *
}
};
const auto face_worker = [&](const auto & cell,
const unsigned int &f,
const unsigned int &sf,
const auto & ncell,
const unsigned int &nf,
const unsigned int &nsf,
auto & scratch_data,
auto & copy_data) {
scratch_data.
reinit(cell, f, sf, ncell, nf, nsf);
const unsigned int n_q_points = q_points.size();
copy_data.face_data.emplace_back();
CopyDataFace & copy_data_face = copy_data.face_data.back();
copy_data_face.cell_matrix.reinit(n_dofs_face, n_dofs_face);
const double extent1 = cell->measure() / cell->face(f)->measure();
const double extent2 = ncell->measure() / ncell->face(nf)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent2);
{
for (unsigned int i = 0; i < n_dofs_face; ++i)
for (unsigned int j = 0; j < n_dofs_face; ++j)
copy_data_face.cell_matrix(i, j) +=
(-diffusion_coefficient *
- diffusion_coefficient *
+ diffusion_coefficient * penalty *
) *
}
};
const auto copier = [&](const auto &c) {
c.cell_rhs,
c.local_dof_indices,
system_matrix,
system_rhs);
for (auto &cdf : c.face_data)
{
cdf.joint_dof_indices,
system_matrix);
}
};
ScratchData scratch_data(
mapping, fe, quadrature, cell_flags, face_quadrature, face_flags);
CopyData copy_data;
dof_handler.end(),
cell_worker,
copier,
scratch_data,
copy_data,
boundary_worker,
face_worker);
}
template <int dim>
void SIPGLaplace<dim>::solve()
{
A_direct.
vmult(solution, system_rhs);
}
template <int dim>
void SIPGLaplace<dim>::output_results(const unsigned int cycle) const
{
".vtu";
std::ofstream output(filename);
}
template <int dim>
void SIPGLaplace<dim>::compute_error_estimate()
{
const auto cell_worker =
[&](const auto &cell, auto &scratch_data, auto ©_data) {
copy_data.cell_index = cell->active_cell_index();
const auto & q_points = fe_v.get_quadrature_points();
const unsigned int n_q_points = q_points.size();
const std::vector<double> &JxW = fe_v.get_JxW_values();
std::vector<Tensor<2, dim>>
hessians(n_q_points);
fe_v.get_function_hessians(solution,
hessians);
std::vector<double> rhs(n_q_points);
rhs_function->value_list(q_points, rhs);
const double hk = cell->diameter();
double residual_norm_square = 0;
{
const double residual =
residual_norm_square += residual * residual * JxW[
point];
}
copy_data.value = hk * hk * residual_norm_square;
};
const auto boundary_worker = [&](const auto & cell,
const unsigned int &face_no,
auto & scratch_data,
auto & copy_data) {
const unsigned n_q_points = q_points.size();
std::vector<double> g(n_q_points);
exact_solution->value_list(q_points, g);
std::vector<double> sol_u(n_q_points);
const double extent1 = cell->measure() / cell->face(face_no)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent1);
double difference_norm_square = 0.;
{
difference_norm_square += diff * diff * JxW[
point];
}
copy_data.value += penalty * difference_norm_square;
};
const auto face_worker = [&](const auto & cell,
const unsigned int &f,
const unsigned int &sf,
const auto & ncell,
const unsigned int &nf,
const unsigned int &nsf,
auto & scratch_data,
auto & copy_data) {
scratch_data.
reinit(cell, f, sf, ncell, nf, nsf);
copy_data.face_data.emplace_back();
CopyDataFace ©_data_face = copy_data.face_data.back();
copy_data_face.cell_indices[0] = cell->active_cell_index();
copy_data_face.cell_indices[1] = ncell->active_cell_index();
const unsigned int n_q_points = q_points.size();
std::vector<double> jump(n_q_points);
get_function_jump(fe_iv, solution, jump);
std::vector<Tensor<1, dim>> grad_jump(n_q_points);
get_function_gradient_jump(fe_iv, solution, grad_jump);
const double h = cell->face(f)->diameter();
const double extent1 = cell->measure() / cell->face(f)->measure();
const double extent2 = ncell->measure() / ncell->face(nf)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent2);
double flux_jump_square = 0;
double u_jump_square = 0;
{
const double flux_jump = grad_jump[
point] * normals[
point];
flux_jump_square +=
diffusion_coefficient * flux_jump * flux_jump * JxW[
point];
}
copy_data_face.values[0] =
0.5 * h * (flux_jump_square + penalty * u_jump_square);
copy_data_face.values[1] = copy_data_face.values[0];
};
const auto copier = [&](const auto ©_data) {
estimated_error_square_per_cell[copy_data.cell_index] +=
copy_data.value;
for (auto &cdf : copy_data.face_data)
for (unsigned int j = 0; j < 2; ++j)
estimated_error_square_per_cell[cdf.cell_indices[j]] += cdf.values[j];
};
estimated_error_square_per_cell.reinit(
triangulation.n_active_cells());
ScratchData scratch_data(
mapping, fe, quadrature, cell_flags, face_quadrature, face_flags);
CopyData copy_data;
dof_handler.end(),
cell_worker,
copier,
scratch_data,
copy_data,
boundary_worker,
face_worker);
}
template <int dim>
double SIPGLaplace<dim>::compute_energy_norm_error()
{
energy_norm_square_per_cell.reinit(
triangulation.n_active_cells());
const auto cell_worker =
[&](const auto &cell, auto &scratch_data, auto ©_data) {
copy_data.cell_index = cell->active_cell_index();
const auto & q_points = fe_v.get_quadrature_points();
const unsigned int n_q_points = q_points.size();
const std::vector<double> &JxW = fe_v.get_JxW_values();
std::vector<Tensor<1, dim>> grad_u(n_q_points);
fe_v.get_function_gradients(solution, grad_u);
std::vector<Tensor<1, dim>> grad_exact(n_q_points);
exact_solution->gradient_list(q_points, grad_exact);
double norm_square = 0;
{
norm_square +=
}
copy_data.value = diffusion_coefficient * norm_square;
};
const auto boundary_worker = [&](const auto & cell,
const unsigned int &face_no,
auto & scratch_data,
auto & copy_data) {
const unsigned n_q_points = q_points.size();
std::vector<double> g(n_q_points);
exact_solution->value_list(q_points, g);
std::vector<double> sol_u(n_q_points);
const double extent1 = cell->measure() / cell->face(face_no)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent1);
double difference_norm_square = 0.;
{
difference_norm_square += diff * diff * JxW[
point];
}
copy_data.value += penalty * difference_norm_square;
};
const auto face_worker = [&](const auto & cell,
const unsigned int &f,
const unsigned int &sf,
const auto & ncell,
const unsigned int &nf,
const unsigned int &nsf,
auto & scratch_data,
auto & copy_data) {
scratch_data.
reinit(cell, f, sf, ncell, nf, nsf);
copy_data.face_data.emplace_back();
CopyDataFace ©_data_face = copy_data.face_data.back();
copy_data_face.cell_indices[0] = cell->active_cell_index();
copy_data_face.cell_indices[1] = ncell->active_cell_index();
const unsigned int n_q_points = q_points.size();
std::vector<double> jump(n_q_points);
get_function_jump(fe_iv, solution, jump);
const double extent1 = cell->measure() / cell->face(f)->measure();
const double extent2 = ncell->measure() / ncell->face(nf)->measure();
const double penalty = get_penalty_factor(degree, extent1, extent2);
double u_jump_square = 0;
{
}
copy_data_face.values[0] = 0.5 * penalty * u_jump_square;
copy_data_face.values[1] = copy_data_face.values[0];
};
const auto copier = [&](const auto ©_data) {
energy_norm_square_per_cell[copy_data.cell_index] += copy_data.value;
for (auto &cdf : copy_data.face_data)
for (unsigned int j = 0; j < 2; ++j)
energy_norm_square_per_cell[cdf.cell_indices[j]] += cdf.values[j];
};
const ScratchData scratch_data(mapping,
fe,
quadrature_overintegration,
cell_flags,
face_quadrature_overintegration,
face_flags);
CopyData copy_data;
dof_handler.end(),
cell_worker,
copier,
scratch_data,
copy_data,
boundary_worker,
face_worker);
const double energy_error =
std::sqrt(energy_norm_square_per_cell.l1_norm());
return energy_error;
}
template <int dim>
void SIPGLaplace<dim>::refine_grid()
{
const double refinement_fraction = 0.1;
triangulation, estimated_error_square_per_cell, refinement_fraction, 0.);
}
template <int dim>
void SIPGLaplace<dim>::compute_errors()
{
double L2_error, H1_error, energy_error;
{
dof_handler,
solution,
*(exact_solution.get()),
difference_per_cell,
quadrature_overintegration,
difference_per_cell,
convergence_table.add_value("L2", L2_error);
}
{
dof_handler,
solution,
*(exact_solution.get()),
difference_per_cell,
quadrature_overintegration,
difference_per_cell,
convergence_table.add_value("H1", H1_error);
}
{
energy_error = compute_energy_norm_error();
convergence_table.add_value("Energy", energy_error);
}
std::cout << " Error in the L2 norm : " << L2_error << std::endl
<< " Error in the H1 seminorm : " << H1_error << std::endl
<< " Error in the energy norm : " << energy_error
<< std::endl;
}
template <int dim>
{
const unsigned int max_cycle =
(test_case == TestCase::convergence_rate ? 6 : 20);
for (unsigned int cycle = 0; cycle < max_cycle; ++cycle)
{
std::cout << "Cycle " << cycle << std::endl;
switch (test_case)
{
case TestCase::convergence_rate:
{
if (cycle == 0)
{
}
else
{
}
break;
}
case TestCase::l_singularity:
{
if (cycle == 0)
{
}
else
{
refine_grid();
}
break;
}
default:
{
}
}
std::cout << " Number of active cells : "
setup_system();
std::cout << " Number of degrees of freedom : " << dof_handler.n_dofs()
<< std::endl;
assemble_system();
solve();
output_results(cycle);
{
convergence_table.add_value("cycle", cycle);
convergence_table.add_value(
"cells",
triangulation.n_active_cells());
convergence_table.add_value("dofs", dof_handler.n_dofs());
}
compute_errors();
if (test_case == TestCase::l_singularity)
{
compute_error_estimate();
std::cout << " Estimated error : "
<<
std::sqrt(estimated_error_square_per_cell.l1_norm())
<< std::endl;
convergence_table.add_value(
"Estimator",
std::sqrt(estimated_error_square_per_cell.l1_norm()));
}
std::cout << std::endl;
}
convergence_table.set_precision("L2", 3);
convergence_table.set_precision("H1", 3);
convergence_table.set_precision("Energy", 3);
convergence_table.set_scientific("L2", true);
convergence_table.set_scientific("H1", true);
convergence_table.set_scientific("Energy", true);
if (test_case == TestCase::convergence_rate)
{
convergence_table.evaluate_convergence_rates(
convergence_table.evaluate_convergence_rates(
}
if (test_case == TestCase::l_singularity)
{
convergence_table.set_precision("Estimator", 3);
convergence_table.set_scientific("Estimator", true);
}
std::cout << "degree = " << degree << std::endl;
convergence_table.write_text(
std::cout, TableHandler::TextOutputFormat::org_mode_table);
}
}
int main()
{
try
{
using namespace Step74;
const TestCase test_case = TestCase::l_singularity;
SIPGLaplace<2> problem(test_case);
problem.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
};
return 0;
}


