This tutorial depends on step-22.
This program grew out of a student project by Abner Salgado at Texas A&M University. Most of the work for this program is by him.
Introduction
Motivation
The purpose of this program is to show how to effectively solve the incompressible time-dependent Navier-Stokes equations. These equations describe the flow of a viscous incompressible fluid and read
\begin{align*}
u_t + u \cdot \nabla u - \nu \Delta u + \nabla p = f, \\
\nabla \cdot u = 0,
\end{align*}
where u represents the velocity of the flow and p the pressure. This system of equations is supplemented by the initial condition
u |_{t=0} = u_0,
with u_0 sufficiently smooth and solenoidal, and suitable boundary conditions. For instance, an admissible boundary condition, is
u|_{\partial\Omega} = u_b.
It is possible to prescribe other boundary conditions as well. In the test case that we solve here the boundary is partitioned into two disjoint subsets \partial\Omega = \Gamma_1 \cup \Gamma_2 and we have
u|_{\Gamma_1} = u_b,
and
u\times n|_{\Gamma_2} = 0, \quad p|_{\Gamma_2} = 0
where n is the outer unit normal. The boundary conditions on \Gamma_2 are often used to model outflow conditions.
In previous tutorial programs (see for instance step-20 and step-22) we have seen how to solve the time-independent Stokes equations using a Schur complement approach. For the time-dependent case, after time discretization, we would arrive at a system like
\begin{align*}
\frac1\tau u^k - \nu \Delta u^k + \nabla p^k = F^k, \\
\nabla \cdot u^k = 0,
\end{align*}
where \tau is the time-step. Although the structure of this system is similar to the Stokes system and thus it could be solved using a Schur complement approach, it turns out that the condition number of the Schur complement is proportional to \tau^{-2}. This makes the system very difficult to solve, and means that for the Navier-Stokes equations, this is not a useful avenue to the solution.
Projection methods
Rather, we need to come up with a different approach to solve the time-dependent Navier-Stokes equations. The difficulty in their solution comes from the fact that the velocity and the pressure are coupled through the constraint
\nabla \cdot u = 0,
for which the pressure is the Lagrange multiplier. Projection methods aim at decoupling this constraint from the diffusion (Laplace) operator.
Let us shortly describe how the projection methods look like in a semi-discrete setting. The objective is to obtain a sequence of velocities \{u^k\} and pressures \{p^k\}. We will also obtain a sequence \{\phi^k\} of auxiliary variables. Suppose that from the initial conditions, and an application of a first order method we have found (u^0,p^0,\phi^0=0) and (u^1,p^1,\phi^1=p^1-p^0). Then the projection method consists of the following steps:
-
Step 0: Extrapolation. Define:
u^\star = 2u^k - u^{k-1}, \quad p^\sharp = p^k + \frac43 \phi^k - \frac13 \phi^{k-1}.
-
Step 1: Diffusion step. We find u^{k+1} that solves the single linear equation
\frac1{2\tau}\left( 3u^{k+1} - 4u^k + u^{k-1} \right)
+ u^\star \cdot\nabla u^{k+1} + \frac12 \left( \nabla \cdot u^\star \right) u^{k+1}
-\nu \Delta u^{k+1} + \nabla p^\sharp
= f^{k+1},
\quad
u^{k+1}|_{\Gamma_1} = u_b,
\quad
u^{k+1} \times n|_{\Gamma_2} = 0.
-
Step 2: Projection. Find \phi^{k+1} that solves
\Delta \phi^{k+1} = \frac3{2\tau} \nabla \cdot u^{k+1},
\quad
\partial_n \phi^{k+1}|_{\Gamma_1} = 0,
\quad
\phi^{k+1}|_{\Gamma_2} = 0
-
Step 3: Pressure correction. Here we have two options:
Without going into details, let us remark a few things about the projection methods that we have just described:
-
The advection term u\cdot\nabla u is replaced by its skew symmetric form
u \cdot \nabla u + \frac12 \left( \nabla\cdot u \right) u.
This is consistent with the continuous equation (because \nabla\cdot u = 0, though this is not true pointwise for the discrete solution) and it is needed to guarantee unconditional stability of the time-stepping scheme. Moreover, to linearize the term we use the second order extrapolation u^\star of u^{k+1}.
-
The projection step is a realization of the Helmholtz decomposition
L^2(\Omega)^d = H \oplus \nabla H^1_{\Gamma_2}(\Omega),
where
H = \left\{ v \in L^2(\Omega)^d:\ \nabla\cdot v =0, \ v\cdot n|_{\Gamma_1} = 0 \right\},
and
H^1_{\Gamma_2}(\Omega) = \left\{ q \in H^1(\Omega):\ q|_{\Gamma_2} = 0 \right\}.
Indeed, if we use this decomposition on u^{k+1} we obtain
u^{k+1} = v^{k+1} + \nabla \left( \frac{2\tau}{3} \phi^{k+1} \right),
with v^{k+1}\in H. Taking the divergence of this equation we arrive at the projection equation.
-
The more accurate of the two variants outlined above is the rotational one. However, the program below implements both variants. Moreover, in the author's experience, the standard form is the one that should be used if, for instance, the viscosity \nu is variable.
The standard incremental scheme and the rotational incremental scheme were first considered by van Kan in
-
J. van Kan, "A second-order accurate pressure-correction scheme for viscous incompressible flow", SIAM Journal on Scientific and Statistical Computing, vol. 7, no. 3, pp. 870–891, 1986
and is analyzed by Guermond in
-
J.-L. Guermond, "Un résultat de convergence d’ordre deux en temps pour
l’approximation des équations de Navier–Stokes par une technique de projection incrémentale", ESAIM: Mathematical Modelling and Numerical Analysis, vol. 33, no. 1, pp. 169–189, 1999
for the case \nu = 1. It turns out that this technique suffers from unphysical boundary conditions for the kinematic pressure that lead to reduced rates of convergence. To prevent this, Timmermans et al. proposed in
-
L. Timmermans, P. Minev, and F. Van De Vosse, "An approximate projection scheme for incompressible flow using spectral elements", International Journal for Numerical Methods in Fluids, vol. 22, no. 7, pp. 673–688, 1996
the rotational pressure-correction projection method that uses a divergence correction for the kinematic pressure. A thorough analysis for scheme has first been performed in
-
J.-L. Guermond and J. Shen, "On the error estimates for the rotational pressure-correction projection methods", Mathematics of Computation, vol. 73, no. 248, pp. 1719–1737, 2004
for the Stokes problem.
The Fully Discrete Setting
To obtain a fully discrete setting of the method we, as always, need a variational formulation. There is one subtle issue here given the nature of the boundary conditions. When we multiply the equation by a suitable test function one of the term that arises is
-\nu \int_\Omega \Delta u \cdot v.
If we, say, had Dirichlet boundary conditions on the whole boundary then after integration by parts we would obtain
-\nu \int_\Omega \Delta u \cdot v = \nu \int_\Omega \nabla u : \nabla v
- \int_{\partial\Omega} \partial_n u \cdot v
= \nu \int_\Omega \nabla u : \nabla v.
One of the advantages of this formulation is that it fully decouples the components of the velocity. Moreover, they all share the same system matrix. This can be exploited in the program.
However, given the nonstandard boundary conditions, to be able to take them into account we need to use the following identity
\Delta u = \nabla\nabla\cdot u - \nabla\times\nabla\times u,
so that when we integrate by parts and take into account the boundary conditions we obtain
-\nu \int_\Omega \Delta u \cdot v = \nu \int_\Omega \left[ \nabla \cdot u \nabla \cdot v
+ \nabla \times u \nabla \times v \right],
which is the form that we would have to use. Notice that this couples the components of the velocity. Moreover, to enforce the boundary condition on the pressure, we need to rewrite
\int_\Omega \nabla p \cdot v = -\int_\Omega p \nabla \cdot v + \int_{\Gamma_1} p v\cdot n
+ \int_{\Gamma_2} p v\cdot n
= -\int_\Omega p \nabla \cdot v,
where the boundary integral in \Gamma_1 equals zero given the boundary conditions for the velocity, and the one in \Gamma_2 given the boundary conditions for the pressure.
In the simplified case where the boundary \Gamma_2 is parallel to a coordinate axis, which holds for the testcase that we carry out below, it can actually be shown that
\nu \int_\Omega \nabla u : \nabla v = \nu \int_\Omega \left[ \nabla \cdot u \nabla \cdot v
+ \nabla \times u \nabla \times v \right].
This issue is not very often addressed in the literature. For more information the reader can consult, for instance,
-
J.-L. GUERMOND, L. QUARTAPELLE, On the approximation of the unsteady Navier-Stokes equations by finite element projection methods, Numer. Math., 80 (1998) 207-238
-
J.-L. GUERMOND, P. MINEV, J. SHEN, Error analysis of pressure-correction schemes for the Navier-Stokes equations with open boundary conditions, SIAM J. Numer. Anal., 43 1 (2005) 239–258.
Implementation
Our implementation of the projection methods follows verbatim the description given above. We must note, however, that as opposed to most other problems that have several solution components, we do not use vector-valued finite elements. Instead, we use separate finite elements the components of the velocity and the pressure, respectively, and use different DoFHandler's for those as well. The main reason for doing this is that, as we see from the description of the scheme, the dim components of the velocity and the pressure are decoupled. As a consequence, the equations for all the velocity components look all the same, have the same system matrix, and can be solved in parallel. Obviously, this approach has also its disadvantages. For instance, we need to keep several DoFHandlers and iterators synchronized when assembling matrices and right hand sides; obtaining quantities that are inherent to vector-valued functions (e.g. divergences) becomes a little awkward, and others.
The Testcase
The testcase that we use for this program consists of the flow around a square obstacle. The geometry is as follows:

with H=4.1, making the geometry slightly non-symmetric.
We impose no-slip boundary conditions on both the top and bottom walls and the obstacle. On the left side we have the inflow boundary condition
u =
\left( \begin{array}{c} 4 U_m y (H-y)/H^2 \\ 0 \end{array} \right),
with U_m = 1.5, i.e. the inflow boundary conditions correspond to Poiseuille flow for this configuration. Finally, on the right vertical wall we impose the condition that the vertical component of the velocity and the pressure should both be zero. The final time T=10.
The commented program
Include files
We start by including all the necessary deal.II header files and some C++ related ones. Each one of them has been discussed in previous tutorial programs, so we will not get into details here.
#include <fstream>
#include <cmath>
#include <iostream>
Finally this is as in all previous programs:
Run time parameters
Since our method has several parameters that can be fine-tuned we put them into an external file, so that they can be determined at run-time.
This includes, in particular, the formulation of the equation for the auxiliary variable \phi, for which we declare an enum. Next, we declare a class that is going to read and store all the parameters that our program needs to run.
namespace RunTimeParameters
{
enum class Method
{
standard,
rotational
};
class Data_Storage
{
public:
Data_Storage();
void read_data(const std::string &filename);
Method form;
double dt;
double initial_time;
double final_time;
double Reynolds;
unsigned int n_global_refines;
unsigned int pressure_degree;
unsigned int vel_max_iterations;
unsigned int vel_Krylov_size;
unsigned int vel_off_diagonals;
unsigned int vel_update_prec;
double vel_eps;
double vel_diag_strength;
bool verbose;
unsigned int output_interval;
protected:
};
In the constructor of this class we declare all the parameters. The details of how this works have been discussed elsewhere, for example in step-29.
Data_Storage::Data_Storage()
: form(Method::rotational)
, initial_time(0.)
, final_time(1.)
, Reynolds(1.)
, n_global_refines(0)
, pressure_degree(1)
, vel_max_iterations(1000)
, vel_Krylov_size(30)
, vel_off_diagonals(60)
, vel_update_prec(15)
, vel_diag_strength(0.01)
, verbose(true)
, output_interval(15)
{
prm.declare_entry("Method_Form",
"rotational",
" Used to select the type of method that we are going "
"to use. ");
prm.enter_subsection("Physical data");
{
prm.declare_entry("initial_time",
"0.",
" The initial time of the simulation. ");
prm.declare_entry("final_time",
"1.",
" The final time of the simulation. ");
prm.declare_entry("Reynolds",
"1.",
" The Reynolds number. ");
}
prm.leave_subsection();
prm.enter_subsection("Time step data");
{
prm.declare_entry("dt",
"5e-4",
" The time step size. ");
}
prm.leave_subsection();
prm.enter_subsection("Space discretization");
{
prm.declare_entry("n_of_refines",
"0",
" The number of global refines we do on the mesh. ");
prm.declare_entry("pressure_fe_degree",
"1",
" The polynomial degree for the pressure space. ");
}
prm.leave_subsection();
prm.enter_subsection("Data solve velocity");
{
prm.declare_entry(
"max_iterations",
"1000",
" The maximal number of iterations GMRES must make. ");
prm.declare_entry("eps",
"1e-12",
" The stopping criterion. ");
prm.declare_entry("Krylov_size",
"30",
" The size of the Krylov subspace to be used. ");
prm.declare_entry("off_diagonals",
"60",
" The number of off-diagonal elements ILU must "
"compute. ");
prm.declare_entry("diag_strength",
"0.01",
" Diagonal strengthening coefficient. ");
prm.declare_entry("update_prec",
"15",
" This number indicates how often we need to "
"update the preconditioner");
}
prm.leave_subsection();
prm.declare_entry("verbose",
"true",
" This indicates whether the output of the solution "
"process should be verbose. ");
prm.declare_entry("output_interval",
"1",
" This indicates between how many time steps we print "
"the solution. ");
}
void Data_Storage::read_data(const std::string &filename)
{
std::ifstream file(filename);
prm.parse_input(file);
if (prm.get("Method_Form") == std::string("rotational"))
form = Method::rotational;
else
form = Method::standard;
prm.enter_subsection("Physical data");
{
initial_time = prm.get_double("initial_time");
final_time = prm.get_double("final_time");
Reynolds = prm.get_double("Reynolds");
}
prm.leave_subsection();
prm.enter_subsection("Time step data");
{
dt = prm.get_double("dt");
}
prm.leave_subsection();
prm.enter_subsection("Space discretization");
{
n_global_refines = prm.get_integer("n_of_refines");
pressure_degree = prm.get_integer("pressure_fe_degree");
}
prm.leave_subsection();
prm.enter_subsection("Data solve velocity");
{
vel_max_iterations = prm.get_integer("max_iterations");
vel_eps = prm.get_double("eps");
vel_Krylov_size = prm.get_integer("Krylov_size");
vel_off_diagonals = prm.get_integer("off_diagonals");
vel_diag_strength = prm.get_double("diag_strength");
vel_update_prec = prm.get_integer("update_prec");
}
prm.leave_subsection();
verbose = prm.get_bool("verbose");
output_interval = prm.get_integer("output_interval");
}
}
static ::ExceptionBase & ExcFileNotOpen(std::string arg1)
#define AssertThrow(cond, exc)
SymmetricTensor< 2, dim, Number > e(const Tensor< 2, dim, Number > &F)
Equation data
In the next namespace, we declare the initial and boundary conditions:
As we have chosen a completely decoupled formulation, we will not take advantage of deal.II's capabilities to handle vector valued problems. We do, however, want to use an interface for the equation data that is somehow dimension independent. To be able to do that, our functions should be able to know on which spatial component we are currently working, and we should be able to have a common interface to do that. The following class is an attempt in that direction.
template <int dim>
class MultiComponentFunction :
public Function<dim>
{
public:
MultiComponentFunction(const double initial_time = 0.);
void set_component(
const unsigned int d);
protected:
unsigned int comp;
};
template <int dim>
MultiComponentFunction<dim>::MultiComponentFunction(
const double initial_time)
, comp(0)
{}
template <int dim>
void MultiComponentFunction<dim>::set_component(
const unsigned int d)
{
}
static ::ExceptionBase & ExcIndexRange(int arg1, int arg2, int arg3)
#define Assert(cond, exc)
SymmetricTensor< 2, dim, Number > d(const Tensor< 2, dim, Number > &F, const Tensor< 2, dim, Number > &dF_dt)
With this class defined, we declare classes that describe the boundary conditions for velocity and pressure:
template <int dim>
class Velocity : public MultiComponentFunction<dim>
{
public:
Velocity(const double initial_time = 0.0);
const unsigned int component = 0) const override;
virtual void value_list(
const std::vector<
Point<dim>> &points,
const unsigned int component = 0) const override;
};
template <int dim>
Velocity<dim>::Velocity(const double initial_time)
: MultiComponentFunction<dim>(initial_time)
{}
template <int dim>
void Velocity<dim>::value_list(
const std::vector<
Point<dim>> &points,
const unsigned int) const
{
const unsigned int n_points = points.size();
for (unsigned int i = 0; i < n_points; ++i)
values[i] = Velocity<dim>::value(points[i]);
}
template <int dim>
double Velocity<dim>::value(
const Point<dim> &p,
const unsigned int)
const
{
if (this->comp == 0)
{
const double Um = 1.5;
const double H = 4.1;
return 4. * Um * p(1) * (H - p(1)) / (H * H);
}
else
return 0.;
}
template <int dim>
{
public:
Pressure(const double initial_time = 0.0);
const unsigned int component = 0) const override;
const unsigned int component = 0) const override;
};
template <int dim>
Pressure<dim>::Pressure(const double initial_time)
{}
template <int dim>
const unsigned int component) const
{
(void)component;
return 25. - p(0);
}
template <int dim>
void Pressure<dim>::value_list(
const std::vector<
Point<dim>> &points,
const unsigned int component) const
{
(void)component;
const unsigned int n_points = points.size();
for (unsigned int i = 0; i < n_points; ++i)
values[i] = Pressure<dim>::value(points[i]);
}
}
virtual void value_list(const std::vector< Point< dim > > &points, std::vector< RangeNumberType > &values, const unsigned int component=0) const
virtual RangeNumberType value(const Point< dim > &p, const unsigned int component=0) const
#define AssertIndexRange(index, range)
static ::ExceptionBase & ExcDimensionMismatch(std::size_t arg1, std::size_t arg2)
The NavierStokesProjection class
Now for the main class of the program. It implements the various versions of the projection method for Navier-Stokes equations. The names for all the methods and member variables should be self-explanatory, taking into account the implementation details given in the introduction.
template <int dim>
class NavierStokesProjection
{
public:
NavierStokesProjection(const RunTimeParameters::Data_Storage &data);
void run(
const bool verbose =
false,
const unsigned int n_plots = 10);
protected:
RunTimeParameters::Method type;
const unsigned int deg;
const double dt;
const double t_0;
const double Re;
EquationData::Velocity<dim> vel_exact;
std::map<types::global_dof_index, double> boundary_values;
std::vector<types::boundary_id> boundary_ids;
double,
double,
<< " The time step " << arg1 << " is out of range."
<< std::endl
<< " The permitted range is (0," << arg2 << "]");
void create_triangulation_and_dofs(const unsigned int n_refines);
void initialize();
void interpolate_velocity();
void diffusion_step(const bool reinit_prec);
void projection_step(const bool reinit_prec);
void update_pressure(const bool reinit_prec);
private:
unsigned int vel_max_its;
unsigned int vel_Krylov_size;
unsigned int vel_off_diagonals;
unsigned int vel_update_prec;
double vel_eps;
double vel_diag_strength;
void initialize_velocity_matrices();
void initialize_pressure_matrices();
#define DeclException2(Exception2, type1, type2, outsequence)
void run(const Iterator &begin, const typename identity< Iterator >::type &end, Worker worker, Copier copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const unsigned int queue_length, const unsigned int chunk_size)
const ::parallel::distributed::Triangulation< dim, spacedim > * triangulation
The next few structures and functions are for doing various things in parallel. They follow the scheme laid out in Parallel computing with multiple processors accessing shared memory, using the WorkStream class. As explained there, this requires us to declare two structures for each of the assemblers, a per-task data and a scratch data structure. These are then handed over to functions that assemble local contributions and that copy these local contributions to the global objects.
One of the things that are specific to this program is that we don't just have a single DoFHandler object that represents both the velocities and the pressure, but we use individual DoFHandler objects for these two kinds of variables. We pay for this optimization when we want to assemble terms that involve both variables, such as the divergence of the velocity and the gradient of the pressure, times the respective test functions. When doing so, we can't just anymore use a single FEValues object, but rather we need two, and they need to be initialized with cell iterators that point to the same cell in the triangulation but different DoFHandlers.
To do this in practice, we declare a "synchronous" iterator – an object that internally consists of several (in our case two) iterators, and each time the synchronous iteration is moved forward one step, each of the iterators stored internally is moved forward one step as well, thereby always staying in sync. As it so happens, there is a deal.II class that facilitates this sort of thing. (What is important here is to know that two DoFHandler objects built on the same triangulation will walk over the cells of the triangulation in the same order.)
using IteratorTuple =
std::tuple<typename DoFHandler<dim>::active_cell_iterator,
void initialize_gradient_operator();
struct InitGradPerTaskData
{
unsigned int vel_dpc;
unsigned int pres_dpc;
std::vector<types::global_dof_index> vel_local_dof_indices;
std::vector<types::global_dof_index> pres_local_dof_indices;
InitGradPerTaskData(const unsigned int dd,
const unsigned int vdpc,
const unsigned int pdpc)
, vel_dpc(vdpc)
, pres_dpc(pdpc)
, local_grad(vdpc, pdpc)
, vel_local_dof_indices(vdpc)
, pres_local_dof_indices(pdpc)
{}
};
struct InitGradScratchData
{
unsigned int nqp;
: nqp(quad.size())
, fe_val_vel(fe_v, quad, flags_v)
, fe_val_pres(fe_p, quad, flags_p)
{}
InitGradScratchData(const InitGradScratchData &data)
: nqp(data.nqp)
, fe_val_vel(data.fe_val_vel.get_fe(),
data.fe_val_vel.get_quadrature(),
data.fe_val_vel.get_update_flags())
, fe_val_pres(data.fe_val_pres.get_fe(),
data.fe_val_pres.get_quadrature(),
data.fe_val_pres.get_update_flags())
{}
};
void assemble_one_cell_of_gradient(const IteratorPair & SI,
InitGradScratchData &scratch,
InitGradPerTaskData &data);
void copy_gradient_local_to_global(const InitGradPerTaskData &data);
typename ActiveSelector::active_cell_iterator active_cell_iterator
The same general layout also applies to the following classes and functions implementing the assembly of the advection term:
void assemble_advection_term();
struct AdvectionPerTaskData
{
std::vector<types::global_dof_index> local_dof_indices;
AdvectionPerTaskData(const unsigned int dpc)
: local_advection(dpc, dpc)
, local_dof_indices(dpc)
{}
};
struct AdvectionScratchData
{
unsigned int nqp;
unsigned int dpc;
std::vector<Point<dim>> u_star_local;
std::vector<Tensor<1, dim>> grad_u_star;
std::vector<double> u_star_tmp;
: nqp(quad.size())
, dpc(fe.n_dofs_per_cell())
, u_star_local(nqp)
, grad_u_star(nqp)
, u_star_tmp(nqp)
, fe_val(fe, quad, flags)
{}
AdvectionScratchData(const AdvectionScratchData &data)
: nqp(data.nqp)
, dpc(data.dpc)
, u_star_local(nqp)
, grad_u_star(nqp)
, u_star_tmp(nqp)
, fe_val(data.fe_val.get_fe(),
data.fe_val.get_quadrature(),
data.fe_val.get_update_flags())
{}
};
void assemble_one_cell_of_advection(
AdvectionScratchData & scratch,
AdvectionPerTaskData & data);
void copy_advection_local_to_global(const AdvectionPerTaskData &data);
The final few functions implement the diffusion solve as well as postprocessing the output, including computing the curl of the velocity:
void diffusion_component_solve(
const unsigned int d);
void output_results(const unsigned int step);
void assemble_vorticity(const bool reinit_prec);
};
NavierStokesProjection::NavierStokesProjection
In the constructor, we just read all the data from the Data_Storage object that is passed as an argument, verify that the data we read is reasonable and, finally, create the triangulation and load the initial data.
template <int dim>
NavierStokesProjection<dim>::NavierStokesProjection(
const RunTimeParameters::Data_Storage &data)
: type(data.form)
, deg(data.pressure_degree)
, dt(data.dt)
, t_0(data.initial_time)
, Re(data.Reynolds)
, vel_exact(data.initial_time)
, fe_velocity(deg + 1)
, fe_pressure(deg)
, quadrature_pressure(deg + 1)
, quadrature_velocity(deg + 2)
, vel_max_its(data.vel_max_iterations)
, vel_Krylov_size(data.vel_Krylov_size)
, vel_off_diagonals(data.vel_off_diagonals)
, vel_update_prec(data.vel_update_prec)
, vel_eps(data.vel_eps)
, vel_diag_strength(data.vel_diag_strength)
{
if (deg < 1)
std::cout
<< " WARNING: The chosen pair of finite element spaces is not stable."
<< std::endl
<< " The obtained results will be nonsense" << std::endl;
AssertThrow(!((dt <= 0.) || (dt > .5 *
T)), ExcInvalidTimeStep(dt, .5 *
T));
create_triangulation_and_dofs(data.n_global_refines);
initialize();
}
NavierStokesProjection::create_triangulation_and_dofs
The method that creates the triangulation and refines it the needed number of times. After creating the triangulation, it creates the mesh dependent data, i.e. it distributes degrees of freedom and renumbers them, and initializes the matrices and vectors that we will use.
template <int dim>
void NavierStokesProjection<dim>::create_triangulation_and_dofs(
const unsigned int n_refines)
{
{
std::string filename = "nsbench2.inp";
std::ifstream file(filename);
}
std::cout << "Number of refines = " << n_refines << std::endl;
std::cout <<
"Number of active cells: " <<
triangulation.n_active_cells()
<< std::endl;
dof_handler_velocity.distribute_dofs(fe_velocity);
dof_handler_pressure.distribute_dofs(fe_pressure);
initialize_velocity_matrices();
initialize_pressure_matrices();
initialize_gradient_operator();
pres_n.reinit(dof_handler_pressure.n_dofs());
pres_n_minus_1.reinit(dof_handler_pressure.n_dofs());
phi_n.reinit(dof_handler_pressure.n_dofs());
phi_n_minus_1.reinit(dof_handler_pressure.n_dofs());
pres_tmp.reinit(dof_handler_pressure.n_dofs());
for (
unsigned int d = 0;
d < dim; ++
d)
{
u_n[
d].reinit(dof_handler_velocity.n_dofs());
u_n_minus_1[
d].reinit(dof_handler_velocity.n_dofs());
u_star[
d].reinit(dof_handler_velocity.n_dofs());
force[
d].reinit(dof_handler_velocity.n_dofs());
}
v_tmp.reinit(dof_handler_velocity.n_dofs());
rot_u.reinit(dof_handler_velocity.n_dofs());
std::cout << "dim (X_h) = " << (dof_handler_velocity.n_dofs() * dim)
<< std::endl
<< "dim (M_h) = " << dof_handler_pressure.n_dofs()
<< std::endl
<< "Re = " << Re << std::endl
<< std::endl;
}
void attach_triangulation(Triangulation< dim, spacedim > &tria)
void read_ucd(std::istream &in, const bool apply_all_indicators_to_manifolds=false)
void Cuthill_McKee(DoFHandler< dim, spacedim > &dof_handler, const bool reversed_numbering=false, const bool use_constraints=false)
NavierStokesProjection::initialize
This method creates the constant matrices and loads the initial data
template <int dim>
void NavierStokesProjection<dim>::initialize()
{
vel_Laplace_plus_Mass = 0.;
vel_Laplace_plus_Mass.add(1. / Re, vel_Laplace);
vel_Laplace_plus_Mass.add(1.5 / dt, vel_Mass);
EquationData::Pressure<dim> pres(t_0);
pres.advance_time(dt);
phi_n = 0.;
phi_n_minus_1 = 0.;
for (
unsigned int d = 0;
d < dim; ++
d)
{
vel_exact.set_time(t_0);
vel_exact.set_component(
d);
vel_exact,
vel_exact.advance_time(dt);
}
}
NavierStokesProjection::initialize_*_matrices
In this set of methods we initialize the sparsity patterns, the constraints (if any) and assemble the matrices that do not depend on the timestep dt. Note that for the Laplace and mass matrices, we can use functions in the library that do this. Because the expensive operations of this function – creating the two matrices – are entirely independent, we could in principle mark them as tasks that can be worked on in parallel using the Threads::new_task functions. We won't do that here since these functions internally already are parallelized, and in particular because the current function is only called once per program run and so does not incur a cost in each time step. The necessary modifications would be quite straightforward, however.
template <int dim>
void NavierStokesProjection<dim>::initialize_velocity_matrices()
{
{
dof_handler_velocity.n_dofs());
sparsity_pattern_velocity.copy_from(dsp);
}
vel_Laplace_plus_Mass.reinit(sparsity_pattern_velocity);
for (
unsigned int d = 0;
d < dim; ++
d)
vel_it_matrix[
d].
reinit(sparsity_pattern_velocity);
vel_Mass.reinit(sparsity_pattern_velocity);
vel_Laplace.reinit(sparsity_pattern_velocity);
vel_Advection.reinit(sparsity_pattern_velocity);
quadrature_velocity,
vel_Mass);
quadrature_velocity,
vel_Laplace);
}
void make_sparsity_pattern(const DoFHandler< dim, spacedim > &dof_handler, SparsityPatternType &sparsity_pattern, const AffineConstraints< number > &constraints=AffineConstraints< number >(), const bool keep_constrained_dofs=true, const types::subdomain_id subdomain_id=numbers::invalid_subdomain_id)
void create_laplace_matrix(const Mapping< dim, spacedim > &mapping, const DoFHandler< dim, spacedim > &dof, const Quadrature< dim > &q, SparseMatrix< double > &matrix, const Function< spacedim > *const a=nullptr, const AffineConstraints< double > &constraints=AffineConstraints< double >())
void create_mass_matrix(const Mapping< dim, spacedim > &mapping, const DoFHandler< dim, spacedim > &dof, const Quadrature< dim > &q, SparseMatrix< number > &matrix, const Function< spacedim, number > *const a=nullptr, const AffineConstraints< number > &constraints=AffineConstraints< number >())
void reinit(MatrixBlock< MatrixType > &v, const BlockSparsityPattern &p)
The initialization of the matrices that act on the pressure space is similar to the ones that act on the velocity space.
template <int dim>
void NavierStokesProjection<dim>::initialize_pressure_matrices()
{
{
dof_handler_pressure.n_dofs());
sparsity_pattern_pressure.copy_from(dsp);
}
pres_Laplace.reinit(sparsity_pattern_pressure);
pres_iterative.reinit(sparsity_pattern_pressure);
pres_Mass.reinit(sparsity_pattern_pressure);
quadrature_pressure,
pres_Laplace);
quadrature_pressure,
pres_Mass);
}
For the gradient operator, we start by initializing the sparsity pattern and compressing it. It is important to notice here that the gradient operator acts from the pressure space into the velocity space, so we have to deal with two different finite element spaces. To keep the loops synchronized, we use the alias that we have defined before, namely PairedIterators and IteratorPair.
template <int dim>
void NavierStokesProjection<dim>::initialize_gradient_operator()
{
{
dof_handler_pressure.n_dofs());
dof_handler_pressure,
dsp);
sparsity_pattern_pres_vel.copy_from(dsp);
}
InitGradPerTaskData per_task_data(0,
fe_velocity.n_dofs_per_cell(),
fe_pressure.n_dofs_per_cell());
InitGradScratchData scratch_data(fe_velocity,
fe_pressure,
quadrature_velocity,
for (
unsigned int d = 0;
d < dim; ++
d)
{
pres_Diff[
d].reinit(sparsity_pattern_pres_vel);
IteratorPair(IteratorTuple(dof_handler_velocity.begin_active(),
dof_handler_pressure.begin_active())),
IteratorPair(IteratorTuple(dof_handler_velocity.end(),
dof_handler_pressure.end())),
*this,
&NavierStokesProjection<dim>::assemble_one_cell_of_gradient,
&NavierStokesProjection<dim>::copy_gradient_local_to_global,
scratch_data,
per_task_data);
}
}
template <int dim>
void NavierStokesProjection<dim>::assemble_one_cell_of_gradient(
const IteratorPair & SI,
InitGradScratchData &scratch,
InitGradPerTaskData &data)
{
scratch.fe_val_vel.reinit(std::get<0>(*SI));
scratch.fe_val_pres.reinit(std::get<1>(*SI));
std::get<0>(*SI)->get_dof_indices(data.vel_local_dof_indices);
std::get<1>(*SI)->get_dof_indices(data.pres_local_dof_indices);
data.local_grad = 0.;
for (unsigned int q = 0; q < scratch.nqp; ++q)
{
for (unsigned int i = 0; i < data.vel_dpc; ++i)
for (unsigned int j = 0; j < data.pres_dpc; ++j)
data.local_grad(i, j) +=
-scratch.fe_val_vel.JxW(q) *
scratch.fe_val_vel.shape_grad(i, q)[data.d] *
scratch.fe_val_pres.shape_value(j, q);
}
}
template <int dim>
void NavierStokesProjection<dim>::copy_gradient_local_to_global(
const InitGradPerTaskData &data)
{
for (unsigned int i = 0; i < data.vel_dpc; ++i)
for (unsigned int j = 0; j < data.pres_dpc; ++j)
pres_Diff[data.d].add(data.vel_local_dof_indices[i],
data.pres_local_dof_indices[j],
data.local_grad(i, j));
}
@ update_values
Shape function values.
@ update_JxW_values
Transformed quadrature weights.
@ update_gradients
Shape function gradients.
void run(const std::vector< std::vector< Iterator > > &colored_iterators, Worker worker, Copier copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const unsigned int queue_length=2 *MultithreadInfo::n_threads(), const unsigned int chunk_size=8)
NavierStokesProjection::run
This is the time marching function, which starting at t_0 advances in time using the projection method with time step dt until T.
Its second parameter, verbose indicates whether the function should output information what it is doing at any given moment: for example, it will say whether we are working on the diffusion, projection substep; updating preconditioners etc. Rather than implementing this output using code like
we use the ConditionalOStream class to do that for us. That class takes an output stream and a condition that indicates whether the things you pass to it should be passed through to the given output stream, or should just be ignored. This way, above code simply becomes
and does the right thing in either case.
template <int dim>
const unsigned int output_interval)
{
const auto n_steps =
static_cast<unsigned int>((
T - t_0) / dt);
vel_exact.set_time(2. * dt);
output_results(1);
for (unsigned int n = 2; n <= n_steps; ++n)
{
if (n % output_interval == 0)
{
verbose_cout << "Plotting Solution" << std::endl;
output_results(n);
}
std::cout << "Step = " << n << " Time = " << (n * dt) << std::endl;
verbose_cout << " Interpolating the velocity " << std::endl;
interpolate_velocity();
verbose_cout << " Diffusion Step" << std::endl;
if (n % vel_update_prec == 0)
verbose_cout << " With reinitialization of the preconditioner"
<< std::endl;
diffusion_step((n % vel_update_prec == 0) || (n == 2));
verbose_cout << " Projection Step" << std::endl;
projection_step((n == 2));
verbose_cout << " Updating the Pressure" << std::endl;
update_pressure((n == 2));
vel_exact.advance_time(dt);
}
output_results(n_steps);
}
template <int dim>
void NavierStokesProjection<dim>::interpolate_velocity()
{
for (
unsigned int d = 0;
d < dim; ++
d)
{
u_star[
d].equ(2., u_n[
d]);
u_star[
d] -= u_n_minus_1[
d];
}
}
NavierStokesProjection::diffusion_step
The implementation of a diffusion step. Note that the expensive operation is the diffusion solve at the end of the function, which we have to do once for each velocity component. To accelerate things a bit, we allow to do this in parallel, using the Threads::new_task function which makes sure that the dim solves are all taken care of and are scheduled to available processors: if your machine has more than one processor core and no other parts of this program are using resources currently, then the diffusion solves will run in parallel. On the other hand, if your system has only one processor core then running things in parallel would be inefficient (since it leads, for example, to cache congestion) and things will be executed sequentially.
template <int dim>
void NavierStokesProjection<dim>::diffusion_step(const bool reinit_prec)
{
pres_tmp.equ(-1., pres_n);
pres_tmp.add(-4. / 3., phi_n, 1. / 3., phi_n_minus_1);
assemble_advection_term();
for (
unsigned int d = 0;
d < dim; ++
d)
{
v_tmp.equ(2. / dt, u_n[
d]);
v_tmp.add(-.5 / dt, u_n_minus_1[
d]);
vel_Mass.vmult_add(force[
d], v_tmp);
pres_Diff[
d].vmult_add(force[
d], pres_tmp);
vel_it_matrix[
d].copy_from(vel_Laplace_plus_Mass);
vel_it_matrix[
d].add(1., vel_Advection);
vel_exact.set_component(
d);
boundary_values.clear();
{
{
case 1:
dof_handler_velocity,
boundary_values);
break;
case 2:
vel_exact,
boundary_values);
break;
case 3:
dof_handler_velocity,
boundary_values);
break;
case 4:
dof_handler_velocity,
boundary_values);
break;
default:
}
}
}
for (
unsigned int d = 0;
d < dim; ++
d)
{
if (reinit_prec)
prec_velocity[
d].initialize(vel_it_matrix[
d],
vel_diag_strength, vel_off_diagonals));
&NavierStokesProjection<dim>::diffusion_component_solve, *
this,
d);
}
}
template <int dim>
void
NavierStokesProjection<dim>::diffusion_component_solve(
const unsigned int d)
{
solver_control,
gmres.solve(vel_it_matrix[
d], u_n[
d], force[
d], prec_velocity[
d]);
}
static ::ExceptionBase & ExcNotImplemented()
typename SparseLUDecomposition< number >::AdditionalData AdditionalData
Task< RT > new_task(const std::function< RT()> &function)
std::vector< value_type > l2_norm(const typename ::Triangulation< dim, spacedim >::cell_iterator &parent, const value_type parent_value)
NavierStokesProjection::assemble_advection_term
The following few functions deal with assembling the advection terms, which is the part of the system matrix for the diffusion step that changes at every time step. As mentioned above, we will run the assembly loop over all cells in parallel, using the WorkStream class and other facilities as described in the documentation module on Parallel computing with multiple processors accessing shared memory.
template <int dim>
void NavierStokesProjection<dim>::assemble_advection_term()
{
vel_Advection = 0.;
AdvectionPerTaskData data(fe_velocity.n_dofs_per_cell());
AdvectionScratchData scratch(fe_velocity,
quadrature_velocity,
dof_handler_velocity.begin_active(),
dof_handler_velocity.end(),
*this,
&NavierStokesProjection<dim>::assemble_one_cell_of_advection,
&NavierStokesProjection<dim>::copy_advection_local_to_global,
scratch,
data);
}
template <int dim>
void NavierStokesProjection<dim>::assemble_one_cell_of_advection(
AdvectionScratchData & scratch,
AdvectionPerTaskData & data)
{
scratch.fe_val.reinit(cell);
cell->get_dof_indices(data.local_dof_indices);
for (
unsigned int d = 0;
d < dim; ++
d)
{
scratch.fe_val.get_function_values(u_star[
d], scratch.u_star_tmp);
for (unsigned int q = 0; q < scratch.nqp; ++q)
scratch.u_star_local[q](
d) = scratch.u_star_tmp[q];
}
for (
unsigned int d = 0;
d < dim; ++
d)
{
scratch.fe_val.get_function_gradients(u_star[
d], scratch.grad_u_star);
for (unsigned int q = 0; q < scratch.nqp; ++q)
{
scratch.u_star_tmp[q] = 0.;
scratch.u_star_tmp[q] += scratch.grad_u_star[q][
d];
}
}
data.local_advection = 0.;
for (unsigned int q = 0; q < scratch.nqp; ++q)
for (unsigned int i = 0; i < scratch.dpc; ++i)
for (unsigned int j = 0; j < scratch.dpc; ++j)
data.local_advection(i, j) += (scratch.u_star_local[q] *
scratch.fe_val.shape_grad(j, q) *
scratch.fe_val.shape_value(i, q)
+
0.5 *
scratch.u_star_tmp[q] *
scratch.fe_val.shape_value(i, q) *
scratch.fe_val.shape_value(j, q))
* scratch.fe_val.JxW(q);
}
template <int dim>
void NavierStokesProjection<dim>::copy_advection_local_to_global(
const AdvectionPerTaskData &data)
{
for (unsigned int i = 0; i < fe_velocity.n_dofs_per_cell(); ++i)
for (unsigned int j = 0; j < fe_velocity.n_dofs_per_cell(); ++j)
vel_Advection.add(data.local_dof_indices[i],
data.local_dof_indices[j],
data.local_advection(i, j));
}
NavierStokesProjection::projection_step
This implements the projection step:
template <int dim>
void NavierStokesProjection<dim>::projection_step(const bool reinit_prec)
{
pres_iterative.copy_from(pres_Laplace);
pres_tmp = 0.;
for (
unsigned d = 0;
d < dim; ++
d)
pres_Diff[
d].Tvmult_add(pres_tmp, u_n[
d]);
phi_n_minus_1 = phi_n;
static std::map<types::global_dof_index, double> bval;
if (reinit_prec)
3,
bval);
if (reinit_prec)
prec_pres_Laplace.initialize(pres_iterative,
vel_diag_strength, vel_off_diagonals));
SolverControl solvercontrol(vel_max_its, vel_eps * pres_tmp.l2_norm());
cg.solve(pres_iterative, phi_n, pres_tmp, prec_pres_Laplace);
phi_n *= 1.5 / dt;
}
NavierStokesProjection::update_pressure
This is the pressure update step of the projection method. It implements the standard formulation of the method, that is
p^{n+1} = p^n +
\phi^{n+1},
or the rotational form, which is
p^{n+1} = p^n +
\phi^{n+1} - \frac{1}{Re} \nabla\cdot u^{n+1}.
template <int dim>
void NavierStokesProjection<dim>::update_pressure(const bool reinit_prec)
{
pres_n_minus_1 = pres_n;
switch (type)
{
case RunTimeParameters::Method::standard:
pres_n += phi_n;
break;
case RunTimeParameters::Method::rotational:
if (reinit_prec)
prec_mass.initialize(pres_Mass);
pres_n = pres_tmp;
prec_mass.solve(pres_n);
pres_n.sadd(1. / Re, 1., pres_n_minus_1);
pres_n += phi_n;
break;
default:
};
}
NavierStokesProjection::output_results
This method plots the current solution. The main difficulty is that we want to create a single output file that contains the data for all velocity components, the pressure, and also the vorticity of the flow. On the other hand, velocities and the pressure live on separate DoFHandler objects, and so can't be written to the same file using a single DataOut object. As a consequence, we have to work a bit harder to get the various pieces of data into a single DoFHandler object, and then use that to drive graphical output.
We will not elaborate on this process here, but rather refer to step-32, where a similar procedure is used (and is documented) to create a joint DoFHandler object for all variables.
Let us also note that we here compute the vorticity as a scalar quantity in a separate function, using the L^2 projection of the quantity \text{curl} u onto the finite element space used for the components of the velocity. In principle, however, we could also have computed as a pointwise quantity from the velocity, and do so through the DataPostprocessor mechanism discussed in step-29 and step-33.
template <int dim>
void NavierStokesProjection<dim>::output_results(const unsigned int step)
{
assemble_vorticity((step == 1));
fe_velocity, dim, fe_pressure, 1, fe_velocity, 1);
joint_dof_handler.distribute_dofs(joint_fe);
Assert(joint_dof_handler.n_dofs() ==
((dim + 1) * dof_handler_velocity.n_dofs() +
dof_handler_pressure.n_dofs()),
std::vector<types::global_dof_index> loc_joint_dof_indices(
joint_fe.n_dofs_per_cell()),
loc_vel_dof_indices(fe_velocity.n_dofs_per_cell()),
loc_pres_dof_indices(fe_pressure.n_dofs_per_cell());
joint_cell = joint_dof_handler.begin_active(),
joint_endc = joint_dof_handler.end(),
vel_cell = dof_handler_velocity.begin_active(),
pres_cell = dof_handler_pressure.begin_active();
for (; joint_cell != joint_endc; ++joint_cell, ++vel_cell, ++pres_cell)
{
joint_cell->get_dof_indices(loc_joint_dof_indices);
vel_cell->get_dof_indices(loc_vel_dof_indices);
pres_cell->get_dof_indices(loc_pres_dof_indices);
for (unsigned int i = 0; i < joint_fe.n_dofs_per_cell(); ++i)
switch (joint_fe.system_to_base_index(i).first.first)
{
case 0:
Assert(joint_fe.system_to_base_index(i).first.second < dim,
joint_solution(loc_joint_dof_indices[i]) =
u_n[joint_fe.system_to_base_index(i).first.second](
loc_vel_dof_indices[joint_fe.system_to_base_index(i)
.second]);
break;
case 1:
Assert(joint_fe.system_to_base_index(i).first.second == 0,
joint_solution(loc_joint_dof_indices[i]) =
pres_n(loc_pres_dof_indices[joint_fe.system_to_base_index(i)
.second]);
break;
case 2:
Assert(joint_fe.system_to_base_index(i).first.second == 0,
joint_solution(loc_joint_dof_indices[i]) = rot_u(
loc_vel_dof_indices[joint_fe.system_to_base_index(i).second]);
break;
default:
}
}
std::vector<std::string> joint_solution_names(dim, "v");
joint_solution_names.emplace_back("p");
joint_solution_names.emplace_back("rot_u");
std::vector<DataComponentInterpretation::DataComponentInterpretation>
component_interpretation(
component_interpretation[dim] =
component_interpretation[dim + 1] =
joint_solution_names,
component_interpretation);
".vtk");
}
void attach_dof_handler(const DoFHandlerType &)
void add_data_vector(const VectorType &data, const std::vector< std::string > &names, const DataVectorType type=type_automatic, const std::vector< DataComponentInterpretation::DataComponentInterpretation > &data_component_interpretation=std::vector< DataComponentInterpretation::DataComponentInterpretation >())
virtual void build_patches(const unsigned int n_subdivisions=0)
static ::ExceptionBase & ExcInternalError()
void write_vtk(std::ostream &out) const
@ component_is_part_of_vector
std::string int_to_string(const unsigned int value, const unsigned int digits=numbers::invalid_unsigned_int)
Following is the helper function that computes the vorticity by projecting the term \text{curl} u onto the finite element space used for the components of the velocity. The function is only called whenever we generate graphical output, so not very often, and as a consequence we didn't bother parallelizing it using the WorkStream concept as we do for the other assembly functions. That should not be overly complicated, however, if needed. Moreover, the implementation that we have here only works for 2d, so we bail if that is not the case.
template <int dim>
void NavierStokesProjection<dim>::assemble_vorticity(const bool reinit_prec)
{
if (reinit_prec)
prec_vel_mass.initialize(vel_Mass);
quadrature_velocity,
const unsigned int dpc = fe_velocity.n_dofs_per_cell(),
nqp = quadrature_velocity.size();
std::vector<types::global_dof_index> ldi(dpc);
std::vector<Tensor<1, dim>> grad_u1(nqp), grad_u2(nqp);
rot_u = 0.;
for (const auto &cell : dof_handler_velocity.active_cell_iterators())
{
fe_val_vel.reinit(cell);
cell->get_dof_indices(ldi);
fe_val_vel.get_function_gradients(u_n[0], grad_u1);
fe_val_vel.get_function_gradients(u_n[1], grad_u2);
loc_rot = 0.;
for (unsigned int q = 0; q < nqp; ++q)
for (unsigned int i = 0; i < dpc; ++i)
loc_rot(i) += (grad_u2[q][0] - grad_u1[q][1]) *
fe_val_vel.shape_value(i, q) *
fe_val_vel.JxW(q);
for (unsigned int i = 0; i < dpc; ++i)
rot_u(ldi[i]) += loc_rot(i);
}
prec_vel_mass.solve(rot_u);
}
}
The main function
The main function looks very much like in all the other tutorial programs, so there is little to comment on here:
int main()
{
try
{
using namespace Step35;
RunTimeParameters::Data_Storage data;
data.read_data("parameter-file.prm");
NavierStokesProjection<2> test(data);
test.run(data.verbose, data.output_interval);
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
std::cout << "----------------------------------------------------"
<< std::endl
<< "Apparently everything went fine!" << std::endl
<< "Don't forget to brush your teeth :-)" << std::endl
<< std::endl;
return 0;
}
unsigned int depth_console(const unsigned int n)
Results
Re = 100
We run the code with the following parameter-file.prm, which can be found in the same directory as the source:
# First a global definition
# the type of method we want to use
set Method_Form = rotational
subsection Physical data
# In this subsection we declare the physical data
# The initial and final time, and the Reynolds number
set initial_time = 0.
set final_time = 25.
set Reynolds = 100
end
subsection Time step data
# In this subsection we declare the data that is to be used for time discretization,
# i.e. the time step dt
set dt = 5e-3
end
subsection Space discretization
# In this subsection we declare the data that is relevant to the space discretization
# we set the number of global refines the triangulation must have
# and the degree k of the pair Q_(k+1)--Q_k of velocity--pressure finite element spaces
set n_of_refines = 3
set pressure_fe_degree = 1
end
subsection Data solve velocity
# In this section we declare the parameters that are going to control the solution process
# for the velocity.
set max_iterations = 1000 # maximal number of iterations that GMRES must make
set eps = 1e-6 # stopping criterion
set Krylov_size = 30 # size of the Krylov subspace to be used in GMRES
set off_diagonals = 60 # number of off diagonals that ILU must compute
set diag_strength = 0.01 # diagonal strengthening value
set update_prec = 10 # this number indicates how often the preconditioner must be updated
end
#The output frequency
set output = 50
#Finally we set the verbosity level
set verbose = false
Since the verbose parameter is set to false, we do not get any kind of output besides the number of the time step the program is currently working on. If we were to set it to true we would get information on what the program is doing and how many steps each iterative process had to make to converge, etc.
Let us plot the obtained results for t=1,5,12,20,25 (i.e. time steps 200, 1000, 2400, 4000, and 5000), where in the left column we show the vorticity and in the right the velocity field:
The images show nicely the development and extension of a vortex chain behind the obstacles, with the sign of the vorticity indicating whether this is a left or right turning vortex.
Re = 500
We can change the Reynolds number, Re, in the parameter file to a value of 500. Doing so, and reducing the time step somewhat as well, yields the following images at times t=20,40:
For this larger Reynolds number, we observe unphysical oscillations, especially for the vorticity. The discretization scheme has now difficulties in correctly resolving the flow, which should still be laminar and well-organized. These phenomena are typical of discretization schemes that lack robustness in under-resolved scenarios, where under-resolved means that the Reynolds number computed with the mesh size instead of the physical dimensions of the geometry is large. We look at a zoom at the region behind the obstacle, and the mesh size we have there:
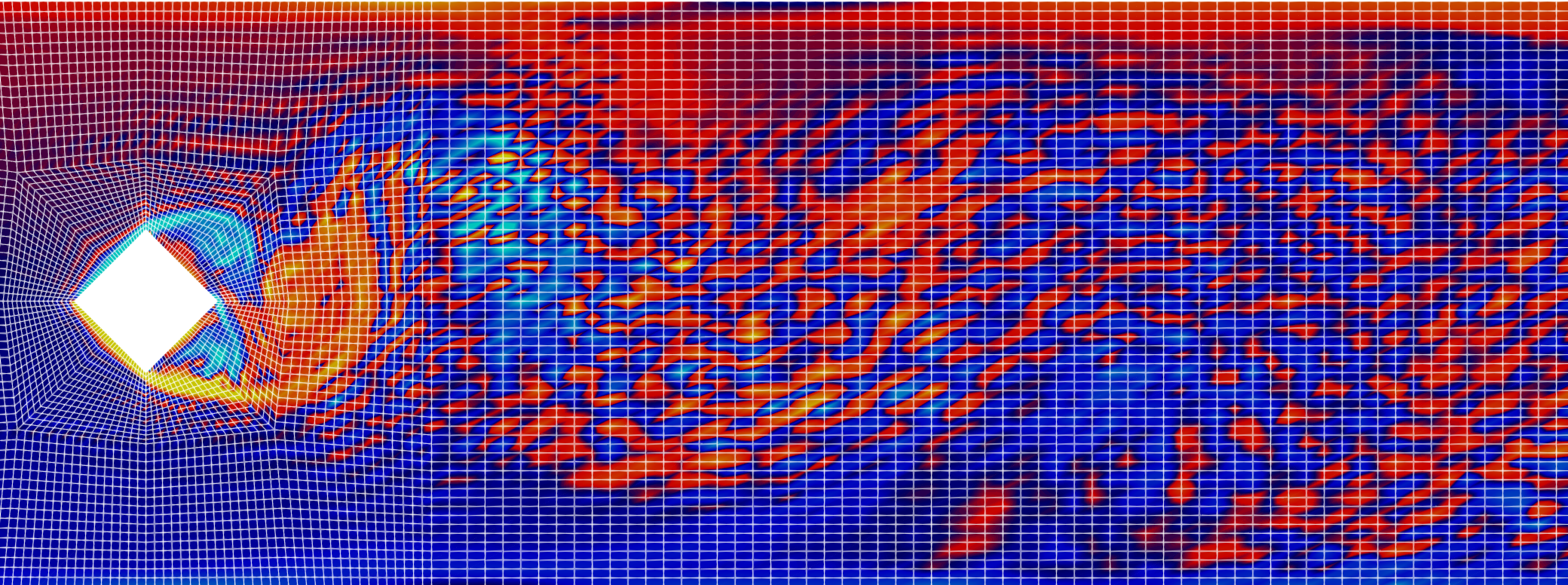
We can easily test our hypothesis by re-running the simulation with one more mesh refinement set in the parameter file :

Indeed, the vorticity field now looks much smoother. While we can expect that further refining the mesh will suppress the remaining oscillations as well, one should take measures to obtain a robust scheme in the limit of coarse resolutions, as described below.
Possibilities for extensions
This program can be extended in the following directions:
-
Adaptive mesh refinement: As we have seen, we computed everything on a single fixed mesh. Using adaptive mesh refinement can lead to increased accuracy while not significantly increasing the computational time.
-
Adaptive time-stepping: Although there apparently is currently no theory about projection methods with variable time step, practice shows that they perform very well.
-
High Reynolds numbers: As we can see from the results, increasing the Reynolds number changes significantly the behavior of the discretization scheme. Using well-known stabilization techniques we could be able to compute the flow in this, or many other problems, when the Reynolds number is very large and where computational costs demand spatial resolutions for which the flow is only marginally resolved, especially for 3D turbulent flows.
-
Variable density incompressible flows: There are projection-like methods for the case of incompressible flows with variable density. Such flows play a role if fluids of different density mix, for example fresh water and salt water, or alcohol and water.
-
Compressible Navier-Stokes equations: These equations are relevant for cases where velocities are high enough so that the fluid becomes compressible, but not fast enough that we get into a regime where viscosity becomes negligible and the Navier-Stokes equations need to be replaced by the hyperbolic Euler equations of gas dynamics. Compressibility starts to become a factor if the velocity becomes greater than about one third of the speed of sound, so it is not a factor for almost all terrestrial vehicles. On the other hand, commercial jetliners fly at about 85 per cent of the speed of sound, and flow over the wings becomes significantly supersonic, a regime in which the compressible Navier-Stokes equations are not applicable any more either. There are significant applications for the range in between, however, such as for small aircraft or the fast trains in many European and East Asian countries.
The plain program
#include <fstream>
#include <cmath>
#include <iostream>
namespace Step35
{
namespace RunTimeParameters
{
enum class Method
{
standard,
rotational
};
class Data_Storage
{
public:
Data_Storage();
void read_data(const std::string &filename);
Method form;
double dt;
double initial_time;
double final_time;
double Reynolds;
unsigned int n_global_refines;
unsigned int pressure_degree;
unsigned int vel_max_iterations;
unsigned int vel_Krylov_size;
unsigned int vel_off_diagonals;
unsigned int vel_update_prec;
double vel_eps;
double vel_diag_strength;
bool verbose;
unsigned int output_interval;
protected:
};
Data_Storage::Data_Storage()
: form(Method::rotational)
, initial_time(0.)
, final_time(1.)
, Reynolds(1.)
, n_global_refines(0)
, pressure_degree(1)
, vel_max_iterations(1000)
, vel_Krylov_size(30)
, vel_off_diagonals(60)
, vel_update_prec(15)
, vel_diag_strength(0.01)
, verbose(true)
, output_interval(15)
{
prm.declare_entry("Method_Form",
"rotational",
" Used to select the type of method that we are going "
"to use. ");
prm.enter_subsection("Physical data");
{
prm.declare_entry("initial_time",
"0.",
" The initial time of the simulation. ");
prm.declare_entry("final_time",
"1.",
" The final time of the simulation. ");
prm.declare_entry("Reynolds",
"1.",
" The Reynolds number. ");
}
prm.leave_subsection();
prm.enter_subsection("Time step data");
{
prm.declare_entry("dt",
"5e-4",
" The time step size. ");
}
prm.leave_subsection();
prm.enter_subsection("Space discretization");
{
prm.declare_entry("n_of_refines",
"0",
" The number of global refines we do on the mesh. ");
prm.declare_entry("pressure_fe_degree",
"1",
" The polynomial degree for the pressure space. ");
}
prm.leave_subsection();
prm.enter_subsection("Data solve velocity");
{
prm.declare_entry(
"max_iterations",
"1000",
" The maximal number of iterations GMRES must make. ");
prm.declare_entry("eps",
"1e-12",
" The stopping criterion. ");
prm.declare_entry("Krylov_size",
"30",
" The size of the Krylov subspace to be used. ");
prm.declare_entry("off_diagonals",
"60",
" The number of off-diagonal elements ILU must "
"compute. ");
prm.declare_entry("diag_strength",
"0.01",
" Diagonal strengthening coefficient. ");
prm.declare_entry("update_prec",
"15",
" This number indicates how often we need to "
"update the preconditioner");
}
prm.leave_subsection();
prm.declare_entry("verbose",
"true",
" This indicates whether the output of the solution "
"process should be verbose. ");
prm.declare_entry("output_interval",
"1",
" This indicates between how many time steps we print "
"the solution. ");
}
void Data_Storage::read_data(const std::string &filename)
{
std::ifstream file(filename);
prm.parse_input(file);
if (prm.get("Method_Form") == std::string("rotational"))
form = Method::rotational;
else
form = Method::standard;
prm.enter_subsection("Physical data");
{
initial_time = prm.get_double("initial_time");
final_time = prm.get_double("final_time");
Reynolds = prm.get_double("Reynolds");
}
prm.leave_subsection();
prm.enter_subsection("Time step data");
{
dt = prm.get_double("dt");
}
prm.leave_subsection();
prm.enter_subsection("Space discretization");
{
n_global_refines = prm.get_integer("n_of_refines");
pressure_degree = prm.get_integer("pressure_fe_degree");
}
prm.leave_subsection();
prm.enter_subsection("Data solve velocity");
{
vel_max_iterations = prm.get_integer("max_iterations");
vel_eps = prm.get_double("eps");
vel_Krylov_size = prm.get_integer("Krylov_size");
vel_off_diagonals = prm.get_integer("off_diagonals");
vel_diag_strength = prm.get_double("diag_strength");
vel_update_prec = prm.get_integer("update_prec");
}
prm.leave_subsection();
verbose = prm.get_bool("verbose");
output_interval = prm.get_integer("output_interval");
}
}
namespace EquationData
{
template <int dim>
class MultiComponentFunction :
public Function<dim>
{
public:
MultiComponentFunction(const double initial_time = 0.);
void set_component(
const unsigned int d);
protected:
unsigned int comp;
};
template <int dim>
MultiComponentFunction<dim>::MultiComponentFunction(
const double initial_time)
, comp(0)
{}
template <int dim>
void MultiComponentFunction<dim>::set_component(
const unsigned int d)
{
}
template <int dim>
class Velocity : public MultiComponentFunction<dim>
{
public:
Velocity(const double initial_time = 0.0);
const unsigned int component = 0) const override;
virtual void value_list(
const std::vector<
Point<dim>> &points,
const unsigned int component = 0) const override;
};
template <int dim>
Velocity<dim>::Velocity(const double initial_time)
: MultiComponentFunction<dim>(initial_time)
{}
template <int dim>
void Velocity<dim>::value_list(
const std::vector<
Point<dim>> &points,
const unsigned int) const
{
const unsigned int n_points = points.size();
for (unsigned int i = 0; i < n_points; ++i)
values[i] = Velocity<dim>::value(points[i]);
}
template <int dim>
double Velocity<dim>::value(
const Point<dim> &p,
const unsigned int)
const
{
if (this->comp == 0)
{
const double Um = 1.5;
const double H = 4.1;
return 4. * Um * p(1) * (H - p(1)) / (H * H);
}
else
return 0.;
}
template <int dim>
{
public:
Pressure(const double initial_time = 0.0);
const unsigned int component = 0) const override;
const unsigned int component = 0) const override;
};
template <int dim>
Pressure<dim>::Pressure(const double initial_time)
{}
template <int dim>
const unsigned int component) const
{
(void)component;
return 25. - p(0);
}
template <int dim>
void Pressure<dim>::value_list(
const std::vector<
Point<dim>> &points,
const unsigned int component) const
{
(void)component;
const unsigned int n_points = points.size();
for (unsigned int i = 0; i < n_points; ++i)
values[i] = Pressure<dim>::value(points[i]);
}
}
template <int dim>
class NavierStokesProjection
{
public:
NavierStokesProjection(const RunTimeParameters::Data_Storage &data);
void run(
const bool verbose =
false,
const unsigned int n_plots = 10);
protected:
RunTimeParameters::Method type;
const unsigned int deg;
const double dt;
const double t_0;
const double Re;
EquationData::Velocity<dim> vel_exact;
std::map<types::global_dof_index, double> boundary_values;
std::vector<types::boundary_id> boundary_ids;
double,
double,
<< " The time step " << arg1 << " is out of range."
<< std::endl
<< " The permitted range is (0," << arg2 << "]");
void create_triangulation_and_dofs(const unsigned int n_refines);
void initialize();
void interpolate_velocity();
void diffusion_step(const bool reinit_prec);
void projection_step(const bool reinit_prec);
void update_pressure(const bool reinit_prec);
private:
unsigned int vel_max_its;
unsigned int vel_Krylov_size;
unsigned int vel_off_diagonals;
unsigned int vel_update_prec;
double vel_eps;
double vel_diag_strength;
void initialize_velocity_matrices();
void initialize_pressure_matrices();
using IteratorTuple =
std::tuple<typename DoFHandler<dim>::active_cell_iterator,
void initialize_gradient_operator();
struct InitGradPerTaskData
{
unsigned int vel_dpc;
unsigned int pres_dpc;
std::vector<types::global_dof_index> vel_local_dof_indices;
std::vector<types::global_dof_index> pres_local_dof_indices;
InitGradPerTaskData(const unsigned int dd,
const unsigned int vdpc,
const unsigned int pdpc)
, vel_dpc(vdpc)
, pres_dpc(pdpc)
, local_grad(vdpc, pdpc)
, vel_local_dof_indices(vdpc)
, pres_local_dof_indices(pdpc)
{}
};
struct InitGradScratchData
{
unsigned int nqp;
: nqp(quad.size())
, fe_val_vel(fe_v, quad, flags_v)
, fe_val_pres(fe_p, quad, flags_p)
{}
InitGradScratchData(const InitGradScratchData &data)
: nqp(data.nqp)
, fe_val_vel(data.fe_val_vel.get_fe(),
data.fe_val_vel.get_quadrature(),
data.fe_val_vel.get_update_flags())
, fe_val_pres(data.fe_val_pres.get_fe(),
data.fe_val_pres.get_quadrature(),
data.fe_val_pres.get_update_flags())
{}
};
void assemble_one_cell_of_gradient(const IteratorPair & SI,
InitGradScratchData &scratch,
InitGradPerTaskData &data);
void copy_gradient_local_to_global(const InitGradPerTaskData &data);
void assemble_advection_term();
struct AdvectionPerTaskData
{
std::vector<types::global_dof_index> local_dof_indices;
AdvectionPerTaskData(const unsigned int dpc)
: local_advection(dpc, dpc)
, local_dof_indices(dpc)
{}
};
struct AdvectionScratchData
{
unsigned int nqp;
unsigned int dpc;
std::vector<Point<dim>> u_star_local;
std::vector<Tensor<1, dim>> grad_u_star;
std::vector<double> u_star_tmp;
: nqp(quad.size())
, dpc(fe.n_dofs_per_cell())
, u_star_local(nqp)
, grad_u_star(nqp)
, u_star_tmp(nqp)
, fe_val(fe, quad, flags)
{}
AdvectionScratchData(const AdvectionScratchData &data)
: nqp(data.nqp)
, dpc(data.dpc)
, u_star_local(nqp)
, grad_u_star(nqp)
, u_star_tmp(nqp)
, fe_val(data.fe_val.get_fe(),
data.fe_val.get_quadrature(),
data.fe_val.get_update_flags())
{}
};
void assemble_one_cell_of_advection(
AdvectionScratchData & scratch,
AdvectionPerTaskData & data);
void copy_advection_local_to_global(const AdvectionPerTaskData &data);
void diffusion_component_solve(
const unsigned int d);
void output_results(const unsigned int step);
void assemble_vorticity(const bool reinit_prec);
};
template <int dim>
NavierStokesProjection<dim>::NavierStokesProjection(
const RunTimeParameters::Data_Storage &data)
: type(data.form)
, deg(data.pressure_degree)
, dt(data.dt)
, t_0(data.initial_time)
, Re(data.Reynolds)
, vel_exact(data.initial_time)
, fe_velocity(deg + 1)
, fe_pressure(deg)
, quadrature_pressure(deg + 1)
, quadrature_velocity(deg + 2)
, vel_max_its(data.vel_max_iterations)
, vel_Krylov_size(data.vel_Krylov_size)
, vel_off_diagonals(data.vel_off_diagonals)
, vel_update_prec(data.vel_update_prec)
, vel_eps(data.vel_eps)
, vel_diag_strength(data.vel_diag_strength)
{
if (deg < 1)
std::cout
<< " WARNING: The chosen pair of finite element spaces is not stable."
<< std::endl
<< " The obtained results will be nonsense" << std::endl;
AssertThrow(!((dt <= 0.) || (dt > .5 *
T)), ExcInvalidTimeStep(dt, .5 *
T));
create_triangulation_and_dofs(data.n_global_refines);
initialize();
}
template <int dim>
void NavierStokesProjection<dim>::create_triangulation_and_dofs(
const unsigned int n_refines)
{
{
std::string filename = "nsbench2.inp";
std::ifstream file(filename);
}
std::cout << "Number of refines = " << n_refines << std::endl;
std::cout <<
"Number of active cells: " <<
triangulation.n_active_cells()
<< std::endl;
dof_handler_velocity.distribute_dofs(fe_velocity);
dof_handler_pressure.distribute_dofs(fe_pressure);
initialize_velocity_matrices();
initialize_pressure_matrices();
initialize_gradient_operator();
pres_n.reinit(dof_handler_pressure.n_dofs());
pres_n_minus_1.reinit(dof_handler_pressure.n_dofs());
phi_n.reinit(dof_handler_pressure.n_dofs());
phi_n_minus_1.reinit(dof_handler_pressure.n_dofs());
pres_tmp.reinit(dof_handler_pressure.n_dofs());
for (
unsigned int d = 0;
d < dim; ++
d)
{
u_n[
d].reinit(dof_handler_velocity.n_dofs());
u_n_minus_1[
d].reinit(dof_handler_velocity.n_dofs());
u_star[
d].reinit(dof_handler_velocity.n_dofs());
force[
d].reinit(dof_handler_velocity.n_dofs());
}
v_tmp.reinit(dof_handler_velocity.n_dofs());
rot_u.reinit(dof_handler_velocity.n_dofs());
std::cout << "dim (X_h) = " << (dof_handler_velocity.n_dofs() * dim)
<< std::endl
<< "dim (M_h) = " << dof_handler_pressure.n_dofs()
<< std::endl
<< "Re = " << Re << std::endl
<< std::endl;
}
template <int dim>
void NavierStokesProjection<dim>::initialize()
{
vel_Laplace_plus_Mass = 0.;
vel_Laplace_plus_Mass.add(1. / Re, vel_Laplace);
vel_Laplace_plus_Mass.add(1.5 / dt, vel_Mass);
EquationData::Pressure<dim> pres(t_0);
pres.advance_time(dt);
phi_n = 0.;
phi_n_minus_1 = 0.;
for (
unsigned int d = 0;
d < dim; ++
d)
{
vel_exact.set_time(t_0);
vel_exact.set_component(
d);
vel_exact,
vel_exact.advance_time(dt);
}
}
template <int dim>
void NavierStokesProjection<dim>::initialize_velocity_matrices()
{
{
dof_handler_velocity.n_dofs());
sparsity_pattern_velocity.copy_from(dsp);
}
vel_Laplace_plus_Mass.reinit(sparsity_pattern_velocity);
for (
unsigned int d = 0;
d < dim; ++
d)
vel_it_matrix[
d].
reinit(sparsity_pattern_velocity);
vel_Mass.reinit(sparsity_pattern_velocity);
vel_Laplace.reinit(sparsity_pattern_velocity);
vel_Advection.reinit(sparsity_pattern_velocity);
quadrature_velocity,
vel_Mass);
quadrature_velocity,
vel_Laplace);
}
template <int dim>
void NavierStokesProjection<dim>::initialize_pressure_matrices()
{
{
dof_handler_pressure.n_dofs());
sparsity_pattern_pressure.copy_from(dsp);
}
pres_Laplace.reinit(sparsity_pattern_pressure);
pres_iterative.reinit(sparsity_pattern_pressure);
pres_Mass.reinit(sparsity_pattern_pressure);
quadrature_pressure,
pres_Laplace);
quadrature_pressure,
pres_Mass);
}
template <int dim>
void NavierStokesProjection<dim>::initialize_gradient_operator()
{
{
dof_handler_pressure.n_dofs());
dof_handler_pressure,
dsp);
sparsity_pattern_pres_vel.copy_from(dsp);
}
InitGradPerTaskData per_task_data(0,
fe_velocity.n_dofs_per_cell(),
fe_pressure.n_dofs_per_cell());
InitGradScratchData scratch_data(fe_velocity,
fe_pressure,
quadrature_velocity,
for (
unsigned int d = 0;
d < dim; ++
d)
{
pres_Diff[
d].reinit(sparsity_pattern_pres_vel);
IteratorPair(IteratorTuple(dof_handler_velocity.begin_active(),
dof_handler_pressure.begin_active())),
IteratorPair(IteratorTuple(dof_handler_velocity.end(),
dof_handler_pressure.end())),
*this,
&NavierStokesProjection<dim>::assemble_one_cell_of_gradient,
&NavierStokesProjection<dim>::copy_gradient_local_to_global,
scratch_data,
per_task_data);
}
}
template <int dim>
void NavierStokesProjection<dim>::assemble_one_cell_of_gradient(
const IteratorPair & SI,
InitGradScratchData &scratch,
InitGradPerTaskData &data)
{
scratch.fe_val_vel.reinit(std::get<0>(*SI));
scratch.fe_val_pres.reinit(std::get<1>(*SI));
std::get<0>(*SI)->get_dof_indices(data.vel_local_dof_indices);
std::get<1>(*SI)->get_dof_indices(data.pres_local_dof_indices);
data.local_grad = 0.;
for (unsigned int q = 0; q < scratch.nqp; ++q)
{
for (unsigned int i = 0; i < data.vel_dpc; ++i)
for (unsigned int j = 0; j < data.pres_dpc; ++j)
data.local_grad(i, j) +=
-scratch.fe_val_vel.JxW(q) *
scratch.fe_val_vel.shape_grad(i, q)[data.d] *
scratch.fe_val_pres.shape_value(j, q);
}
}
template <int dim>
void NavierStokesProjection<dim>::copy_gradient_local_to_global(
const InitGradPerTaskData &data)
{
for (unsigned int i = 0; i < data.vel_dpc; ++i)
for (unsigned int j = 0; j < data.pres_dpc; ++j)
pres_Diff[data.d].add(data.vel_local_dof_indices[i],
data.pres_local_dof_indices[j],
data.local_grad(i, j));
}
template <int dim>
const unsigned int output_interval)
{
const auto n_steps =
static_cast<unsigned int>((
T - t_0) / dt);
vel_exact.set_time(2. * dt);
output_results(1);
for (unsigned int n = 2; n <= n_steps; ++n)
{
if (n % output_interval == 0)
{
verbose_cout << "Plotting Solution" << std::endl;
output_results(n);
}
std::cout << "Step = " << n << " Time = " << (n * dt) << std::endl;
verbose_cout << " Interpolating the velocity " << std::endl;
interpolate_velocity();
verbose_cout << " Diffusion Step" << std::endl;
if (n % vel_update_prec == 0)
verbose_cout << " With reinitialization of the preconditioner"
<< std::endl;
diffusion_step((n % vel_update_prec == 0) || (n == 2));
verbose_cout << " Projection Step" << std::endl;
projection_step((n == 2));
verbose_cout << " Updating the Pressure" << std::endl;
update_pressure((n == 2));
vel_exact.advance_time(dt);
}
output_results(n_steps);
}
template <int dim>
void NavierStokesProjection<dim>::interpolate_velocity()
{
for (
unsigned int d = 0;
d < dim; ++
d)
{
u_star[
d].equ(2., u_n[
d]);
u_star[
d] -= u_n_minus_1[
d];
}
}
template <int dim>
void NavierStokesProjection<dim>::diffusion_step(const bool reinit_prec)
{
pres_tmp.equ(-1., pres_n);
pres_tmp.add(-4. / 3., phi_n, 1. / 3., phi_n_minus_1);
assemble_advection_term();
for (
unsigned int d = 0;
d < dim; ++
d)
{
v_tmp.equ(2. / dt, u_n[
d]);
v_tmp.add(-.5 / dt, u_n_minus_1[
d]);
vel_Mass.vmult_add(force[
d], v_tmp);
pres_Diff[
d].vmult_add(force[
d], pres_tmp);
vel_it_matrix[
d].copy_from(vel_Laplace_plus_Mass);
vel_it_matrix[
d].add(1., vel_Advection);
vel_exact.set_component(
d);
boundary_values.clear();
{
{
case 1:
dof_handler_velocity,
boundary_values);
break;
case 2:
vel_exact,
boundary_values);
break;
case 3:
dof_handler_velocity,
boundary_values);
break;
case 4:
dof_handler_velocity,
boundary_values);
break;
default:
}
}
}
for (
unsigned int d = 0;
d < dim; ++
d)
{
if (reinit_prec)
prec_velocity[
d].initialize(vel_it_matrix[
d],
vel_diag_strength, vel_off_diagonals));
&NavierStokesProjection<dim>::diffusion_component_solve, *
this,
d);
}
}
template <int dim>
void
NavierStokesProjection<dim>::diffusion_component_solve(
const unsigned int d)
{
solver_control,
gmres.solve(vel_it_matrix[
d], u_n[
d], force[
d], prec_velocity[
d]);
}
template <int dim>
void NavierStokesProjection<dim>::assemble_advection_term()
{
vel_Advection = 0.;
AdvectionPerTaskData data(fe_velocity.n_dofs_per_cell());
AdvectionScratchData scratch(fe_velocity,
quadrature_velocity,
dof_handler_velocity.begin_active(),
dof_handler_velocity.end(),
*this,
&NavierStokesProjection<dim>::assemble_one_cell_of_advection,
&NavierStokesProjection<dim>::copy_advection_local_to_global,
scratch,
data);
}
template <int dim>
void NavierStokesProjection<dim>::assemble_one_cell_of_advection(
AdvectionScratchData & scratch,
AdvectionPerTaskData & data)
{
scratch.fe_val.reinit(cell);
cell->get_dof_indices(data.local_dof_indices);
for (
unsigned int d = 0;
d < dim; ++
d)
{
scratch.fe_val.get_function_values(u_star[
d], scratch.u_star_tmp);
for (unsigned int q = 0; q < scratch.nqp; ++q)
scratch.u_star_local[q](
d) = scratch.u_star_tmp[q];
}
for (
unsigned int d = 0;
d < dim; ++
d)
{
scratch.fe_val.get_function_gradients(u_star[
d], scratch.grad_u_star);
for (unsigned int q = 0; q < scratch.nqp; ++q)
{
scratch.u_star_tmp[q] = 0.;
scratch.u_star_tmp[q] += scratch.grad_u_star[q][
d];
}
}
data.local_advection = 0.;
for (unsigned int q = 0; q < scratch.nqp; ++q)
for (unsigned int i = 0; i < scratch.dpc; ++i)
for (unsigned int j = 0; j < scratch.dpc; ++j)
data.local_advection(i, j) += (scratch.u_star_local[q] *
scratch.fe_val.shape_grad(j, q) *
scratch.fe_val.shape_value(i, q)
+
0.5 *
scratch.u_star_tmp[q] *
scratch.fe_val.shape_value(i, q) *
scratch.fe_val.shape_value(j, q))
* scratch.fe_val.JxW(q);
}
template <int dim>
void NavierStokesProjection<dim>::copy_advection_local_to_global(
const AdvectionPerTaskData &data)
{
for (unsigned int i = 0; i < fe_velocity.n_dofs_per_cell(); ++i)
for (unsigned int j = 0; j < fe_velocity.n_dofs_per_cell(); ++j)
vel_Advection.add(data.local_dof_indices[i],
data.local_dof_indices[j],
data.local_advection(i, j));
}
template <int dim>
void NavierStokesProjection<dim>::projection_step(const bool reinit_prec)
{
pres_iterative.copy_from(pres_Laplace);
pres_tmp = 0.;
for (
unsigned d = 0;
d < dim; ++
d)
pres_Diff[
d].Tvmult_add(pres_tmp, u_n[
d]);
phi_n_minus_1 = phi_n;
static std::map<types::global_dof_index, double> bval;
if (reinit_prec)
3,
bval);
if (reinit_prec)
prec_pres_Laplace.initialize(pres_iterative,
vel_diag_strength, vel_off_diagonals));
SolverControl solvercontrol(vel_max_its, vel_eps * pres_tmp.l2_norm());
cg.solve(pres_iterative, phi_n, pres_tmp, prec_pres_Laplace);
phi_n *= 1.5 / dt;
}
template <int dim>
void NavierStokesProjection<dim>::update_pressure(const bool reinit_prec)
{
pres_n_minus_1 = pres_n;
switch (type)
{
case RunTimeParameters::Method::standard:
pres_n += phi_n;
break;
case RunTimeParameters::Method::rotational:
if (reinit_prec)
prec_mass.initialize(pres_Mass);
pres_n = pres_tmp;
prec_mass.solve(pres_n);
pres_n.sadd(1. / Re, 1., pres_n_minus_1);
pres_n += phi_n;
break;
default:
};
}
template <int dim>
void NavierStokesProjection<dim>::output_results(const unsigned int step)
{
assemble_vorticity((step == 1));
fe_velocity, dim, fe_pressure, 1, fe_velocity, 1);
joint_dof_handler.distribute_dofs(joint_fe);
Assert(joint_dof_handler.n_dofs() ==
((dim + 1) * dof_handler_velocity.n_dofs() +
dof_handler_pressure.n_dofs()),
std::vector<types::global_dof_index> loc_joint_dof_indices(
joint_fe.n_dofs_per_cell()),
loc_vel_dof_indices(fe_velocity.n_dofs_per_cell()),
loc_pres_dof_indices(fe_pressure.n_dofs_per_cell());
joint_cell = joint_dof_handler.begin_active(),
joint_endc = joint_dof_handler.end(),
vel_cell = dof_handler_velocity.begin_active(),
pres_cell = dof_handler_pressure.begin_active();
for (; joint_cell != joint_endc; ++joint_cell, ++vel_cell, ++pres_cell)
{
joint_cell->get_dof_indices(loc_joint_dof_indices);
vel_cell->get_dof_indices(loc_vel_dof_indices);
pres_cell->get_dof_indices(loc_pres_dof_indices);
for (unsigned int i = 0; i < joint_fe.n_dofs_per_cell(); ++i)
switch (joint_fe.system_to_base_index(i).first.first)
{
case 0:
Assert(joint_fe.system_to_base_index(i).first.second < dim,
joint_solution(loc_joint_dof_indices[i]) =
u_n[joint_fe.system_to_base_index(i).first.second](
loc_vel_dof_indices[joint_fe.system_to_base_index(i)
.second]);
break;
case 1:
Assert(joint_fe.system_to_base_index(i).first.second == 0,
joint_solution(loc_joint_dof_indices[i]) =
pres_n(loc_pres_dof_indices[joint_fe.system_to_base_index(i)
.second]);
break;
case 2:
Assert(joint_fe.system_to_base_index(i).first.second == 0,
joint_solution(loc_joint_dof_indices[i]) = rot_u(
loc_vel_dof_indices[joint_fe.system_to_base_index(i).second]);
break;
default:
}
}
std::vector<std::string> joint_solution_names(dim, "v");
joint_solution_names.emplace_back("p");
joint_solution_names.emplace_back("rot_u");
std::vector<DataComponentInterpretation::DataComponentInterpretation>
component_interpretation(
component_interpretation[dim] =
component_interpretation[dim + 1] =
joint_solution_names,
component_interpretation);
".vtk");
}
template <int dim>
void NavierStokesProjection<dim>::assemble_vorticity(const bool reinit_prec)
{
if (reinit_prec)
prec_vel_mass.initialize(vel_Mass);
quadrature_velocity,
const unsigned int dpc = fe_velocity.n_dofs_per_cell(),
nqp = quadrature_velocity.size();
std::vector<types::global_dof_index> ldi(dpc);
std::vector<Tensor<1, dim>> grad_u1(nqp), grad_u2(nqp);
rot_u = 0.;
for (const auto &cell : dof_handler_velocity.active_cell_iterators())
{
fe_val_vel.reinit(cell);
cell->get_dof_indices(ldi);
fe_val_vel.get_function_gradients(u_n[0], grad_u1);
fe_val_vel.get_function_gradients(u_n[1], grad_u2);
loc_rot = 0.;
for (unsigned int q = 0; q < nqp; ++q)
for (unsigned int i = 0; i < dpc; ++i)
loc_rot(i) += (grad_u2[q][0] - grad_u1[q][1]) *
fe_val_vel.shape_value(i, q) *
fe_val_vel.JxW(q);
for (unsigned int i = 0; i < dpc; ++i)
rot_u(ldi[i]) += loc_rot(i);
}
prec_vel_mass.solve(rot_u);
}
}
int main()
{
try
{
using namespace Step35;
RunTimeParameters::Data_Storage data;
data.read_data("parameter-file.prm");
NavierStokesProjection<2> test(data);
test.run(data.verbose, data.output_interval);
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
std::cout << "----------------------------------------------------"
<< std::endl
<< "Apparently everything went fine!" << std::endl
<< "Don't forget to brush your teeth :-)" << std::endl
<< std::endl;
return 0;
}


















