 |
Reference documentation for deal.II version 9.3.3
|
 |
Reference documentation for deal.II version 9.3.3
|
#include <deal.II/grid/manifold_lib.h>
Public Types | |
| using | FaceVertexNormals = std::array< Tensor< 1, spacedim >, GeometryInfo< dim >::vertices_per_face > |
Public Member Functions | |
| TransfiniteInterpolationManifold () | |
| virtual | ~TransfiniteInterpolationManifold () override |
| virtual std::unique_ptr< Manifold< dim, spacedim > > | clone () const override |
| void | initialize (const Triangulation< dim, spacedim > &triangulation) |
| virtual Point< spacedim > | get_new_point (const ArrayView< const Point< spacedim > > &surrounding_points, const ArrayView< const double > &weights) const override |
| virtual void | get_new_points (const ArrayView< const Point< spacedim > > &surrounding_points, const Table< 2, double > &weights, ArrayView< Point< spacedim > > new_points) const override |
| Point< 1 > | get_new_point_on_quad (const Triangulation< 1, 1 >::quad_iterator &) const |
| Point< 2 > | get_new_point_on_quad (const Triangulation< 1, 2 >::quad_iterator &) const |
| Point< 3 > | get_new_point_on_quad (const Triangulation< 1, 3 >::quad_iterator &) const |
| Point< 3 > | get_new_point_on_hex (const Triangulation< 3, 3 >::hex_iterator &hex) const |
| Point< 1 > | get_new_point_on_face (const Triangulation< 1, 1 >::face_iterator &) const |
| Point< 2 > | get_new_point_on_face (const Triangulation< 1, 2 >::face_iterator &) const |
| Point< 3 > | get_new_point_on_face (const Triangulation< 1, 3 >::face_iterator &) const |
| Tensor< 1, 2 > | normal_vector (const Triangulation< 2, 2 >::face_iterator &face, const Point< 2 > &p) const |
| Tensor< 1, 3 > | normal_vector (const Triangulation< 3, 3 >::face_iterator &face, const Point< 3 > &p) const |
| void | get_normals_at_vertices (const Triangulation< 2, 2 >::face_iterator &face, FaceVertexNormals &n) const |
| void | get_normals_at_vertices (const Triangulation< 3, 3 >::face_iterator &face, FaceVertexNormals &n) const |
Computing the location of points. | |
| virtual Point< spacedim > | get_intermediate_point (const Point< spacedim > &p1, const Point< spacedim > &p2, const double w) const |
| virtual Point< spacedim > | project_to_manifold (const ArrayView< const Point< spacedim > > &surrounding_points, const Point< spacedim > &candidate) const |
| virtual Point< spacedim > | get_new_point_on_line (const typename Triangulation< dim, spacedim >::line_iterator &line) const |
| virtual Point< spacedim > | get_new_point_on_quad (const typename Triangulation< dim, spacedim >::quad_iterator &quad) const |
| virtual Point< spacedim > | get_new_point_on_hex (const typename Triangulation< dim, spacedim >::hex_iterator &hex) const |
| Point< spacedim > | get_new_point_on_face (const typename Triangulation< dim, spacedim >::face_iterator &face) const |
| Point< spacedim > | get_new_point_on_cell (const typename Triangulation< dim, spacedim >::cell_iterator &cell) const |
Computing tangent vectors | |
| virtual Tensor< 1, spacedim > | get_tangent_vector (const Point< spacedim > &x1, const Point< spacedim > &x2) const |
Computing normal vectors | |
| virtual Tensor< 1, spacedim > | normal_vector (const typename Triangulation< dim, spacedim >::face_iterator &face, const Point< spacedim > &p) const |
| virtual void | get_normals_at_vertices (const typename Triangulation< dim, spacedim >::face_iterator &face, FaceVertexNormals &face_vertex_normals) const |
Private Member Functions | |
| std::array< unsigned int, 20 > | get_possible_cells_around_points (const ArrayView< const Point< spacedim > > &surrounding_points) const |
| Triangulation< dim, spacedim >::cell_iterator | compute_chart_points (const ArrayView< const Point< spacedim > > &surrounding_points, ArrayView< Point< dim > > chart_points) const |
| Point< dim > | pull_back (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const Point< spacedim > &p, const Point< dim > &initial_guess) const |
| Point< spacedim > | push_forward (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const Point< dim > &chart_point) const |
| DerivativeForm< 1, dim, spacedim > | push_forward_gradient (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const Point< dim > &chart_point, const Point< spacedim > &pushed_forward_chart_point) const |
Private Attributes | |
| const Triangulation< dim, spacedim > * | triangulation |
| int | level_coarse |
| std::vector< bool > | coarse_cell_is_flat |
| FlatManifold< dim > | chart_manifold |
| std::vector< internal::MappingQGenericImplementation::InverseQuadraticApproximation< dim, spacedim > > | quadratic_approximation |
| boost::signals2::connection | clear_signal |
Subscriptor functionality | |
Classes derived from Subscriptor provide a facility to subscribe to this object. This is mostly used by the SmartPointer class. | |
| std::atomic< unsigned int > | counter |
| std::map< std::string, unsigned int > | counter_map |
| std::vector< std::atomic< bool > * > | validity_pointers |
| const std::type_info * | object_info |
| void | subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const |
| void | unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const |
| unsigned int | n_subscriptions () const |
| template<typename StreamType > | |
| void | list_subscribers (StreamType &stream) const |
| void | list_subscribers () const |
| template<class Archive > | |
| void | serialize (Archive &ar, const unsigned int version) |
| void | check_no_subscribers () const noexcept |
| using | map_value_type = decltype(counter_map)::value_type |
| using | map_iterator = decltype(counter_map)::iterator |
| static std::mutex | mutex |
| static ::ExceptionBase & | ExcInUse (int arg1, std::string arg2, std::string arg3) |
| static ::ExceptionBase & | ExcNoSubscriber (std::string arg1, std::string arg2) |
A mapping class that extends curved boundary descriptions into the interior of the computational domain. The outer curved boundary description is assumed to be given by another manifold (e.g. a polar manifold on a circle). The mechanism to extend the boundary information is a so-called transfinite interpolation. The use of this class is discussed extensively in step-65.
The formula for extending such a description in 2D is, for example, described on Wikipedia. Given a point (u,v) on the chart, the image of this point in real space is given by
\begin{align*} \mathbf S(u,v) &= (1-v)\mathbf c_0(u)+v \mathbf c_1(u) + (1-u)\mathbf c_2(v) + u \mathbf c_3(v) \\ &\quad - \left[(1-u)(1-v) \mathbf x_0 + u(1-v) \mathbf x_1 + (1-u)v \mathbf x_2 + uv \mathbf x_3 \right] \end{align*}
where \bf x_0, \bf x_1, \bf x_2, \bf x_3 denote the four bounding vertices bounding the image space and \bf c_0, \bf c_1, \bf c_2, \bf c_3 are the four curves describing the lines of the cell. If a curved manifold is attached to any of these lines, the evaluation is done according to Manifold::get_new_point() with the two end points of the line and appropriate weight. In 3D, the generalization of this formula is implemented, creating a weighted sum of the vertices (positive contribution), the lines (negative), and the faces (positive contribution).
This manifold is usually attached to a coarse mesh and then places new points as a combination of the descriptions on the boundaries, weighted appropriately according to the position of the point in the original chart coordinates (u,v). This manifold should be preferred over setting only a curved manifold on the boundary of a mesh in most situations as it yields more uniform mesh distributions as the mesh is refined because it switches from a curved description to a straight description over all children of the initial coarse cell this manifold was attached to. This way, the curved nature of the manifold that is originally contained in one coarse mesh layer will be applied to more than one fine mesh layer once the mesh gets refined. Note that the mechanisms of TransfiniteInterpolationManifold are also built into the MappingQGeneric class when only a surface of a cell is subject to a curved description, ensuring that even the default case without this manifold gets optimal convergence rates when applying curved boundary descriptions.
If no curved boundaries surround a coarse cell, this class reduces to a flat manifold description.
To give an example of using this class, the following code attaches a transfinite manifold to a circle:
In this code, we first set all manifold ids to the id of the transfinite interpolation, and then re-set the manifold ids on the boundary to identify the curved boundary described by the polar manifold. With this code, one gets a really nice mesh:
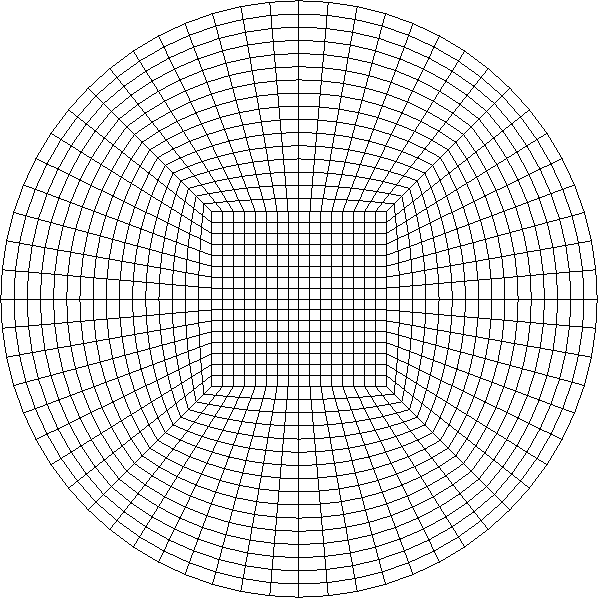
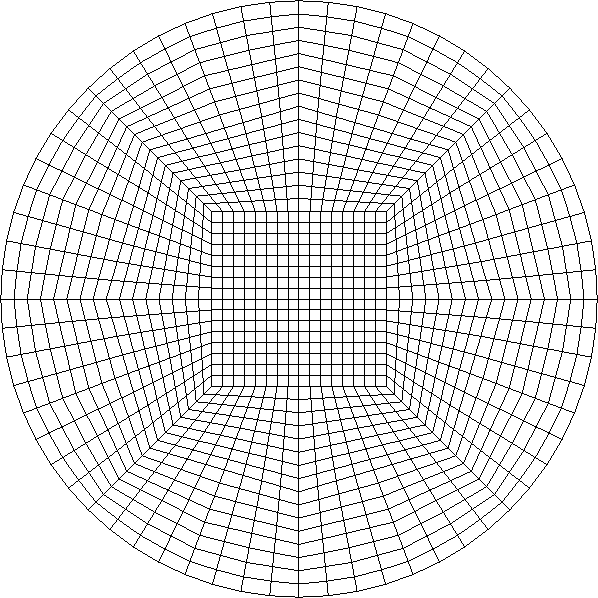
which is obviously much nicer than the polar manifold applied to just the boundary:
This manifold is used in a few GridGenerator functions, including GridGenerator::channel_with_cylinder.
In the implementation of this class, the manifolds surrounding a coarse cell are queried repeatedly to compute points on their interior. For optimal mesh quality, those manifolds should be compatible with a chart notion. For example, computing a point that is 0.25 along the line between two vertices using the weights 0.25 and 0.75 for the two vertices should give the same result as first computing the mid point at 0.5 and then again compute the midpoint between the first vertex and coarse mid point. This is the case for most of the manifold classes provided by deal.II, such as SphericalManifold or PolarManifold, but it might be violated by naive implementations. In case the quality of the manifold is not good enough, upon mesh refinement it may happen that the transformation to a chart inside the get_new_point() or get_new_points() methods produces points that are outside the unit cell. Then this class throws an exception of type Mapping::ExcTransformationFailed. In that case, the mesh should be refined before attaching this class, as done in the following example:
Definition at line 965 of file manifold_lib.h.
|
inherited |
Type keeping information about the normals at the vertices of a face of a cell. Thus, there are GeometryInfo<dim>::vertices_per_face normal vectors, that define the tangent spaces of the boundary at the vertices. Note that the vectors stored in this object are not required to be normalized, nor to actually point outward, as one often will only want to check for orthogonality to define the tangent plane; if a function requires the normals to be normalized, then it must do so itself.
For obvious reasons, this type is not useful in 1d.
Definition at line 306 of file manifold.h.
| TransfiniteInterpolationManifold< dim, spacedim >::TransfiniteInterpolationManifold |
Constructor.
Definition at line 1643 of file manifold_lib.cc.
|
overridevirtual |
Destructor.
Definition at line 1654 of file manifold_lib.cc.
|
overridevirtual |
Make a clone of this Manifold object.
Implements Manifold< dim, dim >.
Definition at line 1664 of file manifold_lib.cc.
| void TransfiniteInterpolationManifold< dim, spacedim >::initialize | ( | const Triangulation< dim, spacedim > & | triangulation | ) |
Initializes the manifold with a coarse mesh. The prerequisite for using this class is that the input triangulation is uniformly refined and the manifold is later attached to the same triangulation.
Whenever the assignment of manifold ids changes on the level of the triangulation which this class was initialized with, initialize() must be called again to update the manifold ids connected to the coarse cells.
Definition at line 1676 of file manifold_lib.cc.
|
overridevirtual |
Return the point which shall become the new vertex surrounded by the given points surrounding_points. weights contains appropriate weights for the surrounding points according to which the manifold determines the new point's position.
The implementation in this class overrides the method in the base class and computes the new point by a transfinite interpolation. The first step in the implementation is to identify the coarse cell on which the surrounding points are located. Then, the coordinates are transformed to the unit coordinates on the coarse cell by a Newton iteration, where the new point is then computed according to the weights. Finally, it is pushed forward to the real space according to the transfinite interpolation.
Reimplemented from Manifold< dim, dim >.
Definition at line 2580 of file manifold_lib.cc.
|
overridevirtual |
Compute a new set of points that interpolate between the given points surrounding_points. weights is a table with as many columns as surrounding_points.size(). The number of columns in weights must match the length of new_points.
The implementation in this class overrides the method in the base class and computes the new point by a transfinite interpolation. The first step in the implementation is to identify the coarse cell on which the surrounding points are located. Then, the coordinates are transformed to the unit coordinates on the coarse cell by a Newton iteration, where the new points are then computed according to the weights. Finally, the is pushed forward to the real space according to the transfinite interpolation.
The implementation does not allow for surrounding_points and new_points to point to the same vector, so make sure to pass different objects into the function.
Reimplemented from Manifold< dim, dim >.
Definition at line 2600 of file manifold_lib.cc.
|
private |
Internal function to identify the most suitable cells (=charts) where the given surrounding points are located. We use a cheap algorithm to identify the cells and rank the cells by probability before we actually do the search inside the relevant cells. The cells are sorted by the distance of a Q1 approximation of the inverse mapping to the unit cell of the surrounding points. We expect at most 20 cells (it should be up to 8 candidates on a 3D structured mesh and a bit more on unstructured ones, typically we only get two or three), so get an array with 20 entries of a the indices cell->index().
Definition at line 2233 of file manifold_lib.cc.
|
private |
Finalizes the identification of the correct chart and populates chart_points with the pullbacks of the surrounding points. This method internally calls get_possible_cells_around_points().
Return an iterator to the cell on which the chart is defined.
Definition at line 2319 of file manifold_lib.cc.
|
private |
Pull back operation into the unit coordinates on the given coarse cell.
This method is currently based on a Newton-like iteration to find the point in the origin. One may speed up the iteration by providing a good initial guess as the third argument. If no better point is known, use cell->real_to_unit_cell_affine_approximation(p)
Definition at line 2082 of file manifold_lib.cc.
|
private |
Push forward operation.
Definition at line 2032 of file manifold_lib.cc.
|
private |
Gradient of the push_forward method.
Definition at line 2053 of file manifold_lib.cc.
|
virtualinherited |
Return an intermediate point between two given points. Overloading this function allows the default pair-wise reduction implementation of the method get_new_point() that takes a Quadrature object as input to work properly.
An implementation of this function should returns a parametric curve on the manifold, joining the points p1 and p2, with parameter w in the interval [0,1]. In particular get_intermediate_point(p1, p2, 0.0) should return p1 and get_intermediate_point(p1, p2, 1.0) should return p2.
In its default implementation, this function calls the project_to_manifold() method with the convex combination of p1 and p2. User classes can get away by simply implementing the project_to_manifold() method.
Reimplemented in ChartManifold< dim, spacedim, chartdim >, and SphericalManifold< dim, spacedim >.
|
virtualinherited |
Given a point which lies close to the given manifold, it modifies it and projects it to manifold itself.
This class is used by the default implementation of the function get_new_point() and should be implemented by derived classes. The default implementation simply throws an exception if called.
If your manifold is simple, you could implement this function only, and the default behavior should work out of the box.
Reimplemented in FlatManifold< dim, spacedim >.
|
virtualinherited |
Backward compatibility interface. Return the point which shall become the new middle vertex of the two children of a regular line. In 2D, this line is a line at the boundary, while in 3d, it is bounding a face at the boundary (the lines therefore is also on the boundary).
The default implementation of this function passes its argument to the Manifolds::get_default_points_and_weights() function, and then calls the Manifold<dim,spacedim>::get_new_point() function. User derived classes can overload Manifold<dim,spacedim>::get_new_point() or Manifold<dim,spacedim>::project_to_manifold(), which is called by the default implementation of Manifold<dim,spacedim>::get_new_point().
|
virtualinherited |
Backward compatibility interface. Return the point which shall become the common point of the four children of a quad at the boundary in three or more spatial dimensions. This function therefore is only useful in at least three dimensions and should not be called for lower dimensions.
This function is called after the four lines bounding the given quad are refined, so you may want to use the information provided by quad->line(i)->child(j), i=0...3, j=0,1.
The default implementation of this function passes its argument to the Manifolds::get_default_points_and_weights() function, and then calls the Manifold<dim,spacedim>::get_new_point() function. User derived classes can overload Manifold<dim,spacedim>::get_new_point() or Manifold<dim,spacedim>::project_to_manifold(), which is called by the default implementation of Manifold<dim,spacedim>::get_new_point().
|
inherited |
Definition at line 419 of file manifold.cc.
|
inherited |
Definition at line 430 of file manifold.cc.
|
inherited |
Definition at line 441 of file manifold.cc.
|
virtualinherited |
Backward compatibility interface. Return the point which shall become the common point of the eight children of a hex in three or spatial dimensions. This function therefore is only useful in at least three dimensions and should not be called for lower dimensions.
This function is called after the all the bounding objects of the given hex are refined, so you may want to use the information provided by hex->quad(i)->line(j)->child(k), i=0...5, j=0...3, k=0,1.
The default implementation of this function passes its argument to the Manifolds::get_default_points_and_weights() function, and then calls the Manifold<dim,spacedim>::get_new_point() function. User derived classes can overload Manifold<dim,spacedim>::get_new_point() or Manifold<dim,spacedim>::project_to_manifold(), which is called by the default implementation of Manifold<dim,spacedim>::get_new_point().
|
inherited |
Definition at line 463 of file manifold.cc.
|
inherited |
Backward compatibility interface. Depending on dim=2 or dim=3 this function calls the get_new_point_on_line or the get_new_point_on_quad function. It throws an exception for dim=1. This wrapper allows dimension independent programming.
|
inherited |
Definition at line 386 of file manifold.cc.
|
inherited |
Definition at line 397 of file manifold.cc.
|
inherited |
Definition at line 408 of file manifold.cc.
|
inherited |
Backward compatibility interface. Depending on dim=1, dim=2 or dim=3 this function calls the get_new_point_on_line, get_new_point_on_quad or the get_new_point_on_hex function. This wrapper allows dimension independent programming.
|
virtualinherited |
Return a vector that, at \mathbf x_1, is tangential to the geodesic that connects two points \mathbf x_1,\mathbf x_2. The geodesic is the shortest line between these two points, where "shortest" is defined via a metric specific to a particular implementation of this class in a derived class. For example, in the case of a FlatManifold, the shortest line between two points is just the straight line, and in this case the tangent vector is just the difference \mathbf d=\mathbf x_2-\mathbf x_1. On the other hand, for a manifold that describes a surface embedded in a higher dimensional space (e.g., the surface of a sphere), then the tangent vector is tangential to the surface, and consequently may point in a different direction than the straight line that connects the two points.
While tangent vectors are often normalized to unit length, the vectors returned by this function are normalized as described in the introduction of this class. Specifically, if \mathbf s(t) traces out the geodesic between the two points where \mathbf x_1 = \mathbf s(0) and \mathbf x_2 = \mathbf s(1), then the returned vector must equal \mathbf s'(0). In other words, the norm of the returned vector also encodes, in some sense, the length of the geodesic because a curve \mathbf s(t) must move "faster" if the two points it connects between arguments t=0 and t=1 are farther apart.
The default implementation of this function approximates \mathbf s'(0) \approx \frac{\mathbf s(\epsilon)-\mathbf x_1}{\epsilon} for a small value of \epsilon, and the evaluation of \mathbf s(\epsilon) is done by calling get_new_point(). If possible, derived classes should override this function by an implementation of the exact derivative.
| x1 | The first point that describes the geodesic, and the one at which the "direction" is to be evaluated. |
| x2 | The second point that describes the geodesic. |
Reimplemented in FlatManifold< dim, spacedim >, ChartManifold< dim, spacedim, chartdim >, and SphericalManifold< dim, spacedim >.
|
virtualinherited |
Return the normal vector to a face embedded in this manifold, at the point p. If p is not in fact on the surface, but only close-by, try to return something reasonable, for example the normal vector at the surface point closest to p. (The point p will in fact not normally lie on the actual surface, but rather be a quadrature point mapped by some polynomial mapping; the mapped surface, however, will not usually coincide with the actual surface.)
This function only makes sense if dim==spacedim because otherwise there is no unique normal vector but in fact a (spacedim-dim+1)-dimensional tangent space of vectors that are all both normal to the face and normal to the dim-dimensional surface that lives in spacedim-dimensional space. For example, think of a two-dimensional mesh that covers a two-dimensional surface in three-dimensional space. In that case, each face (edge) is one-dimensional, and there are two linearly independent vectors that are both normal to the edge: one is normal to the edge and tangent to the surface (intuitively, that would be the one that points from the current cell to the neighboring one, if the surface was locally flat), and the other one is rooted in the edge but points perpendicular to the surface (which is also perpendicular to the edge that lives within the surface). Thus, because there are no obviously correct semantics for this function if spacedim is greater than dim, the function will simply throw an error in that situation.
The face iterator gives an indication which face this function is supposed to compute the normal vector for. This is useful if the boundary of the domain is composed of different nondifferential pieces (for example when using the FlatManifold class to approximate a geometry that is completely described by the coarse mesh, with piecewise (bi-)linear components between the vertices, but where the boundary may have a kink at the vertices itself).
Reimplemented in FlatManifold< dim, spacedim >, and SphericalManifold< dim, spacedim >.
|
inherited |
Definition at line 145 of file manifold.cc.
|
inherited |
Definition at line 166 of file manifold.cc.
|
virtualinherited |
Compute the normal vectors to the boundary at each vertex of the given face embedded in the Manifold. It is not required that the normal vectors be normed somehow. Neither is it required that the normals actually point outward.
This function is needed to compute data for C1 mappings. The default implementation calls normal_vector() on each vertex.
Note that when computing normal vectors at a vertex where the boundary is not differentiable, you have to make sure that you compute the one-sided limits, i.e. limit with respect to points inside the given face.
|
inherited |
Definition at line 251 of file manifold.cc.
|
inherited |
Definition at line 273 of file manifold.cc.
|
private |
The underlying triangulation.
Definition at line 1126 of file manifold_lib.h.
|
private |
The level of the mesh cells where the transfinite approximation is applied, usually level 0.
Definition at line 1132 of file manifold_lib.h.
|
private |
In case there all surrounding manifolds are the transfinite manifold or have default (invalid) manifold id, the manifold degenerates to a flat manifold and we can choose cheaper algorithms for the push_forward method.
Definition at line 1139 of file manifold_lib.h.
|
private |
A flat manifold used to compute new points in the chart space where we use a FlatManifold description.
Definition at line 1145 of file manifold_lib.h.
|
private |
A vector of quadratic approximations to the inverse map from real points to chart points for each of the coarse mesh cells.
Definition at line 1153 of file manifold_lib.h.
|
private |
The connection to Triangulation::signals::clear that must be reset once this class goes out of scope.
Definition at line 1159 of file manifold_lib.h.