DataPostprocessorVector< dim > Class Template Reference

#include <deal.II/numerics/data_postprocessor.h>

Inheritance diagram for DataPostprocessorVector< dim >:

Public Member Functions
	DataPostprocessorVector (const std::string &name, const UpdateFlags update_flags)
virtual std::vector< std::string >	get_names () const override
virtual std::vector< DataComponentInterpretation::DataComponentInterpretation >	get_data_component_interpretation () const override
virtual UpdateFlags	get_needed_update_flags () const override
virtual void	evaluate_scalar_field (const DataPostprocessorInputs::Scalar< dim > &input_data, std::vector< Vector< double > > &computed_quantities) const
virtual void	evaluate_vector_field (const DataPostprocessorInputs::Vector< dim > &input_data, std::vector< Vector< double > > &computed_quantities) const

Private Attributes
const std::string	name
const UpdateFlags	update_flags

Subscriptor functionality
Classes derived from Subscriptor provide a facility to subscribe to this object. This is mostly used by the SmartPointer class.
std::atomic< unsigned int >	counter
std::map< std::string, unsigned int >	counter_map
std::vector< std::atomic< bool > * >	validity_pointers
const std::type_info *	object_info
void	subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const
void	unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const
unsigned int	n_subscriptions () const
template<typename StreamType >
void	list_subscribers (StreamType &stream) const
void	list_subscribers () const
template<class Archive >
void	serialize (Archive &ar, const unsigned int version)
using	map_value_type = decltype(counter_map)::value_type
using	map_iterator = decltype(counter_map)::iterator
static std::mutex	mutex
static ::ExceptionBase &	ExcInUse (int arg1, std::string arg2, std::string arg3)
static ::ExceptionBase &	ExcNoSubscriber (std::string arg1, std::string arg2)
void	check_no_subscribers () const noexcept

Detailed Description

template<int dim>
class DataPostprocessorVector< dim >

This class provides a simpler interface to the functionality offered by the DataPostprocessor class in case one wants to compute only a single vector quantity (defined as having exactly dim components) from the finite element field passed to the DataOut class. For this particular case, it is clear what the returned value of DataPostprocessor::get_data_component_interpretation() should be and we pass the values returned by get_names() and get_needed_update_flags() to the constructor so that derived classes do not have to implement these functions by hand.

All derived classes have to do is implement a constructor and overload either DataPostprocessor::evaluate_scalar_field() or DataPostprocessor::evaluate_vector_field() as discussed in the DataPostprocessor class's documentation.

An example of how the closely related class DataPostprocessorScalar is used can be found in step-29. An example of how the DataPostprocessorTensor class can be used is found in the documentation of that class.

An example

A common example of what one wants to do with postprocessors is to visualize not just the value of the solution, but the gradient. This is, in fact, precisely what step-19 needs, and it consequently uses the code below almost verbatim. Let's, for simplicity, assume that you have only a scalar solution. In fact, because it's readily available, let us simply take the step-6 solver to produce such a scalar solution. The gradient is a vector (with exactly dim components), so the current class fits the bill to produce the gradient through postprocessing. Then, the following code snippet implements everything you need to have to visualize the gradient:

template <int dim>
class GradientPostprocessor : public DataPostprocessorVector<dim>
{
public:
  GradientPostprocessor ()
    :
    // call the constructor of the base class. call the variable to
    // be output "grad_u" and make sure that DataOut provides us
    // with the gradients:
    DataPostprocessorVector<dim> ("grad_u",
                                  update_gradients)
  {}
 
  virtual
  void
  evaluate_scalar_field
  (const DataPostprocessorInputs::Scalar<dim> &input_data,
   std::vector<Vector<double> > &computed_quantities) const override
  {
    // ensure that there really are as many output slots
    // as there are points at which DataOut provides the
    // gradients:
    AssertDimension (input_data.solution_gradients.size(),
                     computed_quantities.size());
 
    // then loop over all of these inputs:
    for (unsigned int p=0; p<input_data.solution_gradients.size(); ++p)
      {
        // ensure that each output slot has exactly 'dim'
        // components (as should be expected, given that we
        // want to create vector-valued outputs), and copy the
        // gradients of the solution at the evaluation points
        // into the output slots:
        AssertDimension (computed_quantities[p].size(), dim);
        for (unsigned int d=0; d<dim; ++d)
          computed_quantities[p][d]
            = input_data.solution_gradients[p][d];
      }
  }
};

The only thing that is necessary is to add another output to the call of DataOut::add_vector() in the run() function of the Step6 class of that example program. The corresponding code snippet would then look like this (where we also use VTU as the file format to output the data):

GradientPostprocessor<dim> gradient_postprocessor;
 
DataOut<dim> data_out;
data_out.attach_dof_handler (dof_handler);
data_out.add_data_vector (solution, "solution");
data_out.add_data_vector (solution, gradient_postprocessor);
data_out.build_patches ();
 
std::ofstream output ("solution.vtu");
data_out.write_vtu (output);

This leads to the following output for the solution and the gradients (you may want to compare with the solution shown in the results section of step-6; the current data is generated on a coarser mesh for simplicity):

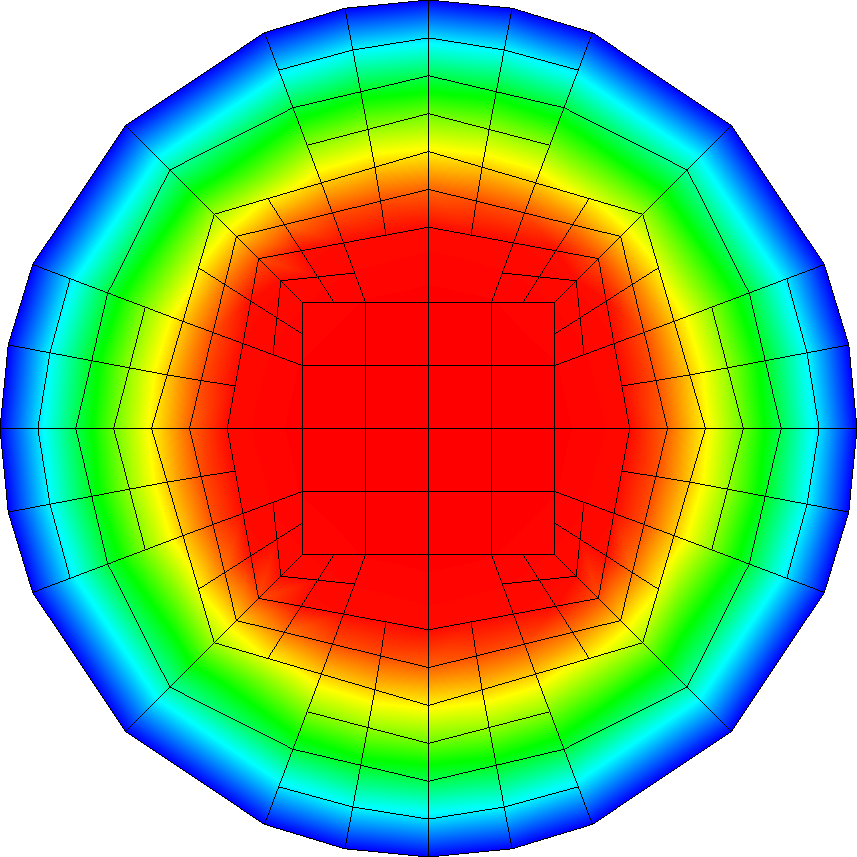
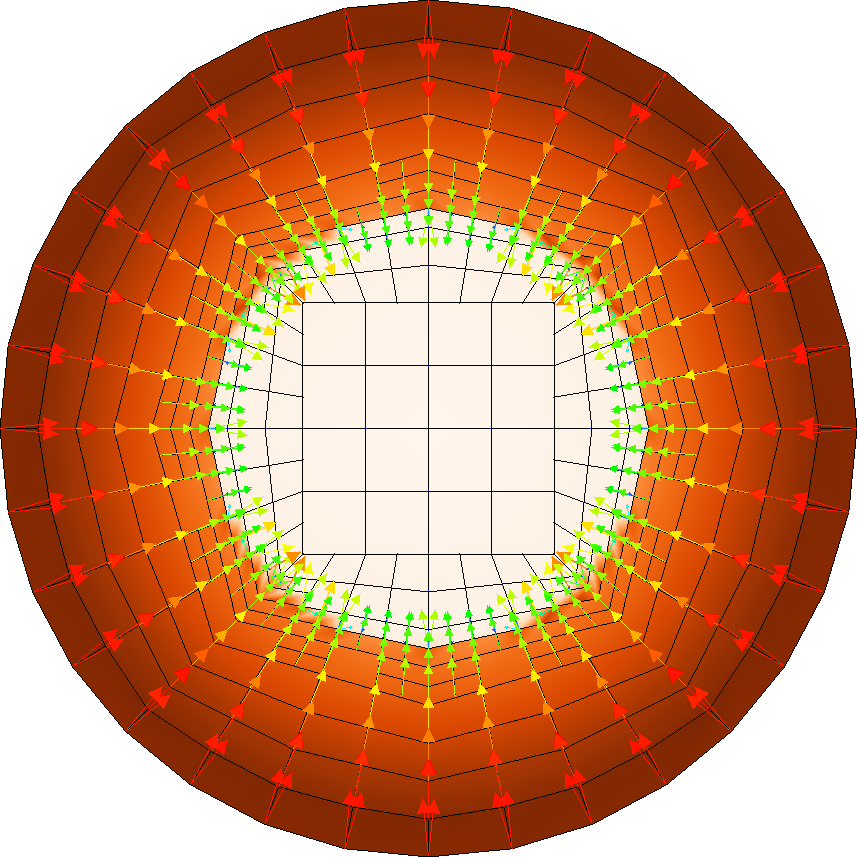
In the second image, the background color corresponds to the magnitude of the gradient vector and the vector glyphs to the gradient itself. It may be surprising at first to see that from each vertex, multiple vectors originate, going in different directions. But that is because the solution is only continuous: in general, the gradient is discontinuous across edges, and so the multiple vectors originating from each vertex simply represent the differing gradients of the solution at each adjacent cell.

The output above – namely, the gradient \(\nabla u\) of the solution – corresponds to the temperature gradient if one interpreted step-6 as solving a steady-state heat transfer problem. It is very small in the central part of the domain because in step-6 we are solving an equation that has a coefficient \(a(\mathbf x)\) that is large in the central part and small on the outside. This can be thought as a material that conducts heat well, and consequently the temperature gradient is small. On the other hand, the "heat flux" corresponds to the quantity \(a(\mathbf x) \nabla u(\mathbf x)\). For the solution of that equation, the flux should be continuous across the interface. This is easily verified by the following modification of the postprocessor:

template <int dim>
class HeatFluxPostprocessor : public DataPostprocessorVector<dim>
{
public:
  HeatFluxPostprocessor ()
    :
    // like above, but now also make sure that DataOut provides
    // us with coordinates of the evaluation points:
    DataPostprocessorVector<dim> ("heat_flux",
                                  update_gradients | update_quadrature_points)
  {}
 
  virtual
  void
  evaluate_scalar_field
  (const DataPostprocessorInputs::Scalar<dim> &input_data,
   std::vector<Vector<double> > &computed_quantities) const override
  {
    AssertDimension (input_data.solution_gradients.size(),
                     computed_quantities.size());
 
    for (unsigned int p=0; p<input_data.solution_gradients.size(); ++p)
      {
        AssertDimension (computed_quantities[p].size(), dim);
        for (unsigned int d=0; d<dim; ++d)
          // like above, but also multiply the gradients with
          // the coefficient evaluated at the current point:
          computed_quantities[p][d]
            = coefficient (input_data.evaluation_points[p]) *
              input_data.solution_gradients[p][d];
      }
  }
};

With this postprocessor, we get the following picture of the heat flux:

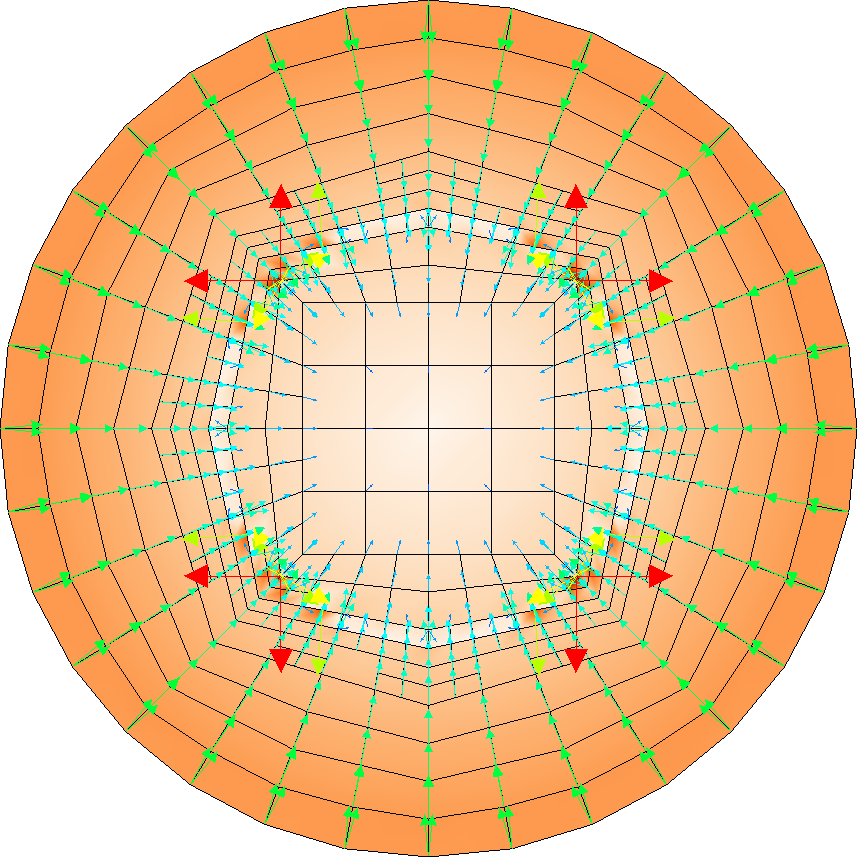
As the background color shows, the gradient times the coefficient is now a continuous function. There are (large) vectors around the interface where the coefficient jumps (at half the distance between the center of the disk to the perimeter) that seem to point in the wrong direction; this is an artifact of the fact that the solution has a discontinuous gradient at these points and that the numerical solution on the current grid does not adequately resolve this interface. This, however, is not important to the current discussion.

Extension to the gradients of vector-valued problems

The example above uses a scalar solution and its gradient as an example. On the other hand, one may want to do something similar for the gradient of a vector-valued displacement field (such as the strain or stress of a displacement field, like those computed in step-8, step-17, step-18, or step-44). In that case, the solution is already vector valued and the stress is a (symmetric) tensor.

deal.II does not currently support outputting tensor-valued quantities, but they can of course be output as a collection of scalar-valued components of the tensor. This can be facilitated using the DataPostprocessorTensor class. The documentation of that class contains an example.

Definition at line 889 of file data_postprocessor.h.

Constructor & Destructor Documentation

DataPostprocessorVector()

template<int dim>

DataPostprocessorVector< dim >::DataPostprocessorVector	(	const std::string &	name,
		const UpdateFlags	update_flags
	)

Constructor. Take the name of the single vector variable computed by classes derived from the current one, as well as the update flags necessary to compute this quantity.

Parameters

name

The name by which the vector variable computed by this class should be made available in graphical output files.

update_flags

This has to be a combination of update_values, update_gradients, update_hessians and update_quadrature_points. Note that the flag update_quadrature_points updates DataPostprocessorInputs::CommonInputs::evaluation_points. If the DataPostprocessor is to be used in combination with DataOutFaces, you may also ask for a update of normals via the update_normal_vectors flag. The description of the flags can be found at UpdateFlags.

Definition at line 99 of file data_postprocessor.cc.

Member Function Documentation

get_names()

template<int dim>

std::vector< std::string > DataPostprocessorVector< dim >::get_names

overridevirtual

Return the vector of strings describing the names of the computed quantities. Given the purpose of this class, this is a vector with dim entries all equal to the name given to the constructor.

Implements DataPostprocessor< dim >.

Definition at line 110 of file data_postprocessor.cc.

get_data_component_interpretation()

template<int dim>

std::vector< DataComponentInterpretation::DataComponentInterpretation > DataPostprocessorVector< dim >::get_data_component_interpretation

overridevirtual

This function returns information about how the individual components of output files that consist of more than one data set are to be interpreted. Since the current class is meant to be used for a single vector result variable, the returned value is obviously DataComponentInterpretation::component_is_part repeated dim times.

Reimplemented from DataPostprocessor< dim >.

Definition at line 119 of file data_postprocessor.cc.

get_needed_update_flags()

template<int dim>

UpdateFlags DataPostprocessorVector< dim >::get_needed_update_flags

overridevirtual

Return which data has to be provided to compute the derived quantities. The flags returned here are the ones passed to the constructor of this class.

Implements DataPostprocessor< dim >.

Definition at line 128 of file data_postprocessor.cc.

evaluate_scalar_field()

template<int dim>

void DataPostprocessor< dim >::evaluate_scalar_field ( const DataPostprocessorInputs::Scalar< dim > &  input_data, std::vector< Vector< double > > &  computed_quantities  ) const

virtualinherited

This is the main function which actually performs the postprocessing. The second argument is a reference to the postprocessed data which already has correct size and must be filled by this function.

The function takes the values, gradients, and higher derivatives of the solution at all evaluation points, as well as other data such as the cell, via the first argument. Not all of the member vectors of this argument will be filled with data – in fact, derivatives and other quantities will only be contain valid data if the corresponding flags are returned by an overridden version of the get_needed_update_flags() function (implemented in a user's derived class). Otherwise those vectors will be in an unspecified state.

This function is called when the finite element field that is being converted into graphical data by DataOut or similar classes represents scalar data, i.e., if the finite element in use has only a single real-valued vector component.

Definition at line 26 of file data_postprocessor.cc.

evaluate_vector_field()

template<int dim>

void DataPostprocessor< dim >::evaluate_vector_field ( const DataPostprocessorInputs::Vector< dim > &  input_data, std::vector< Vector< double > > &  computed_quantities  ) const

virtualinherited

Same as the evaluate_scalar_field() function, but this function is called when the original data vector represents vector data, i.e., the finite element in use has multiple vector components. This function is also called if the finite element is scalar but the solution vector is complex-valued. If the solution vector to be visualized is complex-valued (whether scalar or not), then the input data contains first all real parts of the solution vector at each evaluation point, and then all imaginary parts.

Definition at line 37 of file data_postprocessor.cc.

Member Data Documentation

name

template<int dim>

const std::string DataPostprocessorVector< dim >::name

private

Copies of the two arguments given to the constructor of this class.

Definition at line 940 of file data_postprocessor.h.

update_flags

template<int dim>

const UpdateFlags DataPostprocessorVector< dim >::update_flags

private

Definition at line 941 of file data_postprocessor.h.

---

The documentation for this class was generated from the following files:

• include/deal.II/numerics/data_postprocessor.h
• source/numerics/data_postprocessor.cc