Functions
template<typename NumberType >
std::array< NumberType, 3 >	givens_rotation (const NumberType &x, const NumberType &y)

template<typename NumberType >
std::array< NumberType, 3 >	hyperbolic_rotation (const NumberType &x, const NumberType &y)

template<typename OperatorType , typename VectorType >
double	lanczos_largest_eigenvalue (const OperatorType &H, const VectorType &v0, const unsigned int k, VectorMemory< VectorType > &vector_memory, std::vector< double > *eigenvalues=nullptr)

template<typename OperatorType , typename VectorType >
void	chebyshev_filter (VectorType &x, const OperatorType &H, const unsigned int n, const std::pair< double, double > unwanted_spectrum, const double tau, VectorMemory< VectorType > &vector_memory)

Detailed Description

A collection of linear-algebra utilities.

Function Documentation

◆ givens_rotation()

template<typename NumberType >

std::array<NumberType, 3> Utilities::LinearAlgebra::givens_rotation	(	const NumberType &	x,
		const NumberType &	y
	)

Return the elements of a continuous Givens rotation matrix and the norm of the input vector.

That is for a given pair x and y, return \(c\) , \(s\) and \(\sqrt{x^2+y^2}\) such that

\[ \begin{bmatrix} c & s \\ -s & c \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \sqrt{x^2+y^2} \\ 0 \end{bmatrix} \]

Note: The function is implemented for real valued numbers only.

Author: Denis Davydov, 2017

◆ hyperbolic_rotation()

template<typename NumberType >

std::array<NumberType, 3> Utilities::LinearAlgebra::hyperbolic_rotation	(	const NumberType &	x,
		const NumberType &	y
	)

Return the elements of a hyperbolic rotation matrix.

That is for a given pair x and y, return \(c\) , \(s\) and \(r\) such that

\[ \begin{bmatrix} c & -s \\ -s & c \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} r \\ 0 \end{bmatrix} \]

Real valued solution only exists if \(|x|>|g|\), the function will throw an error otherwise.

Note: The function is implemented for real valued numbers only.

Author: Denis Davydov, 2017

◆ lanczos_largest_eigenvalue()

template<typename OperatorType , typename VectorType >

double Utilities::LinearAlgebra::lanczos_largest_eigenvalue	(	const OperatorType &	H,
		const VectorType &	v0,
		const unsigned int	k,
		VectorMemory< VectorType > &	vector_memory,
		std::vector< double > *	eigenvalues = `nullptr`
	)

Estimate an upper bound for the largest eigenvalue of H by a k -step Lanczos process starting from the initial vector v0. Typical values of k are below 10. This estimator computes a k-step Lanczos decomposition \(H V_k=V_k T_k+f_k e_k^T\) where \(V_k\) contains k Lanczos basis, \(V_k^TV_k=I_k\), \(T_k\) is the tridiagonal Lanczos matrix, \(f_k\) is a residual vector \(f_k^TV_k=0\), and \(e_k\) is the k-th canonical basis of \(R^k\). The returned value is \( ||T_k||_2 + ||f_k||_2\). If eigenvalues is not nullptr, the eigenvalues of \(T_k\) will be written there.

vector_memory is used to allocate memory for temporary vectors. OperatorType has to provide vmult operation with VectorType.

This function implements the algorithm from

@article{Zhou2006,
  Title   = {Self-consistent-field Calculations Using Chebyshev-filtered
             Subspace Iteration},
  Author  = {Zhou, Yunkai and Saad, Yousef and Tiago, Murilo L. and
             Chelikowsky, James R.},
  Journal = {Journal of Computational Physics},
  Year    = {2006},
  Volume  = {219},
  Pages   = {172--184},
}

Note: This function uses Lapack routines to compute the largest eigenvalue of \(T_k\).; This function provides an alternate estimate to that obtained from several steps of SolverCG with SolverCG<VectorType>::connect_eigenvalues_slot().

Author: Denis Davydov, 2017

◆ chebyshev_filter()

template<typename OperatorType , typename VectorType >

void Utilities::LinearAlgebra::chebyshev_filter	(	VectorType &	x,
		const OperatorType &	H,
		const unsigned int	n,
		const std::pair< double, double >	unwanted_spectrum,
		const double	tau,
		VectorMemory< VectorType > &	vector_memory
	)

Apply Chebyshev polynomial of the operator H to x. For a non-defective operator \(H\) with a complete set of eigenpairs \(H \psi_i = \lambda_i \psi_i\), the action of a polynomial filter \(p\) is given by \(p(H)x =\sum_i a_i p(\lambda_i) \psi_i\), where \(x=: \sum_i a_i \psi_i\). Thus by appropriately choosing the polynomial filter, one can alter the eigenmodes contained in \(x\).

This function uses Chebyshev polynomials of first kind. Below is an example of polynomial \(T_n(x)\) of degree \(n=8\) normalized to unity at \(-1.2\).

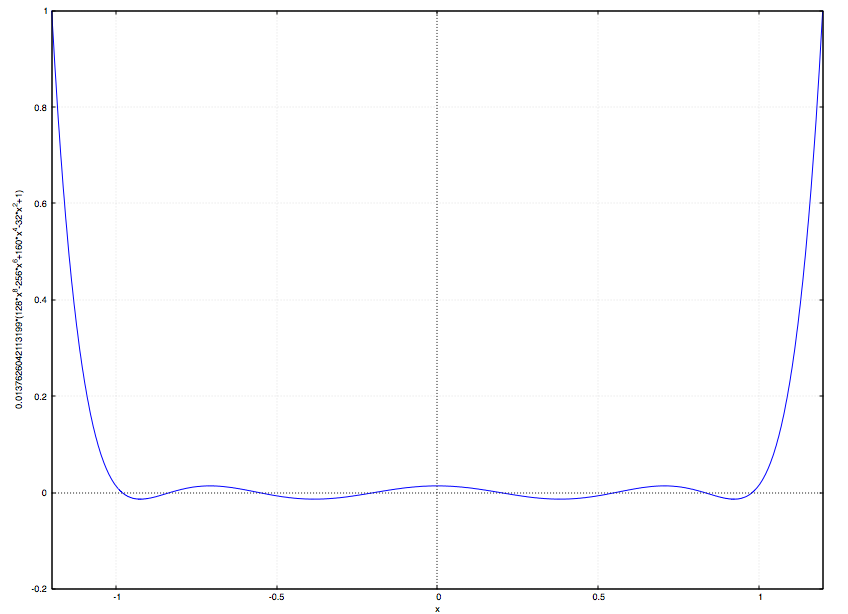
By introducing a linear mapping \(L\) from unwanted_spectrum to \([-1,1]\), we can dump the corresponding modes in x. The higher the polynomial degree \(n\), the more rapid it grows outside of the \([-1,1]\). In order to avoid numerical overflow, we normalize polynomial filter to unity at tau. Thus, the filtered operator is \(p(H) = T_n(L(H))/T_n(L(\tau))\).

The action of the Chebyshev filter only requires evaluation of vmult() of H and is based on the recursion equation for Chebyshev polynomial of degree \(n\): \(T_{n}(x) = 2x T_{n-1}(x) - T_{n-2}(x)\) with \(T_0(x)=1\) and \(T_1(x)=x\).

vector_memory is used to allocate memory for temporary objects.

This function implements the algorithm (with a minor fix of sign of \(\sigma_1\)) from

@article{Zhou2014,
  Title   = {Chebyshev-filtered subspace iteration method free of sparse
             diagonalization for solving the Kohn--Sham equation},
  Author  = {Zhou, Yunkai and Chelikowsky, James R and Saad, Yousef},
  Journal = {Journal of Computational Physics},
  Year    = {2014},
  Volume  = {274},
  Pages   = {770--782},
}

Note: If tau is equal to std::numeric_limits<double>::infinity(), no normalization will be performed.

Author: Denis Davydov, 2017