ScaLAPACKMatrix< NumberType > Class Template Reference

#include <deal.II/lac/scalapack.h>

Inheritance diagram for ScaLAPACKMatrix< NumberType >:

Public Types
using	size_type = unsigned int

Public Member Functions
	ScaLAPACKMatrix (const size_type n_rows, const size_type n_columns, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::general)
	ScaLAPACKMatrix (const size_type size, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::symmetric)
	ScaLAPACKMatrix (const std::string &filename, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32)
	~ScaLAPACKMatrix () override=default
void	reinit (const size_type n_rows, const size_type n_columns, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::general)
void	reinit (const size_type size, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::symmetric)
void	set_property (const LAPACKSupport::Property property)
LAPACKSupport::Property	get_property () const
LAPACKSupport::State	get_state () const
ScaLAPACKMatrix< NumberType > &	operator= (const FullMatrix< NumberType > &)
void	copy_from (const LAPACKFullMatrix< NumberType > &matrix, const unsigned int rank)
void	copy_to (FullMatrix< NumberType > &matrix) const
void	copy_to (LAPACKFullMatrix< NumberType > &matrix, const unsigned int rank) const
void	copy_to (ScaLAPACKMatrix< NumberType > &dest) const
void	copy_to (ScaLAPACKMatrix< NumberType > &B, const std::pair< unsigned int, unsigned int > &offset_A, const std::pair< unsigned int, unsigned int > &offset_B, const std::pair< unsigned int, unsigned int > &submatrix_size) const
void	copy_transposed (const ScaLAPACKMatrix< NumberType > &B)
void	add (const ScaLAPACKMatrix< NumberType > &B, const NumberType a=0., const NumberType b=1., const bool transpose_B=false)
void	add (const NumberType b, const ScaLAPACKMatrix< NumberType > &B)
void	Tadd (const NumberType b, const ScaLAPACKMatrix< NumberType > &B)
void	mult (const NumberType b, const ScaLAPACKMatrix< NumberType > &B, const NumberType c, ScaLAPACKMatrix< NumberType > &C, const bool transpose_A=false, const bool transpose_B=false) const
void	mmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
void	Tmmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
void	mTmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
void	TmTmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const
void	save (const std::string &filename, const std::pair< unsigned int, unsigned int > &chunk_size=std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int)) const
void	load (const std::string &filename)
void	compute_cholesky_factorization ()
void	compute_lu_factorization ()
void	invert ()
std::vector< NumberType >	eigenpairs_symmetric_by_index (const std::pair< unsigned int, unsigned int > &index_limits, const bool compute_eigenvectors)
std::vector< NumberType >	eigenpairs_symmetric_by_value (const std::pair< NumberType, NumberType > &value_limits, const bool compute_eigenvectors)
std::vector< NumberType >	eigenpairs_symmetric_by_index_MRRR (const std::pair< unsigned int, unsigned int > &index_limits, const bool compute_eigenvectors)
std::vector< NumberType >	eigenpairs_symmetric_by_value_MRRR (const std::pair< NumberType, NumberType > &value_limits, const bool compute_eigenvectors)
std::vector< NumberType >	compute_SVD (ScaLAPACKMatrix< NumberType > *U=nullptr, ScaLAPACKMatrix< NumberType > *VT=nullptr)
void	least_squares (ScaLAPACKMatrix< NumberType > &B, const bool transpose=false)
unsigned int	pseudoinverse (const NumberType ratio)
NumberType	reciprocal_condition_number (const NumberType a_norm) const
NumberType	l1_norm () const
NumberType	linfty_norm () const
NumberType	frobenius_norm () const
size_type	m () const
size_type	n () const
unsigned int	local_m () const
unsigned int	local_n () const
unsigned int	global_row (const unsigned int loc_row) const
unsigned int	global_column (const unsigned int loc_column) const
NumberType	local_el (const unsigned int loc_row, const unsigned int loc_column) const
NumberType &	local_el (const unsigned int loc_row, const unsigned int loc_column)
template<class InputVector >
void	scale_columns (const InputVector &factors)
template<class InputVector >
void	scale_rows (const InputVector &factors)

Private Member Functions
NumberType	norm_symmetric (const char type) const
NumberType	norm_general (const char type) const
std::vector< NumberType >	eigenpairs_symmetric (const bool compute_eigenvectors, const std::pair< unsigned int, unsigned int > &index_limits=std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int), const std::pair< NumberType, NumberType > &value_limits=std::make_pair(std::numeric_limits< NumberType >::quiet_NaN(), std::numeric_limits< NumberType >::quiet_NaN()))
std::vector< NumberType >	eigenpairs_symmetric_MRRR (const bool compute_eigenvectors, const std::pair< unsigned int, unsigned int > &index_limits=std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int), const std::pair< NumberType, NumberType > &value_limits=std::make_pair(std::numeric_limits< NumberType >::quiet_NaN(), std::numeric_limits< NumberType >::quiet_NaN()))

Private Attributes
LAPACKSupport::State	state
LAPACKSupport::Property	property
std::shared_ptr< const Utilities::MPI::ProcessGrid >	grid
int	n_rows
int	n_columns
int	row_block_size
int	column_block_size
int	n_local_rows
int	n_local_columns
int	descriptor [9]
std::vector< NumberType >	work
std::vector< int >	iwork
std::vector< int >	ipiv
const char	uplo
const int	first_process_row
const int	first_process_column
const int	submatrix_row
const int	submatrix_column
Threads::Mutex	mutex

Additional Inherited Members
Protected Types inherited from TransposeTable< NumberType >
using	size_type = typename TableBase< 2, NumberType >::size_type
using	value_type = typename AlignedVector< NumberType >::value_type
using	reference = typename AlignedVector< NumberType >::reference
using	const_reference = typename AlignedVector< NumberType >::const_reference
using	const_iterator = MatrixTableIterators::Iterator< TransposeTable< NumberType >, true, MatrixTableIterators::Storage::column_major >
using	iterator = MatrixTableIterators::Iterator< TransposeTable< NumberType >, false, MatrixTableIterators::Storage::column_major >
Protected Types inherited from TableBase< 2, NumberType >
using	size_type = typename AlignedVector< NumberType >::size_type
Protected Member Functions inherited from TransposeTable< NumberType >
reference	el (const size_type i, const size_type j)
const_reference	el (const size_type i, const size_type j) const
	TransposeTable ()=default
	TransposeTable (const size_type size1, const size_type size2)
void	reinit (const size_type size1, const size_type size2, const bool omit_default_initialization=false)
const_reference	operator() (const size_type i, const size_type j) const
reference	operator() (const size_type i, const size_type j)
size_type	n_rows () const
size_type	n_cols () const
iterator	begin ()
const_iterator	begin () const
iterator	end ()
const_iterator	end () const
Protected Member Functions inherited from TableBase< 2, NumberType >
size_type	position (const TableIndices< N > &indices) const
AlignedVector< NumberType >::reference	el (const TableIndices< N > &indices)
AlignedVector< NumberType >::const_reference	el (const TableIndices< N > &indices) const
	TableBase ()=default
	TableBase (const TableIndices< N > &sizes)
	TableBase (const TableIndices< N > &sizes, InputIterator entries, const bool C_style_indexing=true)
	TableBase (const TableBase< N, NumberType > &src)
	TableBase (const TableBase< N, T2 > &src)
	TableBase (TableBase< N, NumberType > &&src) noexcept
	~TableBase () override=default
TableBase< N, NumberType > &	operator= (const TableBase< N, NumberType > &src)
TableBase< N, NumberType > &	operator= (const TableBase< N, T2 > &src)
TableBase< N, NumberType > &	operator= (TableBase< N, NumberType > &&src) noexcept
bool	operator== (const TableBase< N, NumberType > &T2) const
void	reset_values ()
void	reinit (const TableIndices< N > &new_size, const bool omit_default_initialization=false)
size_type	size (const unsigned int i) const
const TableIndices< N > &	size () const
size_type	n_elements () const
bool	empty () const
void	fill (InputIterator entries, const bool C_style_indexing=true)
void	fill (const NumberType &value)
AlignedVector< NumberType >::reference	operator() (const TableIndices< N > &indices)
AlignedVector< NumberType >::const_reference	operator() (const TableIndices< N > &indices) const
void	swap (TableBase< N, NumberType > &v)
std::size_t	memory_consumption () const
void	serialize (Archive &ar, const unsigned int version)
Protected Member Functions inherited from Subscriptor
	Subscriptor ()
	Subscriptor (const Subscriptor &)
	Subscriptor (Subscriptor &&) noexcept
virtual	~Subscriptor ()
Subscriptor &	operator= (const Subscriptor &)
Subscriptor &	operator= (Subscriptor &&) noexcept
void	subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const
void	unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const
unsigned int	n_subscriptions () const
template<typename StreamType >
void	list_subscribers (StreamType &stream) const
void	list_subscribers () const
template<class Archive >
void	serialize (Archive &ar, const unsigned int version)
Static Protected Member Functions inherited from Subscriptor
static ::ExceptionBase &	ExcInUse (int arg1, std::string arg2, std::string arg3)
static ::ExceptionBase &	ExcNoSubscriber (std::string arg1, std::string arg2)
Protected Attributes inherited from TableBase< 2, NumberType >
AlignedVector< NumberType >	values
TableIndices< N >	table_size

Detailed Description

template<typename NumberType>
class ScaLAPACKMatrix< NumberType >

A wrapper class around ScaLAPACK parallel dense linear algebra.

ScaLAPACK assumes that matrices are distributed according to the block-cyclic decomposition scheme. An \(M\) by \(N\) matrix is first decomposed into \(\lceil M / MB \rceil\) by \(\lceil N / NB \rceil\) blocks which are then uniformly distributed across the 2D process grid with \(p q \le Np\) processes, where \(p,q\) are grid dimensions and \(Np\) is the total number of processes. The parameters MB and NB are referred to as row and column block size and determine the granularity of the block-cyclic distribution.

In the following the block-cyclic distribution of a \(10 \times 9\) matrix onto a \(3\times 3\) Cartesian process grid with block sizes \(\text{MB}=\text{NB}=2\) is displayed.

Block-Cyclic Distribution

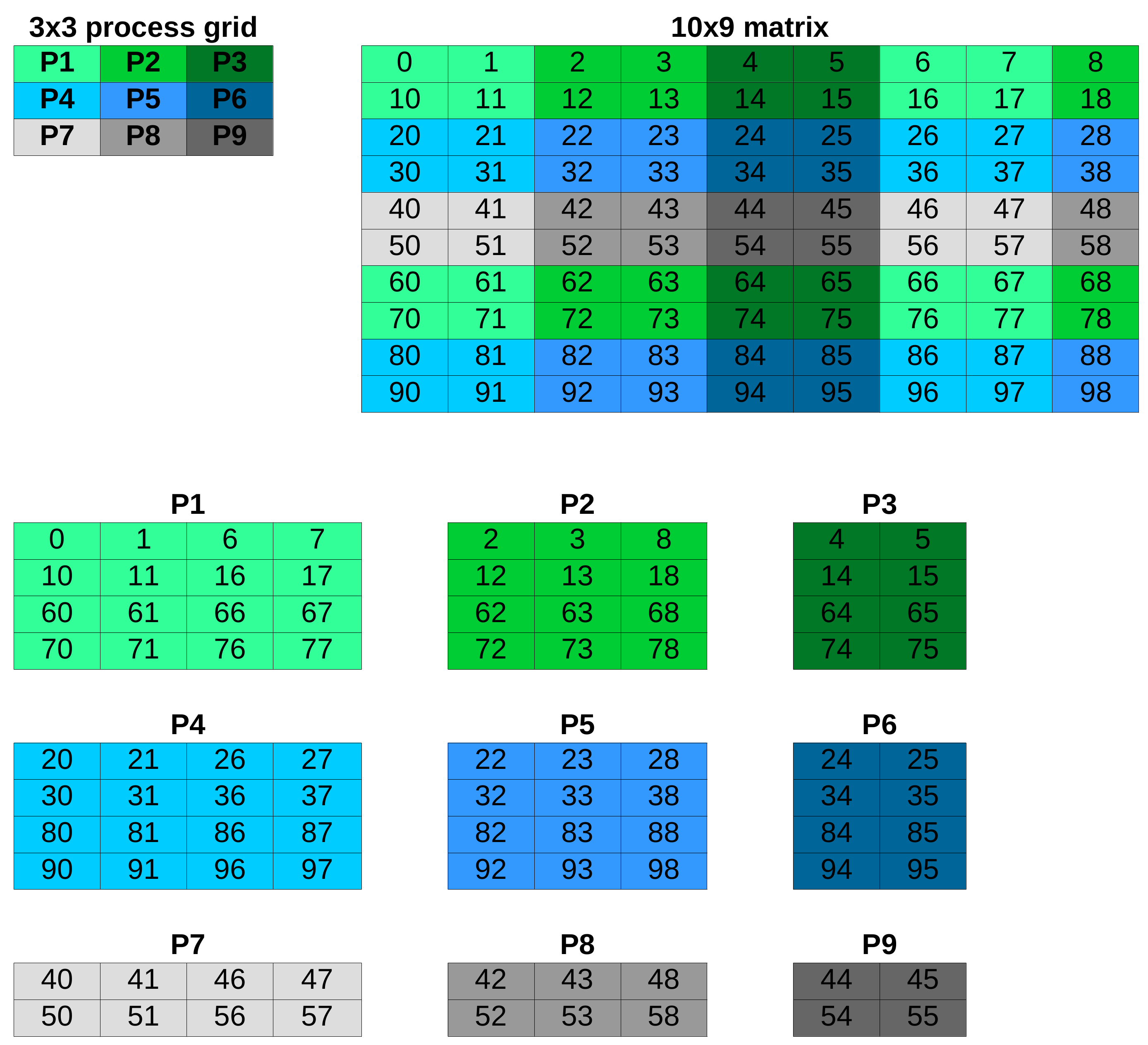
Note that the odd number of columns of the local matrices owned by the processes P2, P5 and P8 accounts for \(N=9\) not being an integral multiple of \(\text{NB}=2\).

The choice of the block sizes is a compromise between a sufficiently large size for efficient local/serial BLAS, but one that is also small enough to achieve good parallel load balance.

Below we show a strong scaling example of ScaLAPACKMatrix::invert() on up to 5 nodes each composed of two Intel Xeon 2660v2 IvyBridge sockets 2.20GHz, 10 cores/socket. Calculations are performed on square processor grids 1x1, 2x2, 3x3, 4x4, 5x5, 6x6, 7x7, 8x8, 9x9, 10x10.

Author

Denis Davydov, Benjamin Brands, 2017

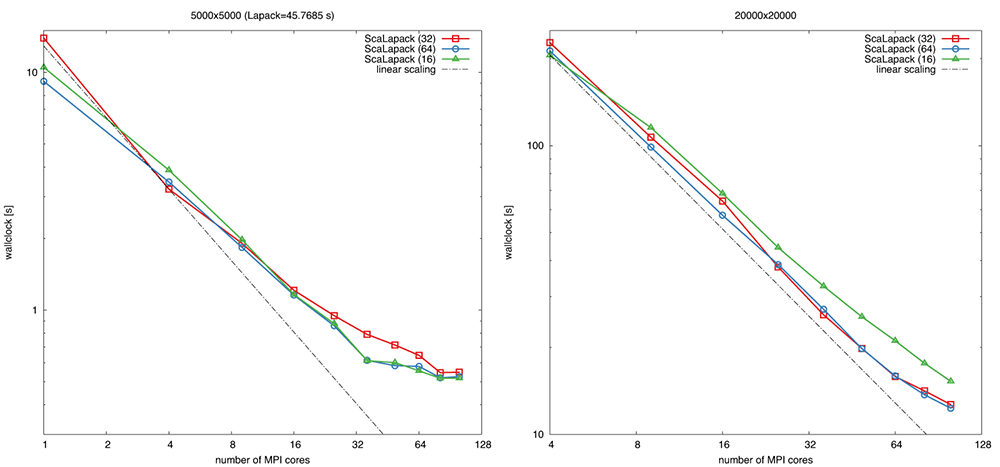
Definition at line 31 of file process_grid.h.

Member Typedef Documentation

size_type

template<typename NumberType>

using ScaLAPACKMatrix< NumberType >::size_type = unsigned int

Declare the type for container size.

Definition at line 83 of file scalapack.h.

Constructor & Destructor Documentation

ScaLAPACKMatrix() [1/3]

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix	(	const size_type	n_rows,
		const size_type	n_columns,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	row_block_size = 32,
		const size_type	column_block_size = 32,
		const LAPACKSupport::Property	property = LAPACKSupport::Property::general
	)

Constructor for a rectangular matrix with n_rows and n_cols and distributed using the grid process_grid.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 79 of file scalapack.cc.

ScaLAPACKMatrix() [2/3]

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix	(	const size_type	size,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	block_size = 32,
		const LAPACKSupport::Property	property = LAPACKSupport::Property::symmetric
	)

Constructor for a square matrix of size size, and distributed using the process grid in process_grid.

The parameter block_size is used for the block-cyclic distribution of the matrix. An identical block size is used for the rows and columns of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 104 of file scalapack.cc.

ScaLAPACKMatrix() [3/3]

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix	(	const std::string &	filename,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	row_block_size = 32,
		const size_type	column_block_size = 32
	)

Constructor for a general rectangular matrix that is read from the file filename and distributed using the grid process_grid.

Loads the matrix from file filename using HDF5. In case that deal.II was built without HDF5 a call to this function will cause an exception to be thrown.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 120 of file scalapack.cc.

~ScaLAPACKMatrix()

template<typename NumberType>

ScaLAPACKMatrix< NumberType >::~ScaLAPACKMatrix ( )

overridedefault

Destructor

Member Function Documentation

reinit() [1/2]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::reinit	(	const size_type	n_rows,
		const size_type	n_columns,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	row_block_size = 32,
		const size_type	column_block_size = 32,
		const LAPACKSupport::Property	property = LAPACKSupport::Property::general
	)

Initialize the rectangular matrix with n_rows and n_cols and distributed using the grid process_grid.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 215 of file scalapack.cc.

reinit() [2/2]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::reinit	(	const size_type	size,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	block_size = 32,
		const LAPACKSupport::Property	property = LAPACKSupport::Property::symmetric
	)

Initialize the square matrix of size size and distributed using the grid process_grid.

The parameter block_size is used for the block-cyclic distribution of the matrix. An identical block size is used for the rows and columns of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 289 of file scalapack.cc.

set_property()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::set_property

(

const LAPACKSupport::Property

property

)

Assign property to this matrix.

Definition at line 302 of file scalapack.cc.

get_property()

template<typename NumberType >

LAPACKSupport::Property ScaLAPACKMatrix< NumberType >::get_property

(

)

const

Return current property of this matrix

Definition at line 312 of file scalapack.cc.

get_state()

template<typename NumberType >

LAPACKSupport::State ScaLAPACKMatrix< NumberType >::get_state

(

)

const

Return current state of this matrix

Definition at line 321 of file scalapack.cc.

operator=()

template<typename NumberType >

ScaLAPACKMatrix< NumberType > & ScaLAPACKMatrix< NumberType >::operator=

(

const FullMatrix< NumberType > &

matrix

)

Assignment operator from a regular FullMatrix.

Note

This function should only be used for relatively small matrix dimensions. It is primarily intended for debugging purposes.

Definition at line 330 of file scalapack.cc.

copy_from()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_from	(	const LAPACKFullMatrix< NumberType > &	matrix,
		const unsigned int	rank
	)

Copies the content of the locally owned matrix to the distributed matrix. The distributed matrix and matrix on process rank must have matching dimensions.

For all processes except the process with rank rank the serial matrix is not referenced. The user has to ensure that all processes call this with identical rank. The rank refers to a process of the MPI communicator used to create the process grid of the distributed matrix.

Definition at line 361 of file scalapack.cc.

copy_to() [1/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to

(

FullMatrix< NumberType > &

matrix

)

const

Copy the contents of the distributed matrix into matrix.

Note

This function should only be used for relatively small matrix dimensions. It is primarily intended for debugging purposes.

Definition at line 659 of file scalapack.cc.

copy_to() [2/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to	(	LAPACKFullMatrix< NumberType > &	matrix,
		const unsigned int	rank
	)		const

Copies the content of the distributed matrix into the locally replicated matrix on the process with rank rank. For all processes except rank matrix is not referenced. The distributed matrix and matrix on the process rank must have matching dimensions.

The user has to ensure that all processes call this with identical rank. The rank refers to a process of the MPI communicator used to create the process grid of the distributed matrix.

Definition at line 528 of file scalapack.cc.

copy_to() [3/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to

(

ScaLAPACKMatrix< NumberType > &

dest

)

const

Copy the contents of the distributed matrix into a differently distributed matrix dest. The function also works for matrices with different process grids or block-cyclic distributions.

Definition at line 845 of file scalapack.cc.

copy_to() [4/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to	(	ScaLAPACKMatrix< NumberType > &	B,
		const std::pair< unsigned int, unsigned int > &	offset_A,
		const std::pair< unsigned int, unsigned int > &	offset_B,
		const std::pair< unsigned int, unsigned int > &	submatrix_size
	)		const

Copy a submatrix (subset) of the distributed matrix A to a submatrix of the distributed matrix B.

• The global row and column index of the first element of the submatrix A is provided by offset_A with row index=offset_A.first and column index=offset_A.second.
• The global row and column index of the first element of the submatrix B is provided by offset_B with row index=offset_B.first and column index=offset_B.second.
• The dimension of the submatrix to be copied is given by submatrix_size with number of rows=submatrix_size.first and number of columns=submatrix_size.second.

If it is necessary to copy complete matrices with an identical block-cyclic distribution, use ScaLAPACKMatrix<NumberType>::copy_to(ScaLAPACKMatrix<NumberType> &dest) with only one argument to avoid communication.

The underlying process grids of the matrices A and B must have been built with the same MPI communicator.

Definition at line 716 of file scalapack.cc.

copy_transposed()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_transposed

(

const ScaLAPACKMatrix< NumberType > &

B

)

Transposing assignment: \(\mathbf{A} = \mathbf{B}^T\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

The following alignment conditions have to be fulfilled: \(MB_A=NB_B\) and \(NB_A=MB_B\).

Definition at line 974 of file scalapack.cc.

add() [1/2]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::add	(	const ScaLAPACKMatrix< NumberType > &	B,
		const NumberType	a = 0.,
		const NumberType	b = 1.,
		const bool	transpose_B = false
	)

The operations based on the input parameter transpose_B and the alignment conditions are summarized in the following table:

transpose_B	Block Sizes	Operation
false	\(MB_A=MB_B\) \(NB_A=NB_B\)	\(\mathbf{A} = a \mathbf{A} + b \mathbf{B}\)
true	\(MB_A=NB_B\) \(NB_A=MB_B\)	\(\mathbf{A} = a \mathbf{A} + b \mathbf{B}^T\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

Definition at line 984 of file scalapack.cc.

add() [2/2]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::add	(	const NumberType	b,
		const ScaLAPACKMatrix< NumberType > &	B
	)

Matrix-addition: \(\mathbf{A} = \mathbf{A} + b\, \mathbf{B}\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

The following alignment conditions have to be fulfilled: \(MB_A=MB_B\) and \(NB_A=NB_B\).

Definition at line 1040 of file scalapack.cc.

Tadd()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::Tadd	(	const NumberType	b,
		const ScaLAPACKMatrix< NumberType > &	B
	)

Matrix-addition: \(\mathbf{A} = \mathbf{A} + b\, \mathbf{B}^T\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

The following alignment conditions have to be fulfilled: \(MB_A=NB_B\) and \(NB_A=MB_B\).

Definition at line 1050 of file scalapack.cc.

mult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::mult	(	const NumberType	b,
		const ScaLAPACKMatrix< NumberType > &	B,
		const NumberType	c,
		ScaLAPACKMatrix< NumberType > &	C,
		const bool	transpose_A = false,
		const bool	transpose_B = false
	)		const

Matrix-matrix-multiplication:

The operations based on the input parameters and the alignment conditions are summarized in the following table:

transpose_A	transpose_B	Block Sizes	Operation
false	false	\(MB_A=MB_C\) \(NB_A=MB_B\) \(NB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A} \cdot \mathbf{B} + c \mathbf{C}\)
false	true	\(MB_A=MB_C\) \(NB_A=NB_B\) \(MB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A} \cdot \mathbf{B}^T + c \mathbf{C}\)
true	false	\(MB_A=MB_B\) \(NB_A=MB_C\) \(NB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A}^T \cdot \mathbf{B} + c \mathbf{C}\)
true	true	\(MB_A=NB_B\) \(NB_A=MB_C\) \(MB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A}^T \cdot \mathbf{B}^T + c \mathbf{C}\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The matrices \(\mathbf{A}\), \(\mathbf{B}\) and \(\mathbf{C}\) must have the same process grid.

Definition at line 1060 of file scalapack.cc.

mmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::mmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = false
	)		const

Matrix-matrix-multiplication.

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A} \cdot \mathbf{B}\)

else \(\mathbf{C} = \mathbf{A} \cdot \mathbf{B}\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=MB_C\), \(NB_A=MB_B\) and \(NB_B=NB_C\).

Definition at line 1177 of file scalapack.cc.

Tmmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::Tmmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = false
	)		const

Matrix-matrix-multiplication using transpose of \(\mathbf{A}\).

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A}^T \cdot \mathbf{B}\)

else \(\mathbf{C} = \mathbf{A}^T \cdot \mathbf{B}\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=MB_B\), \(NB_A=MB_C\) and \(NB_B=NB_C\).

Definition at line 1191 of file scalapack.cc.

mTmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::mTmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = false
	)		const

Matrix-matrix-multiplication using the transpose of \(\mathbf{B}\).

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A} \cdot \mathbf{B}^T\)

else \(\mathbf{C} = \mathbf{A} \cdot \mathbf{B}^T\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=MB_C\), \(NB_A=NB_B\) and \(MB_B=NB_C\).

Definition at line 1205 of file scalapack.cc.

TmTmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::TmTmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = false
	)		const

Matrix-matrix-multiplication using transpose of \(\mathbf{A}\) and \(\mathbf{B}\).

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A}^T \cdot \mathbf{B}^T\)

else \(\mathbf{C} = \mathbf{A}^T \cdot \mathbf{B}^T\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=NB_B\), \(NB_A=MB_C\) and \(MB_B=NB_C\).

Definition at line 1219 of file scalapack.cc.

save()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::save	(	const std::string &	filename,
		const std::pair< unsigned int, unsigned int > &	chunk_size = std::make_pair(numbers::invalid_unsigned_int,                        numbers::invalid_unsigned_int)
	)		const

Stores the distributed matrix in filename using HDF5.

In case that deal.II was built without HDF5 a call to this function will cause an exception to be thrown.

If HDF5 was built with MPI, parallel I/O is used to save the matrix. Otherwise, just one process will do the output. This means that internally the distributed matrix is copied to one process, which does the output. Therefore, the matrix has to fit into the memory of one process.

To tweak the I/O performance, especially for parallel I/O, the user may define the optional parameter chunk_size. All MPI processes need to call the function with the same value. The matrix is written in chunks to the file, therefore the properties of the system define the optimal chunk size. Internally, HDF5 splits the matrix into chunk_size.first x chunk_size.second sized blocks, with chunk_size.first being the number of rows of a chunk and chunk_size.second the number of columns.

Definition at line 2601 of file scalapack.cc.

load()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::load

(

const std::string &

filename

)

Loads the distributed matrix from file filename using HDF5. In case that deal.II was built without HDF5 a call to this function will cause an exception to be thrown.

The matrix must have the same dimensions as the matrix stored in the file.

If HDF5 was build with MPI, parallel I/O is used to load the matrix. Otherwise, just one process will load the matrix from storage and distribute the content to the other processes subsequently.

Definition at line 3036 of file scalapack.cc.

compute_cholesky_factorization()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::compute_cholesky_factorization

(

)

Compute the Cholesky factorization of the matrix using ScaLAPACK function pXpotrf. The result of the factorization is stored in this object.

Definition at line 1233 of file scalapack.cc.

compute_lu_factorization()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::compute_lu_factorization

(

)

Compute the LU factorization of the matrix using ScaLAPACK function pXgetrf and partial pivoting with row interchanges. The result of the factorization is stored in this object.

Definition at line 1266 of file scalapack.cc.

invert()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::invert

(

)

Invert the matrix by first computing a Cholesky for symmetric matrices or a LU factorization for general matrices and then building the actual inverse using pXpotri or pXgetri. If the matrix is triangular, the LU factorization step is skipped, and pXtrtri is used directly.

If a Cholesky or LU factorization has been applied previously, pXpotri or pXgetri are called directly.

The inverse is stored in this object.

Definition at line 1307 of file scalapack.cc.

eigenpairs_symmetric_by_index()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_index	(	const std::pair< unsigned int, unsigned int > &	index_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\).

The eigenvalues/eigenvectors are selected by prescribing a range of indices index_limits.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

If all eigenvalues/eigenvectors have to be computed, pass the closed interval \( \left[ 0, M-1 \right] \) in index_limits.

Pass the closed interval \( \left[ M-r, M-1 \right] \) if the \(r\) largest eigenvalues/eigenvectors are desired.

Definition at line 1423 of file scalapack.cc.

eigenpairs_symmetric_by_value()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_value	(	const std::pair< NumberType, NumberType > &	value_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors. The eigenvalues/eigenvectors are selected by prescribing a range of values value_limits for the eigenvalues.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

Definition at line 1446 of file scalapack.cc.

eigenpairs_symmetric_by_index_MRRR()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_index_MRRR	(	const std::pair< unsigned int, unsigned int > &	index_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\) using the MRRR algorithm.

The eigenvalues/eigenvectors are selected by prescribing a range of indices index_limits.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

If all eigenvalues/eigenvectors have to be computed, pass the closed interval \( \left[ 0, M-1 \right] \) in index_limits.

Pass the closed interval \( \left[ M-r, M-1 \right] \) if the \(r\) largest eigenvalues/eigenvectors are desired.

Definition at line 1756 of file scalapack.cc.

eigenpairs_symmetric_by_value_MRRR()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_value_MRRR	(	const std::pair< NumberType, NumberType > &	value_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\) using the MRRR algorithm. The eigenvalues/eigenvectors are selected by prescribing a range of values value_limits for the eigenvalues.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

Definition at line 1779 of file scalapack.cc.

compute_SVD()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::compute_SVD	(	ScaLAPACKMatrix< NumberType > *	U = nullptr,
		ScaLAPACKMatrix< NumberType > *	VT = nullptr
	)

Computing the singular value decomposition (SVD) of a matrix \(\mathbf{A} \in \mathbb{R}^{M \times N}\), optionally computing the left and/or right singular vectors. The SVD is written as \(\mathbf{A} = \mathbf{U} \cdot \mathbf{\Sigma} \cdot \mathbf{V}^T\) with \(\mathbf{\Sigma} \in \mathbb{R}^{M \times N}\) as a diagonal matrix, \(\mathbf{U} \in \mathbb{R}^{M \times M}\) and \(\mathbf{V} \in \mathbb{R}^{M \times M}\) as orthogonal matrices. The diagonal elements of \(\mathbf{\Sigma}\) are the singular values of \(A\) and the columns of \(\mathbf{U}\) and \(\mathbf{V}\) are the corresponding left and right singular vectors, respectively. The singular values are returned in decreasing order and only the first \(\min(M,N)\) columns of \(\mathbf{U}\) and rows of \(\mathbf{V}^T\) are computed.

Upon return the content of the matrix is unusable. The matrix \(\mathbf{A}\) must have identical block cyclic distribution for the rows and column.

If left singular vectors are required matrices \(\mathbf{A}\) and \(\mathbf{U}\) have to be constructed with the same process grid and block cyclic distribution. If right singular vectors are required matrices \(\mathbf{A}\) and \(\mathbf{V}^T\) have to be constructed with the same process grid and block cyclic distribution.

To avoid computing the left and/or right singular vectors the function accepts nullptr for U and/or VT.

Definition at line 2007 of file scalapack.cc.

least_squares()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::least_squares	(	ScaLAPACKMatrix< NumberType > &	B,
		const bool	transpose = false
	)

Solving overdetermined or underdetermined real linear systems involving matrix \(\mathbf{A} \in \mathbb{R}^{M \times N}\), or its transpose \(\mathbf{A}^T\), using a QR or LQ factorization of \(\mathbf{A}\) for \(N_{\rm RHS}\) RHS vectors in the columns of matrix \(\mathbf{B}\)

It is assumed that \(\mathbf{A}\) has full rank: \(\rm{rank}(\mathbf{A}) = \min(M,N)\).

The following options are supported:

1. If(!transpose) and \(M \geq N\): least squares solution of overdetermined system \(\min \Vert \mathbf{B} - \mathbf{A}\cdot \mathbf{X}\Vert\).
   Upon exit the rows \(0\) to \(N-1\) of \(\mathbf{B}\) contain the least square solution vectors. The residual sum of squares for each column is given by the sum of squares of elements \(N\) to \(M-1\) in that column.
2. If(!transpose) and \(M < N\): find minimum norm solutions of underdetermined systems \(\mathbf{A} \cdot \mathbf{X} = \mathbf{B}\).
   Upon exit the columns of \(\mathbf{B}\) contain the minimum norm solution vectors.
3. If(transpose) and \(M \geq N\): find minimum norm solutions of underdetermined system \( \mathbf{A}^\top \cdot \mathbf{X} = \mathbf{B}\).
   Upon exit the columns of \(\mathbf{B}\) contain the minimum norm solution vectors.
4. If(transpose) and \(M < N\): least squares solution of overdetermined system \(\min \Vert \mathbf{B} - \mathbf{A}^\top \cdot \mathbf{X}\Vert\).
   Upon exit the rows \(0\) to \(M-1\) contain the least square solution vectors. The residual sum of squares for each column is given by the sum of squares of elements \(M\) to \(N-1\) in that column.

If(!tranpose) then \(\mathbf{B} \in \mathbb{R}^{M \times N_{\rm RHS}}\), otherwise \(\mathbf{B} \in \mathbb{R}^{N \times N_{\rm RHS}}\). The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have an identical block cyclic distribution for rows and columns.

Definition at line 2127 of file scalapack.cc.

pseudoinverse()

template<typename NumberType >

unsigned int ScaLAPACKMatrix< NumberType >::pseudoinverse

(

const NumberType

ratio

)

Compute the pseudoinverse \(\mathbf{A}^+ \in \mathbb{R}^{N \times M}\) (Moore-Penrose inverse) of a real matrix \(\mathbf{A} \in \mathbb{R}^{M \times N}\) using the singular value decomposition \(\mathbf{A} = \mathbf{U} \cdot \mathbf{\Sigma} \cdot \mathbf{V}^T\).

Unlike the inverse, the pseudoinverse \(\mathbf{A}^+ = \mathbf{V} \cdot \mathbf{\Sigma}^+ \cdot \mathbf{U}^T\) exists for both rectangular as well as singular matrices \(\mathbf{A}\).

For a rectangular \(\mathbf{\Sigma}\) the pseudoinverse is computed by taking the reciprocal of each non-zero element on the diagonal, leaving the zeros in place, and then transposing \(\mathbf{\Sigma}\). For the numerical computation only the singular values \(\sigma_i > \sigma_{\text{max}} \, \text{ratio}\) are taken into account. Upon successful exit, the function returns the number of singular values fulfilling that condition. That value can be interpreted as the rank of \(\mathbf{A}\).

Upon return this object contains the pseudoinverse \(\mathbf{A}^+ \in \mathbb{R}^{N \times M}\).

The following alignment conditions have to be fulfilled: \(MB_A = NB_A\).

Definition at line 2219 of file scalapack.cc.

reciprocal_condition_number()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::reciprocal_condition_number

(

const NumberType

a_norm

)

const

Estimate the condition number of a SPD matrix in the \(l_1\)-norm. The matrix has to be in the Cholesky state (see compute_cholesky_factorization()). The reciprocal of the condition number is returned in order to avoid the possibility of overflow when the condition number is very large.

a_norm must contain the \(l_1\)-norm of the matrix prior to calling Cholesky factorization (see l1_norm()).

Note

An alternative is to compute the inverse of the matrix explicitly and manually construct \(k_1 = ||\mathbf{A}||_1 \, ||\mathbf{A}^{-1}||_1\).

Definition at line 2306 of file scalapack.cc.

l1_norm()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::l1_norm

(

)

const

Compute the \(l_1\)-norm of the matrix.

Definition at line 2368 of file scalapack.cc.

linfty_norm()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::linfty_norm

(

)

const

Compute the \(l_{\infty}\) norm of the matrix.

Definition at line 2382 of file scalapack.cc.

frobenius_norm()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::frobenius_norm

(

)

const

Compute the Frobenius norm of the matrix.

Definition at line 2396 of file scalapack.cc.

m()

template<typename NumberType>

size_type ScaLAPACKMatrix< NumberType >::m

(

)

const

Number of rows of the \(M \times N\) matrix.

n()

template<typename NumberType>

size_type ScaLAPACKMatrix< NumberType >::n

(

)

const

Number of columns of the \(M \times N\) matrix.

local_m()

template<typename NumberType>

unsigned int ScaLAPACKMatrix< NumberType >::local_m

(

)

const

Number of local rows on this MPI processes.

local_n()

template<typename NumberType>

unsigned int ScaLAPACKMatrix< NumberType >::local_n

(

)

const

Number of local columns on this MPI process.

global_row()

template<typename NumberType >

unsigned int ScaLAPACKMatrix< NumberType >::global_row

(

const unsigned int

loc_row

)

const

Return the global row number for the given local row loc_row .

Definition at line 493 of file scalapack.cc.

global_column()

template<typename NumberType >

unsigned int ScaLAPACKMatrix< NumberType >::global_column

(

const unsigned int

loc_column

)

const

Return the global column number for the given local column loc_column.

Definition at line 510 of file scalapack.cc.

local_el() [1/2]

template<typename NumberType>

NumberType ScaLAPACKMatrix< NumberType >::local_el	(	const unsigned int	loc_row,
		const unsigned int	loc_column
	)		const

Read access to local element.

local_el() [2/2]

template<typename NumberType>

NumberType& ScaLAPACKMatrix< NumberType >::local_el	(	const unsigned int	loc_row,
		const unsigned int	loc_column
	)

Write access to local element.

scale_columns()

template<typename NumberType >

template<class InputVector >

void ScaLAPACKMatrix< NumberType >::scale_columns

(

const InputVector &

factors

)

Scale the columns of the distributed matrix by the scalars provided in the array factors.

The array factors must have as many entries as the matrix columns.

Copies of factors have to be available on all processes of the underlying MPI communicator.

Note

The fundamental prerequisite for the InputVector is that it must be possible to create an ArrayView from it; this is satisfied by the std::vector and Vector classes.

Definition at line 3489 of file scalapack.cc.

scale_rows()

template<typename NumberType >

template<class InputVector >

void ScaLAPACKMatrix< NumberType >::scale_rows

(

const InputVector &

factors

)

Scale the rows of the distributed matrix by the scalars provided in the array factors.

The array factors must have as many entries as the matrix rows.

Copies of factors have to be available on all processes of the underlying MPI communicator.

Note

The fundamental prerequisite for the InputVector is that it must be possible to create an ArrayView from it; this is satisfied by the std::vector and Vector classes.

Definition at line 3500 of file scalapack.cc.

norm_symmetric()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::norm_symmetric ( const char  type ) const

private

Calculate the norm of a distributed symmetric dense matrix using ScaLAPACK's internal function.

Definition at line 2469 of file scalapack.cc.

norm_general()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::norm_general ( const char  type ) const

private

Calculate the norm of a distributed dense matrix using ScaLAPACK's internal function.

Definition at line 2410 of file scalapack.cc.

eigenpairs_symmetric()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric ( const bool  compute_eigenvectors, const std::pair< unsigned int, unsigned int > &  index_limits = std::make_pair(numbers::invalid_unsigned_int,                     numbers::invalid_unsigned_int), const std::pair< NumberType, NumberType > &  value_limits = std::make_pair(std::numeric_limits<NumberType>::quiet_NaN(),                     std::numeric_limits<NumberType>::quiet_NaN())  )

private

Computing selected eigenvalues and, optionally, the eigenvectors. The eigenvalues/eigenvectors are selected by either prescribing a range of indices index_limits or a range of values value_limits for the eigenvalues. The function will throw an exception if both ranges are prescribed (meaning that both ranges differ from the default value) as this ambiguity is prohibited. If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

Definition at line 1466 of file scalapack.cc.

eigenpairs_symmetric_MRRR()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_MRRR ( const bool  compute_eigenvectors, const std::pair< unsigned int, unsigned int > &  index_limits = std::make_pair(numbers::invalid_unsigned_int,                     numbers::invalid_unsigned_int), const std::pair< NumberType, NumberType > &  value_limits = std::make_pair(std::numeric_limits<NumberType>::quiet_NaN(),                     std::numeric_limits<NumberType>::quiet_NaN())  )

private

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\) using the MRRR algorithm. The eigenvalues/eigenvectors are selected by either prescribing a range of indices index_limits or a range of values value_limits for the eigenvalues. The function will throw an exception if both ranges are prescribed (meaning that both ranges differ from the default value) as this ambiguity is prohibited.

By calling this function the original content of the matrix will be overwritten. If requested, the eigenvectors are stored in the columns of the matrix. Also in the case that just the eigenvalues are required, the content of the matrix will be overwritten.

If successful, the computed eigenvalues are arranged in ascending order.

Note

Due to a bug in Netlib-ScaLAPACK, either all or no eigenvectors can be computed. Therefore, the input index_limits has to be set accordingly. Using Intel-MKL this restriction is not required.

Definition at line 1797 of file scalapack.cc.

Member Data Documentation

state

template<typename NumberType>

LAPACKSupport::State ScaLAPACKMatrix< NumberType >::state

private

Since ScaLAPACK operations notoriously change the meaning of the matrix entries, we record the current state after the last operation here.

Definition at line 889 of file scalapack.h.

property

template<typename NumberType>

LAPACKSupport::Property ScaLAPACKMatrix< NumberType >::property

private

Additional property of the matrix which may help to select more efficient ScaLAPACK functions.

Definition at line 895 of file scalapack.h.

grid

template<typename NumberType>

std::shared_ptr<const Utilities::MPI::ProcessGrid> ScaLAPACKMatrix< NumberType >::grid

private

A shared pointer to a Utilities::MPI::ProcessGrid object which contains a BLACS context and a MPI communicator, as well as other necessary data structures.

Definition at line 902 of file scalapack.h.

n_rows

template<typename NumberType>

int ScaLAPACKMatrix< NumberType >::n_rows

private

Number of rows in the matrix.

Definition at line 907 of file scalapack.h.

n_columns

template<typename NumberType>

int ScaLAPACKMatrix< NumberType >::n_columns

private

Number of columns in the matrix.

Definition at line 912 of file scalapack.h.

row_block_size

template<typename NumberType>

int ScaLAPACKMatrix< NumberType >::row_block_size

private

Row block size.

Definition at line 917 of file scalapack.h.

column_block_size

template<typename NumberType>

int ScaLAPACKMatrix< NumberType >::column_block_size

private

Column block size.

Definition at line 922 of file scalapack.h.

n_local_rows

template<typename NumberType>

int ScaLAPACKMatrix< NumberType >::n_local_rows

private

Number of rows in the matrix owned by the current process.

Definition at line 927 of file scalapack.h.

n_local_columns

template<typename NumberType>

int ScaLAPACKMatrix< NumberType >::n_local_columns

private

Number of columns in the matrix owned by the current process.

Definition at line 932 of file scalapack.h.

descriptor

template<typename NumberType>

int ScaLAPACKMatrix< NumberType >::descriptor[9]

private

ScaLAPACK description vector.

Definition at line 937 of file scalapack.h.

work

template<typename NumberType>

std::vector<NumberType> ScaLAPACKMatrix< NumberType >::work

mutableprivate

Workspace array.

Definition at line 942 of file scalapack.h.

iwork

template<typename NumberType>

std::vector<int> ScaLAPACKMatrix< NumberType >::iwork

mutableprivate

Integer workspace array.

Definition at line 947 of file scalapack.h.

ipiv

template<typename NumberType>

std::vector<int> ScaLAPACKMatrix< NumberType >::ipiv

private

Integer array holding pivoting information required by ScaLAPACK's matrix factorization routines.

Definition at line 953 of file scalapack.h.

uplo

template<typename NumberType>

const char ScaLAPACKMatrix< NumberType >::uplo

private

A character to define where elements are stored in case ScaLAPACK operations support this.

Definition at line 959 of file scalapack.h.

first_process_row

template<typename NumberType>

const int ScaLAPACKMatrix< NumberType >::first_process_row

private

The process row of the process grid over which the first row of the global matrix is distributed.

Definition at line 965 of file scalapack.h.

first_process_column

template<typename NumberType>

const int ScaLAPACKMatrix< NumberType >::first_process_column

private

The process column of the process grid over which the first column of the global matrix is distributed.

Definition at line 971 of file scalapack.h.

submatrix_row

template<typename NumberType>

const int ScaLAPACKMatrix< NumberType >::submatrix_row

private

Global row index that determines where to start a submatrix. Currently this equals unity, as we don't use submatrices.

Definition at line 977 of file scalapack.h.

submatrix_column

template<typename NumberType>

const int ScaLAPACKMatrix< NumberType >::submatrix_column

private

Global column index that determines where to start a submatrix. Currently this equals unity, as we don't use submatrices.

Definition at line 983 of file scalapack.h.

mutex

template<typename NumberType>

Threads::Mutex ScaLAPACKMatrix< NumberType >::mutex

mutableprivate

Thread mutex.

Definition at line 988 of file scalapack.h.

---

The documentation for this class was generated from the following files:

• deal.II/base/process_grid.h
• deal.II/lac/scalapack.h
• source/lac/scalapack.cc