PolynomialsRT_Bubbles< dim > Class Template Reference

#include <deal.II/base/polynomials_rt_bubbles.h>

Public Member Functions
	PolynomialsRT_Bubbles (const unsigned int k)
void	compute (const Point< dim > &unit_point, std::vector< Tensor< 1, dim >> &values, std::vector< Tensor< 2, dim >> &grads, std::vector< Tensor< 3, dim >> &grad_grads, std::vector< Tensor< 4, dim >> &third_derivatives, std::vector< Tensor< 5, dim >> &fourth_derivatives) const
unsigned int	n () const
unsigned int	degree () const
std::string	name () const

Static Public Member Functions
static unsigned int	compute_n_pols (const unsigned int degree)

Private Attributes
const unsigned int	my_degree
const PolynomialsRaviartThomas< dim >	raviart_thomas_space
std::vector< Polynomials::Polynomial< double > >	monomials
unsigned int	n_pols

Detailed Description

template<int dim>
class PolynomialsRT_Bubbles< dim >

This class implements the H^div-conforming, vector-valued enhanced Raviart-Thomas polynomials.

Similarly to the classical Raviart-Thomas space, the enhanced Raviart-Thomas polynomials are constructed such that the divergence is in the tensor product polynomial space Q_k-1.

This space is of the form V_k = RT_k-1 + B_k, where B_k is defined as follows:

In 2D:

\begin{align*} B_k^1(E) = \text{span}\left\{x^{a_1-1} y^{a_2}\begin{pmatrix} (a_2+1) x \\ -a_1 y \end{pmatrix}\text{ : } a_2=k \right\} \\ B_k^2(E) = \text{span}\left\{x^{b_1} y^{b_2-1}\begin{pmatrix} -b_2 x \\ (b_1+1) y \end{pmatrix}\text{ : } b_1=k \right\} \end{align*}

In 3D:

\begin{align*} B_k^1(E) = \text{span}\left\{x^{a_1-1} y^{a_2} z^{a_3}\begin{pmatrix} (a_2+a_3+2) x \\ -a_1 y \\ -a_1 z \end{pmatrix}\text{ : } a_2=k \text{ or } a_3=k \right\},\\ B_k^2(E) = \text{span}\left\{x^{b_1} y^{b_2-1} z^{b_3}\begin{pmatrix} -b_2 x \\ (b_1+b_3+2) y \\ -b_2 z \end{pmatrix}\text{ : } b_1=k \text{ or } b_3=k \right\},\\ B_k^3(E) = \text{span}\left\{x^{c_1}y^{c_2}z^{c_3-1}\begin{pmatrix} -c_3 x \\ -c_3y \\ (c_1+c_2+2)z \end{pmatrix}\text{ : } c_1=k \text{ or } c_2=k \right\}, \end{align*}

where \(0 \le a_1, a_2, a_3 \le k\).

Note

Unlike the classical Raviart-Thomas space, the lowest order for the enhanced space is 1, similarly to the Brezzi-Douglas-Marini (BDM) polynomial space.

The total dimension of the space dim(V_k) = d*(k+1)^d, where d is the space dimension. This allows to associate shape functions with the Gauss-Lobatto quadrature points as shown in the figures below.

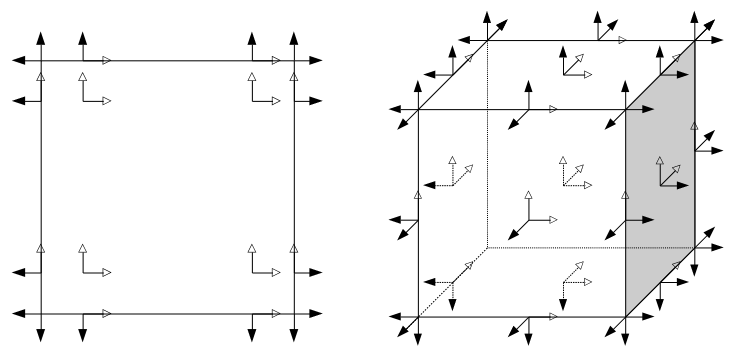
Left - \(2D,\,k=3\), right - \(3D,\,k=2\).

Author

Eldar Khattatov

Date

2018

Definition at line 87 of file polynomials_rt_bubbles.h.

Constructor & Destructor Documentation

PolynomialsRT_Bubbles()

template<int dim>

PolynomialsRT_Bubbles< dim >::PolynomialsRT_Bubbles

(

const unsigned int

k

)

Constructor. Creates all basis functions for RT_bubbles polynomials of given degree.

Definition at line 29 of file polynomials_rt_bubbles.cc.

Member Function Documentation

compute()

template<int dim>

void PolynomialsRT_Bubbles< dim >::compute	(	const Point< dim > &	unit_point,
		std::vector< Tensor< 1, dim >> &	values,
		std::vector< Tensor< 2, dim >> &	grads,
		std::vector< Tensor< 3, dim >> &	grad_grads,
		std::vector< Tensor< 4, dim >> &	third_derivatives,
		std::vector< Tensor< 5, dim >> &	fourth_derivatives
	)		const

Computes the value and the first and second derivatives of each RT_bubbles polynomial at unit_point.

The size of the vectors must either be zero or equal n(). In the first case, the function will not compute these values.

If you need values or derivatives of all tensor product polynomials then use this function, rather than using any of the compute_value, compute_grad or compute_grad_grad functions, see below, in a loop over all tensor product polynomials.

Definition at line 45 of file polynomials_rt_bubbles.cc.

n()

template<int dim>

unsigned int PolynomialsRT_Bubbles< dim >::n ( ) const

inline

Returns the number of enhanced Raviart-Thomas polynomials.

Definition at line 170 of file polynomials_rt_bubbles.h.

degree()

template<int dim>

unsigned int PolynomialsRT_Bubbles< dim >::degree ( ) const

inline

Returns the degree of the RT_bubble space, which is one less than the highest polynomial degree.

Definition at line 179 of file polynomials_rt_bubbles.h.

name()

template<int dim>

std::string PolynomialsRT_Bubbles< dim >::name ( ) const

inline

Return the name of the space, which is RT_Bubbles.

Definition at line 188 of file polynomials_rt_bubbles.h.

compute_n_pols()

template<int dim>

unsigned int PolynomialsRT_Bubbles< dim >::compute_n_pols ( const unsigned int  degree )

static

Return the number of polynomials in the space RT_Bubbles(degree) without requiring to build an object of PolynomialsRT-Bubbles. This is required by the FiniteElement classes.

Definition at line 836 of file polynomials_rt_bubbles.cc.

Member Data Documentation

my_degree

template<int dim>

const unsigned int PolynomialsRT_Bubbles< dim >::my_degree

private

The degree of this object as given to the constructor.

Definition at line 147 of file polynomials_rt_bubbles.h.

raviart_thomas_space

template<int dim>

const PolynomialsRaviartThomas<dim> PolynomialsRT_Bubbles< dim >::raviart_thomas_space

private

An object representing the Raviart-Thomas part of the space

Definition at line 152 of file polynomials_rt_bubbles.h.

monomials

template<int dim>

std::vector<Polynomials::Polynomial<double> > PolynomialsRT_Bubbles< dim >::monomials

private

Storage for monomials, we need all polynomials from degree zero to k+1.

Definition at line 158 of file polynomials_rt_bubbles.h.

n_pols

template<int dim>

unsigned int PolynomialsRT_Bubbles< dim >::n_pols

private

Number of RT_Bubbles polynomials.

Definition at line 163 of file polynomials_rt_bubbles.h.

---

The documentation for this class was generated from the following files:

• deal.II/base/polynomials_rt_bubbles.h
• source/base/polynomials_rt_bubbles.cc