 |
Reference documentation for deal.II version 9.1.1
|
|
Reference documentation for deal.II version 9.1.1
|
#include <deal.II/grid/manifold_lib.h>
Public Member Functions | |
| EllipticalManifold (const Point< spacedim > ¢er, const Tensor< 1, spacedim > &major_axis_direction, const double eccentricity) | |
| virtual std::unique_ptr< Manifold< dim, spacedim > > | clone () const override |
| virtual Point< spacedim > | pull_back (const Point< spacedim > &space_point) const override |
| virtual Point< spacedim > | push_forward (const Point< spacedim > &chart_point) const override |
| virtual DerivativeForm< 1, spacedim, spacedim > | push_forward_gradient (const Point< spacedim > &chart_point) const override |
 Public Member Functions inherited from ChartManifold< dim, spacedim, spacedim > | |
| ChartManifold (const Tensor< 1, chartdim > &periodicity=Tensor< 1, chartdim >()) | |
| virtual | ~ChartManifold () override=default |
| virtual Point< spacedim > | get_intermediate_point (const Point< spacedim > &p1, const Point< spacedim > &p2, const double w) const override |
| virtual Point< spacedim > | get_new_point (const ArrayView< const Point< spacedim >> &surrounding_points, const ArrayView< const double > &weights) const override |
| virtual void | get_new_points (const ArrayView< const Point< spacedim >> &surrounding_points, const Table< 2, double > &weights, ArrayView< Point< spacedim >> new_points) const override |
| virtual Point< spacedim > | push_forward (const Point< chartdim > &chart_point) const=0 |
| virtual DerivativeForm< 1, chartdim, spacedim > | push_forward_gradient (const Point< chartdim > &chart_point) const |
| virtual Tensor< 1, spacedim > | get_tangent_vector (const Point< spacedim > &x1, const Point< spacedim > &x2) const override |
| const Tensor< 1, chartdim > & | get_periodicity () const |
| Public Member Functions inherited from Manifold< dim, spacedim > | |
| virtual | ~Manifold () override=default |
| virtual Point< spacedim > | project_to_manifold (const ArrayView< const Point< spacedim >> &surrounding_points, const Point< spacedim > &candidate) const |
| virtual Point< spacedim > | get_new_point_on_line (const typename Triangulation< dim, spacedim >::line_iterator &line) const |
| virtual Point< spacedim > | get_new_point_on_quad (const typename Triangulation< dim, spacedim >::quad_iterator &quad) const |
| virtual Point< spacedim > | get_new_point_on_hex (const typename Triangulation< dim, spacedim >::hex_iterator &hex) const |
| Point< spacedim > | get_new_point_on_face (const typename Triangulation< dim, spacedim >::face_iterator &face) const |
| Point< spacedim > | get_new_point_on_cell (const typename Triangulation< dim, spacedim >::cell_iterator &cell) const |
| virtual Tensor< 1, spacedim > | normal_vector (const typename Triangulation< dim, spacedim >::face_iterator &face, const Point< spacedim > &p) const |
| virtual void | get_normals_at_vertices (const typename Triangulation< dim, spacedim >::face_iterator &face, FaceVertexNormals &face_vertex_normals) const |
| Public Member Functions inherited from Subscriptor | |
| Subscriptor () | |
| Subscriptor (const Subscriptor &) | |
| Subscriptor (Subscriptor &&) noexcept | |
| virtual | ~Subscriptor () |
| Subscriptor & | operator= (const Subscriptor &) |
| Subscriptor & | operator= (Subscriptor &&) noexcept |
| void | subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const |
| void | unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const |
| unsigned int | n_subscriptions () const |
| template<typename StreamType > | |
| void | list_subscribers (StreamType &stream) const |
| void | list_subscribers () const |
| template<class Archive > | |
| void | serialize (Archive &ar, const unsigned int version) |
Protected Attributes | |
| Tensor< 1, spacedim > | direction |
| const Point< spacedim > | center |
| const double | cosh_u |
Static Private Member Functions | |
| static Tensor< 1, spacedim > | get_periodicity () |
Additional Inherited Members | |
| Public Types inherited from Manifold< dim, spacedim > | |
| using | FaceVertexNormals = std::array< Tensor< 1, spacedim >, GeometryInfo< dim >::vertices_per_face > |
| Static Public Member Functions inherited from Subscriptor | |
| static ::ExceptionBase & | ExcInUse (int arg1, std::string arg2, std::string arg3) |
| static ::ExceptionBase & | ExcNoSubscriber (std::string arg1, std::string arg2) |
Elliptical manifold description derived from ChartManifold. More information on the elliptical coordinate system can be found at Wikipedia .
This is based on the definition of elliptic coordinates \((u,v)\)
\[ \left\lbrace\begin{aligned} x &= x_0 + c \cosh(u) \cos(v) \\ y &= y_0 + c \sinh(u) \sin(v) \end{aligned}\right. \]
in which \((x_0,y_0)\) are coordinates of the center of the cartesian system.
The current implementation uses coordinates \((c,v)\), instead of \((u,v)\), and fixes \(u\) according to a given eccentricity. Therefore, this choice of coordinates generates an elliptical manifold characterized by a constant eccentricity: \(e=\frac{1}{\cosh(u)}\), with \(e\in\left]0,1\right[\).
The constructor of this class will throw an exception if both dim and spacedim are different from two.
This manifold can be used to produce hyper_shells with elliptical curvature. As an example, the test elliptical_manifold_01 produces the following triangulation:
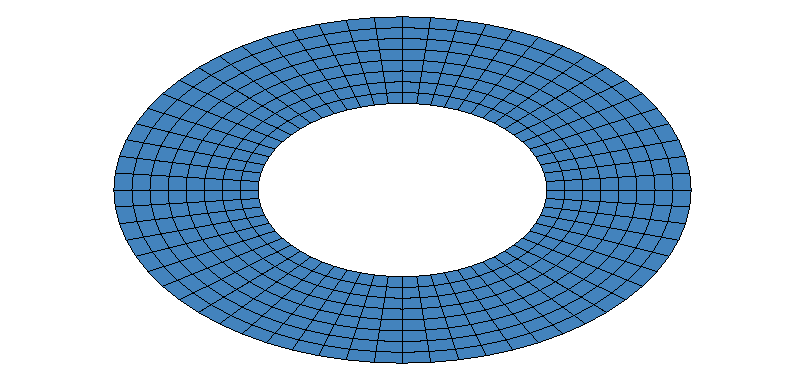
Definition at line 500 of file manifold_lib.h.
| EllipticalManifold< dim, spacedim >::EllipticalManifold | ( | const Point< spacedim > & | center, |
| const Tensor< 1, spacedim > & | major_axis_direction, | ||
| const double | eccentricity | ||
| ) |
Constructor that takes the center of the manifold system, the direction of the major axis, and the manifold eccentricity. The default major axis is the x-axis. The manifold is rotated in order to align the major axis to the direction specified in input.
| center | Center of the manifold. |
| major_axis_direction | Direction of the major axis of the manifold. |
| eccentricity | Eccentricity of the manifold \(e\in\left]0,1\right[\). |
Definition at line 1148 of file manifold_lib.cc.
|
overridevirtual |
Return a copy of this manifold.
Every derived class should implement this operation in a sensible manner.
Implements Manifold< dim, spacedim >.
Definition at line 1176 of file manifold_lib.cc.
|
overridevirtual |
Pull back the given point in spacedim to the Euclidean chartdim dimensional space.
Refer to the general documentation of this class for more information.
Implements ChartManifold< dim, spacedim, spacedim >.
Definition at line 1228 of file manifold_lib.cc.
|
overridevirtual |
Given a point in the chartdim dimensional Euclidean space, this method returns a point on the manifold embedded in the spacedim Euclidean space.
Refer to the general documentation of this class for more information.
Definition at line 1200 of file manifold_lib.cc.
|
overridevirtual |
Given a point in the chartdim dimensional Euclidean space, this method returns the derivatives of the function \(F\) that maps from the chartdim-dimensional to the spacedim-dimensional space. In other words, it is a matrix of size \(\text{spacedim}\times\text{chartdim}\).
This function is used in the computations required by the get_tangent_vector() function. Since not all users of the Manifold class interface will require calling that function, the current function is implemented but will trigger an exception whenever called. This allows derived classes to avoid implementing the push_forward_gradient function if this functionality is not needed in the user program.
Refer to the general documentation of this class for more information.
Definition at line 1270 of file manifold_lib.cc.
|
staticprivate |
Return the periodicity associated with the submanifold.
For \(\text{dim}=2\) and \(\text{spacedim}=2\), the first coordinate is non-periodic, while the second coordinate has a periodicity of \(2\pi\).
Definition at line 1187 of file manifold_lib.cc.
|
protected |
The direction vector of the major axis.
Definition at line 545 of file manifold_lib.h.
|
protected |
The center of the manifold.
Definition at line 549 of file manifold_lib.h.
|
protected |
Parameters deriving from the eccentricity of the manifold.
Definition at line 553 of file manifold_lib.h.
1.8.14