 |
Reference documentation for deal.II version 8.5.1
|
 |
Reference documentation for deal.II version 8.5.1
|
Classes | |
| struct | PeriodicFacePair |
Functions | |
Information about meshes and cells | |
| template<int dim, int spacedim> | |
| double | diameter (const Triangulation< dim, spacedim > &tria) |
| template<int dim, int spacedim> | |
| double | volume (const Triangulation< dim, spacedim > &tria, const Mapping< dim, spacedim > &mapping=(StaticMappingQ1< dim, spacedim >::mapping)) |
| template<int dim, int spacedim> | |
| double | minimal_cell_diameter (const Triangulation< dim, spacedim > &triangulation) |
| template<int dim, int spacedim> | |
| double | maximal_cell_diameter (const Triangulation< dim, spacedim > &triangulation) |
| template<int dim> | |
| double | cell_measure (const std::vector< Point< dim > > &all_vertices, const unsigned int(&vertex_indices)[GeometryInfo< dim >::vertices_per_cell]) |
| template<int dim, typename T > | |
| double | cell_measure (const T &,...) |
Functions supporting the creation of meshes | |
| template<int dim, int spacedim> | |
| void | delete_unused_vertices (std::vector< Point< spacedim > > &vertices, std::vector< CellData< dim > > &cells, SubCellData &subcelldata) |
| template<int dim, int spacedim> | |
| void | delete_duplicated_vertices (std::vector< Point< spacedim > > &all_vertices, std::vector< CellData< dim > > &cells, SubCellData &subcelldata, std::vector< unsigned int > &considered_vertices, const double tol=1e-12) |
Rotating, stretching and otherwise transforming meshes | |
| template<int dim, typename Transformation , int spacedim> | |
| void | transform (const Transformation &transformation, Triangulation< dim, spacedim > &triangulation) |
| template<int dim, int spacedim> | |
| void | shift (const Tensor< 1, spacedim > &shift_vector, Triangulation< dim, spacedim > &triangulation) |
| void | rotate (const double angle, Triangulation< 2 > &triangulation) |
| template<int dim> | |
| void | rotate (const double angle, const unsigned int axis, Triangulation< dim, 3 > &triangulation) |
| template<int dim> | |
| void | laplace_transform (const std::map< unsigned int, Point< dim > > &new_points, Triangulation< dim > &tria, const Function< dim, double > *coefficient=0, const bool solve_for_absolute_positions=false) |
| template<int dim, int spacedim> | |
| std::map< unsigned int, Point< spacedim > > | get_all_vertices_at_boundary (const Triangulation< dim, spacedim > &tria) |
| template<int dim, int spacedim> | |
| void | scale (const double scaling_factor, Triangulation< dim, spacedim > &triangulation) |
| template<int dim, int spacedim> | |
| void | distort_random (const double factor, Triangulation< dim, spacedim > &triangulation, const bool keep_boundary=true) |
| template<int dim, int spacedim> | |
| void | remove_hanging_nodes (Triangulation< dim, spacedim > &tria, const bool isotropic=false, const unsigned int max_iterations=100) |
| template<int dim, int spacedim> | |
| void | remove_anisotropy (Triangulation< dim, spacedim > &tria, const double max_ratio=1.6180339887, const unsigned int max_iterations=5) |
Finding cells and vertices of a triangulation | |
| template<int dim, template< int, int > class MeshType, int spacedim> | |
| unsigned int | find_closest_vertex (const MeshType< dim, spacedim > &mesh, const Point< spacedim > &p) |
| template<int dim, template< int, int > class MeshType, int spacedim> | |
| std::vector< typename MeshType< dim, spacedim >::active_cell_iterator > | find_cells_adjacent_to_vertex (const MeshType< dim, spacedim > &container, const unsigned int vertex_index) |
| template<int dim, template< int, int > class MeshType, int spacedim> | |
| MeshType< dim, spacedim >::active_cell_iterator | find_active_cell_around_point (const MeshType< dim, spacedim > &mesh, const Point< spacedim > &p) |
| template<int dim, template< int, int > class MeshType, int spacedim> | |
| std::pair< typename MeshType< dim, spacedim >::active_cell_iterator, Point< dim > > | find_active_cell_around_point (const Mapping< dim, spacedim > &mapping, const MeshType< dim, spacedim > &mesh, const Point< spacedim > &p) |
| template<int dim, int spacedim> | |
| std::pair< typename hp::DoFHandler< dim, spacedim >::active_cell_iterator, Point< dim > > | find_active_cell_around_point (const hp::MappingCollection< dim, spacedim > &mapping, const hp::DoFHandler< dim, spacedim > &mesh, const Point< spacedim > &p) |
| template<class MeshType > | |
| std::vector< typename MeshType::active_cell_iterator > | get_active_child_cells (const typename MeshType::cell_iterator &cell) |
| template<class MeshType > | |
| void | get_active_neighbors (const typename MeshType::active_cell_iterator &cell, std::vector< typename MeshType::active_cell_iterator > &active_neighbors) |
| template<class MeshType > | |
| std::vector< typename MeshType::active_cell_iterator > | compute_active_cell_halo_layer (const MeshType &mesh, const std_cxx11::function< bool(const typename MeshType::active_cell_iterator &)> &predicate) |
| template<class MeshType > | |
| std::vector< typename MeshType::active_cell_iterator > | compute_ghost_cell_halo_layer (const MeshType &mesh) |
| template<int dim, int spacedim> | |
| std::vector< std::set< typename Triangulation< dim, spacedim >::active_cell_iterator > > | vertex_to_cell_map (const Triangulation< dim, spacedim > &triangulation) |
| template<int dim, int spacedim> | |
| std::map< unsigned int, types::global_vertex_index > | compute_local_to_global_vertex_index_map (const parallel::distributed::Triangulation< dim, spacedim > &triangulation) |
| template<int dim, int spacedim> | |
| std::pair< unsigned int, double > | get_longest_direction (typename Triangulation< dim, spacedim >::active_cell_iterator cell) |
Partitions and subdomains of triangulations | |
| template<int dim, int spacedim> | |
| void | get_face_connectivity_of_cells (const Triangulation< dim, spacedim > &triangulation, DynamicSparsityPattern &connectivity) |
| template<int dim, int spacedim> | |
| void | get_face_connectivity_of_cells (const Triangulation< dim, spacedim > &triangulation, SparsityPattern &connectivity) 1 |
| template<int dim, int spacedim> | |
| void | get_vertex_connectivity_of_cells (const Triangulation< dim, spacedim > &triangulation, DynamicSparsityPattern &connectivity) |
| template<int dim, int spacedim> | |
| void | partition_triangulation (const unsigned int n_partitions, Triangulation< dim, spacedim > &triangulation) |
| template<int dim, int spacedim> | |
| void | partition_triangulation (const unsigned int n_partitions, const SparsityPattern &cell_connection_graph, Triangulation< dim, spacedim > &triangulation) |
| template<int dim, int spacedim> | |
| void | get_subdomain_association (const Triangulation< dim, spacedim > &triangulation, std::vector< types::subdomain_id > &subdomain) |
| template<int dim, int spacedim> | |
| unsigned int | count_cells_with_subdomain_association (const Triangulation< dim, spacedim > &triangulation, const types::subdomain_id subdomain) |
| template<int dim, int spacedim> | |
| std::vector< bool > | get_locally_owned_vertices (const Triangulation< dim, spacedim > &triangulation) |
Comparing different meshes | |
| template<typename MeshType > | |
| std::list< std::pair< typename MeshType::cell_iterator, typename MeshType::cell_iterator > > | get_finest_common_cells (const MeshType &mesh_1, const MeshType &mesh_2) |
| template<int dim, int spacedim> | |
| bool | have_same_coarse_mesh (const Triangulation< dim, spacedim > &mesh_1, const Triangulation< dim, spacedim > &mesh_2) |
| template<typename MeshType > | |
| bool | have_same_coarse_mesh (const MeshType &mesh_1, const MeshType &mesh_2) |
Dealing with distorted cells | |
| template<int dim, int spacedim> | |
| Triangulation< dim, spacedim >::DistortedCellList | fix_up_distorted_child_cells (const typename Triangulation< dim, spacedim >::DistortedCellList &distorted_cells, Triangulation< dim, spacedim > &triangulation) |
Extracting and creating patches of cells surrounding a single cell, | |
and creating triangulation out of them | |
| template<class MeshType > | |
| std::vector< typename MeshType::active_cell_iterator > | get_patch_around_cell (const typename MeshType::active_cell_iterator &cell) |
| template<class Container > | |
| std::vector< typename Container::cell_iterator > | get_cells_at_coarsest_common_level (const std::vector< typename Container::active_cell_iterator > &patch_cells) |
| template<class Container > | |
| void | build_triangulation_from_patch (const std::vector< typename Container::active_cell_iterator > &patch, Triangulation< Container::dimension, Container::space_dimension > &local_triangulation, std::map< typename Triangulation< Container::dimension, Container::space_dimension >::active_cell_iterator, typename Container::active_cell_iterator > &patch_to_global_tria_map) |
| template<class DoFHandlerType > | |
| std::map< types::global_dof_index, std::vector< typename DoFHandlerType::active_cell_iterator > > | get_dof_to_support_patch_map (DoFHandlerType &dof_handler) |
Dealing with periodic domains | |
| template<typename FaceIterator > | |
| bool | orthogonal_equality (std::bitset< 3 > &orientation, const FaceIterator &face1, const FaceIterator &face2, const int direction, const Tensor< 1, FaceIterator::AccessorType::space_dimension > &offset=Tensor< 1, FaceIterator::AccessorType::space_dimension >(), const FullMatrix< double > &matrix=FullMatrix< double >()) |
| template<typename FaceIterator > | |
| bool | orthogonal_equality (const FaceIterator &face1, const FaceIterator &face2, const int direction, const Tensor< 2, FaceIterator::AccessorType::space_dimension > &offset=Tensor< 1, FaceIterator::AccessorType::space_dimension >(), const FullMatrix< double > &matrix=FullMatrix< double >()) |
| template<typename MeshType > | |
| void | collect_periodic_faces (const MeshType &mesh, const types::boundary_id b_id1, const types::boundary_id b_id2, const int direction, std::vector< PeriodicFacePair< typename MeshType::cell_iterator > > &matched_pairs, const Tensor< 1, MeshType::space_dimension > &offset=::Tensor< 1, MeshType::space_dimension >(), const FullMatrix< double > &matrix=FullMatrix< double >()) |
| template<typename MeshType > | |
| void | collect_periodic_faces (const MeshType &mesh, const types::boundary_id b_id, const int direction, std::vector< PeriodicFacePair< typename MeshType::cell_iterator > > &matched_pairs, const ::Tensor< 1, MeshType::space_dimension > &offset=::Tensor< 1, MeshType::space_dimension >(), const FullMatrix< double > &matrix=FullMatrix< double >()) |
Dealing with boundary and manifold ids | |
| template<int dim, int spacedim> | |
| void | copy_boundary_to_manifold_id (Triangulation< dim, spacedim > &tria, const bool reset_boundary_ids=false) |
| template<int dim, int spacedim> | |
| void | copy_material_to_manifold_id (Triangulation< dim, spacedim > &tria, const bool compute_face_ids=false) |
Exceptions | |
| static ::ExceptionBase & | ExcInvalidNumberOfPartitions (int arg1) |
| static ::ExceptionBase & | ExcNonExistentSubdomain (int arg1) |
| static ::ExceptionBase & | ExcTriangulationHasBeenRefined () |
| static ::ExceptionBase & | ExcScalingFactorNotPositive (double arg1) |
| template<int N> | |
| static ::ExceptionBase & | ExcPointNotFoundInCoarseGrid (Point< N > arg1) |
| template<int N> | |
| static ::ExceptionBase & | ExcPointNotFound (Point< N > arg1) |
| static ::ExceptionBase & | ExcVertexNotUsed (unsigned int arg1) |
This namespace is a collection of algorithms working on triangulations, such as shifting or rotating triangulations, but also finding a cell that contains a given point. See the descriptions of the individual functions for more information.
| double GridTools::diameter | ( | const Triangulation< dim, spacedim > & | tria | ) |
Return the diameter of a triangulation. The diameter is computed using only the vertices, i.e. if the diameter should be larger than the maximal distance between boundary vertices due to a higher order mapping, then this function will not catch this.
Definition at line 66 of file grid_tools.cc.
| double GridTools::volume | ( | const Triangulation< dim, spacedim > & | tria, |
| const Mapping< dim, spacedim > & | mapping = (StaticMappingQ1<dim,spacedim>::mapping) |
||
| ) |
Compute the volume (i.e. the dim-dimensional measure) of the triangulation. We compute the measure using the integral \sum_K \int_K 1 \; dx where K are the cells of the given triangulation. The integral is approximated via quadrature for which we need the mapping argument.
If the triangulation is a dim-dimensional one embedded in a higher dimensional space of dimension spacedim, then the value returned is the dim-dimensional measure. For example, for a two-dimensional triangulation in three-dimensional space, the value returned is the area of the surface so described. (This obviously makes sense since the spacedim-dimensional measure of a dim-dimensional triangulation would always be zero if dim < spacedim.
This function also works for objects of type parallel::distributed::Triangulation, in which case the function is a collective operation.
| tria | The triangulation. |
| mapping | An optional argument used to denote the mapping that should be used when describing whether cells are bounded by straight or curved faces. The default is to use a Q_1 mapping, which corresponds to straight lines bounding the cells. |
Definition at line 121 of file grid_tools.cc.
| double GridTools::minimal_cell_diameter | ( | const Triangulation< dim, spacedim > & | triangulation | ) |
Return the diameter of the smallest active cell of a triangulation. See step-24 for an example of use of this function.
Definition at line 2335 of file grid_tools.cc.
| double GridTools::maximal_cell_diameter | ( | const Triangulation< dim, spacedim > & | triangulation | ) |
Return the diameter of the largest active cell of a triangulation.
Definition at line 2350 of file grid_tools.cc.
| double GridTools::cell_measure | ( | const std::vector< Point< dim > > & | all_vertices, |
| const unsigned int(&) | vertex_indices[GeometryInfo< dim >::vertices_per_cell] | ||
| ) |
Given a list of vertices (typically obtained using Triangulation::get_vertices) as the first, and a list of vertex indices that characterize a single cell as the second argument, return the measure (area, volume) of this cell. If this is a real cell, then you can get the same result using cell->measure(), but this function also works for cells that do not exist except that you make it up by naming its vertices from the list.
| double GridTools::cell_measure | ( | const T & | , |
| ... | |||
| ) |
A version of the last function that can accept input for nonzero codimension cases. This function only exists to aid generic programming and calling it will just raise an exception.
| void GridTools::delete_unused_vertices | ( | std::vector< Point< spacedim > > & | vertices, |
| std::vector< CellData< dim > > & | cells, | ||
| SubCellData & | subcelldata | ||
| ) |
Remove vertices that are not referenced by any of the cells. This function is called by all GridIn::read_* functions to eliminate vertices that are listed in the input files but are not used by the cells in the input file. While these vertices should not be in the input from the beginning, they sometimes are, most often when some cells have been removed by hand without wanting to update the vertex lists, as they might be lengthy.
This function is called by all GridIn::read_* functions as the triangulation class requires them to be called with used vertices only. This is so, since the vertices are copied verbatim by that class, so we have to eliminate unused vertices beforehand.
Not implemented for the codimension one case.
Definition at line 368 of file grid_tools.cc.
| void GridTools::delete_duplicated_vertices | ( | std::vector< Point< spacedim > > & | all_vertices, |
| std::vector< CellData< dim > > & | cells, | ||
| SubCellData & | subcelldata, | ||
| std::vector< unsigned int > & | considered_vertices, | ||
| const double | tol = 1e-12 |
||
| ) |
Remove vertices that are duplicated, due to the input of a structured grid, for example. If these vertices are not removed, the faces bounded by these vertices become part of the boundary, even if they are in the interior of the mesh.
This function is called by some GridIn::read_* functions. Only the vertices with indices in considered_vertices are tested for equality. This speeds up the algorithm, which is quadratic and thus quite slow to begin with. However, if you wish to consider all vertices, simply pass an empty vector.
Two vertices are considered equal if their difference in each coordinate direction is less than tol.
Definition at line 464 of file grid_tools.cc.
| void GridTools::transform | ( | const Transformation & | transformation, |
| Triangulation< dim, spacedim > & | triangulation | ||
| ) |
Transform the vertices of the given triangulation by applying the function object provided as first argument to all its vertices.
The transformation given as argument is used to transform each vertex. Its respective type has to offer a function-like syntax, i.e. the predicate is either an object of a type that has an operator(), or it is a pointer to the function. In either case, argument and return value have to be of type Point<spacedim>.
This function is used in the "Possibilities for extensions" section of step-38. It is also used in step-49 and step-53.
| void GridTools::shift | ( | const Tensor< 1, spacedim > & | shift_vector, |
| Triangulation< dim, spacedim > & | triangulation | ||
| ) |
Shift each vertex of the triangulation by the given shift vector. This function uses the transform() function above, so the requirements on the triangulation stated there hold for this function as well.
Definition at line 625 of file grid_tools.cc.
| void GridTools::rotate | ( | const double | angle, |
| Triangulation< 2 > & | triangulation | ||
| ) |
Rotate all vertices of the given two-dimensional triangulation in counter-clockwise sense around the origin of the coordinate system by the given angle (given in radians, rather than degrees). This function uses the transform() function above, so the requirements on the triangulation stated there hold for this function as well.
Definition at line 634 of file grid_tools.cc.
| void GridTools::rotate | ( | const double | angle, |
| const unsigned int | axis, | ||
| Triangulation< dim, 3 > & | triangulation | ||
| ) |
Rotate all vertices of the given triangulation in counter-clockwise direction around the axis with the given index. Otherwise like the function above.
| [in] | angle | Angle in radians to rotate the Triangulation by. |
| [in] | axis | Index of the coordinate axis to rotate around, keeping that coordinate fixed (0=x axis, 1=y axis, 2=z axis). |
| [in,out] | triangulation | The Triangulation object to rotate. |
Definition at line 642 of file grid_tools.cc.
| void GridTools::laplace_transform | ( | const std::map< unsigned int, Point< dim > > & | new_points, |
| Triangulation< dim > & | tria, | ||
| const Function< dim, double > * | coefficient = 0, |
||
| const bool | solve_for_absolute_positions = false |
||
| ) |
Transform the given triangulation smoothly to a different domain where, typically, each of the vertices at the boundary of the triangulation is mapped to the corresponding points in the new_points map.
The unknown displacement field u_d(\mathbf x) in direction d is obtained from the minimization problem
\min\, \int \frac{1}{2} c(\mathbf x) \mathbf \nabla u_d(\mathbf x) \cdot \mathbf \nabla u_d(\mathbf x) \,\rm d x
subject to prescribed constraints. The minimizer is obtained by solving the Laplace equation of the dim components of a displacement field that maps the current domain into one described by new_points . Linear finite elements with four Gaussian quadrature points in each direction are used. The difference between the vertex positions specified in new_points and their current value in tria therefore represents the prescribed values of this displacement field at the boundary of the domain, or more precisely at all of those locations for which new_points provides values (which may be at part of the boundary, or even in the interior of the domain). The function then evaluates this displacement field at each unconstrained vertex and uses it to place the mapped vertex where the displacement field locates it. Because the solution of the Laplace equation is smooth, this guarantees a smooth mapping from the old domain to the new one.
| [in] | new_points | The locations where a subset of the existing vertices are to be placed. Typically, this would be a map from the vertex indices of all nodes on the boundary to their new locations, thus completely specifying the geometry of the mapped domain. However, it may also include interior points if necessary and it does not need to include all boundary vertices (although you then lose control over the exact shape of the mapped domain). |
| [in,out] | tria | The Triangulation object. This object is changed in- place, i.e., the previous locations of vertices are overwritten. |
| [in] | coefficient | An optional coefficient for the Laplace problem. Larger values make cells less prone to deformation (effectively increasing their stiffness). The coefficient is evaluated in the coordinate system of the old, undeformed configuration of the triangulation as input, i.e., before the transformation is applied. Should this function be provided, sensible results can only be expected if all coefficients are positive. |
| [in] | solve_for_absolute_positions | If set to true, the minimization problem is formulated with respect to the final vertex positions as opposed to their displacement. The two formulations are equivalent for the homogeneous problem (default value of coefficient), but they result in very different mesh motion otherwise. Since in most cases one will be using a non-constant coefficient in displacement formulation, the default value of this parameter is false. |
| std::map< unsigned int, Point< spacedim > > GridTools::get_all_vertices_at_boundary | ( | const Triangulation< dim, spacedim > & | tria | ) |
Return a std::map with all vertices of faces located in the boundary
| [in] | tria | The Triangulation object. |
Definition at line 799 of file grid_tools.cc.
| void GridTools::scale | ( | const double | scaling_factor, |
| Triangulation< dim, spacedim > & | triangulation | ||
| ) |
Scale the entire triangulation by the given factor. To preserve the orientation of the triangulation, the factor must be positive.
This function uses the transform() function above, so the requirements on the triangulation stated there hold for this function as well.
Definition at line 653 of file grid_tools.cc.
| void GridTools::distort_random | ( | const double | factor, |
| Triangulation< dim, spacedim > & | triangulation, | ||
| const bool | keep_boundary = true |
||
| ) |
Distort the given triangulation by randomly moving around all the vertices of the grid. The direction of movement of each vertex is random, while the length of the shift vector has a value of factor times the minimal length of the active edges adjacent to this vertex. Note that factor should obviously be well below 0.5.
If keep_boundary is set to true (which is the default), then boundary vertices are not moved.
Distort a triangulation in some random way.
Definition at line 831 of file grid_tools.cc.
| void GridTools::remove_hanging_nodes | ( | Triangulation< dim, spacedim > & | tria, |
| const bool | isotropic = false, |
||
| const unsigned int | max_iterations = 100 |
||
| ) |
Remove hanging nodes from a grid. If the isotropic parameter is set to false (default) this function detects cells with hanging nodes and refines the neighbours in the direction that removes hanging nodes. If the isotropic parameter is set to true, the neighbours refinement is made in each directions. In order to remove all hanging nodes this procedure has to be repeated: this could require a large number of iterations. To avoid this a max number (max_iterations) of iteration is provided.
Consider the following grid:
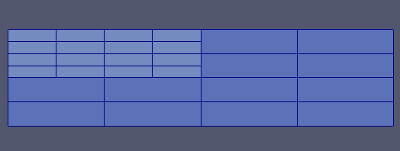
isotropic == false would return:
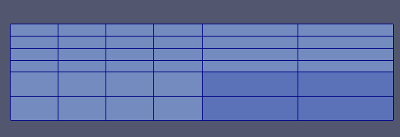
isotropic == true would return:

| [in,out] | tria | Triangulation to refine. |
| [in] | isotropic | If true refine cells in each directions, otherwise (default value) refine the cell in the direction that removes hanging node. |
| [in] | max_iterations | At each step only closest cells to hanging nodes are refined. The code may require a lot of iterations to remove all hanging nodes. max_iterations is the maximum number of iteration allowed. If max_iterations == numbers::invalid_unsigned_int this function continues refining until there are no hanging nodes. |
Definition at line 3943 of file grid_tools.cc.
| void GridTools::remove_anisotropy | ( | Triangulation< dim, spacedim > & | tria, |
| const double | max_ratio = 1.6180339887, |
||
| const unsigned int | max_iterations = 5 |
||
| ) |
Refine a mesh anisotropically such that the resulting mesh is composed by cells with maximum ratio between dimensions less than max_ratio. This procedure requires an algorithm that may not terminate. Consequently, it is possible to set a maximum number of iterations through the max_iterations parameter.
Starting from a cell like this:

This function would return:
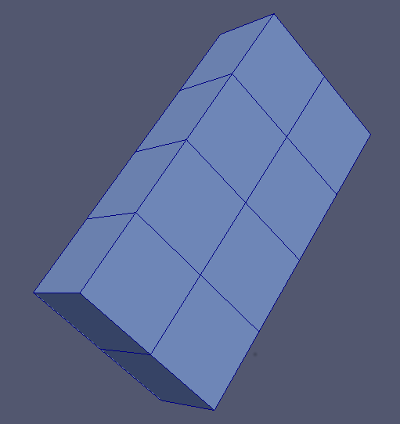
| [in,out] | tria | Triangulation to refine. |
| [in] | max_ratio | Maximum value allowed among the ratio between the dimensions of each cell. |
| [in] | max_iterations | Maximum number of iterations allowed. |
Definition at line 3978 of file grid_tools.cc.
| unsigned int GridTools::find_closest_vertex | ( | const MeshType< dim, spacedim > & | mesh, |
| const Point< spacedim > & | p | ||
| ) |
Find and return the number of the used vertex in a given mesh that is located closest to a given point.
| mesh | A variable of a type that satisfies the requirements of the MeshType concept. |
| p | The point for which we want to find the closest vertex. |
Definition at line 1053 of file grid_tools.cc.
| std::vector< typename MeshType< dim, spacedim >::active_cell_iterator > GridTools::find_cells_adjacent_to_vertex | ( | const MeshType< dim, spacedim > & | container, |
| const unsigned int | vertex_index | ||
| ) |
Find and return a vector of iterators to active cells that surround a given vertex with index vertex_index.
For locally refined grids, the vertex itself might not be a vertex of all adjacent cells that are returned. However, it will always be either a vertex of a cell or be a hanging node located on a face or an edge of it.
| container | A variable of a type that satisfies the requirements of the MeshType concept. |
| vertex_index | The index of the vertex for which we try to find adjacent cells. |
Definition at line 1100 of file grid_tools.cc.
| MeshType< dim, spacedim >::active_cell_iterator GridTools::find_active_cell_around_point | ( | const MeshType< dim, spacedim > & | mesh, |
| const Point< spacedim > & | p | ||
| ) |
Find and return an iterator to the active cell that surrounds a given point.
This is solely a wrapper function for the function of same name below. A Q1 mapping is used for the boundary, and the iterator to the cell in which the point resides is returned.
It is recommended to use the other version of this function, as it simultaneously delivers the local coordinate of the given point without additional computational cost.
| mesh | A variable of a type that satisfies the requirements of the MeshType concept. |
| p | The point for which we want to find the surrounding cell. |
Definition at line 1298 of file grid_tools.cc.
| std::pair< typename MeshType< dim, spacedim >::active_cell_iterator, Point< dim > > GridTools::find_active_cell_around_point | ( | const Mapping< dim, spacedim > & | mapping, |
| const MeshType< dim, spacedim > & | mesh, | ||
| const Point< spacedim > & | p | ||
| ) |
Find and return an iterator to the active cell that surrounds a given point p.
The algorithm used in this function proceeds by first looking for vertex located closest to the given point, see find_closest_vertex(). Secondly, all adjacent cells to this point are found in the mesh, see find_cells_adjacent_to_vertex(). Lastly, for each of these cells, it is tested whether the point is inside. This check is performed using arbitrary boundary mappings. Still, it is possible that due to roundoff errors, the point cannot be located exactly inside the unit cell. In this case, even points at a very small distance outside the unit cell are allowed.
If a point lies on the boundary of two or more cells, then the algorithm tries to identify the cell that is of highest refinement level.
| mapping | The mapping used to determine whether the given point is inside a given cell. |
| mesh | A variable of a type that satisfies the requirements of the MeshType concept. |
| p | The point for which we want to find the surrounding cell. |
Definition at line 1314 of file grid_tools.cc.
| std::pair< typename hp::DoFHandler< dim, spacedim >::active_cell_iterator, Point< dim > > GridTools::find_active_cell_around_point | ( | const hp::MappingCollection< dim, spacedim > & | mapping, |
| const hp::DoFHandler< dim, spacedim > & | mesh, | ||
| const Point< spacedim > & | p | ||
| ) |
A version of the previous function where we use that mapping on a given cell that corresponds to the active finite element index of that cell. This is obviously only useful for hp problems, since the active finite element index for all other DoF handlers is always zero.
Definition at line 1426 of file grid_tools.cc.
| std::vector<typename MeshType::active_cell_iterator> GridTools::get_active_child_cells | ( | const typename MeshType::cell_iterator & | cell | ) |
Return a list of all descendants of the given cell that are active. For example, if the current cell is once refined but none of its children are any further refined, then the returned list will contain all its children.
If the current cell is already active, then the returned list is empty (because the cell has no children that may be active).
| MeshType | A type that satisfies the requirements of the MeshType concept. |
| cell | An iterator pointing to a cell of the mesh. |
| void GridTools::get_active_neighbors | ( | const typename MeshType::active_cell_iterator & | cell, |
| std::vector< typename MeshType::active_cell_iterator > & | active_neighbors | ||
| ) |
Extract the active cells around a given cell cell and return them in the vector active_neighbors.
| MeshType | A type that satisfies the requirements of the MeshType concept. |
| [in] | cell | An iterator pointing to a cell of the mesh. |
| [out] | active_neighbors | A list of active descendants of the given cell |
| std::vector< typename MeshType::active_cell_iterator > GridTools::compute_active_cell_halo_layer | ( | const MeshType & | mesh, |
| const std_cxx11::function< bool(const typename MeshType::active_cell_iterator &)> & | predicate | ||
| ) |
Extract and return the active cell layer around a subdomain (set of active cells) in the mesh (i.e. those that share a common set of vertices with the subdomain but are not a part of it). Here, the "subdomain" consists of exactly all of those cells for which the predicate returns true.
An example of a custom predicate is one that checks for a given material id
and we can then extract the layer of cells around this material with the following call:
Predicates that are frequently useful can be found in namespace IteratorFilters. For example, it is possible to extracting a layer based on material id
or based on a set of active FE indices for an hp::DoFHandler
Note that in the last two examples we ensure that the predicate returns true only for locally owned cells. This means that the halo layer will not contain any artificial cells.
| MeshType | A type that satisfies the requirements of the MeshType concept. |
| [in] | mesh | A mesh (i.e. objects of type Triangulation, DoFHandler, or hp::DoFHandler). |
| [in] | predicate | A function (or object of a type with an operator()) defining the subdomain around which the halo layer is to be extracted. It is a function that takes in an active cell and returns a boolean. |
Definition at line 1583 of file grid_tools.cc.
| std::vector< typename MeshType::active_cell_iterator > GridTools::compute_ghost_cell_halo_layer | ( | const MeshType & | mesh | ) |
Extract and return ghost cells which are the active cell layer around all locally owned cells. This is most relevant for parallel::shared::Triangulation where it will return a subset of all ghost cells on a processor, but for parallel::distributed::Triangulation this will return all the ghost cells.
| MeshType | A type that satisfies the requirements of the MeshType concept. |
| [in] | mesh | A mesh (i.e. objects of type Triangulation, DoFHandler, or hp::DoFHandler). |
Definition at line 1621 of file grid_tools.cc.
| std::vector< std::set< typename Triangulation< dim, spacedim >::active_cell_iterator > > GridTools::vertex_to_cell_map | ( | const Triangulation< dim, spacedim > & | triangulation | ) |
Return the adjacent cells of all the vertices. If a vertex is also a hanging node, the associated coarse cell is also returned. The vertices are ordered by the vertex index. This is the number returned by the function cell->vertex_index(). Notice that only the indices marked in the array returned by Triangulation<dim,spacedim>::get_used_vertices() are used.
Definition at line 1643 of file grid_tools.cc.
| std::map< unsigned int, types::global_vertex_index > GridTools::compute_local_to_global_vertex_index_map | ( | const parallel::distributed::Triangulation< dim, spacedim > & | triangulation | ) |
Compute a globally unique index for each vertex and hanging node associated with a locally owned active cell. The vertices of a ghost cell that are hanging nodes of a locally owned cells have a global index. However, the other vertices of the cells that do not touch an active cell do not have a global index on this processor.
The key of the map is the local index of the vertex and the value is the global index. The indices need to be recomputed after refinement or coarsening and may be different.
Definition at line 1687 of file grid_tools.cc.
| std::pair< unsigned int, double > GridTools::get_longest_direction | ( | typename Triangulation< dim, spacedim >::active_cell_iterator | cell | ) |
Return the highest value among ratios between extents in each of the coordinate directions of a cell. Moreover, return the dimension relative to the highest elongation.
| [in] | cell | an iterator pointing to the cell. |
first value is the dimension of the highest elongation and the second value is the ratio among the dimensions of the cell.Definition at line 3913 of file grid_tools.cc.
| void GridTools::get_face_connectivity_of_cells | ( | const Triangulation< dim, spacedim > & | triangulation, |
| DynamicSparsityPattern & | connectivity | ||
| ) |
Produce a sparsity pattern in which nonzero entries indicate that two cells are connected via a common face. The diagonal entries of the sparsity pattern are also set.
The rows and columns refer to the cells as they are traversed in their natural order using cell iterators.
Definition at line 1971 of file grid_tools.cc.
| void GridTools::get_face_connectivity_of_cells | ( | const Triangulation< dim, spacedim > & | triangulation, |
| SparsityPattern & | connectivity | ||
| ) |
As above, but filling a SparsityPattern object instead.
Definition at line 2018 of file grid_tools.cc.
| void GridTools::get_vertex_connectivity_of_cells | ( | const Triangulation< dim, spacedim > & | triangulation, |
| DynamicSparsityPattern & | connectivity | ||
| ) |
Produce a sparsity pattern in which nonzero entries indicate that two cells are connected via a common vertex. The diagonal entries of the sparsity pattern are also set.
The rows and columns refer to the cells as they are traversed in their natural order using cell iterators.
Definition at line 2030 of file grid_tools.cc.
| void GridTools::partition_triangulation | ( | const unsigned int | n_partitions, |
| Triangulation< dim, spacedim > & | triangulation | ||
| ) |
Use the METIS partitioner to generate a partitioning of the active cells making up the entire domain. After calling this function, the subdomain ids of all active cells will have values between zero and n_partitions-1. You can access the subdomain id of a cell by using cell->subdomain_id().
This function will generate an error if METIS is not installed unless n_partitions is one. I.e., you can write a program so that it runs in the single-processor single-partition case without METIS installed, and only requires METIS when multiple partitions are required.
Definition at line 2056 of file grid_tools.cc.
| void GridTools::partition_triangulation | ( | const unsigned int | n_partitions, |
| const SparsityPattern & | cell_connection_graph, | ||
| Triangulation< dim, spacedim > & | triangulation | ||
| ) |
This function does the same as the previous one, i.e. it partitions a triangulation using METIS into a number of subdomains identified by the cell->subdomain_id() flag.
The difference to the previous function is the second argument, a sparsity pattern that represents the connectivity pattern between cells.
While the function above builds it directly from the triangulation by considering which cells neighbor each other, this function can take a more refined connectivity graph. The sparsity pattern needs to be of size N\times N, where N is the number of active cells in the triangulation. If the sparsity pattern contains an entry at position (i,j), then this means that cells i and j (in the order in which they are traversed by active cell iterators) are to be considered connected; METIS will then try to partition the domain in such a way that (i) the subdomains are of roughly equal size, and (ii) a minimal number of connections are broken.
This function is mainly useful in cases where connections between cells exist that are not present in the triangulation alone (otherwise the previous function would be the simpler one to use). Such connections may include that certain parts of the boundary of a domain are coupled through symmetric boundary conditions or integrals (e.g. friction contact between the two sides of a crack in the domain), or if a numerical scheme is used that not only connects immediate neighbors but a larger neighborhood of cells (e.g. when solving integral equations).
In addition, this function may be useful in cases where the default sparsity pattern is not entirely sufficient. This can happen because the default is to just consider face neighbors, not neighboring cells that are connected by edges or vertices. While the latter couple when using continuous finite elements, they are typically still closely connected in the neighborship graph, and METIS will not usually cut important connections in this case. However, if there are vertices in the mesh where many cells (many more than the common 4 or 6 in 2d and 3d, respectively) come together, then there will be a significant number of cells that are connected across a vertex, but several degrees removed in the connectivity graph built only using face neighbors. In a case like this, METIS may sometimes make bad decisions and you may want to build your own connectivity graph.
Definition at line 2095 of file grid_tools.cc.
| void GridTools::get_subdomain_association | ( | const Triangulation< dim, spacedim > & | triangulation, |
| std::vector< types::subdomain_id > & | subdomain | ||
| ) |
For each active cell, return in the output array to which subdomain (as given by the cell->subdomain_id() function) it belongs. The output array is supposed to have the right size already when calling this function.
This function returns the association of each cell with one subdomain. If you are looking for the association of each DoF with a subdomain, use the DoFTools::get_subdomain_association function.
Definition at line 2140 of file grid_tools.cc.
| unsigned int GridTools::count_cells_with_subdomain_association | ( | const Triangulation< dim, spacedim > & | triangulation, |
| const types::subdomain_id | subdomain | ||
| ) |
Count how many cells are uniquely associated with the given subdomain index.
This function may return zero if there are no cells with the given subdomain index. This can happen, for example, if you try to partition a coarse mesh into more partitions (one for each processor) than there are cells in the mesh.
This function returns the number of cells associated with one subdomain. If you are looking for the association of DoFs with this subdomain, use the DoFTools::count_dofs_with_subdomain_association function.
Definition at line 2155 of file grid_tools.cc.
| std::vector< bool > GridTools::get_locally_owned_vertices | ( | const Triangulation< dim, spacedim > & | triangulation | ) |
For a triangulation, return a mask that represents which of its vertices are "owned" by the current process in the same way as we talk about locally owned cells or degrees of freedom (see GlossLocallyOwnedCell and GlossLocallyOwnedDof). For the purpose of this function, we define a locally owned vertex as follows: a vertex is owned by that processor with the smallest subdomain id (which equals the MPI rank of that processor) among all owners of cells adjacent to this vertex. In other words, vertices that are in the interior of a partition of the triangulation are owned by the owner of this partition; for vertices that lie on the boundary between two or more partitions, the owner is the processor with the least subdomain_id among all adjacent subdomains.
For sequential triangulations (as opposed to, for example, parallel::distributed::Triangulation), every user vertex is of course owned by the current processor, i.e., the function returns Triangulation::get_used_vertices(). For parallel triangulations, the returned mask is a subset of what Triangulation::get_used_vertices() returns.
| triangulation | The triangulation of which the function evaluates which vertices are locally owned. |
Definition at line 2172 of file grid_tools.cc.
| std::list< std::pair< typename MeshType::cell_iterator, typename MeshType::cell_iterator > > GridTools::get_finest_common_cells | ( | const MeshType & | mesh_1, |
| const MeshType & | mesh_2 | ||
| ) |
Given two meshes (i.e. objects of type Triangulation, DoFHandler, or hp::DoFHandler) that are based on the same coarse mesh, this function figures out a set of cells that are matched between the two meshes and where at most one of the meshes is more refined on this cell. In other words, it finds the smallest cells that are common to both meshes, and that together completely cover the domain.
This function is useful, for example, in time-dependent or nonlinear application, where one has to integrate a solution defined on one mesh (e.g., the one from the previous time step or nonlinear iteration) against the shape functions of another mesh (the next time step, the next nonlinear iteration). If, for example, the new mesh is finer, then one has to obtain the solution on the coarse mesh (mesh_1) and interpolate it to the children of the corresponding cell of mesh_2. Conversely, if the new mesh is coarser, one has to express the coarse cell shape function by a linear combination of fine cell shape functions. In either case, one needs to loop over the finest cells that are common to both triangulations. This function returns a list of pairs of matching iterators to cells in the two meshes that can be used to this end.
Note that the list of these iterators is not necessarily ordered, and does also not necessarily coincide with the order in which cells are traversed in one, or both, of the meshes given as arguments.
| MeshType | A type that satisfies the requirements of the MeshType concept. |
Definition at line 2202 of file grid_tools.cc.
| bool GridTools::have_same_coarse_mesh | ( | const Triangulation< dim, spacedim > & | mesh_1, |
| const Triangulation< dim, spacedim > & | mesh_2 | ||
| ) |
Return true if the two triangulations are based on the same coarse mesh. This is determined by checking whether they have the same number of cells on the coarsest level, and then checking that they have the same vertices.
The two meshes may have different refinement histories beyond the coarse mesh.
Definition at line 2293 of file grid_tools.cc.
| bool GridTools::have_same_coarse_mesh | ( | const MeshType & | mesh_1, |
| const MeshType & | mesh_2 | ||
| ) |
The same function as above, but working on arguments of type DoFHandler, or hp::DoFHandler. This function is provided to allow calling have_same_coarse_mesh for all types of containers representing triangulations or the classes built on triangulations.
| MeshType | A type that satisfies the requirements of the MeshType concept. |
Definition at line 2324 of file grid_tools.cc.
| Triangulation< dim, spacedim >::DistortedCellList GridTools::fix_up_distorted_child_cells | ( | const typename Triangulation< dim, spacedim >::DistortedCellList & | distorted_cells, |
| Triangulation< dim, spacedim > & | triangulation | ||
| ) |
Given a triangulation and a list of cells whose children have become distorted as a result of mesh refinement, try to fix these cells up by moving the center node around.
The function returns a list of cells with distorted children that couldn't be fixed up for whatever reason. The returned list is therefore a subset of the input argument.
For a definition of the concept of distorted cells, see the glossary entry. The first argument passed to the current function is typically the exception thrown by the Triangulation::execute_coarsening_and_refinement function.
Definition at line 2894 of file grid_tools.cc.
| std::vector< typename MeshType::active_cell_iterator > GridTools::get_patch_around_cell | ( | const typename MeshType::active_cell_iterator & | cell | ) |
This function returns a list of all the active neighbor cells of the given, active cell. Here, a neighbor is defined as one having at least part of a face in common with the given cell, but not edge (in 3d) or vertex neighbors (in 2d and 3d).
The first element of the returned list is the cell provided as argument. The remaining ones are neighbors: The function loops over all faces of that given cell and checks if that face is not on the boundary of the domain. Then, if the neighbor cell does not have any children (i.e., it is either at the same refinement level as the current cell, or coarser) then this neighbor cell is added to the list of cells. Otherwise, if the neighbor cell is refined and therefore has children, then this function loops over all subfaces of current face adds the neighbors behind these sub-faces to the list to be returned.
| MeshType | A type that satisfies the requirements of the MeshType concept. In C++, the compiler can not determine MeshType from the function call. You need to specify it as an explicit template argument following the function name. |
| [in] | cell | An iterator pointing to a cell of the mesh. |
Definition at line 2931 of file grid_tools.cc.
| std::vector< typename Container::cell_iterator > GridTools::get_cells_at_coarsest_common_level | ( | const std::vector< typename Container::active_cell_iterator > & | patch_cells | ) |
This function takes a vector of active cells (hereafter named patch_cells) as input argument, and returns a vector of their parent cells with the coarsest common level of refinement. In other words, find that set of cells living at the same refinement level so that all cells in the input vector are children of the cells in the set, or are in the set itself.
| Container | In C++, the compiler can not determine the type of Container from the function call. You need to specify it as an explicit template argument following the function name. This type has to satisfy the requirements of a mesh container (see ConceptMeshType). |
| [in] | patch_cells | A vector of active cells for which this function finds the parents at the coarsest common level. This vector of cells typically results from calling the function GridTools::get_patch_around_cell(). |
Definition at line 2974 of file grid_tools.cc.
| void GridTools::build_triangulation_from_patch | ( | const std::vector< typename Container::active_cell_iterator > & | patch, |
| Triangulation< Container::dimension, Container::space_dimension > & | local_triangulation, | ||
| std::map< typename Triangulation< Container::dimension, Container::space_dimension >::active_cell_iterator, typename Container::active_cell_iterator > & | patch_to_global_tria_map | ||
| ) |
This function constructs a Triangulation (named local_triangulation) from a given vector of active cells. This vector (which we think of the cells corresponding to a "patch") contains active cells that are part of an existing global Triangulation. The goal of this function is to build a local Triangulation that contains only the active cells given in patch (and potentially a minimum number of additional cells required to form a valid Triangulation). The function also returns a map that allows to identify the cells in the output Triangulation and corresponding cells in the input list.
The function copies the location of vertices of cells from the cells of the source triangulation to the triangulation that is built from the list of patch cells. This adds support for triangulations which have been perturbed or smoothed in some manner which makes the triangulation deviate from the standard deal.ii refinement strategy of placing new vertices at midpoints of faces or edges.
The operation implemented by this function is frequently used in the definition of error estimators that need to solve "local" problems on each cell and its neighbors. A similar construction is necessary in the definition of the Clement interpolation operator in which one needs to solve a local problem on all cells within the support of a shape function. This function then builds a complete Triangulation from a list of cells that make up such a patch; one can then later attach a DoFHandler to such a Triangulation.
If the list of input cells contains only cells at the same refinement level, then the output Triangulation simply consists of a Triangulation containing only exactly these patch cells. On the other hand, if the input cells live on different refinement levels, i.e., the Triangulation of which they are part is adaptively refined, then the construction of the output Triangulation is not so simple because the coarsest level of a Triangulation can not contain hanging nodes. Rather, we first have to find the common refinement level of all input cells, along with their common parents (see GridTools::get_cells_at_coarsest_common_level()), build a Triangulation from those, and then adaptively refine it so that the input cells all also exist in the output Triangulation.
A consequence of this procedure is that that output Triangulation may contain more active cells than the ones that exist in the input vector. On the other hand, one typically wants to solve the local problem not on the entire output Triangulation, but only on those cells of it that correspond to cells in the input list. In this case, a user typically wants to assign degrees of freedom only on cells that are part of the "patch", and somehow ignore those excessive cells. The current function supports this common requirement by setting the user flag for the cells in the output Triangulation that match with cells in the input list. Cells which are not part of the original patch will not have their user_flag set; we can then avoid assigning degrees of freedom using the FE_Nothing<dim> element.
| Container | In C++, the compiler can not determine the type of Container from the function call. You need to specify it as an explicit template argument following the function name. This type that satisfies the requirements of a mesh container (see ConceptMeshType). |
| [in] | patch | A vector of active cells from a common triangulation. These cells may or may not all be at the same refinement level. |
| [out] | local_triangulation | A triangulation whose active cells correspond to the given vector of active cells in patch. |
| [out] | patch_to_global_tria_map | A map between the local triangulation which is built as explained above, and the cell iterators in the input list. |
Definition at line 3013 of file grid_tools.cc.
| std::map< types::global_dof_index, std::vector< typename DoFHandlerType::active_cell_iterator > > GridTools::get_dof_to_support_patch_map | ( | DoFHandlerType & | dof_handler | ) |
This function runs through the degrees of freedom defined by the DoFHandlerType and for each dof constructs a vector of active_cell_iterators representing the cells of support of the associated basis element at that degree of freedom. This function was originally designed for the implementation of local projections, for instance the Clement interpolant, in conjunction with other local patch functions like GridTools::build_triangulation_from_patch.
DoFHandlerType's built on top of Triangulation or parallel:distributed::Triangulation are supported and handled appropriately.
The result is the patch of cells representing the support of the basis element associated to the degree of freedom. For instance using an FE_Q finite element, we obtain the standard patch of cells touching the degree of freedom and then add other cells that take care of possible hanging node constraints. Using a FE_DGQ finite element, the degrees of freedom are logically considered to be "interior" to the cells so the patch would consist exclusively of the single cell on which the degree of freedom is located.
| DoFHandlerType | The DoFHandlerType should be a DoFHandler or hp::DoFHandler. |
| [in] | dof_handler | The DoFHandlerType which could be built on a Triangulation or a parallel::distributed::Triangulation with a finite element that has degrees of freedom that are logically associated to a vertex, line, quad, or hex. |
Definition at line 3193 of file grid_tools.cc.
|
inline |
An orthogonal equality test for faces.
face1 and face2 are considered equal, if a one to one matching between its vertices can be achieved via an orthogonal equality relation.
Here, two vertices v_1 and v_2 are considered equal, if M\cdot v_1 + offset - v_2 is parallel to the unit vector in unit direction direction. If the parameter matrix is a reference to a spacedim x spacedim matrix, M is set to matrix, otherwise M is the identity matrix.
If the matching was successful, the relative orientation of face1 with respect to face2 is returned in the bitset orientation, where
In 2D face_orientation is always true, face_rotation is always false, and face_flip has the meaning of line_flip. More precisely in 3d:
face_orientation: true if face1 and face2 have the same orientation. Otherwise, the vertex indices of face1 match the vertex indices of face2 in the following manner:
face_flip: true if the matched vertices are rotated by 180 degrees:
face_rotation: true if the matched vertices are rotated by 90 degrees counterclockwise:
and any combination of that... More information on the topic can be found in the glossary article.
Definition at line 3577 of file grid_tools.cc.
| bool GridTools::orthogonal_equality | ( | const FaceIterator & | face1, |
| const FaceIterator & | face2, | ||
| const int | direction, | ||
| const Tensor< 2, FaceIterator::AccessorType::space_dimension > & | offset = Tensor< 1, FaceIterator::AccessorType::space_dimension >(), |
||
| const FullMatrix< double > & | matrix = FullMatrix< double >() |
||
| ) |
Same function as above, but doesn't return the actual orientation
| void GridTools::collect_periodic_faces | ( | const MeshType & | mesh, |
| const types::boundary_id | b_id1, | ||
| const types::boundary_id | b_id2, | ||
| const int | direction, | ||
| std::vector< PeriodicFacePair< typename MeshType::cell_iterator > > & | matched_pairs, | ||
| const Tensor< 1, MeshType::space_dimension > & | offset = ::Tensor<1,MeshType::space_dimension>(), |
||
| const FullMatrix< double > & | matrix = FullMatrix<double>() |
||
| ) |
This function will collect periodic face pairs on the coarsest mesh level of the given mesh (a Triangulation or DoFHandler) and add them to the vector matched_pairs leaving the original contents intact.
Define a 'first' boundary as all boundary faces having boundary_id b_id1 and a 'second' boundary consisting of all faces belonging to b_id2.
This function tries to match all faces belonging to the first boundary with faces belonging to the second boundary with the help of orthogonal_equality().
The bitset that is returned inside of PeriodicFacePair encodes the relative orientation of the first face with respect to the second face, see the documentation of orthogonal_equality() for further details.
The direction refers to the space direction in which periodicity is enforced. When maching periodic faces this vector component is ignored.
The offset is a vector tangential to the faces that is added to the location of vertices of the 'first' boundary when attempting to match them to the corresponding vertices of the 'second' boundary. This can be used to implement conditions such as u(0,y)=u(1,y+1).
Optionally, a dim\times dim rotation matrix can be specified that describes how vector valued DoFs of the first face should be modified prior to constraining to the DoFs of the second face. The matrix is used in two places. First, matrix will be supplied to orthogonal_equality() and used for matching faces: Two vertices v_1 and v_2 match if \text{matrix}\cdot v_1 + \text{offset} - v_2 is parallel to the unit vector in unit direction direction. (For more details see DoFTools::make_periodicity_constraints(), the glossary glossary entry on periodic conditions and step-45). Second, matrix will be stored in the PeriodicFacePair collection matched_pairs for further use.
| MeshType | A type that satisfies the requirements of the MeshType concept. |
matched_pairs (and existing entries will be preserved), it is possible to call this function several times with different boundary ids to generate a vector with all periodic pairs.Definition at line 3707 of file grid_tools.cc.
| void GridTools::collect_periodic_faces | ( | const MeshType & | mesh, |
| const types::boundary_id | b_id, | ||
| const int | direction, | ||
| std::vector< PeriodicFacePair< typename MeshType::cell_iterator > > & | matched_pairs, | ||
| const ::Tensor< 1, MeshType::space_dimension > & | offset = ::Tensor< 1, MeshType::space_dimension >(), |
||
| const FullMatrix< double > & | matrix = FullMatrix< double >() |
||
| ) |
This compatibility version of collect_periodic_faces() only works on grids with cells in standard orientation.
Instead of defining a 'first' and 'second' boundary with the help of two boundary_ids this function defines a 'left' boundary as all faces with local face index 2*dimension and boundary indicator b_id and, similarly, a 'right' boundary consisting of all face with local face index 2*dimension+1 and boundary indicator b_id.
This function will collect periodic face pairs on the coarsest mesh level and add them to matched_pairs leaving the original contents intact.
See above function for further details.
 1.8.14
1.8.14