 |
Reference documentation for deal.II version 8.5.1
|
 |
Reference documentation for deal.II version 8.5.1
|
Functions | |
| void | Triangulation< dim, spacedim >::set_manifold (const types::manifold_id number, const Manifold< dim, spacedim > &manifold_object) |
| void | Triangulation< dim, spacedim >::set_manifold (const types::manifold_id number) |
| void | Triangulation< dim, spacedim >::set_all_manifold_ids (const types::manifold_id number) |
| void | Triangulation< dim, spacedim >::set_all_manifold_ids_on_boundary (const types::manifold_id number) |
| void | Triangulation< dim, spacedim >::set_all_manifold_ids_on_boundary (const types::boundary_id b_id, const types::manifold_id number) |
| const Manifold< dim, spacedim > & | Triangulation< dim, spacedim >::get_manifold (const types::manifold_id number) const |
| std::vector< types::manifold_id > | Triangulation< dim, spacedim >::get_manifold_ids () const |
Dealing with boundary and manifold ids | |
| template<int dim, int spacedim> | |
| void | GridTools::copy_boundary_to_manifold_id (Triangulation< dim, spacedim > &tria, const bool reset_boundary_ids=false) |
| template<int dim, int spacedim> | |
| void | GridTools::copy_material_to_manifold_id (Triangulation< dim, spacedim > &tria, const bool compute_face_ids=false) |
Dealing with manifold indicators | |
| void | TriaAccessor< structdim, dim, spacedim >::set_manifold_id (const types::manifold_id) const |
| void | TriaAccessor< structdim, dim, spacedim >::set_all_manifold_ids (const types::manifold_id) const |
Dealing with boundary indicators | |
| void | TriaAccessor< 0, 1, spacedim >::set_all_manifold_ids (const types::manifold_id) |
The classes in this module are concerned with the description of the manifold in which the domain that a Triangulation describes lives. This manifold description is necessary in two contexts:
Mesh refinement: Whenever a cell is refined, it is necessary to introduce new vertices in the Triangulation. In the simplest case, one assumes that the objects that make up the Triangulation are straight line segments, a bi-linear surface or a tri-linear volume. The next vertex is then simply put into the middle of the old ones (where "middle" means a suitable average of the locations of the pre-existing vertices). This is the default behavior of the Triangulation class, and is described by the FlatManifold class.
On the other hand, if one deals with curved geometries, or geometries which require a denser refinement in some direction, this is not the appropriate thing to do. The classes derived from the Manifold base class therefore describe the geometry of a domain. One can then attach an object of a class derived from this base class to the Triangulation object using the Triangulation::set_manifold() function associating it with a manifold id (see types::manifold_id), use this manifold id on the cells, faces or edges of the triangulation that should be described by this manifold using the TriaAccessor::set_manifold_id() function, and then the Triangulation will ask the manifold object where a new vertex to be located on a cell, face or edge so attributed should be located upon mesh refinement. Several classes already exist to support the most common geometries, e.g., CylinderManifold, or PolarManifold, which represent respectively the geometry obtained when describing your space in cylindrical coordinates or in polar coordinates.
Integration: When using higher order finite element methods, it is often necessary to compute cell terms (like cell contributions to the matrix and right hand side of the linear system) using curved approximations of the boundary, rather than the straight line approximation. The actual implementation of such curved elements happens in the Mapping class (see the Mappings between reference and real cell module), which however obtains its information about the boundary of the domain from the classes described here. The same is, of course, true when integrating boundary terms (e.g., inhomogenous Neumann boundary conditions).
In deal.II, a Manifold is seen as a collection of points, together with a notion of distance between points (on the manifold). New points are typically obtained by providing a local coordinate system on the manifold, identifying existing points in the local coordinate system (pulling them back using the local map to obtain their local coordinates), find the new point in the local coordinate system by weighted sums of the existing points, and transforming back the point in the real space (pushing it forward using the local map). The main class that implements this mechanism is the ChartManifold class, and this is the class that users will likely overload for complex geometries.
While this process is non trivial in most cases of interest, for most of the trivial geometries, like cylinders, spheres or shells, deal.II provides reasonable implementations. More complicated examples can be described using the techniques shown in step-53 and step-54.
The boundary of a Triangulation is a special case of Manifold, for which additional information can be useful in user codes, such as normal vectors to surfaces or to curves. If your coarse mesh is reasonably shaped, you might be interested in only attaching a manifold description to boundary portion of your domain. This can be done using the Triangulation::set_boundary() function, which take as arguments a Boundary object (derived from Manifold). Notice that Triangulation uses only the Manifold interface, not the Boundary interface. Other tools, however, might need to compute exact normals at quadrature points, and therefore a wrapper to query Boundary objects is provided.
A simple example why dealing with curved geometries is already provided by step-1, though it is not elaborated there. For example, consider this small variation of the second_grid() function shown there, where we simply refine every cell several times and do not deal with boundaries at all:
This code leads to a mesh that looks like this:
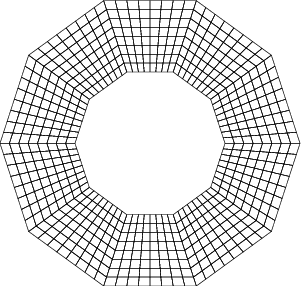
Our intention was to get a mesh that resembles a ring. However, since we did not describe this to the triangulation, what happens is that we start with the 10 coarse cells in circumferential direction we told GridGenerator::hyper_shell() to create, and each of these is then 3 times globally refined. Each time refinement requires a new vertex, it is placed in the middle of the existing ones, regardless of what we may have intended (but omitted to describe in code).
This is easily remedied. step-1 already shows how to do this. Consider this code:
This code is better, producing the following mesh:
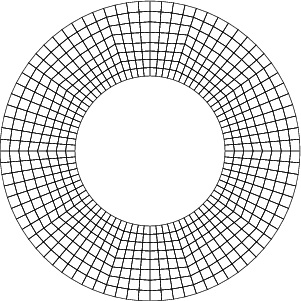
The mesh looks better in that it faithfully reproduces the circular inner and outer boundaries of the domain. However, it is still possible to identify the original 10 cells by the kinks in the tangential lines. They result from the fact that every time a cell is refined, new vertices on interior lines are just placed into the middle of the existing line (the boundary lines are handled differently because we have attached boundary objects). In other words, they end up in places that may be in the geometric middle of a straight line, but not on a circle around the center.
This can be remedied by assigning a manifold description not only to the lines along the boundary, but also to the radial lines and cells (which, in turn, will inherit it to the new lines that are created upon mesh refinement). This code achieves this:
This leads to the following mesh:
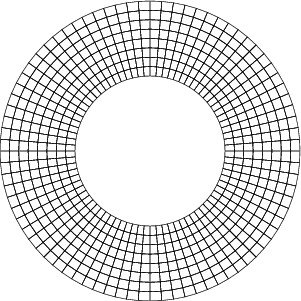
So why does this matter? After all, the last two meshes describe the exact same domain and we know that upon mesh refinement we obtain the correct solution regardless of the choice of cells, as long as the diameter of the largest cell goes to zero.
There are two answers to this question. First, the numerical effort of solving a partial differential equation to a certain accuracy typically depends on the quality of cells since the constant C in error estimates of the form \|u-u_h\|_{H^1} \le Ch^p \|u\|_{H^{p+1}} depends on factors such as the maximal ratio of radii of the smallest circumscribed to largest inscribed circle over all cells (for triangles; or a suitable generalization for other types of cells). Thus, it is worthwhile creating meshes with cells that are as well-formed as possible. This is arguably not so much of an issue for the meshes shown above, but is sometimes an issue. Consider, for example, the following code and mesh:
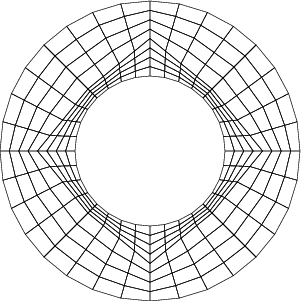
Here, we create only four circumferential cells in the beginning, and refining them leads to the mesh shown. Clearly, here we have cells with bad aspect ratios.
If we drive this further and start with a coarse mesh of only three cells (which may be inappropriate here, since we know that it is not sufficient, but may also be impossible to avoid for complex geometries generated in mesh generators), then we obtain the following mesh:
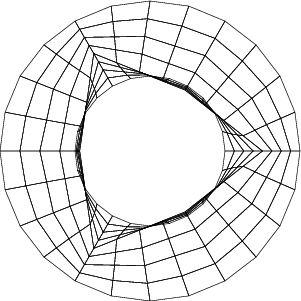
This mesh neither has the correct geometry after refinement, nor do all cells have positive area as is necessary for the finite element method to work. However, even when starting with such in inopportune mesh, we can make things work by attaching a suitable geometry description not only to the boundary but also to interior cells and edges, using the same code as above:
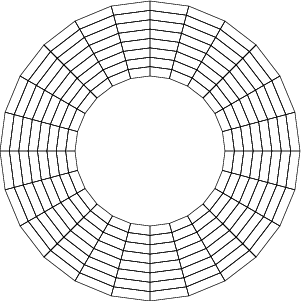
Here, even starting with an initial, inappropriately chosen mesh retains our ability to adequately refine the mesh into one that will serve us well. This example may be manufactured here, but it is relevant, for example in the context of what GridGenerator::hyper_shell() produces in 3d (see the documentation of this function). It is also germane to the cases discussed in the glossary entry on distorted cells.
| void GridTools::copy_boundary_to_manifold_id | ( | Triangulation< dim, spacedim > & | tria, |
| const bool | reset_boundary_ids = false |
||
| ) |
Copy boundary ids to manifold ids on faces and edges at the boundary. The default manifold_id for new Triangulation objects is numbers::invalid_manifold_id. This function copies the boundary_ids of the boundary faces and edges to the manifold_ids of the same faces and edges, allowing the user to change the boundary_ids and use them for boundary conditions regardless of the geometry, which will use manifold_ids to create new points. Only active cells will be iterated over. This is a function you'd typically call when there is only one active level on your Triangulation. Mesh refinement will then inherit these indicators to child cells, faces, and edges.
The optional parameter reset_boundary_ids, indicates whether this function should reset the boundary_ids of boundary faces and edges to its default value 0 after copying its value to the manifold_id. By default, boundary_ids are left untouched.
Definition at line 3844 of file grid_tools.cc.
| void GridTools::copy_material_to_manifold_id | ( | Triangulation< dim, spacedim > & | tria, |
| const bool | compute_face_ids = false |
||
| ) |
Copy material ids to manifold ids. The default manifold_id for new Triangulation objects is numbers::invalid_manifold_id. When refinements occurs, the Triangulation asks where to locate new points to the underlying manifold.
When reading a Triangulation from a supported input format, typical information that can be stored in a file are boundary conditions for boundary faces (which we store in the boundary_id of the faces), material types for cells (which we store in the material_id of the cells) and in some cases subdomain ids for cells (which we store in the subdomain_id of the cell).
If you read one of these grids into a Triangulation, you might still want to use the material_id specified in the input file as a manifold_id description. In this case you can associate a Manifold object to internal cells, and this object will be used by the Triangulation to query Manifold objects for new points. This function iterates over active cells and copies the material_ids to the manifold_ids.
The optional parameter compute_face_ids, indicates whether this function should also set the manifold_ids of the faces (both for internal faces and for faces on the boundary). If set to true, then each face will get a manifold_id equal to the minimum of the surrounding manifold_ids, ensuring that a unique manifold id is selected for each face of the Triangulation. By default, face manifold_ids are not computed.
Definition at line 3887 of file grid_tools.cc.
| void Triangulation< dim, spacedim >::set_manifold | ( | const types::manifold_id | number, |
| const Manifold< dim, spacedim > & | manifold_object | ||
| ) |
Assign a manifold object to a certain part of the the triangulation. If an object with manifold number number is refined, this object is used to find the location of new vertices (see the results section of step-49 for a more in-depth discussion of this, with examples). It is also used for non-linear (i.e.: non-Q1) transformations of cells to the unit cell in shape function calculations.
The manifold_object is not copied and MUST persist until the triangulation is destroyed. This is also true for triangulations generated from this one by copy_triangulation.
It is possible to remove or replace the boundary object during the lifetime of a non-empty triangulation. Usually, this is done before the first refinement and is dangerous afterwards. Removal of a manifold object is done by set_manifold(number), i.e. the function of same name but only one argument. This operation then replaces the manifold object given before by a straight manifold approximation.
| void Triangulation< dim, spacedim >::set_manifold | ( | const types::manifold_id | number | ) |
Reset those parts of the triangulation with the given manifold_id to use a FlatManifold object. This is the default state of a triangulation, and undoes assignment of a different Manifold object by the function of same name and two arguments.
| void Triangulation< dim, spacedim >::set_all_manifold_ids | ( | const types::manifold_id | number | ) |
Set the manifold_id of all cells and faces to the given argument.
| void Triangulation< dim, spacedim >::set_all_manifold_ids_on_boundary | ( | const types::manifold_id | number | ) |
Set the manifold_id of all boundary faces to the given argument.
| void Triangulation< dim, spacedim >::set_all_manifold_ids_on_boundary | ( | const types::boundary_id | b_id, |
| const types::manifold_id | number | ||
| ) |
Set the manifold_id of all boundary faces and edges with given boundary_id b_id to the given manifold_id number.
| const Manifold< dim, spacedim > & Triangulation< dim, spacedim >::get_manifold | ( | const types::manifold_id | number | ) | const |
Return a constant reference to a Manifold object used for this triangulation. Number is the same as in set_manifold
| std::vector< types::manifold_id > Triangulation< dim, spacedim >::get_manifold_ids | ( | ) | const |
Return a vector containing all manifold indicators assigned to the objects of this Triangulation. Note, that each manifold indicator is reported only once. The size of the return vector will represent the number of different indicators (which is greater or equal one).
| void TriaAccessor< structdim, dim, spacedim >::set_manifold_id | ( | const types::manifold_id | ) | const |
Set the manifold indicator. The same applies as for the manifold_id() function.
Note that it only sets the manifold object of the current object itself, not the indicators of the ones that bound it, nor of its children. For example, in 3d, if this function is called on a face, then the manifold indicator of the 4 edges that bound the face remain unchanged. If you want to set the manifold indicators of face, edges and all children at the same time, use the set_all_manifold_ids() function.
| void TriaAccessor< structdim, dim, spacedim >::set_all_manifold_ids | ( | const types::manifold_id | ) | const |
Do as set_manifold_id() but also set the manifold indicators of the objects that bound the current object. For example, in 3d, if set_manifold_id() is called on a face, then the manifold indicator of the 4 edges that bound the face remain unchanged. On the other hand, the manifold indicators of face and edges are all set at the same time using the current function.
| void TriaAccessor< 0, 1, spacedim >::set_all_manifold_ids | ( | const types::manifold_id | ) |
Set the manifold indicator of this object and all of its lower- dimensional sub-objects. Since this object only represents a single vertex, there are no lower-dimensional object and this function is equivalent to calling set_manifold_id() with the same argument.
 1.8.14
1.8.14