|
| | LowStorageRungeKutta ()=default |
| |
| | LowStorageRungeKutta (const runge_kutta_method method) |
| |
| void | initialize (const runge_kutta_method method) override |
| |
| double | evolve_one_time_step (const std::function< VectorType(const double, const VectorType &)> &f, const std::function< VectorType(const double, const double, const VectorType &)> &id_minus_tau_J_inverse, double t, double delta_t, VectorType &y) override |
| |
| double | evolve_one_time_step (const std::function< VectorType(const double, const VectorType &)> &f, double t, double delta_t, VectorType &solution, VectorType &vec_ri, VectorType &vec_ki) |
| |
| void | get_coefficients (std::vector< double > &a, std::vector< double > &b, std::vector< double > &c) const |
| |
| const Status & | get_status () const override |
| |
| double | evolve_one_time_step (std::vector< std::function< VectorType(const double, const VectorType &)> > &F, std::vector< std::function< VectorType(const double, const double, const VectorType &)> > &J_inverse, double t, double delta_t, VectorType &y) override |
| |
template<typename VectorType>
class TimeStepping::LowStorageRungeKutta< VectorType >
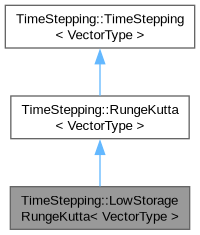
The LowStorageRungeKutta class is derived from RungeKutta and implements a specific class of explicit methods. The main advantages of low-storage methods are the reduced memory consumption and the reduced memory access.
Definition at line 410 of file time_stepping.h.
template<typename VectorType >
| double TimeStepping::LowStorageRungeKutta< VectorType >::evolve_one_time_step |
( |
const std::function< VectorType(const double, const VectorType &)> & | f, |
|
|
const std::function< VectorType(const double, const double, const VectorType &)> & | id_minus_tau_J_inverse, |
|
|
double | t, |
|
|
double | delta_t, |
|
|
VectorType & | y ) |
|
overridevirtual |
This function is used to advance from time t to t+ delta_t. f is the function \( f(t,y) \) that should be integrated, the input parameters are the time t and the vector y and the output is value of f at this point. id_minus_tau_J_inverse is a function that computes \(
inv(I-\tau J)\) where \( I \) is the identity matrix, \( \tau \) is given, and \( J \) is the Jacobian \( \frac{\partial f}{\partial y} \). The input parameters are the time, \( \tau \), and a vector. The output is the value of function at this point. evolve_one_time_step returns the time at the end of the time step.
Implements TimeStepping::RungeKutta< VectorType >.
template<typename VectorType >
| double TimeStepping::RungeKutta< VectorType >::evolve_one_time_step |
( |
std::vector< std::function< VectorType(const double, const VectorType &)> > & | F, |
|
|
std::vector< std::function< VectorType(const double, const double, const VectorType &)> > & | J_inverse, |
|
|
double | t, |
|
|
double | delta_t, |
|
|
VectorType & | y ) |
|
overridevirtualinherited |
This function is used to advance from time t to t+ delta_t. F is a vector of functions \( f(t,y) \) that should be integrated, the input parameters are the time t and the vector y and the output is value of f at this point. J_inverse is a vector functions that compute the inverse of the Jacobians associated to the implicit problems. The input parameters are the time, \( \tau \), and a vector. The output is the value of function at this point. This function returns the time at the end of the time step. When using Runge-Kutta methods, F and J_inverse can only contain one element.
Implements TimeStepping::TimeStepping< VectorType >.
1.11.0