Reference documentation for deal.II version 9.6.0
\(\newcommand{\dealvcentcolon}{\mathrel{\mathop{:}}}\) \(\newcommand{\dealcoloneq}{\dealvcentcolon\mathrel{\mkern-1.2mu}=}\) \(\newcommand{\jump}[1]{\left[\!\left[ #1 \right]\!\right]}\) \(\newcommand{\average}[1]{\left\{\!\left\{ #1 \right\}\!\right\}}\)
Loading...
Searching...
No Matches
Classes | Public Types | Public Member Functions | Static Public Member Functions | Private Types | Private Member Functions | Static Private Member Functions | Private Attributes | Static Private Attributes | Friends | List of all members
PreconditionBlockJacobi< MatrixType, inverse_type > Class Template Reference
Linear algebra classes | Linear algebra classes » Matrix classes » Preconditioners and Relaxation Operators

#include <deal.II/lac/precondition_block.h>

Inheritance diagram for PreconditionBlockJacobi< MatrixType, inverse_type >:
Inheritance graph
[legend]

Classes

class  const_iterator
 

Public Types

using size_type = types::global_dof_index
 

Public Member Functions

template<typename number2 >
void vmult (Vector< number2 > &, const Vector< number2 > &) const
 
template<typename number2 >
void Tvmult (Vector< number2 > &, const Vector< number2 > &) const
 
template<typename number2 >
void vmult_add (Vector< number2 > &, const Vector< number2 > &) const
 
template<typename number2 >
void Tvmult_add (Vector< number2 > &, const Vector< number2 > &) const
 
template<typename number2 >
void step (Vector< number2 > &dst, const Vector< number2 > &rhs) const
 
template<typename number2 >
void Tstep (Vector< number2 > &dst, const Vector< number2 > &rhs) const
 
const_iterator begin () const
 
const_iterator end () const
 
const_iterator begin (const size_type r) const
 
const_iterator end (const size_type r) const
 
template<class Archive >
void serialize (Archive &ar, const unsigned int version)
 
Subscriptor functionality

Classes derived from Subscriptor provide a facility to subscribe to this object. This is mostly used by the SmartPointer class.

void subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const
 
void unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const
 
unsigned int n_subscriptions () const
 
template<typename StreamType >
void list_subscribers (StreamType &stream) const
 
void list_subscribers () const
 

Static Public Member Functions

static ::ExceptionBase & ExcInUse (int arg1, std::string arg2, std::string arg3)
 
static ::ExceptionBase & ExcNoSubscriber (std::string arg1, std::string arg2)
 

Private Types

using number = typename MatrixType::value_type
 
using map_value_type = decltype(counter_map)::value_type
 
using map_iterator = decltype(counter_map)::iterator
 
using value_type
 
enum  Inversion
 

Private Member Functions

template<typename number2 >
void do_vmult (Vector< number2 > &, const Vector< number2 > &, bool adding) const
 
void check_no_subscribers () const noexcept
 
void initialize (const MatrixType &A, const AdditionalData parameters)
 
void initialize (const MatrixType &A, const std::vector< size_type > &permutation, const std::vector< size_type > &inverse_permutation, const AdditionalData parameters)
 
void set_permutation (const std::vector< size_type > &permutation, const std::vector< size_type > &inverse_permutation)
 
void invert_permuted_diagblocks ()
 
void clear ()
 
bool empty () const
 
value_type el (size_type i, size_type j) const
 
void invert_diagblocks ()
 
void forward_step (Vector< number2 > &dst, const Vector< number2 > &prev, const Vector< number2 > &src, const bool transpose_diagonal) const
 
void backward_step (Vector< number2 > &dst, const Vector< number2 > &prev, const Vector< number2 > &src, const bool transpose_diagonal) const
 
size_type block_size () const
 
std::size_t memory_consumption () const
 
void reinit (unsigned int nblocks, size_type blocksize, bool compress, Inversion method=gauss_jordan)
 
void inverses_computed (bool are_they)
 
bool same_diagonal () const
 
bool store_diagonals () const
 
bool inverses_ready () const
 
unsigned int size () const
 
void inverse_vmult (size_type i, Vector< number2 > &dst, const Vector< number2 > &src) const
 
void inverse_Tvmult (size_type i, Vector< number2 > &dst, const Vector< number2 > &src) const
 
FullMatrix< typename MatrixType::value_type > & inverse (size_type i)
 
const FullMatrix< typename MatrixType::value_type > & inverse (size_type i) const
 
Householder< typename MatrixType::value_type > & inverse_householder (size_type i)
 
const Householder< typename MatrixType::value_type > & inverse_householder (size_type i) const
 
LAPACKFullMatrix< typename MatrixType::value_type > & inverse_svd (size_type i)
 
const LAPACKFullMatrix< typename MatrixType::value_type > & inverse_svd (size_type i) const
 
FullMatrix< typename MatrixType::value_type > & diagonal (size_type i)
 
const FullMatrix< typename MatrixType::value_type > & diagonal (size_type i) const
 
void log_statistics () const
 

Static Private Member Functions

static ::ExceptionBase & ExcWrongBlockSize (int arg1, int arg2)
 
static ::ExceptionBase & ExcInverseMatricesAlreadyExist ()
 
static ::ExceptionBase & ExcDiagonalsNotStored ()
 
static ::ExceptionBase & ExcInverseNotAvailable ()
 

Private Attributes

std::atomic< unsigned int > counter
 
std::map< std::string, unsigned int > counter_map
 
std::vector< std::atomic< bool > * > validity_pointers
 
const std::type_info * object_info
 
size_type blocksize
 
SmartPointer< const MatrixType, PreconditionBlock< MatrixType, typename MatrixType::value_type > > A
 
double relaxation
 
std::vector< size_type > permutation
 
std::vector< size_type > inverse_permutation
 
Inversion inversion
 
unsigned int n_diagonal_blocks
 
std::vector< FullMatrix< typename MatrixType::value_type > > var_inverse_full
 
std::vector< Householder< typename MatrixType::value_type > > var_inverse_householder
 
std::vector< LAPACKFullMatrix< typename MatrixType::value_type > > var_inverse_svd
 
std::vector< FullMatrix< typename MatrixType::value_type > > var_diagonal
 
bool var_store_diagonals
 
bool var_same_diagonal
 
bool var_inverses_ready
 

Static Private Attributes

static std::mutex mutex
 

Friends

class Accessor
 
class const_iterator
 

Detailed Description

template<typename MatrixType, typename inverse_type = typename MatrixType::value_type>
class PreconditionBlockJacobi< MatrixType, inverse_type >

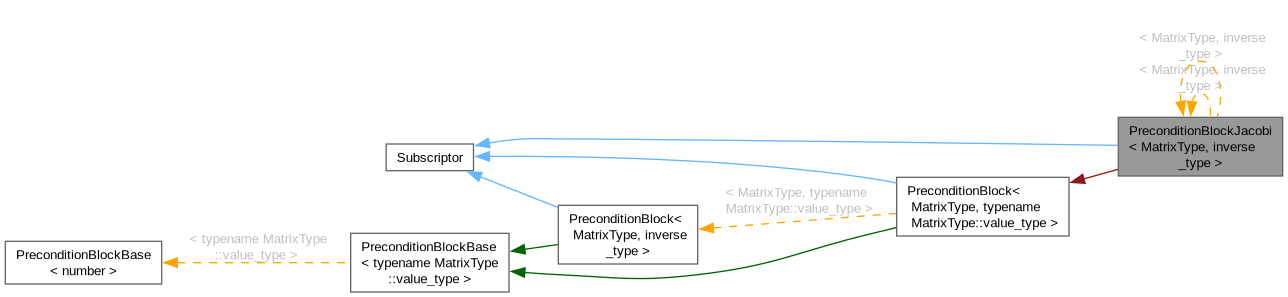
Block Jacobi preconditioning. See PreconditionBlock for requirements on the matrix. This class satisfies the relaxation concept.

Note
Instantiations for this template are provided for <float> and <double>; others can be generated in application programs (see the section on Template instantiations in the manual).

Definition at line 378 of file precondition_block.h.

Member Typedef Documentation

◆ number

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
using PreconditionBlockJacobi< MatrixType, inverse_type >::number = typename MatrixType::value_type
private

Define number type of matrix.

Definition at line 386 of file precondition_block.h.

◆ size_type

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
using PreconditionBlockJacobi< MatrixType, inverse_type >::size_type = types::global_dof_index

Declare type for container size.

Definition at line 392 of file precondition_block.h.

◆ map_value_type

using Subscriptor::map_value_type = decltype(counter_map)::value_type
privateinherited

The data type used in counter_map.

Definition at line 229 of file subscriptor.h.

◆ map_iterator

using Subscriptor::map_iterator = decltype(counter_map)::iterator
privateinherited

The iterator type used in counter_map.

Definition at line 234 of file subscriptor.h.

◆ value_type

using PreconditionBlock< MatrixType, typename MatrixType::value_type >::value_type
privateinherited

Value type for inverse matrices.

Definition at line 94 of file precondition_block.h.

Member Enumeration Documentation

◆ Inversion

enum PreconditionBlockBase::Inversion
inherited

Choose a method for inverting the blocks, and thus the data type for the inverses.

Definition at line 70 of file precondition_block_base.h.

Member Function Documentation

◆ vmult()

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
template<typename number2 >
template void PreconditionBlockJacobi< MatrixType, inverse_type >::vmult< double > ( Vector< number2 > & ,
const Vector< number2 > &  ) const

Execute block Jacobi preconditioning.

This function will automatically use the inverse matrices if they exist, if not then BlockJacobi will need much time inverting the diagonal block matrices in each preconditioning step.

◆ Tvmult()

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
template<typename number2 >
template void PreconditionBlockJacobi< MatrixType, inverse_type >::Tvmult< double > ( Vector< number2 > & ,
const Vector< number2 > &  ) const

Same as vmult, since Jacobi is symmetric.

◆ vmult_add()

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
template<typename number2 >
template void PreconditionBlockJacobi< MatrixType, inverse_type >::vmult_add< double > ( Vector< number2 > & ,
const Vector< number2 > &  ) const

Execute block Jacobi preconditioning, adding to dst.

This function will automatically use the inverse matrices if they exist, if not then BlockJacobi will need much time inverting the diagonal block matrices in each preconditioning step.

◆ Tvmult_add()

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
template<typename number2 >
template void PreconditionBlockJacobi< MatrixType, inverse_type >::Tvmult_add< double > ( Vector< number2 > & ,
const Vector< number2 > &  ) const

Same as vmult_add, since Jacobi is symmetric.

◆ step()

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
template<typename number2 >
void PreconditionBlockJacobi< MatrixType, inverse_type >::step ( Vector< number2 > & dst,
const Vector< number2 > & rhs ) const

Perform one step of the Jacobi iteration.

◆ Tstep()

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
template<typename number2 >
void PreconditionBlockJacobi< MatrixType, inverse_type >::Tstep ( Vector< number2 > & dst,
const Vector< number2 > & rhs ) const

Perform one step of the Jacobi iteration.

◆ begin() [1/2]

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
const_iterator PreconditionBlockJacobi< MatrixType, inverse_type >::begin ( ) const

Iterator starting at the first entry.

◆ end() [1/2]

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
const_iterator PreconditionBlockJacobi< MatrixType, inverse_type >::end ( ) const

Final iterator.

◆ begin() [2/2]

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
const_iterator PreconditionBlockJacobi< MatrixType, inverse_type >::begin ( const size_type r) const

Iterator starting at the first entry of row r.

◆ end() [2/2]

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
const_iterator PreconditionBlockJacobi< MatrixType, inverse_type >::end ( const size_type r) const

Final iterator of row r.

◆ do_vmult()

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
template<typename number2 >
void PreconditionBlockJacobi< MatrixType, inverse_type >::do_vmult ( Vector< number2 > & ,
const Vector< number2 > & ,
bool adding ) const
private

Actual implementation of the preconditioner.

Depending on adding, the result of preconditioning is added to the destination vector.

◆ subscribe()

void Subscriptor::subscribe ( std::atomic< bool > *const validity,
const std::string & identifier = "" ) const
inherited

Subscribes a user of the object by storing the pointer validity. The subscriber may be identified by text supplied as identifier.

Definition at line 135 of file subscriptor.cc.

◆ unsubscribe()

void Subscriptor::unsubscribe ( std::atomic< bool > *const validity,
const std::string & identifier = "" ) const
inherited

Unsubscribes a user from the object.

Note
The identifier and the validity pointer must be the same as the one supplied to subscribe().

Definition at line 155 of file subscriptor.cc.

◆ n_subscriptions()

unsigned int Subscriptor::n_subscriptions ( ) const
inlineinherited

Return the present number of subscriptions to this object. This allows to use this class for reference counted lifetime determination where the last one to unsubscribe also deletes the object.

Definition at line 300 of file subscriptor.h.

◆ list_subscribers() [1/2]

template<typename StreamType >
void Subscriptor::list_subscribers ( StreamType & stream) const
inlineinherited

List the subscribers to the input stream.

Definition at line 317 of file subscriptor.h.

◆ list_subscribers() [2/2]

void Subscriptor::list_subscribers ( ) const
inherited

List the subscribers to deallog.

Definition at line 203 of file subscriptor.cc.

◆ serialize()

template<class Archive >
void Subscriptor::serialize ( Archive & ar,
const unsigned int version )
inlineinherited

Read or write the data of this object to or from a stream for the purpose of serialization using the BOOST serialization library.

This function does not actually serialize any of the member variables of this class. The reason is that what this class stores is only who subscribes to this object, but who does so at the time of storing the contents of this object does not necessarily have anything to do with who subscribes to the object when it is restored. Consequently, we do not want to overwrite the subscribers at the time of restoring, and then there is no reason to write the subscribers out in the first place.

Definition at line 309 of file subscriptor.h.

◆ check_no_subscribers()

void Subscriptor::check_no_subscribers ( ) const
privatenoexceptinherited

Check that there are no objects subscribing to this object. If this check passes then it is safe to destroy the current object. It this check fails then this function will either abort or print an error message to deallog (by using the AssertNothrow mechanism), but will not throw an exception.

Note
Since this function is just a consistency check it does nothing in release mode.
If this function is called when there is an uncaught exception then, rather than aborting, this function prints an error message to the standard error stream and returns.

Definition at line 52 of file subscriptor.cc.

◆ initialize() [1/2]

void PreconditionBlock< MatrixType, typename MatrixType::value_type >::initialize ( const MatrixType & A,
const AdditionalData parameters )
inherited

Initialize matrix and block size. We store the matrix and the block size in the preconditioner object. In a second step, the inverses of the diagonal blocks may be computed.

Additionally, a relaxation parameter for derived classes may be provided.

◆ initialize() [2/2]

void PreconditionBlock< MatrixType, typename MatrixType::value_type >::initialize ( const MatrixType & A,
const std::vector< size_type > & permutation,
const std::vector< size_type > & inverse_permutation,
const AdditionalData parameters )
protectedinherited

Initialize matrix and block size for permuted preconditioning. Additionally to the parameters of the other initialize() function, we hand over two index vectors with the permutation and its inverse. For the meaning of these vectors see PreconditionBlockSOR.

In a second step, the inverses of the diagonal blocks may be computed. Make sure you use invert_permuted_diagblocks() to yield consistent data.

Additionally, a relaxation parameter for derived classes may be provided.

◆ set_permutation()

void PreconditionBlock< MatrixType, typename MatrixType::value_type >::set_permutation ( const std::vector< size_type > & permutation,
const std::vector< size_type > & inverse_permutation )
protectedinherited

Set either the permutation of rows or the permutation of blocks, depending on the size of the vector.

If the size of the permutation vectors is equal to the dimension of the linear system, it is assumed that rows are permuted individually. In this case, set_permutation() must be called before initialize(), since the diagonal blocks are built from the permuted entries of the matrix.

If the size of the permutation vector is not equal to the dimension of the system, the diagonal blocks are computed from the unpermuted entries. Instead, the relaxation methods step() and Tstep() are executed applying the blocks in the order given by the permutation vector. They will throw an exception if length of this vector is not equal to the number of blocks.

Note
Permutation of blocks can only be applied to the relaxation operators step() and Tstep(), not to the preconditioning operators vmult() and Tvmult().
It is safe to call set_permutation() before initialize(), while the other order is only admissible for block permutation.

◆ invert_permuted_diagblocks()

void PreconditionBlock< MatrixType, typename MatrixType::value_type >::invert_permuted_diagblocks ( )
protectedinherited

Replacement of invert_diagblocks() for permuted preconditioning.

◆ clear()

void PreconditionBlock< MatrixType, typename MatrixType::value_type >::clear ( )
inherited

Deletes the inverse diagonal block matrices if existent, sets the blocksize to 0, hence leaves the class in the state that it had directly after calling the constructor.

◆ empty()

bool PreconditionBlock< MatrixType, typename MatrixType::value_type >::empty ( ) const
inherited

Check whether the object is empty.

◆ el()

value_type PreconditionBlock< MatrixType, typename MatrixType::value_type >::el ( size_type i,
size_type j ) const
inherited

Read-only access to entries. This function is only possible if the inverse diagonal blocks are stored.

◆ invert_diagblocks()

void PreconditionBlock< MatrixType, typename MatrixType::value_type >::invert_diagblocks ( )
inherited

Stores the inverse of the diagonal blocks in inverse. This costs some additional memory - for DG methods about 1/3 (for double inverses) or 1/6 (for float inverses) of that used for the matrix - but it makes the preconditioning much faster.

It is not allowed to call this function twice (will produce an error) before a call of clear(...) because at the second time there already exist the inverse matrices.

After this function is called, the lock on the matrix given through the use_matrix function is released, i.e. you may overwrite of delete it. You may want to do this in case you use this matrix to precondition another matrix.

◆ forward_step()

void PreconditionBlock< MatrixType, typename MatrixType::value_type >::forward_step ( Vector< number2 > & dst,
const Vector< number2 > & prev,
const Vector< number2 > & src,
const bool transpose_diagonal ) const
inherited

Perform one block relaxation step in forward numbering.

Depending on the arguments dst and pref, this performs an SOR step (both reference the same vector) of a Jacobi step (both different vectors). For the Jacobi step, the calling function must copy dst to pref after this.

Note
If a permutation is set, it is automatically honored by this function.

◆ backward_step()

void PreconditionBlock< MatrixType, typename MatrixType::value_type >::backward_step ( Vector< number2 > & dst,
const Vector< number2 > & prev,
const Vector< number2 > & src,
const bool transpose_diagonal ) const
inherited

Perform one block relaxation step in backward numbering.

Depending on the arguments dst and pref, this performs an SOR step (both reference the same vector) of a Jacobi step (both different vectors). For the Jacobi step, the calling function must copy dst to pref after this.

Note
If a permutation is set, it is automatically honored by this function.

◆ block_size()

size_type PreconditionBlock< MatrixType, typename MatrixType::value_type >::block_size ( ) const
inherited

Return the size of the blocks.

◆ memory_consumption()

std::size_t PreconditionBlock< MatrixType, typename MatrixType::value_type >::memory_consumption ( ) const
inherited

Determine an estimate for the memory consumption (in bytes) of this object.

◆ ExcWrongBlockSize()

static ::ExceptionBase & PreconditionBlock< MatrixType, typename MatrixType::value_type >::ExcWrongBlockSize ( int arg1,
int arg2 )
staticinherited

For non-overlapping block preconditioners, the block size must divide the matrix size. If not, this exception gets thrown.

Note
The message that will be printed by this exception reads:
<< "The blocksize " << arg1 << " and the size of the matrix " << arg2 << " do not match."

◆ ExcInverseMatricesAlreadyExist()

static ::ExceptionBase & PreconditionBlock< MatrixType, typename MatrixType::value_type >::ExcInverseMatricesAlreadyExist ( )
staticinherited

Exception

◆ reinit()

void PreconditionBlockBase< typename MatrixType::value_type >::reinit ( unsigned int nblocks,
size_type blocksize,
bool compress,
Inversion method = gauss_jordan )
inlineinherited

Resize to this number of diagonal blocks with the given block size. If compress is true, then only one block will be stored.

Definition at line 110 of file precondition_block_base.h.

◆ inverses_computed()

void PreconditionBlockBase< typename MatrixType::value_type >::inverses_computed ( bool are_they)
inlineinherited

Tell the class that inverses are computed.

Definition at line 119 of file precondition_block_base.h.

◆ same_diagonal()

bool PreconditionBlockBase< typename MatrixType::value_type >::same_diagonal ( ) const
inlineinherited

Does the matrix use only one diagonal block?

Definition at line 125 of file precondition_block_base.h.

◆ store_diagonals()

bool PreconditionBlockBase< typename MatrixType::value_type >::store_diagonals ( ) const
inlineinherited

Check, whether diagonal blocks (not their inverses) should be stored.

Definition at line 131 of file precondition_block_base.h.

◆ inverses_ready()

bool PreconditionBlockBase< typename MatrixType::value_type >::inverses_ready ( ) const
inlineinherited

Return true, if inverses are ready for use.

Definition at line 137 of file precondition_block_base.h.

◆ size()

unsigned int PreconditionBlockBase< typename MatrixType::value_type >::size ( ) const
inlineinherited

The number of blocks.

Definition at line 143 of file precondition_block_base.h.

◆ inverse_vmult()

void PreconditionBlockBase< typename MatrixType::value_type >::inverse_vmult ( size_type i,
Vector< number2 > & dst,
const Vector< number2 > & src ) const
inlineinherited

Multiply with the inverse block at position i.

Definition at line 150 of file precondition_block_base.h.

◆ inverse_Tvmult()

void PreconditionBlockBase< typename MatrixType::value_type >::inverse_Tvmult ( size_type i,
Vector< number2 > & dst,
const Vector< number2 > & src ) const
inlineinherited

Multiply with the transposed inverse block at position i.

Definition at line 159 of file precondition_block_base.h.

◆ inverse() [1/2]

FullMatrix< typename MatrixType::value_type > & PreconditionBlockBase< typename MatrixType::value_type >::inverse ( size_type i)
inlineinherited

Access to the inverse diagonal blocks if Inversion is gauss_jordan.

Definition at line 167 of file precondition_block_base.h.

◆ inverse() [2/2]

const FullMatrix< typename MatrixType::value_type > & PreconditionBlockBase< typename MatrixType::value_type >::inverse ( size_type i) const
inlineinherited

Access to the inverse diagonal blocks.

Definition at line 185 of file precondition_block_base.h.

◆ inverse_householder() [1/2]

Householder< typename MatrixType::value_type > & PreconditionBlockBase< typename MatrixType::value_type >::inverse_householder ( size_type i)
inlineinherited

Access to the inverse diagonal blocks if Inversion is householder.

Definition at line 173 of file precondition_block_base.h.

◆ inverse_householder() [2/2]

const Householder< typename MatrixType::value_type > & PreconditionBlockBase< typename MatrixType::value_type >::inverse_householder ( size_type i) const
inlineinherited

Access to the inverse diagonal blocks if Inversion is householder.

Definition at line 191 of file precondition_block_base.h.

◆ inverse_svd() [1/2]

LAPACKFullMatrix< typename MatrixType::value_type > & PreconditionBlockBase< typename MatrixType::value_type >::inverse_svd ( size_type i)
inlineinherited

Access to the inverse diagonal blocks if Inversion is householder.

Definition at line 179 of file precondition_block_base.h.

◆ inverse_svd() [2/2]

const LAPACKFullMatrix< typename MatrixType::value_type > & PreconditionBlockBase< typename MatrixType::value_type >::inverse_svd ( size_type i) const
inlineinherited

Access to the inverse diagonal blocks if Inversion is householder.

Definition at line 197 of file precondition_block_base.h.

◆ diagonal() [1/2]

FullMatrix< typename MatrixType::value_type > & PreconditionBlockBase< typename MatrixType::value_type >::diagonal ( size_type i)
inlineinherited

Access to the diagonal blocks.

Definition at line 203 of file precondition_block_base.h.

◆ diagonal() [2/2]

const FullMatrix< typename MatrixType::value_type > & PreconditionBlockBase< typename MatrixType::value_type >::diagonal ( size_type i) const
inlineinherited

Access to the diagonal blocks.

Definition at line 209 of file precondition_block_base.h.

◆ log_statistics()

void PreconditionBlockBase< typename MatrixType::value_type >::log_statistics ( ) const
inlineinherited

Print some statistics about the inverses to deallog. Output depends on Inversion. It is richest for svd, where we obtain statistics on extremal singular values and condition numbers.

Definition at line 217 of file precondition_block_base.h.

◆ ExcDiagonalsNotStored()

static ::ExceptionBase & PreconditionBlockBase< typename MatrixType::value_type >::ExcDiagonalsNotStored ( )
staticinherited

You are trying to access a diagonal block (not its inverse), but you decided not to store the diagonal blocks.

◆ ExcInverseNotAvailable()

static ::ExceptionBase & PreconditionBlockBase< typename MatrixType::value_type >::ExcInverseNotAvailable ( )
staticinherited

You are accessing a diagonal block, assuming that it has a certain type. But, the method used for inverting the diagonal blocks does not use this type

Friends And Related Symbol Documentation

◆ Accessor

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
friend class Accessor
friend

Definition at line 614 of file precondition_block.h.

◆ const_iterator

template<typename MatrixType , typename inverse_type = typename MatrixType::value_type>
friend class const_iterator
friend

Definition at line 615 of file precondition_block.h.

Member Data Documentation

◆ counter

std::atomic<unsigned int> Subscriptor::counter
mutableprivateinherited

Store the number of objects which subscribed to this object. Initially, this number is zero, and upon destruction it shall be zero again (i.e. all objects which subscribed should have unsubscribed again).

The creator (and owner) of an object is counted in the map below if HE manages to supply identification.

We use the mutable keyword in order to allow subscription to constant objects also.

This counter may be read from and written to concurrently in multithreaded code: hence we use the std::atomic class template.

Definition at line 218 of file subscriptor.h.

◆ counter_map

std::map<std::string, unsigned int> Subscriptor::counter_map
mutableprivateinherited

In this map, we count subscriptions for each different identification string supplied to subscribe().

Definition at line 224 of file subscriptor.h.

◆ validity_pointers

std::vector<std::atomic<bool> *> Subscriptor::validity_pointers
mutableprivateinherited

In this vector, we store pointers to the validity bool in the SmartPointer objects that subscribe to this class.

Definition at line 240 of file subscriptor.h.

◆ object_info

const std::type_info* Subscriptor::object_info
mutableprivateinherited

Pointer to the typeinfo object of this object, from which we can later deduce the class name. Since this information on the derived class is neither available in the destructor, nor in the constructor, we obtain it in between and store it here.

Definition at line 248 of file subscriptor.h.

◆ mutex

std::mutex Subscriptor::mutex
staticprivateinherited

A mutex used to ensure data consistency when accessing the mutable members of this class. This lock is used in the subscribe() and unsubscribe() functions, as well as in list_subscribers().

Definition at line 271 of file subscriptor.h.

◆ blocksize

size_type PreconditionBlock< MatrixType, typename MatrixType::value_type >::blocksize
protectedinherited

Size of the blocks. Each diagonal block is assumed to be of the same size.

Definition at line 338 of file precondition_block.h.

◆ A

SmartPointer<const MatrixType, PreconditionBlock<MatrixType, typename MatrixType::value_type> > PreconditionBlock< MatrixType, typename MatrixType::value_type >::A
protectedinherited

Pointer to the matrix. Make sure that the matrix exists as long as this class needs it, i.e. until calling invert_diagblocks, or (if the inverse matrices should not be stored) until the last call of the preconditoining vmult function of the derived classes.

Definition at line 346 of file precondition_block.h.

◆ relaxation

double PreconditionBlock< MatrixType, typename MatrixType::value_type >::relaxation
protectedinherited

Relaxation parameter to be used by derived classes.

Definition at line 350 of file precondition_block.h.

◆ permutation

std::vector<size_type> PreconditionBlock< MatrixType, typename MatrixType::value_type >::permutation
protectedinherited

The permutation vector

Definition at line 355 of file precondition_block.h.

◆ inverse_permutation

std::vector<size_type> PreconditionBlock< MatrixType, typename MatrixType::value_type >::inverse_permutation
protectedinherited

The inverse permutation vector

Definition at line 360 of file precondition_block.h.

◆ inversion

Inversion PreconditionBlockBase< typename MatrixType::value_type >::inversion
protectedinherited

The method used for inverting blocks.

Definition at line 243 of file precondition_block_base.h.

◆ n_diagonal_blocks

unsigned int PreconditionBlockBase< typename MatrixType::value_type >::n_diagonal_blocks
privateinherited

The number of (inverse) diagonal blocks, if only one is stored.

Definition at line 249 of file precondition_block_base.h.

◆ var_inverse_full

std::vector<FullMatrix<typename MatrixType::value_type> > PreconditionBlockBase< typename MatrixType::value_type >::var_inverse_full
privateinherited

Storage of the inverse matrices of the diagonal blocks matrices as FullMatrix<number> matrices, if Inversion gauss_jordan is used. Using number=float saves memory in comparison with number=double, but may introduce numerical instability.

Definition at line 257 of file precondition_block_base.h.

◆ var_inverse_householder

std::vector<Householder<typename MatrixType::value_type> > PreconditionBlockBase< typename MatrixType::value_type >::var_inverse_householder
privateinherited

Storage of the inverse matrices of the diagonal blocks matrices as Householder matrices if Inversion householder is used. Using number=float saves memory in comparison with number=double, but may introduce numerical instability.

Definition at line 265 of file precondition_block_base.h.

◆ var_inverse_svd

std::vector<LAPACKFullMatrix<typename MatrixType::value_type> > PreconditionBlockBase< typename MatrixType::value_type >::var_inverse_svd
privateinherited

Storage of the inverse matrices of the diagonal blocks matrices as LAPACKFullMatrix matrices if Inversion svd is used. Using number=float saves memory in comparison with number=double, but may introduce numerical instability.

Definition at line 273 of file precondition_block_base.h.

◆ var_diagonal

std::vector<FullMatrix<typename MatrixType::value_type> > PreconditionBlockBase< typename MatrixType::value_type >::var_diagonal
privateinherited

Storage of the original diagonal blocks.

Used by the blocked SSOR method.

Definition at line 280 of file precondition_block_base.h.

◆ var_store_diagonals

bool PreconditionBlockBase< typename MatrixType::value_type >::var_store_diagonals
privateinherited

This is true, if the field var_diagonal is to be used.

Definition at line 286 of file precondition_block_base.h.

◆ var_same_diagonal

bool PreconditionBlockBase< typename MatrixType::value_type >::var_same_diagonal
privateinherited

This is true, if only one inverse is stored.

Definition at line 291 of file precondition_block_base.h.

◆ var_inverses_ready

bool PreconditionBlockBase< typename MatrixType::value_type >::var_inverses_ready
privateinherited

The inverse matrices are usable. Set by the parent class via inverses_computed().

Definition at line 297 of file precondition_block_base.h.

The documentation for this class was generated from the following files:
Generated by doxygen 1.11.0