PolynomialsRT_Bubbles< dim > Class Template Reference

#include <deal.II/base/polynomials_rt_bubbles.h>

Inheritance diagram for PolynomialsRT_Bubbles< dim >:

Public Member Functions
	PolynomialsRT_Bubbles (const unsigned int k)
void	evaluate (const Point< dim > &unit_point, std::vector< Tensor< 1, dim > > &values, std::vector< Tensor< 2, dim > > &grads, std::vector< Tensor< 3, dim > > &grad_grads, std::vector< Tensor< 4, dim > > &third_derivatives, std::vector< Tensor< 5, dim > > &fourth_derivatives) const override
std::string	name () const override
virtual std::unique_ptr< TensorPolynomialsBase< dim > >	clone () const override
unsigned int	n () const
unsigned int	degree () const

Static Public Member Functions
static unsigned int	n_polynomials (const unsigned int degree)

Private Attributes
const PolynomialsRaviartThomas< dim >	raviart_thomas_space
std::vector< Polynomials::Polynomial< double > >	monomials
const unsigned int	polynomial_degree
const unsigned int	n_pols

Detailed Description

template<int dim>
class PolynomialsRT_Bubbles< dim >

This class implements the H^div-conforming, vector-valued enhanced Raviart-Thomas polynomials.

Similarly to the classical Raviart-Thomas space, the enhanced Raviart-Thomas polynomials are constructed such that the divergence is in the tensor product polynomial space Q_k-1.

This space is of the form V_k = RT_k-1 + B_k, where B_k is defined as follows:

In 2d:

\begin{align*} B_k^1(E) = \text{span}\left\{x^{a_1-1} y^{a_2}\begin{pmatrix} (a_2+1) x \\ -a_1 y \end{pmatrix}\text{ : } a_2=k \right\} \\ B_k^2(E) = \text{span}\left\{x^{b_1} y^{b_2-1}\begin{pmatrix} -b_2 x \\ (b_1+1) y \end{pmatrix}\text{ : } b_1=k \right\} \end{align*}

In 3d:

\begin{align*} B_k^1(E) = \text{span}\left\{x^{a_1-1} y^{a_2} z^{a_3}\begin{pmatrix} (a_2+a_3+2) x \\ -a_1 y \\ -a_1 z \end{pmatrix}\text{ : } a_2=k \text{ or } a_3=k \right\},\\ B_k^2(E) = \text{span}\left\{x^{b_1} y^{b_2-1} z^{b_3}\begin{pmatrix} -b_2 x \\ (b_1+b_3+2) y \\ -b_2 z \end{pmatrix}\text{ : } b_1=k \text{ or } b_3=k \right\},\\ B_k^3(E) = \text{span}\left\{x^{c_1}y^{c_2}z^{c_3-1}\begin{pmatrix} -c_3 x \\ -c_3y \\ (c_1+c_2+2)z \end{pmatrix}\text{ : } c_1=k \text{ or } c_2=k \right\}, \end{align*}

where \(0 \le a_1, a_2, a_3 \le k\).

Note

Unlike the classical Raviart-Thomas space, the lowest order for the enhanced space is 1, similarly to the Brezzi-Douglas-Marini (BDM) polynomial space.

The total dimension of the space dim(V_k) = d*(k+1)^d, where d is the space dimension. This allows to associate shape functions with the Gauss-Lobatto quadrature points as shown in the figures below.

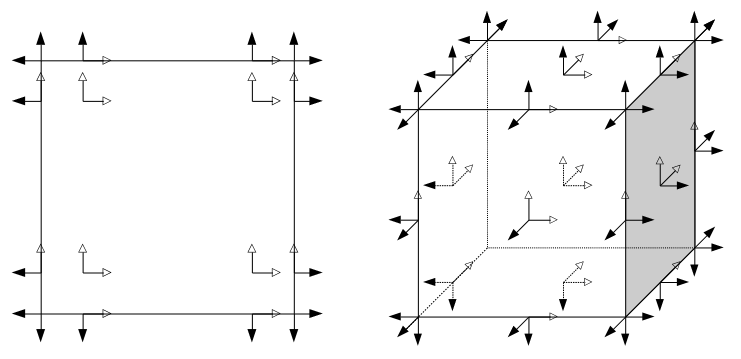
Left - \(2d,\,k=3\), right - \(3d,\,k=2\).

Definition at line 90 of file polynomials_rt_bubbles.h.

Constructor & Destructor Documentation

PolynomialsRT_Bubbles()

template<int dim>

PolynomialsRT_Bubbles< dim >::PolynomialsRT_Bubbles

(

const unsigned int

k

)

Constructor. Creates all basis functions for RT_bubbles polynomials of given degree.

Definition at line 28 of file polynomials_rt_bubbles.cc.

Member Function Documentation

evaluate()

template<int dim>

void PolynomialsRT_Bubbles< dim >::evaluate ( const Point< dim > & unit_point, std::vector< Tensor< 1, dim > > & values, std::vector< Tensor< 2, dim > > & grads, std::vector< Tensor< 3, dim > > & grad_grads, std::vector< Tensor< 4, dim > > & third_derivatives, std::vector< Tensor< 5, dim > > & fourth_derivatives ) const

overridevirtual

Computes the value and the first and second derivatives of each RT_bubbles polynomial at unit_point.

The size of the vectors must either be zero or equal n(). In the first case, the function will not compute these values.

Implements TensorPolynomialsBase< dim >.

Definition at line 43 of file polynomials_rt_bubbles.cc.

name()

template<int dim>

std::string PolynomialsRT_Bubbles< dim >::name ( ) const

inlineoverridevirtual

Return the name of the space, which is RT_Bubbles.

Implements TensorPolynomialsBase< dim >.

Definition at line 150 of file polynomials_rt_bubbles.h.

n_polynomials()

template<int dim>

unsigned int PolynomialsRT_Bubbles< dim >::n_polynomials ( const unsigned int degree )

static

Return the number of polynomials in the space RT_Bubbles(degree) without requiring to build an object of PolynomialsRT-Bubbles. This is required by the FiniteElement classes.

Definition at line 841 of file polynomials_rt_bubbles.cc.

clone()

template<int dim>

std::unique_ptr< TensorPolynomialsBase< dim > > PolynomialsRT_Bubbles< dim >::clone ( ) const

overridevirtual

A sort of virtual copy constructor, this function returns a copy of the polynomial space object. Derived classes need to override the function here in this base class and return an object of the same type as the derived class.

Some places in the library, for example the constructors of FE_PolyTensor, need to make copies of polynomial spaces without knowing their exact type. They do so through this function.

Implements TensorPolynomialsBase< dim >.

Definition at line 853 of file polynomials_rt_bubbles.cc.

n()

template<int dim>

unsigned int TensorPolynomialsBase< dim >::n ( ) const

inlineinherited

Return the number of polynomials.

Definition at line 151 of file tensor_polynomials_base.h.

degree()

template<int dim>

unsigned int TensorPolynomialsBase< dim >::degree ( ) const

inlineinherited

Return the highest polynomial degree of polynomials represented by this class. A derived class may override this if its value is different from my_degree.

Definition at line 160 of file tensor_polynomials_base.h.

Member Data Documentation

raviart_thomas_space

template<int dim>

const PolynomialsRaviartThomas<dim> PolynomialsRT_Bubbles< dim >::raviart_thomas_space

private

An object representing the Raviart-Thomas part of the space

Definition at line 138 of file polynomials_rt_bubbles.h.

monomials

template<int dim>

std::vector<Polynomials::Polynomial<double> > PolynomialsRT_Bubbles< dim >::monomials

private

Storage for monomials, we need all polynomials from degree zero to k+1.

Definition at line 144 of file polynomials_rt_bubbles.h.

polynomial_degree

template<int dim>

const unsigned int TensorPolynomialsBase< dim >::polynomial_degree

privateinherited

The highest polynomial degree of this functions represented by this object.

Definition at line 139 of file tensor_polynomials_base.h.

n_pols

template<int dim>

const unsigned int TensorPolynomialsBase< dim >::n_pols

privateinherited

The number of polynomials represented by this object.

Definition at line 144 of file tensor_polynomials_base.h.

---

The documentation for this class was generated from the following files:

• include/deal.II/base/polynomials_rt_bubbles.h
• source/base/polynomials_rt_bubbles.cc