 |
Reference documentation for deal.II version 9.4.1
|
 |
Reference documentation for deal.II version 9.4.1
|
This tutorial depends on step-12.
| Table of contents | |
|---|---|
The material is based upon work partially supported by eSSENCE of e-Science and the Swedish Research Council under grants 2014-6088 (Kreiss) and 2017-05038 (Massing).
In this example, we show how to use the cut finite element method (CutFEM) in deal.II. For illustration, we want to solve the simplest possible problem, so we again consider Poisson's equation:
\begin{align*} -\Delta u &= f \qquad && \text{in }\, \Omega, \\ u &= u_D \qquad && \text{on }\, \Gamma = \partial \Omega, \end{align*}
where we choose \(f(x) = 4\) and \(u_D(x) = 1\). CutFEM is an immersed method. In this context, "immersed" means that the mesh is unfitted to the geometry of the domain, \(\Omega\). Instead, \(\Omega\) floats freely on top of a uniform background mesh, \(\mathcal{T}^h\).
Since we no longer use the mesh to describe the geometry of the domain, we need some other way to represent it. This can be done in several ways but here we assume that \(\Omega\) is described by a level set function, \(\psi : \mathbb{R}^{\text{dim}} \to \mathbb{R}\) such that
\begin{align*} \Omega &= \{x \in \mathbb{R}^{\text{dim}} : \psi(x) < 0 \}, \\ \Gamma &= \{x \in \mathbb{R}^{\text{dim}} : \psi(x) = 0 \}. \end{align*}
For simplicity, we choose \(\Omega\) to be a unit disk, so that
\begin{equation*} \psi(x) = \| x \| - 1. \end{equation*}
As can be seen from the figure below, the level set function is negative for points in \(\Omega\), zero on the boundary, and positive everywhere else.
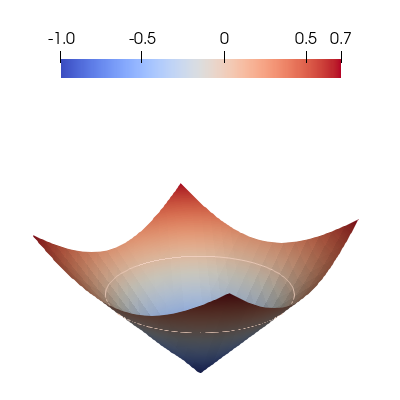
To solve this problem, we want to distribute degrees of freedom over the smallest submesh, \(\mathcal{T}_\Omega^h\), that completely covers the domain:
\begin{equation*} \mathcal{T}_\Omega^h = \{ T \in \mathcal{T}^{h} : T \cap \Omega \neq \emptyset \}. \end{equation*}
This is usually referred to as the "active mesh".
The finite element space where we want to find our numerical solution, \(u_h\), is now
\begin{equation*} V_\Omega^h = \{ v \in C(\mathcal{N}_\Omega^h) : v \in Q_p(T), \, T \in \mathcal{T}_\Omega^h \}, \end{equation*}
where
\begin{equation*} \mathcal{N}_\Omega^h = \bigcup_{T \in \mathcal{T}_\Omega^h} \overline{T}, \end{equation*}
and \(\overline{T}\) denotes the closure of \(T\). The set \(\mathcal{N}_\Omega^h\) is sometimes referred to as the "fictitious domain". Since \(\Omega \subset \mathcal{N}_\Omega^h\), we see that the numerical solution is defined over a slightly larger region than the analytical solution.
In this type of immersed finite element method, the standard way to apply boundary conditions is using Nitsche's method. Multiplying the PDE with a test function, \(v_h \in V_\Omega^h\), and integrating by parts over \(\Omega\), as usual, gives us
\begin{equation*} (\nabla u_h, \nabla v_h)_\Omega - (\partial_n u_h, v_h)_\Gamma = (f,v)_\Omega. \end{equation*}
Let \(\gamma_D > 0\) be a scalar penalty parameter and let \(h\) be some measure of the local cell size. We now note that the following terms are consistent with the Dirichlet boundary condition:
\begin{align*} -(u_h, \partial_n v_h)_\Gamma &= -(u_D, \partial_n v_h)_\Gamma, \\ \left (\frac{\gamma_D}{h} u_h, v_h \right )_\Gamma &= \left (\frac{\gamma_D}{h}u_D, v_h \right )_\Gamma. \end{align*}
Thus, we can add these to the weak formulation to enforce the boundary condition. This leads to the following weak formulation: Find \(u_h \in V_\Omega^h\) such that
\begin{equation*} a_h(u_h, v_h) = L_h(v_h), \quad \forall v_h \in V_\Omega^h, \end{equation*}
where
\begin{align*} a_h(u_h, v_h) &= (\nabla u_h, \nabla v_h)_\Omega - (\partial_n u_h, v_h)_\Gamma - (u_h, \partial_n v_h)_\Gamma + \left (\frac{\gamma_D}{h} u_h, v_h \right )_\Gamma, \\ L_h(v_h) &= (f,v)_\Omega + \left (u_D, \frac{\gamma_D}{h} v_h -\partial_n v_h \right )_\Gamma. \end{align*}
In this formulation, there is one big difference, compared to a standard boundary-fitted finite element method. On each cell, we need to integrate over the part of the domain and the part of the boundary that falls within the cell. Thus, on each cell intersected by \(\Gamma\), we need special quadrature rules that only integrate over these parts of the cell, that is, over \(T \cap \Omega\) and \(T \cap \Gamma\).
Since \(\Omega \cap T\) is the part of the cell that lies inside the domain, we shall refer to the following regions
\begin{align*} \{x \in T : \psi(x) < 0 \}, \\ \{x \in T : \psi(x) > 0 \}, \\ \{x \in T : \psi(x) = 0 \}, \end{align*}
as the "inside", "outside" and the "surface region" of the cell \(T\).
The above finite element method that uses the bilinear form \(a_h(\cdot, \cdot)\) is sometimes referred to as the "naive weak formulation" because it suffers from the so-called "small cut problem". Depending on how \(\Omega\) is located relative to \(\mathcal{T}_h\), a cut between a cell, \(T \in \mathcal{T}_h\), and \(\Omega\) can become arbitrarily small: \(|\Omega \cap T | \rightarrow 0\). For Neumann boundary conditions, the consequence is that the stiffness matrix can become arbitrarily ill-conditioned as the cut-size approaches zero. For a Dirichlet condition, the situation is even worse. For any finite choice of Nitsche constant, \(\gamma_D\), the bilinear form \(a_h(\cdot,\cdot)\) loses coercivity as the size of a cell cut approaches zero. This makes the above weak formulation essentially useless because as we refine we typically can not control how the cells intersect \(\Gamma\). One way to avoid this problem is to add a so-called ghost penalty term, \(g_h\), to the weak formulation (see e.g. [38] and [39]). This leads to the stabilized cut finite element method, which reads: Find \(u_h \in V_\Omega^h\) such that
\begin{equation*} A_h(u_h, v_h) = L_h(v_h), \quad \forall v_h \in V_\Omega^h, \end{equation*}
where
\begin{equation*} A_h(u_h,v_h) = a_h(u_h,v_h) + g_h(u_h, v_h). \end{equation*}
The point of this ghost penalty is that it makes the numerical method essentially independent of how \(\Omega\) relates to the background mesh. In particular, \(A_h\) can be shown to be continuous and coercive, with constants that do not depend on how \(\Omega\) intersects \(\mathcal{T}^h\). To define the ghost penalty, let \(\mathcal{T}_\Gamma^h\) be the set of intersected cells:
\begin{equation*} \mathcal{T}_{\Gamma}^h = \{ T \in \mathcal{T}_{\Omega}^{h} : T \cap \Gamma \neq \emptyset \}, \end{equation*}
and let \(\mathcal{F}_h\) denote the interior faces of the intersected cells in the active mesh:
\begin{equation*} \mathcal{F}_h = \{ F = \overline{T}_+ \cap \overline{T}_- : \, T_+ \in \mathcal{T}_{\Gamma}^h, \, T_- \in \mathcal{T}_{\Omega}^h \}. \end{equation*}
The ghost penalty acts on these faces and reads
\begin{equation*} g_h(u_h,v_h) = \gamma_A \sum_{F \in \mathcal{F}_h} g_F(u_h, v_h), \end{equation*}
where \(g_F\) is the face-wise ghost penalty:
\begin{equation*} g_F(u_h, v_h) = \gamma_A \sum_{k=0}^p \left(\frac{h_F^{2k-1}}{k!^2}[\partial_n^k u_h], [\partial_n^k v_h] \right)_F. \end{equation*}
Here, \(\gamma_A\) is a penalty parameter and \(h_F\) is some measure of the face size. We see that \(g_F\) penalizes the jumps in the face-normal derivatives, \(\partial_n^k\), over \(F = \overline{T}_+ \cap \overline{T}_-\). Since we include all normal derivatives up to the polynomial degree, we weakly force the piecewise polynomial to behave as a single polynomial over \(\overline{T}_+ \cup \overline{T}_-\). Hand-wavingly speaking, this is the reason why we obtain a cut-independent method when we enforce \(g_F(u_h, v_h) = 0\) over the faces in \(\mathcal{F}_h\). Here, we shall use a continuous space of \(Q_1\)-elements, so the ghost penalty is reduced to
\begin{equation*} g_h(u_h,v_h) = \gamma_A \sum_{F \in \mathcal{F}_h} (h_F [\partial_n u_h], [\partial_n v_h])_F. \end{equation*}
A typical use case of a level set method is a problem where the domain is advected in a velocity field, such that the domain deforms with time. For such a problem, one would typically solve for an approximation of the level set function, \(\psi_h \in V^h\), in a separate finite element space over the whole background mesh:
\begin{equation*} V^h = \{ v \in C(\mathcal{N}^h) : v \in Q_p(T), \, T \in \mathcal{T}^h \}, \end{equation*}
where \(\mathcal{N}^h = \bigcup_{T \in \mathcal{T}^h} \overline{T}\). Even if we solve a much simpler problem with a stationary domain in this tutorial, we shall, just to illustrate, still use a discrete level set function for the Poisson problem. Technically, this is a so-called "variational crime" because we are actually not using the bilinear form \(a_h\) but instead
\begin{equation*} a_h^\star(u_h, v_h) = (\nabla u_h, \nabla v_h)_{\Omega_h} - (\partial_n u_h, v_h)_{\Gamma_h} + \ldots \end{equation*}
This is an approximation of \(a_h\) since we integrate over the approximations of the geometry that we get via the discrete level set function:
\begin{align*} \Omega_h &= \{x \in \mathbb{R}^{\text{dim}} : \psi_h(x) < 0 \}, \\ \Gamma_h &= \{x \in \mathbb{R}^{\text{dim}} : \psi_h(x) = 0 \}. \end{align*}
Using \(\Omega_h\) instead of \(\Omega\) in the method will give rise to a larger error in the numerical solution. This is often referred to as the "geometrical error". However, when the same element order, \(p\), is used in \(V^h\) and \(V_\Omega^h\), one can often show that the method gives the same order of convergence as if the exact domain would have been used. Furthermore, deal.II allows us to independently choose a more accurate geometry representation with a higher-order level set function, compared to the function space for solving the Poisson equation.
Even if we have used \(\mathcal{T}_\Omega^h\) to define the finite element space, we will not create this submesh in practice. As in step-46, we shall instead use the hp-framework. To create \(V_\Omega^h\), we first add an FE_Q and an FE_Nothing element to an hp::FECollection. We then iterate over each cell, \(T\), and depending on whether \(T\) belongs to \(\mathcal{T}_\Omega^h\) or not, we set the active_fe_index to either 0 or 1. To do so, we need to determine if a given cell is in \(\mathcal{T}_\Omega^h\) or not. For this purpose, we will use the class NonMatching::MeshClassifier. The MeshClassifier takes the discrete level set function, described as a (DoFHandler, Vector)-pair, as arguments to its constructor:
When we call the reclassify() function on an object of this class, each active cell and face is associated with one of the values {inside, outside, intersected} of the enum NonMatching::LocationToLevelSet. Here, "inside" means that the level set function is negative over the whole cell so that it lies completely inside the domain. Analogously, "outside" means that \(\psi\) is positive over the whole cell, and "intersected" means that \(\psi\) varies in sign over \(T\) so that the zero-contour of \(\psi\) goes through \(T\).
| LocationToLevelSet | \(\psi(x)\) for \(x \in T\) | Relation to \(\Omega\) |
|---|---|---|
| inside | \(\psi(x) < 0\) | \(T \cap \Omega = T\) |
| outside | \(0 < \psi(x)\) | \(T \cap \Omega = \emptyset\) |
| intersected | \(\psi(x)\) varies in sign | \(T \cap \Gamma \neq \emptyset\) |
Each active face is classified in the same way, according to how the sign of \(\psi\) varies over the face. MeshClassifier lets you query this information for a given cell/face via its MeshClassifier::location_to_level_set() methods:
The first include files have all been treated in previous examples.
The first new header contains some common level set functions. For example, the spherical geometry that we use here.
We also need 3 new headers from the NonMatching namespace.
We then define the main class that solves the Laplace problem.
We need two separate DoFHandlers. The first manages the DoFs for the discrete level set function that describes the geometry of the domain.
The second DoFHandler manages the DoFs for the solution of the Poisson equation.
We generate a background mesh with perfectly Cartesian cells. Our domain is a unit disc centered at the origin, so we need to make the background mesh a bit larger than \([-1, 1]^{\text{dim}}\) to completely cover \(\Omega\).
The discrete level set function is defined on the whole background mesh. Thus, to set up the DoFHandler for the level set function, we distribute DoFs over all elements in \(\mathcal{T}_h\). We then set up the discrete level set function by interpolating onto this finite element space.
To set up the finite element space \(V_\Omega^h\), we will use 2 different elements: FE_Q and FE_Nothing. For better readability we define an enum for the indices in the order we store them in the hp::FECollection.
We then use the MeshClassifier to check LocationToLevelSet for each cell in the mesh and tell the DoFHandler to use FE_Q on elements that are inside or intersected, and FE_Nothing on the elements that are outside.
The added ghost penalty results in a sparsity pattern similar to a DG method with a symmetric-interior-penalty term. Thus, we can use the make_flux_sparsity_pattern() function to create it. However, since the ghost-penalty terms only act on the faces in \(\mathcal{F}_h\), we can pass in a lambda function that tells make_flux_sparsity_pattern() over which faces the flux-terms appear. This gives us a sparsity pattern with minimal number of entries. When passing a lambda function, make_flux_sparsity_pattern requires us to also pass cell and face coupling tables to it. If the problem was vector-valued, these tables would allow us to couple only some of the vector components. This is discussed in step-46.
The following function describes which faces are part of the set \(\mathcal{F}_h\). That is, it returns true if the face of the incoming cell belongs to the set \(\mathcal{F}_h\).
Since the ghost penalty is similar to a DG flux term, the simplest way to assemble it is to use an FEInterfaceValues object.
As we iterate over the cells in the mesh, we would in principle have to do the following on each cell, \(T\),
To make the assembly easier, we use the class NonMatching::FEValues, which does the above steps 1 and 2 for us. The algorithm [135] that is used to generate the quadrature rules on the intersected cells uses a 1-dimensional quadrature rule as base. Thus, we pass a 1D Gauss–Legendre quadrature to the constructor of NonMatching::FEValues. On the non-intersected cells, a tensor product of this 1D-quadrature will be used.
As stated in the introduction, each cell has 3 different regions: inside, surface, and outside, where the level set function in each region is negative, zero, and positive. We need an UpdateFlags variable for each such region. These are stored on an object of type NonMatching::RegionUpdateFlags, which we pass to NonMatching::FEValues.
As we iterate over the cells, we don't need to do anything on the cells that have FENothing elements. To disregard them we use an iterator filter.
First, we call the reinit function of our NonMatching::FEValues object. In the background, NonMatching::FEValues uses the MeshClassifier passed to its constructor to check if the incoming cell is intersected. If that is the case, NonMatching::FEValues calls the NonMatching::QuadratureGenerator in the background to create the immersed quadrature rules.
After calling reinit, we can retrieve a FEValues object with quadrature points that corresponds to integrating over the inside region of the cell. This is the object we use to do the local assembly. This is similar to how hp::FEValues builds FEValues objects. However, one difference here is that the FEValues object is returned as an optional. This is a type that wraps an object that may or may not be present. This requires us to add an if-statement to check if the returned optional contains a value, before we use it. This might seem odd at first. Why does the function not just return a reference to a const FEValues<dim>? The reason is that in an immersed method, we have essentially no control of how the cuts occur. Even if the cell is formally intersected: \(T \cap \Omega \neq \emptyset\), it might be that the cut is only of floating point size \(|T \cap \Omega| \sim \epsilon\). When this is the case, we can not expect that the algorithm that generates the quadrature rule produces anything useful. It can happen that the algorithm produces 0 quadrature points. When this happens, the returned optional will not contain a value, even if the cell is formally intersected.
In the same way, we can use NonMatching::FEValues to retrieve an FEFaceValues-like object to integrate over \(T \cap \Gamma\). The only thing that is new here is the type of the object. The transformation from quadrature weights to JxW-values is different for surfaces, so we need a new class: NonMatching::FEImmersedSurfaceValues. In addition to the ordinary functions shape_value(..), shape_grad(..), etc., one can use its normal_vector(..)-function to get an outward normal to the immersed surface, \(\Gamma\). In terms of the level set function, this normal reads
\begin{equation*} n = \frac{\nabla \psi}{\| \nabla \psi \|}. \end{equation*}
An additional benefit of std::optional is that we do not need any other check for whether we are on intersected cells: In case we are on an inside cell, we get an empty object here.
The assembly of the ghost penalty term is straight forward. As we iterate over the local faces, we first check if the current face belongs to the set \(\mathcal{F}_h\). The actual assembly is simple using FEInterfaceValues. Assembling in this we will traverse each internal face in the mesh twice, so in order to get the penalty constant we expect, we multiply the penalty term with a factor 1/2.
Since both DoFHandler instances use the same triangulation, we can add both the level set function and the solution to the same vtu-file. Further, we do not want to output the cells that have LocationToLevelSet value outside. To disregard them, we write a small lambda function and use the set_cell_selection function of the DataOut class.
To test that the implementation works as expected, we want to compute the error in the solution in the \(L^2\)-norm. The analytical solution to the Poisson problem stated in the introduction reads
\begin{align*} u(x) = 1 - \frac{2}{\text{dim}}(\| x \|^2 - 1) , \qquad x \in \overline{\Omega}. \end{align*}
We first create a function corresponding to the analytical solution:
Of course, the analytical solution, and thus also the error, is only defined in \(\overline{\Omega}\). Thus, to compute the \(L^2\)-error we must proceed in the same way as when we assembled the linear system. We first create an NonMatching::FEValues object.
We then iterate iterate over the cells that have LocationToLevelSetValue value inside or intersected again. For each quadrature point, we compute the pointwise error and use this to compute the integral.
Finally, we do a convergence study to check that the \(L^2\)-error decreases with the expected rate. We refine the background mesh a few times. In each refinement cycle, we solve the problem, compute the error, and add the \(L^2\)-error and the mesh size to a ConvergenceTable.
The numerical solution for one of the refinements is shown in the below figure. The zero-contour of the level set function is shown as a white line. On the intersected cells, we see that the numerical solution has a value also outside \(\overline{\Omega}\). As mentioned earlier, this extension of the solution is artificial.
The results of the convergence study is shown in the table below. We see that the \(L^2\) error decreases as we refine and that the estimated order of convergence, EOC, is close to 2.
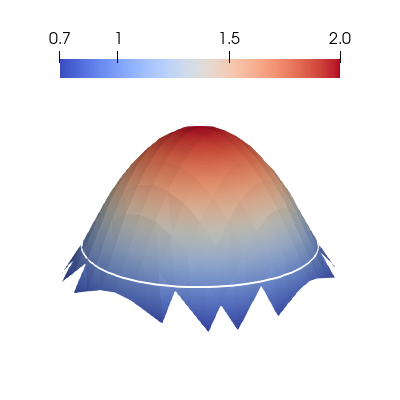
| Cycle | Mesh size | \(L^2\)-Error | EOC |
|---|---|---|---|
| 0 | 0.3025 | 8.0657e-02 | - |
| 1 | 0.1513 | 1.8711e-02 | 2.11 |
| 2 | 0.0756 | 4.1624e-03 | 2.17 |
| 3 | 0.0378 | 9.3979e-04 | 2.15 |