This tutorial depends on step-15.
This program was contributed by Wolfgang Bangerth, Colorado State University.
This material is based upon work partially supported by National Science Foundation grants OAC-1835673, DMS-1821210, and EAR-1925595; and by the Computational Infrastructure in Geodynamics initiative (CIG), through the National Science Foundation under Award No. EAR-1550901 and The University of California-Davis.
Introduction
The step-15 program solved the following, nonlinear equation describing the minimal surface problem:
\begin{align*}
-\nabla \cdot \left( \frac{1}{\sqrt{1+|\nabla u|^{2}}}\nabla u \right) &= 0 \qquad
\qquad &&\textrm{in} ~ \Omega
\\
u&=g \qquad\qquad &&\textrm{on} ~ \partial \Omega.
\end{align*}
step-15 uses a Newton method, and Newton's method works by repeatedly solving a linearized problem for an update \delta u_k – called the "search direction" –, computing a "step length" \alpha_k, and then combining them to compute the new guess for the solution via
\begin{align*}
u_{k+1} = u_k + \alpha_k \, \delta u_k.
\end{align*}
In the course of the discussions in step-15, we found that it is awkward to compute the step length, and so just settled for simple choice: Always choose \alpha_k=0.1. This is of course not efficient: We know that we can only realize Newton's quadratic convergence rate if we eventually are able to choose \alpha_k=1, though we may have to choose it smaller for the first few iterations where we are still too far away to use this long a step length.
Among the goals of this program is therefore to address this shortcoming. Since line search algorithms are not entirely trivial to implement, one does as one should do anyway: Import complicated functionality from an external library. To this end, we will make use of the interfaces deal.II has to one of the big nonlinear solver packages, namely the KINSOL sub-package of the SUNDIALS suite. SUNDIALS is, at its heart, a package meant to solve complex ordinary differential equations (ODEs) and differential-algebraic equations (DAEs), and the deal.II interfaces allow for this via the classes in the SUNDIALS namespace: Notably the SUNDIALS::ARKode and SUNDIALS::IDA classes. But, because that is an important step in the solution of ODEs and DAEs with implicit methods, SUNDIALS also has a solver for nonlinear problems called KINSOL, and deal.II has an interface to it in the form of the SUNDIALS::KINSOL class. This is what we will use for the solution of our problem.
But SUNDIALS isn't just a convenient way for us to avoid writing a line search algorithm. In general, the solution of nonlinear problems is quite expensive, and one typically wants to save as much compute time as possible. One way one can achieve this is as follows: The algorithm in step-15 discretizes the problem and then in every iteration solves a linear system of the form
\begin{align*}
J_k \, \delta U_k = -F_k
\end{align*}
where F_k is the residual vector computed using the current vector of nodal values U_k, J_k is its derivative (called the "Jacobian"), and \delta U_k is the update vector that corresponds to the function \delta u_k mentioned above. The construction of J_k,F_k has been thoroughly discussed in step-15, as has the way to solve the linear system in each Newton iteration. So let us focus on another aspect of the nonlinear solution procedure: Computing F_k is expensive, and assembling the matrix J_k even more so. Do we actually need to do that in every iteration? It turns out that in many applications, this is not actually necessary: These methods often converge even if we replace J_k by an approximation \tilde J_k and solve
\begin{align*}
\tilde J_k \, \widetilde{\delta U}_k = -F_k
\end{align*}
instead, then update
\begin{align*}
U_{k+1} = U_k + \alpha_k \, \widetilde{\delta U}_k.
\end{align*}
This may require an iteration or two more because our update \widetilde{\delta U}_k is not quite as good as \delta U_k, but it may still be a win because we don't have to assemble J_k quite as often.
What kind of approximation \tilde J_k would we like for J_k? Theory says that as U_k converges to the exact solution U^\ast, we need to ensure that \tilde J_k needs to converge to J^\ast = \nabla F(U^\ast). In particular, since J_k\rightarrow J^\ast, a valid choice is \tilde J_k = J_k. But so is choosing \tilde J_k = J_k every, say, fifth iteration k=0,5,10,\ldots and for the other iterations, we choose \tilde J_k equal to the last computed J_{k'}. This is what we will do here: we will just re-use \tilde J_{k-1} from the previous iteration, which may again be what we had used in the iteration before that, \tilde J_{k-2}.
This scheme becomes even more interesting if, for the solution of the linear system with J_k, we don't just have to assemble a matrix, but also compute a good preconditioner. For example, if we were to use a sparse LU decomposition via the SparseDirectUMFPACK class, or used a geometric or algebraic multigrid. In those cases, we would also not have to update the preconditioner, whose computation may have taken about as long or longer than the assembly of the matrix in the first place. Indeed, with this mindset, we should probably think about using the best preconditioner we can think of, even though their construction is typically quite expensive: We will hope to amortize the cost of computing this preconditioner by applying it to more than one just one linear solve.
The big question is, of course: By what criterion do we decide whether we can get away with the approximation \tilde J_k based on a previously computed Jacobian matrix J_{k-s} that goes back s steps, or whether we need to – at least in this iteration – actually re-compute the Jacobian J_k and the corresponding preconditioner? This is, like the issue with line search, one that requires a non-trivial amount of code that monitors the convergence of the overall algorithm. We could implement these sorts of things ourselves, but we probably shouldn't: KINSOL already does that for us. It will tell our code when to "update" the Jacobian matrix.
One last consideration if we were to use an iterative solver instead of the sparse direct one mentioned above: Not only is it possible to get away with replacing J_k by some approximation \tilde J_k when solving for the update \delta U_k, but one can also ask whether it is necessary to solve the linear system
\begin{align*}
\tilde J_k \widetilde{\delta U}_k = -F_k
\end{align*}
to high accuracy. The thinking goes like this: While our current solution U_k is still far away from U^\ast, why would we solve this linear system particularly accurately? The update U_{k+1}=U_k + \widetilde{\delta U}_k is likely still going to be far away from the exact solution, so why spend much time on solving the linear system to great accuracy? This is the kind of thinking that underlies algorithms such as the "Eisenstat-Walker trick" [141] in which one is given a tolerance to which the linear system above in iteration k has to be solved, with this tolerance dependent on the progress in the overall nonlinear solver. As before, one could try to implement this oneself, but KINSOL already provides this kind of information for us – though we will not use it in this program since we use a direct solver that requires no solver tolerance and just solves the linear system exactly up to round-off.
As a summary of all of these considerations, we could say the following: There is no need to reinvent the wheel. Just like deal.II provides a vast amount of finite-element functionality, SUNDIALS' KINSOL package provides a vast amount of nonlinear solver functionality, and we better use it.
How deal.II interfaces with KINSOL
KINSOL, like many similar packages, works in a pretty abstract way. At its core, it sees a nonlinear problem of the form
\begin{align*}
F(U) = 0
\end{align*}
and constructs a sequence of iterates U_k which, in general, are vectors of the same length as the vector returned by the function F. To do this, there are a few things it needs from the user:
- A way to resize a given vector to the correct size.
- A way to evaluate, for a given vector U, the function F(U). This function is generally called the "residual" operation because the goal is of course to find a point U^\ast for which F(U^\ast)=0; if F(U) returns a nonzero vector, then this is the "residual" (i.e., the "rest", or whatever is "left over"). The function that will do this is in essence the same as the computation of the right hand side vector in step-15, but with an important difference: There, the right hand side denoted the negative of the residual, so we have to switch a sign.
- A way to compute the matrix J_k if that is necessary in the current iteration, along with possibly a preconditioner or other data structures (e.g., a sparse decomposition via SparseDirectUMFPACK if that's what we choose to use to solve a linear system). This operation will generally be called the "setup" operation.
- A way to solve a linear system \tilde J_k x = b with whatever matrix \tilde J_k was last computed. This operation will generally be called the "solve" operation.
All of these operations need to be provided to KINSOL by std::function objects that take the appropriate set of arguments and that generally return an integer that indicates success (a zero return value) or failure (a nonzero return value). Specifically, the objects we will access are the SUNDIALS::KINSOL::reinit_vector, SUNDIALS::KINSOL::residual, SUNDIALS::KINSOL::setup_jacobian, and SUNDIALS::KINSOL::solve_jacobian_system member variables. (See the documentation of these variables for their details.) In our implementation, we will use lambda functions to implement these "callbacks" that in turn can call member functions; KINSOL will then call these callbacks whenever its internal algorithms think it is useful.
Details of the implementation
The majority of the code of this tutorial program is as in step-15, and we will not comment on it in much detail. There is really just one aspect one has to pay some attention to, namely how to compute F(U) given a vector U on the one hand, and J(U) given a vector U separately. At first, this seems trivial: We just take the assemble_system() function and in the one case throw out all code that deals with the matrix and in the other case with the right hand side vector. There: Problem solved.
But it isn't quite as simple. That's because the two are not independent if we have nonzero Dirichlet boundary values, as we do here. The linear system we want to solve contains both interior and boundary degrees of freedom, and when eliminating those degrees of freedom from those that are truly "free", using for example AffineConstraints::distribute_local_to_global(), we need to know the matrix when assembling the right hand side vector.
Of course, this completely contravenes the original intent: To not assemble the matrix if we can get away without it. We solve this problem as follows:
- We set the starting guess for the solution vector, U_0, to one where boundary degrees of freedom already have their correct values.
- This implies that all updates can have zero updates for these degrees of freedom, and we can build both residual vectors F(U_k) and Jacobian matrices J_k that corresponds to linear systems whose solutions are zero in these vector components. For this special case, the assembly of matrix and right hand side vectors is independent, and can be broken into separate functions.
There is an assumption here that whenever KINSOL asks for a linear solver with the (approximation of the) Jacobian, that this will be for for an update \delta U (which has zero boundary values), a multiple of which will be added to the solution (which already has the right boundary values). This may not be true and if so, we might have to rethink our approach. That said, it turns out that in practice this is exactly what KINSOL does when using a Newton method, and so our approach is successful.
The commented program
Include files
This program starts out like most others with well known include files. Compared to the step-15 program from which most of what we do here is copied, the only difference is the include of the header files from which we import the SparseDirectUMFPACK class and the actual interface to KINSOL:
#include <fstream>
#include <iostream>
namespace Step77
{
The MinimalSurfaceProblem class template
Similarly, the main class of this program is essentially a copy of the one in step-15. The class does, however, split the computation of the Jacobian (system) matrix (and its factorization using a direct solver) and residual into separate functions for the reasons outlined in the introduction. For the same reason, the class also has a pointer to a factorization of the Jacobian matrix that is reset every time we update the Jacobian matrix.
(If you are wondering why the program uses a direct object for the Jacobian matrix but a pointer for the factorization: Every time KINSOL requests that the Jacobian be updated, we can simply write jacobian_matrix=0; to reset it to an empty matrix that we can then fill again. On the other hand, the SparseDirectUMFPACK class does not have any way to throw away its content or to replace it with a new factorization, and so we use a pointer: We just throw away the whole object and create a new one whenever we have a new Jacobian matrix to factor.)
Finally, the class has a timer variable that we will use to assess how long the different parts of the program take so that we can assess whether KINSOL's tendency to not rebuild the matrix and its factorization makes sense. We will discuss this in the "Results" section below.
template <int dim>
class MinimalSurfaceProblem
{
public:
MinimalSurfaceProblem();
void run();
private:
void setup_system(const bool initial_step);
const double tolerance);
void refine_mesh();
void output_results(const unsigned int refinement_cycle);
void set_boundary_values();
void compute_and_factorize_jacobian(
const Vector<double> &evaluation_point);
std::unique_ptr<SparseDirectUMFPACK> jacobian_matrix_factorization;
};
const ::parallel::distributed::Triangulation< dim, spacedim > * triangulation
Boundary condition
The classes implementing boundary values are a copy from step-15:
template <int dim>
class BoundaryValues :
public Function<dim>
{
public:
const unsigned int component = 0) const override;
};
template <int dim>
double BoundaryValues<dim>::value(
const Point<dim> &p,
const unsigned int ) const
{
}
virtual RangeNumberType value(const Point< dim > &p, const unsigned int component=0) const
static constexpr double PI
::VectorizedArray< Number, width > sin(const ::VectorizedArray< Number, width > &)
The MinimalSurfaceProblem class implementation
Constructor and set up functions
The following few functions are also essentially copies of what step-15 already does, and so there is little to discuss.
template <int dim>
MinimalSurfaceProblem<dim>::MinimalSurfaceProblem()
, fe(1)
{}
template <int dim>
void MinimalSurfaceProblem<dim>::setup_system(const bool initial_step)
{
if (initial_step)
{
dof_handler.distribute_dofs(fe);
current_solution.reinit(dof_handler.n_dofs());
hanging_node_constraints.clear();
hanging_node_constraints);
hanging_node_constraints.close();
}
hanging_node_constraints.condense(dsp);
sparsity_pattern.copy_from(dsp);
jacobian_matrix.reinit(sparsity_pattern);
jacobian_matrix_factorization.reset();
}
void make_hanging_node_constraints(const DoFHandler< dim, spacedim > &dof_handler, AffineConstraints< number > &constraints)
void make_sparsity_pattern(const DoFHandler< dim, spacedim > &dof_handler, SparsityPatternType &sparsity_pattern, const AffineConstraints< number > &constraints=AffineConstraints< number >(), const bool keep_constrained_dofs=true, const types::subdomain_id subdomain_id=numbers::invalid_subdomain_id)
Assembling and factorizing the Jacobian matrix
The following function is then responsible for assembling and factorizing the Jacobian matrix. The first half of the function is in essence the assemble_system() function of step-15, except that it does not deal with also forming a right hand side vector (i.e., the residual) since we do not always have to do these operations at the same time.
We put the whole assembly functionality into a code block enclosed by curly braces so that we can use a TimerOutput::Scope variable to measure how much time is spent in this code block, excluding everything that happens in this function after the matching closing brace }.
template <int dim>
void MinimalSurfaceProblem<dim>::compute_and_factorize_jacobian(
{
{
std::cout << " Computing Jacobian matrix" << std::endl;
jacobian_matrix = 0;
quadrature_formula,
const unsigned int dofs_per_cell = fe.n_dofs_per_cell();
const unsigned int n_q_points = quadrature_formula.size();
std::vector<Tensor<1, dim>> evaluation_point_gradients(n_q_points);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
for (const auto &cell : dof_handler.active_cell_iterators())
{
cell_matrix = 0;
fe_values.reinit(cell);
fe_values.get_function_gradients(evaluation_point,
evaluation_point_gradients);
for (unsigned int q = 0; q < n_q_points; ++q)
{
const double coeff =
1.0 /
std::sqrt(1 + evaluation_point_gradients[q] *
evaluation_point_gradients[q]);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
for (unsigned int j = 0; j < dofs_per_cell; ++j)
cell_matrix(i, j) +=
(((fe_values.shape_grad(i, q)
* coeff
* fe_values.shape_grad(j, q))
-
(fe_values.shape_grad(i, q)
* coeff * coeff * coeff
*
(fe_values.shape_grad(j, q)
* evaluation_point_gradients[q])
* evaluation_point_gradients[q]))
* fe_values.JxW(q));
}
}
cell->get_dof_indices(local_dof_indices);
hanging_node_constraints.distribute_local_to_global(cell_matrix,
local_dof_indices,
jacobian_matrix);
}
std::map<types::global_dof_index, double> boundary_values;
0,
boundary_values);
jacobian_matrix,
dummy_solution,
dummy_rhs);
}
@ update_JxW_values
Transformed quadrature weights.
@ update_gradients
Shape function gradients.
@ update_quadrature_points
Transformed quadrature points.
::VectorizedArray< Number, width > sqrt(const ::VectorizedArray< Number, width > &)
The second half of the function then deals with factorizing the so-computed matrix. To do this, we first create a new SparseDirectUMFPACK object and by assigning it to the member variable jacobian_matrix_factorization, we also destroy whatever object that pointer previously pointed to (if any). Then we tell the object to factorize the Jacobian.
As above, we enclose this block of code into curly braces and use a timer to assess how long this part of the program takes.
(Strictly speaking, we don't actually need the matrix any more after we are done here, and could throw the matrix object away. A code intended to be memory efficient would do this, and only create the matrix object in this function, rather than as a member variable of the surrounding class. We omit this step here because using the same coding style as in previous tutorial programs breeds familiarity with the common style and helps make these tutorial programs easier to read.)
{
std::cout << " Factorizing Jacobian matrix" << std::endl;
jacobian_matrix_factorization = std::make_unique<SparseDirectUMFPACK>();
jacobian_matrix_factorization->factorize(jacobian_matrix);
}
}
Computing the residual vector
The second part of what assemble_system() used to do in step-15 is computing the residual vector, i.e., the right hand side vector of the Newton linear systems. We have broken this out of the previous function, but the following function will be easy to understand if you understood what assemble_system() in step-15 did. Importantly, however, we need to compute the residual not linearized around the current solution vector, but whatever we get from KINSOL. This is necessary for operations such as line search where we want to know what the residual F(U^k + \alpha_k \delta
U^K) is for different values of \alpha_k; KINSOL in those cases simply gives us the argument to the function F and we then compute the residual F(\cdot) at this point.
The function prints the norm of the so-computed residual at the end as a way for us to follow along the progress of the program.
template <int dim>
void MinimalSurfaceProblem<dim>::compute_residual(
{
std::cout << " Computing residual vector..." << std::flush;
quadrature_formula,
const unsigned int dofs_per_cell = fe.n_dofs_per_cell();
const unsigned int n_q_points = quadrature_formula.size();
std::vector<Tensor<1, dim>> evaluation_point_gradients(n_q_points);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
for (const auto &cell : dof_handler.active_cell_iterators())
{
cell_residual = 0;
fe_values.reinit(cell);
fe_values.get_function_gradients(evaluation_point,
evaluation_point_gradients);
for (unsigned int q = 0; q < n_q_points; ++q)
{
const double coeff =
1.0 /
std::sqrt(1 + evaluation_point_gradients[q] *
evaluation_point_gradients[q]);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
cell_residual(i) =
(fe_values.shape_grad(i, q)
* coeff
* evaluation_point_gradients[q]
* fe_values.JxW(q));
}
cell->get_dof_indices(local_dof_indices);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
residual(local_dof_indices[i]) += cell_residual(i);
}
hanging_node_constraints.condense(residual);
residual(i) = 0;
residual(i) = 0;
std::cout <<
" norm=" << residual.
l2_norm() << std::endl;
}
real_type l2_norm() const
Solving linear systems with the Jacobian matrix
Next up is the function that implements the solution of a linear system with the Jacobian matrix. Since we have already factored the matrix when we built the matrix, solving a linear system comes down to applying the inverse matrix to the given right hand side vector: This is what the SparseDirectUMFPACK::vmult() function does that we use here. Following this, we have to make sure that we also address the values of hanging nodes in the solution vector, and this is done using AffineConstraints::distribute().
The function takes an additional, but unused, argument tolerance that indicates how accurately we have to solve the linear system. The meaning of this argument is discussed in the introduction in the context of the "Eisenstat Walker trick", but since we are using a direct rather than an iterative solver, we are not using this opportunity to solve linear systems only inexactly.
template <int dim>
const double )
{
std::cout << " Solving linear system" << std::endl;
jacobian_matrix_factorization->vmult(solution, rhs);
hanging_node_constraints.distribute(solution);
}
Refining the mesh, setting boundary values, and generating graphical output
The following three functions are again simply copies of the ones in step-15:
template <int dim>
void MinimalSurfaceProblem<dim>::refine_mesh()
{
dof_handler,
current_solution,
estimated_error_per_cell);
estimated_error_per_cell,
0.3,
0.03);
solution_transfer.prepare_for_coarsening_and_refinement(current_solution);
dof_handler.distribute_dofs(fe);
solution_transfer.interpolate(current_solution, tmp);
current_solution = std::move(tmp);
hanging_node_constraints.clear();
hanging_node_constraints);
hanging_node_constraints.close();
hanging_node_constraints.distribute(current_solution);
set_boundary_values();
setup_system(false);
}
template <int dim>
void MinimalSurfaceProblem<dim>::set_boundary_values()
{
std::map<types::global_dof_index, double> boundary_values;
0,
BoundaryValues<dim>(),
boundary_values);
for (const auto &boundary_value : boundary_values)
current_solution(boundary_value.first) = boundary_value.second;
hanging_node_constraints.distribute(current_solution);
}
template <int dim>
void MinimalSurfaceProblem<dim>::output_results(
const unsigned int refinement_cycle)
{
const std::string filename =
std::ofstream output(filename);
}
void attach_dof_handler(const DoFHandler< dim, spacedim > &)
void add_data_vector(const VectorType &data, const std::vector< std::string > &names, const DataVectorType type=type_automatic, const std::vector< DataComponentInterpretation::DataComponentInterpretation > &data_component_interpretation={})
virtual void build_patches(const unsigned int n_subdivisions=0)
static void estimate(const Mapping< dim, spacedim > &mapping, const DoFHandler< dim, spacedim > &dof, const Quadrature< dim - 1 > &quadrature, const std::map< types::boundary_id, const Function< spacedim, typename InputVector::value_type > * > &neumann_bc, const InputVector &solution, Vector< float > &error, const ComponentMask &component_mask=ComponentMask(), const Function< spacedim > *coefficients=nullptr, const unsigned int n_threads=numbers::invalid_unsigned_int, const types::subdomain_id subdomain_id=numbers::invalid_subdomain_id, const types::material_id material_id=numbers::invalid_material_id, const Strategy strategy=cell_diameter_over_24)
void write_vtu(std::ostream &out) const
void refine_and_coarsen_fixed_number(Triangulation< dim, spacedim > &triangulation, const Vector< Number > &criteria, const double top_fraction_of_cells, const double bottom_fraction_of_cells, const unsigned int max_n_cells=std::numeric_limits< unsigned int >::max())
std::string int_to_string(const unsigned int value, const unsigned int digits=numbers::invalid_unsigned_int)
The run() function and the overall logic of the program
The only function that really is interesting in this program is the one that drives the overall algorithm of starting on a coarse mesh, doing some mesh refinement cycles, and on each mesh using KINSOL to find the solution of the nonlinear algebraic equation we obtain from discretization on this mesh. The refine_mesh() function above makes sure that the solution on one mesh is used as the starting guess on the next mesh. We also use a TimerOutput object to measure how much time every operation on each mesh costs, and reset the timer at the beginning of each cycle.
As discussed in the introduction, it is not necessary to solve problems on coarse meshes particularly accurately since these will only solve as starting guesses for the next mesh. As a consequence, we will use a target tolerance of \tau=10^{-3} \frac{1}{10^k} for the kth mesh refinement cycle.
All of this is encoded in the first part of this function:
template <int dim>
void MinimalSurfaceProblem<dim>::run()
{
setup_system(true);
set_boundary_values();
for (unsigned int refinement_cycle = 0; refinement_cycle < 6;
++refinement_cycle)
{
computing_timer.reset();
std::cout << "Mesh refinement step " << refinement_cycle << std::endl;
if (refinement_cycle != 0)
refine_mesh();
const double target_tolerance = 1e-3 *
std::pow(0.1, refinement_cycle);
std::cout << " Target_tolerance: " << target_tolerance << std::endl
<< std::endl;
void hyper_ball(Triangulation< dim > &tria, const Point< dim > ¢er=Point< dim >(), const double radius=1., const bool attach_spherical_manifold_on_boundary_cells=false)
::VectorizedArray< Number, width > pow(const ::VectorizedArray< Number, width > &, const Number p)
This is where the fun starts. At the top we create the KINSOL solver object and feed it with an object that encodes a number of additional specifics (of which we only change the nonlinear tolerance we want to reach; but you might want to look into what other members the SUNDIALS::KINSOL::AdditionalData class has and play with them).
{
additional_data;
additional_data.function_tolerance = target_tolerance;
Then we have to describe the operations that were already mentioned in the introduction. In essence, we have to teach KINSOL how to (i) resize a vector to the correct size, (ii) compute the residual vector, (iii) compute the Jacobian matrix (during which we also compute its factorization), and (iv) solve a linear system with the Jacobian.
All four of these operations are represented by member variables of the SUNDIALS::KINSOL class that are of type std::function, i.e., they are objects to which we can assign a pointer to a function or, as we do here, a "lambda function" that takes the appropriate arguments and returns the appropriate information. By convention, KINSOL wants that functions doing something nontrivial return an integer where zero indicates success. It turns out that we can do all of this in just 25 lines of code.
(If you're not familiar what "lambda functions" are, take a look at step-12 or at the wikipedia page on the subject. The idea of lambda functions is that one wants to define a function with a certain set of arguments, but (i) not make it a named functions because, typically, the function is used in only one place and it seems unnecessary to give it a global name; and (ii) that the function has access to some of the variables that exist at the place where it is defined, including member variables. The syntax of lambda functions is awkward, but ultimately quite useful.)
At the very end of the code block we then tell KINSOL to go to work and solve our problem. The member functions called from the 'residual', 'setup_jacobian', and 'solve_jacobian_system' functions will then print output to screen that allows us to follow along with the progress of the program.
x.reinit(dof_handler.n_dofs());
};
nonlinear_solver.residual =
compute_residual(evaluation_point, residual);
return 0;
};
nonlinear_solver.setup_jacobian =
compute_and_factorize_jacobian(current_u);
return 0;
};
const double tolerance) {
this->solve(rhs, dst, tolerance);
return 0;
};
nonlinear_solver.solve(current_solution);
}
The rest is then just house-keeping: Writing data to a file for visualizing, and showing a summary of the timing collected so that we can interpret how long each operation has taken, how often it was executed, etc:
output_results(refinement_cycle);
computing_timer.print_summary();
std::cout << std::endl;
}
}
}
int main()
{
try
{
using namespace Step77;
MinimalSurfaceProblem<2> laplace_problem_2d;
laplace_problem_2d.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
Results
When running the program, you get output that looks like this:
Mesh refinement step 0
Target_tolerance: 0.001
Computing residual vector... norm=0.231202
Computing Jacobian matrix
Factorizing Jacobian matrix
Solving linear system
Computing residual vector... norm=0.231202
Computing residual vector... norm=0.171585
Solving linear system
Computing residual vector... norm=0.171585
Computing residual vector... norm=0.127245
Computing residual vector... norm=0.0796471
Solving linear system
Computing residual vector... norm=0.0796471
Computing residual vector... norm=0.0625301
Solving linear system
Computing residual vector... norm=0.0625301
Computing residual vector... norm=0.0498864
Solving linear system
Computing residual vector... norm=0.0498864
Computing residual vector... norm=0.0407765
Solving linear system
Computing residual vector... norm=0.0407765
Computing residual vector... norm=0.0341589
Solving linear system
Computing residual vector... norm=0.0341589
Computing residual vector... norm=0.0292867
Solving linear system
Computing residual vector... norm=0.0292867
Computing residual vector... norm=0.0256309
Computing residual vector... norm=0.0223448
Solving linear system
Computing residual vector... norm=0.0223448
Computing residual vector... norm=0.0202797
Computing residual vector... norm=0.0183817
Solving linear system
Computing residual vector... norm=0.0183817
Computing residual vector... norm=0.0170464
Computing residual vector... norm=0.0157967
Computing Jacobian matrix
Factorizing Jacobian matrix
Solving linear system
Computing residual vector... norm=0.0157967
Computing residual vector... norm=0.0141572
Computing residual vector... norm=0.012657
Solving linear system
Computing residual vector... norm=0.012657
Computing residual vector... norm=0.0116863
Computing residual vector... norm=0.0107696
Solving linear system
Computing residual vector... norm=0.0107696
Computing residual vector... norm=0.0100986
Computing residual vector... norm=0.00944829
Computing residual vector... norm=0.00822576
Solving linear system
Computing residual vector... norm=0.00822576
Computing residual vector... norm=0.00781983
Computing residual vector... norm=0.00741619
Computing residual vector... norm=0.00661792
Solving linear system
Computing residual vector... norm=0.00661792
Computing residual vector... norm=0.00630571
Computing residual vector... norm=0.00599457
Computing residual vector... norm=0.00537663
Solving linear system
Computing residual vector... norm=0.00537663
Computing residual vector... norm=0.00512813
Computing residual vector... norm=0.00488033
Computing residual vector... norm=0.00438751
Computing residual vector... norm=0.00342052
Solving linear system
Computing residual vector... norm=0.00342052
Computing residual vector... norm=0.00326581
Computing residual vector... norm=0.00311176
Computing residual vector... norm=0.00280617
Computing residual vector... norm=0.00220992
Solving linear system
Computing residual vector... norm=0.00220992
Computing residual vector... norm=0.00209976
Computing residual vector... norm=0.00199943
Solving linear system
Computing residual vector... norm=0.00199942
Computing residual vector... norm=0.00190953
Computing residual vector... norm=0.00182005
Computing residual vector... norm=0.00164259
Computing residual vector... norm=0.00129652
+---------------------------------------------+------------+------------+
| Total wallclock time elapsed since start | 0.192s | |
| | | |
| Section | no. calls | wall time | % of total |
+---------------------------------+-----------+------------+------------+
| assembling the Jacobian | 2 | 0.0141s | 7.4% |
| assembling the residual | 61 | 0.168s | 88% |
| factorizing the Jacobian | 2 | 0.0016s | 0.83% |
| graphical output | 1 | 0.00385s | 2% |
| linear system solve | 19 | 0.0013s | 0.68% |
+---------------------------------+-----------+------------+------------+
Mesh refinement step 1
Target_tolerance: 0.0001
Computing residual vector... norm=0.0883422
Computing Jacobian matrix
Factorizing Jacobian matrix
Solving linear system
Computing residual vector... norm=0.0883422
Computing residual vector... norm=0.0607066
Solving linear system
Computing residual vector... norm=0.0607066
Computing residual vector... norm=0.0437266
Solving linear system
Computing residual vector... norm=0.0437266
Computing residual vector... norm=0.0327999
Solving linear system
Computing residual vector... norm=0.0327999
Computing residual vector... norm=0.0255418
Solving linear system
Computing residual vector... norm=0.0255417
Computing residual vector... norm=0.0206042
Solving linear system
Computing residual vector... norm=0.0206042
Computing residual vector... norm=0.0171602
Solving linear system
Computing residual vector... norm=0.0171602
Computing residual vector... norm=0.014689
Solving linear system
[...]
The way this should be interpreted is most easily explained by looking at the first few lines of the output on the first mesh:
Mesh refinement step 0
Mesh refinement step 0
Target_tolerance: 0.001
Computing residual vector... norm=0.231202
Computing Jacobian matrix
Factorizing Jacobian matrix
Solving linear system
Computing residual vector... norm=0.231202
Computing residual vector... norm=0.171585
Solving linear system
Computing residual vector... norm=0.171585
Computing residual vector... norm=0.127245
Computing residual vector... norm=0.0796471
Solving linear system
Computing residual vector... norm=0.0796471
...
What is happening is this:
- In the first residual computation, KINSOL computes the residual to see whether the desired tolerance has been reached. The answer is no, so it requests the user program to compute the Jacobian matrix (and the function then also factorizes the matrix via SparseDirectUMFPACK).
- KINSOL then instructs us to solve a linear system of the form J_k \, \delta U_k = -F_k with this matrix and the previously computed residual vector.
- It is then time to determine how far we want to go in this direction, i.e., do line search. To this end, KINSOL requires us to compute the residual vector F(U_k + \alpha_k \delta U_k) for different step lengths \alpha_k. For the first step above, it finds an acceptable \alpha_k after two tries, the second time around it takes three tries.
- Having found a suitable updated solution U_{k+1}, the process is repeated except now KINSOL is happy with the current Jacobian matrix and does not instruct us to re-build the matrix and its factorization, and instead asks us to solve a linear system with that same matrix.
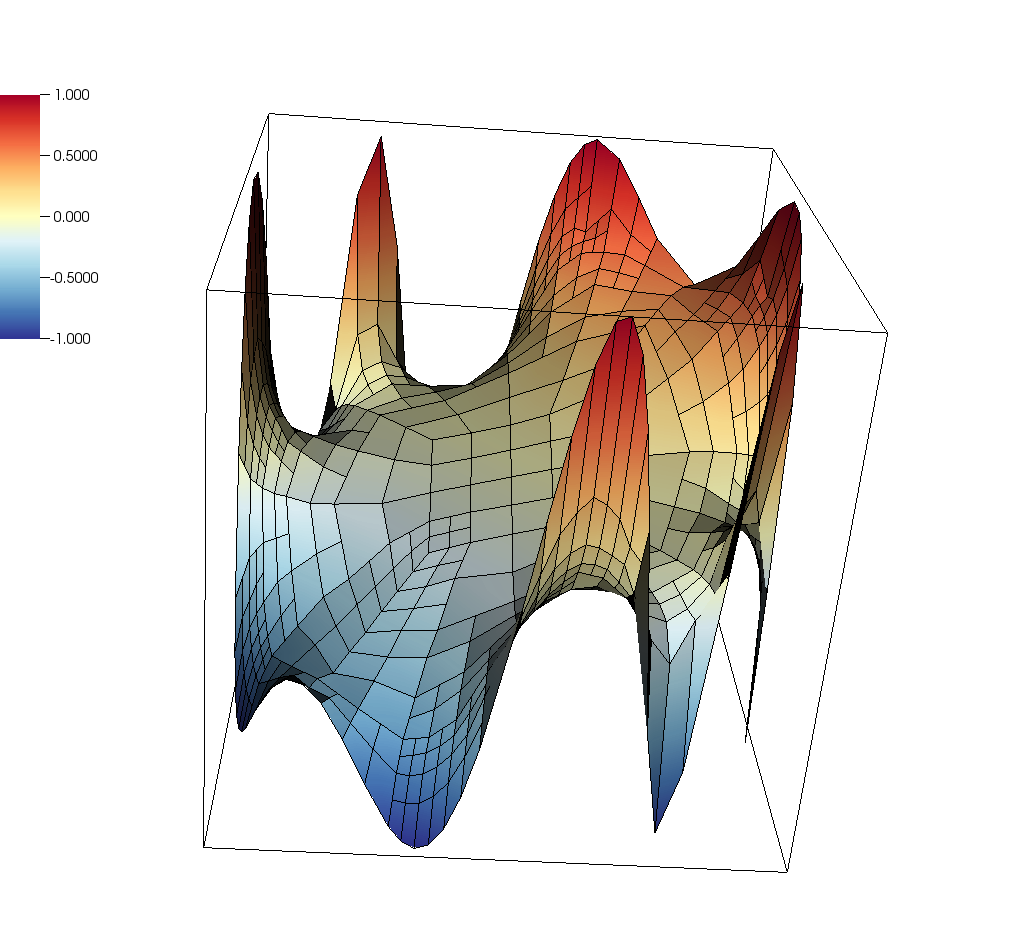
The program also writes the solution to a VTU file at the end of each mesh refinement cycle, and it looks as follows:
The key takeaway messages of this program are the following:
- The solution is the same as the one we computed in step-15, i.e., the interfaces to SUNDIALS' KINSOL package really did what they were supposed to do. This should not come as a surprise, but the important point is that we don't have to spend the time implementing the complex algorithms that underlie advanced nonlinear solvers ourselves.
- KINSOL is able to avoid all sorts of operations such as rebuilding the Jacobian matrix when that is not actually necessary. Comparing the number of linear solves in the output above with the number of times we rebuild the Jacobian and compute its factorization should make it clear that this leads to very substantial savings in terms of compute times, without us having to implement the intricacies of algorithms that determine when we need to rebuild this information.
Possibilities for extensions
For all but the small problems we consider here, a sparse direct solver requires too much time and memory – we need an iterative solver like we use in many other programs. The trade-off between constructing an expensive preconditioner (say, a geometric or algebraic multigrid method) is different in the current case, however: Since we can re-use the same matrix for numerous linear solves, we can do the same for the preconditioner and putting more work into building a good preconditioner can more easily be justified than if we used it only for a single linear solve as one does for many other situations.
But iterative solvers also afford other opportunities. For example (and as discussed briefly in the introduction), we may not need to solve to very high accuracy (small tolerances) in early nonlinear iterations as long as we are still far away from the actual solution. This was the basis of the Eisenstat-Walker trick mentioned there.
KINSOL provides the function that does the linear solution with a target tolerance that needs to be reached. We ignore it in the program above because the direct solver we use does not need a tolerance and instead solves the linear system exactly (up to round-off, of course), but iterative solvers could make use of this kind of information – and, in fact, should.
The plain program
#include <fstream>
#include <iostream>
namespace Step77
{
template <int dim>
class MinimalSurfaceProblem
{
public:
MinimalSurfaceProblem();
void run();
private:
void setup_system(const bool initial_step);
const double tolerance);
void refine_mesh();
void output_results(const unsigned int refinement_cycle);
void set_boundary_values();
void compute_and_factorize_jacobian(
const Vector<double> &evaluation_point);
std::unique_ptr<SparseDirectUMFPACK> jacobian_matrix_factorization;
};
template <int dim>
class BoundaryValues :
public Function<dim>
{
public:
const unsigned int component = 0) const override;
};
template <int dim>
double BoundaryValues<dim>::value(
const Point<dim> &p,
const unsigned int ) const
{
}
template <int dim>
MinimalSurfaceProblem<dim>::MinimalSurfaceProblem()
, fe(1)
{}
template <int dim>
void MinimalSurfaceProblem<dim>::setup_system(const bool initial_step)
{
if (initial_step)
{
dof_handler.distribute_dofs(fe);
current_solution.reinit(dof_handler.n_dofs());
hanging_node_constraints.clear();
hanging_node_constraints);
hanging_node_constraints.close();
}
hanging_node_constraints.condense(dsp);
sparsity_pattern.copy_from(dsp);
jacobian_matrix.reinit(sparsity_pattern);
jacobian_matrix_factorization.reset();
}
template <int dim>
void MinimalSurfaceProblem<dim>::compute_and_factorize_jacobian(
{
{
std::cout << " Computing Jacobian matrix" << std::endl;
jacobian_matrix = 0;
quadrature_formula,
const unsigned int dofs_per_cell = fe.n_dofs_per_cell();
const unsigned int n_q_points = quadrature_formula.size();
std::vector<Tensor<1, dim>> evaluation_point_gradients(n_q_points);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
fe_values.get_function_gradients(evaluation_point,
evaluation_point_gradients);
for (unsigned int q = 0; q < n_q_points; ++q)
{
const double coeff =
1.0 /
std::sqrt(1 + evaluation_point_gradients[q] *
evaluation_point_gradients[q]);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
for (unsigned int j = 0; j < dofs_per_cell; ++j)
(((fe_values.shape_grad(i, q)
* coeff
* fe_values.shape_grad(j, q))
-
(fe_values.shape_grad(i, q)
* coeff * coeff * coeff
*
(fe_values.shape_grad(j, q)
* evaluation_point_gradients[q])
* evaluation_point_gradients[q]))
* fe_values.JxW(q));
}
}
cell->get_dof_indices(local_dof_indices);
hanging_node_constraints.distribute_local_to_global(cell_matrix,
local_dof_indices,
jacobian_matrix);
}
std::map<types::global_dof_index, double> boundary_values;
0,
boundary_values);
jacobian_matrix,
dummy_solution,
dummy_rhs);
}
{
std::cout << " Factorizing Jacobian matrix" << std::endl;
jacobian_matrix_factorization = std::make_unique<SparseDirectUMFPACK>();
jacobian_matrix_factorization->factorize(jacobian_matrix);
}
}
template <int dim>
void MinimalSurfaceProblem<dim>::compute_residual(
{
std::cout << " Computing residual vector..." << std::flush;
quadrature_formula,
const unsigned int dofs_per_cell = fe.n_dofs_per_cell();
const unsigned int n_q_points = quadrature_formula.size();
std::vector<Tensor<1, dim>> evaluation_point_gradients(n_q_points);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
fe_values.get_function_gradients(evaluation_point,
evaluation_point_gradients);
for (unsigned int q = 0; q < n_q_points; ++q)
{
const double coeff =
1.0 /
std::sqrt(1 + evaluation_point_gradients[q] *
evaluation_point_gradients[q]);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
(fe_values.shape_grad(i, q)
* coeff
* evaluation_point_gradients[q]
* fe_values.JxW(q));
}
cell->get_dof_indices(local_dof_indices);
for (unsigned int i = 0; i < dofs_per_cell; ++i)
}
hanging_node_constraints.condense(residual);
residual(i) = 0;
residual(i) = 0;
std::cout <<
" norm=" << residual.
l2_norm() << std::endl;
}
template <int dim>
const double )
{
std::cout << " Solving linear system" << std::endl;
jacobian_matrix_factorization->vmult(solution, rhs);
hanging_node_constraints.distribute(solution);
}
template <int dim>
void MinimalSurfaceProblem<dim>::refine_mesh()
{
dof_handler,
current_solution,
estimated_error_per_cell);
estimated_error_per_cell,
0.3,
0.03);
solution_transfer.prepare_for_coarsening_and_refinement(current_solution);
dof_handler.distribute_dofs(fe);
solution_transfer.interpolate(current_solution, tmp);
current_solution = std::move(tmp);
hanging_node_constraints.clear();
hanging_node_constraints);
hanging_node_constraints.close();
hanging_node_constraints.distribute(current_solution);
set_boundary_values();
setup_system(false);
}
template <int dim>
void MinimalSurfaceProblem<dim>::set_boundary_values()
{
std::map<types::global_dof_index, double> boundary_values;
0,
BoundaryValues<dim>(),
boundary_values);
for (const auto &boundary_value : boundary_values)
current_solution(boundary_value.first) = boundary_value.second;
hanging_node_constraints.distribute(current_solution);
}
template <int dim>
void MinimalSurfaceProblem<dim>::output_results(
const unsigned int refinement_cycle)
{
const std::string filename =
std::ofstream output(filename);
}
template <int dim>
void MinimalSurfaceProblem<dim>::run()
{
setup_system(true);
set_boundary_values();
for (unsigned int refinement_cycle = 0; refinement_cycle < 6;
++refinement_cycle)
{
computing_timer.reset();
std::cout << "Mesh refinement step " << refinement_cycle << std::endl;
if (refinement_cycle != 0)
refine_mesh();
const double target_tolerance = 1
e-3 *
std::pow(0.1, refinement_cycle);
std::cout << " Target_tolerance: " << target_tolerance << std::endl
<< std::endl;
{
additional_data;
additional_data.function_tolerance = target_tolerance;
x.reinit(dof_handler.n_dofs());
};
nonlinear_solver.residual =
compute_residual(evaluation_point, residual);
return 0;
};
nonlinear_solver.setup_jacobian =
compute_and_factorize_jacobian(current_u);
return 0;
};
const double tolerance) {
this->solve(rhs, dst, tolerance);
return 0;
};
nonlinear_solver.solve(current_solution);
}
output_results(refinement_cycle);
computing_timer.print_summary();
std::cout << std::endl;
}
}
}
int main()
{
try
{
using namespace Step77;
MinimalSurfaceProblem<2> laplace_problem_2d;
laplace_problem_2d.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
void cell_matrix(FullMatrix< double > &M, const FEValuesBase< dim > &fe, const FEValuesBase< dim > &fetest, const ArrayView< const std::vector< double > > &velocity, const double factor=1.)
void cell_residual(Vector< double > &result, const FEValuesBase< dim > &fe, const std::vector< Tensor< 1, dim > > &input, const ArrayView< const std::vector< double > > &velocity, double factor=1.)
SymmetricTensor< 2, dim, Number > e(const Tensor< 2, dim, Number > &F)