CGALWrappers Namespace Reference

Classes
struct	AdditionalData
struct	AdditionalData< 2 >

Typedefs
using	ConcurrencyTag = CGAL::Sequential_tag

Enumerations
enum class	FacetTopology { facet_vertices_on_surface = CGAL::FACET_VERTICES_ON_SURFACE , facet_vertices_on_same_surface_patch , facet_vertices_on_same_surface_patch_with_adjacency_check }
enum class	BooleanOperation { compute_corefinement = 1 << 0 , compute_difference = 1 << 1 , compute_intersection = 1 << 2 , compute_union = 1 << 3 }

Functions
template<typename CGALPointType , int dim, int spacedim>
void	dealii_cell_to_cgal_surface_mesh (const typename ::Triangulation< dim, spacedim >::cell_iterator &cell, const ::Mapping< dim, spacedim > &mapping, CGAL::Surface_mesh< CGALPointType > &mesh)
template<typename CGALPointType , int dim, int spacedim>
void	dealii_tria_to_cgal_surface_mesh (const ::Triangulation< dim, spacedim > &triangulation, CGAL::Surface_mesh< CGALPointType > &mesh)
template<typename C3t3 >
void	cgal_surface_mesh_to_cgal_triangulation (CGAL::Surface_mesh< typename C3t3::Point::Point > &surface_mesh, C3t3 &triangulation, const AdditionalData< 3 > &data=AdditionalData< 3 >{})
template<typename CGALPointType >
void	compute_boolean_operation (const CGAL::Surface_mesh< CGALPointType > &surface_mesh_1, const CGAL::Surface_mesh< CGALPointType > &surface_mesh_2, const BooleanOperation &boolean_operation, CGAL::Surface_mesh< CGALPointType > &output_surface_mesh)
template<typename CGALTriangulationType >
::Quadrature< CGALTriangulationType::Point::Ambient_dimension::value >	compute_quadrature (const CGALTriangulationType &tria, const unsigned int degree)
template<int dim0, int dim1, int spacedim>
::Quadrature< spacedim >	compute_quadrature_on_boolean_operation (const typename ::Triangulation< dim0, spacedim >::cell_iterator &cell0, const typename ::Triangulation< dim1, spacedim >::cell_iterator &cell1, const unsigned int degree, const BooleanOperation &bool_op, const Mapping< dim0, spacedim > &mapping0=(::ReferenceCells::get_hypercube< dim0 >() .template get_default_linear_mapping< dim0, spacedim >()), const Mapping< dim1, spacedim > &mapping1=(::ReferenceCells::get_hypercube< dim1 >() .template get_default_linear_mapping< dim1, spacedim >()))
template<int dim0, int dim1, int spacedim>
::Quadrature< spacedim >	compute_quadrature_on_intersection (const typename ::Triangulation< dim0, spacedim >::cell_iterator &cell0, const typename ::Triangulation< dim1, spacedim >::cell_iterator &cell1, const unsigned int degree, const Mapping< dim0, spacedim > &mapping0, const Mapping< dim1, spacedim > &mapping1)
template<typename CGALPointType >
void	remesh_surface (CGAL::Surface_mesh< CGALPointType > &surface_mesh, const AdditionalData< 3 > &data=AdditionalData< 3 >{})

Detailed Description

Interface to the Computational Geometry Algorithm Library (CGAL).

CGAL is a software project that provides easy access to efficient and reliable geometric algorithms. The library offers data structures and algorithms like triangulations, Voronoi diagrams, Boolean operations on polygons and polyhedra, point set processing, arrangements of curves, surface and volume mesh generation, geometry processing, alpha shapes, convex hull algorithms, shape reconstruction, AABB and KD trees...

You can learn more about the CGAL library at https://www.cgal.org/

Typedef Documentation

ConcurrencyTag

using CGALWrappers::ConcurrencyTag = typedef CGAL::Sequential_tag

Definition at line 79 of file utilities.h.

Enumeration Type Documentation

FacetTopology

enum class CGALWrappers::FacetTopology

strong

Enumerator
facet_vertices_on_surface	Each vertex of the facet have to be on the surface, on a curve, or on a corner.
facet_vertices_on_same_surface_patch	The three vertices of a facet belonging to a surface patch s have to be on the same surface patch s, on a curve or on a corner.
facet_vertices_on_same_surface_patch_with_adjacency_check	The three vertices of a facet belonging to a surface patch s have to be on the same surface patch s, or on a curve incident to the surface patch s or on a corner incident to the surface patch s.

Definition at line 31 of file additional_data.h.

BooleanOperation

enum class CGALWrappers::BooleanOperation

strong

An enum type given to functions that compute boolean operations between geometrical objects, defined by triangulated surface grids.

As an example, we show all supported boolean operations applied to a hedra (the union of two pyramids) and a cube.

Enumerator
compute_corefinement	Given two triangulated surfaces, refine the first surface until its intersection with the second surface is captured exactly by the refinement
compute_difference	Given two triangulated surfaces, compute the boolean difference of the first surface minus the second surface
compute_intersection	Given two triangulated surfaces, compute their intersection
compute_union	Given two triangulated surfaces, compute their union

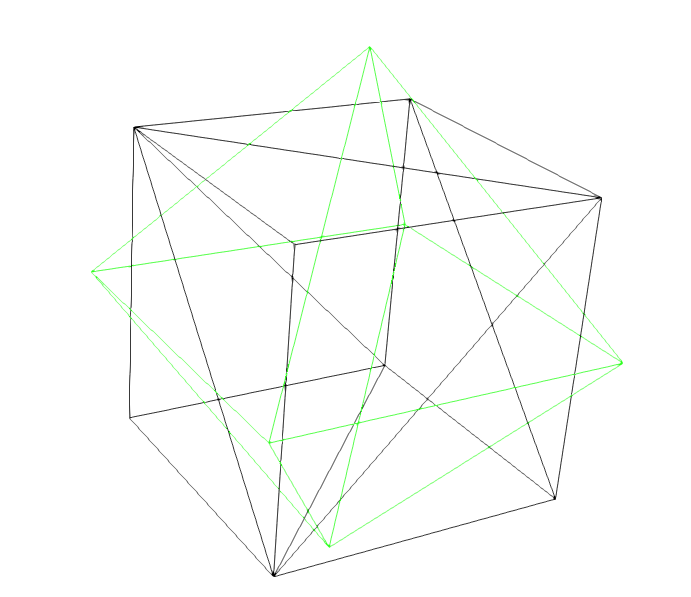
Definition at line 91 of file utilities.h.

Function Documentation

dealii_cell_to_cgal_surface_mesh()

template<typename CGALPointType , int dim, int spacedim>

void CGALWrappers::dealii_cell_to_cgal_surface_mesh	(	const typename ::Triangulation< dim, spacedim >::cell_iterator &	cell,
		const ::Mapping< dim, spacedim > &	mapping,
		CGAL::Surface_mesh< CGALPointType > &	mesh
	)

Build a CGAL::Surface_mesh from a deal.II cell.

The class Surface_mesh implements a halfedge data structure and can be used to represent polyhedral surfaces. It is an edge-centered data structure capable of maintaining incidence information of vertices, edges, and faces. Each edge is represented by two halfedges with opposite orientation. The orientation of a face is chosen so that the halfedges around a face are oriented counterclockwise.

More information on this class is available at https://doc.cgal.org/latest/Surface_mesh/index.html

The function will throw an exception in dimension one. In dimension two, it generates a surface mesh of the quadrilateral cell or of the triangle cell, while in dimension three it will generate the surface mesh of the cell, i.e., a polyhedral mesh containing the faces of the input cell.

The generated mesh is useful when performing geometric operations using CGAL::Polygon_mesh_processing, i.e., to compute boolean operations on cells, splitting, cutting, slicing, etc.

For examples on how to use the resulting CGAL::Surface_mesh see https://doc.cgal.org/latest/Polygon_mesh_processing/

Parameters

[in]	cell	The input deal.II cell iterator
[in]	mapping	The mapping used to map the vertices of the cell
[out]	mesh	The output CGAL::Surface_mesh

dealii_tria_to_cgal_surface_mesh()

template<typename CGALPointType , int dim, int spacedim>

void CGALWrappers::dealii_tria_to_cgal_surface_mesh	(	const ::Triangulation< dim, spacedim > &	triangulation,
		CGAL::Surface_mesh< CGALPointType > &	mesh
	)

Convert a deal.II triangulation to a CGAL::Surface_mesh. The output depends on the intrinsic dimension of the input deal.II triangulation.

In 2D, i.e. with a Triangulation<2> or a Triangulation<2,3>, the output is the CGAL::Surface_mesh describing the whole triangulation.

In 3D, the boundary the of the deal.II Triangulation is converted to a CGAL::Surface_mesh by looping over all the boundary faces.

Parameters

[in]	triangulation	The input deal.II triangulation.
[out]	mesh	The output CGAL::Surface_mesh.

cgal_surface_mesh_to_cgal_triangulation()

template<typename C3t3 >

void CGALWrappers::cgal_surface_mesh_to_cgal_triangulation	(	CGAL::Surface_mesh< typename C3t3::Point::Point > &	surface_mesh,
		C3t3 &	triangulation,
		const AdditionalData< 3 > &	data = AdditionalData< 3 >{}
	)

Given a closed CGAL::Surface_mesh, this function fills the region bounded by the surface with tets.

Parameters

[in]	surface_mesh	The (closed) surface mesh bounding the volume that has to be filled.
[out]	triangulation	The output triangulation filled with tetrahedra.
[in]	data	AdditionalData object to pass to the CGAL::make_mesh_3 function. See the documentation of that struct for a description of those parameters.

compute_boolean_operation()

template<typename CGALPointType >

void CGALWrappers::compute_boolean_operation	(	const CGAL::Surface_mesh< CGALPointType > &	surface_mesh_1,
		const CGAL::Surface_mesh< CGALPointType > &	surface_mesh_2,
		const BooleanOperation &	boolean_operation,
		CGAL::Surface_mesh< CGALPointType > &	output_surface_mesh
	)

Given two triangulated surface meshes that bound two volumes, execute a boolean operation on them, and store the result in a third surface mesh.

Quoting from CGAL documentation (https://doc.cgal.org/latest/Polygon_mesh_processing/index.html#title14):

‍Given a closed triangulated surface mesh, each connected component splits the 3D space into two subspaces. The vertex sequence of each face of a component is seen either clockwise or counterclockwise from these two subspaces. The subspace that sees the sequence clockwise (resp. counterclockwise) is on the negative (resp. positive) side of the component.

‍Given a closed triangulated surface mesh surface with no self-intersections, we say that surface bounds a volume if each subspace lies exclusively on the positive (or negative) side of all the incident connected components of surface. The volume bounded by surface is the union of all subspaces that are on negative sides of their incident connected components of surface.

‍There is no restriction on the topology of the input volumes. However, there are some requirements on the input to guarantee that the operation is possible. First, the input meshes must not self-intersect. Second, the operation is possible only if the output can be bounded by a manifold triangulated surface mesh. In particular this means that the output volume has no part with zero thickness. Mathematically speaking, the intersection with an infinitesimally small ball centered in the output volume is a topological ball. At the surface level this means that no non-manifold vertex or edge is allowed in the output. For example, it is not possible to compute the union of two cubes that are disjoint but sharing an edge.

See BooleanOperation for a list of available operations, with the corresponding examples.

Parameters

[in]	surface_mesh_1	The first surface mesh.
[in]	surface_mesh_2	The second surface mesh.
[in]	boolean_operation	See BooleanOperation for the list of the allowed operations.
[out]	output_surface_mesh	The surface mesh with the result of the boolean operation.

compute_quadrature()

template<typename CGALTriangulationType >

::Quadrature< CGALTriangulationType::Point::Ambient_dimension::value > CGALWrappers::compute_quadrature	(	const CGALTriangulationType &	tria,
		const unsigned int	degree
	)

Given a CGAL Triangulation describing a polyhedral region, create a Quadrature rule to integrate over the polygon by looping through all the vertices and exploiting QGaussSimplex.

Parameters

[in]	tria	The CGAL triangulation object describing the polyhedral region.
[in]	degree	Desired degree of the Quadrature rule on each element of the polyhedral.

Returns

A global Quadrature rule that allows to integrate over the polyhedron.

compute_quadrature_on_boolean_operation()

template<int dim0, int dim1, int spacedim>

::Quadrature< spacedim > CGALWrappers::compute_quadrature_on_boolean_operation	(	const typename ::Triangulation< dim0, spacedim >::cell_iterator &	cell0,
		const typename ::Triangulation< dim1, spacedim >::cell_iterator &	cell1,
		const unsigned int	degree,
		const BooleanOperation &	bool_op,
		const Mapping< dim0, spacedim > &	mapping0 = (::ReferenceCells::get_hypercube< dim0 >() .template get_default_linear_mapping< dim0, spacedim >()),
		const Mapping< dim1, spacedim > &	mapping1 = (::ReferenceCells::get_hypercube< dim1 >() .template get_default_linear_mapping< dim1, spacedim >())
	)

Compute a Quadrature formula over the polygonal/polyhedral region described by a BooleanOperation between two deal.II cell_iterator objects. The degree of the Quadrature rule is specified by the argument degree. This function splits the polygon/polyhedron into simplices and collects QGaussSimplex quadrature rules.

Parameters

[in]	cell0	A cell_iterator to the first deal.II cell.
[in]	cell1	A cell_iterator to the second deal.II cell.
[in]	degree	The degree of accuracy you wish to get for the global quadrature formula.
[in]	bool_op	The BooleanOperation to be performed.
[in]	mapping0	Mapping object for the first cell.
[in]	mapping1	Mapping object for the first cell.

Returns

[out] Quadrature<spacedim> The global quadrature rule on the polygon/polyhedron.

compute_quadrature_on_intersection()

template<int dim0, int dim1, int spacedim>

::Quadrature< spacedim > CGALWrappers::compute_quadrature_on_intersection	(	const typename ::Triangulation< dim0, spacedim >::cell_iterator &	cell0,
		const typename ::Triangulation< dim1, spacedim >::cell_iterator &	cell1,
		const unsigned int	degree,
		const Mapping< dim0, spacedim > &	mapping0,
		const Mapping< dim1, spacedim > &	mapping1
	)

A specialization of the function above when the BooleanOperation is an intersection. The rationale behind this specialization is that deal.II affine cells are convex sets, and as the intersection of convex sets is itself convex, this function internally exploits this to use a cheaper way to mesh the inside.

Parameters

[in]	cell0	A cell_iterator to the first deal.II cell.
[in]	cell1	A cell_iterator to the second deal.II cell.
[in]	mapping0	Mapping object for the first cell.
[in]	mapping1	Mapping object for the first cell.
[in]	degree	The degree of accuracy you wish to get for the global quadrature formula.

Returns

[out] Quadrature<spacedim> The global quadrature rule on the polygon/polyhedron.

remesh_surface()

template<typename CGALPointType >

void CGALWrappers::remesh_surface	(	CGAL::Surface_mesh< CGALPointType > &	surface_mesh,
		const AdditionalData< 3 > &	data = AdditionalData< 3 >{}
	)

Remesh a CGAL::Surface_mesh.

If the domain has 1-dimensional exposed features, the criteria includes a sizing field to guide the sampling of 1-dimensional features with protecting balls centers.

• CGAL::parameters::edge_size.

This utility should be exploited to improve the quality of a mesh coming from boolean operations. As an example, consider two CGAL::Surface_mesh objects describing two hyper_spheres that intersect non-trivially. After computing their corefinement and union with compute_boolean_operation(), the resulting mesh is the following:

Clearly, elements (triangles) like the ones arising along the intersection of the two spheres should be avoided as they're quite degenerate and would decrease the accuracy of the results. A call to the present function will try to remesh the surface, according to the given named parameters, to improve its quality. In the present case, the result is the following:

Parameters

	surface_mesh	The input CGAL::Surface_mesh.
[in]	data	AdditionalData object to pass to the CGAL::make_mesh_3 function. See the documentation of that struct for a description of those parameters.