This program was contributed by Manuel Quezada de Luna <manuel.quezada.dl@gmail.com>.
It comes without any warranty or support by its authors or the authors of deal.II.
This program is part of the deal.II code gallery and consists of the following files (click to inspect):
Pictures from this code gallery program
Annotated version of Readme.md
Two Phase Flow
General description of the problem
We consider the problem of two-phase incompressible flow. We start with an initial state of two phases (fluids) that define density and viscosity fields. Using these fields we solve the incompressible Navier-Stokes equations to obtain a velocity field.
We use the initial state to define a representation of the interface via a Level Set function \(\phi\in[-1, 1]\). The zero level set \(\{\phi=0\}\) defines the interface of the phases. Positive values of the level set function represent water while negative values represent air.
Using the velocity field from the Navier-Stokes equations we transport the level set function. To do this we assume the velocity is divergence free and write the transport equation in conservation form.
Using the advected level set function we reconstruct density and viscosity fields. We repeat the process until the final desired time.
The Navier-Stokes equations are solved using a projection scheme based on [1]. To solve the level set we use continuous Galerkin Finite Elements with high-order stabilization based on the entropy residual of the solution [2] and artificial compression inspired by [3] and [4].
General description of the code
Driver code: MultiPhase
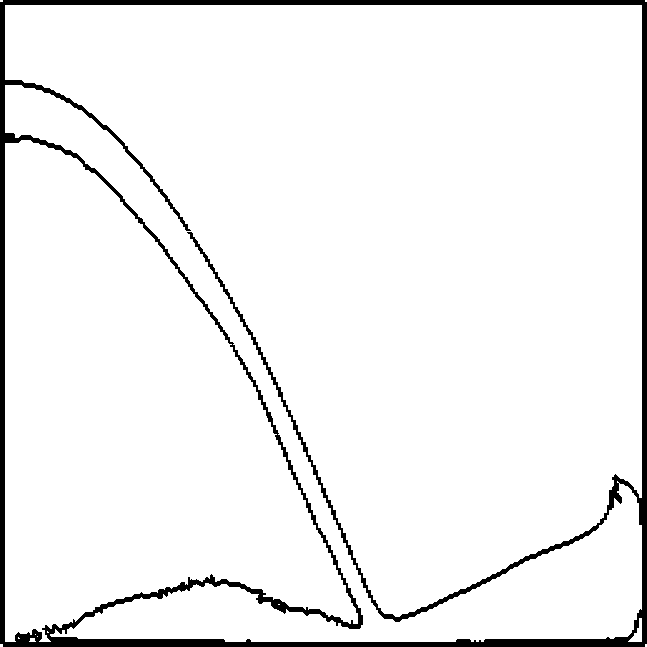
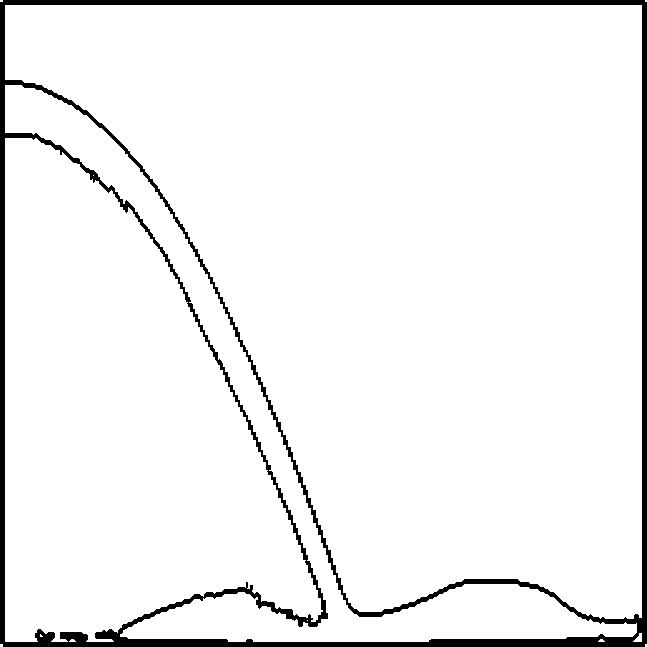
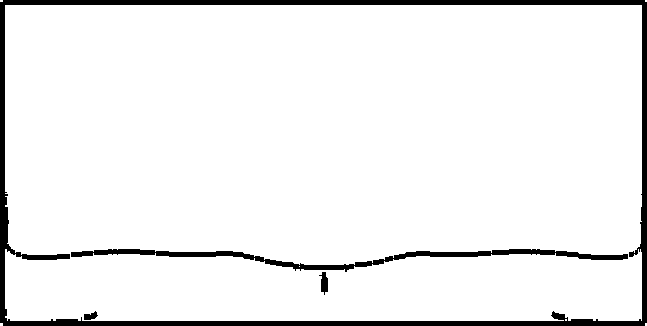
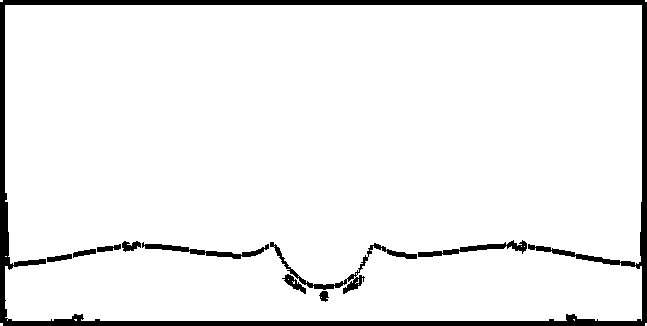
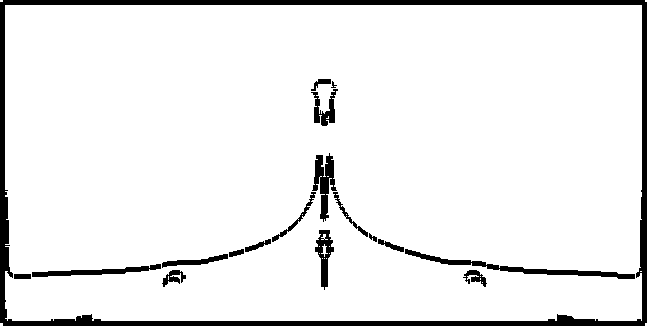
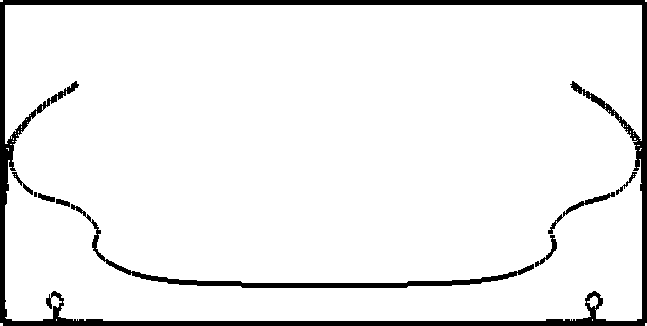
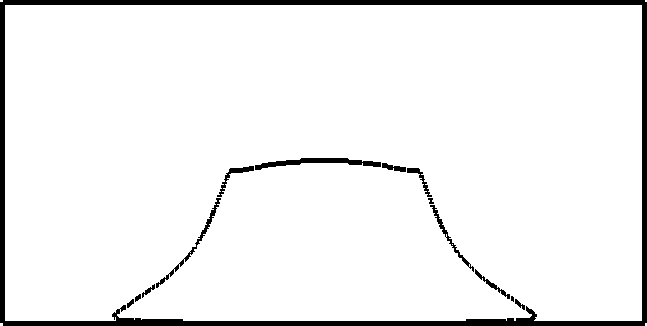
The driver code of the simulation is the run function within MultiPhase.cc. The general idea is to define here everything that has to do with the problem, set all the (physical and numerical) parameters and perform the time loop. The run function does the following: Set some physical parameters like final time, density and viscosity coefficients, etc. and numerical parameters like cfl, numerical constants, algorithms to be used, etc. Creates the geometry for the specified problem. Currently we have the following problems: Breaking Dam problem in 2D. Filling a tank in 2D. Small wave perturbation in 2D. Falling drop in 2D. Creates an object of the class NavierStokesSolver and an object of the class LevelSetSolver.
Set the initial condition for each of the solvers. Performs the time loop. Within the time loop we do the following: Pass the current level set function to the Navier Stokes Solver. Ask the Navier Stokes Solver to perform one time step. Get the velocity field from the Navier Stokes Solver. Pass the velocity field to the Level Set Solver. Ask the Level Set Solver to perform one time step. Get the level set function from the Level Set Solver. Repeat until the final time. Output the solution at the requested times.
Navier Stokes Solver
The NavierStokesSolver class is responsible for solving the Navier Stokes equation for just one time step. It requires density and viscosity information. This information can be passed by either a function or by passing a vector containing the DOFs of the level set function. For this reason the class contains the following two constructors: First constructor. Here we have to pass density and viscosity constants for the two phases. In addition, we have to pass a vector of DOFs defining the level set function. This constructor is meant to be used during the two-phase flow simulations. Second constructor. Here we have to pass functions to define the viscosity and density fields. This is meant to test the convergence properties of the method (and to validate the implementation).
Level Set Solver
The LevelSetSolver.cc code is responsible for solving the Level Set for just one time step. It requires information about the velocity field and provides the transported level set function. The velocity field can be interpolated (outside of this class) from a given function to test the method (and to validate the implementation). Alternatively, the velocity can be provided from the solution of the Navier-Stokes equations (for the two phase flow simulations).
Testing the Navier Stokes Solver
The TestNavierStokes.cc code is used to test the convergence (in time) of the Navier-Stokes solver. To run it uncomment the line SET(TARGET "TestNavierStokes") within CMakeLists.txt (and make sure to comment SET(TARGET "TestLevelSet") and SET(TARGET "MultiPhase"). Then cmake and compile. The convergence can be done in 2 or 3 dimensions. Different exact solutions (and force terms) are used in each case. The dimension can be set in the line TestNavierStokes<2> test_navier_stokes(degree_LS, degree_U) within the main function.
Testing the Level Set Solver
The TestLevelSet.cc code is used to test the level set solver. To run it uncomment the corresponding line within CMakeLists.txt. Then cmake and compile. There are currently just two problems implemented: diagonal advection and circular rotation. If the velocity is independent of time set the flag VARIABLE_VELOCITY to zero to avoid interpolating the velocity field at every time step.
Utility files
The files utilities.cc, utilities_test_LS.cc and utilities_test_NS.cc contain functions required in MultiPhase.cc, TestLevelSet.cc and TestNavierStokes.cc respectively. The script clean.sh ereases all files created by cmake, compile and run any example.
References
[1] J.-L. Guermond and A. Salgado. A splitting method for incompressible flows with variable density based on a pressure Poisson equation. Journal of Computational Physics, 228(8):2834–2846, 2009.
[2] J.-L. Guermond, R. Pasquetti, and B. Popov. Entropy viscosity method for nonlinear conservation laws. Journal of Computational Physics, 230(11):4248– 4267, 2011.
[3] A. Harten. The artificial compression method for computation of shocks and contact discontinuities. I. Single conservation laws. Communications on Pure and Applied Mathematics, 30(5):611–638, 1977.
[4] A. Harten. The artificial compression method for computation of shocks and contact discontinuities. III. Self-adjusting hybrid schemes. Mathematics of Computation, 32:363–389, 1978.
Annotated version of LevelSetSolver.cc
#include <fstream>
#include <iostream>
#include <memory>
FLAGS
#define NUM_ITER 1
#define CHECK_MAX_PRINCIPLE 0
LOG FOR LEVEL SET FROM -1 to 1
#define ENTROPY(phi) std::log(std::abs(1-phi*phi)+1E-14)
#define ENTROPY_GRAD(phi,phix) 2*phi*phix*((1-phi*phi>=0) ? -1 : 1)/(std::abs(1-phi*phi)+1E-14)
////////////////////////////////////////////////////// ////////////////// TRANSPORT SOLVER ////////////////// ////////////////////////////////////////////////////// This is a solver for the transpor solver. We assume the velocity is divergence free and solve the equation in conservation form. /////////////////////////////// -------— NOTATION -------— /////////////////////////////// We use notation popular in the literature of conservation laws. For this reason the solution is denoted as u, unm1, unp1, etc. and the velocity is treated as vx, vy and vz.
template <int dim>
class LevelSetSolver
{
public:
//////////////////// INITIAL CONDITIONS ////////////////////
///////////////////// BOUNDARY CONDITIONS /////////////////////
void set_boundary_conditions(std::vector<types::global_dof_index> &boundary_values_id_u,
std::vector<double> boundary_values_u);
////////////// SET VELOCITY //////////////
/////////////////// SET AND GET ALPHA ///////////////////
/////////////// NTH TIME STEP ///////////////
/////// SETUP ///////
void setup();
LevelSetSolver (const unsigned int degree_LS,
const unsigned int degree_U,
const double time_step,
const double cK,
const double cE,
const bool verbose,
std::string ALGORITHM,
const unsigned int TIME_INTEGRATION,
~LevelSetSolver();
private:
const ::parallel::distributed::Triangulation< dim, spacedim > * triangulation
//////////////////////////////////// ASSEMBLE MASS (and other) MATRICES ////////////////////////////////////
void assemble_ML();
void invert_ML();
void assemble_MC();
////////////////////////////////// LOW ORDER METHOD (DiJ Viscosity) //////////////////////////////////
void assemble_C_Matrix();
/////////////////// ENTROPY VISCOSITY ///////////////////
void assemble_EntRes_Matrix();
/////////////////////// FOR MAXIMUM PRINCIPLE ///////////////////////
/////////////////// COMPUTE SOLUTIONS ///////////////////
std::string algorithm);
std::string algorithm);
/////////// UTILITIES ///////////
void get_sparsity_pattern();
void get_map_from_Q1_to_Q2();
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner,
void save_old_solution();
void save_old_vel_solution();
/////////////////// MY PETSC WRAPPERS ///////////////////
const std::vector<types::global_dof_index> &indices,
std::vector<PetscScalar> &values);
const std::vector<types::global_dof_index> &indices,
std::map<types::global_dof_index, types::global_dof_index> &map_from_Q1_to_Q2,
std::vector<PetscScalar> &values);
FINITE ELEMENT SPACE
int degree_MAX;
int degree_LS;
int degree_U;
OPERATORS times SOLUTION VECTOR
MASS MATRIX
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> MC_preconditioner;
BOUNDARIES
std::vector<types::global_dof_index> boundary_values_id_u;
std::vector<double> boundary_values_u;
////////// MATRICES ////////// FOR FIRST ORDER VISCOSITY
FOR ENTROPY VISCOSITY
FOR FCT (flux and limited flux)
FOR ITERATIVE FCT
GHOSTED VECTORS
NON-GHOSTED VECTORS
LUMPED MASS MATRIX
CONSTRAINTS
TIME STEPPING
SOME PARAMETERS
double cE, cK;
double solver_tolerance;
double entropy_normalization_factor;
UTILITIES
bool verbose;
std::string ALGORITHM;
unsigned int TIME_INTEGRATION;
std::map<types::global_dof_index, types::global_dof_index> map_from_Q1_to_Q2;
std::map<types::global_dof_index, std::vector<types::global_dof_index> > sparsity_pattern;
};
template <int dim>
LevelSetSolver<dim>::LevelSetSolver (const unsigned int degree_LS,
const unsigned int degree_U,
const double time_step,
const double cK,
const double cE,
const bool verbose,
std::string ALGORITHM,
const unsigned int TIME_INTEGRATION,
:
mpi_communicator (mpi_communicator),
degree_LS(degree_LS),
fe_LS (degree_LS),
degree_U(degree_U),
fe_U (degree_U),
time_step(time_step),
cE(cE),
cK(cK),
verbose(verbose),
ALGORITHM(ALGORITHM),
TIME_INTEGRATION(TIME_INTEGRATION),
pcout (
std::cout,(
Utilities::MPI::this_mpi_process(mpi_communicator)== 0))
{
pcout << "********** LEVEL SET SETUP **********" << std::endl;
setup();
}
template <int dim>
LevelSetSolver<dim>::~LevelSetSolver ()
{
dof_handler_LS.clear ();
dof_handler_U.clear ();
}
/////////////////////////////////////////////////////// /////////////////// PUBLIC FUNCTIONS ////////////////// /////////////////////////////////////////////////////// //////////////////////////////////// //////// INITIAL CONDITIONS //////// ////////////////////////////////////
template<int dim>
{
this->un = un;
this->locally_relevant_solution_vx = locally_relevant_solution_vx;
this->locally_relevant_solution_vy = locally_relevant_solution_vy;
initialize old vectors with current solution, this just happens the first time
unm1 = un;
locally_relevant_solution_vx_old = locally_relevant_solution_vx;
locally_relevant_solution_vy_old = locally_relevant_solution_vy;
}
template<int dim>
{
this->un = un;
this->locally_relevant_solution_vx = locally_relevant_solution_vx;
this->locally_relevant_solution_vy = locally_relevant_solution_vy;
this->locally_relevant_solution_vz = locally_relevant_solution_vz;
initialize old vectors with current solution, this just happens the first time
unm1 = un;
locally_relevant_solution_vx_old = locally_relevant_solution_vx;
locally_relevant_solution_vy_old = locally_relevant_solution_vy;
locally_relevant_solution_vz_old = locally_relevant_solution_vz;
}
///////////////////////////////////// //////// BOUNDARY CONDITIONS //////// /////////////////////////////////////
template <int dim>
void LevelSetSolver<dim>::set_boundary_conditions(std::vector<types::global_dof_index> &boundary_values_id_u,
std::vector<double> boundary_values_u)
{
this->boundary_values_id_u = boundary_values_id_u;
this->boundary_values_u = boundary_values_u;
}
////////////////////////////// //////// SET VELOCITY //////// //////////////////////////////
SAVE OLD SOLUTION
update velocity
this->locally_relevant_solution_vx=locally_relevant_solution_vx;
this->locally_relevant_solution_vy=locally_relevant_solution_vy;
}
template <int dim>
{
SAVE OLD SOLUTION
update velocity
this->locally_relevant_solution_vx=locally_relevant_solution_vx;
this->locally_relevant_solution_vy=locally_relevant_solution_vy;
this->locally_relevant_solution_vz=locally_relevant_solution_vz;
}
/////////////////////////////// //////// SET AND GET U //////// ///////////////////////////////
---------------------------— COMPUTE SOLUTIONS ---------------------------—
template <int dim>
void LevelSetSolver<dim>::nth_time_step()
{
assemble_EntRes_Matrix();
COMPUTE SOLUTION
if (TIME_INTEGRATION==FORWARD_EULER)
compute_solution(unp1,un,ALGORITHM);
else
compute_solution_SSP33(unp1,un,ALGORITHM);
BOUNDARY CONDITIONS
unp1.set(boundary_values_id_u,boundary_values_u);
CHECK MAXIMUM PRINCIPLE
if (CHECK_MAX_PRINCIPLE)
{
compute_bounds(un);
check_max_principle(unp1);
}
pcout << "*********************************************************************... " << unp1.min() << ", " << unp1.max() << std::endl;
---------------------------— SETUP ---------------------------—
template <int dim>
void LevelSetSolver<dim>::setup()
{
solver_tolerance=1E-6;
degree_MAX =
std::max(degree_LS,degree_U);
::VectorizedArray< Number, width > max(const ::VectorizedArray< Number, width > &, const ::VectorizedArray< Number, width > &)
//////////////////////// SETUP FOR DOF HANDLERS //////////////////////// setup system LS
dof_handler_LS.distribute_dofs (fe_LS);
locally_owned_dofs_LS = dof_handler_LS.locally_owned_dofs ();
setup system U
dof_handler_U.distribute_dofs (fe_U);
locally_owned_dofs_U = dof_handler_U.locally_owned_dofs ();
////////////////// INIT CONSTRAINTS //////////////////
constraints.clear ();
constraints.reinit (locally_relevant_dofs_LS);
constraints.close ();
void make_hanging_node_constraints(const DoFHandler< dim, spacedim > &dof_handler, AffineConstraints< number > &constraints)
///////////////////// NON-GHOSTED VECTORS /////////////////////
MPP_uL_solution.reinit(locally_owned_dofs_LS,mpi_communicator);
NMPP_uH_solution.reinit(locally_owned_dofs_LS,mpi_communicator);
RHS.reinit(locally_owned_dofs_LS,mpi_communicator);
uStage1_nonGhosted.reinit (locally_owned_dofs_LS,mpi_communicator);
uStage2_nonGhosted.reinit (locally_owned_dofs_LS,mpi_communicator);
unp1.reinit (locally_owned_dofs_LS,mpi_communicator);
MPP_uH_solution.reinit (locally_owned_dofs_LS,mpi_communicator);
vectors for lumped mass matrix
ML_vector.reinit(locally_owned_dofs_LS,mpi_communicator);
inverse_ML_vector.reinit(locally_owned_dofs_LS,mpi_communicator);
ones_vector.reinit(locally_owned_dofs_LS,mpi_communicator);
ones_vector = 1.;
operators times solution
K_times_solution.reinit(locally_owned_dofs_LS,mpi_communicator);
DL_times_solution.reinit(locally_owned_dofs_LS,mpi_communicator);
DH_times_solution.reinit(locally_owned_dofs_LS,mpi_communicator);
LIMITERS (FCT)
R_pos_vector_nonGhosted.reinit (locally_owned_dofs_LS,mpi_communicator);
R_neg_vector_nonGhosted.reinit (locally_owned_dofs_LS,mpi_communicator);
umin_vector.reinit (locally_owned_dofs_LS,mpi_communicator);
umax_vector.reinit (locally_owned_dofs_LS,mpi_communicator);
///////////////////////////////////////////////////// GHOSTED VECTORS (used within some assemble process) /////////////////////////////////////////////////////
uStage1.reinit (locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
uStage2.reinit (locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
unm1.reinit (locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
un.reinit (locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
MPP_uL_solution_ghosted.reinit (locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
MPP_uLkp1_solution_ghosted.reinit (locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
NMPP_uH_solution_ghosted.reinit (locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
init vectors for vx
locally_relevant_solution_vx.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
locally_relevant_solution_vx_old.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
init vectors for vy
locally_relevant_solution_vy.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
locally_relevant_solution_vy_old.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
init vectors for vz
locally_relevant_solution_vz.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
locally_relevant_solution_vz_old.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
LIMITERS (FCT)
R_pos_vector.reinit(locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
R_neg_vector.reinit(locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
//////////////// SETUP MATRICES //////////////// MATRICES
dof_handler_LS.locally_owned_dofs(),
mpi_communicator,
locally_relevant_dofs_LS);
MC_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
Cx_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
CTx_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
Cy_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
CTy_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
if (dim==3)
{
Cz_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
CTz_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
}
dLij_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
EntRes_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
SuppSize_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
dCij_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
A_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
LxA_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
Akp1_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
LxAkp1_matrix.reinit (dof_handler_LS.locally_owned_dofs(),
dof_handler_LS.locally_owned_dofs(),
dsp, mpi_communicator);
void make_sparsity_pattern(const DoFHandler< dim, spacedim > &dof_handler, SparsityPatternType &sparsity_pattern, const AffineConstraints< number > &constraints=AffineConstraints< number >(), const bool keep_constrained_dofs=true, const types::subdomain_id subdomain_id=numbers::invalid_subdomain_id)
COMPUTE MASS MATRICES (AND OTHERS) FOR FIRST TIME STEP
assemble_ML();
invert_ML();
assemble_MC();
assemble_C_Matrix();
get mat for DOFs between Q1 and Q2
get_map_from_Q1_to_Q2();
get_sparsity_pattern();
}
---------------------------— MASS MATRICES ---------------------------—
template<int dim>
void LevelSetSolver<dim>::assemble_ML()
{
ML_vector=0;
const unsigned int dofs_per_cell = fe_LS.dofs_per_cell;
const unsigned int n_q_points = quadrature_formula.size();
std::vector<types::global_dof_index> local_dof_indices (dofs_per_cell);
cell_LS = dof_handler_LS.begin_active(),
endc_LS = dof_handler_LS.end();
for (; cell_LS!=endc_LS; ++cell_LS)
if (cell_LS->is_locally_owned())
{
cell_ML = 0;
fe_values_LS.reinit (cell_LS);
for (unsigned int q_point=0; q_point<n_q_points; ++q_point)
{
const double JxW = fe_values_LS.JxW(q_point);
for (unsigned int i=0; i<dofs_per_cell; ++i)
cell_ML (i) += fe_values_LS.shape_value(i,q_point)*JxW;
}
@ update_values
Shape function values.
@ update_JxW_values
Transformed quadrature weights.
@ update_gradients
Shape function gradients.
@ update_quadrature_points
Transformed quadrature points.
typename ActiveSelector::active_cell_iterator active_cell_iterator
distribute
cell_LS->get_dof_indices (local_dof_indices);
constraints.distribute_local_to_global (cell_ML,local_dof_indices,ML_vector);
}
compress
}
template<int dim>
void LevelSetSolver<dim>::invert_ML()
{
loop on locally owned i-DOFs (rows)
for (; idofs_iter!=locally_owned_dofs_LS.end(); ++idofs_iter)
{
int gi = *idofs_iter;
inverse_ML_vector(gi) = 1./ML_vector(gi);
}
}
template<int dim>
void LevelSetSolver<dim>::assemble_MC()
{
MC_matrix=0;
const unsigned int dofs_per_cell = fe_LS.dofs_per_cell;
const unsigned int n_q_points = quadrature_formula.size();
std::vector<types::global_dof_index> local_dof_indices (dofs_per_cell);
std::vector<double> shape_values(dofs_per_cell);
endc_LS = dof_handler_LS.end();
for (; cell_LS!=endc_LS; ++cell_LS)
if (cell_LS->is_locally_owned())
{
cell_MC = 0;
fe_values_LS.reinit (cell_LS);
for (unsigned int q_point=0; q_point<n_q_points; ++q_point)
{
const double JxW = fe_values_LS.JxW(q_point);
for (unsigned int i=0; i<dofs_per_cell; ++i)
shape_values[i] = fe_values_LS.shape_value(i,q_point);
for (unsigned int i=0; i<dofs_per_cell; ++i)
for (unsigned int j=0; j<dofs_per_cell; ++j)
cell_MC(i,j) += shape_values[i]*shape_values[j]*JxW;
}
active_cell_iterator begin_active(const unsigned int level=0) const
distribute
cell_LS->get_dof_indices (local_dof_indices);
constraints.distribute_local_to_global (cell_MC,local_dof_indices,MC_matrix);
}
compress
---------------------------— LO METHOD (Dij Viscosity) ---------------------------—
template <int dim>
void LevelSetSolver<dim>::assemble_C_Matrix ()
{
Cx_matrix=0;
CTx_matrix=0;
Cy_matrix=0;
CTy_matrix=0;
Cz_matrix=0;
CTz_matrix=0;
const unsigned int dofs_per_cell_LS = fe_LS.dofs_per_cell;
const unsigned int n_q_points = quadrature_formula.size();
std::vector<Tensor<1, dim> > shape_grads_LS(dofs_per_cell_LS);
std::vector<double> shape_values_LS(dofs_per_cell_LS);
std::vector<types::global_dof_index> local_dof_indices_LS (dofs_per_cell_LS);
endc_LS = dof_handler_LS.
end();
for (; cell_LS!=endc_LS; ++cell_LS)
if (cell_LS->is_locally_owned())
{
cell_Cij_x = 0;
cell_Cij_y = 0;
cell_Cji_x = 0;
cell_Cji_y = 0;
if (dim==3)
{
cell_Cij_z = 0;
cell_Cji_z = 0;
}
fe_values_LS.reinit (cell_LS);
cell_LS->get_dof_indices (local_dof_indices_LS);
for (unsigned int q_point=0; q_point<n_q_points; ++q_point)
{
const double JxW = fe_values_LS.JxW(q_point);
for (unsigned int i=0; i<dofs_per_cell_LS; ++i)
{
shape_values_LS[i] = fe_values_LS.shape_value(i,q_point);
shape_grads_LS [i] = fe_values_LS.shape_grad (i,q_point);
}
for (unsigned int i=0; i<dofs_per_cell_LS; ++i)
for (unsigned int j=0; j < dofs_per_cell_LS; ++j)
{
cell_Cij_x(i,j) += (shape_grads_LS[j][0])*shape_values_LS[i]*JxW;
cell_Cij_y(i,j) += (shape_grads_LS[j][1])*shape_values_LS[i]*JxW;
cell_Cji_x(i,j) += (shape_grads_LS[i][0])*shape_values_LS[j]*JxW;
cell_Cji_y(i,j) += (shape_grads_LS[i][1])*shape_values_LS[j]*JxW;
if (dim==3)
{
cell_Cij_z(i,j) += (shape_grads_LS[j][2])*shape_values_LS[i]*JxW;
cell_Cji_z(i,j) += (shape_grads_LS[i][2])*shape_values_LS[j]*JxW;
}
}
}
cell_iterator end() const
Distribute
constraints.distribute_local_to_global(cell_Cij_x,local_dof_indices_LS,Cx_matrix);
constraints.distribute_local_to_global(cell_Cji_x,local_dof_indices_LS,CTx_matrix);
constraints.distribute_local_to_global(cell_Cij_y,local_dof_indices_LS,Cy_matrix);
constraints.distribute_local_to_global(cell_Cji_y,local_dof_indices_LS,CTy_matrix);
if (dim==3)
{
constraints.distribute_local_to_global(cell_Cij_z,local_dof_indices_LS,Cz_matrix);
constraints.distribute_local_to_global(cell_Cji_z,local_dof_indices_LS,CTz_matrix);
}
}
COMPRESS
if (dim==3)
{
}
}
template<int dim>
{
K_times_solution = 0;
const unsigned int dofs_per_cell = fe_LS.dofs_per_cell;
const unsigned int n_q_points = quadrature_formula.size();
std::vector<Tensor<1,dim> > un_grads (n_q_points);
std::vector<double> old_vx_values (n_q_points);
std::vector<double> old_vy_values (n_q_points);
std::vector<double> old_vz_values (n_q_points);
std::vector<double> shape_values(dofs_per_cell);
std::vector<Tensor<1,dim> > shape_grads(dofs_per_cell);
std::vector<types::global_dof_index> indices_LS (dofs_per_cell);
loop on cells
endc_LS = dof_handler_LS.
end();
cell_U = dof_handler_U.begin_active();
for (; cell_LS!=endc_LS; ++cell_U, ++cell_LS)
if (cell_LS->is_locally_owned())
{
cell_K_times_solution=0;
fe_values_LS.reinit (cell_LS);
cell_LS->get_dof_indices (indices_LS);
fe_values_LS.get_function_gradients(solution,un_grads);
fe_values_U.get_function_values(locally_relevant_solution_vx,old_vx_values);
fe_values_U.get_function_values(locally_relevant_solution_vy,old_vy_values);
if (dim==3) fe_values_U.get_function_values(locally_relevant_solution_vz,old_vz_values);
void reinit(const Triangulation< dim, spacedim > &tria)
compute cell_K_times_solution
for (unsigned int q_point=0; q_point<n_q_points; ++q_point)
{
v[0] = old_vx_values[q_point];
v[1] = old_vy_values[q_point];
if (dim==3) v[2] = old_vz_values[q_point];
for (unsigned int i=0; i<dofs_per_cell; ++i)
cell_K_times_solution(i) += (v*un_grads[q_point])
*fe_values_LS.shape_value(i,q_point)*fe_values_LS.JxW(q_point);
}
distribute
constraints.distribute_local_to_global (cell_K_times_solution, indices_LS, K_times_solution);
}
}
template <int dim>
void LevelSetSolver<dim>::assemble_K_DL_DH_times_vector
{
K_times_solution=0;
DL_times_solution=0;
DH_times_solution=0;
dLij_matrix = 0;
dCij_matrix = 0;
PetscInt ncolumns;
const PetscInt *gj;
const PetscScalar *Cxi, *Cyi, *Czi, *CTxi, *CTyi, *CTzi;
const PetscScalar *EntResi, *SuppSizei, *MCi;
double solni;
loop on locally owned i-DOFs (rows)
for (; idofs_iter!=locally_owned_dofs_LS.end(); ++idofs_iter)
{
PetscInt gi = *idofs_iter;
double ith_K_times_solution = 0;
read velocity of i-th DOF
vi[0] = locally_relevant_solution_vx(map_from_Q1_to_Q2[gi]);
vi[1] = locally_relevant_solution_vy(map_from_Q1_to_Q2[gi]);
if (dim==3) vi[2] = locally_relevant_solution_vz(map_from_Q1_to_Q2[gi]);
solni = solution(gi);
get i-th row of C matrices
MatGetRow(Cx_matrix,gi,&ncolumns,&gj,&Cxi);
MatGetRow(Cy_matrix,gi,&ncolumns,&gj,&Cyi);
MatGetRow(CTx_matrix,gi,&ncolumns,&gj,&CTxi);
MatGetRow(CTy_matrix,gi,&ncolumns,&gj,&CTyi);
if (dim==3)
{
MatGetRow(Cz_matrix,gi,&ncolumns,&gj,&Czi);
MatGetRow(CTz_matrix,gi,&ncolumns,&gj,&CTzi);
}
MatGetRow(EntRes_matrix,gi,&ncolumns,&gj,&EntResi);
MatGetRow(SuppSize_matrix,gi,&ncolumns,&gj,&SuppSizei);
MatGetRow(MC_matrix,gi,&ncolumns,&gj,&MCi);
get vector values for column indices
const std::vector<types::global_dof_index> gj_indices (gj,gj+ncolumns);
std::vector<double> soln(ncolumns);
std::vector<double> vx(ncolumns);
std::vector<double> vy(ncolumns);
std::vector<double> vz(ncolumns);
get_vector_values(solution,gj_indices,soln);
get_vector_values(locally_relevant_solution_vx,gj_indices,map_from_Q1_to_Q2,vx);
get_vector_values(locally_relevant_solution_vy,gj_indices,map_from_Q1_to_Q2,vy);
if (dim==3)
get_vector_values(locally_relevant_solution_vz,gj_indices,map_from_Q1_to_Q2,vz);
Array for i-th row of matrices
std::vector<double> dLi(ncolumns), dCi(ncolumns);
double dLii = 0, dCii = 0;
loop on sparsity pattern of i-th DOF
for (int j =0; j < ncolumns; ++j)
{
C[0] = Cxi[j];
C[1] = Cyi[j];
CT[0]= CTxi[j];
CT[1]= CTyi[j];
vj[0] = vx[j];
vj[1] = vy[j];
if (dim==3)
{
C[2] = Czi[j];
CT[2] = CTzi[j];
vj[2] = vz[j];
}
ith_K_times_solution += soln[j]*(vj*C);
low order dissipative matrix
dLii -= dLi[j];
::VectorizedArray< Number, width > abs(const ::VectorizedArray< Number, width > &)
high order dissipative matrix (entropy viscosity)
cE*
std::abs(EntResi[j])/(entropy_normalization_factor*MCi[j]/SuppSizei[j]));
::VectorizedArray< Number, width > min(const ::VectorizedArray< Number, width > &, const ::VectorizedArray< Number, width > &)
high order compression matrix
dCii -= dCi[j];
}
}
::VectorizedArray< Number, width > pow(const ::VectorizedArray< Number, width > &, const Number p)
save K times solution vector K_times_solution(gi)=ith_K_times_solution; save i-th row of matrices on global matrices
MatSetValuesRow(dLij_matrix,gi,&dLi[0]);
dLij_matrix.set(gi,gi,dLii);
MatSetValuesRow(dCij_matrix,gi,&dCi[0]);
dCij_matrix.set(gi,gi,dCii);
Restore matrices after reading rows
MatRestoreRow(Cx_matrix,gi,&ncolumns,&gj,&Cxi);
MatRestoreRow(Cy_matrix,gi,&ncolumns,&gj,&Cyi);
MatRestoreRow(CTx_matrix,gi,&ncolumns,&gj,&CTxi);
MatRestoreRow(CTy_matrix,gi,&ncolumns,&gj,&CTyi);
if (dim==3)
{
MatRestoreRow(Cz_matrix,gi,&ncolumns,&gj,&Czi);
MatRestoreRow(CTz_matrix,gi,&ncolumns,&gj,&CTzi);
}
MatRestoreRow(EntRes_matrix,gi,&ncolumns,&gj,&EntResi);
MatRestoreRow(SuppSize_matrix,gi,&ncolumns,&gj,&SuppSizei);
MatRestoreRow(MC_matrix,gi,&ncolumns,&gj,&MCi);
}
compress K_times_solution.compress(VectorOperation::insert);
get matrices times vector
dLij_matrix.vmult(DL_times_solution,solution);
dCij_matrix.vmult(DH_times_solution,solution);
}
---------------------------— ENTROPY VISCOSITY ---------------------------—
template <int dim>
void LevelSetSolver<dim>::assemble_EntRes_Matrix ()
{
EntRes_matrix=0;
entropy_normalization_factor=0;
SuppSize_matrix=0;
const unsigned int dofs_per_cell_LS = fe_LS.dofs_per_cell;
const unsigned int n_q_points = quadrature_formula.size();
std::vector<double> uqn (n_q_points);
std::vector<double> uqnm1 (n_q_points);
std::vector<Tensor<1,dim> > guqn (n_q_points);
std::vector<Tensor<1,dim> > guqnm1 (n_q_points);
std::vector<double> vxqn (n_q_points);
std::vector<double> vyqn (n_q_points);
std::vector<double> vzqn (n_q_points);
std::vector<double> vxqnm1 (n_q_points);
std::vector<double> vyqnm1 (n_q_points);
std::vector<double> vzqnm1 (n_q_points);
std::vector<Tensor<1, dim> > shape_grads_LS(dofs_per_cell_LS);
std::vector<double> shape_values_LS(dofs_per_cell_LS);
std::vector<types::global_dof_index> local_dof_indices_LS (dofs_per_cell_LS);
endc_LS = dof_handler_LS.
end();
double Rk;
double max_entropy=-1E10, min_entropy=1E10;
double cell_max_entropy, cell_min_entropy;
double cell_entropy_mass, entropy_mass=0;
double cell_volume_double, volume=0;
for (; cell_LS!=endc_LS; ++cell_LS, ++cell_U)
if (cell_LS->is_locally_owned())
{
cell_entropy_mass = 0;
cell_volume_double = 0;
cell_max_entropy = -1E10;
cell_min_entropy = 1E10;
cell_EntRes = 0;
cell_volume = 0;
get solutions at quadrature points
fe_values_LS.reinit(cell_LS);
cell_LS->get_dof_indices (local_dof_indices_LS);
fe_values_LS.get_function_values(un,uqn);
fe_values_LS.get_function_values(unm1,uqnm1);
fe_values_LS.get_function_gradients(un,guqn);
fe_values_LS.get_function_gradients(unm1,guqnm1);
fe_values_U.get_function_values(locally_relevant_solution_vx,vxqn);
fe_values_U.get_function_values(locally_relevant_solution_vy,vyqn);
if (dim==3) fe_values_U.get_function_values(locally_relevant_solution_vz,vzqn);
fe_values_U.get_function_values(locally_relevant_solution_vx_old,vxqnm1);
fe_values_U.get_function_values(locally_relevant_solution_vy_old,vyqnm1);
if (dim==3) fe_values_U.get_function_values(locally_relevant_solution_vz_old,vzqnm1);
for (unsigned int q=0; q<n_q_points; ++q)
{
Rk = 1./time_step*(ENTROPY(uqn[q])-ENTROPY(uqnm1[q]))
+(vxqn[q]*ENTROPY_GRAD(uqn[q],guqn[q][0])+vyqn[q]*ENTROPY_GRAD(uqn[q],guqn[q][1]))/2.
+(vxqnm1[q]*ENTROPY_GRAD(uqnm1[q],guqnm1[q][0])+vyqnm1[q]*ENTROPY_GRAD(uqnm1[q],guqnm1[q][1]))/2.;
if (dim==3)
Rk += 0.5*(vzqn[q]*ENTROPY_GRAD(uqn[q],guqn[q][2])+vzqnm1[q]*ENTROPY_GRAD(uqnm1[q],guqnm1[q][2]));
const double JxW = fe_values_LS.JxW(q);
for (unsigned int i=0; i<dofs_per_cell_LS; ++i)
{
shape_values_LS[i] = fe_values_LS.shape_value(i,q);
shape_grads_LS [i] = fe_values_LS.shape_grad (i,q);
}
for (unsigned int i=0; i<dofs_per_cell_LS; ++i)
for (unsigned int j=0; j < dofs_per_cell_LS; ++j)
{
cell_EntRes (i,j) += Rk*shape_values_LS[i]*shape_values_LS[j]*JxW;
cell_volume (i,j) += JxW;
}
cell_entropy_mass += ENTROPY(uqn[q])*JxW;
cell_volume_double += JxW;
cell_min_entropy =
std::min(cell_min_entropy,ENTROPY(uqn[q]));
cell_max_entropy =
std::max(cell_max_entropy,ENTROPY(uqn[q]));
}
entropy_mass += cell_entropy_mass;
min_entropy =
std::min(min_entropy,cell_min_entropy);
max_entropy =
std::max(max_entropy,cell_max_entropy);
Distribute
constraints.distribute_local_to_global(cell_EntRes,local_dof_indices_LS,EntRes_matrix);
constraints.distribute_local_to_global(cell_volume,local_dof_indices_LS,SuppSize_matrix);
}
ENTROPY NORM FACTOR
}
T min(const T &t, const MPI_Comm &mpi_communicator)
T sum(const T &t, const MPI_Comm &mpi_communicator)
T max(const T &t, const MPI_Comm &mpi_communicator)
---------------------------— TO CHECK MAX PRINCIPLE ---------------------------—
template<int dim>
{
umin_vector = 0;
umax_vector = 0;
loop on locally owned i-DOFs (rows)
for (; idofs_iter!=locally_owned_dofs_LS.end(); ++idofs_iter)
{
int gi = *idofs_iter;
get solution at DOFs on the sparsity pattern of i-th DOF
std::vector<types::global_dof_index> gj_indices = sparsity_pattern[gi];
std::vector<double> soln(gj_indices.size());
get_vector_values(un_solution,gj_indices,soln);
compute bounds, ith row of flux matrix, P vectors
double mini=1E10, maxi=-1E10;
for (unsigned int j =0; j < gj_indices.size(); ++j)
{
bounds
}
umin_vector(gi) = mini;
umax_vector(gi) = maxi;
}
}
template<int dim>
{
compute min and max vectors
const unsigned int dofs_per_cell = fe_LS.dofs_per_cell;
std::vector<types::global_dof_index> local_dof_indices (dofs_per_cell);
double tol=1e-10;
endc_LS = dof_handler_LS.
end();
for (; cell_LS!=endc_LS; ++cell_LS)
if (cell_LS->is_locally_owned() && !cell_LS->at_boundary())
{
cell_LS->get_dof_indices(local_dof_indices);
for (unsigned int i=0; i<dofs_per_cell; ++i)
if (locally_owned_dofs_LS.is_element(local_dof_indices[i]))
{
double solni = unp1_solution(local_dof_indices[i]);
if (solni - umin_vector(local_dof_indices[i]) < -tol || umax_vector(local_dof_indices[i]) - solni < -tol)
{
pcout << "MAX Principle violated" << std::endl;
abort();
}
}
}
}
---------------------------— COMPUTE SOLUTIONS ---------------------------—
template<int dim>
void LevelSetSolver<dim>::compute_MPP_uL_and_NMPP_uH
{
NON-GHOSTED VECTORS: MPP_uL_solution, NMPP_uH_solution GHOSTED VECTORS: un_solution
MPP_uL_solution=un_solution;
NMPP_uH_solution=un_solution;
assemble RHS VECTORS
assemble_K_times_vector(un_solution);
assemble_K_DL_DH_times_vector(un_solution);
///////////////////////// COMPUTE MPP u1 solution /////////////////////////
MPP_uL_solution.
scale(ML_vector);
MPP_uL_solution.
add(-time_step,K_times_solution);
MPP_uL_solution.
add(-time_step,DL_times_solution);
MPP_uL_solution.
scale(inverse_ML_vector);
void scale(const VectorBase &scaling_factors)
void add(const std::vector< size_type > &indices, const std::vector< PetscScalar > &values)
////////////////////////////// COMPUTE GALERKIN u2 solution //////////////////////////////
MC_matrix.vmult(RHS,un_solution);
RHS.add(-time_step,K_times_solution,-time_step,DH_times_solution);
solve(constraints,MC_matrix,MC_preconditioner,NMPP_uH_solution,RHS);
}
template <int dim>
void LevelSetSolver<dim>::compute_MPP_uH
{
MPP_uH_solution=0;
loop on locally owned i-DOFs (rows)
PetscInt ncolumns;
const PetscInt *gj;
const PetscScalar *MCi, *dLi, *dCi;
double solni, mi, solLi, solHi;
for (; idofs_iter!=locally_owned_dofs_LS.end(); ++idofs_iter)
{
int gi = *idofs_iter;
read vectors at i-th DOF
solni=solution(gi);
solHi=NMPP_uH_solution_ghosted(gi);
solLi=MPP_uL_solution_ghosted(gi);
mi=ML_vector(gi);
get i-th row of matrices
MatGetRow(MC_matrix,gi,&ncolumns,&gj,&MCi);
MatGetRow(dLij_matrix,gi,&ncolumns,&gj,&dLi);
MatGetRow(dCij_matrix,gi,&ncolumns,&gj,&dCi);
get vector values for support of i-th DOF
const std::vector<types::global_dof_index> gj_indices (gj,gj+ncolumns);
std::vector<double> soln(ncolumns);
std::vector<double> solH(ncolumns);
get_vector_values(solution,gj_indices,soln);
get_vector_values(NMPP_uH_solution_ghosted,gj_indices,solH);
Array for i-th row of matrices
std::vector<double> Ai(ncolumns);
compute bounds, ith row of flux matrix, P vectors
double mini=1E10, maxi=-1E10;
double Pposi=0 ,Pnegi=0;
for (int j =0; j < ncolumns; ++j)
{
bounds
i-th row of flux matrix A
Ai[j] = (((gi==gj[j]) ? 1 : 0)*mi - MCi[j])*(solH[j]-soln[j] - (solHi-solni))
+time_step*(dLi[j]-dCi[j])*(soln[j]-solni);
compute P vectors
Pposi += Ai[j]*((Ai[j] > 0) ? 1. : 0.);
Pnegi += Ai[j]*((Ai[j] < 0) ? 1. : 0.);
}
save i-th row of flux matrix A
MatSetValuesRow(A_matrix,gi,&Ai[0]);
compute Q vectors
double Qposi = mi*(maxi-solLi);
double Qnegi = mi*(mini-solLi);
compute R vectors
R_pos_vector_nonGhosted(gi) = ((Pposi==0) ? 1. :
std::min(1.0,Qposi/Pposi));
R_neg_vector_nonGhosted(gi) = ((Pnegi==0) ? 1. :
std::min(1.0,Qnegi/Pnegi));
Restore matrices after reading rows
MatRestoreRow(MC_matrix,gi,&ncolumns,&gj,&MCi);
MatRestoreRow(dLij_matrix,gi,&ncolumns,&gj,&dLi);
MatRestoreRow(dCij_matrix,gi,&ncolumns,&gj,&dCi);
}
compress A matrix
compress R vectors
update ghost values for R vectors
R_pos_vector = R_pos_vector_nonGhosted;
R_neg_vector = R_neg_vector_nonGhosted;
compute limiters. NOTE: this is a different loop due to need of i- and j-th entries of R vectors
const double *Ai;
double Rposi, Rnegi;
idofs_iter=locally_owned_dofs_LS.begin();
for (; idofs_iter!=locally_owned_dofs_LS.end(); ++idofs_iter)
{
int gi = *idofs_iter;
Rposi = R_pos_vector(gi);
Rnegi = R_neg_vector(gi);
get i-th row of A matrix
MatGetRow(A_matrix,gi,&ncolumns,&gj,&Ai);
get vector values for column indices
const std::vector<types::global_dof_index> gj_indices (gj,gj+ncolumns);
std::vector<double> Rpos(ncolumns);
std::vector<double> Rneg(ncolumns);
get_vector_values(R_pos_vector,gj_indices,Rpos);
get_vector_values(R_neg_vector,gj_indices,Rneg);
Array for i-th row of A_times_L matrix
std::vector<double> LxAi(ncolumns);
loop in sparsity pattern of i-th DOF
for (int j =0; j < ncolumns; ++j)
LxAi[j] = Ai[j] * ((Ai[j]>0) ?
std::min(Rposi,Rneg[j]) :
std::min(Rnegi,Rpos[j]));
save i-th row of LxA
MatSetValuesRow(LxA_matrix,gi,&LxAi[0]);
restore A matrix after reading it
MatRestoreRow(A_matrix,gi,&ncolumns,&gj,&Ai);
}
LxA_matrix.vmult(MPP_uH_solution,ones_vector);
MPP_uH_solution.
scale(inverse_ML_vector);
MPP_uH_solution.
add(1.0,MPP_uL_solution_ghosted);
}
template<int dim>
void LevelSetSolver<dim>::compute_MPP_uH_with_iterated_FCT
{
MPP_uH_solution=0;
compute_MPP_uH(MPP_uH_solution,MPP_uL_solution_ghosted,NMPP_uH_solution_ghosted,un_solution);
if (NUM_ITER>0)
{
Akp1_matrix.copy_from(A_matrix);
LxAkp1_matrix.copy_from(LxA_matrix);
loop in num of FCT iterations
PetscInt ncolumns;
const PetscInt *gj;
const PetscScalar *Akp1i;
double mi;
for (int iter=0; iter<NUM_ITER; ++iter)
{
MPP_uLkp1_solution_ghosted = MPP_uH_solution;
Akp1_matrix.
add(-1.0, LxAkp1_matrix);
loop on locally owned i-DOFs (rows)
for (; idofs_iter!=locally_owned_dofs_LS.end(); ++idofs_iter)
{
int gi = *idofs_iter;
read vectors at i-th DOF
mi=ML_vector(gi);
double solLi = MPP_uLkp1_solution_ghosted(gi);
get i-th row of matrices
MatGetRow(Akp1_matrix,gi,&ncolumns,&gj,&Akp1i);
get vector values for support of i-th DOF
const std::vector<types::global_dof_index> gj_indices (gj,gj+ncolumns);
std::vector<double> soln(ncolumns);
get_vector_values(un_solution,gj_indices,soln);
compute bounds, ith row of flux matrix, P vectors
double mini=1E10, maxi=-1E10;
double Pposi=0 ,Pnegi=0;
for (int j =0; j < ncolumns; ++j)
{
bounds
compute P vectors
Pposi += Akp1i[j]*((Akp1i[j] > 0) ? 1. : 0.);
Pnegi += Akp1i[j]*((Akp1i[j] < 0) ? 1. : 0.);
}
compute Q vectors
double Qposi = mi*(maxi-solLi);
double Qnegi = mi*(mini-solLi);
compute R vectors
R_pos_vector_nonGhosted(gi) = ((Pposi==0) ? 1. :
std::min(1.0,Qposi/Pposi));
R_neg_vector_nonGhosted(gi) = ((Pnegi==0) ? 1. :
std::min(1.0,Qnegi/Pnegi));
Restore matrices after reading rows
MatRestoreRow(Akp1_matrix,gi,&ncolumns,&gj,&Akp1i);
}
compress R vectors
update ghost values for R vectors
R_pos_vector = R_pos_vector_nonGhosted;
R_neg_vector = R_neg_vector_nonGhosted;
compute limiters. NOTE: this is a different loop due to need of i- and j-th entries of R vectors
double Rposi, Rnegi;
idofs_iter=locally_owned_dofs_LS.begin();
for (; idofs_iter!=locally_owned_dofs_LS.end(); ++idofs_iter)
{
int gi = *idofs_iter;
Rposi = R_pos_vector(gi);
Rnegi = R_neg_vector(gi);
get i-th row of Akp1 matrix
MatGetRow(Akp1_matrix,gi,&ncolumns,&gj,&Akp1i);
get vector values for column indices
const std::vector<types::global_dof_index> gj_indices(gj,gj+ncolumns);
std::vector<double> Rpos(ncolumns);
std::vector<double> Rneg(ncolumns);
get_vector_values(R_pos_vector,gj_indices,Rpos);
get_vector_values(R_neg_vector,gj_indices,Rneg);
Array for i-th row of LxAkp1 matrix
std::vector<double> LxAkp1i(ncolumns);
for (int j =0; j < ncolumns; ++j)
LxAkp1i[j] = Akp1i[j] * ((Akp1i[j]>0) ?
std::min(Rposi,Rneg[j]) :
std::min(Rnegi,Rpos[j]));
save i-th row of LxA
MatSetValuesRow(LxAkp1_matrix,gi,&LxAkp1i[0]);
restore A matrix after reading it
MatRestoreRow(Akp1_matrix,gi,&ncolumns,&gj,&Akp1i);
}
LxAkp1_matrix.vmult(MPP_uH_solution,ones_vector);
MPP_uH_solution.
scale(inverse_ML_vector);
MPP_uH_solution.
add(1.0,MPP_uLkp1_solution_ghosted);
}
}
}
template<int dim>
std::string algorithm)
{
unp1=0;
COMPUTE MPP LOW-ORDER SOLN and NMPP HIGH-ORDER SOLN
compute_MPP_uL_and_NMPP_uH(MPP_uL_solution,NMPP_uH_solution,un);
if (algorithm.compare("MPP_u1")==0)
unp1=MPP_uL_solution;
else if (algorithm.compare("NMPP_uH")==0)
unp1=NMPP_uH_solution;
else if (algorithm.compare("MPP_uH")==0)
{
MPP_uL_solution_ghosted = MPP_uL_solution;
NMPP_uH_solution_ghosted=NMPP_uH_solution;
compute_MPP_uH_with_iterated_FCT(MPP_uH_solution,MPP_uL_solution_ghosted,NMPP_uH_solution_ghosted,un);
unp1=MPP_uH_solution;
}
else
{
pcout << "Error in algorithm" << std::endl;
abort();
}
}
template<int dim>
std::string algorithm)
{
GHOSTED VECTORS: un NON-GHOSTED VECTORS: unp1
unp1=0;
uStage1=0., uStage2=0.;
uStage1_nonGhosted=0., uStage2_nonGhosted=0.;
///////////// FIRST STAGE ///////////// u1=un-dt*RH*un
compute_solution(uStage1_nonGhosted,un,algorithm);
uStage1=uStage1_nonGhosted;
////////////// SECOND STAGE ////////////// u2=3/4*un+1/4*(u1-dt*RH*u1)
compute_solution(uStage2_nonGhosted,uStage1,algorithm);
uStage2_nonGhosted*=1./4;
uStage2_nonGhosted.add(3./4,un);
uStage2=uStage2_nonGhosted;
///////////// THIRD STAGE ///////////// unp1=1/3*un+2/3*(u2-dt*RH*u2)
compute_solution(unp1,uStage2,algorithm);
unp1*=2./3;
}
---------------------------— UTILITIES ---------------------------—
template<int dim>
void LevelSetSolver<dim>::get_sparsity_pattern()
{
loop on DOFs
PetscInt ncolumns;
const PetscInt *gj;
const PetscScalar *MCi;
for (; idofs_iter!=locally_owned_dofs_LS.end(); ++idofs_iter)
{
PetscInt gi = *idofs_iter;
get i-th row of mass matrix (dummy, I just need the indices gj)
MatGetRow(MC_matrix,gi,&ncolumns,&gj,&MCi);
sparsity_pattern[gi] = std::vector<types::global_dof_index>(gj,gj+ncolumns);
MatRestoreRow(MC_matrix,gi,&ncolumns,&gj,&MCi);
}
}
template<int dim>
void LevelSetSolver<dim>::get_map_from_Q1_to_Q2()
{
map_from_Q1_to_Q2.clear();
const unsigned int dofs_per_cell_LS = fe_LS.dofs_per_cell;
std::vector<types::global_dof_index> local_dof_indices_LS (dofs_per_cell_LS);
const unsigned int dofs_per_cell_U = fe_U.dofs_per_cell;
std::vector<types::global_dof_index> local_dof_indices_U (dofs_per_cell_U);
endc_LS = dof_handler_LS.
end();
for (; cell_LS!=endc_LS; ++cell_LS, ++cell_U)
if (!cell_LS->is_artificial())
{
cell_LS->get_dof_indices(local_dof_indices_LS);
cell_U->get_dof_indices(local_dof_indices_U);
for (unsigned int i=0; i<dofs_per_cell_LS; ++i)
map_from_Q1_to_Q2[local_dof_indices_LS[i]] = local_dof_indices_U[i];
}
}
template <int dim>
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner,
{
all vectors are NON-GHOSTED
SolverControl solver_control (dof_handler_LS.n_dofs(), solver_tolerance);
constraints.
distribute (completely_distributed_solution);
solver.solve (Matrix, completely_distributed_solution, rhs, *preconditioner);
constraints.
distribute (completely_distributed_solution);
if (verbose==true) pcout << " Solved in " << solver_control.last_step() << " iterations." << std::endl;
}
template <int dim>
void LevelSetSolver<dim>::save_old_solution()
{
unm1 = un;
un = unp1;
}
template <int dim>
void LevelSetSolver<dim>::save_old_vel_solution()
{
locally_relevant_solution_vx_old = locally_relevant_solution_vx;
locally_relevant_solution_vy_old = locally_relevant_solution_vy;
if (dim==3)
locally_relevant_solution_vz_old = locally_relevant_solution_vz;
}
void distribute(VectorType &vec) const
---------------------------— MY PETSC WRAPPERS ---------------------------—
template<int dim>
const std::vector<types::global_dof_index> &indices,
std::vector<PetscScalar> &values)
{
PETSc wrapper to get sets of values from a petsc vector. we assume the vector is ghosted We need to figure out which elements we own locally. Then get a pointer to the elements that are stored here (both the ones we own as well as the ghost elements). In this array, the locally owned elements come first followed by the ghost elements whose position we can get from an index set
IndexSet ghost_indices = locally_relevant_dofs_LS;
PetscInt n_idx, begin, end, i;
n_idx = indices.size();
VecGetOwnershipRange (vector, &begin, &end);
Vec solution_in_local_form = PETSC_NULL;
VecGhostGetLocalForm(vector, &solution_in_local_form);
PetscScalar *soln;
VecGetArray(solution_in_local_form, &soln);
for (i = 0; i < n_idx; ++i)
{
int index = indices[i];
if (index >= begin && index < end)
values[i] = *(soln+index-begin);
else
{
values[i] = *(soln+ghostidx+end-begin);
}
}
VecRestoreArray(solution_in_local_form, &soln);
VecGhostRestoreLocalForm(vector, &solution_in_local_form);
}
template<int dim>
const std::vector<types::global_dof_index> &indices,
std::map<types::global_dof_index, types::global_dof_index> &map_from_Q1_to_Q2,
std::vector<PetscScalar> &values)
{
size_type index_within_set(const size_type global_index) const
void subtract_set(const IndexSet &other)
THIS IS MEANT TO BE USED WITH VELOCITY VECTORS PETSc wrapper to get sets of values from a petsc vector. we assume the vector is ghosted We need to figure out which elements we own locally. Then get a pointer to the elements that are stored here (both the ones we own as well as the ghost elements). In this array, the locally owned elements come first followed by the ghost elements whose position we can get from an index set
IndexSet ghost_indices = locally_relevant_dofs_U;
PetscInt n_idx, begin, end, i;
n_idx = indices.size();
VecGetOwnershipRange (vector, &begin, &end);
Vec solution_in_local_form = PETSC_NULL;
VecGhostGetLocalForm(vector, &solution_in_local_form);
PetscScalar *soln;
VecGetArray(solution_in_local_form, &soln);
for (i = 0; i < n_idx; ++i)
{
int index = map_from_Q1_to_Q2[indices[i]];
if (index >= begin && index < end)
values[i] = *(soln+index-begin);
else
{
values[i] = *(soln+ghostidx+end-begin);
}
}
VecRestoreArray(solution_in_local_form, &soln);
VecGhostRestoreLocalForm(vector, &solution_in_local_form);
}
Annotated version of MultiPhase.cc
#include <fstream>
#include <iostream>
/////////////////////// FOR TRANSPORT PROBLEM /////////////////////// TIME_INTEGRATION
#define FORWARD_EULER 0
#define SSP33 1
PROBLEM
#define FILLING_TANK 0
#define BREAKING_DAM 1
#define FALLING_DROP 2
#define SMALL_WAVE_PERTURBATION 3
#include "NavierStokesSolver.cc"
#include "LevelSetSolver.cc"
#include "utilities.cc"
/////////////////////////////////////////////////// /////////////////// MAIN CLASS //////////////////// ///////////////////////////////////////////////////
template <int dim>
class MultiPhase
{
public:
MultiPhase (const unsigned int degree_LS,
const unsigned int degree_U);
~MultiPhase ();
void run ();
private:
void set_boundary_inlet();
void get_boundary_values_U();
void get_boundary_values_phi(std::vector<types::global_dof_index> &boundary_values_id_phi,
std::vector<double> &boundary_values_phi);
void output_results();
void output_vectors();
void output_rho();
void setup();
void initial_condition();
void init_constraints();
int degree_LS;
int degree_U;
SOLUTION VECTORS
BOUNDARY VECTORS
std::vector<types::global_dof_index> boundary_values_id_u;
std::vector<types::global_dof_index> boundary_values_id_v;
std::vector<types::global_dof_index> boundary_values_id_phi;
std::vector<double> boundary_values_u;
std::vector<double> boundary_values_v;
std::vector<double> boundary_values_phi;
double time;
double time_step;
double final_time;
unsigned int timestep_number;
double cfl;
double umax;
double min_h;
double sharpness;
int sharpness_integer;
unsigned int n_refinement;
unsigned int output_number;
double output_time;
bool get_output;
bool verbose;
FOR NAVIER STOKES
double rho_fluid;
double nu_fluid;
double rho_air;
double nu_air;
double nu;
double eps;
FOR TRANSPORT
double cK;
double cE;
unsigned int TRANSPORT_TIME_INTEGRATION;
std::string ALGORITHM;
unsigned int PROBLEM;
};
template <int dim>
MultiPhase<dim>::MultiPhase (const unsigned int degree_LS,
const unsigned int degree_U)
:
mpi_communicator (MPI_COMM_WORLD),
degree_LS(degree_LS),
fe_LS (degree_LS),
degree_U(degree_U),
fe_U (degree_U),
fe_P (degree_U-1),
pcout (
std::cout,(
Utilities::MPI::this_mpi_process(mpi_communicator)== 0))
{}
template <int dim>
MultiPhase<dim>::~MultiPhase ()
{
dof_handler_LS.clear ();
dof_handler_U.clear ();
dof_handler_P.clear ();
}
///////////////////////////////////// /////////////// SETUP /////////////// /////////////////////////////////////
template <int dim>
void MultiPhase<dim>::setup()
{
setup system LS
dof_handler_LS.distribute_dofs (fe_LS);
locally_owned_dofs_LS = dof_handler_LS.locally_owned_dofs ();
locally_relevant_dofs_LS);
setup system U
dof_handler_U.distribute_dofs (fe_U);
locally_owned_dofs_U = dof_handler_U.locally_owned_dofs ();
locally_relevant_dofs_U);
setup system P
dof_handler_P.distribute_dofs (fe_P);
locally_owned_dofs_P = dof_handler_P.locally_owned_dofs ();
locally_relevant_dofs_P);
init vectors for phi
locally_relevant_solution_phi.reinit(locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
locally_relevant_solution_phi = 0;
completely_distributed_solution_phi.reinit (locally_owned_dofs_P,mpi_communicator);
init vectors for u
locally_relevant_solution_u.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
locally_relevant_solution_u = 0;
completely_distributed_solution_u.reinit (locally_owned_dofs_U,mpi_communicator);
init vectors for v
locally_relevant_solution_v.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
locally_relevant_solution_v = 0;
completely_distributed_solution_v.reinit (locally_owned_dofs_U,mpi_communicator);
init vectors for p
locally_relevant_solution_p.reinit (locally_owned_dofs_P,locally_relevant_dofs_P,mpi_communicator);
locally_relevant_solution_p = 0;
completely_distributed_solution_p.reinit (locally_owned_dofs_P,mpi_communicator);
INIT CONSTRAINTS
init_constraints();
}
template <int dim>
void MultiPhase<dim>::initial_condition()
{
time=0;
Initial conditions init condition for phi
completely_distributed_solution_phi = 0;
InitialPhi<dim>(PROBLEM, sharpness),
completely_distributed_solution_phi);
constraints.
distribute (completely_distributed_solution_phi);
locally_relevant_solution_phi = completely_distributed_solution_phi;
init condition for u=0
completely_distributed_solution_u = 0;
completely_distributed_solution_u);
constraints.
distribute (completely_distributed_solution_u);
locally_relevant_solution_u = completely_distributed_solution_u;
init condition for v
completely_distributed_solution_v = 0;
completely_distributed_solution_v);
constraints.
distribute (completely_distributed_solution_v);
locally_relevant_solution_v = completely_distributed_solution_v;
init condition for p
completely_distributed_solution_p = 0;
completely_distributed_solution_p);
constraints.
distribute (completely_distributed_solution_p);
locally_relevant_solution_p = completely_distributed_solution_p;
}
template <int dim>
void MultiPhase<dim>::init_constraints()
{
constraints.
reinit (locally_relevant_dofs_LS);
}
template <int dim>
void MultiPhase<dim>::get_boundary_values_U()
{
std::map<types::global_dof_index, double> map_boundary_values_u;
std::map<types::global_dof_index, double> map_boundary_values_v;
std::map<types::global_dof_index, double> map_boundary_values_w;
void reinit(const IndexSet &local_constraints=IndexSet())
NO-SLIP CONDITION
if (PROBLEM==BREAKING_DAM || PROBLEM==FALLING_DROP)
{
LEFT
RIGHT
BOTTOM
TOP
}
else if (PROBLEM==SMALL_WAVE_PERTURBATION)
{
no slip in bottom and top and slip in left and right LEFT
RIGHT
BOTTOM
TOP
}
else if (PROBLEM==FILLING_TANK)
{
LEFT: entry in x, zero in y
RIGHT: no-slip condition
BOTTOM: non-slip
TOP: exit in y, zero in x
}
else
{
pcout << "Error in type of PROBLEM at Boundary Conditions" << std::endl;
abort();
}
boundary_values_id_u.resize(map_boundary_values_u.size());
boundary_values_id_v.resize(map_boundary_values_v.size());
boundary_values_u.resize(map_boundary_values_u.size());
boundary_values_v.resize(map_boundary_values_v.size());
std::map<types::global_dof_index,double>::const_iterator boundary_value_u =map_boundary_values_u.begin();
std::map<types::global_dof_index,double>::const_iterator boundary_value_v =map_boundary_values_v.begin();
for (int i=0; boundary_value_u !=map_boundary_values_u.end(); ++boundary_value_u, ++i)
{
boundary_values_id_u[i]=boundary_value_u->first;
boundary_values_u[i]=boundary_value_u->second;
}
for (int i=0; boundary_value_v !=map_boundary_values_v.end(); ++boundary_value_v, ++i)
{
boundary_values_id_v[i]=boundary_value_v->first;
boundary_values_v[i]=boundary_value_v->second;
}
}
template <int dim>
void MultiPhase<dim>::set_boundary_inlet()
{
const QGauss<dim-1> face_quadrature_formula(1);
const unsigned int n_face_q_points = face_quadrature_formula.size();
std::vector<double> u_value (n_face_q_points);
std::vector<double> v_value (n_face_q_points);
endc_U = dof_handler_U.end();
for (; cell_U!=endc_U; ++cell_U)
if (cell_U->is_locally_owned())
for (unsigned int face=0; face<GeometryInfo<dim>::faces_per_cell; ++face)
if (cell_U->face(face)->at_boundary())
{
fe_face_values.reinit(cell_U,face);
fe_face_values.get_function_values(locally_relevant_solution_u,u_value);
fe_face_values.get_function_values(locally_relevant_solution_v,v_value);
u[0]=u_value[0];
u[1]=v_value[0];
if (fe_face_values.normal_vector(0)*u < -1e-14)
cell_U->face(face)->set_boundary_id(10);
}
}
template <int dim>
void MultiPhase<dim>::get_boundary_values_phi(std::vector<types::global_dof_index> &boundary_values_id_phi,
std::vector<double> &boundary_values_phi)
{
std::map<types::global_dof_index, double> map_boundary_values_phi;
set_boundary_inlet();
boundary_values_id_phi.resize(map_boundary_values_phi.size());
boundary_values_phi.resize(map_boundary_values_phi.size());
std::map<types::global_dof_index,double>::const_iterator boundary_value_phi = map_boundary_values_phi.begin();
for (int i=0; boundary_value_phi !=map_boundary_values_phi.end(); ++boundary_value_phi, ++i)
{
boundary_values_id_phi[i]=boundary_value_phi->first;
boundary_values_phi[i]=boundary_value_phi->second;
}
}
template<int dim>
void MultiPhase<dim>::output_results()
{
@ update_normal_vectors
Normal vectors.
output_vectors();
output_rho();
output_number++;
}
template <int dim>
void MultiPhase<dim>::output_vectors()
{
const std::string filename = ("sol_vectors-" +
"." +
std::ofstream output ((filename + ".vtu").c_str());
{
std::vector<std::string> filenames;
for (unsigned int i=0;
++i)
filenames.push_back ("sol_vectors-" +
"." +
".vtu");
std::ofstream master_output ((filename + ".pvtu").c_str());
}
}
template <int dim>
void MultiPhase<dim>::output_rho()
{
Postprocessor<dim> postprocessor(eps,rho_air,rho_fluid);
const std::string filename = ("sol_rho-" +
"." +
std::ofstream output ((filename + ".vtu").c_str());
{
std::vector<std::string> filenames;
for (unsigned int i=0;
++i)
filenames.push_back ("sol_rho-" +
"." +
".vtu");
std::ofstream master_output ((filename + ".pvtu").c_str());
}
}
template <int dim>
void MultiPhase<dim>::run()
{
void attach_dof_handler(const DoFHandler< dim, spacedim > &)
void add_data_vector(const VectorType &data, const std::vector< std::string > &names, const DataVectorType type=type_automatic, const std::vector< DataComponentInterpretation::DataComponentInterpretation > &data_component_interpretation={})
virtual void build_patches(const unsigned int n_subdivisions=0)
void write_pvtu_record(std::ostream &out, const std::vector< std::string > &piece_names) const
void write_vtu(std::ostream &out) const
unsigned int this_mpi_process(const MPI_Comm &mpi_communicator)
unsigned int n_mpi_processes(const MPI_Comm &mpi_communicator)
std::string int_to_string(const unsigned int value, const unsigned int digits=numbers::invalid_unsigned_int)
//////////////////// GENERAL PARAMETERS ////////////////////
umax=1;
cfl=0.1;
verbose = true;
get_output = true;
output_number = 0;
n_refinement=8;
output_time = 0.1;
final_time = 10.0;
////////////////////////////////////////// PARAMETERS FOR THE NAVIER STOKES PROBLEM //////////////////////////////////////////
rho_fluid = 1000.;
nu_fluid = 1.0;
rho_air = 1.0;
nu_air = 1.8e-2;
PROBLEM=BREAKING_DAM;
PROBLEM=FILLING_TANK; PROBLEM=SMALL_WAVE_PERTURBATION; PROBLEM=FALLING_DROP;
ForceTerms<dim> force_function(std::vector<double> {0.0,-1.0});
////////////////////////////////// PARAMETERS FOR TRANSPORT PROBLEM //////////////////////////////////
cK = 1.0;
cE = 1.0;
sharpness_integer=10;
TRANSPORT_TIME_INTEGRATION=FORWARD_EULER;
TRANSPORT_TIME_INTEGRATION=SSP33;
ALGORITHM = "MPP_u1"; ALGORITHM = "NMPP_uH";
ADJUST PARAMETERS ACCORDING TO PROBLEM
if (PROBLEM==FALLING_DROP)
n_refinement=7;
////////// GEOMETRY //////////
if (PROBLEM==FILLING_TANK)
else if (PROBLEM==BREAKING_DAM || PROBLEM==SMALL_WAVE_PERTURBATION)
{
std::vector< unsigned int > repetitions;
repetitions.push_back(2);
repetitions.push_back(1);
}
else if (PROBLEM==FALLING_DROP)
{
std::vector< unsigned int > repetitions;
repetitions.push_back(1);
repetitions.push_back(4);
}
void hyper_rectangle(Triangulation< dim, spacedim > &tria, const Point< dim > &p1, const Point< dim > &p2, const bool colorize=false)
void subdivided_hyper_rectangle(Triangulation< dim, spacedim > &tria, const std::vector< unsigned int > &repetitions, const Point< dim > &p1, const Point< dim > &p2, const bool colorize=false)
SETUP
PARAMETERS FOR TIME STEPPING
time_step = cfl*min_h/umax;
eps=1.*min_h;
sharpness=sharpness_integer*min_h;
::VectorizedArray< Number, width > sqrt(const ::VectorizedArray< Number, width > &)
INITIAL CONDITIONS
initial_condition();
output_results();
NAVIER STOKES SOLVER
NavierStokesSolver<dim> navier_stokes (degree_LS,degree_U,
time_step,eps,
rho_air,nu_air,
rho_fluid,nu_fluid,
force_function,
verbose,
BOUNDARY CONDITIONS FOR NAVIER STOKES
get_boundary_values_U();
navier_stokes.set_boundary_conditions(boundary_values_id_u, boundary_values_id_v,
boundary_values_u, boundary_values_v);
set INITIAL CONDITION within NAVIER STOKES
navier_stokes.initial_condition(locally_relevant_solution_phi,
locally_relevant_solution_u,
locally_relevant_solution_v,
locally_relevant_solution_p);
TRANSPORT SOLVER
LevelSetSolver<dim> transport_solver (degree_LS,degree_U,
time_step,cK,cE,
verbose,
ALGORITHM,
TRANSPORT_TIME_INTEGRATION,
mpi_communicator);
BOUNDARY CONDITIONS FOR PHI
get_boundary_values_phi(boundary_values_id_phi,boundary_values_phi);
transport_solver.set_boundary_conditions(boundary_values_id_phi,boundary_values_phi);
set INITIAL CONDITION within TRANSPORT PROBLEM
transport_solver.initial_condition(locally_relevant_solution_phi,
locally_relevant_solution_u,
locally_relevant_solution_v);
int dofs_U = 2*dof_handler_U.n_dofs();
int dofs_P = 2*dof_handler_P.n_dofs();
int dofs_LS = dof_handler_LS.n_dofs();
int dofs_TOTAL = dofs_U+dofs_P+dofs_LS;
NO BOUNDARY CONDITIONS for LEVEL SET
pcout << "Cfl: " << cfl << "; umax: " << umax << "; min h: " << min_h
<< "; time step: " << time_step << std::endl;
pcout << " Number of active cells: "
<< " Number of degrees of freedom: " << std::endl
<< " U: " << dofs_U << std::endl
<< " P: " << dofs_P << std::endl
<< " LS: " << dofs_LS << std::endl
<< " TOTAL: " << dofs_TOTAL
<< std::endl;
TIME STEPPING
for (timestep_number=1, time=time_step; time<=final_time;
time+=time_step,++timestep_number)
{
pcout << "Time step " << timestep_number
<< " at t=" << time
<< std::endl;
GET NAVIER STOKES VELOCITY
navier_stokes.set_phi(locally_relevant_solution_phi);
navier_stokes.nth_time_step();
navier_stokes.get_velocity(locally_relevant_solution_u,locally_relevant_solution_v);
transport_solver.set_velocity(locally_relevant_solution_u,locally_relevant_solution_v);
GET LEVEL SET SOLUTION
transport_solver.nth_time_step();
transport_solver.get_unp1(locally_relevant_solution_phi);
if (get_output && time-(output_number)*output_time>0)
output_results();
}
navier_stokes.get_velocity(locally_relevant_solution_u, locally_relevant_solution_v);
transport_solver.get_unp1(locally_relevant_solution_phi);
if (get_output)
output_results();
}
int main(int argc, char *argv[])
{
try
{
PetscInitialize(&argc, &argv, PETSC_NULL, PETSC_NULL);
{
unsigned int degree_LS = 1;
unsigned int degree_U = 2;
MultiPhase<2> multi_phase(degree_LS, degree_U);
multi_phase.run();
}
PetscFinalize();
}
catch (std::exception &exc)
{
std::cerr << std::endl << std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl << std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
unsigned int depth_console(const unsigned int n)
Annotated version of NavierStokesSolver.cc
#include <fstream>
#include <iostream>
#include <memory>
#define MAX_NUM_ITER_TO_RECOMPUTE_PRECONDITIONER 10
///////////////////////////////////////////////////////////// /////////////////// NAVIER STOKES SOLVER //////////////////// /////////////////////////////////////////////////////////////
template<int dim>
class NavierStokesSolver
{
public:
constructor for using LEVEL SET
NavierStokesSolver(const unsigned int degree_LS,
const unsigned int degree_U,
const double time_step,
const double eps,
const double rho_air,
const double nu_air,
const double rho_fluid,
const double nu_fluid,
const bool verbose,
constructor for NOT LEVEL SET
NavierStokesSolver(const unsigned int degree_LS,
const unsigned int degree_U,
const double time_step,
const bool verbose,
rho and nu functions
initial conditions
boundary conditions
void set_boundary_conditions(std::vector<types::global_dof_index> boundary_values_id_u,
std::vector<types::global_dof_index> boundary_values_id_v, std::vector<double> boundary_values_u,
std::vector<double> boundary_values_v);
void set_boundary_conditions(std::vector<types::global_dof_index> boundary_values_id_u,
std::vector<types::global_dof_index> boundary_values_id_v,
std::vector<types::global_dof_index> boundary_values_id_w, std::vector<double> boundary_values_u,
std::vector<double> boundary_values_v, std::vector<double> boundary_values_w);
DO STEPS
SETUP
void setup();
~NavierStokesSolver();
private:
SETUP AND INITIAL CONDITION
void setup_DOF();
void setup_VECTORS();
void init_constraints();
ASSEMBLE SYSTEMS
void assemble_system_U();
void assemble_system_dpsi_q();
SOLVERS
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner,
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner,
GET DIFFERENT FIELDS
void get_rho_and_nu(double phi);
void get_velocity();
void get_pressure();
OTHERS
void save_old_solution();
int degree_LS;
int degree_U;
double rho_air;
double nu_air;
double rho_fluid;
double nu_fluid;
double time_step;
double eps;
bool verbose;
unsigned int LEVEL_SET;
unsigned int RHO_TIMES_RHS;
double rho_min;
double rho_value;
double nu_value;
double h;
double umax;
int degree_MAX;
std::vector<types::global_dof_index> boundary_values_id_u;
std::vector<types::global_dof_index> boundary_values_id_v;
std::vector<types::global_dof_index> boundary_values_id_w;
std::vector<double> boundary_values_u;
std::vector<double> boundary_values_v;
std::vector<double> boundary_values_w;
bool rebuild_Matrix_U;
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner_Matrix_u;
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner_Matrix_v;
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner_Matrix_w;
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner_S;
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner_M;
bool rebuild_S_M;
bool rebuild_Matrix_U_preconditioners;
bool rebuild_S_M_preconditioners;
};
CONSTRUCTOR FOR LEVEL SET
template<int dim>
NavierStokesSolver<dim>::NavierStokesSolver(const unsigned int degree_LS,
const unsigned int degree_U,
const double time_step,
const double eps,
const double rho_air,
const double nu_air,
const double rho_fluid,
const double nu_fluid,
const bool verbose,
:
mpi_communicator(mpi_communicator),
degree_LS(degree_LS),
fe_LS(degree_LS),
degree_U(degree_U),
fe_U(degree_U),
fe_P(degree_U-1),
force_function(force_function),
This is dummy since rho and nu functions won't be used
rho_function(force_function),
nu_function(force_function),
rho_air(rho_air),
nu_air(nu_air),
rho_fluid(rho_fluid),
nu_fluid(nu_fluid),
time_step(time_step),
eps(eps),
verbose(verbose),
LEVEL_SET(1),
RHO_TIMES_RHS(1),
rebuild_Matrix_U(true),
rebuild_S_M(true),
rebuild_Matrix_U_preconditioners(true),
rebuild_S_M_preconditioners(true)
{setup();}
CONSTRUCTOR NOT FOR LEVEL SET
template<int dim>
NavierStokesSolver<dim>::NavierStokesSolver(const unsigned int degree_LS,
const unsigned int degree_U,
const double time_step,
const bool verbose,
mpi_communicator(mpi_communicator),
degree_LS(degree_LS),
fe_LS(degree_LS),
degree_U(degree_U),
fe_U(degree_U),
fe_P(degree_U-1),
force_function(force_function),
rho_function(rho_function),
nu_function(nu_function),
time_step(time_step),
verbose(verbose),
LEVEL_SET(0),
RHO_TIMES_RHS(0),
pcout(
std::cout,(
Utilities::MPI::this_mpi_process(mpi_communicator)==0)),
rebuild_Matrix_U(true),
rebuild_S_M(true),
rebuild_Matrix_U_preconditioners(true),
rebuild_S_M_preconditioners(true)
{setup();}
template<int dim>
NavierStokesSolver<dim>::~NavierStokesSolver()
{
dof_handler_LS.clear();
dof_handler_U.clear();
dof_handler_P.clear();
}
///////////////////////////////////////////////////////// ////////////////// SETTERS AND GETTERS ////////////////// /////////////////////////////////////////////////////////
template<int dim>
void NavierStokesSolver<dim>::set_rho_and_nu_functions(
const Function<dim> &rho_function,
{
this->rho_function=rho_function;
this->nu_function=nu_function;
}
template<int dim>
{
this->locally_relevant_solution_phi=locally_relevant_solution_phi;
this->locally_relevant_solution_u=locally_relevant_solution_u;
this->locally_relevant_solution_v=locally_relevant_solution_v;
this->locally_relevant_solution_p=locally_relevant_solution_p;
set old vectors to the initial condition (just for first time step)
save_old_solution();
}
template<int dim>
{
this->locally_relevant_solution_phi=locally_relevant_solution_phi;
this->locally_relevant_solution_u=locally_relevant_solution_u;
this->locally_relevant_solution_v=locally_relevant_solution_v;
this->locally_relevant_solution_w=locally_relevant_solution_w;
this->locally_relevant_solution_p=locally_relevant_solution_p;
set old vectors to the initial condition (just for first time step)
save_old_solution();
}
template<int dim>
void NavierStokesSolver<dim>::set_boundary_conditions(std::vector<types::global_dof_index> boundary_values_id_u,
std::vector<types::global_dof_index> boundary_values_id_v,
std::vector<double> boundary_values_u,
std::vector<double> boundary_values_v)
{
this->boundary_values_id_u=boundary_values_id_u;
this->boundary_values_id_v=boundary_values_id_v;
this->boundary_values_u=boundary_values_u;
this->boundary_values_v=boundary_values_v;
}
template<int dim>
void NavierStokesSolver<dim>::set_boundary_conditions(std::vector<types::global_dof_index> boundary_values_id_u,
std::vector<types::global_dof_index> boundary_values_id_v,
std::vector<types::global_dof_index> boundary_values_id_w,
std::vector<double> boundary_values_u,
std::vector<double> boundary_values_v,
std::vector<double> boundary_values_w)
{
this->boundary_values_id_u=boundary_values_id_u;
this->boundary_values_id_v=boundary_values_id_v;
this->boundary_values_id_w=boundary_values_id_w;
this->boundary_values_u=boundary_values_u;
this->boundary_values_v=boundary_values_v;
this->boundary_values_w=boundary_values_w;
}
template<int dim>
{
this->locally_relevant_solution_u=locally_relevant_solution_u;
this->locally_relevant_solution_v=locally_relevant_solution_v;
}
template<int dim>
{
this->locally_relevant_solution_u=locally_relevant_solution_u;
this->locally_relevant_solution_v=locally_relevant_solution_v;
this->locally_relevant_solution_w=locally_relevant_solution_w;
}
template<int dim>
{
this->locally_relevant_solution_phi=locally_relevant_solution_phi;
}
template<int dim>
void NavierStokesSolver<dim>::get_rho_and_nu(double phi)
{
double H=0;
get rho, nu
if (phi>eps)
H=1;
else if (phi<-eps)
H=-1;
else
H=phi/eps;
rho_value=rho_fluid*(1+H)/2.+rho_air*(1-H)/2.;
nu_value=nu_fluid*(1+H)/2.+nu_air*(1-H)/2.;
rho_value=rho_fluid*(1+phi)/2.+rho_air*(1-phi)/2.; nu_value=nu_fluid*(1+phi)/2.+nu_air*(1-phi)/2.;
}
template<int dim>
{
locally_relevant_solution_p=this->locally_relevant_solution_p;
}
template<int dim>
{
locally_relevant_solution_u=this->locally_relevant_solution_u;
locally_relevant_solution_v=this->locally_relevant_solution_v;
}
template<int dim>
{
locally_relevant_solution_u=this->locally_relevant_solution_u;
locally_relevant_solution_v=this->locally_relevant_solution_v;
locally_relevant_solution_w=this->locally_relevant_solution_w;
}
/////////////////////////////////////////////////// /////////// SETUP AND INITIAL CONDITION /////////// ///////////////////////////////////////////////////
template<int dim>
void NavierStokesSolver<dim>::setup()
{
pcout<<"***** SETUP IN NAVIER STOKES SOLVER *****"<<std::endl;
setup_DOF();
init_constraints();
setup_VECTORS();
}
template<int dim>
void NavierStokesSolver<dim>::setup_DOF()
{
rho_min = 1.;
degree_MAX=
std::max(degree_LS,degree_U);
setup system LS
dof_handler_LS.distribute_dofs(fe_LS);
locally_owned_dofs_LS=dof_handler_LS.locally_owned_dofs();
setup system U
dof_handler_U.distribute_dofs(fe_U);
locally_owned_dofs_U=dof_handler_U.locally_owned_dofs();
setup system P
dof_handler_P.distribute_dofs(fe_P);
locally_owned_dofs_P=dof_handler_P.locally_owned_dofs();
}
template<int dim>
void NavierStokesSolver<dim>::setup_VECTORS()
{
init vectors for phi
locally_relevant_solution_phi.reinit(locally_owned_dofs_LS,locally_relevant_dofs_LS,
mpi_communicator);
locally_relevant_solution_phi=0;
init vectors for u
locally_relevant_solution_u.reinit(locally_owned_dofs_U,locally_relevant_dofs_U,
mpi_communicator);
locally_relevant_solution_u=0;
completely_distributed_solution_u.reinit(locally_owned_dofs_U,mpi_communicator);
system_rhs_u.reinit(locally_owned_dofs_U,mpi_communicator);
init vectors for u_old
locally_relevant_solution_u_old.reinit(locally_owned_dofs_U,locally_relevant_dofs_U,
mpi_communicator);
locally_relevant_solution_u_old=0;
init vectors for v
locally_relevant_solution_v.reinit(locally_owned_dofs_U,locally_relevant_dofs_U,
mpi_communicator);
locally_relevant_solution_v=0;
completely_distributed_solution_v.reinit(locally_owned_dofs_U,mpi_communicator);
system_rhs_v.reinit(locally_owned_dofs_U,mpi_communicator);
init vectors for v_old
locally_relevant_solution_v_old.reinit(locally_owned_dofs_U,locally_relevant_dofs_U,
mpi_communicator);
locally_relevant_solution_v_old=0;
init vectors for w
locally_relevant_solution_w.reinit(locally_owned_dofs_U,locally_relevant_dofs_U,
mpi_communicator);
locally_relevant_solution_w=0;
completely_distributed_solution_w.reinit(locally_owned_dofs_U,mpi_communicator);
system_rhs_w.reinit(locally_owned_dofs_U,mpi_communicator);
init vectors for w_old
locally_relevant_solution_w_old.reinit(locally_owned_dofs_U,locally_relevant_dofs_U,
mpi_communicator);
locally_relevant_solution_w_old=0;
init vectors for dpsi
locally_relevant_solution_psi.reinit(locally_owned_dofs_P,locally_relevant_dofs_P,
mpi_communicator);
locally_relevant_solution_psi=0;
system_rhs_psi.reinit(locally_owned_dofs_P,mpi_communicator);
init vectors for dpsi old
locally_relevant_solution_psi_old.reinit(locally_owned_dofs_P,locally_relevant_dofs_P,
mpi_communicator);
locally_relevant_solution_psi_old=0;
init vectors for q
completely_distributed_solution_q.reinit(locally_owned_dofs_P,mpi_communicator);
system_rhs_q.reinit(locally_owned_dofs_P,mpi_communicator);
init vectors for psi
completely_distributed_solution_psi.reinit(locally_owned_dofs_P,mpi_communicator);
init vectors for p
locally_relevant_solution_p.reinit(locally_owned_dofs_P,locally_relevant_dofs_P,
mpi_communicator);
locally_relevant_solution_p=0;
completely_distributed_solution_p.reinit(locally_owned_dofs_P,mpi_communicator);
//////////////////////// Initialize constraints ////////////////////////
////////////////// Sparsity pattern ////////////////// sparsity pattern for A
dof_handler_U.locally_owned_dofs(),
mpi_communicator,
locally_relevant_dofs_U);
system_Matrix_u.reinit(dof_handler_U.locally_owned_dofs(),
dof_handler_U.locally_owned_dofs(),
dsp_Matrix,
mpi_communicator);
system_Matrix_v.reinit(dof_handler_U.locally_owned_dofs(),
dof_handler_U.locally_owned_dofs(),
dsp_Matrix,
mpi_communicator);
system_Matrix_w.reinit(dof_handler_U.locally_owned_dofs(),
dof_handler_U.locally_owned_dofs(),
dsp_Matrix,
mpi_communicator);
rebuild_Matrix_U=true;
sparsity pattern for S
dof_handler_P.locally_owned_dofs(),
mpi_communicator,
locally_relevant_dofs_P);
system_S.reinit(dof_handler_P.locally_owned_dofs(),
dof_handler_P.locally_owned_dofs(),
dsp_S,
mpi_communicator);
sparsity pattern for M
dof_handler_P.locally_owned_dofs(),
mpi_communicator,
locally_relevant_dofs_P);
system_M.reinit(dof_handler_P.locally_owned_dofs(),
dof_handler_P.locally_owned_dofs(),
dsp_M,
mpi_communicator);
rebuild_S_M=true;
}
template<int dim>
void NavierStokesSolver<dim>::init_constraints()
{
grl constraints
constraints.
reinit(locally_relevant_dofs_U);
constraints for dpsi
constraints_psi.clear();
constraints_psi.reinit(locally_relevant_dofs_P);
if (constraints_psi.can_store_line(0)) constraints_psi.add_line(0); //constraint u0 = 0
constraints_psi.close();
}
/////////////////////////////////////////////////// //////////////// ASSEMBLE SYSTEMS ///////////////// ///////////////////////////////////////////////////
template<int dim>
void NavierStokesSolver<dim>::assemble_system_U()
{
if (rebuild_Matrix_U==true)
{
system_Matrix_u=0;
system_Matrix_v=0;
system_Matrix_w=0;
}
system_rhs_u=0;
system_rhs_v=0;
system_rhs_w=0;
const unsigned int dofs_per_cell=fe_U.dofs_per_cell;
const unsigned int n_q_points=quadrature_formula.size();
std::vector<double> phiqnp1(n_q_points);
std::vector<double> uqn(n_q_points);
std::vector<double> uqnm1(n_q_points);
std::vector<double> vqn(n_q_points);
std::vector<double> vqnm1(n_q_points);
std::vector<double> wqn(n_q_points);
std::vector<double> wqnm1(n_q_points);
FOR Explicit nonlinearity std::vector<Tensor<1, dim> > grad_un(n_q_points); std::vector<Tensor<1, dim> > grad_vn(n_q_points); std::vector<Tensor<1, dim> > grad_wn(n_q_points); Tensor<1, dim> Un;
std::vector<Tensor<1, dim> > grad_pqn(n_q_points);
std::vector<Tensor<1, dim> > grad_psiqn(n_q_points);
std::vector<Tensor<1, dim> > grad_psiqnm1(n_q_points);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
std::vector<Tensor<1, dim> > shape_grad(dofs_per_cell);
std::vector<double> shape_value(dofs_per_cell);
double force_u;
double force_v;
double force_w;
double pressure_grad_u;
double pressure_grad_v;
double pressure_grad_w;
double u_star=0;
double v_star=0;
double w_star=0;
double rho_star;
double rho;
cell_U=dof_handler_U.
begin_active(), endc_U=dof_handler_U.end();
for (; cell_U!=endc_U; ++cell_U,++cell_P,++cell_LS)
if (cell_U->is_locally_owned())
{
cell_A_u=0;
cell_rhs_u=0;
cell_rhs_v=0;
cell_rhs_w=0;
fe_values_LS.reinit(cell_LS);
fe_values_U.reinit(cell_U);
fe_values_P.reinit(cell_P);
get function values for LS
fe_values_LS.get_function_values(locally_relevant_solution_phi,phiqnp1);
get function values for U
fe_values_U.get_function_values(locally_relevant_solution_u,uqn);
fe_values_U.get_function_values(locally_relevant_solution_u_old,uqnm1);
fe_values_U.get_function_values(locally_relevant_solution_v,vqn);
fe_values_U.get_function_values(locally_relevant_solution_v_old,vqnm1);
if (dim==3)
{
fe_values_U.get_function_values(locally_relevant_solution_w,wqn);
fe_values_U.get_function_values(locally_relevant_solution_w_old,wqnm1);
}
For explicit nonlinearity get gradient values for U fe_values_U.get_function_gradients(locally_relevant_solution_u,grad_un); fe_values_U.get_function_gradients(locally_relevant_solution_v,grad_vn); if (dim==3) fe_values_U.get_function_gradients(locally_relevant_solution_w,grad_wn);
get values and gradients for p and dpsi
fe_values_P.get_function_gradients(locally_relevant_solution_p,grad_pqn);
fe_values_P.get_function_gradients(locally_relevant_solution_psi,grad_psiqn);
fe_values_P.get_function_gradients(locally_relevant_solution_psi_old,grad_psiqnm1);
for (unsigned int q_point=0; q_point<n_q_points; ++q_point)
{
const double JxW=fe_values_U.JxW(q_point);
for (unsigned int i=0; i<dofs_per_cell; ++i)
{
shape_grad[i]=fe_values_U.shape_grad(i,q_point);
shape_value[i]=fe_values_U.shape_value(i,q_point);
}
pressure_grad_u=(grad_pqn[q_point][0]+4./3*grad_psiqn[q_point][0]-1./3*grad_psiqnm1[q_point][0]);
pressure_grad_v=(grad_pqn[q_point][1]+4./3*grad_psiqn[q_point][1]-1./3*grad_psiqnm1[q_point][1]);
if (dim==3)
pressure_grad_w=(grad_pqn[q_point][2]+4./3*grad_psiqn[q_point][2]-1./3*grad_psiqnm1[q_point][2]);
if (LEVEL_SET==1)
get_rho_and_nu(phiqnp1[q_point]);
else
{
rho_value=rho_function.value(fe_values_U.quadrature_point(q_point));
nu_value=nu_function.value(fe_values_U.quadrature_point(q_point));
}
Non-linearity: for semi-implicit
u_star=2*uqn[q_point]-uqnm1[q_point];
v_star=2*vqn[q_point]-vqnm1[q_point];
if (dim==3)
w_star=2*wqn[q_point]-wqnm1[q_point];
for explicit nonlinearity Un[0] = uqn[q_point]; Un[1] = vqn[q_point]; if (dim==3) Un[2] = wqn[q_point];
double nonlinearity_u = Un*grad_un[q_point]; double nonlinearity_v = Un*grad_vn[q_point]; double nonlinearity_w = 0; if (dim==3) nonlinearity_w = Un*grad_wn[q_point];
rho_star=rho_value;
rho=rho_value;
FORCE TERMS
force_function.
vector_value(fe_values_U.quadrature_point(q_point),force_terms);
force_u=force_terms[0];
force_v=force_terms[1];
if (dim==3)
force_w=force_terms[2];
if (RHO_TIMES_RHS==1)
{
force_u*=rho;
force_v*=rho;
if (dim==3)
force_w*=rho;
}
for (unsigned int i=0; i<dofs_per_cell; ++i)
{
cell_rhs_u(i)+=((4./3*rho*uqn[q_point]-1./3*rho*uqnm1[q_point]
+2./3*time_step*(force_u-pressure_grad_u)
virtual void vector_value(const Point< dim > &p, Vector< RangeNumberType > &values) const
-2./3*time_step*rho*nonlinearity_u
)*shape_value[i])*JxW;
cell_rhs_v(i)+=((4./3*rho*vqn[q_point]-1./3*rho*vqnm1[q_point]
+2./3*time_step*(force_v-pressure_grad_v)
-2./3*time_step*rho*nonlinearity_v
)*shape_value[i])*JxW;
if (dim==3)
cell_rhs_w(i)+=((4./3*rho*wqn[q_point]-1./3*rho*wqnm1[q_point]
+2./3*time_step*(force_w-pressure_grad_w)
-2./3*time_step*rho*nonlinearity_w
)*shape_value[i])*JxW;
if (rebuild_Matrix_U==true)
for (unsigned int j=0; j<dofs_per_cell; ++j)
{
if (dim==2)
cell_A_u(i,j)+=(rho_star*shape_value[i]*shape_value[j]
+2./3*time_step*nu_value*(shape_grad[i]*shape_grad[j])
+2./3*time_step*rho*shape_value[i]
*(u_star*shape_grad[j][0]+v_star*shape_grad[j][1])
)*JxW;
else
cell_A_u(i,j)+=(rho_star*shape_value[i]*shape_value[j]
+2./3*time_step*nu_value*(shape_grad[i]*shape_grad[j])
+2./3*time_step*rho*shape_value[i]
*(u_star*shape_grad[j][0]+v_star*shape_grad[j][1]+w_star*shape_grad[j][2])
)*JxW;
}
}
}
cell_U->get_dof_indices(local_dof_indices);
distribute
if (rebuild_Matrix_U==true)
if (dim==3)
}
if (rebuild_Matrix_U==true)
{
system_Matrix_v.copy_from(system_Matrix_u);
if (dim==3)
system_Matrix_w.copy_from(system_Matrix_u);
}
void distribute_local_to_global(const InVector &local_vector, const std::vector< size_type > &local_dof_indices, OutVector &global_vector) const
BOUNDARY CONDITIONS
system_rhs_u.set(boundary_values_id_u,boundary_values_u);
system_rhs_v.set(boundary_values_id_v,boundary_values_v);
if (dim==3)
{
system_rhs_w.set(boundary_values_id_w,boundary_values_w);
}
if (rebuild_Matrix_U)
{
system_Matrix_u.clear_rows(boundary_values_id_u,1);
system_Matrix_v.clear_rows(boundary_values_id_v,1);
if (dim==3)
system_Matrix_w.clear_rows(boundary_values_id_w,1);
if (rebuild_Matrix_U_preconditioners)
{
PRECONDITIONERS
rebuild_Matrix_U_preconditioners=false;
if (dim==3)
}
}
rebuild_Matrix_U=true;
}
template<int dim>
void NavierStokesSolver<dim>::assemble_system_dpsi_q()
{
if (rebuild_S_M==true)
{
system_S=0;
system_M=0;
}
system_rhs_psi=0;
system_rhs_q=0;
const unsigned int dofs_per_cell=fe_P.dofs_per_cell;
const unsigned int n_q_points=quadrature_formula.size();
std::vector<double> phiqnp1(n_q_points);
std::vector<Tensor<1, dim> > gunp1(n_q_points);
std::vector<Tensor<1, dim> > gvnp1(n_q_points);
std::vector<Tensor<1, dim> > gwnp1(n_q_points);
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
std::vector<double> shape_value(dofs_per_cell);
std::vector<Tensor<1, dim> > shape_grad(dofs_per_cell);
cell_P=dof_handler_P.begin_active(), endc_P=dof_handler_P.end();
for (; cell_P!=endc_P; ++cell_P,++cell_U,++cell_LS)
if (cell_P->is_locally_owned())
{
cell_S=0;
cell_M=0;
cell_rhs_psi=0;
cell_rhs_q=0;
fe_values_P.reinit(cell_P);
fe_values_U.reinit(cell_U);
fe_values_LS.reinit(cell_LS);
get function values for LS
fe_values_LS.get_function_values(locally_relevant_solution_phi,phiqnp1);
get function grads for u and v
fe_values_U.get_function_gradients(locally_relevant_solution_u,gunp1);
fe_values_U.get_function_gradients(locally_relevant_solution_v,gvnp1);
if (dim==3)
fe_values_U.get_function_gradients(locally_relevant_solution_w,gwnp1);
for (unsigned int q_point=0; q_point<n_q_points; ++q_point)
{
const double JxW=fe_values_P.JxW(q_point);
double divU = gunp1[q_point][0]+gvnp1[q_point][1];
if (dim==3) divU += gwnp1[q_point][2];
for (unsigned int i=0; i<dofs_per_cell; ++i)
{
shape_value[i]=fe_values_P.shape_value(i,q_point);
shape_grad[i]=fe_values_P.shape_grad(i,q_point);
}
if (LEVEL_SET==1)
get_rho_and_nu (phiqnp1[q_point]);
else
nu_value=nu_function.value(fe_values_U.quadrature_point(q_point));
for (unsigned int i=0; i<dofs_per_cell; ++i)
{
cell_rhs_psi(i)+=-3./2./time_step*rho_min*divU*shape_value[i]*JxW;
cell_rhs_q(i)-=nu_value*divU*shape_value[i]*JxW;
if (rebuild_S_M==true)
{
for (unsigned int j=0; j<dofs_per_cell; ++j)
if (i==j)
{
cell_S(i,j)+=shape_grad[i]*shape_grad[j]*JxW+1E-10;
cell_M(i,j)+=shape_value[i]*shape_value[j]*JxW;
}
else
{
cell_S(i,j)+=shape_grad[i]*shape_grad[j]*JxW;
cell_M(i,j)+=shape_value[i]*shape_value[j]*JxW;
}
}
}
}
cell_P->get_dof_indices(local_dof_indices);
Distribute
if (rebuild_S_M==true)
{
constraints_psi.distribute_local_to_global(cell_S,local_dof_indices,system_S);
constraints_psi.distribute_local_to_global(cell_M,local_dof_indices,system_M);
}
constraints_psi.distribute_local_to_global(cell_rhs_q,local_dof_indices,system_rhs_q);
constraints_psi.distribute_local_to_global(cell_rhs_psi,local_dof_indices,system_rhs_psi);
}
if (rebuild_S_M==true)
{
if (rebuild_S_M_preconditioners)
{
rebuild_S_M_preconditioners=false;
}
}
rebuild_S_M=false;
}
/////////////////////////////////////////////////// ///////////////////// SOLVERS ///////////////////// ///////////////////////////////////////////////////
template<int dim>
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner,
{
PETScWrappers::SolverCG solver(solver_control, mpi_communicator); PETScWrappers::SolverGMRES solver(solver_control, mpi_communicator); PETScWrappers::SolverChebychev solver(solver_control, mpi_communicator);
constraints.
distribute(completely_distributed_solution);
solver.solve(Matrix,completely_distributed_solution,rhs,*preconditioner);
constraints.
distribute(completely_distributed_solution);
if (solver_control.last_step() > MAX_NUM_ITER_TO_RECOMPUTE_PRECONDITIONER)
rebuild_Matrix_U_preconditioners=true;
if (verbose==true)
pcout<<" Solved U in "<<solver_control.last_step()<<" iterations."<<std::endl;
}
template<int dim>
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner,
{
PETScWrappers::SolverGMRES solver(solver_control, mpi_communicator);
constraints.
distribute(completely_distributed_solution);
solver.solve(Matrix,completely_distributed_solution,rhs,*preconditioner);
constraints.
distribute(completely_distributed_solution);
if (solver_control.last_step() > MAX_NUM_ITER_TO_RECOMPUTE_PRECONDITIONER)
rebuild_S_M_preconditioners=true;
if (verbose==true)
pcout<<" Solved P in "<<solver_control.last_step()<<" iterations."<<std::endl;
}
/////////////////////////////////////////////////// ////////////// get different fields /////////////// ///////////////////////////////////////////////////
template<int dim>
void NavierStokesSolver<dim>::get_velocity()
{
assemble_system_U();
save_old_solution();
solve_U(constraints,system_Matrix_u,preconditioner_Matrix_u,completely_distributed_solution_u,system_rhs_u);
locally_relevant_solution_u=completely_distributed_solution_u;
solve_U(constraints,system_Matrix_v,preconditioner_Matrix_v,completely_distributed_solution_v,system_rhs_v);
locally_relevant_solution_v=completely_distributed_solution_v;
if (dim==3)
{
solve_U(constraints,system_Matrix_w,preconditioner_Matrix_w,completely_distributed_solution_w,system_rhs_w);
locally_relevant_solution_w=completely_distributed_solution_w;
}
}
template<int dim>
void NavierStokesSolver<dim>::get_pressure()
{
GET DPSI
assemble_system_dpsi_q();
solve_P(constraints_psi,system_S,preconditioner_S,completely_distributed_solution_psi,system_rhs_psi);
locally_relevant_solution_psi=completely_distributed_solution_psi;
SOLVE Q
solve_P(constraints,system_M,preconditioner_M,completely_distributed_solution_q,system_rhs_q);
UPDATE THE PRESSURE
completely_distributed_solution_p.add(1,completely_distributed_solution_psi);
completely_distributed_solution_p.add(1,completely_distributed_solution_q);
locally_relevant_solution_p = completely_distributed_solution_p;
}
/////////////////////////////////////////////////// ///////////////////// DO STEPS //////////////////// ///////////////////////////////////////////////////
template<int dim>
void NavierStokesSolver<dim>::nth_time_step()
{
get_velocity();
get_pressure();
}
/////////////////////////////////////////////////// ////////////////////// OTHERS ///////////////////// ///////////////////////////////////////////////////
template<int dim>
void NavierStokesSolver<dim>::save_old_solution()
{
locally_relevant_solution_u_old=locally_relevant_solution_u;
locally_relevant_solution_v_old=locally_relevant_solution_v;
locally_relevant_solution_w_old=locally_relevant_solution_w;
locally_relevant_solution_psi_old=locally_relevant_solution_psi;
}
Annotated version of TestLevelSet.cc
#include <fstream>
#include <iostream>
#include <memory>
/////////////////////// FOR TRANSPORT PROBLEM /////////////////////// TIME_INTEGRATION
#define FORWARD_EULER 0
#define SSP33 1
PROBLEM
#define CIRCULAR_ROTATION 0
#define DIAGONAL_ADVECTION 1
OTHER FLAGS
#define VARIABLE_VELOCITY 0
#include "utilities_test_LS.cc"
#include "LevelSetSolver.cc"
/////////////////////////////////////////////////// /////////////////// MAIN CLASS //////////////////// ///////////////////////////////////////////////////
template <int dim>
class TestLevelSet
{
public:
TestLevelSet (const unsigned int degree_LS,
const unsigned int degree_U);
~TestLevelSet ();
void run ();
private:
BOUNDARY
void set_boundary_inlet();
void get_boundary_values_phi(std::vector<unsigned int> &boundary_values_id_phi,
std::vector<double> &boundary_values_phi);
VELOCITY
void get_interpolated_velocity();
SETUP AND INIT CONDITIONS
void setup();
void initial_condition();
void init_constraints();
POST PROCESSING
void output_results();
void output_solution();
SOLUTION VECTORS
BOUNDARY VECTORS
std::vector<unsigned int> boundary_values_id_phi;
std::vector<double> boundary_values_phi;
GENERAL
int degree;
int degree_LS;
int degree_U;
IndexSet locally_owned_dofs_U_disp_field;
IndexSet locally_relevant_dofs_U_disp_field;
double time;
double time_step;
double final_time;
unsigned int timestep_number;
double cfl;
double min_h;
double sharpness;
int sharpness_integer;
unsigned int n_refinement;
unsigned int output_number;
double output_time;
bool get_output;
bool verbose;
FOR TRANSPORT
double cK;
double cE;
unsigned int TRANSPORT_TIME_INTEGRATION;
std::string ALGORITHM;
unsigned int PROBLEM;
FOR RECONSTRUCTION OF MATERIAL FIELDS
double eps, rho_air, rho_fluid;
MASS MATRIX
std::shared_ptr<PETScWrappers::PreconditionBoomerAMG> preconditioner_MC;
};
template <int dim>
TestLevelSet<dim>::TestLevelSet (const unsigned int degree_LS,
const unsigned int degree_U)
:
mpi_communicator (MPI_COMM_WORLD),
degree_LS(degree_LS),
fe_LS (degree_LS),
degree_U(degree_U),
fe_U (degree_U),
fe_U_disp_field(
FE_Q<dim>(degree_U),dim),
pcout (
std::cout,(
Utilities::MPI::this_mpi_process(mpi_communicator)== 0))
{}
template <int dim>
TestLevelSet<dim>::~TestLevelSet ()
{
dof_handler_U_disp_field.clear();
dof_handler_LS.clear ();
dof_handler_U.clear ();
}
VELOCITY //////////
template <int dim>
void TestLevelSet<dim>::get_interpolated_velocity()
{
velocity in x
completely_distributed_solution_u = 0;
ExactU<dim>(PROBLEM,time),
completely_distributed_solution_u);
constraints.
distribute (completely_distributed_solution_u);
locally_relevant_solution_u = completely_distributed_solution_u;
velocity in y
completely_distributed_solution_v = 0;
ExactV<dim>(PROBLEM,time),
completely_distributed_solution_v);
constraints.
distribute (completely_distributed_solution_v);
locally_relevant_solution_v = completely_distributed_solution_v;
if (dim==3)
{
completely_distributed_solution_w = 0;
ExactW<dim>(PROBLEM,time),
completely_distributed_solution_w);
constraints.
distribute (completely_distributed_solution_w);
locally_relevant_solution_w = completely_distributed_solution_w;
}
}
////////// BOUNDARY //////////
template <int dim>
void TestLevelSet<dim>::set_boundary_inlet()
{
const QGauss<dim-1> face_quadrature_formula(1);
const unsigned int n_face_q_points = face_quadrature_formula.size();
std::vector<double> u_value (n_face_q_points);
std::vector<double> v_value (n_face_q_points);
std::vector<double> w_value (n_face_q_points);
cell_U = dof_handler_U.begin_active(),
endc_U = dof_handler_U.end();
for (; cell_U!=endc_U; ++cell_U)
if (cell_U->is_locally_owned())
for (unsigned int face=0; face<GeometryInfo<dim>::faces_per_cell; ++face)
if (cell_U->face(face)->at_boundary())
{
fe_face_values.reinit(cell_U,face);
fe_face_values.get_function_values(locally_relevant_solution_u,u_value);
fe_face_values.get_function_values(locally_relevant_solution_v,v_value);
if (dim==3)
fe_face_values.get_function_values(locally_relevant_solution_w,w_value);
u[0]=u_value[0];
u[1]=v_value[0];
if (dim==3)
u[2]=w_value[0];
if (fe_face_values.normal_vector(0)*u < -1e-14)
cell_U->face(face)->set_boundary_id(10);
}
}
template <int dim>
void TestLevelSet<dim>::get_boundary_values_phi(std::vector<unsigned int> &boundary_values_id_phi,
std::vector<double> &boundary_values_phi)
{
std::map<unsigned int, double> map_boundary_values_phi;
set_boundary_inlet();
boundary_id,BoundaryPhi<dim>(),
map_boundary_values_phi);
boundary_values_id_phi.resize(map_boundary_values_phi.size());
boundary_values_phi.resize(map_boundary_values_phi.size());
std::map<unsigned int,double>::const_iterator boundary_value_phi = map_boundary_values_phi.begin();
for (int i=0; boundary_value_phi !=map_boundary_values_phi.end(); ++boundary_value_phi, ++i)
{
boundary_values_id_phi[i]=boundary_value_phi->first;
boundary_values_phi[i]=boundary_value_phi->second;
}
}
/////////////////////////////// SETUP AND INITIAL CONDITIONS //////////////////////////////
template <int dim>
void TestLevelSet<dim>::setup()
{
setup system LS
dof_handler_LS.distribute_dofs (fe_LS);
locally_owned_dofs_LS = dof_handler_LS.locally_owned_dofs ();
locally_relevant_dofs_LS);
setup system U
dof_handler_U.distribute_dofs (fe_U);
locally_owned_dofs_U = dof_handler_U.locally_owned_dofs ();
locally_relevant_dofs_U);
setup system U for disp field
dof_handler_U_disp_field.distribute_dofs (fe_U_disp_field);
locally_owned_dofs_U_disp_field = dof_handler_U_disp_field.locally_owned_dofs ();
locally_relevant_dofs_U_disp_field);
init vectors for phi
locally_relevant_solution_phi.reinit(locally_owned_dofs_LS,
locally_relevant_dofs_LS,
mpi_communicator);
locally_relevant_solution_phi = 0;
completely_distributed_solution_phi.reinit(mpi_communicator,
dof_handler_LS.n_dofs(),
dof_handler_LS.n_locally_owned_dofs());
init vectors for u
locally_relevant_solution_u.reinit(locally_owned_dofs_U,
locally_relevant_dofs_U,
mpi_communicator);
locally_relevant_solution_u = 0;
completely_distributed_solution_u.reinit(mpi_communicator,
dof_handler_U.n_dofs(),
dof_handler_U.n_locally_owned_dofs());
init vectors for v
locally_relevant_solution_v.reinit(locally_owned_dofs_U,
locally_relevant_dofs_U,
mpi_communicator);
locally_relevant_solution_v = 0;
completely_distributed_solution_v.reinit(mpi_communicator,
dof_handler_U.n_dofs(),
dof_handler_U.n_locally_owned_dofs());
init vectors for w
locally_relevant_solution_w.reinit(locally_owned_dofs_U,
locally_relevant_dofs_U,
mpi_communicator);
locally_relevant_solution_w = 0;
completely_distributed_solution_w.reinit(mpi_communicator,
dof_handler_U.n_dofs(),
dof_handler_U.n_locally_owned_dofs());
init_constraints();
MASS MATRIX
dof_handler_LS.n_locally_owned_dofs_per_processor(),
mpi_communicator,
locally_relevant_dofs_LS);
matrix_MC.reinit (mpi_communicator,
dsp,
dof_handler_LS.n_locally_owned_dofs_per_processor(),
dof_handler_LS.n_locally_owned_dofs_per_processor(),
matrix_MC_tnm1.reinit (mpi_communicator,
dsp,
dof_handler_LS.n_locally_owned_dofs_per_processor(),
dof_handler_LS.n_locally_owned_dofs_per_processor(),
}
template <int dim>
void TestLevelSet<dim>::initial_condition()
{
time=0;
Initial conditions init condition for phi
completely_distributed_solution_phi = 0;
InitialPhi<dim>(PROBLEM, sharpness),
Functions::ZeroFunction<dim>(),
completely_distributed_solution_phi);
constraints.
distribute (completely_distributed_solution_phi);
locally_relevant_solution_phi = completely_distributed_solution_phi;
init condition for u=0
completely_distributed_solution_u = 0;
ExactU<dim>(PROBLEM,time),
completely_distributed_solution_u);
constraints.
distribute (completely_distributed_solution_u);
locally_relevant_solution_u = completely_distributed_solution_u;
init condition for v
completely_distributed_solution_v = 0;
ExactV<dim>(PROBLEM,time),
completely_distributed_solution_v);
constraints.
distribute (completely_distributed_solution_v);
locally_relevant_solution_v = completely_distributed_solution_v;
}
template <int dim>
void TestLevelSet<dim>::init_constraints()
{
constraints.
reinit (locally_relevant_dofs_LS);
constraints_disp_field.clear ();
constraints_disp_field.reinit (locally_relevant_dofs_LS);
constraints_disp_field.close ();
}
///////////////// POST PROCESSING /////////////////
error for phi
solution,
InitialPhi<dim>(PROBLEM,sharpness),
difference_per_cell,
double u_L1_error = difference_per_cell.l1_norm();
solution,
InitialPhi<dim>(PROBLEM,sharpness),
difference_per_cell,
double u_L2_error = difference_per_cell.l2_norm();
pcout << "L1 error: " << u_L1_error << std::endl;
pcout << "L2 error: " << u_L2_error << std::endl;
}
template<int dim>
void TestLevelSet<dim>::output_results()
{
output_solution();
output_number++;
}
template <int dim>
void TestLevelSet<dim>::output_solution()
{
const std::string filename = ("solution-" +
"." +
std::ofstream output ((filename + ".vtu").c_str());
{
std::vector<std::string> filenames;
for (unsigned int i=0;
++i)
filenames.push_back ("solution-" +
"." +
".vtu");
std::ofstream master_output ((filename + ".pvtu").c_str());
}
}
template <int dim>
void TestLevelSet<dim>::run()
{
//////////////////// GENERAL PARAMETERS ////////////////////
cfl=0.1;
verbose = false;
get_output = true;
output_number = 0;
n_refinement=6;
output_time = 0.1;
final_time = 1.0;
PROBLEM=CIRCULAR_ROTATION;
PROBLEM=DIAGONAL_ADVECTION;
double umax = 0;
if (PROBLEM==CIRCULAR_ROTATION)
else
static constexpr double PI
////////////////////////////////// PARAMETERS FOR TRANSPORT PROBLEM //////////////////////////////////
cK = 1.0;
cE = 1.0;
sharpness_integer=1;
TRANSPORT_TIME_INTEGRATION=FORWARD_EULER;
TRANSPORT_TIME_INTEGRATION=SSP33;
ALGORITHM = "MPP_u1";
ALGORITHM = "MPP_uH";
////////// GEOMETRY //////////
if (PROBLEM==CIRCULAR_ROTATION || PROBLEM==DIAGONAL_ADVECTION)
void hyper_cube(Triangulation< dim, spacedim > &tria, const double left=0., const double right=1., const bool colorize=false)
GridGenerator::hyper_rectangle(triangulation, Point<dim>(0.0,0.0), Point<dim>(1.0,1.0), true);
/////// SETUP ///////
for Reconstruction of MATERIAL FIELDS
eps=1*min_h;
sharpness=sharpness_integer*min_h;
rho_fluid = 1000;
rho_air = 1;
GET TIME STEP
time_step = cfl*min_h/umax;
////////////////// TRANSPORT SOLVER //////////////////
LevelSetSolver<dim> level_set (degree_LS,degree_U,
time_step,cK,cE,
verbose,
ALGORITHM,
TRANSPORT_TIME_INTEGRATION,
mpi_communicator);
/////////////////// INITIAL CONDITION ///////////////////
initial_condition();
output_results();
if (dim==2)
level_set.initial_condition(locally_relevant_solution_phi,
locally_relevant_solution_u,locally_relevant_solution_v);
else
level_set.initial_condition(locally_relevant_solution_phi,
locally_relevant_solution_u,locally_relevant_solution_v,locally_relevant_solution_w);
///////////////////////////// BOUNDARY CONDITIONS FOR PHI /////////////////////////////
get_boundary_values_phi(boundary_values_id_phi,boundary_values_phi);
level_set.set_boundary_conditions(boundary_values_id_phi,boundary_values_phi);
OUTPUT DATA REGARDING TIME STEPPING AND MESH
int dofs_LS = dof_handler_LS.
n_dofs();
pcout << "Cfl: " << cfl << std::endl;
pcout << " Number of active cells: "
<< " Number of degrees of freedom: " << std::endl
<< " LS: " << dofs_LS << std::endl;
types::global_dof_index n_dofs() const
TIME STEPPING
timestep_number=0;
time=0;
while (time<final_time)
{
timestep_number++;
if (time+time_step > final_time)
{
pcout << "FINAL TIME STEP... " << std::endl;
time_step = final_time-time;
}
pcout << "Time step " << timestep_number
<< "\twith dt=" << time_step
<< "\tat tn=" << time << std::endl;
////////////// GET VELOCITY // (NS or interpolate from a function) at current time tn //////////////
if (VARIABLE_VELOCITY)
{
get_interpolated_velocity();
SET VELOCITY TO LEVEL SET SOLVER
level_set.set_velocity(locally_relevant_solution_u,locally_relevant_solution_v);
}
//////////////////////// GET LEVEL SET SOLUTION // (at tnp1) ////////////////////////
level_set.nth_time_step();
///////////// UPDATE TIME /////////////
//////// OUTPUT ////////
if (get_output && time-(output_number)*output_time>=0)
{
level_set.get_unp1(locally_relevant_solution_phi);
output_results();
}
}
pcout << "FINAL TIME T=" << time << std::endl;
}
int main(int argc, char *argv[])
{
try
{
PetscInitialize(&argc, &argv, PETSC_NULL, PETSC_NULL);
{
unsigned int degree = 1;
TestLevelSet<2> multiphase(degree, degree);
multiphase.run();
}
PetscFinalize();
}
catch (std::exception &exc)
{
std::cerr << std::endl << std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl << std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
Annotated version of TestNavierStokes.cc
#include <fstream>
#include <iostream>
#include "utilities_test_NS.cc"
#include "NavierStokesSolver.cc"
/////////////////////////////////////////////////// /////////////////// MAIN CLASS //////////////////// ///////////////////////////////////////////////////
template <int dim>
class TestNavierStokes
{
public:
TestNavierStokes (const unsigned int degree_LS,
const unsigned int degree_U);
~TestNavierStokes ();
void run ();
private:
void get_boundary_values_U(double t);
void fix_pressure();
void output_results();
void process_solution(const unsigned int cycle);
void setup();
void initial_condition();
void init_constraints();
std::vector<unsigned int> boundary_values_id_u;
std::vector<unsigned int> boundary_values_id_v;
std::vector<unsigned int> boundary_values_id_w;
std::vector<double> boundary_values_u;
std::vector<double> boundary_values_v;
std::vector<double> boundary_values_w;
double rho_fluid;
double nu_fluid;
double rho_air;
double nu_air;
int degree_LS;
int degree_U;
TimerOutput timer;
double time;
double time_step;
double final_time;
unsigned int timestep_number;
double cfl;
double min_h;
unsigned int n_cycles;
unsigned int n_refinement;
unsigned int output_number;
double output_time;
bool get_output;
double h;
double umax;
bool verbose;
double nu;
};
template <int dim>
TestNavierStokes<dim>::TestNavierStokes (const unsigned int degree_LS,
const unsigned int degree_U)
:
mpi_communicator (MPI_COMM_WORLD),
degree_LS(degree_LS),
fe_LS (degree_LS),
degree_U(degree_U),
fe_U (degree_U),
fe_P (degree_U-1),
timer(std::cout, TimerOutput::summary, TimerOutput::wall_times),
{}
template <int dim>
TestNavierStokes<dim>::~TestNavierStokes ()
{
dof_handler_U.clear ();
dof_handler_P.clear ();
}
///////////////////////////////////// /////////////// SETUP /////////////// /////////////////////////////////////
template <int dim>
void TestNavierStokes<dim>::setup()
{
setup system LS
locally_relevant_dofs_LS);
void distribute_dofs(const FiniteElement< dim, spacedim > &fe)
const IndexSet & locally_owned_dofs() const
setup system U
dof_handler_U.distribute_dofs (fe_U);
locally_owned_dofs_U = dof_handler_U.locally_owned_dofs ();
locally_relevant_dofs_U);
setup system P
dof_handler_P.distribute_dofs (fe_P);
locally_owned_dofs_P = dof_handler_P.locally_owned_dofs ();
locally_relevant_dofs_P);
init_constraints();
init vectors for rho
locally_relevant_solution_rho.reinit (locally_owned_dofs_LS,locally_relevant_dofs_LS,mpi_communicator);
locally_relevant_solution_rho = 0;
completely_distributed_solution_rho.reinit(locally_owned_dofs_LS,mpi_communicator);
init vectors for u
locally_relevant_solution_u.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
locally_relevant_solution_u = 0;
completely_distributed_solution_u.reinit(locally_owned_dofs_U,mpi_communicator);
init vectors for v
locally_relevant_solution_v.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
locally_relevant_solution_v = 0;
completely_distributed_solution_v.reinit(locally_owned_dofs_U,mpi_communicator);
init vectors for w
locally_relevant_solution_w.reinit (locally_owned_dofs_U,locally_relevant_dofs_U,mpi_communicator);
locally_relevant_solution_w = 0;
completely_distributed_solution_w.reinit(locally_owned_dofs_U,mpi_communicator);
init vectors for p
locally_relevant_solution_p.reinit(locally_owned_dofs_P,locally_relevant_dofs_P,mpi_communicator);
locally_relevant_solution_p = 0;
completely_distributed_solution_p.reinit(locally_owned_dofs_P,mpi_communicator);
}
template <int dim>
void TestNavierStokes<dim>::initial_condition()
{
time=0;
Initial conditions init condition for rho
completely_distributed_solution_rho = 0;
RhoFunction<dim>(0),
completely_distributed_solution_rho);
constraints.
distribute (completely_distributed_solution_rho);
locally_relevant_solution_rho = completely_distributed_solution_rho;
init condition for u
completely_distributed_solution_u = 0;
ExactSolution_and_BC_U<dim>(0,0),
completely_distributed_solution_u);
constraints.
distribute (completely_distributed_solution_u);
locally_relevant_solution_u = completely_distributed_solution_u;
init condition for v
completely_distributed_solution_v = 0;
ExactSolution_and_BC_U<dim>(0,1),
completely_distributed_solution_v);
constraints.
distribute (completely_distributed_solution_v);
locally_relevant_solution_v = completely_distributed_solution_v;
init condition for w
if (dim == 3)
{
completely_distributed_solution_w = 0;
ExactSolution_and_BC_U<dim>(0,2),
completely_distributed_solution_w);
constraints.
distribute (completely_distributed_solution_w);
locally_relevant_solution_w = completely_distributed_solution_w;
}
init condition for p
completely_distributed_solution_p = 0;
ExactSolution_p<dim>(0),
completely_distributed_solution_p);
constraints.
distribute (completely_distributed_solution_p);
locally_relevant_solution_p = completely_distributed_solution_p;
}
template <int dim>
void TestNavierStokes<dim>::init_constraints()
{
constraints.
reinit (locally_relevant_dofs_LS);
}
template<int dim>
void TestNavierStokes<dim>::fix_pressure()
{
fix the constant in the pressure
completely_distributed_solution_p = locally_relevant_solution_p;
locally_relevant_solution_p,
0);
if (dim==2)
completely_distributed_solution_p.add(-mean_value+
std::sin(1)*(
std::cos(time)-cos(1+time)));
else
locally_relevant_solution_p = completely_distributed_solution_p;
}
template <int dim>
void TestNavierStokes<dim>::output_results ()
{
for (unsigned int i=0; i<subdomain.size(); ++i)
const std::string filename = ("solution-" +
"." +
std::ofstream output ((filename + ".vtu").c_str());
{
std::vector<std::string> filenames;
for (unsigned int i=0;
++i)
filenames.push_back ("solution-" +
"." +
".vtu");
std::ofstream master_output ((filename + ".pvtu").c_str());
}
output_number++;
}
template <int dim>
void TestNavierStokes<dim>::process_solution(const unsigned int cycle)
{
::VectorizedArray< Number, width > cos(const ::VectorizedArray< Number, width > &)
::VectorizedArray< Number, width > sin(const ::VectorizedArray< Number, width > &)
error for u
locally_relevant_solution_u,
ExactSolution_and_BC_U<dim>(time,0),
difference_per_cell,
double u_L2_error = difference_per_cell.l2_norm();
u_L2_error =
locally_relevant_solution_u,
ExactSolution_and_BC_U<dim>(time,0),
difference_per_cell,
double u_H1_error = difference_per_cell.l2_norm();
u_H1_error =
error for v
locally_relevant_solution_v,
ExactSolution_and_BC_U<dim>(time,1),
difference_per_cell,
double v_L2_error = difference_per_cell.l2_norm();
v_L2_error =
mpi_communicator));
locally_relevant_solution_v,
ExactSolution_and_BC_U<dim>(time,1),
difference_per_cell,
double v_H1_error = difference_per_cell.l2_norm();
v_H1_error =
v_H1_error, mpi_communicator));
error for w
double w_L2_error = 0;
double w_H1_error = 0;
if (dim == 3)
{
locally_relevant_solution_w,
ExactSolution_and_BC_U<dim>(time,2),
difference_per_cell,
w_L2_error = difference_per_cell.l2_norm();
w_L2_error =
mpi_communicator));
locally_relevant_solution_w,
ExactSolution_and_BC_U<dim>(time,2),
difference_per_cell,
w_H1_error = difference_per_cell.l2_norm();
w_H1_error =
w_H1_error, mpi_communicator));
}
error for p
locally_relevant_solution_p,
ExactSolution_p<dim>(time),
difference_per_cell,
double p_L2_error = difference_per_cell.l2_norm();
p_L2_error =
mpi_communicator));
locally_relevant_solution_p,
ExactSolution_p<dim>(time),
difference_per_cell,
double p_H1_error = difference_per_cell.l2_norm();
p_H1_error =
mpi_communicator));
const unsigned int n_active_cells=
triangulation.n_active_cells();
const unsigned int n_dofs_U=dof_handler_U.n_dofs();
const unsigned int n_dofs_P=dof_handler_P.n_dofs();
convergence_table.add_value("cycle", cycle);
convergence_table.add_value("cells", n_active_cells);
convergence_table.add_value("dofs_U", n_dofs_U);
convergence_table.add_value("dofs_P", n_dofs_P);
convergence_table.add_value("dt", time_step);
convergence_table.add_value("u L2", u_L2_error);
convergence_table.add_value("u H1", u_H1_error);
convergence_table.add_value("v L2", v_L2_error);
convergence_table.add_value("v H1", v_H1_error);
if (dim==3)
{
convergence_table.add_value("w L2", w_L2_error);
convergence_table.add_value("w H1", w_H1_error);
}
convergence_table.add_value("p L2", p_L2_error);
convergence_table.add_value("p H1", p_H1_error);
}
template <int dim>
void TestNavierStokes<dim>::get_boundary_values_U(double t)
{
std::map<unsigned int, double> map_boundary_values_u;
std::map<unsigned int, double> map_boundary_values_v;
boundary_values_id_u.resize(map_boundary_values_u.size());
boundary_values_id_v.resize(map_boundary_values_v.size());
boundary_values_u.resize(map_boundary_values_u.size());
boundary_values_v.resize(map_boundary_values_v.size());
std::map<unsigned int,double>::const_iterator boundary_value_u =map_boundary_values_u.begin();
std::map<unsigned int,double>::const_iterator boundary_value_v =map_boundary_values_v.begin();
if (dim==3)
{
std::map<unsigned int, double> map_boundary_values_w;
boundary_values_id_w.resize(map_boundary_values_w.size());
boundary_values_w.resize(map_boundary_values_w.size());
std::map<unsigned int,double>::const_iterator boundary_value_w =map_boundary_values_w.begin();
for (int i=0; boundary_value_w !=map_boundary_values_w.end(); ++boundary_value_w, ++i)
{
boundary_values_id_w[i]=boundary_value_w->first;
boundary_values_w[i]=boundary_value_w->second;
}
}
for (int i=0; boundary_value_u !=map_boundary_values_u.end(); ++boundary_value_u, ++i)
{
boundary_values_id_u[i]=boundary_value_u->first;
boundary_values_u[i]=boundary_value_u->second;
}
for (int i=0; boundary_value_v !=map_boundary_values_v.end(); ++boundary_value_v, ++i)
{
boundary_values_id_v[i]=boundary_value_v->first;
boundary_values_v[i]=boundary_value_v->second;
}
}
template <int dim>
void TestNavierStokes<dim>::run()
{
{
std::cout << "***** CONVERGENCE TEST FOR NS *****" << std::endl;
std::cout << "DEGREE LS: " << degree_LS << std::endl;
std::cout << "DEGREE U: " << degree_U << std::endl;
}
PARAMETERS FOR THE NAVIER STOKES PROBLEM
final_time = 1.0;
time_step=0.1;
n_cycles=6;
n_refinement=6;
ForceTerms<dim> force_function;
RhoFunction<dim> rho_function;
NuFunction<dim> nu_function;
output_time=0.1;
output_number=0;
bool get_output = false;
bool get_error = true;
verbose = true;
for (unsigned int cycle=0; cycle<n_cycles; ++cycle)
{
if (cycle == 0)
{
setup();
initial_condition();
}
else
{
setup();
initial_condition();
time_step*=0.5;
}
output_results();
if (cycle==0)
NavierStokesSolver<dim> navier_stokes (degree_LS,
degree_U,
time_step,
force_function,
rho_function,
nu_function,
verbose,
mpi_communicator);
set INITIAL CONDITION within TRANSPORT PROBLEM
if (dim==2)
navier_stokes.initial_condition(locally_relevant_solution_rho,
locally_relevant_solution_u,
locally_relevant_solution_v,
locally_relevant_solution_p);
else
navier_stokes.initial_condition(locally_relevant_solution_rho,
locally_relevant_solution_u,
locally_relevant_solution_v,
locally_relevant_solution_w,
locally_relevant_solution_p);
pcout << "Cycle " << cycle << ':' << std::endl;
pcout << " Cycle " << cycle
<< " Number of active cells: "
<< " Number of degrees of freedom (velocity): "
<< dof_handler_U.n_dofs() << std::endl
<< std::endl;
TIME STEPPING
timestep_number=0;
time=0;
double time_step_backup=time_step;
while (time<final_time)
{
timestep_number++;
/////////////// GET TIME_STEP ///////////////
if (time+time_step > final_time-1E-10)
{
pcout << "FINAL TIME STEP..." << std::endl;
time_step_backup=time_step;
time_step=final_time-time;
}
pcout << "Time step " << timestep_number
<< "\twith dt=" << time_step
<< "\tat tn=" << time
<< std::endl;
///////////// FORCE TERMS /////////////
force_function.set_time(time+time_step);
///////////////////////////// DENSITY AND VISCOSITY FIELD /////////////////////////////
rho_function.set_time(time+time_step);
nu_function.set_time(time+time_step);
///////////////////// BOUNDARY CONDITIONS /////////////////////
get_boundary_values_U(time+time_step);
if (dim==2) navier_stokes.set_boundary_conditions(boundary_values_id_u, boundary_values_id_v,
boundary_values_u, boundary_values_v);
else navier_stokes.set_boundary_conditions(boundary_values_id_u,
boundary_values_id_v,
boundary_values_id_w,
boundary_values_u, boundary_values_v, boundary_values_w);
////////////// GET SOLUTION //////////////
navier_stokes.nth_time_step();
if (dim==2)
navier_stokes.get_velocity(locally_relevant_solution_u,locally_relevant_solution_v);
else
navier_stokes.get_velocity(locally_relevant_solution_u,
locally_relevant_solution_v,
locally_relevant_solution_w);
navier_stokes.get_pressure(locally_relevant_solution_p);
////////////// FIX PRESSURE //////////////
///////////// UPDATE TIME /////////////
//////// OUTPUT ////////
if (get_output && time-(output_number)*output_time>=1E-10)
output_results();
}
pcout << "FINAL TIME: " << time << std::endl;
time_step=time_step_backup;
if (get_error)
process_solution(cycle);
if (get_error)
{
convergence_table.set_precision("u L2", 2);
convergence_table.set_precision("u H1", 2);
convergence_table.set_scientific("u L2",true);
convergence_table.set_scientific("u H1",true);
convergence_table.set_precision("v L2", 2);
convergence_table.set_precision("v H1", 2);
convergence_table.set_scientific("v L2",true);
convergence_table.set_scientific("v H1",true);
if (dim==3)
{
convergence_table.set_precision("w L2", 2);
convergence_table.set_precision("w H1", 2);
convergence_table.set_scientific("w L2",true);
convergence_table.set_scientific("w H1",true);
}
convergence_table.set_precision("p L2", 2);
convergence_table.set_precision("p H1", 2);
convergence_table.set_scientific("p L2",true);
convergence_table.set_scientific("p H1",true);
convergence_table.set_tex_format("cells","r");
convergence_table.set_tex_format("dofs_U","r");
convergence_table.set_tex_format("dofs_P","r");
convergence_table.set_tex_format("dt","r");
{
std::cout << std::endl;
convergence_table.write_text(std::cout);
}
}
}
}
int main(int argc, char *argv[])
{
try
{
PetscInitialize(&argc, &argv, PETSC_NULL, PETSC_NULL);
{
unsigned int degree_LS = 1;
unsigned int degree_U = 2;
TestNavierStokes<2> test_navier_stokes(degree_LS, degree_U);
test_navier_stokes.run();
}
PetscFinalize();
}
catch (std::exception &exc)
{
std::cerr << std::endl << std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl << std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
Annotated version of clean.sh
rm -rf CMakeFiles CMakeCache.txt Makefile cmake_install.cmake *~
rm -f MultiPhase TestLevelSet TestNavierStokes
rm -f sol*
rm -f *#*
rm -f *.visit
Annotated version of utilities.cc
///////////////////////////////////////////////// ////////////////// INITIAL PHI ////////////////// /////////////////////////////////////////////////
template <int dim>
class InitialPhi :
public Function <dim>
{
public:
InitialPhi (
unsigned int PROBLEM,
double sharpness=0.005) :
Function<dim>(),
sharpness(sharpness),
PROBLEM(PROBLEM) {}
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
double sharpness;
unsigned int PROBLEM;
};
template <int dim>
double InitialPhi<dim>::value (
const Point<dim> &p,
const unsigned int) const
{
double x = p[0];
double y = p[1];
if (PROBLEM==FILLING_TANK)
return 0.5*(-std::tanh((y-0.3)/sharpness)*std::tanh((y-0.35)/sharpness)+1)
*(-std::tanh((x-0.02)/sharpness)+1)-1;
else if (PROBLEM==BREAKING_DAM)
return 0.5*(-std::tanh((x-0.35)/sharpness)*std::tanh((x-0.65)/sharpness)+1)
*(1-std::tanh((y-0.35)/sharpness))-1;
else if (PROBLEM==FALLING_DROP)
{
double x0=0.15;
double y0=0.75;
double r0=0.1;
return 1-(std::tanh((r-r0)/sharpness)+std::tanh((y-0.3)/sharpness));
}
else if (PROBLEM==SMALL_WAVE_PERTURBATION)
{
return -std::tanh((y-wave)/sharpness);
}
else
{
std::cout << "Error in type of PROBLEM" << std::endl;
}
}
virtual RangeNumberType value(const Point< dim > &p, const unsigned int component=0) const
void abort(const ExceptionBase &exc) noexcept
/////////////////////////////////////////////////// ////////////////// FORCE TERMS ///// ////////////// ///////////////////////////////////////////////////
template <int dim>
{
public:
};
///////////////////////////////////////////////// ////////////////// BOUNDARY PHI ///////////////// /////////////////////////////////////////////////
template <int dim>
{
public:
BoundaryPhi (
const double value,
const unsigned int n_components=1) :
Functions::
ConstantFunction<dim>(value,n_components) {}
};
////////////////////////////////////////////////////// ////////////////// BOUNDARY VELOCITY ///////////////// //////////////////////////////////////////////////////
template <int dim>
{
public:
BoundaryU (
unsigned int PROBLEM,
double t=0) :
Function<dim>(), PROBLEM(PROBLEM) {this->
set_time(t);}
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
unsigned PROBLEM;
};
template <int dim>
double BoundaryU<dim>::value (
const Point<dim> &p,
const unsigned int)
const
{
virtual void set_time(const Number new_time)
////////////////// FILLING THE TANK ////////////////// boundary for filling the tank (inlet)
double x = p[0];
double y = p[1];
if (PROBLEM==FILLING_TANK)
{
if (x==0 && y>=0.3 && y<=0.35)
return 0.25;
else
return 0.0;
}
else
{
std::cout << "Error in PROBLEM definition" << std::endl;
abort();
}
}
template <int dim>
{
public:
BoundaryV (
unsigned int PROBLEM,
double t=0) :
Function<dim>(), PROBLEM(PROBLEM) {this->
set_time(t);}
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
unsigned int PROBLEM;
};
template <int dim>
double BoundaryV<dim>::value (
const Point<dim> &p,
const unsigned int)
const
{
boundary for filling the tank (outlet)
double x = p[0];
double y = p[1];
double return_value = 0;
if (PROBLEM==FILLING_TANK)
{
if (y==0.4 && x>=0.3 && x<=0.35)
return_value = 0.25;
}
return return_value;
}
/////////////////////////////////////////////////// ///////////////// POST-PROCESSING ///////////////// ///////////////////////////////////////////////////
template <int dim>
{
public:
Postprocessor(double eps, double rho_air, double rho_fluid)
:
{
this->eps=eps;
this->rho_air=rho_air;
this->rho_fluid=rho_fluid;
}
virtual
void
double eps;
double rho_air;
double rho_fluid;
};
template <int dim>
void
Postprocessor<dim>::
{
const unsigned int n_quadrature_points = input_data.
solution_values.size();
for (unsigned int q=0; q<n_quadrature_points; ++q)
{
double H;
double rho_value;
if (phi_value > eps)
H=1;
else if (phi_value < -eps)
H=-1;
else
rho_value = rho_fluid*(1+H)/2. + rho_air*(1-H)/2.;
computed_quantities[q] = rho_value;
}
}
virtual void evaluate_scalar_field(const DataPostprocessorInputs::Scalar< dim > &input_data, std::vector< Vector< double > > &computed_quantities) const
std::vector< double > solution_values
Annotated version of utilities_test_LS.cc
/////////////////////////////////////////////////// ////////////////// INITIAL PHI ////////////////// ///////////////////////////////////////////////////
template <int dim>
class InitialPhi :
public Function <dim>
{
public:
InitialPhi (
unsigned int PROBLEM,
double sharpness=0.005) :
Function<dim>(),
sharpness(sharpness),
PROBLEM(PROBLEM) {}
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
double sharpness;
unsigned int PROBLEM;
};
template <int dim>
double InitialPhi<dim>::value (
const Point<dim> &p,
const unsigned int) const
{
double x = p[0];
double y = p[1];
double return_value = -1.;
if (PROBLEM==CIRCULAR_ROTATION)
{
double x0=0.5;
double y0=0.75;
double r0=0.15;
return_value = -std::tanh((r-r0)/sharpness);
}
else
{
double x0=0.25;
double y0=0.25;
double r0=0.15;
double r=0;
if (dim==2)
else
{
double z0=0.25;
double z=p[2];
}
return_value = -std::tanh((r-r0)/sharpness);
}
return return_value;
}
///////////////////////////////////////////////// ////////////////// BOUNDARY PHI ///////////////// /////////////////////////////////////////////////
template <int dim>
class BoundaryPhi :
public Function <dim>
{
public:
BoundaryPhi (double t=0)
:
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
};
template <int dim>
double BoundaryPhi<dim>::value (
const Point<dim> &,
const unsigned int)
const
{
return -1.0;
}
virtual RangeNumberType value(const Point< dim > &p, const unsigned int component=0) const override
/////////////////////////////////////////////////// ////////////////// EXACT VELOCITY ///////////////// ///////////////////////////////////////////////////
template <int dim>
{
public:
ExactU (
unsigned int PROBLEM,
double time=0) :
Function<dim>(), PROBLEM(PROBLEM), time(time) {}
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
unsigned PROBLEM;
};
template <int dim>
double ExactU<dim>::value (
const Point<dim> &p,
const unsigned int)
const
{
if (PROBLEM==CIRCULAR_ROTATION)
else
return 1.0;
}
template <int dim>
{
public:
ExactV (
unsigned int PROBLEM,
double time=0) :
Function<dim>(), PROBLEM(PROBLEM), time(time) {}
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
unsigned int PROBLEM;
};
template <int dim>
double ExactV<dim>::value (
const Point<dim> &p,
const unsigned int)
const
{
if (PROBLEM==CIRCULAR_ROTATION)
else
return 1.0;
}
template <int dim>
{
public:
ExactW (
unsigned int PROBLEM,
double time=0) :
Function<dim>(), PROBLEM(PROBLEM), time(time) {}
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
unsigned int PROBLEM;
};
template <int dim>
double ExactW<dim>::value (
const Point<dim> &,
const unsigned int)
const
{
PROBLEM = 3D_DIAGONAL_ADVECTION
Annotated version of utilities_test_NS.cc
/////////////////////////////////////////////////// ////////// EXACT SOLUTION RHO TO TEST NS ////////// ///////////////////////////////////////////////////
template <int dim>
class RhoFunction :
public Function <dim>
{
public:
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
};
template <int dim>
double RhoFunction<dim>::value (
const Point<dim> &p,
const unsigned int) const
{
double return_value = 0;
if (dim==2)
else
return return_value;
}
template <int dim>
class NuFunction :
public Function <dim>
{
public:
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
};
template <int dim>
double NuFunction<dim>::value (
const Point<dim> &,
const unsigned int)
const
{
return 1.;
}
////////////////////////////////////////////////////////////// ///////////////// EXACT SOLUTION U to TEST NS //////////////// //////////////////////////////////////////////////////////////
template <int dim>
class ExactSolution_and_BC_U :
public Function <dim>
{
public:
ExactSolution_and_BC_U (double t=0, int field=0)
:
field(field)
{
}
virtual double value (
const Point<dim> &p,
const unsigned int component=1)
const;
virtual void set_field(int field) {this->field=field;}
int field;
unsigned int type_simulation;
};
template <int dim>
double ExactSolution_and_BC_U<dim>::value (
const Point<dim> &p,
const unsigned int) const
{
double return_value = 0;
double x = p[0];
double y = p[1];
double z = 0;
if (dim == 2)
if (field == 0)
else
else
{
z = p[2];
if (field == 0)
else if (field == 1)
else
}
return return_value;
}
template <int dim>
const unsigned int) const
{
virtual Tensor< 1, dim, RangeNumberType > gradient(const Point< dim > &p, const unsigned int component=0) const
THIS IS USED JUST FOR TESTING NS
double t = this->get_time();
double x = p[0];
double y = p[1];
double z = 0;
if (dim == 2)
if (field == 0)
{
}
else
{
}
else
{
z=p[2];
if (field == 0)
{
}
else if (field == 1)
{
}
else
{
}
}
return return_value;
}
/////////////////////////////////////////////////// ///////// EXACT SOLUTION FOR p TO TEST NS ///////// ///////////////////////////////////////////////////
template <int dim>
class ExactSolution_p :
public Function <dim>
{
public:
virtual double value (
const Point<dim> &p,
const unsigned int component=0)
const;
};
template <int dim>
double ExactSolution_p<dim>::value (
const Point<dim> &p,
const unsigned int)
const
{
double return_value = 0;
if (dim == 2)
else
return_value =
std::sin(p[0]+p[1]+p[2]+t);
return return_value;
}
template <int dim>
{
if (dim == 2)
{
}
else
{
return_value[0] =
std::cos(t+p[0]+p[1]+p[2]);
return_value[1] =
std::cos(t+p[0]+p[1]+p[2]);
return_value[2] =
std::cos(t+p[0]+p[1]+p[2]);
}
return return_value;
}
////////////////////////////////////////////////////////////// ////////////////// FORCE TERMS to TEST NS //////////////////// //////////////////////////////////////////////////////////////
template <int dim>
class ForceTerms :
public Function <dim>
{
public:
ForceTerms (double t=0)
:
{
nu = 1.;
}
double nu;
};
template <int dim>
{
double x = p[0];
double y = p[1];
double z = 0;
if (dim == 2)
{
virtual void vector_value(const Point< dim > &p, Vector< RangeNumberType > &return_value) const override
force in x
force in y
force in x
values[0]=
values[1]=
values[2]=
}
}