#include <deal.II/lac/scalapack.h>

Inheritance diagram for ScaLAPACKMatrix< NumberType >:

Public Types
using	size_type = unsigned int

Public Member Functions
	ScaLAPACKMatrix (const size_type n_rows, const size_type n_columns, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::general)

	ScaLAPACKMatrix (const size_type size, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::symmetric)

	ScaLAPACKMatrix (const std::string &filename, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32)

	~ScaLAPACKMatrix () override=default

void	reinit (const size_type n_rows, const size_type n_columns, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::general)

void	reinit (const size_type size, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::symmetric)

void	set_property (const LAPACKSupport::Property property)

LAPACKSupport::Property	get_property () const

LAPACKSupport::State	get_state () const

ScaLAPACKMatrix< NumberType > &	operator= (const FullMatrix< NumberType > &)

void	copy_from (const LAPACKFullMatrix< NumberType > &matrix, const unsigned int rank)

void	copy_to (FullMatrix< NumberType > &matrix) const

void	copy_to (LAPACKFullMatrix< NumberType > &matrix, const unsigned int rank) const

void	copy_to (ScaLAPACKMatrix< NumberType > &dest) const

void	copy_to (ScaLAPACKMatrix< NumberType > &B, const std::pair< unsigned int, unsigned int > &offset_A, const std::pair< unsigned int, unsigned int > &offset_B, const std::pair< unsigned int, unsigned int > &submatrix_size) const

void	copy_transposed (const ScaLAPACKMatrix< NumberType > &B)

void	add (const ScaLAPACKMatrix< NumberType > &B, const NumberType a=0., const NumberType b=1., const bool transpose_B=false)

void	add (const NumberType b, const ScaLAPACKMatrix< NumberType > &B)

void	Tadd (const NumberType b, const ScaLAPACKMatrix< NumberType > &B)

void	mult (const NumberType b, const ScaLAPACKMatrix< NumberType > &B, const NumberType c, ScaLAPACKMatrix< NumberType > &C, const bool transpose_A=false, const bool transpose_B=false) const

void	mmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const

void	Tmmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const

void	mTmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const

void	TmTmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const

void	save (const std::string &filename, const std::pair< unsigned int, unsigned int > &chunk_size=std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int)) const

void	load (const std::string &filename)

void	compute_cholesky_factorization ()

void	compute_lu_factorization ()

void	invert ()

std::vector< NumberType >	eigenpairs_symmetric_by_index (const std::pair< unsigned int, unsigned int > &index_limits, const bool compute_eigenvectors)

std::vector< NumberType >	eigenpairs_symmetric_by_value (const std::pair< NumberType, NumberType > &value_limits, const bool compute_eigenvectors)

std::vector< NumberType >	eigenpairs_symmetric_by_index_MRRR (const std::pair< unsigned int, unsigned int > &index_limits, const bool compute_eigenvectors)

std::vector< NumberType >	eigenpairs_symmetric_by_value_MRRR (const std::pair< NumberType, NumberType > &value_limits, const bool compute_eigenvectors)

std::vector< NumberType >	compute_SVD (ScaLAPACKMatrix< NumberType > U=nullptr, ScaLAPACKMatrix< NumberType > VT=nullptr)

void	least_squares (ScaLAPACKMatrix< NumberType > &B, const bool transpose=false)

unsigned int	pseudoinverse (const NumberType ratio)

NumberType	reciprocal_condition_number (const NumberType a_norm) const

NumberType	l1_norm () const

NumberType	linfty_norm () const

NumberType	frobenius_norm () const

size_type	m () const

size_type	n () const

unsigned int	local_m () const

unsigned int	local_n () const

unsigned int	global_row (const unsigned int loc_row) const

unsigned int	global_column (const unsigned int loc_column) const

NumberType	local_el (const unsigned int loc_row, const unsigned int loc_column) const

NumberType &	local_el (const unsigned int loc_row, const unsigned int loc_column)

template<class InputVector >
void	scale_columns (const InputVector &factors)

template<class InputVector >
void	scale_rows (const InputVector &factors)

Protected Types
using	value_type = typename AlignedVector< NumberType >::value_type

using	reference = typename AlignedVector< NumberType >::reference

using	const_reference = typename AlignedVector< NumberType >::const_reference

using	const_iterator = MatrixTableIterators::Iterator< TransposeTable< NumberType >, true, MatrixTableIterators::Storage::column_major >

using	iterator = MatrixTableIterators::Iterator< TransposeTable< NumberType >, false, MatrixTableIterators::Storage::column_major >

Protected Member Functions
void	reinit (const size_type size1, const size_type size2, const bool omit_default_initialization=false)

void	reinit (const TableIndices< N > &new_size, const bool omit_default_initialization=false)

const_reference	operator() (const size_type i, const size_type j) const

reference	operator() (const size_type i, const size_type j)

AlignedVector< T >::reference	operator() (const TableIndices< N > &indices)

AlignedVector< T >::const_reference	operator() (const TableIndices< N > &indices) const

size_type	n_rows () const

size_type	n_cols () const

iterator	begin ()

const_iterator	begin () const

iterator	end ()

const_iterator	end () const

reference	el (const size_type i, const size_type j)

const_reference	el (const size_type i, const size_type j) const

AlignedVector< T >::reference	el (const TableIndices< N > &indices)

AlignedVector< T >::const_reference	el (const TableIndices< N > &indices) const

bool	operator== (const TableBase< N, T > &T2) const

void	reset_values ()

void	clear ()

size_type	size (const unsigned int i) const

const TableIndices< N > &	size () const

size_type	n_elements () const

bool	empty () const

template<typename InputIterator >
void	fill (InputIterator entries, const bool C_style_indexing=true)

void	fill (const T &value)

void	replicate_across_communicator (const MPI_Comm &communicator, const unsigned int root_process)

void	swap (TableBase< N, T > &v)

std::size_t	memory_consumption () const

template<class Archive >
void	serialize (Archive &ar, const unsigned int version)

size_type	position (const TableIndices< N > &indices) const

Protected Attributes
AlignedVector< T >	values

TableIndices< N >	table_size

Private Member Functions
NumberType	norm_symmetric (const char type) const

NumberType	norm_general (const char type) const

std::vector< NumberType >	eigenpairs_symmetric (const bool compute_eigenvectors, const std::pair< unsigned int, unsigned int > &index_limits=std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int), const std::pair< NumberType, NumberType > &value_limits=std::make_pair(std::numeric_limits< NumberType >::quiet_NaN(), std::numeric_limits< NumberType >::quiet_NaN()))

std::vector< NumberType >	eigenpairs_symmetric_MRRR (const bool compute_eigenvectors, const std::pair< unsigned int, unsigned int > &index_limits=std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int), const std::pair< NumberType, NumberType > &value_limits=std::make_pair(std::numeric_limits< NumberType >::quiet_NaN(), std::numeric_limits< NumberType >::quiet_NaN()))

void	save_serial (const std::string &filename, const std::pair< unsigned int, unsigned int > &chunk_size) const

void	load_serial (const std::string &filename)

void	save_parallel (const std::string &filename, const std::pair< unsigned int, unsigned int > &chunk_size) const

void	load_parallel (const std::string &filename)

Private Attributes
LAPACKSupport::State	state

LAPACKSupport::Property	property

std::shared_ptr< const Utilities::MPI::ProcessGrid >	grid

int	n_rows

int	n_columns

int	row_block_size

int	column_block_size

int	n_local_rows

int	n_local_columns

int	descriptor [9]

std::vector< NumberType >	work

std::vector< int >	iwork

std::vector< int >	ipiv

const char	uplo

const int	first_process_row

const int	first_process_column

const int	submatrix_row

const int	submatrix_column

Threads::Mutex	mutex

Subscriptor functionality
Classes derived from Subscriptor provide a facility to subscribe to this object. This is mostly used by the SmartPointer class.
std::atomic< unsigned int >	counter

std::map< std::string, unsigned int >	counter_map

std::vector< std::atomic< bool > * >	validity_pointers

const std::type_info *	object_info

void	check_no_subscribers () const noexcept

void	subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

void	unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

unsigned int	n_subscriptions () const

template<typename StreamType >
void	list_subscribers (StreamType &stream) const

void	list_subscribers () const

using	map_value_type = decltype(counter_map)::value_type

using	map_iterator = decltype(counter_map)::iterator

static ::ExceptionBase &	ExcInUse (int arg1, std::string arg2, std::string arg3)

static ::ExceptionBase &	ExcNoSubscriber (std::string arg1, std::string arg2)

Detailed Description

template<typename NumberType>
class ScaLAPACKMatrix< NumberType >

A wrapper class around ScaLAPACK parallel dense linear algebra.

ScaLAPACK assumes that matrices are distributed according to the block-cyclic decomposition scheme. An \(M\) by \(N\) matrix is first decomposed into \(\lceil M / MB \rceil\) by \(\lceil N / NB \rceil\) blocks which are then uniformly distributed across the 2D process grid with \(p q \le Np\) processes, where \(p,q\) are grid dimensions and \(Np\) is the total number of processes. The parameters MB and NB are referred to as row and column block size and determine the granularity of the block-cyclic distribution.

In the following the block-cyclic distribution of a \(10 \times 9\) matrix onto a \(3\times 3\) Cartesian process grid with block sizes \(\text{MB}=\text{NB}=2\) is displayed.

Block-Cyclic Distribution

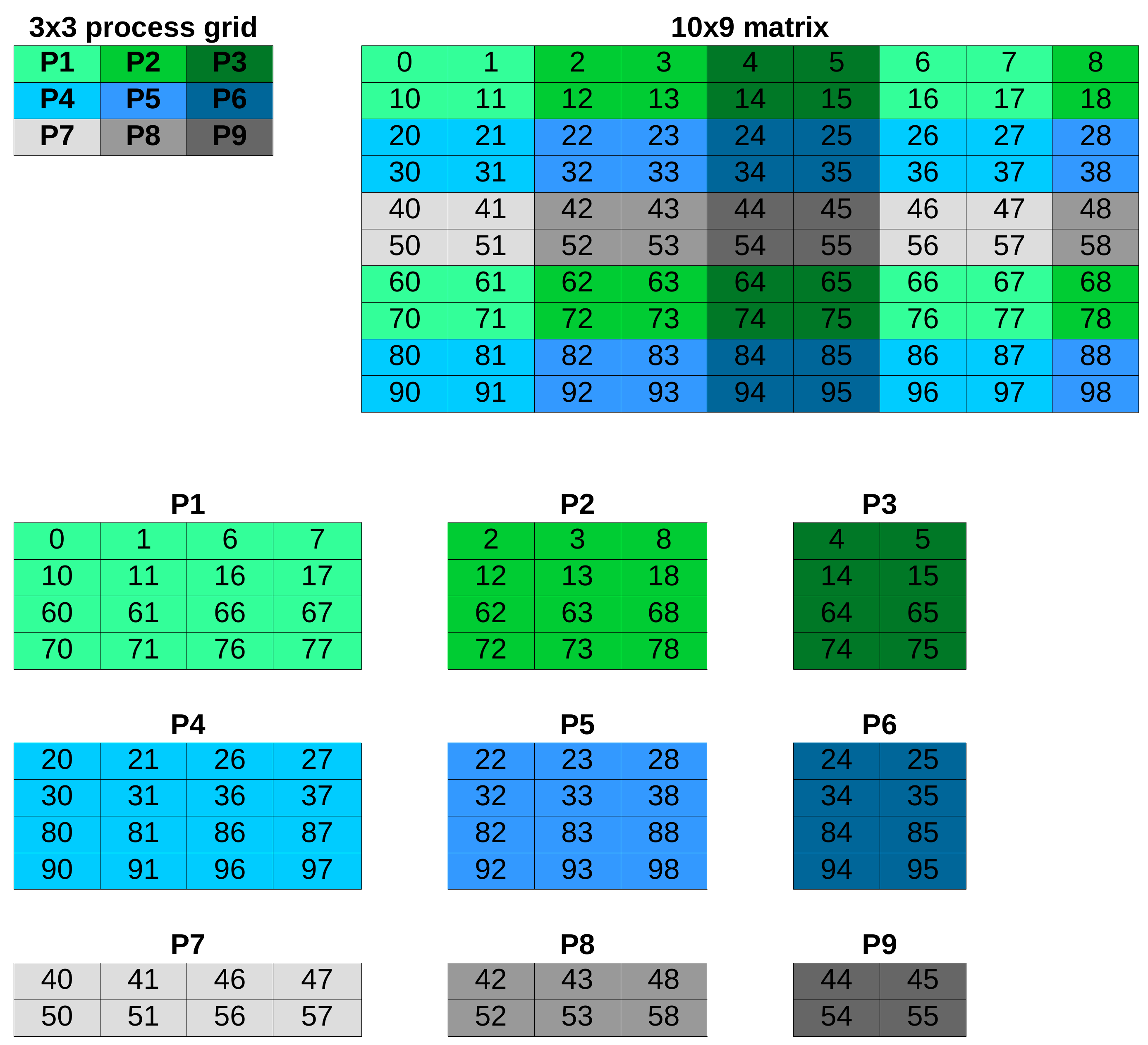
Note that the odd number of columns of the local matrices owned by the processes P2, P5 and P8 accounts for \(N=9\) not being an integral multiple of \(\text{NB}=2\).

The choice of the block sizes is a compromise between a sufficiently large size for efficient local/serial BLAS, but one that is also small enough to achieve good parallel load balance.

Below we show a strong scaling example of ScaLAPACKMatrix::invert() on up to 5 nodes each composed of two Intel Xeon 2660v2 IvyBridge sockets 2.20GHz, 10 cores/socket. Calculations are performed on square processor grids 1x1, 2x2, 3x3, 4x4, 5x5, 6x6, 7x7, 8x8, 9x9, 10x10.

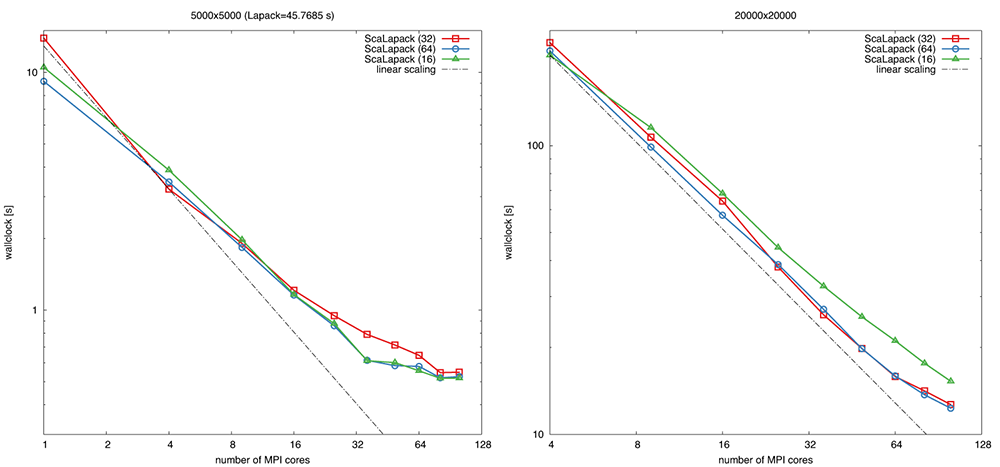
Definition at line 76 of file scalapack.h.

Member Typedef Documentation

◆ size_type

template<typename NumberType >

using ScaLAPACKMatrix< NumberType >::size_type = unsigned int

Declare the type for container size.

Definition at line 82 of file scalapack.h.

◆ value_type

using TransposeTable< NumberType >::value_type = typename AlignedVector<NumberType >::value_type

inherited

Typedef for the values in the table.

Definition at line 1985 of file table.h.

◆ reference

using TransposeTable< NumberType >::reference = typename AlignedVector<NumberType >::reference

inherited

Typedef for the references in the table.

Definition at line 1990 of file table.h.

◆ const_reference

using TransposeTable< NumberType >::const_reference = typename AlignedVector<NumberType >::const_reference

inherited

Typedef for the constant references in the table.

Definition at line 1995 of file table.h.

◆ const_iterator

using TransposeTable< NumberType >::const_iterator = MatrixTableIterators::Iterator<TransposeTable<NumberType >, true, MatrixTableIterators::Storage::column_major>

inherited

Typedef for a constant iterator that traverses the table in column-major order.

Definition at line 2001 of file table.h.

◆ iterator

using TransposeTable< NumberType >::iterator = MatrixTableIterators::Iterator<TransposeTable<NumberType >, false, MatrixTableIterators::Storage::column_major>

inherited

Typedef for an iterator that traverses the table in column-major order.

Definition at line 2009 of file table.h.

Constructor & Destructor Documentation

◆ ScaLAPACKMatrix() [1/3]

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix	(	const size_type	n_rows,
		const size_type	n_columns,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	row_block_size = `32`,
		const size_type	column_block_size = `32`,
		const LAPACKSupport::Property	property = `LAPACKSupport::Property::general`
	)

Constructor for a rectangular matrix with n_rows and n_cols and distributed using the grid process_grid.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 80 of file scalapack.cc.

◆ ScaLAPACKMatrix() [2/3]

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix	(	const size_type	size,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	block_size = `32`,
		const LAPACKSupport::Property	property = `LAPACKSupport::Property::symmetric`
	)

Constructor for a square matrix of size size, and distributed using the process grid in process_grid.

The parameter block_size is used for the block-cyclic distribution of the matrix. An identical block size is used for the rows and columns of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 105 of file scalapack.cc.

◆ ScaLAPACKMatrix() [3/3]

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix	(	const std::string &	filename,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	row_block_size = `32`,
		const size_type	column_block_size = `32`
	)

Constructor for a general rectangular matrix that is read from the file filename and distributed using the grid process_grid.

Loads the matrix from file filename using HDF5. In case that deal.II was built without HDF5 a call to this function will cause an exception to be thrown.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 121 of file scalapack.cc.

◆ ~ScaLAPACKMatrix()

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::~ScaLAPACKMatrix ( )

overridedefault

Destructor

Member Function Documentation

◆ reinit() [1/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::reinit	(	const size_type	n_rows,
		const size_type	n_columns,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	row_block_size = `32`,
		const size_type	column_block_size = `32`,
		const LAPACKSupport::Property	property = `LAPACKSupport::Property::general`
	)

Initialize the rectangular matrix with n_rows and n_cols and distributed using the grid process_grid.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 216 of file scalapack.cc.

◆ reinit() [2/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::reinit	(	const size_type	size,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	block_size = `32`,
		const LAPACKSupport::Property	property = `LAPACKSupport::Property::symmetric`
	)

Initialize the square matrix of size size and distributed using the grid process_grid.

The parameter block_size is used for the block-cyclic distribution of the matrix. An identical block size is used for the rows and columns of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 290 of file scalapack.cc.

◆ set_property()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::set_property ( const LAPACKSupport::Property property )

Assign property to this matrix.

Definition at line 303 of file scalapack.cc.

◆ get_property()

template<typename NumberType >

LAPACKSupport::Property ScaLAPACKMatrix< NumberType >::get_property

Return current property of this matrix

Definition at line 313 of file scalapack.cc.

◆ get_state()

template<typename NumberType >

LAPACKSupport::State ScaLAPACKMatrix< NumberType >::get_state

Return current state of this matrix

Definition at line 322 of file scalapack.cc.

◆ operator=()

template<typename NumberType >

ScaLAPACKMatrix< NumberType > & ScaLAPACKMatrix< NumberType >::operator= ( const FullMatrix< NumberType > & matrix )

Assignment operator from a regular FullMatrix.

Note: This function should only be used for relatively small matrix dimensions. It is primarily intended for debugging purposes.

Definition at line 331 of file scalapack.cc.

◆ copy_from()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_from	(	const LAPACKFullMatrix< NumberType > &	matrix,
		const unsigned int	rank
	)

Copies the content of the locally owned matrix to the distributed matrix. The distributed matrix and matrix on process rank must have matching dimensions.

For all processes except the process with rank rank the serial matrix is not referenced. The user has to ensure that all processes call this with identical rank. The rank refers to a process of the MPI communicator used to create the process grid of the distributed matrix.

Definition at line 362 of file scalapack.cc.

◆ copy_to() [1/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to ( FullMatrix< NumberType > & matrix ) const

Copy the contents of the distributed matrix into matrix.

Note: This function should only be used for relatively small matrix dimensions. It is primarily intended for debugging purposes.

Definition at line 666 of file scalapack.cc.

◆ copy_to() [2/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to	(	LAPACKFullMatrix< NumberType > &	matrix,
		const unsigned int	rank
	)		const

Copies the content of the distributed matrix into the locally replicated matrix on the process with rank rank. For all processes except rank matrix is not referenced. The distributed matrix and matrix on the process rank must have matching dimensions.

The user has to ensure that all processes call this with identical rank. The rank refers to a process of the MPI communicator used to create the process grid of the distributed matrix.

Definition at line 532 of file scalapack.cc.

◆ copy_to() [3/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to ( ScaLAPACKMatrix< NumberType > & dest ) const

Copy the contents of the distributed matrix into a differently distributed matrix dest. The function also works for matrices with different process grids or block-cyclic distributions.

Definition at line 852 of file scalapack.cc.

◆ copy_to() [4/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to	(	ScaLAPACKMatrix< NumberType > &	B,
		const std::pair< unsigned int, unsigned int > &	offset_A,
		const std::pair< unsigned int, unsigned int > &	offset_B,
		const std::pair< unsigned int, unsigned int > &	submatrix_size
	)		const

Copy a submatrix (subset) of the distributed matrix A to a submatrix of the distributed matrix B.

The global row and column index of the first element of the submatrix A is provided by offset_A with row index=offset_A.first and column index=offset_A.second.
The global row and column index of the first element of the submatrix B is provided by offset_B with row index=offset_B.first and column index=offset_B.second.
The dimension of the submatrix to be copied is given by submatrix_size with number of rows=submatrix_size.first and number of columns=submatrix_size.second.

If it is necessary to copy complete matrices with an identical block-cyclic distribution, use ScaLAPACKMatrix<NumberType>::copy_to(ScaLAPACKMatrix<NumberType> &dest) with only one argument to avoid communication.

The underlying process grids of the matrices A and B must have been built with the same MPI communicator.

Definition at line 723 of file scalapack.cc.

◆ copy_transposed()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_transposed ( const ScaLAPACKMatrix< NumberType > & B )

Transposing assignment: \(\mathbf{A} = \mathbf{B}^T\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

The following alignment conditions have to be fulfilled: \(MB_A=NB_B\) and \(NB_A=MB_B\).

Definition at line 980 of file scalapack.cc.

◆ add() [1/2]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::add	(	const ScaLAPACKMatrix< NumberType > &	B,
		const NumberType	a = `0.`,
		const NumberType	b = `1.`,
		const bool	transpose_B = `false`
	)

The operations based on the input parameter transpose_B and the alignment conditions are summarized in the following table:

transpose_B	Block Sizes	Operation
false	\(MB_A=MB_B\) \(NB_A=NB_B\)	\(\mathbf{A} = a \mathbf{A} + b \mathbf{B}\)
true	\(MB_A=NB_B\) \(NB_A=MB_B\)	\(\mathbf{A} = a \mathbf{A} + b \mathbf{B}^T\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

Definition at line 990 of file scalapack.cc.

◆ add() [2/2]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::add	(	const NumberType	b,
		const ScaLAPACKMatrix< NumberType > &	B
	)

Matrix-addition: \(\mathbf{A} = \mathbf{A} + b\, \mathbf{B}\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

The following alignment conditions have to be fulfilled: \(MB_A=MB_B\) and \(NB_A=NB_B\).

Definition at line 1046 of file scalapack.cc.

◆ Tadd()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::Tadd	(	const NumberType	b,
		const ScaLAPACKMatrix< NumberType > &	B
	)

Matrix-addition: \(\mathbf{A} = \mathbf{A} + b\, \mathbf{B}^T\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

The following alignment conditions have to be fulfilled: \(MB_A=NB_B\) and \(NB_A=MB_B\).

Definition at line 1056 of file scalapack.cc.

◆ mult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::mult	(	const NumberType	b,
		const ScaLAPACKMatrix< NumberType > &	B,
		const NumberType	c,
		ScaLAPACKMatrix< NumberType > &	C,
		const bool	transpose_A = `false`,
		const bool	transpose_B = `false`
	)		const

Matrix-matrix-multiplication:

The operations based on the input parameters and the alignment conditions are summarized in the following table:

transpose_A	transpose_B	Block Sizes	Operation
false	false	\(MB_A=MB_C\) \(NB_A=MB_B\) \(NB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A} \cdot \mathbf{B} + c \mathbf{C}\)
false	true	\(MB_A=MB_C\) \(NB_A=NB_B\) \(MB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A} \cdot \mathbf{B}^T + c \mathbf{C}\)
true	false	\(MB_A=MB_B\) \(NB_A=MB_C\) \(NB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A}^T \cdot \mathbf{B} + c \mathbf{C}\)
true	true	\(MB_A=NB_B\) \(NB_A=MB_C\) \(MB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A}^T \cdot \mathbf{B}^T + c \mathbf{C}\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The matrices \(\mathbf{A}\), \(\mathbf{B}\) and \(\mathbf{C}\) must have the same process grid.

Definition at line 1066 of file scalapack.cc.

◆ mmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::mmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = `false`
	)		const

Matrix-matrix-multiplication.

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A} \cdot \mathbf{B}\)

else \(\mathbf{C} = \mathbf{A} \cdot \mathbf{B}\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=MB_C\), \(NB_A=MB_B\) and \(NB_B=NB_C\).

Definition at line 1183 of file scalapack.cc.

◆ Tmmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::Tmmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = `false`
	)		const

Matrix-matrix-multiplication using transpose of \(\mathbf{A}\).

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A}^T \cdot \mathbf{B}\)

else \(\mathbf{C} = \mathbf{A}^T \cdot \mathbf{B}\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=MB_B\), \(NB_A=MB_C\) and \(NB_B=NB_C\).

Definition at line 1197 of file scalapack.cc.

◆ mTmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::mTmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = `false`
	)		const

Matrix-matrix-multiplication using the transpose of \(\mathbf{B}\).

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A} \cdot \mathbf{B}^T\)

else \(\mathbf{C} = \mathbf{A} \cdot \mathbf{B}^T\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=MB_C\), \(NB_A=NB_B\) and \(MB_B=NB_C\).

Definition at line 1211 of file scalapack.cc.

◆ TmTmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::TmTmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = `false`
	)		const

Matrix-matrix-multiplication using transpose of \(\mathbf{A}\) and \(\mathbf{B}\).

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A}^T \cdot \mathbf{B}^T\)

else \(\mathbf{C} = \mathbf{A}^T \cdot \mathbf{B}^T\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=NB_B\), \(NB_A=MB_C\) and \(MB_B=NB_C\).

Definition at line 1225 of file scalapack.cc.

◆ save()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::save	(	const std::string &	filename,
		const std::pair< unsigned int, unsigned int > &	chunk_size = `std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int)`
	)		const

Stores the distributed matrix in filename using HDF5.

In case that deal.II was built without HDF5 a call to this function will cause an exception to be thrown.

If HDF5 was built with MPI, parallel I/O is used to save the matrix. Otherwise, just one process will do the output. This means that internally the distributed matrix is copied to one process, which does the output. Therefore, the matrix has to fit into the memory of one process.

To tweak the I/O performance, especially for parallel I/O, the user may define the optional parameter chunk_size. All MPI processes need to call the function with the same value. The matrix is written in chunks to the file, therefore the properties of the system define the optimal chunk size. Internally, HDF5 splits the matrix into chunk_size.first x chunk_size.second sized blocks, with chunk_size.first being the number of rows of a chunk and chunk_size.second the number of columns.

Definition at line 2607 of file scalapack.cc.

◆ load()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::load ( const std::string & filename )

Loads the distributed matrix from file filename using HDF5. In case that deal.II was built without HDF5 a call to this function will cause an exception to be thrown.

The matrix must have the same dimensions as the matrix stored in the file.

If HDF5 was build with MPI, parallel I/O is used to load the matrix. Otherwise, just one process will load the matrix from storage and distribute the content to the other processes subsequently.

Definition at line 3042 of file scalapack.cc.

◆ compute_cholesky_factorization()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::compute_cholesky_factorization

Compute the Cholesky factorization of the matrix using ScaLAPACK function pXpotrf. The result of the factorization is stored in this object.

Definition at line 1239 of file scalapack.cc.

◆ compute_lu_factorization()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::compute_lu_factorization

Compute the LU factorization of the matrix using ScaLAPACK function pXgetrf and partial pivoting with row interchanges. The result of the factorization is stored in this object.

Definition at line 1272 of file scalapack.cc.

◆ invert()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::invert

Invert the matrix by first computing a Cholesky for symmetric matrices or a LU factorization for general matrices and then building the actual inverse using pXpotri or pXgetri. If the matrix is triangular, the LU factorization step is skipped, and pXtrtri is used directly.

If a Cholesky or LU factorization has been applied previously, pXpotri or pXgetri are called directly.

The inverse is stored in this object.

Definition at line 1313 of file scalapack.cc.

◆ eigenpairs_symmetric_by_index()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_index	(	const std::pair< unsigned int, unsigned int > &	index_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\).

The eigenvalues/eigenvectors are selected by prescribing a range of indices index_limits.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

If all eigenvalues/eigenvectors have to be computed, pass the closed interval \( \left[ 0, M-1 \right] \) in index_limits.

Pass the closed interval \( \left[ M-r, M-1 \right] \) if the \(r\) largest eigenvalues/eigenvectors are desired.

Definition at line 1429 of file scalapack.cc.

◆ eigenpairs_symmetric_by_value()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_value	(	const std::pair< NumberType, NumberType > &	value_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors. The eigenvalues/eigenvectors are selected by prescribing a range of values value_limits for the eigenvalues.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

Definition at line 1452 of file scalapack.cc.

◆ eigenpairs_symmetric_by_index_MRRR()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_index_MRRR	(	const std::pair< unsigned int, unsigned int > &	index_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\) using the MRRR algorithm.

The eigenvalues/eigenvectors are selected by prescribing a range of indices index_limits.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

If all eigenvalues/eigenvectors have to be computed, pass the closed interval \( \left[ 0, M-1 \right] \) in index_limits.

Pass the closed interval \( \left[ M-r, M-1 \right] \) if the \(r\) largest eigenvalues/eigenvectors are desired.

Definition at line 1762 of file scalapack.cc.

◆ eigenpairs_symmetric_by_value_MRRR()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_value_MRRR	(	const std::pair< NumberType, NumberType > &	value_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\) using the MRRR algorithm. The eigenvalues/eigenvectors are selected by prescribing a range of values value_limits for the eigenvalues.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

Definition at line 1785 of file scalapack.cc.

◆ compute_SVD()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::compute_SVD	(	ScaLAPACKMatrix< NumberType > *	U = `nullptr`,
		ScaLAPACKMatrix< NumberType > *	VT = `nullptr`
	)

Computing the singular value decomposition (SVD) of a matrix \(\mathbf{A} \in \mathbb{R}^{M \times N}\), optionally computing the left and/or right singular vectors. The SVD is written as \(\mathbf{A} = \mathbf{U} \cdot \mathbf{\Sigma} \cdot \mathbf{V}^T\) with \(\mathbf{\Sigma} \in \mathbb{R}^{M \times N}\) as a diagonal matrix, \(\mathbf{U} \in \mathbb{R}^{M \times M}\) and \(\mathbf{V} \in \mathbb{R}^{M \times M}\) as orthogonal matrices. The diagonal elements of \(\mathbf{\Sigma}\) are the singular values of \(A\) and the columns of \(\mathbf{U}\) and \(\mathbf{V}\) are the corresponding left and right singular vectors, respectively. The singular values are returned in decreasing order and only the first \(\min(M,N)\) columns of \(\mathbf{U}\) and rows of \(\mathbf{V}^T\) are computed.

Upon return the content of the matrix is unusable. The matrix \(\mathbf{A}\) must have identical block cyclic distribution for the rows and column.

If left singular vectors are required matrices \(\mathbf{A}\) and \(\mathbf{U}\) have to be constructed with the same process grid and block cyclic distribution. If right singular vectors are required matrices \(\mathbf{A}\) and \(\mathbf{V}^T\) have to be constructed with the same process grid and block cyclic distribution.

To avoid computing the left and/or right singular vectors the function accepts nullptr for U and/or VT.

Definition at line 2013 of file scalapack.cc.

◆ least_squares()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::least_squares	(	ScaLAPACKMatrix< NumberType > &	B,
		const bool	transpose = `false`
	)

Solving overdetermined or underdetermined real linear systems involving matrix \(\mathbf{A} \in \mathbb{R}^{M \times N}\), or its transpose \(\mathbf{A}^T\), using a QR or LQ factorization of \(\mathbf{A}\) for \(N_{\rm RHS}\) RHS vectors in the columns of matrix \(\mathbf{B}\)

It is assumed that \(\mathbf{A}\) has full rank: \(\rm{rank}(\mathbf{A}) = \min(M,N)\).

The following options are supported:

If(!transpose) and \(M \geq N\): least squares solution of overdetermined system \(\min \Vert \mathbf{B} - \mathbf{A}\cdot \mathbf{X}\Vert\).
Upon exit the rows \(0\) to \(N-1\) of \(\mathbf{B}\) contain the least square solution vectors. The residual sum of squares for each column is given by the sum of squares of elements \(N\) to \(M-1\) in that column.
If(!transpose) and \(M < N\): find minimum norm solutions of underdetermined systems \(\mathbf{A} \cdot \mathbf{X} = \mathbf{B}\).
Upon exit the columns of \(\mathbf{B}\) contain the minimum norm solution vectors.
If(transpose) and \(M \geq N\): find minimum norm solutions of underdetermined system \( \mathbf{A}^\top \cdot \mathbf{X} = \mathbf{B}\).
Upon exit the columns of \(\mathbf{B}\) contain the minimum norm solution vectors.
If(transpose) and \(M < N\): least squares solution of overdetermined system \(\min \Vert \mathbf{B} - \mathbf{A}^\top \cdot \mathbf{X}\Vert\).
Upon exit the rows \(0\) to \(M-1\) contain the least square solution vectors. The residual sum of squares for each column is given by the sum of squares of elements \(M\) to \(N-1\) in that column.

If(!tranpose) then \(\mathbf{B} \in \mathbb{R}^{M \times N_{\rm RHS}}\), otherwise \(\mathbf{B} \in \mathbb{R}^{N \times N_{\rm RHS}}\). The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have an identical block cyclic distribution for rows and columns.

Definition at line 2133 of file scalapack.cc.

◆ pseudoinverse()

template<typename NumberType >

unsigned int ScaLAPACKMatrix< NumberType >::pseudoinverse ( const NumberType ratio )

Compute the pseudoinverse \(\mathbf{A}^+ \in \mathbb{R}^{N \times M}\) (Moore-Penrose inverse) of a real matrix \(\mathbf{A} \in \mathbb{R}^{M \times N}\) using the singular value decomposition \(\mathbf{A} = \mathbf{U} \cdot \mathbf{\Sigma} \cdot \mathbf{V}^T\).

Unlike the inverse, the pseudoinverse \(\mathbf{A}^+ = \mathbf{V} \cdot \mathbf{\Sigma}^+ \cdot \mathbf{U}^T\) exists for both rectangular as well as singular matrices \(\mathbf{A}\).

For a rectangular \(\mathbf{\Sigma}\) the pseudoinverse is computed by taking the reciprocal of each non-zero element on the diagonal, leaving the zeros in place, and then transposing \(\mathbf{\Sigma}\). For the numerical computation only the singular values \(\sigma_i > \sigma_{\text{max}} \, \text{ratio}\) are taken into account. Upon successful exit, the function returns the number of singular values fulfilling that condition. That value can be interpreted as the rank of \(\mathbf{A}\).

Upon return this object contains the pseudoinverse \(\mathbf{A}^+ \in \mathbb{R}^{N \times M}\).

The following alignment conditions have to be fulfilled: \(MB_A = NB_A\).

Definition at line 2225 of file scalapack.cc.

◆ reciprocal_condition_number()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::reciprocal_condition_number ( const NumberType a_norm ) const

Estimate the condition number of a SPD matrix in the \(l_1\)-norm. The matrix has to be in the Cholesky state (see compute_cholesky_factorization()). The reciprocal of the condition number is returned in order to avoid the possibility of overflow when the condition number is very large.

a_norm must contain the \(l_1\)-norm of the matrix prior to calling Cholesky factorization (see l1_norm()).

Note: An alternative is to compute the inverse of the matrix explicitly and manually construct \(k_1 = ||\mathbf{A}||_1 \, ||\mathbf{A}^{-1}||_1\).

Definition at line 2312 of file scalapack.cc.

◆ l1_norm()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::l1_norm

Compute the \(l_1\)-norm of the matrix.

Definition at line 2374 of file scalapack.cc.

◆ linfty_norm()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::linfty_norm

Compute the \(l_{\infty}\) norm of the matrix.

Definition at line 2388 of file scalapack.cc.

◆ frobenius_norm()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::frobenius_norm

Compute the Frobenius norm of the matrix.

Definition at line 2402 of file scalapack.cc.

◆ m()

template<typename NumberType >

size_type ScaLAPACKMatrix< NumberType >::m ( ) const

Number of rows of the \(M \times N\) matrix.

◆ n()

template<typename NumberType >

size_type ScaLAPACKMatrix< NumberType >::n ( ) const

Number of columns of the \(M \times N\) matrix.

◆ local_m()

template<typename NumberType >

unsigned int ScaLAPACKMatrix< NumberType >::local_m ( ) const

Number of local rows on this MPI processes.

◆ local_n()

template<typename NumberType >

unsigned int ScaLAPACKMatrix< NumberType >::local_n ( ) const

Number of local columns on this MPI process.

◆ global_row()

template<typename NumberType >

unsigned int ScaLAPACKMatrix< NumberType >::global_row ( const unsigned int loc_row ) const

Return the global row number for the given local row loc_row .

Definition at line 497 of file scalapack.cc.

◆ global_column()

template<typename NumberType >

unsigned int ScaLAPACKMatrix< NumberType >::global_column ( const unsigned int loc_column ) const

Return the global column number for the given local column loc_column.

Definition at line 514 of file scalapack.cc.

◆ local_el() [1/2]

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::local_el	(	const unsigned int	loc_row,
		const unsigned int	loc_column
	)		const

Read access to local element.

◆ local_el() [2/2]

template<typename NumberType >

NumberType & ScaLAPACKMatrix< NumberType >::local_el	(	const unsigned int	loc_row,
		const unsigned int	loc_column
	)

Write access to local element.

◆ scale_columns()

template<typename NumberType >

template<class InputVector >

void ScaLAPACKMatrix< NumberType >::scale_columns ( const InputVector & factors )

Scale the columns of the distributed matrix by the scalars provided in the array factors.

The array factors must have as many entries as the matrix columns.

Copies of factors have to be available on all processes of the underlying MPI communicator.

Note: The fundamental prerequisite for the InputVector is that it must be possible to create an ArrayView from it; this is satisfied by the std::vector and Vector classes.

Definition at line 3495 of file scalapack.cc.

◆ scale_rows()

template<typename NumberType >

template<class InputVector >

void ScaLAPACKMatrix< NumberType >::scale_rows ( const InputVector & factors )

Scale the rows of the distributed matrix by the scalars provided in the array factors.

The array factors must have as many entries as the matrix rows.

Copies of factors have to be available on all processes of the underlying MPI communicator.

Note: The fundamental prerequisite for the InputVector is that it must be possible to create an ArrayView from it; this is satisfied by the std::vector and Vector classes.

Definition at line 3506 of file scalapack.cc.

◆ norm_symmetric()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::norm_symmetric ( const char type ) const

private

Calculate the norm of a distributed symmetric dense matrix using ScaLAPACK's internal function.

Definition at line 2475 of file scalapack.cc.

◆ norm_general()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::norm_general ( const char type ) const

private

Calculate the norm of a distributed dense matrix using ScaLAPACK's internal function.

Definition at line 2416 of file scalapack.cc.

◆ eigenpairs_symmetric()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric	(	const bool	compute_eigenvectors,
		const std::pair< unsigned int, unsigned int > &	index_limits = `std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int)`,
		const std::pair< NumberType, NumberType > &	value_limits = `std::make_pair(std::numeric_limits<NumberType>::quiet_NaN(), std::numeric_limits<NumberType>::quiet_NaN())`
	)

private

Computing selected eigenvalues and, optionally, the eigenvectors. The eigenvalues/eigenvectors are selected by either prescribing a range of indices index_limits or a range of values value_limits for the eigenvalues. The function will throw an exception if both ranges are prescribed (meaning that both ranges differ from the default value) as this ambiguity is prohibited. If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

Definition at line 1472 of file scalapack.cc.

◆ eigenpairs_symmetric_MRRR()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_MRRR	(	const bool	compute_eigenvectors,
		const std::pair< unsigned int, unsigned int > &	index_limits = `std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int)`,
		const std::pair< NumberType, NumberType > &	value_limits = `std::make_pair(std::numeric_limits<NumberType>::quiet_NaN(), std::numeric_limits<NumberType>::quiet_NaN())`
	)

private

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\) using the MRRR algorithm. The eigenvalues/eigenvectors are selected by either prescribing a range of indices index_limits or a range of values value_limits for the eigenvalues. The function will throw an exception if both ranges are prescribed (meaning that both ranges differ from the default value) as this ambiguity is prohibited.

By calling this function the original content of the matrix will be overwritten. If requested, the eigenvectors are stored in the columns of the matrix. Also in the case that just the eigenvalues are required, the content of the matrix will be overwritten.

If successful, the computed eigenvalues are arranged in ascending order.

Note: Due to a bug in Netlib-ScaLAPACK, either all or no eigenvectors can be computed. Therefore, the input index_limits has to be set accordingly. Using Intel-MKL this restriction is not required.

Definition at line 1803 of file scalapack.cc.

◆ save_serial()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::save_serial	(	const std::string &	filename,
		const std::pair< unsigned int, unsigned int > &	chunk_size
	)		const

private

Definition at line 2649 of file scalapack.cc.

◆ load_serial()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::load_serial ( const std::string & filename )

private

Definition at line 3063 of file scalapack.cc.

◆ save_parallel()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::save_parallel	(	const std::string &	filename,
		const std::pair< unsigned int, unsigned int > &	chunk_size
	)		const

private

Definition at line 2806 of file scalapack.cc.

◆ load_parallel()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::load_parallel ( const std::string & filename )

private

Definition at line 3241 of file scalapack.cc.

◆ reinit() [3/4]

void TransposeTable< NumberType >::reinit	(	const size_type	size1,
		const size_type	size2,
		const bool	omit_default_initialization = `false`
	)

inherited

Reinitialize the object. This function is mostly here for compatibility with the earlier vector2d class. Passes down to the base class by converting the arguments to the data type requested by the base class.

◆ reinit() [4/4]

template<int N, typename T >

void TableBase< N, T >::reinit	(	const TableIndices< N > &	new_size,
		const bool	omit_default_initialization = `false`
	)

inherited

Set the dimensions of this object to the sizes given in the first argument, and allocate the required memory for table entries to accommodate these sizes. If omit_default_initialization is set to false, all elements of the table are set to a default constructed object for the element type. Otherwise the memory is left in an uninitialized or otherwise undefined state.

◆ operator()() [1/4]

const_reference TransposeTable< NumberType >::operator()	(	const size_type	i,
		const size_type	j
	)		const

inherited

Direct access to one element of the table by specifying all indices at the same time. Range checks are performed.

This version of the function only allows read access.

◆ operator()() [2/4]

reference TransposeTable< NumberType >::operator()	(	const size_type	i,
		const size_type	j
	)

inherited

Direct access to one element of the table by specifying all indices at the same time. Range checks are performed.

This version of the function allows read-write access.

◆ operator()() [3/4]

template<int N, typename T >

AlignedVector< T >::reference TableBase< N, T >::operator() ( const TableIndices< N > & indices )

inherited

Return a read-write reference to the indicated element.

◆ operator()() [4/4]

template<int N, typename T >

AlignedVector< T >::const_reference TableBase< N, T >::operator() ( const TableIndices< N > & indices ) const

inherited

Return the value of the indicated element as a read-only reference.

We return the requested value as a constant reference rather than by value since this object may hold data types that may be large, and we don't know here whether copying is expensive or not.

◆ n_rows()

size_type TransposeTable< NumberType >::n_rows ( ) const

inherited

Number of rows. This function really makes only sense since we have a two-dimensional object here.

◆ n_cols()

size_type TransposeTable< NumberType >::n_cols ( ) const

inherited

Number of columns. This function really makes only sense since we have a two-dimensional object here.

◆ begin() [1/2]

iterator TransposeTable< NumberType >::begin ( )

inherited

Return an iterator pointing to the first entry.

◆ begin() [2/2]

const_iterator TransposeTable< NumberType >::begin ( ) const

inherited

Return a constant iterator pointing to the first entry.

◆ end() [1/2]

iterator TransposeTable< NumberType >::end ( )

inherited

Return an iterator pointing to one past the last entry.

◆ end() [2/2]

const_iterator TransposeTable< NumberType >::end ( ) const

inherited

Return a constant iterator pointing to one past the last entry.

◆ el() [1/4]

reference TransposeTable< NumberType >::el	(	const size_type	i,
		const size_type	j
	)

protectedinherited

Return a read-write reference to the element (i,j).

This function does no bounds checking and is only to be used internally and in functions already checked.

These functions are mainly here for compatibility with a former implementation of these table classes for 2d arrays, then called vector2d.

◆ el() [2/4]

const_reference TransposeTable< NumberType >::el	(	const size_type	i,
		const size_type	j
	)		const

protectedinherited

Return the value of the element (i,j) as a read-only reference.

This function does no bounds checking and is only to be used internally and in functions already checked.

We return the requested value as a constant reference rather than by value since this object may hold data types that may be large, and we don't know here whether copying is expensive or not.

These functions are mainly here for compatibility with a former implementation of these table classes for 2d arrays, then called vector2d.

◆ el() [3/4]

template<int N, typename T >

AlignedVector< T >::reference TableBase< N, T >::el ( const TableIndices< N > & indices )

protectedinherited

Return a read-write reference to the indicated element.

This function does no bounds checking and is only to be used internally and in functions already checked.

◆ el() [4/4]

template<int N, typename T >

AlignedVector< T >::const_reference TableBase< N, T >::el ( const TableIndices< N > & indices ) const

protectedinherited

Return the value of the indicated element as a read-only reference.

This function does no bounds checking and is only to be used internally and in functions already checked.

We return the requested value as a constant reference rather than by value since this object may hold data types that may be large, and we don't know here whether copying is expensive or not.

◆ operator==()

template<int N, typename T >

bool TableBase< N, T >::operator== ( const TableBase< N, T > & T2 ) const

inherited

Test for equality of two tables.

◆ reset_values()

template<int N, typename T >

void TableBase< N, T >::reset_values ( )

inherited

Set all entries to their default value (i.e. copy them over with default constructed objects). Do not change the size of the table, though.

◆ clear()

template<int N, typename T >

void TableBase< N, T >::clear ( )

inherited

Set all dimensions to zero.

◆ size() [1/2]

template<int N, typename T >

size_type TableBase< N, T >::size ( const unsigned int i ) const

inherited

Size of the table in direction i.

◆ size() [2/2]

template<int N, typename T >

const TableIndices< N > & TableBase< N, T >::size ( ) const

inherited

Return the sizes of this object in each direction.

◆ n_elements()

template<int N, typename T >

size_type TableBase< N, T >::n_elements ( ) const

inherited

Return the number of elements stored in this object, which is the product of the extensions in each dimension.

◆ empty()

template<int N, typename T >

bool TableBase< N, T >::empty ( ) const

inherited

Return whether the object is empty, i.e. one of the directions is zero. This is equivalent to n_elements()==0.

◆ fill() [1/2]

template<int N, typename T >

template<typename InputIterator >

void TableBase< N, T >::fill	(	InputIterator	entries,
		const bool	C_style_indexing = `true`
	)

inherited

Fill this table (which is assumed to already have the correct size) from a source given by dereferencing the given forward iterator (which could, for example, be a pointer to the first element of an array, or an inserting std::istream_iterator). The second argument denotes whether the elements pointed to are arranged in a way that corresponds to the last index running fastest or slowest. The default is to use C-style indexing where the last index runs fastest (as opposed to Fortran-style where the first index runs fastest when traversing multidimensional arrays. For example, if you try to fill an object of type Table<2,T>, then calling this function with the default value for the second argument will result in the equivalent of doing

Table<2,T> t;
for (unsigned int i=0; i<t.size(0); ++i)
  for (unsigned int j=0; j<t.size(1); ++j)
    t[i][j] = *entries++;

On the other hand, if the second argument to this function is false, then this would result in code of the following form:

Table<2,T> t;
for (unsigned int j=0; j<t.size(1); ++j)
  for (unsigned int i=0; i<t.size(0); ++i)
    t[i][j] = *entries++;

Note the switched order in which we fill the table elements by traversing the given set of iterators.

Parameters

entries	An iterator to a set of elements from which to initialize this table. It is assumed that iterator can be incremented and dereferenced a sufficient number of times to fill this table.
C_style_indexing	If true, run over elements of the table with the last index changing fastest as we dereference subsequent elements of the input range. If false, change the first index fastest.

◆ fill() [2/2]

template<int N, typename T >

void TableBase< N, T >::fill ( const T & value )

inherited

Fill all table entries with the same value.

◆ replicate_across_communicator()

template<int N, typename T >

void TableBase< N, T >::replicate_across_communicator	(	const MPI_Comm &	communicator,
		const unsigned int	root_process
	)

inherited

This function replicates the state found on the process indicated by root_process across all processes of the MPI communicator. The current state found on any of the processes other than root_process is lost in this process. One can imagine this operation to act like a call to Utilities::MPI::broadcast() from the root process to all other processes, though in practice the function may try to move the data into shared memory regions on each of the machines that host MPI processes and let all MPI processes on this machine then access this shared memory region instead of keeping their own copy. See the general documentation of this class for a code example.

The intent of this function is to quickly exchange large arrays from one process to others, rather than having to compute or create it on all processes. This is specifically the case for data loaded from disk – say, large data tables – that are more easily dealt with by reading once and then distributing across all processes in an MPI universe, than letting each process read the data from disk itself. Specifically, the use of shared memory regions allows for replicating the data only once per multicore machine in the MPI universe, rather than replicating data once for each MPI process. This results in large memory savings if the data is large on today's machines that can easily house several dozen MPI processes per shared memory space.

This function does not imply a model of keeping data on different processes in sync, as LinearAlgebra::distributed::Vector and other vector classes do where there exists a notion of certain elements of the vector owned by each process and possibly ghost elements that are mirrored from its owning process to other processes. Rather, the elements of the current object are simply copied to the other processes, and it is useful to think of this operation as creating a set of const AlignedVector objects on all processes that should not be changed any more after the replication operation, as this is the only way to ensure that the vectors remain the same on all processes. This is particularly true because of the use of shared memory regions where any modification of a vector element on one MPI process may also result in a modification of elements visible on other processes, assuming they are located within one shared memory node.

Note: The use of shared memory between MPI processes requires that the detected MPI installation supports the necessary operations. This is the case for MPI 3.0 and higher.; This function is not cheap. It needs to create sub-communicators of the provided communicator object, which is generally an expensive operation. Likewise, the generation of shared memory spaces is not a cheap operation. As a consequence, this function primarily makes sense when the goal is to share large read-only data tables among processes; examples are data tables that are loaded at start-up time and then used over the course of the run time of the program. In such cases, the start-up cost of running this function can be amortized over time, and the potential memory savings from not having to store the table on each process may be substantial on machines with large core counts on which many MPI processes run on the same machine.; This function only makes sense if the data type T is "self-contained", i.e., all of its information is stored in its member variables, and if none of the member variables are pointers to other parts of the memory. This is because if a type T does have pointers to other parts of memory, then moving T into a shared memory space does not result in the other processes having access to data that the object points to with its member variable pointers: These continue to live only on one process, and are typically in memory areas not accessible to the other processes. As a consequence, the usual use case for this function is to share arrays of simple objects such as doubles or ints.; After calling this function, objects on different MPI processes share a common state. That means that certain operations become "collective", i.e., they must be called on all participating processors at the same time. In particular, you can no longer call resize(), reserve(), or clear() on one MPI process – you have to do so on all processes at the same time, because they have to communicate for these operations. If you do not do so, you will likely get a deadlock that may be difficult to debug. By extension, this rule of only collectively resizing extends to this function itself: You can not call it twice in a row because that implies that first all but the root_process throw away their data, which is not a collective operation. Generally, these restrictions on what can and can not be done hint at the correctness of the comments above: You should treat an AlignedVector on which the current function has been called as const, on which no further operations can be performed until the destructor is called.

◆ swap()

template<int N, typename T >

void TableBase< N, T >::swap ( TableBase< N, T > & v )

inherited

Swap the contents of this table and the other table v. One could do this operation with a temporary variable and copying over the data elements, but this function is significantly more efficient since it only swaps the pointers to the data of the two vectors and therefore does not need to allocate temporary storage and move data around.

This function is analogous to the swap function of all C++ standard containers. Also, there is a global function swap(u,v) that simply calls u.swap(v), again in analogy to standard functions.

◆ memory_consumption()

template<int N, typename T >

std::size_t TableBase< N, T >::memory_consumption ( ) const

inherited

Determine an estimate for the memory consumption (in bytes) of this object.

◆ serialize()

template<int N, typename T >

template<class Archive >

void TableBase< N, T >::serialize	(	Archive &	ar,
		const unsigned int	version
	)

inherited

Write or read the data of this object to or from a stream for the purpose of serialization using the BOOST serialization library.

◆ position()

template<int N, typename T >

size_type TableBase< N, T >::position ( const TableIndices< N > & indices ) const

protectedinherited

Return the position of the indicated element within the array of elements stored one after the other. This function does no index checking.

Member Data Documentation

◆ state

template<typename NumberType >

LAPACKSupport::State ScaLAPACKMatrix< NumberType >::state

private

Since ScaLAPACK operations notoriously change the meaning of the matrix entries, we record the current state after the last operation here.

Definition at line 887 of file scalapack.h.

◆ property

template<typename NumberType >

LAPACKSupport::Property ScaLAPACKMatrix< NumberType >::property

private

Additional property of the matrix which may help to select more efficient ScaLAPACK functions.

Definition at line 893 of file scalapack.h.

◆ grid

template<typename NumberType >

std::shared_ptr<const Utilities::MPI::ProcessGrid> ScaLAPACKMatrix< NumberType >::grid

private

A shared pointer to a Utilities::MPI::ProcessGrid object which contains a BLACS context and a MPI communicator, as well as other necessary data structures.

Definition at line 900 of file scalapack.h.

◆ n_rows

template<typename NumberType >

int ScaLAPACKMatrix< NumberType >::n_rows

private

Number of rows in the matrix.

Definition at line 905 of file scalapack.h.

◆ n_columns

template<typename NumberType >

int ScaLAPACKMatrix< NumberType >::n_columns

private

Number of columns in the matrix.

Definition at line 910 of file scalapack.h.

◆ row_block_size

template<typename NumberType >

int ScaLAPACKMatrix< NumberType >::row_block_size

private

Row block size.

Definition at line 915 of file scalapack.h.

◆ column_block_size

template<typename NumberType >

int ScaLAPACKMatrix< NumberType >::column_block_size

private

Column block size.

Definition at line 920 of file scalapack.h.

◆ n_local_rows

template<typename NumberType >

int ScaLAPACKMatrix< NumberType >::n_local_rows

private

Number of rows in the matrix owned by the current process.

Definition at line 925 of file scalapack.h.

◆ n_local_columns

template<typename NumberType >

int ScaLAPACKMatrix< NumberType >::n_local_columns

private

Number of columns in the matrix owned by the current process.

Definition at line 930 of file scalapack.h.

◆ descriptor

template<typename NumberType >

int ScaLAPACKMatrix< NumberType >::descriptor[9]

private

ScaLAPACK description vector.

Definition at line 935 of file scalapack.h.

◆ work

template<typename NumberType >

std::vector<NumberType> ScaLAPACKMatrix< NumberType >::work

mutableprivate

Workspace array.

Definition at line 940 of file scalapack.h.

◆ iwork

template<typename NumberType >

std::vector<int> ScaLAPACKMatrix< NumberType >::iwork

mutableprivate

Integer workspace array.

Definition at line 945 of file scalapack.h.

◆ ipiv

template<typename NumberType >

std::vector<int> ScaLAPACKMatrix< NumberType >::ipiv

private

Integer array holding pivoting information required by ScaLAPACK's matrix factorization routines.

Definition at line 951 of file scalapack.h.

◆ uplo

template<typename NumberType >

const char ScaLAPACKMatrix< NumberType >::uplo

private

A character to define where elements are stored in case ScaLAPACK operations support this.

Definition at line 957 of file scalapack.h.

◆ first_process_row

template<typename NumberType >

const int ScaLAPACKMatrix< NumberType >::first_process_row

private

The process row of the process grid over which the first row of the global matrix is distributed.

Definition at line 963 of file scalapack.h.

◆ first_process_column

template<typename NumberType >

const int ScaLAPACKMatrix< NumberType >::first_process_column

private

The process column of the process grid over which the first column of the global matrix is distributed.

Definition at line 969 of file scalapack.h.

◆ submatrix_row

template<typename NumberType >

const int ScaLAPACKMatrix< NumberType >::submatrix_row

private

Global row index that determines where to start a submatrix. Currently this equals unity, as we don't use submatrices.

Definition at line 975 of file scalapack.h.

◆ submatrix_column

template<typename NumberType >

const int ScaLAPACKMatrix< NumberType >::submatrix_column

private

Global column index that determines where to start a submatrix. Currently this equals unity, as we don't use submatrices.

Definition at line 981 of file scalapack.h.

◆ mutex

template<typename NumberType >

Threads::Mutex ScaLAPACKMatrix< NumberType >::mutex

mutableprivate

Thread mutex.

Definition at line 986 of file scalapack.h.

◆ values

template<int N, typename T >

AlignedVector<T> TableBase< N, T >::values

protectedinherited

Component-array.

Definition at line 795 of file table.h.

◆ table_size

template<int N, typename T >

TableIndices<N> TableBase< N, T >::table_size

protectedinherited

Size in each direction of the table.

Definition at line 800 of file table.h.

The documentation for this class was generated from the following files:

include/deal.II/lac/scalapack.h
source/lac/scalapack.cc

Public Types

Public Member Functions

Protected Types

Protected Member Functions

Protected Attributes

Private Member Functions

Private Attributes

Subscriptor functionality

Detailed Description

Member Typedef Documentation

◆ size_type

◆ value_type

◆ reference

◆ const_reference

◆ const_iterator

◆ iterator

Constructor & Destructor Documentation

◆ ScaLAPACKMatrix() [1/3]

◆ ScaLAPACKMatrix() [2/3]

◆ ScaLAPACKMatrix() [3/3]

◆ ~ScaLAPACKMatrix()

Member Function Documentation

◆ reinit() [1/4]

◆ reinit() [2/4]

◆ set_property()

◆ get_property()

◆ get_state()

◆ operator=()

◆ copy_from()

◆ copy_to() [1/4]

◆ copy_to() [2/4]

◆ copy_to() [3/4]

◆ copy_to() [4/4]

◆ copy_transposed()

◆ add() [1/2]

◆ add() [2/2]

◆ Tadd()

◆ mult()

◆ mmult()

◆ Tmmult()

◆ mTmult()

◆ TmTmult()

◆ save()

◆ load()

◆ compute_cholesky_factorization()

◆ compute_lu_factorization()

◆ invert()

◆ eigenpairs_symmetric_by_index()

◆ eigenpairs_symmetric_by_value()

◆ eigenpairs_symmetric_by_index_MRRR()

◆ eigenpairs_symmetric_by_value_MRRR()

◆ compute_SVD()

◆ least_squares()

◆ pseudoinverse()

◆ reciprocal_condition_number()

◆ l1_norm()

◆ linfty_norm()

◆ frobenius_norm()

◆ m()

◆ n()

◆ local_m()

◆ local_n()

◆ global_row()

◆ global_column()

◆ local_el() [1/2]

◆ local_el() [2/2]

◆ scale_columns()

◆ scale_rows()

◆ norm_symmetric()

◆ norm_general()

◆ eigenpairs_symmetric()

◆ eigenpairs_symmetric_MRRR()

◆ save_serial()

◆ load_serial()

◆ save_parallel()

◆ load_parallel()

◆ reinit() [3/4]

◆ reinit() [4/4]

◆ operator()() [1/4]

◆ operator()() [2/4]