 |
Reference documentation for deal.II version 9.4.1
|
 |
Reference documentation for deal.II version 9.4.1
|
#include <deal.II/fe/fe_enriched.h>
Classes | |
| class | InternalData |
Public Types | |
| enum | Conformity { unknown = 0x00 , L2 = 0x01 , Hcurl = 0x02 , Hdiv = 0x04 , H1 = Hcurl | Hdiv , H2 = 0x0e } |
Public Member Functions | |
| FE_Enriched (const FiniteElement< dim, spacedim > &fe_base, const FiniteElement< dim, spacedim > &fe_enriched, const Function< spacedim > *enrichment_function) | |
| FE_Enriched (const FiniteElement< dim, spacedim > &fe_base) | |
| FE_Enriched (const FiniteElement< dim, spacedim > *fe_base, const std::vector< const FiniteElement< dim, spacedim > * > &fe_enriched, const std::vector< std::vector< std::function< const Function< spacedim > *(const typename Triangulation< dim, spacedim >::cell_iterator &)> > > &functions) | |
| virtual std::unique_ptr< FiniteElement< dim, spacedim > > | clone () const override |
| virtual UpdateFlags | requires_update_flags (const UpdateFlags update_flags) const override |
| virtual std::string | get_name () const override |
| virtual const FiniteElement< dim, spacedim > & | base_element (const unsigned int index) const override |
| virtual double | shape_value (const unsigned int i, const Point< dim > &p) const override |
| std::pair< std::unique_ptr< FiniteElement< dim, spacedim > >, unsigned int > | operator^ (const unsigned int multiplicity) const |
| const FiniteElement< dim, spacedim > & | operator[] (const unsigned int fe_index) const |
| bool | operator== (const FiniteElementData &) const |
| ReferenceCell | reference_cell () const |
| unsigned int | n_unique_quads () const |
| unsigned int | n_unique_faces () const |
| unsigned int | n_dofs_per_vertex () const |
| unsigned int | n_dofs_per_line () const |
| unsigned int | n_dofs_per_quad (unsigned int face_no=0) const |
| unsigned int | max_dofs_per_quad () const |
| unsigned int | n_dofs_per_hex () const |
| unsigned int | n_dofs_per_face (unsigned int face_no=0, unsigned int child=0) const |
| unsigned int | max_dofs_per_face () const |
| unsigned int | n_dofs_per_cell () const |
| template<int structdim> | |
| unsigned int | n_dofs_per_object (const unsigned int i=0) const |
| unsigned int | n_components () const |
| unsigned int | n_blocks () const |
| const BlockIndices & | block_indices () const |
| unsigned int | tensor_degree () const |
| bool | conforms (const Conformity) const |
| unsigned int | get_first_line_index () const |
| unsigned int | get_first_quad_index (const unsigned int quad_no=0) const |
| unsigned int | get_first_hex_index () const |
| unsigned int | get_first_face_line_index (const unsigned int face_no=0) const |
| unsigned int | get_first_face_quad_index (const unsigned int face_no=0) const |
Transfer matrices | |
| virtual const FullMatrix< double > & | get_restriction_matrix (const unsigned int child, const RefinementCase< dim > &refinement_case=RefinementCase< dim >::isotropic_refinement) const override |
| virtual const FullMatrix< double > & | get_prolongation_matrix (const unsigned int child, const RefinementCase< dim > &refinement_case=RefinementCase< dim >::isotropic_refinement) const override |
Shape function access | |
| virtual double | shape_value_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const |
| virtual Tensor< 1, dim > | shape_grad (const unsigned int i, const Point< dim > &p) const |
| virtual Tensor< 1, dim > | shape_grad_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const |
| virtual Tensor< 2, dim > | shape_grad_grad (const unsigned int i, const Point< dim > &p) const |
| virtual Tensor< 2, dim > | shape_grad_grad_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const |
| virtual Tensor< 3, dim > | shape_3rd_derivative (const unsigned int i, const Point< dim > &p) const |
| virtual Tensor< 3, dim > | shape_3rd_derivative_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const |
| virtual Tensor< 4, dim > | shape_4th_derivative (const unsigned int i, const Point< dim > &p) const |
| virtual Tensor< 4, dim > | shape_4th_derivative_component (const unsigned int i, const Point< dim > &p, const unsigned int component) const |
| virtual bool | has_support_on_face (const unsigned int shape_index, const unsigned int face_index) const |
Transfer and constraint matrices | |
| bool | prolongation_is_implemented () const |
| bool | isotropic_prolongation_is_implemented () const |
| bool | restriction_is_implemented () const |
| bool | isotropic_restriction_is_implemented () const |
| bool | restriction_is_additive (const unsigned int index) const |
| const FullMatrix< double > & | constraints (const ::internal::SubfaceCase< dim > &subface_case=::internal::SubfaceCase< dim >::case_isotropic) const |
| bool | constraints_are_implemented (const ::internal::SubfaceCase< dim > &subface_case=::internal::SubfaceCase< dim >::case_isotropic) const |
| virtual void | get_interpolation_matrix (const FiniteElement< dim, spacedim > &source, FullMatrix< double > &matrix) const |
Functions to support hp-adaptivity | |
| virtual bool | operator== (const FiniteElement< dim, spacedim > &fe) const |
| bool | operator!= (const FiniteElement< dim, spacedim > &) const |
Index computations | |
| std::pair< unsigned int, unsigned int > | system_to_component_index (const unsigned int index) const |
| unsigned int | component_to_system_index (const unsigned int component, const unsigned int index) const |
| std::pair< unsigned int, unsigned int > | face_system_to_component_index (const unsigned int index, const unsigned int face_no=0) const |
| unsigned int | adjust_quad_dof_index_for_face_orientation (const unsigned int index, const unsigned int face_no, const bool face_orientation, const bool face_flip, const bool face_rotation) const |
| virtual unsigned int | face_to_cell_index (const unsigned int face_dof_index, const unsigned int face, const bool face_orientation=true, const bool face_flip=false, const bool face_rotation=false) const |
| unsigned int | adjust_line_dof_index_for_line_orientation (const unsigned int index, const bool line_orientation) const |
| const ComponentMask & | get_nonzero_components (const unsigned int i) const |
| unsigned int | n_nonzero_components (const unsigned int i) const |
| bool | is_primitive () const |
| bool | is_primitive (const unsigned int i) const |
| unsigned int | n_base_elements () const |
| unsigned int | element_multiplicity (const unsigned int index) const |
| const FiniteElement< dim, spacedim > & | get_sub_fe (const ComponentMask &mask) const |
| virtual const FiniteElement< dim, spacedim > & | get_sub_fe (const unsigned int first_component, const unsigned int n_selected_components) const |
| std::pair< std::pair< unsigned int, unsigned int >, unsigned int > | system_to_base_index (const unsigned int index) const |
| std::pair< std::pair< unsigned int, unsigned int >, unsigned int > | face_system_to_base_index (const unsigned int index, const unsigned int face_no=0) const |
| types::global_dof_index | first_block_of_base (const unsigned int b) const |
| std::pair< unsigned int, unsigned int > | component_to_base_index (const unsigned int component) const |
| std::pair< unsigned int, unsigned int > | block_to_base_index (const unsigned int block) const |
| std::pair< unsigned int, types::global_dof_index > | system_to_block_index (const unsigned int component) const |
| unsigned int | component_to_block_index (const unsigned int component) const |
Component and block matrices | |
| ComponentMask | component_mask (const FEValuesExtractors::Scalar &scalar) const |
| ComponentMask | component_mask (const FEValuesExtractors::Vector &vector) const |
| ComponentMask | component_mask (const FEValuesExtractors::SymmetricTensor< 2 > &sym_tensor) const |
| ComponentMask | component_mask (const BlockMask &block_mask) const |
| BlockMask | block_mask (const FEValuesExtractors::Scalar &scalar) const |
| BlockMask | block_mask (const FEValuesExtractors::Vector &vector) const |
| BlockMask | block_mask (const FEValuesExtractors::SymmetricTensor< 2 > &sym_tensor) const |
| BlockMask | block_mask (const ComponentMask &component_mask) const |
| virtual std::pair< Table< 2, bool >, std::vector< unsigned int > > | get_constant_modes () const |
Public Attributes | |
| const unsigned int | dofs_per_vertex |
| const unsigned int | dofs_per_line |
| const unsigned int | dofs_per_quad |
| const unsigned int | dofs_per_hex |
| const unsigned int | first_line_index |
| const unsigned int | first_quad_index |
| const unsigned int | first_hex_index |
| const unsigned int | first_face_line_index |
| const unsigned int | first_face_quad_index |
| const unsigned int | dofs_per_face |
| const unsigned int | dofs_per_cell |
| const unsigned int | components |
| const unsigned int | degree |
| const Conformity | conforming_space |
| const BlockIndices | block_indices_data |
Static Public Attributes | |
| static constexpr unsigned int | space_dimension = spacedim |
| static constexpr unsigned int | dimension = dim |
Private Member Functions | |
| FE_Enriched (const std::vector< const FiniteElement< dim, spacedim > * > &fes, const std::vector< unsigned int > &multiplicities, const std::vector< std::vector< std::function< const Function< spacedim > *(const typename Triangulation< dim, spacedim >::cell_iterator &)> > > &functions) | |
Private Attributes | |
| const ReferenceCell | reference_cell_kind |
| const unsigned int | number_unique_quads |
| const unsigned int | number_unique_faces |
| const std::vector< unsigned int > | n_dofs_on_quad |
| const unsigned int | dofs_per_quad_max |
| const std::vector< unsigned int > | first_index_of_quads |
| const std::vector< unsigned int > | first_line_index_of_faces |
| const std::vector< unsigned int > | first_quad_index_of_faces |
| const std::vector< unsigned int > | n_dofs_on_face |
| const unsigned int | dofs_per_face_max |
Functions to support hp | |
| std::vector< std::vector< std::vector< unsigned int > > > | base_no_mult_local_enriched_dofs |
| const std::vector< std::vector< std::function< const Function< spacedim > *(const typename Triangulation< dim, spacedim >::cell_iterator &)> > > | enrichments |
| const bool | is_enriched |
| const std::unique_ptr< const FESystem< dim, spacedim > > | fe_system |
| virtual bool | hp_constraints_are_implemented () const override |
| virtual void | get_face_interpolation_matrix (const FiniteElement< dim, spacedim > &source, FullMatrix< double > &matrix, const unsigned int face_no=0) const override |
| virtual void | get_subface_interpolation_matrix (const FiniteElement< dim, spacedim > &source, const unsigned int subface, FullMatrix< double > &matrix, const unsigned int face_no=0) const override |
| virtual std::vector< std::pair< unsigned int, unsigned int > > | hp_vertex_dof_identities (const FiniteElement< dim, spacedim > &fe_other) const override |
| virtual std::vector< std::pair< unsigned int, unsigned int > > | hp_line_dof_identities (const FiniteElement< dim, spacedim > &fe_other) const override |
| virtual std::vector< std::pair< unsigned int, unsigned int > > | hp_quad_dof_identities (const FiniteElement< dim, spacedim > &fe_other, const unsigned int face_no=0) const override |
| virtual FiniteElementDomination::Domination | compare_for_domination (const FiniteElement< dim, spacedim > &fe_other, const unsigned int codim=0) const override final |
| const std::vector< std::vector< std::function< const Function< spacedim > *(const typename Triangulation< dim, spacedim >::cell_iterator &)> > > | get_enrichments () const |
| const FESystem< dim, spacedim > & | get_fe_system () const |
| void | initialize (const std::vector< const FiniteElement< dim, spacedim > * > &fes, const std::vector< unsigned int > &multiplicities) |
| template<int dim_1> | |
| void | multiply_by_enrichment (const Quadrature< dim_1 > &quadrature, const InternalData &fe_data, const internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const typename Triangulation< dim, spacedim >::cell_iterator &cell, internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const |
| template<int dim_1> | |
| std::unique_ptr< typename FiniteElement< dim, spacedim >::InternalDataBase > | setup_data (std::unique_ptr< typename FESystem< dim, spacedim >::InternalData > fes_data, const UpdateFlags flags, const Quadrature< dim_1 > &quadrature) const |
| virtual std::unique_ptr< typename FiniteElement< dim, spacedim >::InternalDataBase > | get_data (const UpdateFlags flags, const Mapping< dim, spacedim > &mapping, const Quadrature< dim > &quadrature, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const override |
| virtual std::unique_ptr< typename FiniteElement< dim, spacedim >::InternalDataBase > | get_face_data (const UpdateFlags update_flags, const Mapping< dim, spacedim > &mapping, const hp::QCollection< dim - 1 > &quadrature, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const override |
| virtual std::unique_ptr< typename FiniteElement< dim, spacedim >::InternalDataBase > | get_subface_data (const UpdateFlags update_flags, const Mapping< dim, spacedim > &mapping, const Quadrature< dim - 1 > &quadrature, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const override |
| virtual void | fill_fe_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const CellSimilarity::Similarity cell_similarity, const Quadrature< dim > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const typename FiniteElement< dim, spacedim >::InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const override |
| virtual void | fill_fe_face_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const hp::QCollection< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const typename FiniteElement< dim, spacedim >::InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const override |
| virtual void | fill_fe_subface_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const unsigned int sub_no, const Quadrature< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const typename FiniteElement< dim, spacedim >::InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const override |
Support points and interpolation | |
| std::vector< std::vector< FullMatrix< double > > > | restriction |
| std::vector< std::vector< FullMatrix< double > > > | prolongation |
| FullMatrix< double > | interface_constraints |
| std::vector< Point< dim > > | unit_support_points |
| std::vector< std::vector< Point< dim - 1 > > > | unit_face_support_points |
| std::vector< Point< dim > > | generalized_support_points |
| std::vector< std::vector< Point< dim - 1 > > > | generalized_face_support_points |
| std::vector< Table< 2, int > > | adjust_quad_dof_index_for_face_orientation_table |
| std::vector< int > | adjust_line_dof_index_for_line_orientation_table |
| std::vector< std::pair< unsigned int, unsigned int > > | system_to_component_table |
| std::vector< std::vector< std::pair< unsigned int, unsigned int > > > | face_system_to_component_table |
| std::vector< std::pair< std::pair< unsigned int, unsigned int >, unsigned int > > | system_to_base_table |
| std::vector< std::vector< std::pair< std::pair< unsigned int, unsigned int >, unsigned int > > > | face_system_to_base_table |
| BlockIndices | base_to_block_indices |
| std::vector< std::pair< std::pair< unsigned int, unsigned int >, unsigned int > > | component_to_base_table |
| const std::vector< bool > | restriction_is_additive_flags |
| const std::vector< ComponentMask > | nonzero_components |
| const std::vector< unsigned int > | n_nonzero_components_table |
| const bool | cached_primitivity |
| const std::vector< Point< dim > > & | get_unit_support_points () const |
| bool | has_support_points () const |
| virtual Point< dim > | unit_support_point (const unsigned int index) const |
| const std::vector< Point< dim - 1 > > & | get_unit_face_support_points (const unsigned int face_no=0) const |
| bool | has_face_support_points (const unsigned int face_no=0) const |
| virtual Point< dim - 1 > | unit_face_support_point (const unsigned int index, const unsigned int face_no=0) const |
| const std::vector< Point< dim > > & | get_generalized_support_points () const |
| bool | has_generalized_support_points () const |
| GeometryPrimitive | get_associated_geometry_primitive (const unsigned int cell_dof_index) const |
| virtual void | convert_generalized_support_point_values_to_dof_values (const std::vector< Vector< double > > &support_point_values, std::vector< double > &nodal_values) const |
| virtual std::size_t | memory_consumption () const |
| void | reinit_restriction_and_prolongation_matrices (const bool isotropic_restriction_only=false, const bool isotropic_prolongation_only=false) |
| TableIndices< 2 > | interface_constraints_size () const |
| virtual std::unique_ptr< InternalDataBase > | get_face_data (const UpdateFlags update_flags, const Mapping< dim, spacedim > &mapping, const Quadrature< dim - 1 > &quadrature, internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const |
| virtual void | fill_fe_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const CellSimilarity::Similarity cell_similarity, const Quadrature< dim > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const =0 |
| virtual void | fill_fe_face_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const hp::QCollection< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const |
| virtual void | fill_fe_face_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const Quadrature< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const InternalDataBase &fe_internal, internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const |
| virtual void | fill_fe_subface_values (const typename Triangulation< dim, spacedim >::cell_iterator &cell, const unsigned int face_no, const unsigned int sub_no, const Quadrature< dim - 1 > &quadrature, const Mapping< dim, spacedim > &mapping, const typename Mapping< dim, spacedim >::InternalDataBase &mapping_internal, const ::internal::FEValuesImplementation::MappingRelatedData< dim, spacedim > &mapping_data, const InternalDataBase &fe_internal, ::internal::FEValuesImplementation::FiniteElementRelatedData< dim, spacedim > &output_data) const =0 |
| static ::ExceptionBase & | ExcShapeFunctionNotPrimitive (int arg1) |
| static ::ExceptionBase & | ExcFENotPrimitive () |
| static ::ExceptionBase & | ExcUnitShapeValuesDoNotExist () |
| static ::ExceptionBase & | ExcFEHasNoSupportPoints () |
| static ::ExceptionBase & | ExcEmbeddingVoid () |
| static ::ExceptionBase & | ExcProjectionVoid () |
| static ::ExceptionBase & | ExcWrongInterfaceMatrixSize (int arg1, int arg2) |
| static ::ExceptionBase & | ExcInterpolationNotImplemented () |
| static std::vector< unsigned int > | compute_n_nonzero_components (const std::vector< ComponentMask > &nonzero_components) |
Subscriptor functionality | |
Classes derived from Subscriptor provide a facility to subscribe to this object. This is mostly used by the SmartPointer class. | |
| std::atomic< unsigned int > | counter |
| std::map< std::string, unsigned int > | counter_map |
| std::vector< std::atomic< bool > * > | validity_pointers |
| const std::type_info * | object_info |
| void | subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const |
| void | unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const |
| unsigned int | n_subscriptions () const |
| template<typename StreamType > | |
| void | list_subscribers (StreamType &stream) const |
| void | list_subscribers () const |
| template<class Archive > | |
| void | serialize (Archive &ar, const unsigned int version) |
| void | check_no_subscribers () const noexcept |
| static ::ExceptionBase & | ExcInUse (int arg1, std::string arg2, std::string arg3) |
| static ::ExceptionBase & | ExcNoSubscriber (std::string arg1, std::string arg2) |
| using | map_value_type = decltype(counter_map)::value_type |
| using | map_iterator = decltype(counter_map)::iterator |
| static std::mutex | mutex |
Implementation of a partition of unity finite element method (PUM) by Babuska and Melenk which enriches a standard finite element with an enrichment function multiplied with another (usually linear) finite element:
\[ U(\mathbf x) = \sum_i N_i(\mathbf x) U_i + \sum_j N_j(\mathbf x) \sum_k F_k(\mathbf x) U_{jk} \]
where \( N_i(\mathbf x) \) and \( N_j(\mathbf x) \) are the underlying finite elements (including the mapping from the isoparametric element to the real element); \( F_k(\mathbf x) \) are the scalar enrichment functions in real space (e.g. \( 1/r \), \( \exp(-r) \), etc); \( U_i \) and \( U_{jk} \) are the standard and enriched DoFs. This allows to include in the finite element space a priori knowledge about the partial differential equation being solved which in turn improves the local approximation properties of the spaces. This can be useful for highly oscillatory solutions, problems with domain corners or on unbounded domains or sudden changes of boundary conditions. PUM method uses finite element spaces which satisfy the partition of unity property (e.g. FE_Q). Among other properties this makes the resulting space to reproduce enrichment functions exactly.
The simplest constructor of this class takes two finite element objects and an enrichment function to be used. For example
In this case, standard DoFs are distributed by FE_Q<dim>(2), whereas enriched DoFs are coming from a single finite element FE_Q<dim>(1) used with a single enrichment function function. In this case, the total number of DoFs on the enriched element is the sum of DoFs from FE_Q<dim>(2) and FE_Q<dim>(1).
As an example of an enrichment function, consider \( \exp(-x) \), which leads to the following shape functions on the unit element:
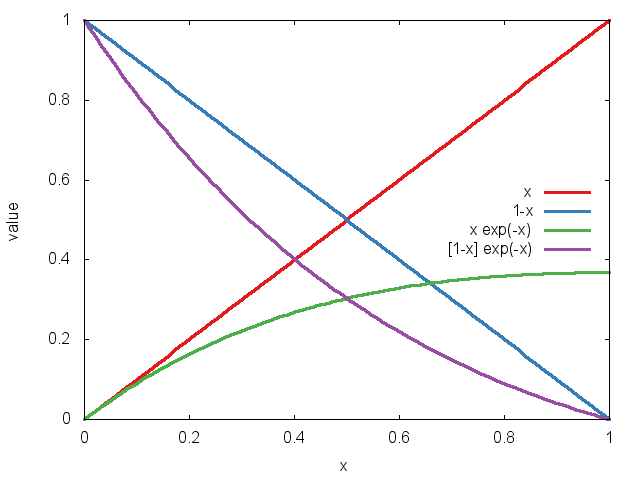
| 
|
| 1d element, base and enriched shape functions. | enriched shape function corresponding to the central vertex. |
Note that evaluation of gradients (hessians) of the enriched shape functions or the finite element field requires evaluation of gradients (gradients and hessians) of the enrichment functions:
\begin{align*} U(\mathbf x) &= \sum_i N_i(\mathbf x) U_i + \sum_{j,k} N_j(\mathbf x) F_k(\mathbf x) U_{jk} \\ \mathbf \nabla U(\mathbf x) &= \sum_i \mathbf \nabla N_i(\mathbf x) U_i + \sum_{j,k} \left[\mathbf \nabla N_j(\mathbf x) F_k(\mathbf x) + N_j(\mathbf x) \mathbf \nabla F_k(\mathbf x) \right] U_{jk} \\ \mathbf \nabla \mathbf \nabla U(\mathbf x) &= \sum_i \mathbf \nabla \mathbf \nabla N_i(\mathbf x) U_i + \sum_{j,k} \left[\mathbf \nabla \mathbf \nabla N_j(\mathbf x) F_k(\mathbf x) + \mathbf \nabla F_k(\mathbf x) \mathbf \nabla N_j(\mathbf x) + \mathbf \nabla N_j(\mathbf x) \mathbf \nabla F_k(\mathbf x) + N_j(\mathbf x) \mathbf \nabla \mathbf \nabla F_k(\mathbf x) \right] U_{jk} \end{align*}
In most applications it is beneficial to introduce enrichments only in some part of the domain (e.g. around a crack tip) and use standard FE (e.g. FE_Q) elsewhere. This can be achieved by using the hp-finite element framework in deal.II that allows for the use of different elements on different cells. To make the resulting space \(C^0\) continuous, it is then necessary for the DoFHandler class and DoFTools::make_hanging_node_constraints() function to be able to figure out what to do at the interface between enriched and non-enriched cells. Specifically, we want the degrees of freedom corresponding to enriched shape functions to be zero at these interfaces. These classes and functions can not to do this automatically, but the effect can be achieved by using not just a regular FE_Q on cells without enrichment, but to wrap the FE_Q into an FE_Enriched object without actually enriching it. This can be done as follows:
This constructor is equivalent to calling
and will result in the correct constraints for enriched DoFs attributed to support points on the interface between the two regions.
When using this class, please cite [52] . The PUM was introduced in [109] and [5] .
The implementation of the class is based on FESystem which is aggregated as a private member. The simplest constructor FE_Enriched<dim> fe(FE_Q<dim>(2), FE_Q<dim>(1),function) will internally initialize FESystem as
Note that it would not be wise to have this class derived from FESystem as the latter concatenates the given elements into different components of a vector element, whereas the current class combines the given elements into the same components. For instance, if two scalar elements are given, the resulting element will be scalar rather than have two components when doing the same with an FESystem.
The ordering of the shape function, interface_constrains, the prolongation (embedding) and the restriction matrices are taken from the FESystem class.
Definition at line 175 of file fe_enriched.h.
|
inherited |
Enumerator for the different types of continuity a finite element may have. Continuity is measured by the Sobolev space containing the constructed finite element space and is also called this way.
Note that certain continuities may imply others. For instance, a function in H1 is in Hcurl and Hdiv as well.
If you are interested in continuity in the classical sense, then the following relations hold:
H1 implies that the function is continuous over cell boundaries.
H2 implies that the function is continuously differentiable over cell boundaries.
In order to test if a finite element conforms to a certain space, use FiniteElementData<dim>::conforms().
| FE_Enriched< dim, spacedim >::FE_Enriched | ( | const FiniteElement< dim, spacedim > & | fe_base, |
| const FiniteElement< dim, spacedim > & | fe_enriched, | ||
| const Function< spacedim > * | enrichment_function | ||
| ) |
Constructor which takes base FiniteElement fe_base and the enrichment FiniteElement fe_enriched which will be multiplied by the enrichment_function.
In case fe_enriched is other than FE_Nothing, the lifetime of the enrichment_function must be at least as long as the FE_Enriched object.
Definition at line 146 of file fe_enriched.cc.
| FE_Enriched< dim, spacedim >::FE_Enriched | ( | const FiniteElement< dim, spacedim > & | fe_base | ) |
Constructor which only wraps the base FE fe_base. As for the enriched finite element space, FE_Nothing is used. Continuity constraints will be automatically generated when this non-enriched element is used in conjunction with enriched finite element within a DoFHandler with hp-capabilities.
See the discussion in the class documentation on how to use this element in the context of hp-finite element methods.
Definition at line 136 of file fe_enriched.cc.
| FE_Enriched< dim, spacedim >::FE_Enriched | ( | const FiniteElement< dim, spacedim > * | fe_base, |
| const std::vector< const FiniteElement< dim, spacedim > * > & | fe_enriched, | ||
| const std::vector< std::vector< std::function< const Function< spacedim > *(const typename Triangulation< dim, spacedim >::cell_iterator &)> > | , | ||
| & | functions | ||
| ) |
Constructor which takes pointer to the base FiniteElement fe_base and a vector of enriched FiniteElement's fe_enriched . fe_enriched[i] finite element will be enriched with functions in functions[i].
This is the most general public constructor which also allows to have different enrichment functions in different disjoint parts of the domain. To that end the last argument provides an association of cell iterator to a Function. This is done to simplify the usage of this class when the number of disjoint domains with different functions is more than a few. Otherwise one would have to use different instance of this class for each disjoint enriched domain.
If you don't plan to use this feature, you can utilize C++11 lambdas to define dummy functions. Below is an example which uses two functions with the first element to be enriched and a single function with the second one.
Definition at line 165 of file fe_enriched.cc.
|
private |
The most general private constructor. The first two input parameters are consistent with those in FESystem. It is used internally only with multiplicities[0]=1, which is a logical requirement for this finite element.
Definition at line 178 of file fe_enriched.cc.
|
overridevirtual |
A sort of virtual copy constructor, this function returns a copy of the finite element object. Derived classes need to override the function here in this base class and return an object of the same type as the derived class.
Some places in the library, for example the constructors of FESystem as well as the hp::FECollection class, need to make copies of finite elements without knowing their exact type. They do so through this function.
Implements FiniteElement< dim, spacedim >.
Definition at line 283 of file fe_enriched.cc.
|
overridevirtual |
Given a set of update flags, compute which other quantities also need to be computed in order to satisfy the request by the given flags. Then return the combination of the original set of flags and those just computed.
As an example, if update_flags contains update_gradients a finite element class will typically require the computation of the inverse of the Jacobian matrix in order to rotate the gradient of shape functions on the reference cell to the real cell. It would then return not just update_gradients, but also update_covariant_transformation, the flag that makes the mapping class produce the inverse of the Jacobian matrix.
An extensive discussion of the interaction between this function and FEValues can be found in the How Mapping, FiniteElement, and FEValues work together documentation module.
Implements FiniteElement< dim, spacedim >.
Definition at line 301 of file fe_enriched.cc.
|
overridevirtual |
Return a string that identifies a finite element.
Implements FiniteElement< dim, spacedim >.
Definition at line 496 of file fe_enriched.cc.
|
overridevirtual |
Access to a composing element. The index needs to be smaller than the number of base elements. In the context of this class, the number of base elements is always more than one: a non-enriched element plus an element to be enriched, which could be FE_Nothing.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 517 of file fe_enriched.cc.
|
overridevirtual |
Return the value of the ith shape function at the point p. p is a point on the reference element.
This function returns meaningful values only for non-enriched element as real-space enrichment requires evaluation of the function at the point in real-space.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 270 of file fe_enriched.cc.
|
overridevirtual |
Projection from a fine grid space onto a coarse grid space.
This function only makes sense when all child elements are also enriched using the same function(s) as the parent element.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 1045 of file fe_enriched.cc.
|
overridevirtual |
Embedding matrix between grids.
This function only makes sense when all child elements are also enriched using the same function(s) as the parent element.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 1035 of file fe_enriched.cc.
|
overridevirtual |
Return whether this element implements hp-constraints.
This function returns true if and only if all its base elements return true for this function.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 887 of file fe_enriched.cc.
|
overridevirtual |
Return the matrix interpolating from a face of one element to the face of the neighboring element. The size of the matrix is then source.dofs_per_face times this->dofs_per_face.
Base elements of this element will have to implement this function. They may only provide interpolation matrices for certain source finite elements, for example those from the same family. If they don't implement interpolation from a given element, then they must throw an exception of type FiniteElement<dim,spacedim>::ExcInterpolationNotImplemented, which will get propagated out from this element.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 895 of file fe_enriched.cc.
|
overridevirtual |
Return the matrix interpolating from a face of one element to the subface of the neighboring element. The size of the matrix is then source.dofs_per_face times this->dofs_per_face.
Base elements of this element will have to implement this function. They may only provide interpolation matrices for certain source finite elements, for example those from the same family. If they don't implement interpolation from a given element, then they must throw an exception of type FiniteElement<dim,spacedim>::ExcInterpolationNotImplemented, which will get propagated out from this element.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 919 of file fe_enriched.cc.
|
overridevirtual |
If, on a vertex, several finite elements are active, the hp-code first assigns the degrees of freedom of each of these FEs different global indices. It then calls this function to find out which of them should get identical values, and consequently can receive the same global DoF index. This function therefore returns a list of identities between DoFs of the present finite element object with the DoFs of fe_other, which is a reference to a finite element object representing one of the other finite elements active on this particular vertex. The function computes which of the degrees of freedom of the two finite element objects are equivalent, both numbered between zero and the corresponding value of n_dofs_per_vertex() of the two finite elements. The first index of each pair denotes one of the vertex dofs of the present element, whereas the second is the corresponding index of the other finite element.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 945 of file fe_enriched.cc.
|
overridevirtual |
Same as hp_vertex_dof_indices(), except that the function treats degrees of freedom on lines.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 963 of file fe_enriched.cc.
|
overridevirtual |
Same as hp_vertex_dof_indices(), except that the function treats degrees of freedom on quads.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 981 of file fe_enriched.cc.
|
finaloverridevirtual |
Return whether this element dominates another one given as argument fe_other, whether it is the other way around, whether neither dominates, or if either could dominate. The codim parameter describes the codimension of the investigated subspace and specifies that it is subject to this comparison. For example, if codim==0 then this function compares which element dominates at the cell level. If codim==1, then the elements are compared at faces, i.e., the comparison happens between the function spaces of the two finite elements as restricted to a face. Larger values of codim work correspondingly.
For a definition of domination, see FiniteElementDomination::Domination and in particular the hp-paper.
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 1001 of file fe_enriched.cc.
| const std::vector< std::vector< std::function< const Function< spacedim > *(const typename Triangulation< dim, spacedim >::cell_iterator &)> > > FE_Enriched< dim, spacedim >::get_enrichments |
Return enrichment functions
Definition at line 262 of file fe_enriched.cc.
| const FESystem< dim, spacedim > & FE_Enriched< dim, spacedim >::get_fe_system |
Return the underlying FESystem object.
Definition at line 879 of file fe_enriched.cc.
|
protected |
Auxiliary function called from get_data, get_face_data and get_subface_data. It take internal data of FESystem object in fes_data and the quadrature rule qudrature.
This function essentially take the internal data from an instance of FESystem class and wraps it into our own InternalData class which additionally has objects to hold values/gradients/hessians of enrichment functions at each quadrature point depending on flags.
Definition at line 325 of file fe_enriched.cc.
|
overrideprotectedvirtual |
Prepare internal data structures and fill in values independent of the cell. Returns a pointer to an object of which the caller of this function (FEValues) then has to assume ownership (which includes destruction when it is no more needed).
Implements FiniteElement< dim, spacedim >.
Definition at line 408 of file fe_enriched.cc.
|
overrideprotectedvirtual |
Like get_data(), but return an object that will later be used for evaluating shape function information at quadrature points on faces of cells. The object will then be used in calls to implementations of FiniteElement::fill_fe_face_values(). See the documentation of get_data() for more information.
The default implementation of this function converts the face quadrature into a cell quadrature with appropriate quadrature point locations, and with that calls the get_data() function above that has to be implemented in derived classes.
| [in] | update_flags | A set of UpdateFlags values that describe what kind of information the FEValues object requests the finite element to compute. This set of flags may also include information that the finite element can not compute, e.g., flags that pertain to data produced by the mapping. An implementation of this function needs to set up all data fields in the returned object that are necessary to produce the finite- element related data specified by these flags, and may already pre- compute part of this information as discussed above. Elements may want to store these update flags (or a subset of these flags) in InternalDataBase::update_each so they know at the time when FiniteElement::fill_fe_face_values() is called what they are supposed to compute |
| [in] | mapping | A reference to the mapping used for computing values and derivatives of shape functions. |
| [in] | quadrature | A reference to the object that describes where the shape functions should be evaluated. |
| [out] | output_data | A reference to the object that FEValues will use in conjunction with the object returned here and where an implementation of FiniteElement::fill_fe_face_values() will place the requested information. This allows the current function to already pre-compute pieces of information that can be computed on the reference cell, as discussed above. FEValues guarantees that this output object and the object returned by the current function will always be used together. |
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 367 of file fe_enriched.cc.
|
overrideprotectedvirtual |
Like get_data(), but return an object that will later be used for evaluating shape function information at quadrature points on children of faces of cells. The object will then be used in calls to implementations of FiniteElement::fill_fe_subface_values(). See the documentation of get_data() for more information.
The default implementation of this function converts the face quadrature into a cell quadrature with appropriate quadrature point locations, and with that calls the get_data() function above that has to be implemented in derived classes.
| [in] | update_flags | A set of UpdateFlags values that describe what kind of information the FEValues object requests the finite element to compute. This set of flags may also include information that the finite element can not compute, e.g., flags that pertain to data produced by the mapping. An implementation of this function needs to set up all data fields in the returned object that are necessary to produce the finite- element related data specified by these flags, and may already pre- compute part of this information as discussed above. Elements may want to store these update flags (or a subset of these flags) in InternalDataBase::update_each so they know at the time when FiniteElement::fill_fe_subface_values() is called what they are supposed to compute |
| [in] | mapping | A reference to the mapping used for computing values and derivatives of shape functions. |
| [in] | quadrature | A reference to the object that describes where the shape functions should be evaluated. |
| [out] | output_data | A reference to the object that FEValues will use in conjunction with the object returned here and where an implementation of FiniteElement::fill_fe_subface_values() will place the requested information. This allows the current function to already pre-compute pieces of information that can be computed on the reference cell, as discussed above. FEValues guarantees that this output object and the object returned by the current function will always be used together. |
Reimplemented from FiniteElement< dim, spacedim >.
Definition at line 388 of file fe_enriched.cc.
|
overrideprotectedvirtual |
Definition at line 525 of file fe_enriched.cc.
|
overrideprotectedvirtual |
Definition at line 560 of file fe_enriched.cc.
|
overrideprotectedvirtual |
Definition at line 597 of file fe_enriched.cc.
|
private |
This function sets up the index table for the system as well as restriction and prolongation matrices.
Definition at line 426 of file fe_enriched.cc.
|
private |
After calling fill_fe_(face/subface_)values this function implements the chain rule to multiply stored shape values/gradient/hessians by those of enrichment function evaluated at quadrature points.
Definition at line 635 of file fe_enriched.cc.
|
inherited |
|
inherited |
This operator returns a reference to the present object if the argument given equals to zero. While this does not seem particularly useful, it is helpful in writing code that works with both DoFHandler and the hp- version hp::DoFHandler, since one can then write code like this:
This code doesn't work in both situations without the present operator because DoFHandler::get_fe() returns a finite element, whereas hp::DoFHandler::get_fe() returns a collection of finite elements that doesn't offer a dofs_per_cell member variable: one first has to select which finite element to work on, which is done using the operator[]. Fortunately, cell->active_fe_index() also works for non-hp-classes and simply returns zero in that case. The present operator[] accepts this zero argument, by returning the finite element with index zero within its collection (that, of course, consists only of the present finite element anyway).
|
virtualinherited |
Just like for shape_value(), but this function will be called when the shape function has more than one non-zero vector component. In that case, this function should return the value of the component-th vector component of the ith shape function at point p.
Reimplemented in FE_DGPNonparametric< dim, spacedim >, FE_NedelecSZ< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, dim >, FE_PolyTensor< dim, spacedim >, FE_PolyTensor< dim, spacedim >, FE_PolyTensor< dim, dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
virtualinherited |
Return the gradient of the ith shape function at the point p. p is a point on the reference element, and likewise the gradient is the gradient on the unit cell with respect to unit cell coordinates. If the finite element is vector-valued, then return the value of the only non-zero component of the vector value of this shape function. If the shape function has more than one non-zero component (which we refer to with the term non-primitive), then derived classes implementing this function should throw an exception of type ExcShapeFunctionNotPrimitive. In that case, use the shape_grad_component() function.
Implementations of this function should throw an exception of type ExcUnitShapeValuesDoNotExist if the shape functions of the FiniteElement under consideration depend on the shape of the cell in real space, i.e., if the shape functions are not defined by mapping from the reference cell. Some non-conforming elements are defined this way, as is the FE_DGPNonparametric class, to name just one example.
The default implementation of this virtual function does exactly this, i.e., it simply throws an exception of type ExcUnitShapeValuesDoNotExist.
Reimplemented in FE_DGPNonparametric< dim, spacedim >, FE_NedelecSZ< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, dim >, FE_PolyTensor< dim, spacedim >, FE_PolyTensor< dim, spacedim >, FE_PolyTensor< dim, dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
virtualinherited |
Just like for shape_grad(), but this function will be called when the shape function has more than one non-zero vector component. In that case, this function should return the gradient of the component-th vector component of the ith shape function at point p.
Reimplemented in FE_DGPNonparametric< dim, spacedim >, FE_NedelecSZ< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, dim >, FE_PolyTensor< dim, spacedim >, FE_PolyTensor< dim, spacedim >, FE_PolyTensor< dim, dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
virtualinherited |
Return the tensor of second derivatives of the ith shape function at point p on the unit cell. The derivatives are derivatives on the unit cell with respect to unit cell coordinates. If the finite element is vector-valued, then return the value of the only non-zero component of the vector value of this shape function. If the shape function has more than one non-zero component (which we refer to with the term non-primitive), then derived classes implementing this function should throw an exception of type ExcShapeFunctionNotPrimitive. In that case, use the shape_grad_grad_component() function.
Implementations of this function should throw an exception of type ExcUnitShapeValuesDoNotExist if the shape functions of the FiniteElement under consideration depend on the shape of the cell in real space, i.e., if the shape functions are not defined by mapping from the reference cell. Some non-conforming elements are defined this way, as is the FE_DGPNonparametric class, to name just one example.
The default implementation of this virtual function does exactly this, i.e., it simply throws an exception of type ExcUnitShapeValuesDoNotExist.
Reimplemented in FE_DGPNonparametric< dim, spacedim >, FE_NedelecSZ< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, dim >, FE_PolyTensor< dim, spacedim >, FE_PolyTensor< dim, spacedim >, FE_PolyTensor< dim, dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
virtualinherited |
Just like for shape_grad_grad(), but this function will be called when the shape function has more than one non-zero vector component. In that case, this function should return the gradient of the component-th vector component of the ith shape function at point p.
Reimplemented in FE_DGPNonparametric< dim, spacedim >, FE_NedelecSZ< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, dim >, FE_PolyTensor< dim, spacedim >, FE_PolyTensor< dim, spacedim >, FE_PolyTensor< dim, dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
virtualinherited |
Return the tensor of third derivatives of the ith shape function at point p on the unit cell. The derivatives are derivatives on the unit cell with respect to unit cell coordinates. If the finite element is vector-valued, then return the value of the only non-zero component of the vector value of this shape function. If the shape function has more than one non-zero component (which we refer to with the term non-primitive), then derived classes implementing this function should throw an exception of type ExcShapeFunctionNotPrimitive. In that case, use the shape_3rd_derivative_component() function.
Implementations of this function should throw an exception of type ExcUnitShapeValuesDoNotExist if the shape functions of the FiniteElement under consideration depend on the shape of the cell in real space, i.e., if the shape functions are not defined by mapping from the reference cell. Some non-conforming elements are defined this way, as is the FE_DGPNonparametric class, to name just one example.
The default implementation of this virtual function does exactly this, i.e., it simply throws an exception of type ExcUnitShapeValuesDoNotExist.
Reimplemented in FE_Poly< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
virtualinherited |
Just like for shape_3rd_derivative(), but this function will be called when the shape function has more than one non-zero vector component. In that case, this function should return the gradient of the component- th vector component of the ith shape function at point p.
Reimplemented in FE_Poly< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
virtualinherited |
Return the tensor of fourth derivatives of the ith shape function at point p on the unit cell. The derivatives are derivatives on the unit cell with respect to unit cell coordinates. If the finite element is vector-valued, then return the value of the only non-zero component of the vector value of this shape function. If the shape function has more than one non-zero component (which we refer to with the term non-primitive), then derived classes implementing this function should throw an exception of type ExcShapeFunctionNotPrimitive. In that case, use the shape_4th_derivative_component() function.
Implementations of this function should throw an exception of type ExcUnitShapeValuesDoNotExist if the shape functions of the FiniteElement under consideration depend on the shape of the cell in real space, i.e., if the shape functions are not defined by mapping from the reference cell. Some non-conforming elements are defined this way, as is the FE_DGPNonparametric class, to name just one example.
The default implementation of this virtual function does exactly this, i.e., it simply throws an exception of type ExcUnitShapeValuesDoNotExist.
Reimplemented in FE_Poly< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
virtualinherited |
Just like for shape_4th_derivative(), but this function will be called when the shape function has more than one non-zero vector component. In that case, this function should return the gradient of the component- th vector component of the ith shape function at point p.
Reimplemented in FE_Poly< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
virtualinherited |
This function returns true, if the shape function shape_index has non-zero function values somewhere on the face face_index. The function is typically used to determine whether some matrix elements resulting from face integrals can be assumed to be zero and may therefore be omitted from integration.
A default implementation is provided in this base class which always returns true. This is the safe way to go.
Reimplemented in FE_DGPMonomial< dim >, FE_DGPMonomial< dim >, FE_Q_Hierarchical< dim >, FE_ABF< dim >, FE_DGVector< PolynomialType, dim, spacedim >, FE_DGVector< PolynomialsBDM< dim >, dim, dim >, FE_DGVector< PolynomialsNedelec< dim >, dim, dim >, FE_DGVector< PolynomialsRaviartThomas< dim >, dim, dim >, FE_DGP< dim, spacedim >, FE_DGPMonomial< dim >, FE_DGPNonparametric< dim, spacedim >, FE_DGQ< dim, spacedim >, FE_DGQ< dim, dim >, FE_FaceQ< dim, spacedim >, FE_FaceQ< 1, spacedim >, FE_FaceP< dim, spacedim >, FE_Nedelec< dim >, FE_Q_Base< dim, spacedim >, FE_Q_Base< dim, dim >, FE_Q_Base< dim, spacedim >, FE_Q_Bubbles< dim, spacedim >, FE_Q_DG0< dim, spacedim >, FE_Q_Hierarchical< dim >, FE_RaviartThomas< dim >, FE_RaviartThomasNodal< dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, FESystem< dim, spacedim >, FE_TraceQ< dim, spacedim >, FE_DGPMonomial< dim >, and FE_Q_Hierarchical< dim >.
|
inherited |
Return whether this element implements its prolongation matrices. The return value also indicates whether a call to the get_prolongation_matrix() function will generate an error or not.
Note, that this function returns true only if the prolongation matrices of the isotropic and all anisotropic refinement cases are implemented. If you are interested in the prolongation matrices for isotropic refinement only, use the isotropic_prolongation_is_implemented function instead.
This function is mostly here in order to allow us to write more efficient test programs which we run on all kinds of weird elements, and for which we simply need to exclude certain tests in case something is not implemented. It will in general probably not be a great help in applications, since there is not much one can do if one needs these features and they are not implemented. This function could be used to check whether a call to get_prolongation_matrix() will succeed; however, one then still needs to cope with the lack of information this just expresses.
|
inherited |
Return whether this element implements its prolongation matrices for isotropic children. The return value also indicates whether a call to the get_prolongation_matrix function will generate an error or not.
This function is mostly here in order to allow us to write more efficient test programs which we run on all kinds of weird elements, and for which we simply need to exclude certain tests in case something is not implemented. It will in general probably not be a great help in applications, since there is not much one can do if one needs these features and they are not implemented. This function could be used to check whether a call to get_prolongation_matrix() will succeed; however, one then still needs to cope with the lack of information this just expresses.
|
inherited |
Return whether this element implements its restriction matrices. The return value also indicates whether a call to the get_restriction_matrix() function will generate an error or not.
Note, that this function returns true only if the restriction matrices of the isotropic and all anisotropic refinement cases are implemented. If you are interested in the restriction matrices for isotropic refinement only, use the isotropic_restriction_is_implemented() function instead.
This function is mostly here in order to allow us to write more efficient test programs which we run on all kinds of weird elements, and for which we simply need to exclude certain tests in case something is not implemented. It will in general probably not be a great help in applications, since there is not much one can do if one needs these features and they are not implemented. This function could be used to check whether a call to get_restriction_matrix() will succeed; however, one then still needs to cope with the lack of information this just expresses.
|
inherited |
Return whether this element implements its restriction matrices for isotropic children. The return value also indicates whether a call to the get_restriction_matrix() function will generate an error or not.
This function is mostly here in order to allow us to write more efficient test programs which we run on all kinds of weird elements, and for which we simply need to exclude certain tests in case something is not implemented. It will in general probably not be a great help in applications, since there is not much one can do if one needs these features and they are not implemented. This function could be used to check whether a call to get_restriction_matrix() will succeed; however, one then still needs to cope with the lack of information this just expresses.
|
inherited |
Access the restriction_is_additive_flags field. See the discussion about restriction matrices in the general class documentation for more information.
The index must be between zero and the number of shape functions of this element.
|
inherited |
Return a read only reference to the matrix that describes the constraints at the interface between a refined and an unrefined cell.
Some finite elements do not (yet) implement hanging node constraints. If this is the case, then this function will generate an exception, since no useful return value can be generated. If you should have a way to live with this, then you might want to use the constraints_are_implemented() function to check up front whether this function will succeed or generate the exception.
|
inherited |
Return whether this element implements its hanging node constraints. The return value also indicates whether a call to the constraints() function will generate an error or not.
This function is mostly here in order to allow us to write more efficient test programs which we run on all kinds of weird elements, and for which we simply need to exclude certain tests in case hanging node constraints are not implemented. It will in general probably not be a great help in applications, since there is not much one can do if one needs hanging node constraints and they are not implemented. This function could be used to check whether a call to constraints() will succeed; however, one then still needs to cope with the lack of information this just expresses.
|
virtualinherited |
Return the matrix interpolating from the given finite element to the present one. The size of the matrix is then dofs_per_cell times source.dofs_per_cell.
Derived elements will have to implement this function. They may only provide interpolation matrices for certain source finite elements, for example those from the same family. If they don't implement interpolation from a given element, then they must throw an exception of type ExcInterpolationNotImplemented.
Reimplemented in FE_Bernstein< dim, spacedim >, FE_DGQ< dim, spacedim >, FE_DGQ< dim, dim >, FE_Q_Base< dim, spacedim >, FE_Q_Base< dim, dim >, FE_Q_Base< dim, spacedim >, FE_Q_Bubbles< dim, spacedim >, FE_Q_DG0< dim, spacedim >, FESystem< dim, spacedim >, FESystem< dim, dim >, FESystem< dim, spacedim >, FE_Nothing< dim, spacedim >, and FE_Nothing< dim, dim >.
|
virtualinherited |
Comparison operator.
The implementation in the current class checks for equality of the following pieces of information between the current object and the one given as argument, in this order:
This covers most cases where elements can differ, but there are cases of derived elements that are different and for which the current function still returns true. For these cases, derived classes should overload this function.
|
inherited |
Comparison operator.
Definition at line 196 of file fe_data.cc.
|
inherited |
Non-equality comparison operator. Defined in terms of the equality comparison operator.
|
inherited |
Compute vector component and index of this shape function within the shape functions corresponding to this component from the index of a shape function within this finite element.
If the element is scalar, then the component is always zero, and the index within this component is equal to the overall index.
If the shape function referenced has more than one non-zero component, then it cannot be associated with one vector component, and an exception of type ExcShapeFunctionNotPrimitive will be raised.
Note that if the element is composed of other (base) elements, and a base element has more than one component but all its shape functions are primitive (i.e. are non-zero in only one component), then this mapping contains valid information. However, the index of a shape function of this element within one component (i.e. the second number of the respective entry of this array) does not indicate the index of the respective shape function within the base element (since that has more than one vector-component). For this information, refer to the system_to_base_table field and the system_to_base_index() function.
See the class description above for an example of how this function is typically used.
The use of this function is explained extensively in the step-8 and step-20 tutorial programs as well as in the Handling vector valued problems module.
|
inherited |
Compute the shape function for the given vector component and index.
If the element is scalar, then the component must be zero, and the index within this component is equal to the overall index.
This is the opposite operation from the system_to_component_index() function.
|
inherited |
Same as system_to_component_index(), but do it for shape functions and their indices on a face. The range of allowed indices is therefore 0..dofs_per_face.
You will rarely need this function in application programs, since almost all application codes only need to deal with cell indices, not face indices. The function is mainly there for use inside the library.
|
inherited |
For faces with non-standard face_orientation in 3D, the dofs on faces (quads) have to be permuted in order to be combined with the correct shape functions. Given a local dof index on a quad, return the local index, if the face has non-standard face_orientation, face_flip or face_rotation. In 2D and 1D there is no need for permutation and consequently an exception is thrown.
|
virtualinherited |
Given an index in the natural ordering of indices on a face, return the index of the same degree of freedom on the cell.
To explain the concept, consider the case where we would like to know whether a degree of freedom on a face, for example as part of an FESystem element, is primitive. Unfortunately, the is_primitive() function in the FiniteElement class takes a cell index, so we would need to find the cell index of the shape function that corresponds to the present face index. This function does that.
Code implementing this would then look like this:
The function takes additional arguments that account for the fact that actual faces can be in their standard ordering with respect to the cell under consideration, or can be flipped, oriented, etc.
| face_dof_index | The index of the degree of freedom on a face. This index must be between zero and dofs_per_face. |
| face | The number of the face this degree of freedom lives on. This number must be between zero and GeometryInfo::faces_per_cell. |
| face_orientation | One part of the description of the orientation of the face. See GlossFaceOrientation. |
| face_flip | One part of the description of the orientation of the face. See GlossFaceOrientation. |
| face_rotation | One part of the description of the orientation of the face. See GlossFaceOrientation. |
Reimplemented in FE_Q_Base< dim, spacedim >, FE_Q_Base< dim, dim >, FE_Q_Base< dim, spacedim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
inherited |
For lines with non-standard line_orientation in 3D, the dofs on lines have to be permuted in order to be combined with the correct shape functions. Given a local dof index on a line, return the local index, if the line has non-standard line_orientation. In 2D and 1D there is no need for permutation, so the given index is simply returned.
|
inherited |
Return in which of the vector components of this finite element the ith shape function is non-zero. The length of the returned array is equal to the number of vector components of this element.
For most finite element spaces, the result of this function will be a vector with exactly one element being true, since for most spaces the individual vector components are independent. In that case, the component with the single zero is also the first element of what system_to_component_index() returns.
Only for those spaces that couple the components, for example to make a shape function divergence free, will there be more than one true entry. Elements for which this is true are called non-primitive (see GlossPrimitive).
|
inherited |
Return in how many vector components the ith shape function is non-zero. This value equals the number of entries equal to true in the result of the get_nonzero_components() function.
For most finite element spaces, the result will be equal to one. It is not equal to one only for those ansatz spaces for which vector-valued shape functions couple the individual components, for example in order to make them divergence-free.
|
inherited |
Return whether the entire finite element is primitive, in the sense that all its shape functions are primitive. If the finite element is scalar, then this is always the case.
Since this is an extremely common operation, the result is cached and returned by this function.
|
inherited |
Return whether the ith shape function is primitive in the sense that the shape function is non-zero in only one vector component. Non- primitive shape functions would then, for example, be those of divergence free ansatz spaces, in which the individual vector components are coupled.
The result of the function is true if and only if the result of n_nonzero_components(i) is equal to one.
|
inherited |
Number of base elements in a mixed discretization.
Note that even for vector valued finite elements, the number of components needs not coincide with the number of base elements, since they may be reused. For example, if you create a FESystem with three identical finite element classes by using the constructor that takes one finite element and a multiplicity, then the number of base elements is still one, although the number of components of the finite element is equal to the multiplicity.
|
inherited |
This index denotes how often the base element index is used in a composed element. If the element is atomic, then the result is always equal to one. See the documentation for the n_base_elements() function for more details.
|
inherited |
Return a reference to a contained finite element that matches the components selected by the given ComponentMask mask.
For an arbitrarily nested FESystem, this function returns the inner-most FiniteElement that matches the given mask. The method fails if the mask does not exactly match one of the contained finite elements. It is most useful if the current object is an FESystem, as the return value can only be this in all other cases.
Note that the returned object can be an FESystem if the mask matches it but not any of the contained objects.
Let us illustrate the function with the an FESystem fe with 7 components:
The following table lists all possible component masks you can use:
| ComponentMask | Result | Description |
|---|---|---|
[true,true,true,true,true,true,true] | FESystem<2>[FESystem<2>[FE_Q<2>(2)^2]-FE_Q<2>(1)-FE_DGP<2>(0)^2-FE_BDM<2>(1)] | fe itself, the whole FESystem |
[true,true,false,false,false,false,false] | FESystem<2>[FE_Q<2>(2)^2] | just the fe_velocity |
[true,false,false,false,false,false,false] | FE_Q<2>(2) | The first component in fe_velocity |
[false,true,false,false,false,false,false] | FE_Q<2>(2) | The second component in fe_velocity |
[false,false,true,false,false,false,false] | FE_Q<2>(1) | fe_pressure |
[false,false,false,true,false,false,false] | FE_DGP<2>(0) | first copy of fe_dg |
[false,false,false,false,true,false,false] | FE_DGP<2>(0) | second copy of fe_dg |
[false,false,false,false,false,true,true] | FE_BDM<2>(1) | both components of fe_nonprim |
|
virtualinherited |
Return a reference to a contained finite element that matches the components n_selected_components components starting at component with index first_component.
See the other get_sub_fe() function above for more details.
Reimplemented in FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
inherited |
Return for shape function index the base element it belongs to, the number of the copy of this base element (which is between zero and the multiplicity of this element), and the index of this shape function within this base element.
If the element is not composed of others, then base and instance are always zero, and the index is equal to the number of the shape function. If the element is composed of single instances of other elements (i.e. all with multiplicity one) all of which are scalar, then base values and dof indices within this element are equal to the system_to_component_table. It differs only in case the element is composed of other elements and at least one of them is vector-valued itself.
See the class documentation above for an example of how this function is typically used.
This function returns valid values also in the case of vector-valued (i.e. non-primitive) shape functions, in contrast to the system_to_component_index() function.
|
inherited |
Same as system_to_base_index(), but for degrees of freedom located on a face. The range of allowed indices is therefore 0..dofs_per_face.
You will rarely need this function in application programs, since almost all application codes only need to deal with cell indices, not face indices. The function is mainly there for use inside the library.
|
inherited |
Given a base element number, return the first block of a BlockVector it would generate.
|
inherited |
For each vector component, return which base element implements this component and which vector component in this base element this is. This information is only of interest for vector-valued finite elements which are composed of several sub-elements. In that case, one may want to obtain information about the element implementing a certain vector component, which can be done using this function and the FESystem::base_element() function.
If this is a scalar finite element, then the return value is always equal to a pair of zeros.
|
inherited |
Return the base element for this block and the number of the copy of the base element.
|
inherited |
The vector block and the index inside the block for this shape function.
|
inherited |
The vector block for this component.
|
inherited |
Return a component mask with as many elements as this object has vector components and of which exactly the one component is true that corresponds to the given argument. See the glossary for more information.
| scalar | An object that represents a single scalar vector component of this finite element. |
|
inherited |
Return a component mask with as many elements as this object has vector components and of which exactly the dim components are true that correspond to the given argument. See the glossary for more information.
| vector | An object that represents dim vector components of this finite element. |
|
inherited |
Return a component mask with as many elements as this object has vector components and of which exactly the dim*(dim+1)/2 components are true that correspond to the given argument. See the glossary for more information.
| sym_tensor | An object that represents dim*(dim+1)/2 components of this finite element that are jointly to be interpreted as forming a symmetric tensor. |
|
inherited |
Given a block mask (see this glossary entry), produce a component mask (see this glossary entry) that represents the components that correspond to the blocks selected in the input argument. This is essentially a conversion operator from BlockMask to ComponentMask.
| block_mask | The mask that selects individual blocks of the finite element |
|
inherited |
Return a block mask with as many elements as this object has blocks and of which exactly the one component is true that corresponds to the given argument. See the glossary for more information.
| scalar | An object that represents a single scalar vector component of this finite element. |
|
inherited |
Return a component mask with as many elements as this object has vector components and of which exactly the dim components are true that correspond to the given argument. See the glossary for more information.
| vector | An object that represents dim vector components of this finite element. |
|
inherited |
Return a component mask with as many elements as this object has vector components and of which exactly the dim*(dim+1)/2 components are true that correspond to the given argument. See the glossary for more information.
| sym_tensor | An object that represents dim*(dim+1)/2 components of this finite element that are jointly to be interpreted as forming a symmetric tensor. |
|
inherited |
Given a component mask (see this glossary entry), produce a block mask (see this glossary entry) that represents the blocks that correspond to the components selected in the input argument. This is essentially a conversion operator from ComponentMask to BlockMask.
| component_mask | The mask that selects individual components of the finite element |
|
virtualinherited |
Return a list of constant modes of the element. The number of rows in the resulting table depends on the elements in use. For standard elements, the table has as many rows as there are components in the element and dofs_per_cell columns. To each component of the finite element, the row in the returned table contains a basis representation of the constant function 1 on the element. However, there are some scalar elements where there is more than one constant mode, e.g. the element FE_Q_DG0.
In order to match the constant modes to the actual components in the element, the returned data structure also returns a vector with as many components as there are constant modes on the element that contains the component number.
Reimplemented in FE_DGP< dim, spacedim >, FE_DGQ< dim, spacedim >, FE_DGQ< dim, dim >, FE_DGQLegendre< dim, spacedim >, FE_FaceQ< dim, spacedim >, FE_FaceQ< 1, spacedim >, FE_FaceP< dim, spacedim >, FE_Nedelec< dim >, FE_Nothing< dim, spacedim >, FE_Nothing< dim, dim >, FE_Q_Base< dim, spacedim >, FE_Q_Base< dim, dim >, FE_Q_Base< dim, spacedim >, FE_Q_DG0< dim, spacedim >, FE_Q_Hierarchical< dim >, FE_RaviartThomas< dim >, FE_SimplexPoly< dim, spacedim >, FE_SimplexPoly< dim, dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, FESystem< dim, spacedim >, and FE_TraceQ< dim, spacedim >.
|
inherited |
Return the support points of the trial functions on the unit cell, if the derived finite element defines them. Finite elements that allow some kind of interpolation operation usually have support points. On the other hand, elements that define their degrees of freedom by, for example, moments on faces, or as derivatives, don't have support points. In that case, the returned field is empty.
If the finite element defines support points, then their number equals the number of degrees of freedom of the element. The order of points in the array matches that returned by the cell->get_dof_indices function.
See the class documentation for details on support points.
FESystem(FE_Q(1),3) for which each support point would appear three times in the returned array.
|
inherited |
Return whether a finite element has defined support points. If the result is true, then a call to the get_unit_support_points() yields a non-empty array.
The result may be false if an element is not defined by interpolating shape functions, for example by P-elements on quadrilaterals. It will usually only be true if the element constructs its shape functions by the requirement that they be one at a certain point and zero at all the points associated with the other shape functions.
In composed elements (i.e. for the FESystem class), the result will be true if all the base elements have defined support points. FE_Nothing is a special case in FESystems, because it has 0 support points and has_support_points() is false, but an FESystem containing an FE_Nothing among other elements will return true.
|
virtualinherited |
Return the position of the support point of the indexth shape function. If it does not exist, raise an exception.
The default implementation simply returns the respective element from the array you get from get_unit_support_points(), but derived elements may overload this function. In particular, note that the FESystem class overloads it so that it can return the support points of individual base elements, if not all the base elements define support points. In this way, you can still ask for certain support points, even if get_unit_support_points() only returns an empty array.
Reimplemented in FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
inherited |
Return the support points of the trial functions on the unit face, if the derived finite element defines some. Finite elements that allow some kind of interpolation operation usually have support points. On the other hand, elements that define their degrees of freedom by, for example, moments on faces, or as derivatives, don't have support points. In that case, the returned field is empty
Note that elements that have support points need not necessarily have some on the faces, even if the interpolation points are located physically on a face. For example, the discontinuous elements have interpolation points on the vertices, and for higher degree elements also on the faces, but they are not defined to be on faces since in that case degrees of freedom from both sides of a face (or from all adjacent elements to a vertex) would be identified with each other, which is not what we would like to have). Logically, these degrees of freedom are therefore defined to belong to the cell, rather than the face or vertex. In that case, the returned element would therefore have length zero.
If the finite element defines support points, then their number equals the number of degrees of freedom on the face (dofs_per_face). The order of points in the array matches that returned by the cell->face(face)->get_dof_indices function.
See the class documentation for details on support points.
|
inherited |
Return whether a finite element has defined support points on faces. If the result is true, then a call to the get_unit_face_support_points() yields a non-empty vector.
For more information, see the documentation for the has_support_points() function.
|
virtualinherited |
The function corresponding to the unit_support_point() function, but for faces. See there for more information.
Reimplemented in FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
inherited |
Return a vector of generalized support points.
See the glossary entry on generalized support points for more information.
|
inherited |
Return whether a finite element has defined generalized support points. If the result is true, then a call to the get_generalized_support_points() yields a non-empty vector.
See the glossary entry on generalized support points for more information.
|
inherited |
For a given degree of freedom, return whether it is logically associated with a vertex, line, quad or hex.
For instance, for continuous finite elements this coincides with the lowest dimensional object the support point of the degree of freedom lies on. To give an example, for \(Q_1\) elements in 3d, every degree of freedom is defined by a shape function that we get by interpolating using support points that lie on the vertices of the cell. The support of these points of course extends to all edges connected to this vertex, as well as the adjacent faces and the cell interior, but we say that logically the degree of freedom is associated with the vertex as this is the lowest- dimensional object it is associated with. Likewise, for \(Q_2\) elements in 3d, the degrees of freedom with support points at edge midpoints would yield a value of GeometryPrimitive::line from this function, whereas those on the centers of faces in 3d would return GeometryPrimitive::quad.
To make this more formal, the kind of object returned by this function represents the object so that the support of the shape function corresponding to the degree of freedom, (i.e., that part of the domain where the function "lives") is the union of all of the cells sharing this object. To return to the example above, for \(Q_2\) in 3d, the shape function with support point at an edge midpoint has support on all cells that share the edge and not only the cells that share the adjacent faces, and consequently the function will return GeometryPrimitive::line.
On the other hand, for discontinuous elements of type \(DGQ_2\), a degree of freedom associated with an interpolation polynomial that has its support point physically located at a line bounding a cell, but is nonzero only on one cell. Consequently, it is logically associated with the interior of that cell (i.e., with a GeometryPrimitive::quad in 2d and a GeometryPrimitive::hex in 3d).
| [in] | cell_dof_index | The index of a shape function or degree of freedom. This index must be in the range [0,dofs_per_cell). |
|
virtualinherited |
Given the values of a function \(f(\mathbf x)\) at the (generalized) support points of the reference cell, this function then computes what the nodal values of the element are, i.e., \(\Psi_i[f]\), where \(\Psi_i\) are the node functionals of the element (see also Node values or node functionals). The values \(\Psi_i[f]\) are then the expansion coefficients for the shape functions of the finite element function that interpolates the given function \(f(x)\), i.e., \( f_h(\mathbf x) = \sum_i \Psi_i[f] \varphi_i(\mathbf x) \) is the finite element interpolant of \(f\) with the current element. The operation described here is used, for example, in the FETools::compute_node_matrix() function.
In more detail, let us assume that the generalized support points (see this glossary entry ) of the current element are \(\hat{\mathbf x}_i\) and that the node functionals associated with the current element are \(\Psi_i[\cdot]\). Then, the fact that the element is based on generalized support points, implies that if we apply \(\Psi_i\) to a (possibly vector-valued) finite element function \(\varphi\), the result must have the form \(\Psi_i[\varphi] = f_i(\varphi(\hat{\mathbf x}_i))\) – in other words, the value of the node functional \(\Psi_i\) applied to \(\varphi\) only depends on the values of \(\varphi\) at \(\hat{\mathbf x}_i\) and not on values anywhere else, or integrals of \(\varphi\), or any other kind of information.
The exact form of \(f_i\) depends on the element. For example, for scalar Lagrange elements, we have that in fact \(\Psi_i[\varphi] = \varphi(\hat{\mathbf x}_i)\). If you combine multiple scalar Lagrange elements via an FESystem object, then \(\Psi_i[\varphi] = \varphi(\hat{\mathbf x}_i)_{c(i)}\) where \(c(i)\) is the result of the FiniteElement::system_to_component_index() function's return value's first component. In these two cases, \(f_i\) is therefore simply the identity (in the scalar case) or a function that selects a particular vector component of its argument. On the other hand, for Raviart-Thomas elements, one would have that \(f_i(\mathbf y) = \mathbf y \cdot \mathbf n_i\) where \(\mathbf n_i\) is the normal vector of the face at which the shape function is defined.
Given all of this, what this function does is the following: If you input a list of values of a function \(\varphi\) at all generalized support points (where each value is in fact a vector of values with as many components as the element has), then this function returns a vector of values obtained by applying the node functionals to these values. In other words, if you pass in \(\{\varphi(\hat{\mathbf x}_i)\}_{i=0}^{N-1}\) then you will get out a vector \(\{\Psi[\varphi]\}_{i=0}^{N-1}\) where \(N\) equals dofs_per_cell.
| [in] | support_point_values | An array of size dofs_per_cell (which equals the number of points the get_generalized_support_points() function will return) where each element is a vector with as many entries as the element has vector components. This array should contain the values of a function at the generalized support points of the current element. |
| [out] | nodal_values | An array of size dofs_per_cell that contains the node functionals of the element applied to the given function. |
Reimplemented in FESystem< dim, spacedim >, FESystem< dim, dim >, FESystem< dim, spacedim >, FE_ABF< dim >, FE_BDM< dim >, FE_BernardiRaugel< dim >, FE_DGQ< dim, spacedim >, FE_DGQ< dim, dim >, FE_DGQArbitraryNodes< dim, spacedim >, FE_FaceQ< dim, spacedim >, FE_Nedelec< dim >, FE_PyramidPoly< dim, spacedim >, FE_PyramidPoly< dim, dim >, FE_Q< dim, spacedim >, FE_Q< dim, dim >, FE_Q_Bubbles< dim, spacedim >, FE_Q_DG0< dim, spacedim >, FE_Q_iso_Q1< dim, spacedim >, FE_RannacherTurek< dim >, FE_RaviartThomas< dim >, FE_RaviartThomasNodal< dim >, FE_RT_Bubbles< dim >, FE_SimplexPoly< dim, spacedim >, FE_SimplexPoly< dim, dim >, FE_TraceQ< dim, spacedim >, FE_WedgePoly< dim, spacedim >, and FE_WedgePoly< dim, dim >.
|
virtualinherited |
Determine an estimate for the memory consumption (in bytes) of this object.
This function is made virtual, since finite element objects are usually accessed through pointers to their base class, rather than the class itself.
Reimplemented in FE_ABF< dim >, FE_DGVector< PolynomialType, dim, spacedim >, FE_DGVector< PolynomialsBDM< dim >, dim, dim >, FE_DGVector< PolynomialsNedelec< dim >, dim, dim >, FE_DGVector< PolynomialsRaviartThomas< dim >, dim, dim >, FE_DGP< dim, spacedim >, FE_DGPMonomial< dim >, FE_DGPNonparametric< dim, spacedim >, FE_Nedelec< dim >, FE_Poly< dim, spacedim >, FE_Poly< dim, spacedim >, FE_Poly< dim, dim >, FE_Q_Hierarchical< dim >, FE_RaviartThomas< dim >, FESystem< dim, spacedim >, FESystem< dim, dim >, and FESystem< dim, spacedim >.
|
protectedinherited |
Reinit the vectors of restriction and prolongation matrices to the right sizes: For every refinement case, except for RefinementCase::no_refinement, and for every child of that refinement case the space of one restriction and prolongation matrix is allocated, see the documentation of the restriction and prolongation vectors for more detail on the actual vector sizes.
| isotropic_restriction_only | only the restriction matrices required for isotropic refinement are reinited to the right size. |
| isotropic_prolongation_only | only the prolongation matrices required for isotropic refinement are reinited to the right size. |
|
protectedinherited |
Return the size of interface constraint matrices. Since this is needed in every derived finite element class when initializing their size, it is placed into this function, to avoid having to recompute the dimension- dependent size of these matrices each time.
Note that some elements do not implement the interface constraints for certain polynomial degrees. In this case, this function still returns the size these matrices should have when implemented, but the actual matrices are empty.
|
staticprotectedinherited |
Given the pattern of nonzero components for each shape function, compute for each entry how many components are non-zero for each shape function. This function is used in the constructor of this class.
|
protectedvirtualinherited |
|
protectedpure virtualinherited |
Compute information about the shape functions on the cell denoted by the first argument. Derived classes will have to implement this function based on the kind of element they represent. It is called by FEValues::reinit().
Conceptually, this function evaluates shape functions and their derivatives at the quadrature points represented by the mapped locations of those described by the quadrature argument to this function. In many cases, computing derivatives of shape functions (and in some cases also computing values of shape functions) requires making use of the mapping from the reference to the real cell; this information can either be taken from the mapping_data object that has been filled for the current cell before this function is called, or by calling the member functions of a Mapping object with the mapping_internal object that also corresponds to the current cell.
The information computed by this function is used to fill the various member variables of the output argument of this function. Which of the member variables of that structure should be filled is determined by the update flags stored in the FiniteElement::InternalDataBase::update_each field of the object passed to this function. These flags are typically set by FiniteElement::get_data(), FiniteElement::get_face_date() and FiniteElement::get_subface_data() (or, more specifically, implementations of these functions in derived classes).
An extensive discussion of the interaction between this function and FEValues can be found in the How Mapping, FiniteElement, and FEValues work together documentation module.
| [in] | cell | The cell of the triangulation for which this function is to compute a mapping from the reference cell to. |
| [in] | cell_similarity | Whether or not the cell given as first argument is simply a translation, rotation, etc of the cell for which this function was called the most recent time. This information is computed simply by matching the vertices (as stored by the Triangulation) between the previous and the current cell. The value passed here may be modified by implementations of this function and should then be returned (see the discussion of the return value of this function). |
| [in] | quadrature | A reference to the quadrature formula in use for the current evaluation. This quadrature object is the same as the one used when creating the internal_data object. The current object is then responsible for evaluating shape functions at the mapped locations of the quadrature points represented by this object. |
| [in] | mapping | A reference to the mapping object used to map from the reference cell to the current cell. This object was used to compute the information in the mapping_data object before the current function was called. It is also the mapping object that created the mapping_internal object via Mapping::get_data(). You will need the reference to this mapping object most often to call Mapping::transform() to transform gradients and higher derivatives from the reference to the current cell. |
| [in] | mapping_internal | An object specific to the mapping object. What the mapping chooses to store in there is of no relevance to the current function, but you may have to pass a reference to this object to certain functions of the Mapping class (e.g., Mapping::transform()) if you need to call them from the current function. |
| [in] | mapping_data | The output object into which the Mapping::fill_fe_values() function wrote the mapping information corresponding to the current cell. This includes, for example, Jacobians of the mapping that may be of relevance to the current function, as well as other information that FEValues::reinit() requested from the mapping. |
| [in] | fe_internal | A reference to an object previously created by get_data() and that may be used to store information the mapping can compute once on the reference cell. See the documentation of the FiniteElement::InternalDataBase class for an extensive description of the purpose of these objects. |
| [out] | output_data | A reference to an object whose member variables should be computed. Not all of the members of this argument need to be filled; which ones need to be filled is determined by the update flags stored inside the fe_internal object. |
fe_internal and output_data objects. In other words, if an implementation of this function knows that it has written a piece of data into the output argument in a previous call, then there is no need to copy it there again in a later call if the implementation knows that this is the same value.
|
protectedvirtualinherited |
This function is the equivalent to FiniteElement::fill_fe_values(), but for faces of cells. See there for an extensive discussion of its purpose. It is called by FEFaceValues::reinit().
| [in] | cell | The cell of the triangulation for which this function is to compute a mapping from the reference cell to. |
| [in] | face_no | The number of the face we are currently considering, indexed among the faces of the cell specified by the previous argument. |
| [in] | quadrature | A reference to the quadrature formula in use for the current evaluation. This quadrature object is the same as the one used when creating the internal_data object. The current object is then responsible for evaluating shape functions at the mapped locations of the quadrature points represented by this object. |
| [in] | mapping | A reference to the mapping object used to map from the reference cell to the current cell. This object was used to compute the information in the mapping_data object before the current function was called. It is also the mapping object that created the mapping_internal object via Mapping::get_data(). You will need the reference to this mapping object most often to call Mapping::transform() to transform gradients and higher derivatives from the reference to the current cell. |
| [in] | mapping_internal | An object specific to the mapping object. What the mapping chooses to store in there is of no relevance to the current function, but you may have to pass a reference to this object to certain functions of the Mapping class (e.g., Mapping::transform()) if you need to call them from the current function. |
| [in] | mapping_data | The output object into which the Mapping::fill_fe_values() function wrote the mapping information corresponding to the current cell. This includes, for example, Jacobians of the mapping that may be of relevance to the current function, as well as other information that FEValues::reinit() requested from the mapping. |
| [in] | fe_internal | A reference to an object previously created by get_data() and that may be used to store information the mapping can compute once on the reference cell. See the documentation of the FiniteElement::InternalDataBase class for an extensive description of the purpose of these objects. |
| [out] | output_data | A reference to an object whose member variables should be computed. Not all of the members of this argument need to be filled; which ones need to be filled is determined by the update flags stored inside the fe_internal object. |
|
protectedvirtualinherited |
|
protectedpure virtualinherited |
This function is the equivalent to FiniteElement::fill_fe_values(), but for the children of faces of cells. See there for an extensive discussion of its purpose. It is called by FESubfaceValues::reinit().
| [in] | cell | The cell of the triangulation for which this function is to compute a mapping from the reference cell to. |
| [in] | face_no | The number of the face we are currently considering, indexed among the faces of the cell specified by the previous argument. |
| [in] | sub_no | The number of the subface, i.e., the number of the child of a face, that we are currently considering, indexed among the children of the face specified by the previous argument. |
| [in] | quadrature | A reference to the quadrature formula in use for the current evaluation. This quadrature object is the same as the one used when creating the internal_data object. The current object is then responsible for evaluating shape functions at the mapped locations of the quadrature points represented by this object. |
| [in] | mapping | A reference to the mapping object used to map from the reference cell to the current cell. This object was used to compute the information in the mapping_data object before the current function was called. It is also the mapping object that created the mapping_internal object via Mapping::get_data(). You will need the reference to this mapping object most often to call Mapping::transform() to transform gradients and higher derivatives from the reference to the current cell. |
| [in] | mapping_internal | An object specific to the mapping object. What the mapping chooses to store in there is of no relevance to the current function, but you may have to pass a reference to this object to certain functions of the Mapping class (e.g., Mapping::transform()) if you need to call them from the current function. |
| [in] | mapping_data | The output object into which the Mapping::fill_fe_values() function wrote the mapping information corresponding to the current cell. This includes, for example, Jacobians of the mapping that may be of relevance to the current function, as well as other information that FEValues::reinit() requested from the mapping. |
| [in] | fe_internal | A reference to an object previously created by get_data() and that may be used to store information the mapping can compute once on the reference cell. See the documentation of the FiniteElement::InternalDataBase class for an extensive description of the purpose of these objects. |
| [out] | output_data | A reference to an object whose member variables should be computed. Not all of the members of this argument need to be filled; which ones need to be filled is determined by the update flags stored inside the fe_internal object. |
|
inherited |
Return the kind of reference cell this element is defined on: For example, whether the element's reference cell is a square or triangle, or similar choices in higher dimensions.
|
inherited |
Number of unique quads. If all quads have the same type, the value is one; else it equals the number of quads.
|
inherited |
Number of unique faces. If all faces have the same type, the value is one; else it equals the number of faces.
|
inherited |
Number of dofs per vertex.
|
inherited |
Number of dofs per line. Not including dofs on lower dimensional objects.
|
inherited |
Number of dofs per quad. Not including dofs on lower dimensional objects.
|
inherited |
Maximum number of dofs per quad. Not including dofs on lower dimensional objects.
|
inherited |
Number of dofs per hex. Not including dofs on lower dimensional objects.
|
inherited |
Number of dofs per face, accumulating degrees of freedom of all lower dimensional objects.
|
inherited |
Maximum number of dofs per face, accumulating degrees of freedom of all lower dimensional objects.
|
inherited |
Number of dofs per cell, accumulating degrees of freedom of all lower dimensional objects.
|
inherited |
Return the number of degrees per structdim-dimensional object. For structdim==0, the function therefore returns dofs_per_vertex, for structdim==1 dofs_per_line, etc. This function is mostly used to allow some template trickery for functions that should work on all sorts of objects without wanting to use the different names (vertex, line, ...) associated with these objects.
|
inherited |
Number of components. See the glossary for more information.
|
inherited |
Number of blocks. See the glossary for more information.
|
inherited |
Detailed information on block sizes.
|
inherited |
Maximal polynomial degree of a shape function in a single coordinate direction.
This function can be used to determine the optimal quadrature rule.
|
inherited |
Test whether a finite element space conforms to a certain Sobolev space.
|
inherited |
Return first index of dof on a line.
|
inherited |
Return first index of dof on a quad.
|
inherited |
Return first index of dof on a hexahedron.
|
inherited |
Return first index of dof on a line for face data.
|
inherited |
Return first index of dof on a quad for face data.
|
protected |
For each finite element i used in enrichment and each enrichment function j associated with it (essentially its multiplicity), base_no_mult_local_enriched_dofs[i][j] contains the associated local DoFs on the FE_Enriched finite element.
Definition at line 521 of file fe_enriched.h.
|
protected |
Enrichment functions. The size of the first vector is the same as the number of FiniteElement spaces used with enrichment. Whereas the size of the inner vector corresponds to the number of enrichment functions associated with a single FiniteElement.
Definition at line 532 of file fe_enriched.h.
|
protected |
Auxiliary variable used to distinguish between the case when we do enrichment and when the class simply wraps another FiniteElement.
This variable is initialized in the constructor by looping over a vector of enrichment elements and checking if all of them are FE_Nothing. If this is the case, then the value is set to false, otherwise it is true.
Definition at line 543 of file fe_enriched.h.
|
private |
The underlying FESystem object.
Definition at line 660 of file fe_enriched.h.
|
staticconstexprinherited |
The dimension of the image space, corresponding to Triangulation.
|
protectedinherited |
Vector of projection matrices. See get_restriction_matrix() above. The constructor initializes these matrices to zero dimensions, which can be changed by derived classes implementing them.
Note, that restriction[refinement_case-1][child] includes the restriction matrix of child child for the RefinementCase refinement_case. Here, we use refinement_case-1 instead of refinement_case as for RefinementCase::no_refinement(=0) there are no restriction matrices available.
|
protectedinherited |
Vector of embedding matrices. See get_prolongation_matrix() above. The constructor initializes these matrices to zero dimensions, which can be changed by derived classes implementing them.
Note, that prolongation[refinement_case-1][child] includes the prolongation matrix of child child for the RefinementCase refinement_case. Here, we use refinement_case-1 instead of refinement_case as for RefinementCase::no_refinement(=0) there are no prolongation matrices available.
|
protectedinherited |
Specify the constraints which the dofs on the two sides of a cell interface underlie if the line connects two cells of which one is refined once.
For further details see the general description of the derived class.
This field is obviously useless in one dimension and has there a zero size.
|
protectedinherited |
List of support points on the unit cell, in case the finite element has any. The constructor leaves this field empty, derived classes may write in some contents.
Finite elements that allow some kind of interpolation operation usually have support points. On the other hand, elements that define their degrees of freedom by, for example, moments on faces, or as derivatives, don't have support points. In that case, this field remains empty.
|
protectedinherited |
Same for the faces. See the description of the get_unit_face_support_points() function for a discussion of what contributes a face support point.
|
protectedinherited |
|
protectedinherited |
|
protectedinherited |
For faces with non-standard face_orientation in 3D, the dofs on faces (quads) have to be permuted in order to be combined with the correct shape functions. Given a local dof index on a quad, return the shift in the local index, if the face has non-standard face_orientation, i.e. old_index + shift = new_index. In 2D and 1D there is no need for permutation so the vector is empty. In 3D it has the size of dofs_per_quad * 8 , where 8 is the number of orientations, a face can be in (all combinations of the three bool flags face_orientation, face_flip and face_rotation).
The constructor of this class fills this table with zeros, i.e., no permutation at all. Derived finite element classes have to fill this Table with the correct values.
|
protectedinherited |
For lines with non-standard line_orientation in 3D, the dofs on lines have to be permuted in order to be combined with the correct shape functions. Given a local dof index on a line, return the shift in the local index, if the line has non-standard line_orientation, i.e. old_index + shift = new_index. In 2D and 1D there is no need for permutation so the vector is empty. In 3D it has the size of dofs_per_line.
The constructor of this class fills this table with zeros, i.e., no permutation at all. Derived finite element classes have to fill this vector with the correct values.
|
protectedinherited |
Store what system_to_component_index() will return.
|
protectedinherited |
Map between linear dofs and component dofs on face. This is filled with default values in the constructor, but derived classes will have to overwrite the information if necessary.
By component, we mean the vector component, not the base element. The information thus makes only sense if a shape function is non-zero in only one component.
|
protectedinherited |
For each shape function, store to which base element and which instance of this base element (in case its multiplicity is greater than one) it belongs, and its index within this base element. If the element is not composed of others, then base and instance are always zero, and the index is equal to the number of the shape function. If the element is composed of single instances of other elements (i.e. all with multiplicity one) all of which are scalar, then base values and dof indices within this element are equal to the system_to_component_table. It differs only in case the element is composed of other elements and at least one of them is vector-valued itself.
This array has valid values also in the case of vector-valued (i.e. non-primitive) shape functions, in contrast to the system_to_component_table.
|
protectedinherited |
|
protectedinherited |
|
protectedinherited |
The base element establishing a component.
For each component number c, the entries have the following meaning:
table[c].first.first c. This is the index you can pass to base_element(). table[c].first.second c. This value is between 0 and the n_components() of this base element. table[c].second c. This value is between 0 and the element_multiplicity() of this base element. This variable is set to the correct size by the constructor of this class, but needs to be initialized by derived classes, unless its size is one and the only entry is a zero, which is the case for scalar elements. In that case, the initialization by the base class is sufficient.
|
protectedinherited |
|
protectedinherited |
For each shape function, give a vector of bools (with size equal to the number of vector components which this finite element has) indicating in which component each of these shape functions is non-zero.
For primitive elements, there is only one non-zero component.
|
protectedinherited |
This array holds how many values in the respective entry of the nonzero_components element are non-zero. The array is thus a short-cut to allow faster access to this information than if we had to count the non-zero entries upon each request for this information. The field is initialized in the constructor of this class.
|
protectedinherited |
|
staticconstexprinherited |
|
privateinherited |
|
privateinherited |
|
privateinherited |
|
inherited |
|
inherited |
|
privateinherited |
|
inherited |
|
privateinherited |
|
inherited |
|
inherited |
|
privateinherited |
|
inherited |
|
inherited |
|
privateinherited |
|
inherited |
|
privateinherited |
|
inherited |
|
privateinherited |
|
inherited |
|
privateinherited |
|
inherited |
|
inherited |
Number of vector components of this finite element, and dimension of the image space. For vector-valued finite elements (i.e. when this number is greater than one), the number of vector components is in many cases equal to the number of base elements glued together with the help of the FESystem class. However, for elements like the Nedelec element, the number is greater than one even though we only have one base element.
|
inherited |
|
inherited |
|
inherited |
Storage for an object describing the sizes of each block of a compound element. For an element which is not an FESystem, this contains only a single block with length dofs_per_cell.