This tutorial depends on step-26.
Introduction
The Black-Scholes equation is a partial differential equation that falls a bit out of the ordinary scheme. It describes what the fair price of a "European
call" stock option is. Without going into too much detail, a stock "option" is a contract one can buy from a bank that allows me, but not requires me, to buy a specific stock at a fixed price K at a fixed future time T in the future. The question one would then want to answer as a buyer of such an option is "How much do I think such a contract is worth?", or as the seller "How much do I need to charge for this contract?", both as a function of the time t<T before the contract is up at time T and as a function of the stock price S. Fischer Black and Myron Scholes derived a partial differential equation for the fair price V(S,t) for such options under the assumption that stock prices exhibit random price fluctuations with a given level of "volatility" plus a background exponential price increase (which one can think of as the inflation rate that simply devalues all money over time). For their work, Black and Scholes received the Nobel Prize in Economic Sciences in 1997, making this the first tutorial program dealing with a problem for which someone has gotten a Nobel Prize [20].
The equation reads as follows:
\begin{align*}
&\frac{\partial V}{\partial t} + \frac{\sigma^2S^2}{2} \
\frac{\partial^2 V}{\partial S^2} + \
rS\frac{\partial V}{\partial S} - rV = 0, \
\quad\quad &&\forall S\in \Omega, t \in (0,T)
\\
&V(0,t) = 0, \
&&\forall t \in (0,T)
\\
&V(S,t) \rightarrow S, \
&& \text{as } S \rightarrow \infty, \forall t \in (0,T)
\\
&V(S,T) = \max(S-K,0) \
&&\forall S \in \Omega
\end{align*}
where
\begin{align*}
V(S,t): && \text{Value of call option at time t and asset price S} \\
\sigma: && \text{Volatility of the underlying asset} \\
r: && \text{Risk free interest rate} \\
K : && \text{Strike price for purchasing asset}
\end{align*}
The way we should interpret this equation is that it is a time-dependent partial differential equation of one "space" variable S as the price of the stock, and V(S,t) is the price of the option at time t if the stock price at that time were S.
Particularities of the equation system
There are a number of oddities in this equation that are worth discussing before moving on to its numerical solution. First, the "spatial" domain \Omega\subset\mathbb{R} is unbounded, and thus S can be unbounded in value. This is because there may be a practical upper bound for stock prices, but not a conceptual one. The boundary conditions V(S,t)\rightarrow S as S\rightarrow \infty can then be interpreted as follows: What is the value of an option that allows me to buy a stock at price K if the stock price (today or at time t=T) is S\gg K? One would expect that it is V\approx S-K plus some adjustment for inflation, or, if we really truly consider huge values of S, we can neglect K and arrive at the statement that the boundary values at the infinite boundary should be of the form V\rightarrow S as stated above.
In practice, for us to use a finite element method to solve this, we are going to need to bound \Omega. Since this equation describes prices, and it doesn't make sense to talk about prices being negative, we will set the lower bound of \Omega to be 0. Then, for an upper bound, we will choose a very large number, one that S is not very likely to ever get to. We will call this S_\text{max}. So, \Omega=[0,S_\text{max}].
Second, after truncating the domain, we need to ask what boundary values we should pose at this now finite boundary. To take care of this, we use "put-call" parity [111]. A "pull option" is one in which we are allowed, but not required, to sell a stock at price K to someone at a future time T. This says
\begin{align*}
V(S,t)+Ke^{-r(T-t)}=P(S,t)+S
\end{align*}
where V(S,t) is the value of the call option, and P(S,t) is the value of the put option. Since we expect P(S,t) \rightarrow 0 as S \rightarrow \infty, this says
\begin{align*}
V(S,t) \rightarrow S-Ke^{-r(T-t)},
\end{align*}
and we can use this as a reasonable boundary condition at our finite point S_\text{max}.
The second complication of the Block-Scholes equation is that we are given a final condition, and not an initial condition. This is because we know what the option is worth at time t=T: If the stock price at T is S<K, then we have no incentive to use our option of buying a price K because we can buy that stock for cheaper on the open market. So V(S,T)=0 for S<K. On the other hand, if at time T we have S>K, then we can buy the stock at price K via the option and immediately sell it again on the market for price S, giving me a profit of S-K. In other words, V(S,T)=S-K for S>K. So, we only know values for V at the end time but not the initial time – in fact, finding out what a fair price at the current time (conventionally taken to be t=0) is what solving these equations is all about.
This means that this is not an equation that is posed going forward in time, but in fact going backward in time. Thus it makes sense to solve this problem in reverse by making the change of variables \tau=T-t where now \tau denotes the time before the strike time T.
With all of this, we finally end up with the following problem:
\begin{align*}
&-\frac{\partial V}{\partial \tau} + \frac{\sigma^2S^2}{2} \
\frac{\partial^2 V}{\partial S^2} + rS\frac{\partial V}{\partial S} - rV=0\
, \quad\quad &&\forall S\in [0,S_\text{max}], \tau \in [0,T]
\\
&V(0,\tau) = 0, \
&&\forall \tau \in [0,T]
\\
&V(S_\text{max},\tau)=S_\text{max}-Ke^{-r\tau}, \
&&\forall \tau \in [0,T]
\\
&V(S,0) = \max(S-K,0) \
&&\forall S \in [0,S_\text{max}]
\end{align*}
Conceptually, this is an advection-diffusion-reaction problem for the variable V: There is both a second-order derivative diffusion term, a first-order derivative advection term, and a zeroth-order reaction term. We can expect this problem to be a little bit forgiving in practice because for realistic values of the coefficients, it is diffusive dominated. But, because of the advective terms in the problem, we will have to be careful with mesh refinement and time step choice. There is also the issue that the diffusion term is written in a non-conservative form and so integration by parts is not immediately obvious. This will be discussed in the next section.
Scheme for the numerical solution
We will solve this problem using an IMEX method. In particular, we first discretize in time with the theta method and will later pick different values of theta for the advective and diffusive terms. Let V^n(S) approximate V(S,\tau_n):
\begin{align*}
0=&-\frac{V^n(S)-V^{n-1}(S)}{k_n} \\
&+\frac{\sigma^2S^2}{2}\left[(1-\theta)\frac{d^2V^{n-1}(S)}{dS^2} + \
\theta \frac{d^2V^{n}(S)}{dS^2}\right] \\
&+rS\left[(1-\theta)\frac{dV^{n-1}(S)}{dS} + \
\theta\frac{dV^{n}(S)}{dS}\right] \\
&-r\left[(1-\theta)V^{n-1}(S) + \theta V^n(S)\right]
\end{align*}
Here, k_n=\tau_n-\tau_{n-1} is the time step size. Given this time discretization, we can proceed to discretize space by multiplying with test functions and then integrating by parts. Because there are some interesting details in this due to the advective and non-advective terms in this equation, this process will be explained in detail.
So, we begin by multiplying by test functions, \{\phi_i(S)\}_{i\in\mathbb{N}}:
\begin{align*}
0=&-\int_0^{S_\text{max}}\phi_i(S)\left[V^n(S)-V^{n-1}(S)\right]dS \\
&+k_n\int_0^{S_\text{max}}\phi_i(S)\left[\frac{\sigma^2S^2}{2} \
\left[(1-\theta)\frac{d^2V^{n-1}(S)}{dS^2} + \
\theta \frac{d^2V^{n}(S)}{dS^2}\right]\right]dS \\
&+k_n\int_0^{S_\text{max}}\phi_i(S)\left[rS\left[(1-\theta)
\frac{dV^{n-1}(S)}{dS}\
+ \theta\frac{dV^{n}(S)}{dS}\right]\right]dS \\
&-k_n\int_0^{S_\text{max}}\phi_i(S)\left[r\left[(1-\theta)V^{n-1}(S)\
+ \theta V^n(S)\right]\right]dS
\end{align*}
As usual, (1) becomes -\textbf{M}V^n+\textbf{M}V^{n-1} and (4) becomes k_n\left[-r(1-\theta)\textbf{M}V^{n-1} - \theta r\textbf{M}V^n\right], where \textbf{M}_{i,j}=\left(\phi_i(S),\phi_j(S)\right), and where we have taken the liberty of denoting by V not only the function V(S) but also the vector of nodal values after discretization.
The interesting parts come from (2) and (3).
For (2), we have:
\begin{align*}
&k_n\int_0^{S_\text{max}}\phi_i(S)\left[\frac{\sigma^2S^2}{2} \
\left[(1-\theta)\frac{d^2V^{n-1}(S)}{dS^2} + \
\theta \frac{d^2V^{n}(S)}{dS^2}\right]\right]dS \\
&=k_n(1-\theta)\int_0^{S_\text{max}}\phi_i(S)\frac{\sigma^2S^2}{2} \
\frac{d^2V^{n-1}(S)}{dS^2} \
+k_n\theta\int_0^{S_\text{max}}\phi_i(S)\frac{\sigma^2S^2}{2} \
\frac{d^2V^{n}(S)}{dS^2}
\end{align*}
There are two integrals here, that are more or less the same, with the differences being a slightly different coefficient in front of the integral, and a different time step for V. Therefore, we will outline this integral in the general case, and account for the differences at the end. So, consider the general integral, which we will solve using integration by parts:
\begin{align*}
&\int_{0}^{S_\text{max}} \phi_i(S)\frac{\sigma^2S^2}{2}
\frac{d^2V^n(S)}{dS^2}dS \\
&= \phi_i(S)\frac{1}{2}\sigma^2S^2\frac{dV^n(S)}{dS}\Bigg|_0^{S_{max}} - \
\int_0^{S_\text{max}} \phi_i(S)\sigma^2S\frac{dV^n(S)}{dS}dS - \
\int_0^{S_\text{max}} \frac{d\phi_i(S)}{dS}\frac{1}{2}\sigma^2S^2 \
\frac{dV^n(S)}{dS}dS \\
&= -\int_0^{S_\text{max}} \phi_i(S)\sigma^2S\frac{dV^n(S)}{dS}dS - \
\int_0^{S_\text{max}} \frac{d\phi_i(S)}{dS}\frac{1}{2}\sigma^2S^2 \
\frac{dV^n(S)}{dS}dS \\
&= -\int_0^{S_\text{max}} \phi_i(S)\sigma^2S \sum_j V_j^n
\frac{d\phi_j(S)}{dS}dS \
-\int_0^{S_\text{max}} \frac{d\phi_i(S)}{dS}\frac{1}{2} \
\sigma^2S^2 \sum_k V_k^n \frac{d\phi_k(S)}{dS}dS \\
&= -\sum_j \sigma^2 \int_0^{S_\text{max}} \phi_i(S)S
\frac{d\phi_j(S)}{dS}dS V_j^n\
- \sum_k \frac{1}{2}\sigma^2 \int_0^{S_\text{max}} \frac{d\phi_i(S)}{dS}S^2\
\frac{d\phi_k}{dS}dS V_k^n \\
&= -\sum_j \sigma^2 \left(\phi_i(S)S, \frac{d\phi_j(S)}{dS}\right) V_j^n \
- \sum_k \frac{1}{2}\sigma^2 \left(\frac{d\phi_i(S)}{dS}S^2,\
\frac{d\phi_k(S)}{dS}\right) V_k^n \\
&= -\sigma^2\textbf{B}V^n - \frac{1}{2}\sigma^2\textbf{D}V^n, \quad\quad \
\textbf{B}_{i,j} = \left(\phi_i(S)S, \frac{d\phi_j(S)}{dS}\right),\
\textbf{D}_{i,j} = \left(\frac{d\phi_i(S)}{dS}S^2,\frac{d\phi_j(S)}{dS}\right)
\end{align*}
So, after adding in the constants and exchanging V^n for V^{n-1} where applicable, we arrive at the following for (2):
\begin{align*}
&k_n\int_0^{S_\text{max}}\phi_i(S)\left[\frac{\sigma^2S^2}{2}
\left[(1-\theta)\
\frac{d^2V^{n-1}(S)}{dS^2} + \
\theta \frac{d^2V^{n}(S)}{dS^2}\right]\right]dS \\
&= k_n\left[-(1-\theta)\sigma^2\textbf{B}V^{n-1}\
-(1-\theta)\frac{1}{2}\sigma^2\textbf{D}V^{n-1} \
-\theta\sigma^2\textbf{B}V^{n}
-\theta\frac{1}{2}\sigma^2\textbf{D}V^{n}\right]
\end{align*}
But, because the matrix \textbf{B} involves an advective term, we will choose \theta=0 there – in other words, we use an explicit Euler method to treat advection. Conversely, since the matrix \textbf{D} involves the diffusive term, we will choose \theta=1/2 there – i.e., we treat diffusion using the second order Crank-Nicolson method.
So, we arrive at the following:
\begin{align*}
k_n\left[-\frac{1}{4}\sigma^2\textbf{D}V^{n-1} \
-\frac{1}{4}\sigma^2\textbf{D}V^n \
- \sigma^2\textbf{B}V^{n-1}\right]
\end{align*}
Now, to handle (3). For this, we will again proceed by considering the general case like above.
\begin{align*}
&\int_{0}^{S_\text{max}} \phi_i(S)rS\frac{dV^n}{dS}dS \\
&= \phi_i(S)rSV^n\Bigg|_0^{S_\text{max}} - \int_0^{S_\text{max}}
\left[r\phi_i(S) \
+ r\frac{d\phi_i(S)}{dS}S \right]V^ndS \\
&= -\int_0^{S_\text{max}} r\phi_i(S)V^ndS - \
\int_0^{S_\text{max}} r\frac{d\phi_i(S)}{dS}SV^ndS \\
&= -\int_0^{S_\text{max}} r\phi_i(S) \sum_j V_j^n\phi_j(S)dS \
-\int_0^{S_\text{max}} rS\frac{d\phi_i(S)}{dS} \sum_k V_k\phi_k(S)dS \\
&= -\sum_j r\left(\phi_i(S), \phi_j(S)\right) V_j^n -\
\sum_k r\left(S\frac{d\phi_i(S)}{dS}, \phi_k(S)\right)V_k^n \\
&= -r\textbf{M}V^n -r\textbf{A}V^n, \quad\quad\
\textbf{M}_{i,j} = \left(\phi_i(S), \phi_j(S)\right),\
\textbf{A}_{i,j} = \left(S\frac{d\phi_i(S)}{dS}, \phi_j(S)\right)
\end{align*}
So, again after adding in the constants and exchanging V^n for V^{n-1} where applicable, we arrive at the following for (3):
\begin{align*}
&k_n\int_0^{S_\text{max}}\phi_i(S)\left[rS\left[(1-\theta)
\frac{dV^{n-1}(S)}{dS} +\
\theta\frac{dV^{n}(S)}{dS}\right]\right]dS \\
&= k_n\left[-(1-\theta)r\textbf{M}V^{n-1} -(1-\theta)r\textbf{A}V^{n-1}\
-\theta r\textbf{M}V^n -\theta r\textbf{A}V^n\right]
\end{align*}
Just as before, we will use \theta=0 for the matrix \textbf{A} and \theta=\frac{1}{2} for the matrix \textbf{M}. So, we arrive at the following for (3):
\begin{align*}
k_n\left[-\frac{1}{2}r\textbf{M}V^{n-1} - \frac{1}{2}r\textbf{M}V^n \
-r\textbf{A}V^{n-1}\right]
\end{align*}
Now, putting everything together, we obtain the following discrete form for the Black-Scholes Equation:
\begin{align*}
0&= \\
&-\textbf{M}V^n+\textbf{M}V^{n-1} \\
& +k_n\left[-\frac{1}{4}\sigma^2\textbf{D}V^{n-1} \
-\frac{1}{4}\sigma^2\textbf{D}V^n \
- \sigma^2\textbf{B}V^n \
-\frac{1}{2}r\textbf{M}V^{n-1} - \frac{1}{2}r\textbf{M}V^n \
-r\textbf{A}V^n \
-r\frac{1}{2}\textbf{M}V^{n-1} - \frac{1}{2} r\textbf{M}V^n\right] \\
&= -\textbf{M}V^n + \textbf{M}V^{n-1} +\
k_n\left[- \frac{1}{4}\sigma^2\textbf{D}V^{n-1} -\
\frac{1}{4}\sigma^2\textbf{D}V^n - r\textbf{M}V^{n-1} -\
r\textbf{M}V^n - \sigma^2\textbf{B}V^{n-1} - r\textbf{A}V^{n-1}\right]
\end{align*}
So, altogether we have:
\begin{equation}
0 = \textbf{M}V^n - \textbf{M}V^{n-1} +\
k_n\left[ \frac{1}{4}\sigma^2\textbf{D}V^{n-1} +\
\frac{1}{4}\sigma^2\textbf{D}V^n + r\textbf{M}V^{n-1} + r\textbf{M}V^n +\
\sigma^2\textbf{B}V^{n-1} + r\textbf{A}V^{n-1}\right]\tag{*}
\end{equation}
As usual, we can write this with the unknown quantities on the left and the known ones on the right. This leads to the following linear system that would have to be solved in each time step:
\begin{align*}
\left[\textbf{M}+\frac{1}{4}k_n\sigma^2\textbf{D}+k_nr\textbf{M}\right]V^n\
=\
\left[-\frac{1}{4}k_n\sigma^2\textbf{D}-\
k_nr\textbf{M}+k_n\sigma^2\textbf{B}-\
k_nr\textbf{A}+\textbf{M}\right]V^{n-1}
\end{align*}
Test Case
For this program, we will use the Method of Manufactured Solutions (MMS) to test that it is working correctly. This means that we will choose our solution to be a certain function similar to step-7. For our case, we will use:
\begin{align*}
V(S,\tau) = -\tau^2 - S^2 + 6\tag{**}
\end{align*}
This means that, using our PDE, we arrive at the following problem:
\begin{align*}
&-\frac{\partial V}{\partial \tau} +\
\frac{\sigma^2S^2}{2}\frac{\partial^2 V}{\partial S^2} +\
rS\frac{\partial V}{\partial S} - rV = f(S,\tau) \\
&V(0,\tau) = -\tau^2 + 6 \\
&V(S_\text{max}, \tau) = -S_\text{max}^2 - \tau^2 + 6 \\
&V(S, 0) = -S^2 + 6
\end{align*}
Where, f(S,\tau) = 2\tau - \sigma^2S^2 - 2rS^2 - r(-\tau^2 - S^2 + 6). This set-up now has right hand sides for the equation itself and for the boundary conditions at S=0 that we did not have before, along with "final" conditions (or, with \tau-time "initial conditions") that do not match the real situation. We will implement this in such a way in the code that it is easy to exchange – the introduction of the changes above is just meant to enable the use of a manufactured solution.
If the program is working correctly, then it should produce (**) as the solution. This does mean that we need to modify our variational form somewhat to account for the non-zero right hand side.
First, we define the following:
\begin{align*}
F^n_i = \left(\phi_i(S), f^n(S)\right), && \text{where } f^n(S) =\
f(S,\tau_n)
\end{align*}
So, we arrive at the new equation:
\begin{align*}
\left[\textbf{M}+\frac{1}{4}k_n\sigma^2\textbf{D}+k_nr\textbf{M}\right]V^n\
=\
\left[-\frac{1}{4}k_n\sigma^2\textbf{D}-\
k_nr\textbf{M}+k_n\sigma^2\textbf{B}-\
k_nr\textbf{A}+\textbf{M}\right]V^{n-1} -\
k_n\left[\frac{1}{2}F^{n-1}+\frac{1}{2}F^n\right]
\end{align*}
We then solve this equation as outlined above.
The commented program
Include files
The program starts with the usual include files, all of which you should have seen before by now:
#include <fstream>
#include <iostream>
Then the usual placing of all content of this program into a namespace and the importation of the deal.II namespace into the one we will work in. We also define an identifier to allow for the MMS code to be run when MMS is defined. Otherwise, the program solves the original problem:
namespace BlackScholesSolver
{
#define MMS
Solution Class
This section creates a class for the known solution when testing using the MMS. Here we are using v(\tau,S) = -\tau^2 -S^2 + 6 for the solution. We need to include the solution equation and the gradient for the H1 seminorm calculation.
template <int dim>
{
public:
Solution(const double maturity_time);
const unsigned int component = 0) const override;
const unsigned int component = 0) const override;
private:
const double maturity_time;
};
template <int dim>
Solution<dim>::Solution(const double maturity_time)
: maturity_time(maturity_time)
{
}
template <int dim>
const unsigned int component) const
{
return -Utilities::fixed_power<2, double>(p(component)) -
Utilities::fixed_power<2, double>(this->
get_time()) + 6;
}
template <int dim>
const unsigned int component) const
{
}
virtual Tensor< 1, dim, RangeNumberType > gradient(const Point< dim > &p, const unsigned int component=0) const
virtual RangeNumberType value(const Point< dim > &p, const unsigned int component=0) const
static ::ExceptionBase & ExcNotImplemented()
#define Assert(cond, exc)
Equation Data
In the following classes and functions, we implement the right hand side and boundary values that define this problem and for which we need function objects. The right hand side is chosen as discussed at the end of the introduction.
First, we handle the initial condition.
template <int dim>
class InitialConditions :
public Function<dim>
{
public:
InitialConditions(const double strike_price);
const unsigned int component = 0) const override;
private:
const double strike_price;
};
template <int dim>
InitialConditions<dim>::InitialConditions(const double strike_price)
: strike_price(strike_price)
{}
template <int dim>
double InitialConditions<dim>::value(
const Point<dim> & p,
const unsigned int component) const
{
#ifdef MMS
return -Utilities::fixed_power<2, double>(p(component)) + 6;
#else
return std::max(p(component) - strike_price, 0.);
#endif
}
::VectorizedArray< Number, width > max(const ::VectorizedArray< Number, width > &, const ::VectorizedArray< Number, width > &)
Next, we handle the left boundary condition.
template <int dim>
class LeftBoundaryValues :
public Function<dim>
{
public:
const unsigned int component = 0) const override;
};
template <int dim>
double LeftBoundaryValues<dim>::value(
const Point<dim> &,
const unsigned int ) const
{
#ifdef MMS
return -Utilities::fixed_power<2, double>(this->
get_time()) + 6;
#else
return 0.;
#endif
}
Then, we handle the right boundary condition.
template <int dim>
class RightBoundaryValues :
public Function<dim>
{
public:
RightBoundaryValues(const double strike_price, const double interest_rate);
const unsigned int component = 0) const override;
private:
const double strike_price;
const double interest_rate;
};
template <int dim>
RightBoundaryValues<dim>::RightBoundaryValues(const double strike_price,
const double interest_rate)
: strike_price(strike_price)
, interest_rate(interest_rate)
{}
template <int dim>
double RightBoundaryValues<dim>::value(
const Point<dim> & p,
const unsigned int component) const
{
#ifdef MMS
return -Utilities::fixed_power<2, double>(p(component)) -
Utilities::fixed_power<2, double>(this->
get_time()) + 6;
#else
return (p(component) - strike_price) *
#endif
}
VectorizedArray< Number, width > exp(const ::VectorizedArray< Number, width > &x)
Finally, we handle the right hand side.
template <int dim>
class RightHandSide :
public Function<dim>
{
public:
RightHandSide(const double asset_volatility, const double interest_rate);
const unsigned int component = 0) const override;
private:
const double asset_volatility;
const double interest_rate;
};
template <int dim>
RightHandSide<dim>::RightHandSide(const double asset_volatility,
const double interest_rate)
: asset_volatility(asset_volatility)
, interest_rate(interest_rate)
{}
template <int dim>
double RightHandSide<dim>::value(
const Point<dim> & p,
const unsigned int component) const
{
#ifdef MMS
Utilities::fixed_power<2, double>(asset_volatility * p(component)) -
2 * interest_rate * Utilities::fixed_power<2, double>(p(component)) -
interest_rate *
(-Utilities::fixed_power<2, double>(p(component)) -
Utilities::fixed_power<2, double>(this->
get_time()) + 6);
#else
(void)p;
(void)component;
return 0.0;
#endif
}
The BlackScholes Class
The next piece is the declaration of the main class of this program. This is very similar to the step-26 tutorial, with some modifications. New matrices had to be added to calculate the A and B matrices, as well as the V_{diff} vector mentioned in the introduction. We also define the parameters used in the problem.
maximum_stock_price: The imposed upper bound on the spatial domain. This is the maximum allowed stock price.maturity_time: The upper bound on the time domain. This is when the option expires.
asset_volatility: The volatility of the stock price.
interest_rate: The risk free interest rate.
strike_price: The agreed upon price that the buyer will have the option of purchasing the stocks at the expiration time.
Some slight differences between this program and step-26 are the creation of the a_matrix and the b_matrix, which is described in the introduction. We then also need to store the current time, the size of the time step, and the number of the current time step. Next, we will store the output into a DataOutStack variable because we will be layering the solution at each time on top of one another to create the solution manifold. Then, we have a variable that stores the current cycle and number of cycles that we will run when calculating the solution. The cycle is one full solution calculation given a mesh. We refine the mesh once in between each cycle to exhibit the convergence properties of our program. Finally, we store the convergence data into a convergence table.
As far as member functions are concerned, we have a function that calculates the convergence information for each cycle, called process_solution. This is just like what is done in step-7.
template <int dim>
class BlackScholes
{
public:
BlackScholes();
private:
void setup_system();
void solve_time_step();
void refine_grid();
void process_solution();
void add_results_for_output();
void write_convergence_table();
const double maximum_stock_price;
const double maturity_time;
const double asset_volatility;
const double interest_rate;
const double strike_price;
double time;
double time_step;
const double theta;
const unsigned int n_cycles;
const unsigned int n_time_steps;
std::vector<std::string> solution_names;
};
void mass_matrix(FullMatrix< double > &M, const FEValuesBase< dim > &fe, const double factor=1.)
void run(const Iterator &begin, const typename identity< Iterator >::type &end, Worker worker, Copier copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const unsigned int queue_length, const unsigned int chunk_size)
const ::parallel::distributed::Triangulation< dim, spacedim > * triangulation
The BlackScholes Implementation
Now, we get to the implementation of the main class. We will set the values for the various parameters used in the problem. These were chosen because they are fairly normal values for these parameters. Although the stock price has no upper bound in reality (it is in fact infinite), we impose an upper bound that is twice the strike price. This is a somewhat arbitrary choice to be twice the strike price, but it is large enough to see the interesting parts of the solution.
template <int dim>
BlackScholes<dim>::BlackScholes()
: maximum_stock_price(1.)
, maturity_time(1.)
, asset_volatility(.2)
, interest_rate(0.05)
, strike_price(0.5)
, fe(1)
, time(0.0)
, theta(0.5)
, n_cycles(4)
, n_time_steps(5000)
{
}
BlackScholes::setup_system
The next function sets up the DoFHandler object, computes the constraints, and sets the linear algebra objects to their correct sizes. We also compute the mass matrix here by calling a function from the library. We will compute the other 3 matrices next, because these need to be computed 'by hand'.
Note, that the time step is initialized here because the maturity time was needed to compute the time step.
template <int dim>
void BlackScholes<dim>::setup_system()
{
dof_handler.distribute_dofs(fe);
time_step = maturity_time / n_time_steps;
constraints.clear();
constraints.close();
dsp,
constraints,
true);
sparsity_pattern.copy_from(dsp);
laplace_matrix.reinit(sparsity_pattern);
a_matrix.reinit(sparsity_pattern);
b_matrix.reinit(sparsity_pattern);
system_matrix.reinit(sparsity_pattern);
void make_hanging_node_constraints(const DoFHandler< dim, spacedim > &dof_handler, AffineConstraints< number > &constraints)
void make_sparsity_pattern(const DoFHandler< dim, spacedim > &dof_handler, SparsityPatternType &sparsity_pattern, const AffineConstraints< number > &constraints=AffineConstraints< number >(), const bool keep_constrained_dofs=true, const types::subdomain_id subdomain_id=numbers::invalid_subdomain_id)
void create_mass_matrix(const Mapping< dim, spacedim > &mapping, const DoFHandler< dim, spacedim > &dof, const Quadrature< dim > &q, SparseMatrix< number > &matrix, const Function< spacedim, number > *const a=nullptr, const AffineConstraints< number > &constraints=AffineConstraints< number >())
Below is the code to create the Laplace matrix with non-constant coefficients. This corresponds to the matrix D in the introduction. This non-constant coefficient is represented in the current_coefficient variable.
const unsigned int dofs_per_cell = fe.dofs_per_cell;
quadrature_formula,
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
for (const unsigned int q_index : fe_values.quadrature_point_indices())
{
const double current_coefficient =
fe_values.quadrature_point(q_index).square();
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
(current_coefficient *
fe_values.shape_grad(i, q_index) *
fe_values.shape_grad(j, q_index) *
fe_values.JxW(q_index));
}
}
cell->get_dof_indices(local_dof_indices);
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
laplace_matrix.add(local_dof_indices[i],
local_dof_indices[j],
}
}
@ update_values
Shape function values.
@ update_JxW_values
Transformed quadrature weights.
@ update_gradients
Shape function gradients.
@ update_quadrature_points
Transformed quadrature points.
void cell_matrix(FullMatrix< double > &M, const FEValuesBase< dim > &fe, const FEValuesBase< dim > &fetest, const ArrayView< const std::vector< double > > &velocity, const double factor=1.)
Now we will create the A matrix. Below is the code to create the matrix A as discussed in the introduction. The non constant coefficient is again represented in the current_coefficient variable.
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
for (const unsigned int q_index : fe_values.quadrature_point_indices())
{
fe_values.quadrature_point(q_index);
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
{
(current_coefficient *
fe_values.shape_grad(i, q_index) *
fe_values.shape_value(j, q_index) *
fe_values.JxW(q_index));
}
}
}
cell->get_dof_indices(local_dof_indices);
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
a_matrix.add(local_dof_indices[i],
local_dof_indices[j],
}
}
Finally we will create the matrix B. Below is the code to create the matrix B as discussed in the introduction. The non constant coefficient is again represented in the current_coefficient variable.
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
for (const unsigned int q_index : fe_values.quadrature_point_indices())
{
fe_values.quadrature_point(q_index);
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
(current_coefficient *
fe_values.shape_value(i, q_index) *
fe_values.shape_grad(j, q_index) *
fe_values.JxW(q_index));
}
}
cell->get_dof_indices(local_dof_indices);
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
b_matrix.add(local_dof_indices[i],
local_dof_indices[j],
}
}
solution.reinit(dof_handler.n_dofs());
system_rhs.reinit(dof_handler.n_dofs());
}
BlackScholes::solve_time_step
The next function is the one that solves the actual linear system for a single time step. The only interesting thing here is that the matrices we have built are symmetric positive definite, so we can use the conjugate gradient method.
template <int dim>
void BlackScholes<dim>::solve_time_step()
{
cg.solve(system_matrix, solution, system_rhs, preconditioner);
constraints.distribute(solution);
}
void initialize(const MatrixType &A, const typename BaseClass::AdditionalData ¶meters=typename BaseClass::AdditionalData())
SymmetricTensor< 2, dim, Number > e(const Tensor< 2, dim, Number > &F)
BlackScholes::add_results_for_output
This is simply the function to stitch the solution pieces together. For this, we create a new layer at each time, and then add the solution vector for that timestep. The function then stitches this together with the old solutions using 'build_patches'.
template <int dim>
void BlackScholes<dim>::add_results_for_output()
{
data_out_stack.new_parameter_value(time, time_step);
data_out_stack.attach_dof_handler(dof_handler);
data_out_stack.add_data_vector(solution, solution_names);
data_out_stack.build_patches(2);
data_out_stack.finish_parameter_value();
}
BlackScholes::refine_grid
It is somewhat unnecessary to have a function for the global refinement that we do. The reason for the function is to allow for the possibility of an adaptive refinement later.
template <int dim>
void BlackScholes<dim>::refine_grid()
{
}
BlackScholes::process_solution
This is where we calculate the convergence and error data to evaluate the effectiveness of the program. Here, we calculate the L^2, H^1 and L^{\infty} norms.
template <int dim>
void BlackScholes<dim>::process_solution()
{
Solution<dim> sol(maturity_time);
sol.set_time(time);
solution,
sol,
difference_per_cell,
const double L2_error =
difference_per_cell,
solution,
sol,
difference_per_cell,
const double H1_error =
difference_per_cell,
solution,
sol,
difference_per_cell,
q_iterated,
const double Linfty_error =
difference_per_cell,
const unsigned int n_dofs = dof_handler.n_dofs();
convergence_table.add_value("dofs", n_dofs);
convergence_table.add_value("L2", L2_error);
convergence_table.add_value("H1", H1_error);
convergence_table.add_value("Linfty", Linfty_error);
}
unsigned int n_active_cells(const internal::TriangulationImplementation::NumberCache< 1 > &c)
BlackScholes::write_convergence_table
This next part is building the convergence and error tables. By this, we need to set the settings for how to output the data that was calculated during BlackScholes::process_solution. First, we will create the headings and set up the cells properly. During this, we will also prescribe the precision of our results. Then we will write the calculated errors based on the L^2, H^1, and L^{\infty} norms to the console and to the error LaTeX file.
template <int dim>
void BlackScholes<dim>::write_convergence_table()
{
convergence_table.set_precision("L2", 3);
convergence_table.set_precision("H1", 3);
convergence_table.set_precision("Linfty", 3);
convergence_table.set_scientific("L2", true);
convergence_table.set_scientific("H1", true);
convergence_table.set_scientific("Linfty", true);
convergence_table.set_tex_caption("cells", "\\# cells");
convergence_table.set_tex_caption("dofs", "\\# dofs");
convergence_table.set_tex_caption("L2", "@fL^2@f-error");
convergence_table.set_tex_caption("H1", "@fH^1@f-error");
convergence_table.set_tex_caption("Linfty", "@fL^\\infty@f-error");
convergence_table.set_tex_format("cells", "r");
convergence_table.set_tex_format("dofs", "r");
std::cout << std::endl;
convergence_table.write_text(std::cout);
std::string error_filename = "error";
error_filename += "-global";
error_filename += ".tex";
std::ofstream error_table_file(error_filename);
convergence_table.write_tex(error_table_file);
Next, we will make the convergence table. We will again write this to the console and to the convergence LaTeX file.
convergence_table.add_column_to_supercolumn("cells", "n cells");
std::vector<std::string> new_order;
new_order.emplace_back("n cells");
new_order.emplace_back("H1");
new_order.emplace_back("L2");
convergence_table.set_column_order(new_order);
convergence_table.evaluate_convergence_rates(
convergence_table.evaluate_convergence_rates(
convergence_table.evaluate_convergence_rates(
convergence_table.evaluate_convergence_rates(
std::cout << std::endl;
convergence_table.write_text(std::cout);
std::string conv_filename = "convergence";
conv_filename += "-global";
switch (fe.degree)
{
case 1:
conv_filename += "-q1";
break;
case 2:
conv_filename += "-q2";
break;
default:
}
conv_filename += ".tex";
std::ofstream table_file(conv_filename);
convergence_table.write_tex(table_file);
}
BlackScholes::run
Now we get to the main driver of the program. This is where we do all the work of looping through the time steps and calculating the solution vector each time. Here at the top, we set the initial refinement value and then create a mesh. Then we refine this mesh once. Next, we set up the data_out_stack object to store our solution. Finally, we start a for loop to loop through the cycles. This lets us recalculate a solution for each successive mesh refinement. At the beginning of each iteration, we need to reset the time and time step number. We introduce an if statement to accomplish this because we don't want to do this on the first iteration.
template <int dim>
{
solution_names.emplace_back("u");
data_out_stack.declare_data_vector(solution_names,
for (unsigned int cycle = 0; cycle < n_cycles; cycle++)
{
if (cycle != 0)
{
refine_grid();
time = 0.0;
}
setup_system();
std::cout << std::endl
<< "===========================================" << std::endl
<< "Cycle " << cycle << ':' << std::endl
<< "Number of active cells: "
<< "Number of degrees of freedom: " << dof_handler.n_dofs()
<< std::endl
<< std::endl;
InitialConditions<dim>(strike_price),
solution);
if (cycle == (n_cycles - 1))
{
add_results_for_output();
}
void hyper_cube(Triangulation< dim, spacedim > &tria, const double left=0., const double right=1., const bool colorize=false)
Next, we run the main loop which runs until we exceed the maturity time. We first compute the right hand side of the equation, which is described in the introduction. Recall that it contains the term \left[-\frac{1}{4}k_n\sigma^2\mathbf{D}-k_nr\mathbf{M}+k_n\sigma^2
\mathbf{B}-k_nr\mathbf{A}+\mathbf{M}\right]V^{n-1}. We put these terms into the variable system_rhs, with the help of a temporary vector:
vmult_result.
reinit(dof_handler.n_dofs());
forcing_terms.
reinit(dof_handler.n_dofs());
for (unsigned int timestep_number = 0; timestep_number < n_time_steps;
++timestep_number)
{
time += time_step;
if (timestep_number % 1000 == 0)
std::cout << "Time step " << timestep_number << " at t=" << time
<< std::endl;
laplace_matrix.vmult(vmult_result, solution);
system_rhs.add(
(-1) * (1 - theta) * time_step *
Utilities::fixed_power<2, double>(asset_volatility) * 0.5,
vmult_result);
system_rhs.add((-1) * (1 - theta) * time_step * interest_rate * 2,
vmult_result);
a_matrix.vmult(vmult_result, solution);
system_rhs.add((-1) * time_step * interest_rate, vmult_result);
b_matrix.vmult(vmult_result, solution);
system_rhs.add(
(-1) * Utilities::fixed_power<2, double>(asset_volatility) *
time_step * 1,
vmult_result);
virtual void reinit(const size_type N, const bool omit_zeroing_entries=false)
The second piece is to compute the contributions of the source terms. This corresponds to the term -k_n\left[\frac{1}{2}F^{n-1}
+\frac{1}{2}F^n\right]. The following code calls VectorTools::create_right_hand_side to compute the vectors F, where we set the time of the right hand side (source) function before we evaluate it. The result of this all ends up in the forcing_terms variable:
RightHandSide<dim> rhs_function(asset_volatility, interest_rate);
rhs_function.set_time(time);
rhs_function,
forcing_terms);
forcing_terms *= time_step * theta;
system_rhs -= forcing_terms;
rhs_function.set_time(time - time_step);
rhs_function,
forcing_terms);
forcing_terms *= time_step * (1 - theta);
system_rhs -= forcing_terms;
Next, we add the forcing terms to the ones that come from the time stepping, and also build the matrix \left[\mathbf{M}+
\frac{1}{4}k_n\sigma^2\mathbf{D}+k_nr\mathbf{M}\right] that we have to invert in each time step. The final piece of these operations is to eliminate hanging node constrained degrees of freedom from the linear system:
system_matrix.add(
(theta)*time_step *
Utilities::fixed_power<2, double>(asset_volatility) * 0.5,
laplace_matrix);
system_matrix.add((time_step)*interest_rate * theta * (1 + 1),
constraints.condense(system_matrix, system_rhs);
There is one more operation we need to do before we can solve it: boundary values. To this end, we create a boundary value object, set the proper time to the one of the current time step, and evaluate it as we have done many times before. The result is used to also set the correct boundary values in the linear system:
{
RightBoundaryValues<dim> right_boundary_function(strike_price,
interest_rate);
LeftBoundaryValues<dim> left_boundary_function;
right_boundary_function.set_time(time);
left_boundary_function.set_time(time);
std::map<types::global_dof_index, double> boundary_values;
0,
left_boundary_function,
boundary_values);
1,
right_boundary_function,
boundary_values);
system_matrix,
solution,
system_rhs);
}
With this out of the way, all we have to do is solve the system, generate graphical data on the last cycle, and create the convergence table data.
solve_time_step();
if (cycle == (n_cycles - 1))
{
add_results_for_output();
}
}
#ifdef MMS
process_solution();
#endif
}
const std::string filename = "solution.vtk";
std::ofstream output(filename);
data_out_stack.write_vtk(output);
#ifdef MMS
write_convergence_table();
#endif
}
}
Having made it this far, there is, again, nothing much to discuss for the main function of this program: it looks like all such functions since step-6.
int main()
{
try
{
using namespace BlackScholesSolver;
BlackScholes<1> black_scholes_solver;
black_scholes_solver.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
Results
Below is the output of the program:
===========================================
Number of active cells: 1
Number of degrees of freedom: 2
Time step 0 at t=0.0002
[...]
Cycle 7:
Number of active cells: 128
Number of degrees of freedom: 129
Time step 0 at t=0.0002
Time step 1000 at t=0.2002
Time step 2000 at t=0.4002
Time step 3000 at t=0.6002
Time step 4000 at t=0.8002
1 2 1.667e-01 5.774e-01 2.222e-01
2 3 3.906e-02 2.889e-01 5.380e-02
4 5 9.679e-03 1.444e-01 1.357e-02
8 9 2.405e-03 7.218e-02 3.419e-03
16 17 5.967e-04 3.609e-02 8.597e-04
32 33 1.457e-04 1.804e-02 2.155e-04
64 65 3.307e-05 9.022e-03 5.388e-05
128 129 5.016e-06 4.511e-03 1.342e-05
1 5.774e-01 - - 1.667e-01 - -
2 2.889e-01 2.00 1.00 3.906e-02 4.27 2.09
4 1.444e-01 2.00 1.00 9.679e-03 4.04 2.01
8 7.218e-02 2.00 1.00 2.405e-03 4.02 2.01
16 3.609e-02 2.00 1.00 5.967e-04 4.03 2.01
32 1.804e-02 2.00 1.00 1.457e-04 4.10 2.03
64 9.022e-03 2.00 1.00 3.307e-05 4.41 2.14
128 4.511e-03 2.00 1.00 5.016e-06 6.59 2.72
void L2(Vector< number > &result, const FEValuesBase< dim > &fe, const std::vector< double > &input, const double factor=1.)
What is more interesting is the output of the convergence tables. They are outputted into the console, as well into a LaTeX file. The convergence tables are shown above. Here, you can see that the the solution has a convergence rate of \mathcal{O}(h) with respect to the H^1-norm, and the solution has a convergence rate of \mathcal{O}(h^2) with respect to the L^2-norm.
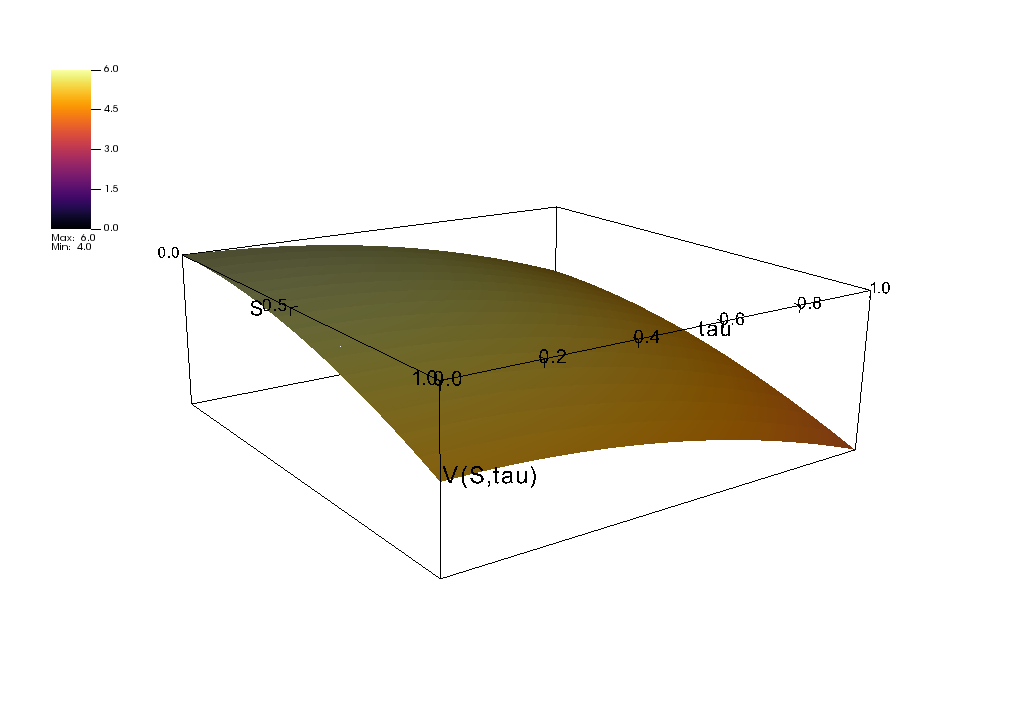
Below is the visualization of the solution.
The plain program
#include <fstream>
#include <iostream>
namespace BlackScholesSolver
{
#define MMS
template <int dim>
{
public:
Solution(const double maturity_time);
const unsigned int component = 0) const override;
const unsigned int component = 0) const override;
private:
const double maturity_time;
};
template <int dim>
Solution<dim>::Solution(const double maturity_time)
: maturity_time(maturity_time)
{
}
template <int dim>
const unsigned int component) const
{
return -Utilities::fixed_power<2, double>(p(component)) -
Utilities::fixed_power<2, double>(this->
get_time()) + 6;
}
template <int dim>
const unsigned int component) const
{
}
template <int dim>
class InitialConditions :
public Function<dim>
{
public:
InitialConditions(const double strike_price);
const unsigned int component = 0) const override;
private:
const double strike_price;
};
template <int dim>
InitialConditions<dim>::InitialConditions(const double strike_price)
: strike_price(strike_price)
{}
template <int dim>
double InitialConditions<dim>::value(
const Point<dim> & p,
const unsigned int component) const
{
#ifdef MMS
return -Utilities::fixed_power<2, double>(p(component)) + 6;
#else
return std::max(p(component) - strike_price, 0.);
#endif
}
template <int dim>
class LeftBoundaryValues :
public Function<dim>
{
public:
const unsigned int component = 0) const override;
};
template <int dim>
double LeftBoundaryValues<dim>::value(
const Point<dim> &,
const unsigned int ) const
{
#ifdef MMS
return -Utilities::fixed_power<2, double>(this->
get_time()) + 6;
#else
return 0.;
#endif
}
template <int dim>
class RightBoundaryValues :
public Function<dim>
{
public:
RightBoundaryValues(const double strike_price, const double interest_rate);
const unsigned int component = 0) const override;
private:
const double strike_price;
const double interest_rate;
};
template <int dim>
RightBoundaryValues<dim>::RightBoundaryValues(const double strike_price,
const double interest_rate)
: strike_price(strike_price)
, interest_rate(interest_rate)
{}
template <int dim>
double RightBoundaryValues<dim>::value(
const Point<dim> & p,
const unsigned int component) const
{
#ifdef MMS
return -Utilities::fixed_power<2, double>(p(component)) -
Utilities::fixed_power<2, double>(this->
get_time()) + 6;
#else
return (p(component) - strike_price) *
#endif
}
template <int dim>
class RightHandSide :
public Function<dim>
{
public:
RightHandSide(const double asset_volatility, const double interest_rate);
const unsigned int component = 0) const override;
private:
const double asset_volatility;
const double interest_rate;
};
template <int dim>
RightHandSide<dim>::RightHandSide(const double asset_volatility,
const double interest_rate)
: asset_volatility(asset_volatility)
, interest_rate(interest_rate)
{}
template <int dim>
double RightHandSide<dim>::value(
const Point<dim> & p,
const unsigned int component) const
{
#ifdef MMS
Utilities::fixed_power<2, double>(asset_volatility * p(component)) -
2 * interest_rate * Utilities::fixed_power<2, double>(p(component)) -
interest_rate *
(-Utilities::fixed_power<2, double>(p(component)) -
Utilities::fixed_power<2, double>(this->
get_time()) + 6);
#else
(void)p;
(void)component;
return 0.0;
#endif
}
template <int dim>
class BlackScholes
{
public:
BlackScholes();
private:
void setup_system();
void solve_time_step();
void refine_grid();
void process_solution();
void add_results_for_output();
void write_convergence_table();
const double maximum_stock_price;
const double maturity_time;
const double asset_volatility;
const double interest_rate;
const double strike_price;
double time;
double time_step;
const double theta;
const unsigned int n_cycles;
const unsigned int n_time_steps;
std::vector<std::string> solution_names;
};
template <int dim>
BlackScholes<dim>::BlackScholes()
: maximum_stock_price(1.)
, maturity_time(1.)
, asset_volatility(.2)
, interest_rate(0.05)
, strike_price(0.5)
, fe(1)
, time(0.0)
, theta(0.5)
, n_cycles(4)
, n_time_steps(5000)
{
}
template <int dim>
void BlackScholes<dim>::setup_system()
{
dof_handler.distribute_dofs(fe);
time_step = maturity_time / n_time_steps;
constraints.clear();
constraints.close();
dsp,
constraints,
true);
sparsity_pattern.copy_from(dsp);
laplace_matrix.reinit(sparsity_pattern);
a_matrix.reinit(sparsity_pattern);
b_matrix.reinit(sparsity_pattern);
system_matrix.reinit(sparsity_pattern);
const unsigned int dofs_per_cell = fe.dofs_per_cell;
quadrature_formula,
std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
for (const unsigned int q_index : fe_values.quadrature_point_indices())
{
const double current_coefficient =
fe_values.quadrature_point(q_index).square();
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
(current_coefficient *
fe_values.shape_grad(i, q_index) *
fe_values.shape_grad(j, q_index) *
fe_values.JxW(q_index));
}
}
cell->get_dof_indices(local_dof_indices);
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
laplace_matrix.add(local_dof_indices[i],
local_dof_indices[j],
}
}
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
for (const unsigned int q_index : fe_values.quadrature_point_indices())
{
fe_values.quadrature_point(q_index);
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
{
(current_coefficient *
fe_values.shape_grad(i, q_index) *
fe_values.shape_value(j, q_index) *
fe_values.JxW(q_index));
}
}
}
cell->get_dof_indices(local_dof_indices);
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
a_matrix.add(local_dof_indices[i],
local_dof_indices[j],
}
}
for (const auto &cell : dof_handler.active_cell_iterators())
{
fe_values.reinit(cell);
for (const unsigned int q_index : fe_values.quadrature_point_indices())
{
fe_values.quadrature_point(q_index);
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
(current_coefficient *
fe_values.shape_value(i, q_index) *
fe_values.shape_grad(j, q_index) *
fe_values.JxW(q_index));
}
}
cell->get_dof_indices(local_dof_indices);
for (const unsigned int i : fe_values.dof_indices())
{
for (const unsigned int j : fe_values.dof_indices())
b_matrix.add(local_dof_indices[i],
local_dof_indices[j],
}
}
solution.reinit(dof_handler.n_dofs());
system_rhs.reinit(dof_handler.n_dofs());
}
template <int dim>
void BlackScholes<dim>::solve_time_step()
{
cg.solve(system_matrix, solution, system_rhs, preconditioner);
constraints.distribute(solution);
}
template <int dim>
void BlackScholes<dim>::add_results_for_output()
{
data_out_stack.new_parameter_value(time, time_step);
data_out_stack.attach_dof_handler(dof_handler);
data_out_stack.add_data_vector(solution, solution_names);
data_out_stack.build_patches(2);
data_out_stack.finish_parameter_value();
}
template <int dim>
void BlackScholes<dim>::refine_grid()
{
}
template <int dim>
void BlackScholes<dim>::process_solution()
{
Solution<dim> sol(maturity_time);
sol.set_time(time);
solution,
sol,
difference_per_cell,
const double L2_error =
difference_per_cell,
solution,
sol,
difference_per_cell,
const double H1_error =
difference_per_cell,
solution,
sol,
difference_per_cell,
q_iterated,
const double Linfty_error =
difference_per_cell,
const unsigned int n_dofs = dof_handler.n_dofs();
convergence_table.add_value("dofs", n_dofs);
convergence_table.add_value("L2", L2_error);
convergence_table.add_value("H1", H1_error);
convergence_table.add_value("Linfty", Linfty_error);
}
template <int dim>
void BlackScholes<dim>::write_convergence_table()
{
convergence_table.set_precision("L2", 3);
convergence_table.set_precision("H1", 3);
convergence_table.set_precision("Linfty", 3);
convergence_table.set_scientific("L2", true);
convergence_table.set_scientific("H1", true);
convergence_table.set_scientific("Linfty", true);
convergence_table.set_tex_caption("cells", "\\# cells");
convergence_table.set_tex_caption("dofs", "\\# dofs");
convergence_table.set_tex_caption("L2", "@f@f$L^2@f@f$-error");
convergence_table.set_tex_caption("H1", "@f@f$H^1@f@f$-error");
convergence_table.set_tex_caption("Linfty", "@f@f$L^\\infty@f@f$-error");
convergence_table.set_tex_format("cells", "r");
convergence_table.set_tex_format("dofs", "r");
std::cout << std::endl;
convergence_table.write_text(std::cout);
std::string error_filename = "error";
error_filename += "-global";
error_filename += ".tex";
std::ofstream error_table_file(error_filename);
convergence_table.write_tex(error_table_file);
convergence_table.add_column_to_supercolumn("cells", "n cells");
std::vector<std::string> new_order;
new_order.emplace_back("n cells");
new_order.emplace_back("H1");
new_order.emplace_back("L2");
convergence_table.set_column_order(new_order);
convergence_table.evaluate_convergence_rates(
convergence_table.evaluate_convergence_rates(
convergence_table.evaluate_convergence_rates(
convergence_table.evaluate_convergence_rates(
std::cout << std::endl;
convergence_table.write_text(std::cout);
std::string conv_filename = "convergence";
conv_filename += "-global";
switch (fe.degree)
{
case 1:
conv_filename += "-q1";
break;
case 2:
conv_filename += "-q2";
break;
default:
}
conv_filename += ".tex";
std::ofstream table_file(conv_filename);
convergence_table.write_tex(table_file);
}
template <int dim>
{
solution_names.emplace_back("u");
data_out_stack.declare_data_vector(solution_names,
for (unsigned int cycle = 0; cycle < n_cycles; cycle++)
{
if (cycle != 0)
{
refine_grid();
time = 0.0;
}
setup_system();
std::cout << std::endl
<< "===========================================" << std::endl
<< "Cycle " << cycle << ':' << std::endl
<< "Number of active cells: "
<< "Number of degrees of freedom: " << dof_handler.n_dofs()
<< std::endl
<< std::endl;
InitialConditions<dim>(strike_price),
solution);
if (cycle == (n_cycles - 1))
{
add_results_for_output();
}
vmult_result.
reinit(dof_handler.n_dofs());
forcing_terms.
reinit(dof_handler.n_dofs());
for (unsigned int timestep_number = 0; timestep_number < n_time_steps;
++timestep_number)
{
time += time_step;
if (timestep_number % 1000 == 0)
std::cout << "Time step " << timestep_number << " at t=" << time
<< std::endl;
laplace_matrix.vmult(vmult_result, solution);
system_rhs.add(
(-1) * (1 - theta) * time_step *
Utilities::fixed_power<2, double>(asset_volatility) * 0.5,
vmult_result);
system_rhs.add((-1) * (1 - theta) * time_step * interest_rate * 2,
vmult_result);
a_matrix.vmult(vmult_result, solution);
system_rhs.add((-1) * time_step * interest_rate, vmult_result);
b_matrix.vmult(vmult_result, solution);
system_rhs.add(
(-1) * Utilities::fixed_power<2, double>(asset_volatility) *
time_step * 1,
vmult_result);
RightHandSide<dim> rhs_function(asset_volatility, interest_rate);
rhs_function.set_time(time);
rhs_function,
forcing_terms);
forcing_terms *= time_step * theta;
system_rhs -= forcing_terms;
rhs_function.set_time(time - time_step);
rhs_function,
forcing_terms);
forcing_terms *= time_step * (1 - theta);
system_rhs -= forcing_terms;
(theta)*time_step *
Utilities::fixed_power<2, double>(asset_volatility) * 0.5,
laplace_matrix);
system_matrix.add((time_step)*interest_rate * theta * (1 + 1),
constraints.condense(system_matrix, system_rhs);
{
RightBoundaryValues<dim> right_boundary_function(strike_price,
interest_rate);
LeftBoundaryValues<dim> left_boundary_function;
right_boundary_function.set_time(time);
left_boundary_function.set_time(time);
std::map<types::global_dof_index, double> boundary_values;
0,
left_boundary_function,
boundary_values);
1,
right_boundary_function,
boundary_values);
system_matrix,
solution,
system_rhs);
}
solve_time_step();
if (cycle == (n_cycles - 1))
{
add_results_for_output();
}
}
#ifdef MMS
process_solution();
#endif
}
const std::string filename = "solution.vtk";
std::ofstream output(filename);
data_out_stack.write_vtk(output);
#ifdef MMS
write_convergence_table();
#endif
}
}
int main()
{
try
{
using namespace BlackScholesSolver;
BlackScholes<1> black_scholes_solver;
black_scholes_solver.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
void add(const std::vector< size_type > &indices, const std::vector< OtherNumber > &values)