Simplex support (experimental)

This module describes the experimental simplex support in deal.II. More...

Classes
class	ScalarLagrangePolynomialPyramid< dim >
class	QGaussSimplex< dim >
class	QWitherdenVincentSimplex< dim >
class	FE_PyramidPoly< dim, spacedim >
class	FE_PyramidP< dim, spacedim >
class	FE_PyramidDGP< dim, spacedim >
class	FE_SimplexPoly< dim, spacedim >
class	FE_SimplexP< dim, spacedim >
class	FE_SimplexDGP< dim, spacedim >
class	FE_WedgePoly< dim, spacedim >
class	FE_WedgeP< dim, spacedim >
class	FE_WedgeDGP< dim, spacedim >
class	MappingFE< dim, spacedim >

Functions
void	GridIn< dim, spacedim >::read_vtk (std::istream &in)
void	GridIn< dim, spacedim >::read_msh (std::istream &in)
void	GridIn< dim, spacedim >::read_msh (const std::string &filename)

Creating meshes from other meshes
template<int dim, int spacedim>
void	GridGenerator::subdivided_hyper_rectangle_with_simplices (Triangulation< dim, spacedim > &tria, const std::vector< unsigned int > &repetitions, const Point< dim > &p1, const Point< dim > &p2, const bool colorize=false)
template<int dim, int spacedim>
void	GridGenerator::subdivided_hyper_cube_with_simplices (Triangulation< dim, spacedim > &tria, const unsigned int repetitions, const double p1=0.0, const double p2=1.0, const bool colorize=false)

Detailed Description

This module describes the experimental simplex support in deal.II.

Simplex and mixed meshes in deal.II are still experimental, i.e., work in progress. Large parts of the library have been ported to be able to operate on such kind of meshes. However, there are still many functions that need to be generalized. You can get a good overview of the ported functionalities by taking a look at the tests in the folder "tests/simplex". In the following, we provide two very basic examples to get started and provide some implementation details.

Example: simplex mesh

The following code shows how to work with simplex meshes:

/* ---------------------------------------------------------------------
 *
 * Copyright (C) 1999 - 2021 by the deal.II authors
 *
 * This file is part of the deal.II library.
 *
 * The deal.II library is free software; you can use it, redistribute
 * it, and/or modify it under the terms of the GNU Lesser General
 * Public License as published by the Free Software Foundation; either
 * version 2.1 of the License, or (at your option) any later version.
 * The full text of the license can be found in the file LICENSE.md at
 * the top level directory of deal.II.
 *
 * ---------------------------------------------------------------------
 *
 * <br>
 *
 * <i>
 * This program was contributed by Peter Munch. This work and the required
 * generalizations of the internal data structures of deal.II form part of the
 * project "Virtual Materials Design" funded by the Helmholtz Association of
 * German Research Centres.
 * </i>
 *
 *
 * <a name="Intro"></a>
 * <h1>Introduction</h1>
 *
 * <h3>Motivation</h3>
 *
 * Many freely available mesh-generation tools produce meshes that consist of
 * simplices (triangles in 2D; tetrahedra in 3D). The reason for this is that
 * generating such kind of meshes for complex geometries is simpler than the
 * generation of hex-only meshes. This tutorial shows how to work on such kind
 * of meshes with the experimental simplex features in deal.II. For this
 * purpose, we solve the Poisson problem from @ref step_3 "step-3" in 2D with a mesh only
 * consisting of triangles.
 *
 *
 * <h3>Working on simplex meshes</h3>
 *
 * To be able to work on simplex meshes, one has to select appropriate finite
 * elements, quadrature rules, and mapping objects. In @ref step_3 "step-3", we used FE_Q,
 * QGauss, and (implicitly by not specifying a mapping) MappingQ1. The
 * equivalent classes for the first two classes in the context of simplices are
 * FE_SimplexP and QGaussSimplex, which we will utilize here. For mapping
 * purposes, we use the class MappingFE, which implements an isoparametric
 * mapping. We initialize it with an FE_SimplexP object so that it can be
 * applied on simplex meshes.
 *
 *
 * <h3>Mesh generation</h3>
 *
 * In contrast to @ref step_3 "step-3", we do not use a function from the GridGenerator
 * namespace, but rather read an externally generated mesh. For this tutorial,
 * we have created the mesh (square with width and height of one) with Gmsh with
 * the following journal file "box_2D_tri.geo":
 *
 * @code
 * Rectangle(1) = {0, 0, 0, 1, 1, 0};
 * Mesh 2;
 * Save "box_2D_tri.msh";
 * @endcode
 *
 * The journal file can be processed by Gmsh generating the actual mesh with the
 * ending ".geo":
 *
 * @code
 * gmsh box_2D_tri.geo
 * @endcode
 *
 * We have included in the tutorial folder both the journal file and the mesh
 * file in the event that one does not have access to Gmsh.
 *
 * The mesh can be simply read by deal.II with methods provided by the GridIn
 * class, as shown below.
 *
 */
 
 
// @sect3{Include files}
 
// Include files, as used in @ref step_3 "step-3":
#include <deal.II/base/function.h>
 
#include <deal.II/dofs/dof_handler.h>
#include <deal.II/dofs/dof_tools.h>
 
#include <deal.II/fe/fe_values.h>
 
#include <deal.II/grid/tria.h>
 
#include <deal.II/lac/dynamic_sparsity_pattern.h>
#include <deal.II/lac/full_matrix.h>
#include <deal.II/lac/precondition.h>
#include <deal.II/lac/solver_cg.h>
#include <deal.II/lac/sparse_matrix.h>
#include <deal.II/lac/vector.h>
 
#include <deal.II/numerics/data_out.h>
#include <deal.II/numerics/matrix_tools.h>
#include <deal.II/numerics/vector_tools.h>
 
#include <fstream>
#include <iostream>
 
// Include files that contain appropriate quadrature rules, finite elements,
// and mapping objects for simplex meshes.
#include <deal.II/base/quadrature_lib.h>
 
#include <deal.II/fe/fe_simplex_p.h>
#include <deal.II/fe/mapping_fe.h>
 
// The following file contains the class GridIn, which allows us to read
// external meshes.
#include <deal.II/grid/grid_in.h>
 
using namespace dealii;
 
// @sect3{The <code>Step3</code> class}
//
// This is the main class of the tutorial. Since it is very similar to the
// version from @ref step_3 "step-3", we will only point out and explain the relevant
// differences that allow to perform simulations on simplex meshes.
 
class Step3
{
public:
  Step3();
 
  void run();
 
private:
  void make_grid();
  void setup_system();
  void assemble_system();
  void solve();
  void output_results() const;
 
  Triangulation<2> triangulation;
 
  // Here, we select a mapping object, a finite element, and a quadrature rule
  // that are compatible with simplex meshes.
  const MappingFE<2>     mapping;
  const FE_SimplexP<2>   fe;
  const QGaussSimplex<2> quadrature_formula;
 
  DoFHandler<2> dof_handler;
 
  SparsityPattern      sparsity_pattern;
  SparseMatrix<double> system_matrix;
 
  Vector<double> solution;
  Vector<double> system_rhs;
};
 
 
// @sect4{Step3::Step3}
//
// In the constructor, we set the polynomial degree of the finite element and
// the number of quadrature points. Furthermore, we initialize the MappingFE
// object with a (linear) FE_SimplexP object so that it can work on simplex
// meshes.
Step3::Step3()
  : mapping(FE_SimplexP<2>(1))
  , fe(2)
  , quadrature_formula(3)
  , dof_handler(triangulation)
{}
 
 
// @sect4{Step3::make_grid}
//
// Read the external mesh file "box_2D_tri.msh" as in @ref step_3 "step-3".
void Step3::make_grid()
{
  GridIn<2>(triangulation).read("box_2D_tri.msh");
 
  std::cout << "Number of active cells: " << triangulation.n_active_cells()
            << std::endl;
}
 
 
// @sect4{Step3::setup_system}
//
// From here on, nothing has changed. Not even, the
// cell integrals have been changed depending on whether one operates on
// hypercube or simplex meshes. This is astonishing and is possible due to the
// design of the following two classes:
//  - DoFHandler: this class stores degrees of freedom in a flexible way and
//    allows simple access to them depending on the element type independent of
//    the cell type.
//  - FEValues: this class hides the details of finite element, quadrature rule,
//    and mapping (even if the implementations are inherently different)
//    behind a unified interface.
void Step3::setup_system()
{
  dof_handler.distribute_dofs(fe);
  std::cout << "Number of degrees of freedom: " << dof_handler.n_dofs()
            << std::endl;
  DynamicSparsityPattern dsp(dof_handler.n_dofs());
  DoFTools::make_sparsity_pattern(dof_handler, dsp);
  sparsity_pattern.copy_from(dsp);
 
  system_matrix.reinit(sparsity_pattern);
 
  solution.reinit(dof_handler.n_dofs());
  system_rhs.reinit(dof_handler.n_dofs());
}
 
 
// @sect4{Step3::assemble_system}
//
// Nothing has changed here.
void Step3::assemble_system()
{
  FEValues<2> fe_values(mapping,
                        fe,
                        quadrature_formula,
                        update_values | update_gradients | update_JxW_values);
 
  const unsigned int dofs_per_cell = fe.n_dofs_per_cell();
  FullMatrix<double> cell_matrix(dofs_per_cell, dofs_per_cell);
  Vector<double>     cell_rhs(dofs_per_cell);
  std::vector<types::global_dof_index> local_dof_indices(dofs_per_cell);
 
  for (const auto &cell : dof_handler.active_cell_iterators())
    {
      fe_values.reinit(cell);
 
      cell_matrix = 0;
      cell_rhs    = 0;
 
      for (const unsigned int q_index : fe_values.quadrature_point_indices())
        {
          for (const unsigned int i : fe_values.dof_indices())
            for (const unsigned int j : fe_values.dof_indices())
              cell_matrix(i, j) +=
                (fe_values.shape_grad(i, q_index) * // grad phi_i(x_q)
                 fe_values.shape_grad(j, q_index) * // grad phi_j(x_q)
                 fe_values.JxW(q_index));           // dx
 
          for (const unsigned int i : fe_values.dof_indices())
            cell_rhs(i) += (fe_values.shape_value(i, q_index) * // phi_i(x_q)
                            1. *                                // f(x_q)
                            fe_values.JxW(q_index));            // dx
        }
      cell->get_dof_indices(local_dof_indices);
 
      for (const unsigned int i : fe_values.dof_indices())
        for (const unsigned int j : fe_values.dof_indices())
          system_matrix.add(local_dof_indices[i],
                            local_dof_indices[j],
                            cell_matrix(i, j));
 
      for (const unsigned int i : fe_values.dof_indices())
        system_rhs(local_dof_indices[i]) += cell_rhs(i);
    }
 
 
  std::map<types::global_dof_index, double> boundary_values;
  VectorTools::interpolate_boundary_values(
    mapping, dof_handler, 0, Functions::ZeroFunction<2>(), boundary_values);
  MatrixTools::apply_boundary_values(boundary_values,
                                     system_matrix,
                                     solution,
                                     system_rhs);
}
 
 
// @sect4{Step3::solve}
//
// Nothing has changed here.
void Step3::solve()
{
  SolverControl            solver_control(1000, 1e-12);
  SolverCG<Vector<double>> solver(solver_control);
  solver.solve(system_matrix, solution, system_rhs, PreconditionIdentity());
}
 
 
// @sect4{Step3::output_results}
//
// Nothing has changed here.
void Step3::output_results() const
{
  DataOut<2> data_out;
 
  DataOutBase::VtkFlags flags;
  flags.write_higher_order_cells = true;
  data_out.set_flags(flags);
 
  data_out.attach_dof_handler(dof_handler);
  data_out.add_data_vector(solution, "solution");
  data_out.build_patches(mapping, 2);
  std::ofstream output("solution.vtk");
  data_out.write_vtk(output);
}
 
 
// @sect4{Step3::run}
//
// Nothing has changed here.
void Step3::run()
{
  make_grid();
  setup_system();
  assemble_system();
  solve();
  output_results();
}
 
 
// @sect3{The <code>main</code> function}
//
// Nothing has changed here.
int main()
{
  deallog.depth_console(2);
 
  Step3 laplace_problem;
  laplace_problem.run();
 
  return 0;
}
 
/*
 * <h1>Results</h1>
 *
 * The following figures show the mesh and the result obtained by executing this
 * program:
 *
 * <table align="center" class="doxtable" style="width:65%">
 *   <tr>
 *     <td>
 *         @image html step_3_simplex_0.png
 *     </td>
 *     <td>
 *         @image html step_3_simplex_1.png
 *     </td>
 *   </tr>
 * </table>
 *
 * Not surprisingly, the result looks as expected.
 *
 *
 * <h3>Possibilities for extensions</h3>
 *
 * In this tutorial, we presented how to use the deal.II simplex infrastructure
 * to solve a simple Poisson problem on a simplex mesh in 2D. In this scope, we
 * could only present a small section of the capabilities. In the following, we
 * point out further capabilities briefly.
 *
 *
 * <h4>3D meshes and codim-1 meshes in 3D</h4>
 *
 * An extension to 3D is quite straightforward. Both FE_SimplexP and
 * QGaussSimplex are implemented in a dimensional-independent way so that simply
 * replacing everywhere dim=2 with dim=3 should work out of the box.
 *
 * Furthermore, embedding of a 2D mesh consisting of triangles in 3D space is
 * possible.
 *
 *
 * <h4>Mixed meshes</h4>
 *
 * In @ref step_3 "step-3", we considered meshes only consisting of quadrilaterals. In this
 * tutorial, we took a look at the case that the mesh only consists of
 * triangles. In the general case (also known as mixed mesh), the mesh consists
 * of both cell types. In 3D, meshes might even consist of more cell types, like
 * wedges/prisms and pyramids. We consider such meshes in the tutorial
 * @ref step_3mixed "step-3mixed".
 *
 *
 * <h4>Alternative finite elements, quadrature rules, and mapping objects</h4>
 *
 * In this tutorial, we used the most basic finite-element, quadrature-rule, and
 * mapping classes. However, more classes are compatible with simplices. The
 * following list gives an overview of these classes:
 * - finite elements: FE_SimplexP, FE_SimplexDGP, FE_SimplexP_Bubbles
 * - quadrature rules: QGaussSimplex, QWitherdenVincentSimplex, QDuffy
 * - mapping objects: MappingFE, MappingFEField
 *
 * It should be also pointed out that FESystems can also handle simplex finite
 * elements which is crucial to solve vector-valued problems, as needed, e.g.,
 * to solve elasticity and fluid problems (see also @ref step_17 "step-17").
 *
 *
 * <h4>Alternative mesh generation approaches</h4>
 *
 * In this tutorial, we have created the mesh externally and read it with the
 * help of GridIn. Since we believe that the main motivation to work on simplex
 * meshes is that one has a complex geometry that can only be meshed with
 * an external tool with simplices, deal.II does not have too many functions in
 * the GridGenerator namespace, targeting simplex meshes. However, we would like
 * to point out the following functions:
 *  - GridGenerator::subdivided_hyper_cube_with_simplices() and
 *    GridGenerator::subdivided_hyper_rectangle_with_simplices(), which fill a
 *    hypercube and a hyperrectangle domain with simplices
 *  - GridGenerator::convert_hypercube_to_simplex_mesh(), which converts meshes
 *    consisting of hypercube cells to simplex meshes by replacing one
 *    quadrilateral with 4 triangles and one hexahedron with 24 tetrahedrons
 *
 *
 * <h4>hp-adaptivity</h4>
 *
 * Here, we considered a mesh without refinements and with all cells assigned
 * the same type of element with the same polynomial degree. However, one is not
 * restricted to this. For further details on hp-methods, see @ref step_27 "step-27".
 *
 *
 * <h4>Parallelization</h4>
 *
 * To parallelize the code, one needs to replace the Triangulation object either
 * with parallel::shared::Triangulation or
 * parallel::fullydistributed::Triangulation and make some minor adjustments, as
 * discussed in @ref step_6 "step-6".
 *
 *
 * <h4>Face integrals and discontinuous Galerkin methods</h4>
 *
 * The classes FEFaceValues and FEInterfaceValues are also compatible with
 * simplex meshes.
 *
 *
 * <h4>Matrix-free operator evaluation</h4>
 *
 * In this tutorial, we showed a matrix-based approach. However, one could also
 * rewrite the code using MatrixFree, FEEvaluation, and FEFaceEvaluation, which
 * are also compatible with simplex meshes.
 *
 */

Example: mixed mesh

The following code shows how to work with mixed meshes:

/* ---------------------------------------------------------------------
 *
 * Copyright (C) 1999 - 2021 by the deal.II authors
 *
 * This file is part of the deal.II library.
 *
 * The deal.II library is free software; you can use it, redistribute
 * it, and/or modify it under the terms of the GNU Lesser General
 * Public License as published by the Free Software Foundation; either
 * version 2.1 of the License, or (at your option) any later version.
 * The full text of the license can be found in the file LICENSE.md at
 * the top level directory of deal.II.
 *
 * ---------------------------------------------------------------------
 *
 * <br>
 *
 * <i>
 * This program was contributed by Peter Munch. This work and the required
 * generalizations of the internal data structures of deal.II form part of the
 * project "Virtual Materials Design" funded by the Helmholtz Association of
 * German Research Centres.
 * </i>
 *
 *
 * <a name="Intro"></a>
 * <h1>Introduction</h1>
 *
 * <h3>Motivation</h3>
 *
 * The motivation for using simplex meshes (as done in @ref step_3simplex "step-3simplex") is
 * straightforward: many freely available mesh-generation tools are very good in
 * creating good-quality meshes in such a format, while they struggle with
 * hex-only meshes. Hex-only meshes, on the other hand, are characterized with
 * better numerical properties (e.g., less degrees of freedom for the same
 * degree of accuracy and possibly better performance since the tensor-product
 * structure can be exploited) and are, as a consequence, the natural choice for
 * rather simple geometries and for meshes described by a coarse mesh with a few
 * cells (like a hyperball) and obtained in their final form through iterative
 * local refinement.
 *
 * Mixed meshes try to combine the best of both worlds by partitioning the
 * geometry in parts that can be easily meshed by hypercube cells
 * (quadrilaterals in 2D, hexahedrons in 3D) and in parts that can not be meshed
 * easily, requiring simplices (triangles in 2D, tetrahedrons in 3D). Since one
 * assumes that the region requiring simplices is rather small compared to the
 * rest of the domain where more efficient and accurate methods can be applied,
 * one can expect that the overall efficiency is hardly impacted by such an
 * approach.
 *
 * One should note that in 3D, one also needs a transition region between
 * hypercube and simplex regions. Here, one can use wedges/prisms and/or
 * pyramids.
 *
 *
 * <h3>Working with mixed meshes</h3>
 *
 * <i>
 * In the following, we concentrate, for the sake of simplicity, on 2D meshes:
 * they can only contain triangles and quadrilaterals. However, as detailed in
 * the outlook, an extension of the presented approach to the 3D case is
 * straightforward.
 * </i>
 *
 * The complexity of working with mixed meshes in 2D results from the fact
 * that it contains of two
 * types of geometrical objects: quadrilaterals and triangles. How to deal with
 * quadrilaterals, we have discussed in @ref step_3 "step-3": we selected an appropriate
 * finite element, quadrature rule and mapping object, e.g., FE_Q, QGauss, and
 * MappingFE (initialized with FE_Q). For simplex meshes, we selected in
 * @ref step_3simplex "step-3simplex" FE_SimplexP, QGaussSimplex, and MappingFE (intialized with
 * FE_SimplexP).
 *
 * For mixed meshes, we need multiple finite elements, quadrature rules, and
 * mapping objects (one set for triangles and one set for quadrilaterals) in the
 * same program. To ease the work with the multitude of objects (in particular
 * in 3D, we need at least four of each), you can collect the objects and group
 * them together in hp::FECollection, hp::QCollection, and
 * hp::MappingCollection.
 *
 * Just like in the context of finite elements, quadrature rules, and mapping
 * objects, we need multiple FEValues objects: the collection of FEValues is
 * called hp::FEValues. It returns the FEValues object needed for the current
 * cell via the method hp::FEValues::get_present_fe_values().
 *
 * For hp::FEValues, to be able to select the right finite element/quadrature
 * rule/ mapping object set, it queries the active_fe_index of the given cell
 * during hp::FEValues::reinit(). The indices have to be set - as shown below -
 * before calling DoFHandler::distribute_dofs() by the user.
 *
 * <i>
 * The namespace name of hp::FECollection, hp::QCollection,
 * hp::MappingCollection, and hp::FEValues indicates that these classes have not
 * been written for mixed meshes in the first place, but for problems where each
 * (hypercube) cell could have a different type of finite element assigned - in
 * the simplest case, all cells have the same element type but different
 * polynomial degrees p (the reason for the letter "p" in "hp"). An extension of
 * this infrastructure to work not only on different element types but also on
 * different geometrical objects was a natural choice. For further details on
 * hp-methods, see @ref step_27 "step-27".
 * </i>
 *
 * <h3>Mesh generation</h3>
 *
 * Just like in @ref step_3simplex "step-3simplex", we read an externally generated mesh. For this
 * tutorial, we have created the mesh (square with width and height of one;
 * quadrilaterals on the left half and triangles on the right half) with Gmsh
 * with the following journal file "box_2D_mixed.geo":
 *
 * @code
 * Rectangle(1) = {0.0, 0, 0, 0.5, 1, 0};
 * Rectangle(2) = {0.5, 0, 0, 0.5, 1, 0};
 * Recombine Surface{1};
 * Physical Surface("All") = {1, 2};
 * Mesh 2;
 * Coherence Mesh;
 * Save "box_2D_mixed.msh";
 * @endcode
 *
 * The journal file can be processed by Gmsh generating the actual mesh with the
 * ending ".msh":
 *
 * @code
 * gmsh box_2D_mixed.geo
 * @endcode
 *
 * We have included in the tutorial folder both the journal file and the mesh
 * file in the event that one does not have access to Gmsh.
 *
 */
 
 
// @sect3{Include files}
 
// Include files, as used in @ref step_3 "step-3":
#include <deal.II/base/function.h>
 
#include <deal.II/dofs/dof_handler.h>
#include <deal.II/dofs/dof_tools.h>
 
#include <deal.II/fe/fe_q.h>
#include <deal.II/fe/fe_values.h>
 
#include <deal.II/grid/tria.h>
 
#include <deal.II/lac/dynamic_sparsity_pattern.h>
#include <deal.II/lac/full_matrix.h>
#include <deal.II/lac/precondition.h>
#include <deal.II/lac/solver_cg.h>
#include <deal.II/lac/sparse_matrix.h>
#include <deal.II/lac/vector.h>
 
#include <deal.II/numerics/data_out.h>
#include <deal.II/numerics/matrix_tools.h>
#include <deal.II/numerics/vector_tools.h>
 
#include <fstream>
#include <iostream>
 
// Include files, as added in @ref step_3simplex "step-3simplex":
#include <deal.II/base/quadrature_lib.h>
 
#include <deal.II/fe/fe_simplex_p.h>
#include <deal.II/fe/mapping_fe.h>
 
#include <deal.II/grid/grid_in.h>
 
// Include files that we need in this tutorial to be able to deal with
// collections of finite elements, quadrature rules, mapping objects, and
// FEValues.
#include <deal.II/hp/fe_collection.h>
#include <deal.II/hp/fe_values.h>
#include <deal.II/hp/mapping_collection.h>
#include <deal.II/hp/q_collection.h>
 
using namespace dealii;
 
// @sect3{The <code>Step3</code> class}
//
// This is the main class of the tutorial. Since it is very similar to the
// version from @ref step_3 "step-3" and @ref step_3simplex "step-3simplex", we will only point out and explain
// the relevant differences that allow to perform simulations on mixed meshes.
 
class Step3
{
public:
  Step3();
 
  void run();
 
private:
  void make_grid();
  void setup_system();
  void assemble_system();
  void solve();
  void output_results() const;
 
  Triangulation<2> triangulation;
 
  // As already explained, we are not working with mapping objects, finite
  // elements, and quadrature rules directly but with collections of them.
  const hp::MappingCollection<2> mapping;
  const hp::FECollection<2>      fe;
  const hp::QCollection<2>       quadrature_formula;
 
  DoFHandler<2> dof_handler;
 
  SparsityPattern      sparsity_pattern;
  SparseMatrix<double> system_matrix;
 
  Vector<double> solution;
  Vector<double> system_rhs;
};
 
 
// @sect4{Step3::Step3}
//
// In the constructor of the Step3 class, we fill the collections. Here, we
// position the objects related to triangles in the first place (index 0) and
// the ones related to quadrilaterals in the second place (index 1).
Step3::Step3()
  : mapping(MappingFE<2>(FE_SimplexP<2>(1)), MappingFE<2>(FE_Q<2>(1)))
  , fe(FE_SimplexP<2>(2), FE_Q<2>(2))
  , quadrature_formula(QGaussSimplex<2>(3), QGauss<2>(3))
  , dof_handler(triangulation)
{}
 
 
// @sect4{Step3::make_grid}
//
// Read the external mesh file "box_2D_mixed.msh" as in @ref step_3simplex "step-3simplex".
void Step3::make_grid()
{
  GridIn<2>(triangulation).read("box_2D_mixed.msh");
 
  std::cout << "Number of active cells: " << triangulation.n_active_cells()
            << std::endl;
}
 
 
// @sect4{Step3::setup_system}
//
// In contrast to @ref step_3 "step-3" and @ref step_3simplex "step-3simplex", we need here a preprocessing step
// that assigns an active_fe_index to each cell consistently according to the
// indices in the collections and the cell type.
void Step3::setup_system()
{
  for (const auto &cell : dof_handler.active_cell_iterators())
    {
      if (cell->reference_cell() == ReferenceCells::Triangle)
        cell->set_active_fe_index(0);
      else if (cell->reference_cell() == ReferenceCells::Quadrilateral)
        cell->set_active_fe_index(1);
      else
        Assert(false, ExcNotImplemented());
    }
 
  dof_handler.distribute_dofs(fe);
  std::cout << "Number of degrees of freedom: " << dof_handler.n_dofs()
            << std::endl;
  DynamicSparsityPattern dsp(dof_handler.n_dofs());
  DoFTools::make_sparsity_pattern(dof_handler, dsp);
  sparsity_pattern.copy_from(dsp);
 
  system_matrix.reinit(sparsity_pattern);
 
  solution.reinit(dof_handler.n_dofs());
  system_rhs.reinit(dof_handler.n_dofs());
}
 
 
// @sect4{Step3::assemble_system}
//
// The following function looks similar to the version in @ref step_3 "step-3" and
// @ref step_3simplex "step-3simplex" with the following two differences:
//  - We do not work with FEValues directly but with the collection class
//    hp::FEValues. It gives us - after it has been initialized with the current
//    cell - a reference to the right FEValues object (constructed
//    with the correct mapping object, finite element, and quadrature rule),
//    which can be used as usual to compute the cell integrals.
//  - The cell-local stiffness matrix and the right-hand-side vector have
//    different sizes depending on the cell type (6 DoFs vs. 9 DoFs) so that
//    they might need to be resized for each cell.
//
// Apart from these two changes, the code has not changed. Not even, the
// cell integrals have been changed depending on whether one operates on
// hypercube, simplex, or mixed meshes.
void Step3::assemble_system()
{
  hp::FEValues<2> hp_fe_values(mapping,
                               fe,
                               quadrature_formula,
                               update_values | update_gradients |
                                 update_JxW_values);
 
  FullMatrix<double>                   cell_matrix;
  Vector<double>                       cell_rhs;
  std::vector<types::global_dof_index> local_dof_indices;
 
  for (const auto &cell : dof_handler.active_cell_iterators())
    {
      hp_fe_values.reinit(cell);
 
      const auto &fe_values = hp_fe_values.get_present_fe_values();
 
      const unsigned int dofs_per_cell = cell->get_fe().n_dofs_per_cell();
      cell_matrix.reinit(dofs_per_cell, dofs_per_cell);
      cell_rhs.reinit(dofs_per_cell);
      local_dof_indices.resize(dofs_per_cell);
 
      cell_matrix = 0;
      cell_rhs    = 0;
 
      for (const unsigned int q_index : fe_values.quadrature_point_indices())
        {
          for (const unsigned int i : fe_values.dof_indices())
            for (const unsigned int j : fe_values.dof_indices())
              cell_matrix(i, j) +=
                (fe_values.shape_grad(i, q_index) * // grad phi_i(x_q)
                 fe_values.shape_grad(j, q_index) * // grad phi_j(x_q)
                 fe_values.JxW(q_index));           // dx
 
          for (const unsigned int i : fe_values.dof_indices())
            cell_rhs(i) += (fe_values.shape_value(i, q_index) * // phi_i(x_q)
                            1. *                                // f(x_q)
                            fe_values.JxW(q_index));            // dx
        }
      cell->get_dof_indices(local_dof_indices);
 
      for (const unsigned int i : fe_values.dof_indices())
        for (const unsigned int j : fe_values.dof_indices())
          system_matrix.add(local_dof_indices[i],
                            local_dof_indices[j],
                            cell_matrix(i, j));
 
      for (const unsigned int i : fe_values.dof_indices())
        system_rhs(local_dof_indices[i]) += cell_rhs(i);
    }
 
 
  std::map<types::global_dof_index, double> boundary_values;
  VectorTools::interpolate_boundary_values(
    mapping, dof_handler, 0, Functions::ZeroFunction<2>(), boundary_values);
  MatrixTools::apply_boundary_values(boundary_values,
                                     system_matrix,
                                     solution,
                                     system_rhs);
}
 
 
// @sect4{Step3::solve}
//
// Nothing has changed here.
void Step3::solve()
{
  SolverControl            solver_control(1000, 1e-12);
  SolverCG<Vector<double>> solver(solver_control);
  solver.solve(system_matrix, solution, system_rhs, PreconditionIdentity());
}
 
 
// @sect4{Step3::output_results}
//
// Nothing has changed here.
void Step3::output_results() const
{
  DataOut<2> data_out;
 
  DataOutBase::VtkFlags flags;
  flags.write_higher_order_cells = true;
  data_out.set_flags(flags);
 
  data_out.attach_dof_handler(dof_handler);
  data_out.add_data_vector(solution, "solution");
  data_out.build_patches(mapping, 2);
  std::ofstream output("solution.vtk");
  data_out.write_vtk(output);
}
 
 
// @sect4{Step3::run}
//
// Nothing has changed here.
void Step3::run()
{
  make_grid();
  setup_system();
  assemble_system();
  solve();
  output_results();
}
 
 
// @sect3{The <code>main</code> function}
//
// Nothing has changed here.
int main()
{
  deallog.depth_console(2);
 
  Step3 laplace_problem;
  laplace_problem.run();
 
  return 0;
}
 

Reference cells

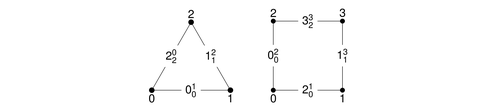
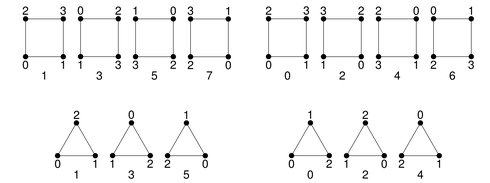
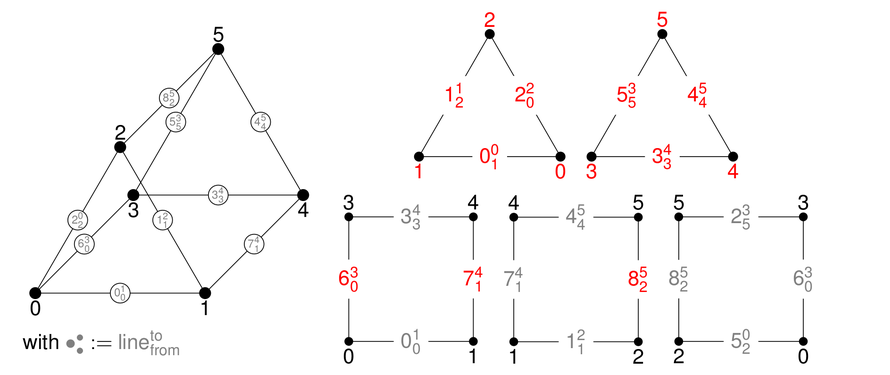
In 2D, we provide triangles and quadrilaterals with the following possible orientations in 3D:

2D: triangle and quadrilateral

Possible orientations of triangles and quadrilaterals in 3D

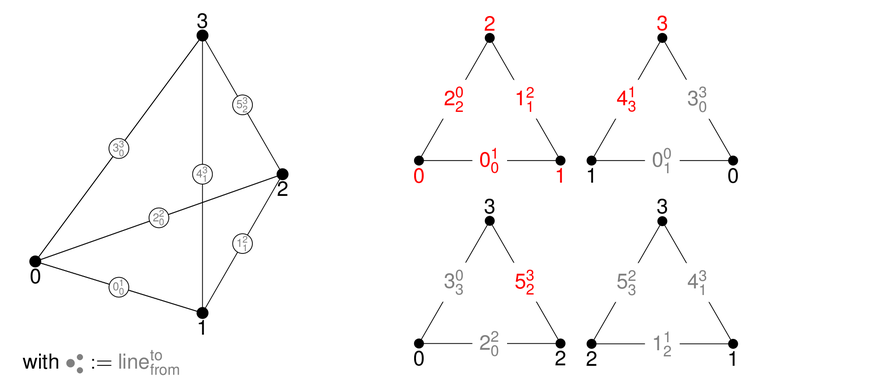
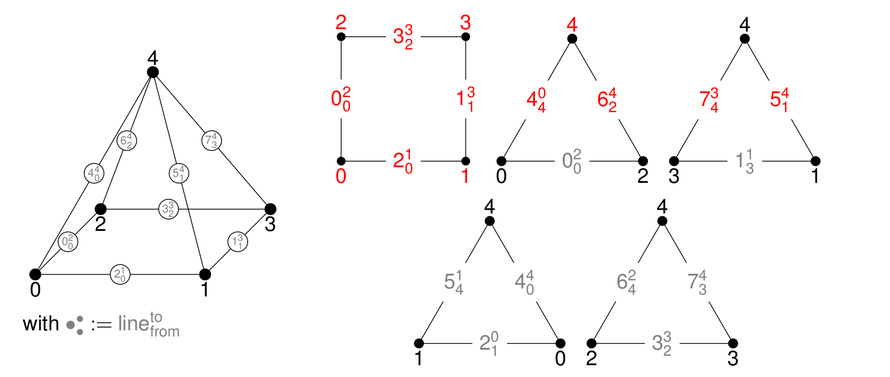
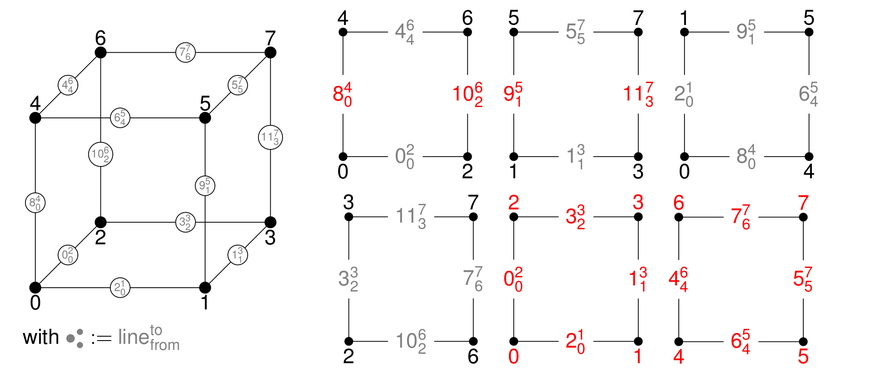
In 3D, tetrahedra, pyramids, wedges, and hexahedra are available:

3D: Tetrahedron

3D: Pyramid

3D: Wedge

3D: Hexahedron

Each surface of a 3D reference cell consists of 2D reference cells. The documentation of the enumeration of the numbering of their vertices and lines are given in the right columns.

Function Documentation

subdivided_hyper_rectangle_with_simplices()

template<int dim, int spacedim>

void GridGenerator::subdivided_hyper_rectangle_with_simplices	(	Triangulation< dim, spacedim > &	tria,
		const std::vector< unsigned int > &	repetitions,
		const Point< dim > &	p1,
		const Point< dim > &	p2,
		const bool	colorize = false
	)

Create a coordinate-parallel brick from the two diagonally opposite corner points p1 and p2. The number of vertices in coordinate direction i is given by repetitions[i]+1.

Note

This function connects internally 4/8 vertices to quadrilateral/hexahedral cells and subdivides these into 2/5 triangular/tetrahedral cells.

Currently, this function only works for dim==spacedim.

subdivided_hyper_cube_with_simplices()

template<int dim, int spacedim>

void GridGenerator::subdivided_hyper_cube_with_simplices	(	Triangulation< dim, spacedim > &	tria,
		const unsigned int	repetitions,
		const double	p1 = 0.0,
		const double	p2 = 1.0,
		const bool	colorize = false
	)

Initialize the given triangulation with a hypercube (square in 2D and cube in 3D) consisting of repetitions cells in each direction. The hypercube volume is the tensor product interval \([left,right]^{\text{dim}}\) in the present number of dimensions, where the limits are given as arguments. They default to zero and unity, then producing the unit hypercube.

Note

This function connects internally 4/8 vertices to quadrilateral/hexahedral cells and subdivides these into 2/5 triangular/tetrahedral cells.

read_vtk()

template<int dim, int spacedim>

void GridIn< dim, spacedim >::read_vtk

(

std::istream &

in

)

Read grid data from a unstructured vtk file. The vtk file may contain the following VTK cell types: VTK_HEXAHEDRON (12), VTK_TETRA (10), VTK_QUAD (9), VTK_TRIANGLE (5), and VTK_LINE (3).

Depending on the template dimension, only some of the above are accepted.

In particular, in three dimensions, this function expects the file to contain

• VTK_HEXAHEDRON/VTK_TETRA cell types
• VTK_QUAD/VTK_TRIANGLE cell types, to specify optional boundary or interior quad faces
• VTK_LINE cell types, to specify optional boundary or interior edges

In two dimensions:

• VTK_QUAD/VTK_TRIANGLE cell types
• VTK_LINE cell types, to specify optional boundary or interior edges

In one dimension

• VTK_LINE cell types

The input file may specify boundary ids, material ids, and manifold ids using the CELL_DATA section of the VTK file format.

This function interprets two types of CELL_DATA contained in the input file: SCALARS MaterialID, used to specify the material_id of the cells, or the boundary_id of the faces and edges, and SCALARS ManifoldID, that can be used to specify the manifold id of any Triangulation object (cell, face, or edge).

The companion GridOut::write_vtk function can be used to write VTK files compatible with this method.

Processing the CELL_TYPES section////////////////////////

Definition at line 128 of file grid_in.cc.

read_msh() [1/2]

template<int dim, int spacedim>

void GridIn< dim, spacedim >::read_msh

(

std::istream &

in

)

Read grid data from an msh file, either version 1 or version 2 of that file format. The Gmsh formats are documented at http://www.gmsh.info/.

Note

The input function of deal.II does not distinguish between newline and other whitespace. Therefore, deal.II will be able to read files in a slightly more general format than Gmsh.

Definition at line 1427 of file grid_in.cc.

read_msh() [2/2]

template<int dim, int spacedim>

void GridIn< dim, spacedim >::read_msh

(

const std::string &

filename

)

Read grid data using Gmsh API. Any file supported by Gmsh can be passed as argument. The format is deduced from the filename extension.

This function interprets non-named physical ids (gmsh format < 4.0) as material or boundary ids (similarly to what happens with the other read_msh() function). If you want to specify non default manifold or boundary ids, you must group all entities that require a non default boundary or manifold id into named physical groups, where the name is interpreted using the function Patterns::Tools::to_value() applied to a std::map<std::string, int>. The keys can be either MaterialID (if the physical group refers to object of dimension dim), BoundaryID (if the group refers to objects of dimension < dim), or ManifoldID.

From the Gmsh documentation, the formats of the physical tags follows the following conventions:

$PhysicalNames // same as MSH version 2
  numPhysicalNames(ASCII int)
  dimension(ASCII int) physicalTag(ASCII int) "name"(127 characters max)
  ...
$EndPhysicalNames

For example, the following snippet of mesh file

MeshFormat
4.1 0 8
$EndMeshFormat
$PhysicalNames
4
1 1 "ManifoldID:0"
1 2 "BoundaryID: -1, ManifoldID: 1"
2 3 "ManifoldID: 1"
2 4 "MaterialID: 2, ManifoldID: 1"
$EndPhysicalNames
$Entities
...

refers to a two dimensional grid where:

• a portion of the boundary of dimension 1 has physical tag 1, and manifold id 0
• some internal faces (lines of dimension 1) have manifold id 1
• some elements have manifold id 1 (and material id equal to the default value, i.e., zero)
• some elements have manifold id 1 and material id equal to 2

If the physical groups are not named, then the behaviour is the same as the other read_msh() function, i.e., the physical tag itself is interpreted as a boundary or material id.

Definition at line 2124 of file grid_in.cc.