#include <deal.II/lac/scalapack.h>

Inheritance diagram for ScaLAPACKMatrix< NumberType >:

Public Types
using	size_type = unsigned int

Public Member Functions
	ScaLAPACKMatrix (const size_type n_rows, const size_type n_columns, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::general)

	ScaLAPACKMatrix (const size_type size, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::symmetric)

	ScaLAPACKMatrix (const std::string &filename, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32)

	~ScaLAPACKMatrix () override=default

void	reinit (const size_type n_rows, const size_type n_columns, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type row_block_size=32, const size_type column_block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::general)

void	reinit (const size_type size, const std::shared_ptr< const Utilities::MPI::ProcessGrid > &process_grid, const size_type block_size=32, const LAPACKSupport::Property property=LAPACKSupport::Property::symmetric)

void	set_property (const LAPACKSupport::Property property)

LAPACKSupport::Property	get_property () const

LAPACKSupport::State	get_state () const

ScaLAPACKMatrix< NumberType > &	operator= (const FullMatrix< NumberType > &)

void	copy_from (const LAPACKFullMatrix< NumberType > &matrix, const unsigned int rank)

void	copy_to (FullMatrix< NumberType > &matrix) const

void	copy_to (LAPACKFullMatrix< NumberType > &matrix, const unsigned int rank) const

void	copy_to (ScaLAPACKMatrix< NumberType > &dest) const

void	copy_to (ScaLAPACKMatrix< NumberType > &B, const std::pair< unsigned int, unsigned int > &offset_A, const std::pair< unsigned int, unsigned int > &offset_B, const std::pair< unsigned int, unsigned int > &submatrix_size) const

void	copy_transposed (const ScaLAPACKMatrix< NumberType > &B)

void	add (const ScaLAPACKMatrix< NumberType > &B, const NumberType a=0., const NumberType b=1., const bool transpose_B=false)

void	add (const NumberType b, const ScaLAPACKMatrix< NumberType > &B)

void	Tadd (const NumberType b, const ScaLAPACKMatrix< NumberType > &B)

void	mult (const NumberType b, const ScaLAPACKMatrix< NumberType > &B, const NumberType c, ScaLAPACKMatrix< NumberType > &C, const bool transpose_A=false, const bool transpose_B=false) const

void	mmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const

void	Tmmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const

void	mTmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const

void	TmTmult (ScaLAPACKMatrix< NumberType > &C, const ScaLAPACKMatrix< NumberType > &B, const bool adding=false) const

void	save (const std::string &filename, const std::pair< unsigned int, unsigned int > &chunk_size=std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int)) const

void	load (const std::string &filename)

void	compute_cholesky_factorization ()

void	compute_lu_factorization ()

void	invert ()

std::vector< NumberType >	eigenpairs_symmetric_by_index (const std::pair< unsigned int, unsigned int > &index_limits, const bool compute_eigenvectors)

std::vector< NumberType >	eigenpairs_symmetric_by_value (const std::pair< NumberType, NumberType > &value_limits, const bool compute_eigenvectors)

std::vector< NumberType >	eigenpairs_symmetric_by_index_MRRR (const std::pair< unsigned int, unsigned int > &index_limits, const bool compute_eigenvectors)

std::vector< NumberType >	eigenpairs_symmetric_by_value_MRRR (const std::pair< NumberType, NumberType > &value_limits, const bool compute_eigenvectors)

std::vector< NumberType >	compute_SVD (ScaLAPACKMatrix< NumberType > U=nullptr, ScaLAPACKMatrix< NumberType > VT=nullptr)

void	least_squares (ScaLAPACKMatrix< NumberType > &B, const bool transpose=false)

unsigned int	pseudoinverse (const NumberType ratio)

NumberType	reciprocal_condition_number (const NumberType a_norm) const

NumberType	l1_norm () const

NumberType	linfty_norm () const

NumberType	frobenius_norm () const

size_type	m () const

size_type	n () const

unsigned int	local_m () const

unsigned int	local_n () const

unsigned int	global_row (const unsigned int loc_row) const

unsigned int	global_column (const unsigned int loc_column) const

NumberType	local_el (const unsigned int loc_row, const unsigned int loc_column) const

NumberType &	local_el (const unsigned int loc_row, const unsigned int loc_column)

template<class InputVector >
void	scale_columns (const InputVector &factors)

template<class InputVector >
void	scale_rows (const InputVector &factors)

Private Member Functions
NumberType	norm_symmetric (const char type) const

NumberType	norm_general (const char type) const

std::vector< NumberType >	eigenpairs_symmetric (const bool compute_eigenvectors, const std::pair< unsigned int, unsigned int > &index_limits=std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int), const std::pair< NumberType, NumberType > &value_limits=std::make_pair(std::numeric_limits< NumberType >::quiet_NaN(), std::numeric_limits< NumberType >::quiet_NaN()))

std::vector< NumberType >	eigenpairs_symmetric_MRRR (const bool compute_eigenvectors, const std::pair< unsigned int, unsigned int > &index_limits=std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int), const std::pair< NumberType, NumberType > &value_limits=std::make_pair(std::numeric_limits< NumberType >::quiet_NaN(), std::numeric_limits< NumberType >::quiet_NaN()))

void	save_serial (const std::string &filename, const std::pair< unsigned int, unsigned int > &chunk_size) const

void	load_serial (const std::string &filename)

void	save_parallel (const std::string &filename, const std::pair< unsigned int, unsigned int > &chunk_size) const

void	load_parallel (const std::string &filename)

Private Attributes
LAPACKSupport::State	state

LAPACKSupport::Property	property

std::shared_ptr< const Utilities::MPI::ProcessGrid >	grid

int	n_rows

int	n_columns

int	row_block_size

int	column_block_size

int	n_local_rows

int	n_local_columns

int	descriptor [9]

std::vector< NumberType >	work

std::vector< int >	iwork

std::vector< int >	ipiv

const char	uplo

const int	first_process_row

const int	first_process_column

const int	submatrix_row

const int	submatrix_column

Threads::Mutex	mutex

Additional Inherited Members
Protected Types inherited from TransposeTable< NumberType >
using	size_type = typename TableBase< 2, NumberType >::size_type

using	value_type = typename AlignedVector< NumberType >::value_type

using	reference = typename AlignedVector< NumberType >::reference

using	const_reference = typename AlignedVector< NumberType >::const_reference

using	const_iterator = MatrixTableIterators::Iterator< TransposeTable< NumberType >, true, MatrixTableIterators::Storage::column_major >

using	iterator = MatrixTableIterators::Iterator< TransposeTable< NumberType >, false, MatrixTableIterators::Storage::column_major >

Protected Types inherited from TableBase< 2, NumberType >
using	value_type = NumberType

using	size_type = typename AlignedVector< NumberType >::size_type

Protected Member Functions inherited from TransposeTable< NumberType >
reference	el (const size_type i, const size_type j)

const_reference	el (const size_type i, const size_type j) const

	TransposeTable ()=default

	TransposeTable (const size_type size1, const size_type size2)

void	reinit (const size_type size1, const size_type size2, const bool omit_default_initialization=false)

const_reference	operator() (const size_type i, const size_type j) const

reference	operator() (const size_type i, const size_type j)

size_type	n_rows () const

size_type	n_cols () const

iterator	begin ()

const_iterator	begin () const

iterator	end ()

const_iterator	end () const

Protected Member Functions inherited from TableBase< 2, NumberType >
size_type	position (const TableIndices< N > &indices) const

AlignedVector< NumberType >::reference	el (const TableIndices< N > &indices)

AlignedVector< NumberType >::const_reference	el (const TableIndices< N > &indices) const

	TableBase ()=default

	TableBase (const TableIndices< N > &sizes)

	TableBase (const TableIndices< N > &sizes, InputIterator entries, const bool C_style_indexing=true)

	TableBase (const TableBase< N, NumberType > &src)

	TableBase (const TableBase< N, T2 > &src)

	TableBase (TableBase< N, NumberType > &&src) noexcept

	~TableBase () override=default

TableBase< N, NumberType > &	operator= (const TableBase< N, NumberType > &src)

TableBase< N, NumberType > &	operator= (const TableBase< N, T2 > &src)

TableBase< N, NumberType > &	operator= (TableBase< N, NumberType > &&src) noexcept

bool	operator== (const TableBase< N, NumberType > &T2) const

void	reset_values ()

void	reinit (const TableIndices< N > &new_size, const bool omit_default_initialization=false)

size_type	size (const unsigned int i) const

const TableIndices< N > &	size () const

size_type	n_elements () const

bool	empty () const

void	fill (InputIterator entries, const bool C_style_indexing=true)

void	fill (const NumberType &value)

AlignedVector< NumberType >::reference	operator() (const TableIndices< N > &indices)

AlignedVector< NumberType >::const_reference	operator() (const TableIndices< N > &indices) const

void	swap (TableBase< N, NumberType > &v)

std::size_t	memory_consumption () const

void	serialize (Archive &ar, const unsigned int version)

Protected Member Functions inherited from Subscriptor
	Subscriptor ()

	Subscriptor (const Subscriptor &)

	Subscriptor (Subscriptor &&) noexcept

virtual	~Subscriptor ()

Subscriptor &	operator= (const Subscriptor &)

Subscriptor &	operator= (Subscriptor &&) noexcept

void	subscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

void	unsubscribe (std::atomic< bool > *const validity, const std::string &identifier="") const

unsigned int	n_subscriptions () const

template<typename StreamType >
void	list_subscribers (StreamType &stream) const

void	list_subscribers () const

template<class Archive >
void	serialize (Archive &ar, const unsigned int version)

Static Protected Member Functions inherited from Subscriptor
static ::ExceptionBase &	ExcInUse (int arg1, std::string arg2, std::string arg3)

static ::ExceptionBase &	ExcNoSubscriber (std::string arg1, std::string arg2)

Protected Attributes inherited from TableBase< 2, NumberType >
AlignedVector< NumberType >	values

TableIndices< N >	table_size

Detailed Description

template<typename NumberType>
class ScaLAPACKMatrix< NumberType >

A wrapper class around ScaLAPACK parallel dense linear algebra.

ScaLAPACK assumes that matrices are distributed according to the block-cyclic decomposition scheme. An \(M\) by \(N\) matrix is first decomposed into \(\lceil M / MB \rceil\) by \(\lceil N / NB \rceil\) blocks which are then uniformly distributed across the 2D process grid with \(p q \le Np\) processes, where \(p,q\) are grid dimensions and \(Np\) is the total number of processes. The parameters MB and NB are referred to as row and column block size and determine the granularity of the block-cyclic distribution.

In the following the block-cyclic distribution of a \(10 \times 9\) matrix onto a \(3\times 3\) Cartesian process grid with block sizes \(\text{MB}=\text{NB}=2\) is displayed.

Block-Cyclic Distribution

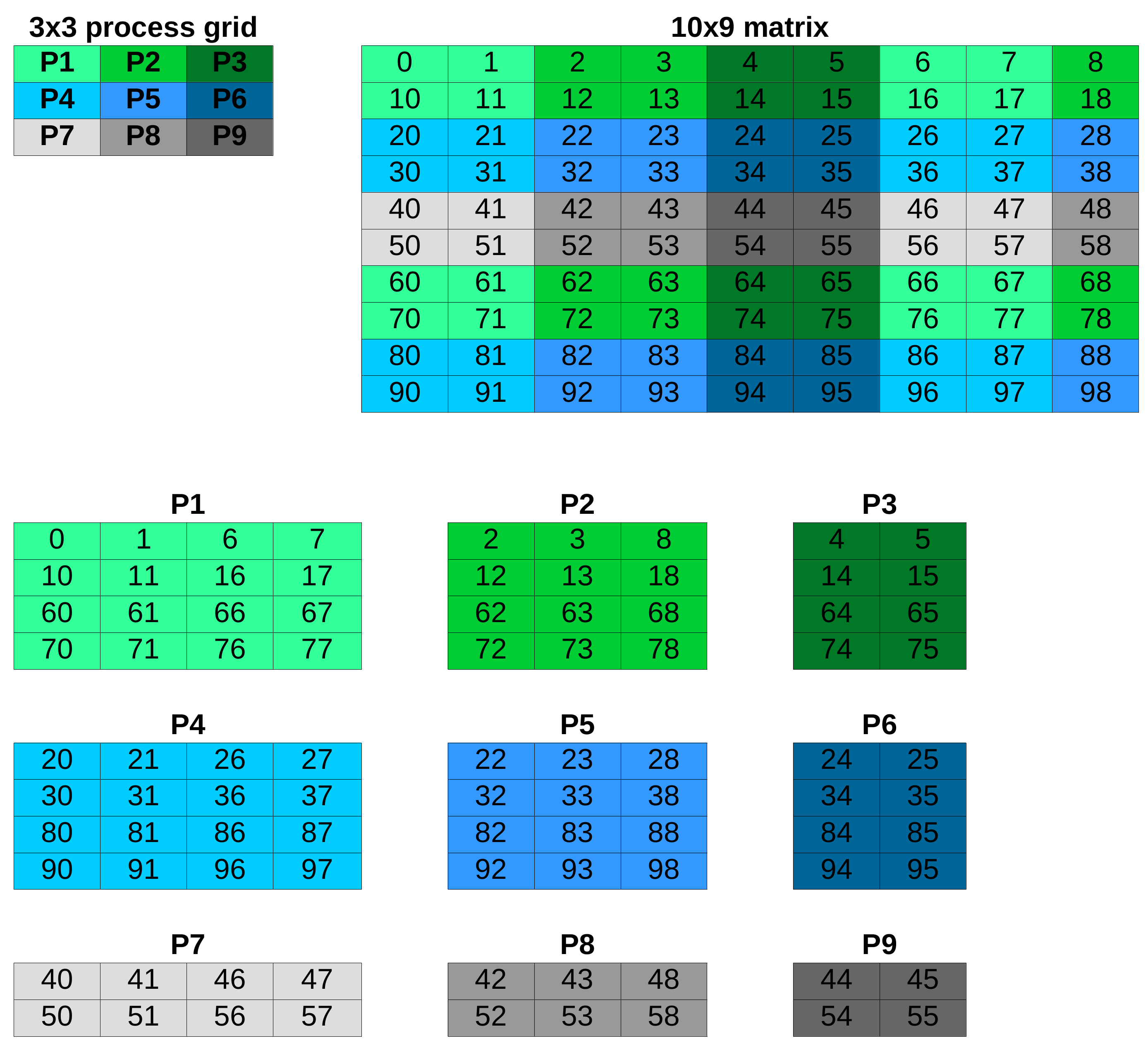
Note that the odd number of columns of the local matrices owned by the processes P2, P5 and P8 accounts for \(N=9\) not being an integral multiple of \(\text{NB}=2\).

The choice of the block sizes is a compromise between a sufficiently large size for efficient local/serial BLAS, but one that is also small enough to achieve good parallel load balance.

Below we show a strong scaling example of ScaLAPACKMatrix::invert() on up to 5 nodes each composed of two Intel Xeon 2660v2 IvyBridge sockets 2.20GHz, 10 cores/socket. Calculations are performed on square processor grids 1x1, 2x2, 3x3, 4x4, 5x5, 6x6, 7x7, 8x8, 9x9, 10x10.

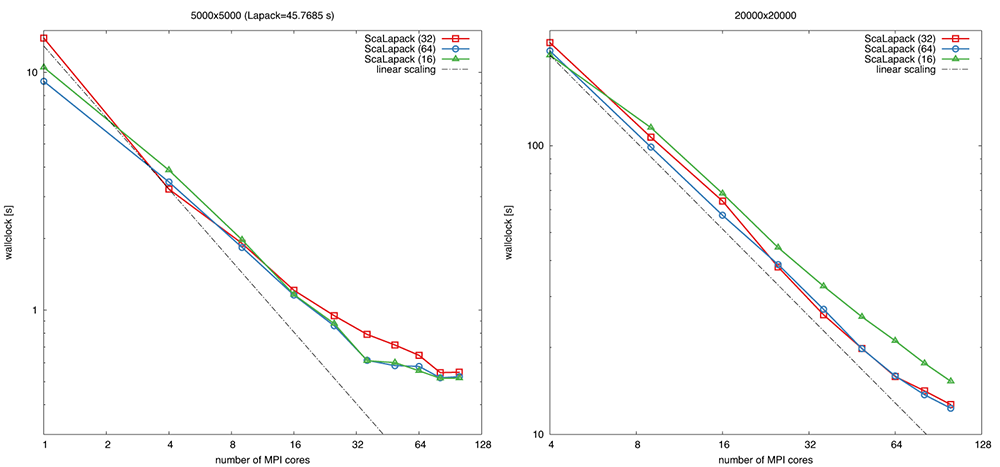
Author: Denis Davydov, Benjamin Brands, 2017

Definition at line 77 of file scalapack.h.

Member Typedef Documentation

◆ size_type

template<typename NumberType >

using ScaLAPACKMatrix< NumberType >::size_type = unsigned int

Declare the type for container size.

Definition at line 83 of file scalapack.h.

Constructor & Destructor Documentation

◆ ScaLAPACKMatrix() [1/3]

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix	(	const size_type	n_rows,
		const size_type	n_columns,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	row_block_size = `32`,
		const size_type	column_block_size = `32`,
		const LAPACKSupport::Property	property = `LAPACKSupport::Property::general`
	)

Constructor for a rectangular matrix with n_rows and n_cols and distributed using the grid process_grid.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 79 of file scalapack.cc.

◆ ScaLAPACKMatrix() [2/3]

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix	(	const size_type	size,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	block_size = `32`,
		const LAPACKSupport::Property	property = `LAPACKSupport::Property::symmetric`
	)

Constructor for a square matrix of size size, and distributed using the process grid in process_grid.

The parameter block_size is used for the block-cyclic distribution of the matrix. An identical block size is used for the rows and columns of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 104 of file scalapack.cc.

◆ ScaLAPACKMatrix() [3/3]

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::ScaLAPACKMatrix	(	const std::string &	filename,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	row_block_size = `32`,
		const size_type	column_block_size = `32`
	)

Constructor for a general rectangular matrix that is read from the file filename and distributed using the grid process_grid.

Loads the matrix from file filename using HDF5. In case that deal.II was built without HDF5 a call to this function will cause an exception to be thrown.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 120 of file scalapack.cc.

◆ ~ScaLAPACKMatrix()

template<typename NumberType >

ScaLAPACKMatrix< NumberType >::~ScaLAPACKMatrix ( )

overridedefault

Destructor

Member Function Documentation

◆ reinit() [1/2]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::reinit	(	const size_type	n_rows,
		const size_type	n_columns,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	row_block_size = `32`,
		const size_type	column_block_size = `32`,
		const LAPACKSupport::Property	property = `LAPACKSupport::Property::general`
	)

Initialize the rectangular matrix with n_rows and n_cols and distributed using the grid process_grid.

The parameters row_block_size and column_block_size are the block sizes used for the block-cyclic distribution of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 215 of file scalapack.cc.

◆ reinit() [2/2]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::reinit	(	const size_type	size,
		const std::shared_ptr< const Utilities::MPI::ProcessGrid > &	process_grid,
		const size_type	block_size = `32`,
		const LAPACKSupport::Property	property = `LAPACKSupport::Property::symmetric`
	)

Initialize the square matrix of size size and distributed using the grid process_grid.

The parameter block_size is used for the block-cyclic distribution of the matrix. An identical block size is used for the rows and columns of the matrix. In general, it is recommended to use powers of \(2\), e.g. \(16,32,64, \dots\).

Definition at line 289 of file scalapack.cc.

◆ set_property()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::set_property ( const LAPACKSupport::Property property )

Assign property to this matrix.

Definition at line 302 of file scalapack.cc.

◆ get_property()

template<typename NumberType >

LAPACKSupport::Property ScaLAPACKMatrix< NumberType >::get_property

Return current property of this matrix

Definition at line 312 of file scalapack.cc.

◆ get_state()

template<typename NumberType >

LAPACKSupport::State ScaLAPACKMatrix< NumberType >::get_state

Return current state of this matrix

Definition at line 321 of file scalapack.cc.

◆ operator=()

template<typename NumberType >

ScaLAPACKMatrix< NumberType > & ScaLAPACKMatrix< NumberType >::operator= ( const FullMatrix< NumberType > & matrix )

Assignment operator from a regular FullMatrix.

Note: This function should only be used for relatively small matrix dimensions. It is primarily intended for debugging purposes.

Definition at line 330 of file scalapack.cc.

◆ copy_from()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_from	(	const LAPACKFullMatrix< NumberType > &	matrix,
		const unsigned int	rank
	)

Copies the content of the locally owned matrix to the distributed matrix. The distributed matrix and matrix on process rank must have matching dimensions.

For all processes except the process with rank rank the serial matrix is not referenced. The user has to ensure that all processes call this with identical rank. The rank refers to a process of the MPI communicator used to create the process grid of the distributed matrix.

Definition at line 361 of file scalapack.cc.

◆ copy_to() [1/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to ( FullMatrix< NumberType > & matrix ) const

Copy the contents of the distributed matrix into matrix.

Note: This function should only be used for relatively small matrix dimensions. It is primarily intended for debugging purposes.

Definition at line 663 of file scalapack.cc.

◆ copy_to() [2/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to	(	LAPACKFullMatrix< NumberType > &	matrix,
		const unsigned int	rank
	)		const

Copies the content of the distributed matrix into the locally replicated matrix on the process with rank rank. For all processes except rank matrix is not referenced. The distributed matrix and matrix on the process rank must have matching dimensions.

The user has to ensure that all processes call this with identical rank. The rank refers to a process of the MPI communicator used to create the process grid of the distributed matrix.

Definition at line 530 of file scalapack.cc.

◆ copy_to() [3/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to ( ScaLAPACKMatrix< NumberType > & dest ) const

Copy the contents of the distributed matrix into a differently distributed matrix dest. The function also works for matrices with different process grids or block-cyclic distributions.

Definition at line 849 of file scalapack.cc.

◆ copy_to() [4/4]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_to	(	ScaLAPACKMatrix< NumberType > &	B,
		const std::pair< unsigned int, unsigned int > &	offset_A,
		const std::pair< unsigned int, unsigned int > &	offset_B,
		const std::pair< unsigned int, unsigned int > &	submatrix_size
	)		const

Copy a submatrix (subset) of the distributed matrix A to a submatrix of the distributed matrix B.

The global row and column index of the first element of the submatrix A is provided by offset_A with row index=offset_A.first and column index=offset_A.second.
The global row and column index of the first element of the submatrix B is provided by offset_B with row index=offset_B.first and column index=offset_B.second.
The dimension of the submatrix to be copied is given by submatrix_size with number of rows=submatrix_size.first and number of columns=submatrix_size.second.

If it is necessary to copy complete matrices with an identical block-cyclic distribution, use ScaLAPACKMatrix<NumberType>::copy_to(ScaLAPACKMatrix<NumberType> &dest) with only one argument to avoid communication.

The underlying process grids of the matrices A and B must have been built with the same MPI communicator.

Definition at line 720 of file scalapack.cc.

◆ copy_transposed()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::copy_transposed ( const ScaLAPACKMatrix< NumberType > & B )

Transposing assignment: \(\mathbf{A} = \mathbf{B}^T\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

The following alignment conditions have to be fulfilled: \(MB_A=NB_B\) and \(NB_A=MB_B\).

Definition at line 980 of file scalapack.cc.

◆ add() [1/2]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::add	(	const ScaLAPACKMatrix< NumberType > &	B,
		const NumberType	a = `0.`,
		const NumberType	b = `1.`,
		const bool	transpose_B = `false`
	)

The operations based on the input parameter transpose_B and the alignment conditions are summarized in the following table:

transpose_B	Block Sizes	Operation
false	\(MB_A=MB_B\) \(NB_A=NB_B\)	\(\mathbf{A} = a \mathbf{A} + b \mathbf{B}\)
true	\(MB_A=NB_B\) \(NB_A=MB_B\)	\(\mathbf{A} = a \mathbf{A} + b \mathbf{B}^T\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

Definition at line 990 of file scalapack.cc.

◆ add() [2/2]

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::add	(	const NumberType	b,
		const ScaLAPACKMatrix< NumberType > &	B
	)

Matrix-addition: \(\mathbf{A} = \mathbf{A} + b\, \mathbf{B}\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

The following alignment conditions have to be fulfilled: \(MB_A=MB_B\) and \(NB_A=NB_B\).

Definition at line 1046 of file scalapack.cc.

◆ Tadd()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::Tadd	(	const NumberType	b,
		const ScaLAPACKMatrix< NumberType > &	B
	)

Matrix-addition: \(\mathbf{A} = \mathbf{A} + b\, \mathbf{B}^T\)

The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have the same process grid.

The following alignment conditions have to be fulfilled: \(MB_A=NB_B\) and \(NB_A=MB_B\).

Definition at line 1056 of file scalapack.cc.

◆ mult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::mult	(	const NumberType	b,
		const ScaLAPACKMatrix< NumberType > &	B,
		const NumberType	c,
		ScaLAPACKMatrix< NumberType > &	C,
		const bool	transpose_A = `false`,
		const bool	transpose_B = `false`
	)		const

Matrix-matrix-multiplication:

The operations based on the input parameters and the alignment conditions are summarized in the following table:

transpose_A	transpose_B	Block Sizes	Operation
false	false	\(MB_A=MB_C\) \(NB_A=MB_B\) \(NB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A} \cdot \mathbf{B} + c \mathbf{C}\)
false	true	\(MB_A=MB_C\) \(NB_A=NB_B\) \(MB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A} \cdot \mathbf{B}^T + c \mathbf{C}\)
true	false	\(MB_A=MB_B\) \(NB_A=MB_C\) \(NB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A}^T \cdot \mathbf{B} + c \mathbf{C}\)
true	true	\(MB_A=NB_B\) \(NB_A=MB_C\) \(MB_B=NB_C\)	\(\mathbf{C} = b \mathbf{A}^T \cdot \mathbf{B}^T + c \mathbf{C}\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The matrices \(\mathbf{A}\), \(\mathbf{B}\) and \(\mathbf{C}\) must have the same process grid.

Definition at line 1066 of file scalapack.cc.

◆ mmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::mmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = `false`
	)		const

Matrix-matrix-multiplication.

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A} \cdot \mathbf{B}\)

else \(\mathbf{C} = \mathbf{A} \cdot \mathbf{B}\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=MB_C\), \(NB_A=MB_B\) and \(NB_B=NB_C\).

Definition at line 1183 of file scalapack.cc.

◆ Tmmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::Tmmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = `false`
	)		const

Matrix-matrix-multiplication using transpose of \(\mathbf{A}\).

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A}^T \cdot \mathbf{B}\)

else \(\mathbf{C} = \mathbf{A}^T \cdot \mathbf{B}\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=MB_B\), \(NB_A=MB_C\) and \(NB_B=NB_C\).

Definition at line 1197 of file scalapack.cc.

◆ mTmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::mTmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = `false`
	)		const

Matrix-matrix-multiplication using the transpose of \(\mathbf{B}\).

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A} \cdot \mathbf{B}^T\)

else \(\mathbf{C} = \mathbf{A} \cdot \mathbf{B}^T\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=MB_C\), \(NB_A=NB_B\) and \(MB_B=NB_C\).

Definition at line 1211 of file scalapack.cc.

◆ TmTmult()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::TmTmult	(	ScaLAPACKMatrix< NumberType > &	C,
		const ScaLAPACKMatrix< NumberType > &	B,
		const bool	adding = `false`
	)		const

Matrix-matrix-multiplication using transpose of \(\mathbf{A}\) and \(\mathbf{B}\).

The optional parameter adding determines whether the result is stored in \(\mathbf{C}\) or added to \(\mathbf{C}\).

if (adding) \(\mathbf{C} = \mathbf{C} + \mathbf{A}^T \cdot \mathbf{B}^T\)

else \(\mathbf{C} = \mathbf{A}^T \cdot \mathbf{B}^T\)

It is assumed that \(\mathbf{A}\) and \(\mathbf{B}\) have compatible sizes and that \(\mathbf{C}\) already has the right size.

The following alignment conditions have to be fulfilled: \(MB_A=NB_B\), \(NB_A=MB_C\) and \(MB_B=NB_C\).

Definition at line 1225 of file scalapack.cc.

◆ save()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::save	(	const std::string &	filename,
		const std::pair< unsigned int, unsigned int > &	chunk_size = `std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int)`
	)		const

Stores the distributed matrix in filename using HDF5.

In case that deal.II was built without HDF5 a call to this function will cause an exception to be thrown.

If HDF5 was built with MPI, parallel I/O is used to save the matrix. Otherwise, just one process will do the output. This means that internally the distributed matrix is copied to one process, which does the output. Therefore, the matrix has to fit into the memory of one process.

To tweak the I/O performance, especially for parallel I/O, the user may define the optional parameter chunk_size. All MPI processes need to call the function with the same value. The matrix is written in chunks to the file, therefore the properties of the system define the optimal chunk size. Internally, HDF5 splits the matrix into chunk_size.first x chunk_size.second sized blocks, with chunk_size.first being the number of rows of a chunk and chunk_size.second the number of columns.

Definition at line 2607 of file scalapack.cc.

◆ load()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::load ( const std::string & filename )

Loads the distributed matrix from file filename using HDF5. In case that deal.II was built without HDF5 a call to this function will cause an exception to be thrown.

The matrix must have the same dimensions as the matrix stored in the file.

If HDF5 was build with MPI, parallel I/O is used to load the matrix. Otherwise, just one process will load the matrix from storage and distribute the content to the other processes subsequently.

Definition at line 3042 of file scalapack.cc.

◆ compute_cholesky_factorization()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::compute_cholesky_factorization

Compute the Cholesky factorization of the matrix using ScaLAPACK function pXpotrf. The result of the factorization is stored in this object.

Definition at line 1239 of file scalapack.cc.

◆ compute_lu_factorization()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::compute_lu_factorization

Compute the LU factorization of the matrix using ScaLAPACK function pXgetrf and partial pivoting with row interchanges. The result of the factorization is stored in this object.

Definition at line 1272 of file scalapack.cc.

◆ invert()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::invert

Invert the matrix by first computing a Cholesky for symmetric matrices or a LU factorization for general matrices and then building the actual inverse using pXpotri or pXgetri. If the matrix is triangular, the LU factorization step is skipped, and pXtrtri is used directly.

If a Cholesky or LU factorization has been applied previously, pXpotri or pXgetri are called directly.

The inverse is stored in this object.

Definition at line 1313 of file scalapack.cc.

◆ eigenpairs_symmetric_by_index()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_index	(	const std::pair< unsigned int, unsigned int > &	index_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\).

The eigenvalues/eigenvectors are selected by prescribing a range of indices index_limits.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

If all eigenvalues/eigenvectors have to be computed, pass the closed interval \( \left[ 0, M-1 \right] \) in index_limits.

Pass the closed interval \( \left[ M-r, M-1 \right] \) if the \(r\) largest eigenvalues/eigenvectors are desired.

Definition at line 1429 of file scalapack.cc.

◆ eigenpairs_symmetric_by_value()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_value	(	const std::pair< NumberType, NumberType > &	value_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors. The eigenvalues/eigenvectors are selected by prescribing a range of values value_limits for the eigenvalues.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

Definition at line 1452 of file scalapack.cc.

◆ eigenpairs_symmetric_by_index_MRRR()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_index_MRRR	(	const std::pair< unsigned int, unsigned int > &	index_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\) using the MRRR algorithm.

The eigenvalues/eigenvectors are selected by prescribing a range of indices index_limits.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

If all eigenvalues/eigenvectors have to be computed, pass the closed interval \( \left[ 0, M-1 \right] \) in index_limits.

Pass the closed interval \( \left[ M-r, M-1 \right] \) if the \(r\) largest eigenvalues/eigenvectors are desired.

Definition at line 1762 of file scalapack.cc.

◆ eigenpairs_symmetric_by_value_MRRR()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_by_value_MRRR	(	const std::pair< NumberType, NumberType > &	value_limits,
		const bool	compute_eigenvectors
	)

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\) using the MRRR algorithm. The eigenvalues/eigenvectors are selected by prescribing a range of values value_limits for the eigenvalues.

If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

Definition at line 1785 of file scalapack.cc.

◆ compute_SVD()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::compute_SVD	(	ScaLAPACKMatrix< NumberType > *	U = `nullptr`,
		ScaLAPACKMatrix< NumberType > *	VT = `nullptr`
	)

Computing the singular value decomposition (SVD) of a matrix \(\mathbf{A} \in \mathbb{R}^{M \times N}\), optionally computing the left and/or right singular vectors. The SVD is written as \(\mathbf{A} = \mathbf{U} \cdot \mathbf{\Sigma} \cdot \mathbf{V}^T\) with \(\mathbf{\Sigma} \in \mathbb{R}^{M \times N}\) as a diagonal matrix, \(\mathbf{U} \in \mathbb{R}^{M \times M}\) and \(\mathbf{V} \in \mathbb{R}^{M \times M}\) as orthogonal matrices. The diagonal elements of \(\mathbf{\Sigma}\) are the singular values of \(A\) and the columns of \(\mathbf{U}\) and \(\mathbf{V}\) are the corresponding left and right singular vectors, respectively. The singular values are returned in decreasing order and only the first \(\min(M,N)\) columns of \(\mathbf{U}\) and rows of \(\mathbf{V}^T\) are computed.

Upon return the content of the matrix is unusable. The matrix \(\mathbf{A}\) must have identical block cyclic distribution for the rows and column.

If left singular vectors are required matrices \(\mathbf{A}\) and \(\mathbf{U}\) have to be constructed with the same process grid and block cyclic distribution. If right singular vectors are required matrices \(\mathbf{A}\) and \(\mathbf{V}^T\) have to be constructed with the same process grid and block cyclic distribution.

To avoid computing the left and/or right singular vectors the function accepts nullptr for U and/or VT.

Definition at line 2013 of file scalapack.cc.

◆ least_squares()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::least_squares	(	ScaLAPACKMatrix< NumberType > &	B,
		const bool	transpose = `false`
	)

Solving overdetermined or underdetermined real linear systems involving matrix \(\mathbf{A} \in \mathbb{R}^{M \times N}\), or its transpose \(\mathbf{A}^T\), using a QR or LQ factorization of \(\mathbf{A}\) for \(N_{\rm RHS}\) RHS vectors in the columns of matrix \(\mathbf{B}\)

It is assumed that \(\mathbf{A}\) has full rank: \(\rm{rank}(\mathbf{A}) = \min(M,N)\).

The following options are supported:

If(!transpose) and \(M \geq N\): least squares solution of overdetermined system \(\min \Vert \mathbf{B} - \mathbf{A}\cdot \mathbf{X}\Vert\).
Upon exit the rows \(0\) to \(N-1\) of \(\mathbf{B}\) contain the least square solution vectors. The residual sum of squares for each column is given by the sum of squares of elements \(N\) to \(M-1\) in that column.
If(!transpose) and \(M < N\): find minimum norm solutions of underdetermined systems \(\mathbf{A} \cdot \mathbf{X} = \mathbf{B}\).
Upon exit the columns of \(\mathbf{B}\) contain the minimum norm solution vectors.
If(transpose) and \(M \geq N\): find minimum norm solutions of underdetermined system \( \mathbf{A}^\top \cdot \mathbf{X} = \mathbf{B}\).
Upon exit the columns of \(\mathbf{B}\) contain the minimum norm solution vectors.
If(transpose) and \(M < N\): least squares solution of overdetermined system \(\min \Vert \mathbf{B} - \mathbf{A}^\top \cdot \mathbf{X}\Vert\).
Upon exit the rows \(0\) to \(M-1\) contain the least square solution vectors. The residual sum of squares for each column is given by the sum of squares of elements \(M\) to \(N-1\) in that column.

If(!tranpose) then \(\mathbf{B} \in \mathbb{R}^{M \times N_{\rm RHS}}\), otherwise \(\mathbf{B} \in \mathbb{R}^{N \times N_{\rm RHS}}\). The matrices \(\mathbf{A}\) and \(\mathbf{B}\) must have an identical block cyclic distribution for rows and columns.

Definition at line 2133 of file scalapack.cc.

◆ pseudoinverse()

template<typename NumberType >

unsigned int ScaLAPACKMatrix< NumberType >::pseudoinverse ( const NumberType ratio )

Compute the pseudoinverse \(\mathbf{A}^+ \in \mathbb{R}^{N \times M}\) (Moore-Penrose inverse) of a real matrix \(\mathbf{A} \in \mathbb{R}^{M \times N}\) using the singular value decomposition \(\mathbf{A} = \mathbf{U} \cdot \mathbf{\Sigma} \cdot \mathbf{V}^T\).

Unlike the inverse, the pseudoinverse \(\mathbf{A}^+ = \mathbf{V} \cdot \mathbf{\Sigma}^+ \cdot \mathbf{U}^T\) exists for both rectangular as well as singular matrices \(\mathbf{A}\).

For a rectangular \(\mathbf{\Sigma}\) the pseudoinverse is computed by taking the reciprocal of each non-zero element on the diagonal, leaving the zeros in place, and then transposing \(\mathbf{\Sigma}\). For the numerical computation only the singular values \(\sigma_i > \sigma_{\text{max}} \, \text{ratio}\) are taken into account. Upon successful exit, the function returns the number of singular values fulfilling that condition. That value can be interpreted as the rank of \(\mathbf{A}\).

Upon return this object contains the pseudoinverse \(\mathbf{A}^+ \in \mathbb{R}^{N \times M}\).

The following alignment conditions have to be fulfilled: \(MB_A = NB_A\).

Definition at line 2225 of file scalapack.cc.

◆ reciprocal_condition_number()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::reciprocal_condition_number ( const NumberType a_norm ) const

Estimate the condition number of a SPD matrix in the \(l_1\)-norm. The matrix has to be in the Cholesky state (see compute_cholesky_factorization()). The reciprocal of the condition number is returned in order to avoid the possibility of overflow when the condition number is very large.

a_norm must contain the \(l_1\)-norm of the matrix prior to calling Cholesky factorization (see l1_norm()).

Note: An alternative is to compute the inverse of the matrix explicitly and manually construct \(k_1 = ||\mathbf{A}||_1 \, ||\mathbf{A}^{-1}||_1\).

Definition at line 2312 of file scalapack.cc.

◆ l1_norm()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::l1_norm

Compute the \(l_1\)-norm of the matrix.

Definition at line 2374 of file scalapack.cc.

◆ linfty_norm()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::linfty_norm

Compute the \(l_{\infty}\) norm of the matrix.

Definition at line 2388 of file scalapack.cc.

◆ frobenius_norm()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::frobenius_norm

Compute the Frobenius norm of the matrix.

Definition at line 2402 of file scalapack.cc.

◆ m()

template<typename NumberType >

size_type ScaLAPACKMatrix< NumberType >::m ( ) const

Number of rows of the \(M \times N\) matrix.

◆ n()

template<typename NumberType >

size_type ScaLAPACKMatrix< NumberType >::n ( ) const

Number of columns of the \(M \times N\) matrix.

◆ local_m()

template<typename NumberType >

unsigned int ScaLAPACKMatrix< NumberType >::local_m ( ) const

Number of local rows on this MPI processes.

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::local_el	(	const unsigned int	loc_row,
		const unsigned int	loc_column
	)		const

Read access to local element.

◆ local_el() [2/2]

template<typename NumberType >

NumberType& ScaLAPACKMatrix< NumberType >::local_el	(	const unsigned int	loc_row,
		const unsigned int	loc_column
	)

Write access to local element.

◆ scale_columns()

template<typename NumberType >

template<class InputVector >

void ScaLAPACKMatrix< NumberType >::scale_columns ( const InputVector & factors )

Scale the columns of the distributed matrix by the scalars provided in the array factors.

The array factors must have as many entries as the matrix columns.

Copies of factors have to be available on all processes of the underlying MPI communicator.

Note: The fundamental prerequisite for the InputVector is that it must be possible to create an ArrayView from it; this is satisfied by the std::vector and Vector classes.

Definition at line 3495 of file scalapack.cc.

◆ scale_rows()

template<typename NumberType >

template<class InputVector >

void ScaLAPACKMatrix< NumberType >::scale_rows ( const InputVector & factors )

Scale the rows of the distributed matrix by the scalars provided in the array factors.

The array factors must have as many entries as the matrix rows.

Copies of factors have to be available on all processes of the underlying MPI communicator.

Note: The fundamental prerequisite for the InputVector is that it must be possible to create an ArrayView from it; this is satisfied by the std::vector and Vector classes.

Definition at line 3506 of file scalapack.cc.

◆ norm_symmetric()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::norm_symmetric ( const char type ) const

private

Calculate the norm of a distributed symmetric dense matrix using ScaLAPACK's internal function.

Definition at line 2475 of file scalapack.cc.

◆ norm_general()

template<typename NumberType >

NumberType ScaLAPACKMatrix< NumberType >::norm_general ( const char type ) const

private

Calculate the norm of a distributed dense matrix using ScaLAPACK's internal function.

Definition at line 2416 of file scalapack.cc.

◆ eigenpairs_symmetric()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric	(	const bool	compute_eigenvectors,
		const std::pair< unsigned int, unsigned int > &	index_limits = `std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int)`,
		const std::pair< NumberType, NumberType > &	value_limits = `std::make_pair(std::numeric_limits<NumberType>::quiet_NaN(), std::numeric_limits<NumberType>::quiet_NaN())`
	)

private

Computing selected eigenvalues and, optionally, the eigenvectors. The eigenvalues/eigenvectors are selected by either prescribing a range of indices index_limits or a range of values value_limits for the eigenvalues. The function will throw an exception if both ranges are prescribed (meaning that both ranges differ from the default value) as this ambiguity is prohibited. If successful, the computed eigenvalues are arranged in ascending order. The eigenvectors are stored in the columns of the matrix, thereby overwriting the original content of the matrix.

Definition at line 1472 of file scalapack.cc.

◆ eigenpairs_symmetric_MRRR()

template<typename NumberType >

std::vector< NumberType > ScaLAPACKMatrix< NumberType >::eigenpairs_symmetric_MRRR	(	const bool	compute_eigenvectors,
		const std::pair< unsigned int, unsigned int > &	index_limits = `std::make_pair(numbers::invalid_unsigned_int, numbers::invalid_unsigned_int)`,
		const std::pair< NumberType, NumberType > &	value_limits = `std::make_pair(std::numeric_limits<NumberType>::quiet_NaN(), std::numeric_limits<NumberType>::quiet_NaN())`
	)

private

Computing selected eigenvalues and, optionally, the eigenvectors of the real symmetric matrix \(\mathbf{A} \in \mathbb{R}^{M \times M}\) using the MRRR algorithm. The eigenvalues/eigenvectors are selected by either prescribing a range of indices index_limits or a range of values value_limits for the eigenvalues. The function will throw an exception if both ranges are prescribed (meaning that both ranges differ from the default value) as this ambiguity is prohibited.

By calling this function the original content of the matrix will be overwritten. If requested, the eigenvectors are stored in the columns of the matrix. Also in the case that just the eigenvalues are required, the content of the matrix will be overwritten.

If successful, the computed eigenvalues are arranged in ascending order.

Note: Due to a bug in Netlib-ScaLAPACK, either all or no eigenvectors can be computed. Therefore, the input index_limits has to be set accordingly. Using Intel-MKL this restriction is not required.

Definition at line 1803 of file scalapack.cc.

◆ save_serial()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::save_serial	(	const std::string &	filename,
		const std::pair< unsigned int, unsigned int > &	chunk_size
	)		const

private

Definition at line 2649 of file scalapack.cc.

◆ load_serial()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::load_serial ( const std::string & filename )

private

Definition at line 3063 of file scalapack.cc.

◆ save_parallel()

template<typename NumberType >

void ScaLAPACKMatrix< NumberType >::save_parallel	(	const std::string &	filename,
		const std::pair< unsigned int, unsigned int > &	chunk_size
	)		const

Thread mutex.

Definition at line 988 of file scalapack.h.

The documentation for this class was generated from the following files:

include/deal.II/lac/scalapack.h
source/lac/scalapack.cc

Public Types

Public Member Functions

Private Member Functions

Private Attributes

Additional Inherited Members

Detailed Description

template<typename NumberType> class ScaLAPACKMatrix< NumberType >

Member Typedef Documentation

◆ size_type

Constructor & Destructor Documentation

◆ ScaLAPACKMatrix() [1/3]

◆ ScaLAPACKMatrix() [2/3]

◆ ScaLAPACKMatrix() [3/3]

◆ ~ScaLAPACKMatrix()

Member Function Documentation

◆ reinit() [1/2]

◆ reinit() [2/2]

◆ set_property()

◆ get_property()

◆ get_state()

◆ operator=()

◆ copy_from()

◆ copy_to() [1/4]

◆ copy_to() [2/4]

◆ copy_to() [3/4]

◆ copy_to() [4/4]

◆ copy_transposed()

◆ add() [1/2]

◆ add() [2/2]

◆ Tadd()

◆ mult()

◆ mmult()

◆ Tmmult()

◆ mTmult()

◆ TmTmult()

◆ save()

◆ load()

◆ compute_cholesky_factorization()

◆ compute_lu_factorization()

◆ invert()

◆ eigenpairs_symmetric_by_index()

◆ eigenpairs_symmetric_by_value()

◆ eigenpairs_symmetric_by_index_MRRR()

◆ eigenpairs_symmetric_by_value_MRRR()

◆ compute_SVD()

◆ least_squares()

◆ pseudoinverse()

◆ reciprocal_condition_number()

◆ l1_norm()

◆ linfty_norm()

◆ frobenius_norm()

◆ m()

◆ n()

◆ local_m()

◆ local_n()

◆ global_row()

◆ global_column()

◆ local_el() [1/2]

◆ local_el() [2/2]

◆ scale_columns()

◆ scale_rows()

◆ norm_symmetric()

◆ norm_general()

◆ eigenpairs_symmetric()

◆ eigenpairs_symmetric_MRRR()

◆ save_serial()

◆ load_serial()

◆ save_parallel()

◆ load_parallel()

Member Data Documentation

◆ state

◆ property

◆ grid

◆ n_rows

◆ n_columns

◆ row_block_size

◆ column_block_size

◆ n_local_rows

◆ n_local_columns

◆ descriptor

template<typename NumberType>
class ScaLAPACKMatrix< NumberType >