 |
Reference documentation for deal.II version 9.0.0
|
|
Reference documentation for deal.II version 9.0.0
|
#include <deal.II/numerics/data_postprocessor.h>
Public Member Functions | |
| DataPostprocessorTensor (const std::string &name, const UpdateFlags update_flags) | |
| virtual std::vector< std::string > | get_names () const |
| virtual std::vector< DataComponentInterpretation::DataComponentInterpretation > | get_data_component_interpretation () const |
| virtual UpdateFlags | get_needed_update_flags () const |
 Public Member Functions inherited from DataPostprocessor< dim > | |
| virtual | ~DataPostprocessor ()=default |
| virtual void | evaluate_scalar_field (const DataPostprocessorInputs::Scalar< dim > &input_data, std::vector< Vector< double > > &computed_quantities) const |
| virtual void | evaluate_vector_field (const DataPostprocessorInputs::Vector< dim > &input_data, std::vector< Vector< double > > &computed_quantities) const |
| Public Member Functions inherited from Subscriptor | |
| Subscriptor () | |
| Subscriptor (const Subscriptor &) | |
| Subscriptor (Subscriptor &&) noexcept | |
| virtual | ~Subscriptor () |
| Subscriptor & | operator= (const Subscriptor &) |
| Subscriptor & | operator= (Subscriptor &&) noexcept |
| void | subscribe (const char *identifier=nullptr) const |
| void | unsubscribe (const char *identifier=nullptr) const |
| unsigned int | n_subscriptions () const |
| void | list_subscribers () const |
| template<class Archive > | |
| void | serialize (Archive &ar, const unsigned int version) |
Private Attributes | |
| const std::string | name |
Additional Inherited Members | |
| Static Public Member Functions inherited from Subscriptor | |
| static ::ExceptionBase & | ExcInUse (int arg1, std::string arg2, std::string arg3) |
| static ::ExceptionBase & | ExcNoSubscriber (std::string arg1, std::string arg2) |
This class provides a simpler interface to the functionality offered by the DataPostprocessor class in case one wants to compute only a single tensor quantity (defined as having exactly dim*dim components) from the finite element field passed to the DataOut class.
For this case, we would like to output all of these components as parts of a tensor-valued quantity. Unfortunately, the various backends that write DataOut data in graphical file formats (see the DataOutBase namespace for what formats can be written) do not support tensor data at the current time. In fact, neither does the DataComponentInterpretation namespace that provides semantic information how individual components of graphical data should be interpreted. Nevertheless, like DataPostprocessorScalar and DataPostprocessorVector, this class helps with setting up what the get_names() and get_needed_update_flags() functions required by the DataPostprocessor base class should return, and so the current class implements these based on information that the constructor of the current class receives from further derived classes.
(In order to visualize this collection of scalar fields that, together, are then supposed to be interpreted as a tensor, one has to (i) use a visualization program that can visualize tensors, and (ii) teach it how to re-combine the scalar fields into tensors. In the case of Visit – see https://wci.llnl.gov/simulation/computer-codes/visit/ – this is done by creating a new "Expression": in essence, one creates a variable, say "grad_u", that is tensor-valued and whose value is given by the expression {{grad_u_xx,grad_u_xy}, {grad_u_yx, grad_u_yy}}, where the referenced variables are the names of scalar fields that, here, are produced by the example below. Visit is then able to visualize this "new" variable as a tensor.)
All derived classes have to do is implement a constructor and overload either DataPostprocessor::evaluate_scalar_field() or DataPostprocessor::evaluate_vector_field().
An example of how the closely related class DataPostprocessorScalar is used can be found in step-29. An example of how the DataPostprocessorVector class can be used is found in the documentation of that class.
A common example of what one wants to do with postprocessors is to visualize not just the value of the solution, but the gradient. This class is meant for tensor-valued outputs, so we will start with a vector-valued solution: the displacement field of step-8. The gradient is a rank-2 tensor (with exactly dim*dim components), so the current class fits the bill to produce the gradient through postprocessing. Then, the following code snippet implements everything you need to have to visualize the gradient:
The only tricky part in this piece of code is how to sort the dim*dim elements of the strain tensor into the one vector of computed output quantities – in other words, how to unroll the elements of the tensor into the vector. This is facilitated by the Tensor::component_to_unrolled_index() function that takes a pair of indices that specify a particular element of the tensor and returns a vector index that is then used in the code above to fill the computed_quantities array.
The last thing that is necessary is to add another output to the call of DataOut::add_vector() in the output_results() function of the Step8 class of that example program. The corresponding code snippet would then look like this:
This leads to the following output for the displacement field (i.e., the solution) and the gradients (you may want to compare with the solution shown in the results section of step-8; the current data is generated on a uniform mesh for simplicity):
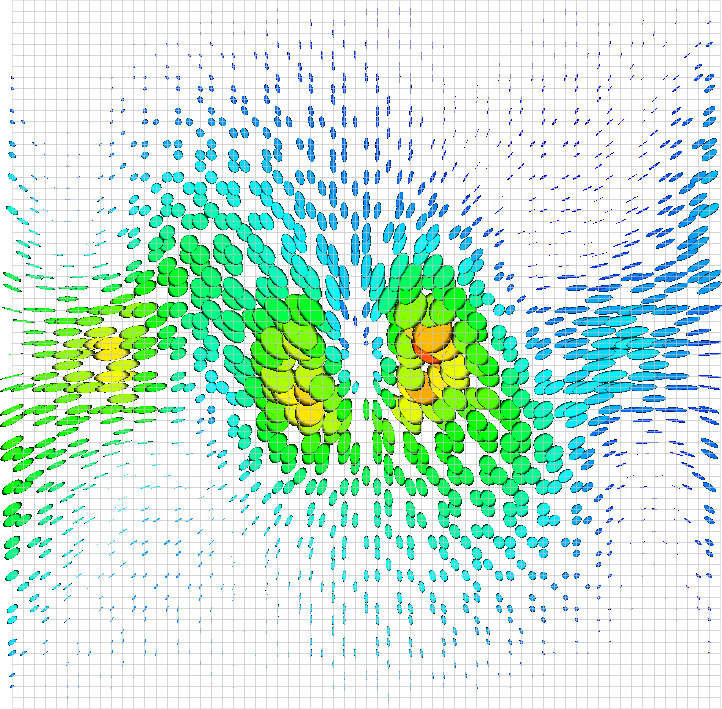
These pictures show an ellipse representing the gradient tensor at, on average, every tenth mesh point. You may want to read through the documentation of the Visit visualization program (see https://wci.llnl.gov/simulation/computer-codes/visit/) for an interpretation of how exactly tensors are visualizated.
In elasticity, one is often interested not in the gradient of the displacement, but in the "strain", i.e., the symmetrized version of the gradient \(\varepsilon=\frac 12 (\nabla u + \nabla u^T)\). This is easily facilitated with the following minor modification:
Using this class in step-8 leads to the following visualization:
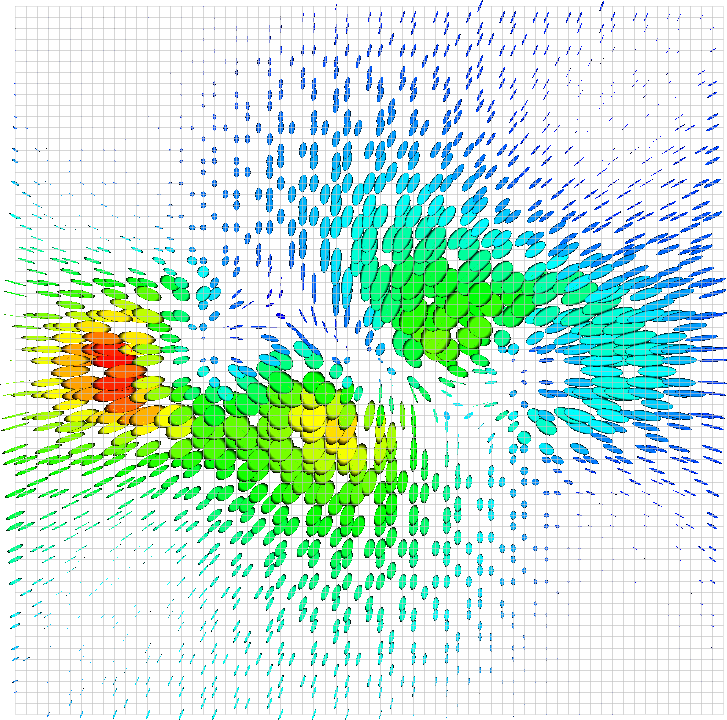
Given how easy it is to output the strain, it would also not be very complicated to write a postprocessor that computes the stress in the solution field as the stress is easily computed from the strain by multiplication with either the strain-stress tensor or, in simple cases, the Lamé constants.
Definition at line 1009 of file data_postprocessor.h.
| DataPostprocessorTensor< dim >::DataPostprocessorTensor | ( | const std::string & | name, |
| const UpdateFlags | update_flags | ||
| ) |
Constructor. Take the name of the single vector variable computed by classes derived from the current one, as well as the update flags necessary to compute this quantity.
| name | The name by which the vector variable computed by this class should be made available in graphical output files. |
| update_flags | This has to be a combination of update_values, update_gradients and update_hessians. If the DataPostprocessor is to be used in combination with DataOutFaces, you may also ask for a update of normals via the update_normal_vectors flag. |
Definition at line 152 of file data_postprocessor.cc.
|
virtual |
Return the vector of strings describing the names of the computed quantities. Given the purpose of this class, this is a vector with dim entries all equal to the name given to the constructor.
Implements DataPostprocessor< dim >.
Definition at line 164 of file data_postprocessor.cc.
|
virtual |
This function returns information about how the individual components of output files that consist of more than one data set are to be interpreted. Since the current class is meant to be used for a single vector result variable, the returned value is obviously DataComponentInterpretation::component_is_part repeated dim times.
Reimplemented from DataPostprocessor< dim >.
Definition at line 182 of file data_postprocessor.cc.
|
virtual |
Return which data has to be provided to compute the derived quantities. The flags returned here are the ones passed to the constructor of this class.
Implements DataPostprocessor< dim >.
Definition at line 193 of file data_postprocessor.cc.
|
private |
Copies of the two arguments given to the constructor of this class.
Definition at line 1056 of file data_postprocessor.h.
1.8.14