#include <deal.II/matrix_free/fe_evaluation.h>

Inheritance diagram for FEEvaluation< dim, fe_degree, n_q_points_1d, n_components_, Number >:

Public Member Functions
	FEEvaluation (const MatrixFree< dim, Number > &matrix_free, const unsigned int fe_no=0, const unsigned int quad_no=0)

	FEEvaluation (const Mapping< dim > &mapping, const FiniteElement< dim > &fe, const Quadrature< 1 > &quadrature, const UpdateFlags update_flags, const unsigned int first_selected_component=0)

	FEEvaluation (const FiniteElement< dim > &fe, const Quadrature< 1 > &quadrature, const UpdateFlags update_flags, const unsigned int first_selected_component=0)

template<int n_components_other>
	FEEvaluation (const FiniteElement< dim > &fe, const FEEvaluationBase< dim, n_components_other, Number > &other, const unsigned int first_selected_component=0)

	FEEvaluation (const FEEvaluation &other)

FEEvaluation &	operator= (const FEEvaluation &other)

void	evaluate (const bool evaluate_values, const bool evaluate_gradients, const bool evaluate_hessians=false)

void	integrate (const bool integrate_values, const bool integrate_gradients)

Point< dim, VectorizedArray< Number > >	quadrature_point (const unsigned int q_point) const

Public Member Functions inherited from FEEvaluationBase< dim, n_components_, Number >
	~FEEvaluationBase ()

void	reinit (const unsigned int cell)

template<typename DoFHandlerType , bool level_dof_access>
void	reinit (const TriaIterator< DoFCellAccessor< DoFHandlerType, level_dof_access > > &cell)

void	reinit (const typename Triangulation< dim >::cell_iterator &cell)

unsigned int	get_cell_data_number () const

internal::MatrixFreeFunctions::CellType	get_cell_type () const

const internal::MatrixFreeFunctions::ShapeInfo< Number > &	get_shape_info () const

void	fill_JxW_values (AlignedVector< VectorizedArray< Number > > &JxW_values) const

template<typename VectorType >
void	read_dof_values (const VectorType &src, const unsigned int first_index=0)

template<typename VectorType >
void	read_dof_values_plain (const VectorType &src, const unsigned int first_index=0)

template<typename VectorType >
void	distribute_local_to_global (VectorType &dst, const unsigned int first_index=0) const

template<typename VectorType >
void	set_dof_values (VectorType &dst, const unsigned int first_index=0) const

value_type	get_dof_value (const unsigned int dof) const

void	submit_dof_value (const value_type val_in, const unsigned int dof)

value_type	get_value (const unsigned int q_point) const

void	submit_value (const value_type val_in, const unsigned int q_point)

gradient_type	get_gradient (const unsigned int q_point) const

void	submit_gradient (const gradient_type grad_in, const unsigned int q_point)

Tensor< 1, n_components_, Tensor< 2, dim, VectorizedArray< Number > > >	get_hessian (const unsigned int q_point) const

gradient_type	get_hessian_diagonal (const unsigned int q_point) const

value_type	get_laplacian (const unsigned int q_point) const

VectorizedArray< Number >	get_divergence (const unsigned int q_point) const

SymmetricTensor< 2, dim, VectorizedArray< Number > >	get_symmetric_gradient (const unsigned int q_point) const

Tensor< 1,(dim==2?1:dim), VectorizedArray< Number > >	get_curl (const unsigned int q_point) const

void	submit_divergence (const VectorizedArray< Number > div_in, const unsigned int q_point)

void	submit_symmetric_gradient (const SymmetricTensor< 2, dim, VectorizedArray< Number > > grad_in, const unsigned int q_point)

void	submit_curl (const Tensor< 1, dim==2?1:dim, VectorizedArray< Number > > curl_in, const unsigned int q_point)

value_type	integrate_value () const

VectorizedArray< Number >	JxW (const unsigned int q_point) const

const VectorizedArray< Number > *	begin_dof_values () const

VectorizedArray< Number > *	begin_dof_values ()

const VectorizedArray< Number > *	begin_values () const

VectorizedArray< Number > *	begin_values ()

const VectorizedArray< Number > *	begin_gradients () const

VectorizedArray< Number > *	begin_gradients ()

const VectorizedArray< Number > *	begin_hessians () const

VectorizedArray< Number > *	begin_hessians ()

const std::vector< unsigned int > &	get_internal_dof_numbering () const

ArrayView< VectorizedArray< Number > >	get_scratch_data () const

Public Attributes
const unsigned int	dofs_per_cell

const unsigned int	n_q_points

Private Member Functions
void	check_template_arguments (const unsigned int fe_no, const unsigned int first_selected_component)

Private Attributes
void(*	evaluate_funct )(const internal::MatrixFreeFunctions::ShapeInfo< Number > &, VectorizedArray< Number > values_dofs_actual[], VectorizedArray< Number > values_quad[], VectorizedArray< Number > gradients_quad[][dim], VectorizedArray< Number > hessians_quad[][(dim (dim+1))/2], VectorizedArray< Number > scratch_data, const bool evaluate_val, const bool evaluate_grad, const bool evaluate_lapl)

void(*	integrate_funct )(const internal::MatrixFreeFunctions::ShapeInfo< Number > &, VectorizedArray< Number > values_dofs_actual[], VectorizedArray< Number > values_quad[], VectorizedArray< Number > gradients_quad[][dim], VectorizedArray< Number > scratch_data, const bool evaluate_val, const bool evaluate_grad)

Additional Inherited Members
Protected Member Functions inherited from FEEvaluationAccess< dim, n_components_, Number >
	FEEvaluationAccess (const MatrixFree< dim, Number > &matrix_free, const unsigned int fe_no, const unsigned int quad_no, const unsigned int fe_degree, const unsigned int n_q_points)

template<int n_components_other>
	FEEvaluationAccess (const Mapping< dim > &mapping, const FiniteElement< dim > &fe, const Quadrature< 1 > &quadrature, const UpdateFlags update_flags, const unsigned int first_selected_component, const FEEvaluationBase< dim, n_components_other, Number > *other)

	FEEvaluationAccess (const FEEvaluationAccess &other)

FEEvaluationAccess &	operator= (const FEEvaluationAccess &other)

Protected Member Functions inherited from FEEvaluationBase< dim, n_components_, Number >
	FEEvaluationBase (const MatrixFree< dim, Number > &matrix_free, const unsigned int fe_no, const unsigned int quad_no, const unsigned int fe_degree, const unsigned int n_q_points)

template<int n_components_other>
	FEEvaluationBase (const Mapping< dim > &mapping, const FiniteElement< dim > &fe, const Quadrature< 1 > &quadrature, const UpdateFlags update_flags, const unsigned int first_selected_component, const FEEvaluationBase< dim, n_components_other, Number > *other)

	FEEvaluationBase (const FEEvaluationBase &other)

FEEvaluationBase &	operator= (const FEEvaluationBase &other)

template<typename VectorType , typename VectorOperation >
void	read_write_operation (const VectorOperation &operation, VectorType *vectors[]) const

template<typename VectorType >
void	read_dof_values_plain (const VectorType *src_data[])

Protected Attributes inherited from FEEvaluationBase< dim, n_components_, Number >
AlignedVector< VectorizedArray< Number > > *	scratch_data_array

VectorizedArray< Number > *	scratch_data

VectorizedArray< Number > *	values_dofs [n_components]

VectorizedArray< Number > *	values_quad [n_components]

VectorizedArray< Number > *	gradients_quad [n_components][dim]

VectorizedArray< Number > *	hessians_quad [n_components][(dim *(dim+1))/2]

const unsigned int	quad_no

const unsigned int	n_fe_components

const unsigned int	active_fe_index

const unsigned int	active_quad_index

const MatrixFree< dim, Number > *	matrix_info

const internal::MatrixFreeFunctions::DoFInfo *	dof_info

const internal::MatrixFreeFunctions::MappingInfo< dim, Number > *	mapping_info

const internal::MatrixFreeFunctions::ShapeInfo< Number > *	data

const Tensor< 1, dim, VectorizedArray< Number > > *	cartesian_data

const Tensor< 2, dim, VectorizedArray< Number > > *	jacobian

const VectorizedArray< Number > *	J_value

const VectorizedArray< Number > *	quadrature_weights

const Point< dim, VectorizedArray< Number > > *	quadrature_points

const Tensor< 2, dim, VectorizedArray< Number > > *	jacobian_grad

const Tensor< 1,(dim >1?dim (dim-1)/2:1), Tensor< 1, dim, VectorizedArray< Number > > >	jacobian_grad_upper

unsigned int	cell

internal::MatrixFreeFunctions::CellType	cell_type

unsigned int	cell_data_number

bool	dof_values_initialized

bool	values_quad_initialized

bool	gradients_quad_initialized

bool	hessians_quad_initialized

bool	values_quad_submitted

bool	gradients_quad_submitted

std_cxx1x::shared_ptr< internal::MatrixFreeFunctions::MappingDataOnTheFly< dim, Number > >	mapped_geometry

std::vector< types::global_dof_index >	old_style_dof_indices

const unsigned int	first_selected_component

std::vector< types::global_dof_index >	local_dof_indices

Detailed Description

template<int dim, int fe_degree, int n_q_points_1d, int n_components_, typename Number>
class FEEvaluation< dim, fe_degree, n_q_points_1d, n_components_, Number >

The class that provides all functions necessary to evaluate functions at quadrature points and cell integrations. In functionality, this class is similar to FEValues, however, it includes a lot of specialized functions that make it much faster (between 5 and 500, depending on the polynomial degree).

Usage and initialization

Fast usage in combination with MatrixFree

The first and foremost way of usage is to initialize this class from a MatrixFree object that caches everything related to the degrees of freedom and the mapping information. This way, it is possible to use vectorization for applying a differential operator for several cells at once.

The capabilities of FEEvaluation span a large spectrum of integration tasks for weak forms. In general, there are two classes of tasks that get done. One is the evaluate path that interpolates from a solution vector to quadrature points:

FEEvaluation<dim,fe_degree> phi(matrix_free);
for (unsigned int cell_index = cell_range.first;
     cell_index < cell_range.second; ++cell_index)
  {
    phi.reinit(cell_index);
    phi.read_dof_values(vector);
    phi.evaluate(true, false);   // interpolate values, but not gradients
    for (unsigned int q_index=0; q_index<phi.n_q_points; ++q_index)
      {
        VectorizedArray<double> val = phi.get_value(q_index);
        // do something with val
      }
  }

Likewise, a gradient of the finite element solution represented by vector can be interpolated to the quadrature points by phi.get_gradient(q). The combination of read_dof_values(), evaluate() and get_value() is similar to what FEValues::get_function_values or FEValues::get_function_gradients does, but it is in general much faster because it makes use of the tensor product, see the description of the evaluation routines below, and can do this operation for several cells at once through vectorization.

The second class of tasks done by FEEvaluation are integration tasks for right hand sides. In finite element computations, these typically consist of multiplying a quantity on quadrature points (a function value, or a field interpolated by the finite element space itself) by a set of test functions and integrating over the cell through summation of the values in each quadrature point, multiplied by the quadrature weight and the Jacobian determinant of the transformation. If a generic Function object is given and we want to compute \(v_i = \int_\Omega \varphi_i f dx\), this is done by the following cell-wise integration:

FEEvaluation<dim,fe_degree> phi(matrix_free);
Function<dim> &function = ...;
for (unsigned int cell_index = cell_range.first;
     cell_index < cell_range.second; ++cell_index)
  {
    phi.reinit(cell_index);
    for (unsigned int q_index=0; q_index<phi.n_q_points; ++q_index)
      {
        Point<dim,VectorizedArray<double> > p_vect =
          phi.quadrature_point(q_index);
        // Need to evaluate function for each component in VectorizedArray
        VectorizedArray<double> f_value;
        for (unsigned int v=0; v<VectorizedArray<double>::n_array_elements; ++v)
          {
            Point<dim> p;
            for (unsigned int d=0; d<dim; ++d)
              p[d] = p_vect[d][v];
            f_value[v] = function.value(p);
          }
        phi.submit_value(f_value, q);
      }
    phi.integrate(true, false);
    phi.distribute_local_to_global(dst);
  }

In this code, the call to phi.submit_value() prepares for the multiplication by the test function prior to the actual integration (inside the submit call, the value to be tested is also multiplied by the determinant of the Jacobian and the quadrature weight). In the integrate() call, an integral contribution tested by each basis function underlying the FEEvaluation object (e.g. the four linear shape functions of FE_Q<2>(1) in 2D) is computed, which gives the vector entries to be summed into the dst vector. Note that the above code needs to explicitly loop over the components in the vectorized array for evaluating the function, which is necessary for interfacing with a generic Function object with double arguments. Simple functions can also be implemented in VectorizedArray form directly as VectorizedArray provides the basic math operations.

For evaluating a bilinear form, the evaluation on a source vector is combined with the integration involving test functions that get written into a result vector. This setting is the context of matrix-free operator evaluation and explained in the step-37 and step-48 tutorial programs.

Note that the two vector accesses through FEEvaluation::read_dof_values and FEEvaluation::distribute_local_to_global resolve constraints on the fly, based on the ConstraintMatrix object specified at the MatrixFree::reinit() call. In case the values in the degrees of freedom are of interest (usually only the values in quadrature points are necessary), these can be accessed through FEEvaluation::get_dof_value(i), where i is the index of the basis function. Note that the numbering of the degrees of freedom for continuous elements in FEEvaluation is different from the ordering in FE_Q (or FEValues) because FEEvaluation needs to access them in lexicographic order, which is the ordering used in FE_DGQ, for instance. Re-indexing would be too expensive because the access inside evaluate() and integrate() is on the critical path in the tensorial evaluation parts. An alternative to filling the DoF values by read_dof_values() before an evaluate() call is to manually assign a value by a set_dof_value() call. Likewise, if the local result of integration should be further processed rather than scattered into a vector by distribute_local_to_global(), one can access it by get_dof_value() after an integrate() call. An example for using the values of an integral in a different context is fast assembly of matrices as shown in the next subsection.

For most operator evaluation tasks that repeatedly go through the mesh, the realization by MatrixFree that combines pre-computed data for the mapping (Jacobian transformations for the geometry description) with on-the-fly evaluation of basis functions is the most efficient way of doing things. In other words, the framework selects a trade-off between memory usage and initialization of objects that is suitable for replacement of matrix-vector products or explicit time integration in a matrix-free way.

Usage without pre-initialized MatrixFree object

The second form of usage is to initialize FEEvaluation from geometry information generated by FEValues. This allows to apply the integration loops on the fly without prior initialization of MatrixFree objects. This can be useful when the memory and initialization cost of MatrixFree is not acceptable, e.g. when a different number of quadrature points should be used for one single evaluation in error computation. Also, when using the routines of this class to assemble matrices the trade-off implied by the MatrixFree class may not be desired. In such a case, the cost to initialize the necessary geometry data on the fly is comparably low and thus avoiding a global object MatrixFree can be useful. When used in this way, reinit methods reminiscent from FEValues with a cell iterator are used. However, note that this model results in working on a single cell at a time, with geometry data duplicated in all components of the vectorized array. Thus, vectorization is only useful when it can apply the same operation on different data, e.g. when performing matrix assembly.

As an example, consider the following code to assemble the contributions to the Laplace matrix:

FEEvaluation<dim,fe_degree> fe_eval (mapping, finite_element,
                                     QGauss<1>(fe_degree+1), flags);
for (cell = dof_handler.begin_active();
     cell != dof_handler.end();
     ++cell)
  {
    fe_eval.reinit(cell);
    for (unsigned int i=0; i<dofs_per_cell;
         i += VectorizedArray<double>::n_array_elements)
      {
        const unsigned int n_items =
          i+VectorizedArray<double>::n_array_elements > dofs_per_cell ?
          (dofs_per_cell - i) : VectorizedArray<double>::n_array_elements;
        // Set n_items unit vectors
        for (unsigned int j=0; j<dofs_per_cell; ++j)
          fe_eval.set_dof_value(VectorizedArray<double>(), j);
        for (unsigned int v=0; v<n_items; ++v)
          {
            VectorizedArray<double> one_value = VectorizedArray<double>();
            one_value[v] = 1.;
            fe_eval.set_dof_value(one_value, i+v);
          }
        // Apply operator on unit vector to generate the next few matrix
        // columns
        fe_eval.evaluate(true, true);
        for (unsigned int q=0; q<n_q_points; ++q)
          {
            fe_eval.submit_value(10.*fe_eval.get_value(q), q);
            fe_eval.submit_gradient(fe_eval.get_gradient(q), q);
          }
        fe_eval.integrate(true, true);
        // Insert computed entries in matrix
        for (unsigned int v=0; v<n_items; ++v)
          for (unsigned int j=0; j<dofs_per_cell; ++j)
            cell_matrix(fe_eval.get_internal_dof_numbering()[j],
                        fe_eval.get_internal_dof_numbering()[i+v])
              = fe_eval.get_dof_value(j)[v];
      }
    ...
  }

This code generates the columns of the cell matrix with the loop over i above. The way this is done is the following: FEEvaluation's routines focus on the evaluation of finite element operators, so for computing a cell matrix out of an operator evaluation it is applied to all the unit vectors on the cell. Applying the operator on a unit vector might seem inefficient but the evaluation routines used here are so quick that they still work much faster than what is possible with FEValues. In particular, the complexity is (fe_degree+1)^2*dim+1 rather than (fe_degree+1)^3*dim .

Due to vectorization, we can generate matrix columns for several unit vectors at a time (e.g. 4). The variable n_items make sure that we do the last iteration where the number of cell dofs is not divisible by the vectorization length correctly. Also note that we need to get the internal dof numbering applied by fe_eval because FEEvaluation internally uses a lexicographic numbering of degrees of freedom as explained above.

Internal data organization

The temporary data for holding the solution values on the local degrees of freedom as well as the interpolated values, gradients, and Hessians on quadrature points is a scratch array provided by MatrixFree::acquire_scratch_data() that is re-used between different calls to FEEvaluation. Therefore, constructing an FEEvaluation object is typically cheap and does not involve any expensive operation. Only a few dozen pointers to the actual data fields are set during construction. Therefore, no negative performance impact arises when creating an FEEvaluation several times per loop, such as at the top of a local_cell_operation operation that is split in small chunks for a parallel for loop, obviating a separate scratch data field for parallel loops as necessary in the loop of WorkStream.

When using the FEEvaluation class in multithreaded mode, the thread local storage of the scratch data in MatrixFree automatically makes sure that each thread gets it private data array. Note, however, that deal.II must be compiled with thread support also when all the thread parallelization is provided externally and not done via deal.II's routines, such as OpenMP. This is because deal.II needs to know the notation of thread local storage. The FEEvaluation kernels have been verified to work within OpenMP loops.

Description of evaluation routines

This class contains specialized evaluation routines for elements based on tensor-product quadrature formulas and tensor-product-like shape functions, including standard FE_Q or FE_DGQ elements and quadrature points symmetric around 0.5 (like Gauss quadrature), FE_DGP elements based on truncated tensor products as well as the faster case of Gauss-Lobatto elements with Gauss-Lobatto quadrature which give diagonal mass matrices and quicker evaluation internally. The main benefit of this class is the evaluation of all shape functions in all quadrature or integration over all shape functions in dim (fe_degree+1)^dim+1 operations instead of the slower (fe_degree+1)^2*dim complexity in the evaluation routines of FEValues. This is done by an algorithm called sum factorization which factors out constant factors during the evaluation along a coordinate direction. This algorithm is the basis of many spectral element algorithms.

Note that many of the operations available through this class are inherited from the base class FEEvaluationBase, in particular reading from and writing to vectors. Also, the class inherits from FEEvaluationAccess that implements access to values, gradients and Hessians of the finite element function on quadrature points.

This class assumes that the shape functions of the FiniteElement under consideration do not depend on the geometry of the cells in real space. Currently, other finite elements cannot be treated with the matrix-free concept.

Degree of finite element as a compile-time parameter

The default usage model of FEEvaluation expects the polynomial degree to be given as a template parameter. This requirement guarantees maximum efficiency: The sum factorization evaluation performs a number of nested short 1D loops of length equal to the polynomial degree plus one. If the loop bounds are known at compile time, the compiler can unroll loops as deemed most efficient by its heuristics. At least the innermost loop is almost always completely unrolled, avoiding the loop overhead.

However, carrying the polynomial degree (and the number of quadrature points) as a template parameter makes things more complicated in codes where different polynomial degrees should be considered, e.g. in application codes where the polynomial degree is given through an input file. The recommended approach for good performance is to create different cell functions, possibly through different operator classes that are derived from a common base class with virtual functions to access the operator evaluation. The program then keeps only a pointer to the common base class after initializing templated derived classes with fixed polynomial degree that are selected from the detected polynomial degree. This approach requires a-priori knowledge of the range of valid degrees and can lead to rather long compile times in programs with many apply functions.

A flexible choice of the polynomial degree based on the information in the element passed to the initialization is also supported by FEEvaluation, even though it runs two to three times more slowly. For this, set the template parameter for the polynomial degree to -1 (and choose an arbitrary number for the number of quadrature points), which switches to the other code path. Internally, an evaluator object with template specialization for -1 is invoked that runs according to run-time bounds, whereas the default case with compile-time bounds given through fe_degree selects another template class without compromising efficiency.

An overview of the performance of FEEvaluation is given in the following figure. It considers the time spent per degree of freedom for evaluating the Laplacian with continuous finite elements using a code similar to the step-37 tutorial program for single-precision arithmetics. The time is based on an experiment on a single core of an Intel Xeon E5-2687W v4, running at 3.4 GHz and measured at problem sizes around 10 million. The plot lists the computational time (around 0.1 seconds) divided by the number of degrees freedom.

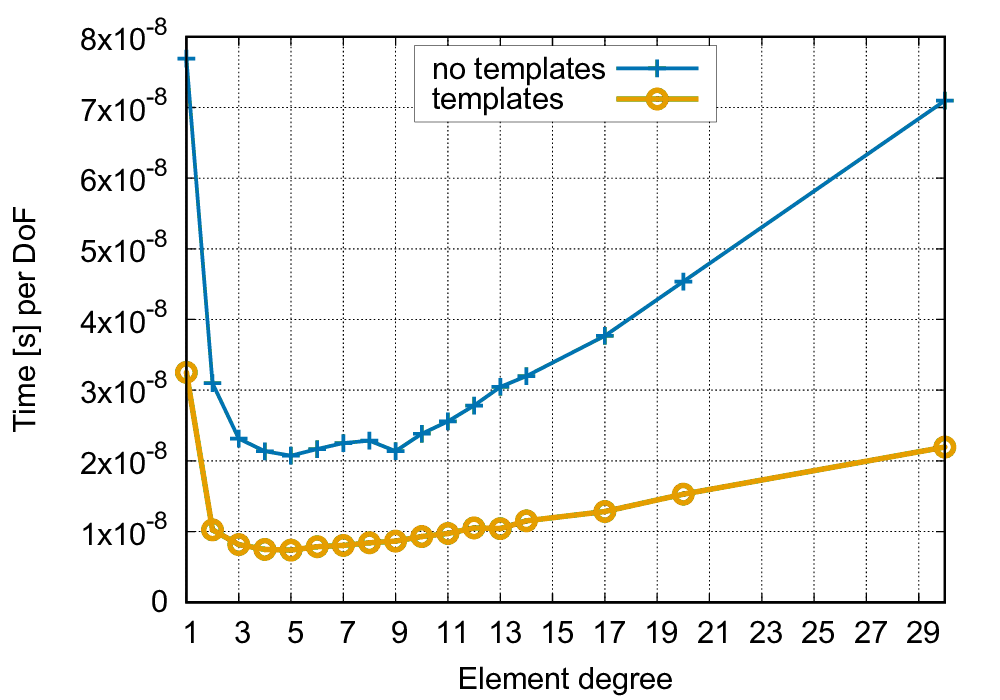
The figure shows that the templated version is between 2.5 and 3 times faster. The fastest turnaround on this setup is for polynomial degree 5 at 7.4e-9 seconds per degree of freedom or 134 million degrees of freedom per second - on a single core. The non-templated version is also fastest at polynomial degree 5 with 2.1e-9 seconds per degree of freedom or 48 million degrees of freedom per second.

Handling multi-component systems

FEEvaluation also allows for treating vector-valued problems through a template parameter on the number of components:

FEEvaluation<dim,fe_degree,n_q_points_1d,n_components> phi(matrix_free);

If used this way, the components can be gathered from several components of an std::vector<VectorType> through the call

phi.read_dof_values(src, 0);

where the 0 means that the vectors starting from the zeroth vector in the std::vector should be used, src[0], src[1], ..., src[n_components-1].

An alternative way for reading multi-component systems is possible if the DoFHandler underlying the MatrixFree data is based on an FESystem of n_components entries. In that case, a single vector is provided for the read_dof_values() and distribute_local_to_global() calls.

An important property of FEEvaluation in multi-component systems is the layout of multiple components in the get_value(), get_gradient(), or get_dof_value() calls. In this case, instead of a scalar return field VectorizedArray<double> a tensor is returned,

get_value -> Tensor<1,n_components,VectorizedArray<double> >

get_gradient -> Tensor<1,n_components,Tensor<1,dim,VectorizedArray<double> > >

In a similar vein, the submit_value() and submit_gradient() calls take tensors of values. Note that there exist specializations for n_components=1 and n_components=dim, which are provided through the base class FEEvaluationAccess. In the scalar case, these provide the scalar return types described above. In the vector-valued case, the gradient is converted from Tensor<1,dim,Tensor<1,dim,VectorizedArray<double> > > to Tensor<2,dim,VectorizedArray<double> >. Furthermore, additional operations such as the diveregence or curl are available.

In case different shape functions are combined, for example mixed finite element formulations in Stokes flow, two FEEvaluation objects are created, one for the velocity and one for the pressure. Those are then combined on quadrature points:

FEEvaluation<dim,degree_p+1,degree_p+2,dim> velocity (data, 0);
FEEvaluation<dim,degree_p,  degree_p+2,1, > pressure (data, 1);
for (unsigned int cell=cell_range.first; cell<cell_range.second; ++cell)
  {
    velocity.reinit (cell);
    velocity.read_dof_values (src.block(0));
    velocity.evaluate (false,true);
    pressure.reinit (cell);
    pressure.read_dof_values (src.block(1));
    pressure.evaluate (true,false);
    for (unsigned int q=0; q<velocity.n_q_points; ++q)
      {
        SymmetricTensor<2,dim,VectorizedArray<double> > sym_grad_u =
          velocity.get_symmetric_gradient (q);
        VectorizedArray<double> pres = pressure.get_value(q);
        VectorizedArray<double> div = -trace(sym_grad_u);
        pressure.submit_value (div, q);
        // subtract p * I
        for (unsigned int d=0; d<dim; ++d)
          sym_grad_u[d][d] -= pres;
        velocity.submit_symmetric_gradient(sym_grad_u, q);
     }
    velocity.integrate (false,true);
    velocity.distribute_local_to_global (dst.block(0));
    pressure.integrate (true,false);
    pressure.distribute_local_to_global (dst.block(1));
  }

This code assumes that a BlockVector of two components describes the velocity and pressure components, respectively. For identifying the different DoFHandler objects for velocity and pressure, the second argument to the FEEvaluation objects specify the respective component 0 for velocity and 1 for pressure. For further examples of vector-valued problems, the deal.II test suite includes a few additional examples as well, e.g. the Stokes operator described above is found at https://github.com/dealii/dealii/blob/master/tests/matrix_free/matrix_vector_stokes_noflux.cc

Handling several integration tasks and data storage in quadrature points

The design of FEEvaluation and MatrixFree separates the geometry from the basis functions. Therefore, several DoFHandler objects (or the same DoFHandler equipped with different constraint objects) can share the same geometry information like in the Stokes example above. All geometry is cached once in MatrixFree, so FEEvaluation does not need to do expensive initialization calls and rather sets a few pointers. This realization is based on the idea that the geometry information is needed only once also when several fields are evaluated, in a departure from FEValues which sets up the internal mapping data for each field. If for example a multi-component PDE involves the shape values on one component and the shape gradient on the other, no efficiency is lost if both are based on the same MatrixFree object where the update flags specify that both update_values , update_gradients , and update_jxw_values are given. The selection of desired quantities of shape values is through the flags in the evaluate() or integrate calls and the access at quadrature points:

phi1.evaluate(true, false);
phi2.evaluate(false, true);
for (unsigned int q_index=0; q_index<phi1.n_q_points; ++q_index)
  {
    VectorizedArray<double> val1 = phi1.get_value(q);
    Tensor<1,dim,VectorizedArray<double> > grad2 = phi2.get_gradient(q);
    Point<dim,VectorizedArray<double> > point = phi1.get_quadrature_point(q);
    // ... some complicated formula combining those three...
  }

In the loop over quadrature points, one can ask any of the two FEEvaluation objects — it does not really matter which one because they only keep pointers to the quadrature point data — to provide the quadrature point location.

This observation also translates to the case when different differential operators are implemented in a program, for example the action of a mass matrix for one phase of the algorithm and the action of a stiffness matrix in another one. Only a single MatrixFree object is necessary, maintaining full efficiency by using different local functions with the respective implementation in separate FEEvaluation objects. In other words, a user does not need to bother about being conservative when providing update_flags to the initialization of MatrixFree for efficiency reasons - no overhead incurs inside FEEvaluation, except for at most one or two more if statements inside the FEEvaluation::reinit() call. Rather, the largest set of flags necessary among all calls is perfectly fine from an efficiency point of view.

For the combination of different fields, including different solution vectors that come from different time steps, it is mandatory that all FEEvaluation objects share the same MatrixFree object. This is because the way cells are looped by MatrixFree::cell_loop() can be different for different DoFHandler or ConstraintMatrix arguments. More precisely, even though the layout is going to be the same in serial, there is no guarantee about the ordering for different DoFHandler/Constraints in the MPI case. The reason is that the algorithm detects cells that need data exchange with MPI and those can change for different elements — FE_Q with hanging node constraints connects to more neighbors than a FE_DGQ element, for instance, and cells which need data exchange are put in different positions inside the cell loop. Of course, if the exact same DoFHandler, ConstraintMatrix, and options (such as the setting for thread parallelism) are set, then the order is going to be the same because the algorithm is deterministic.

Template Parameters

dim	Dimension in which this class is to be used
fe_degree	Degree of the tensor product finite element with fe_degree+1 degrees of freedom per coordinate direction. Can be set to -1 if the degree is not known at compile time, but performance will usually be worse by a factor of 2-3.
n_q_points_1d	Number of points in the quadrature formula in 1D, defaults to fe_degree+1
n_components	Number of vector components when solving a system of PDEs. If the same operation is applied to several components of a PDE (e.g. a vector Laplace equation), they can be applied simultaneously with one call (and often more efficiently). Defaults to 1.
Number	Number format, usually `double` or `float`. Defaults to `double`

Author: Katharina Kormann and Martin Kronbichler, 2010, 2011

Definition at line 53 of file fe_evaluation.h.