# Introduction
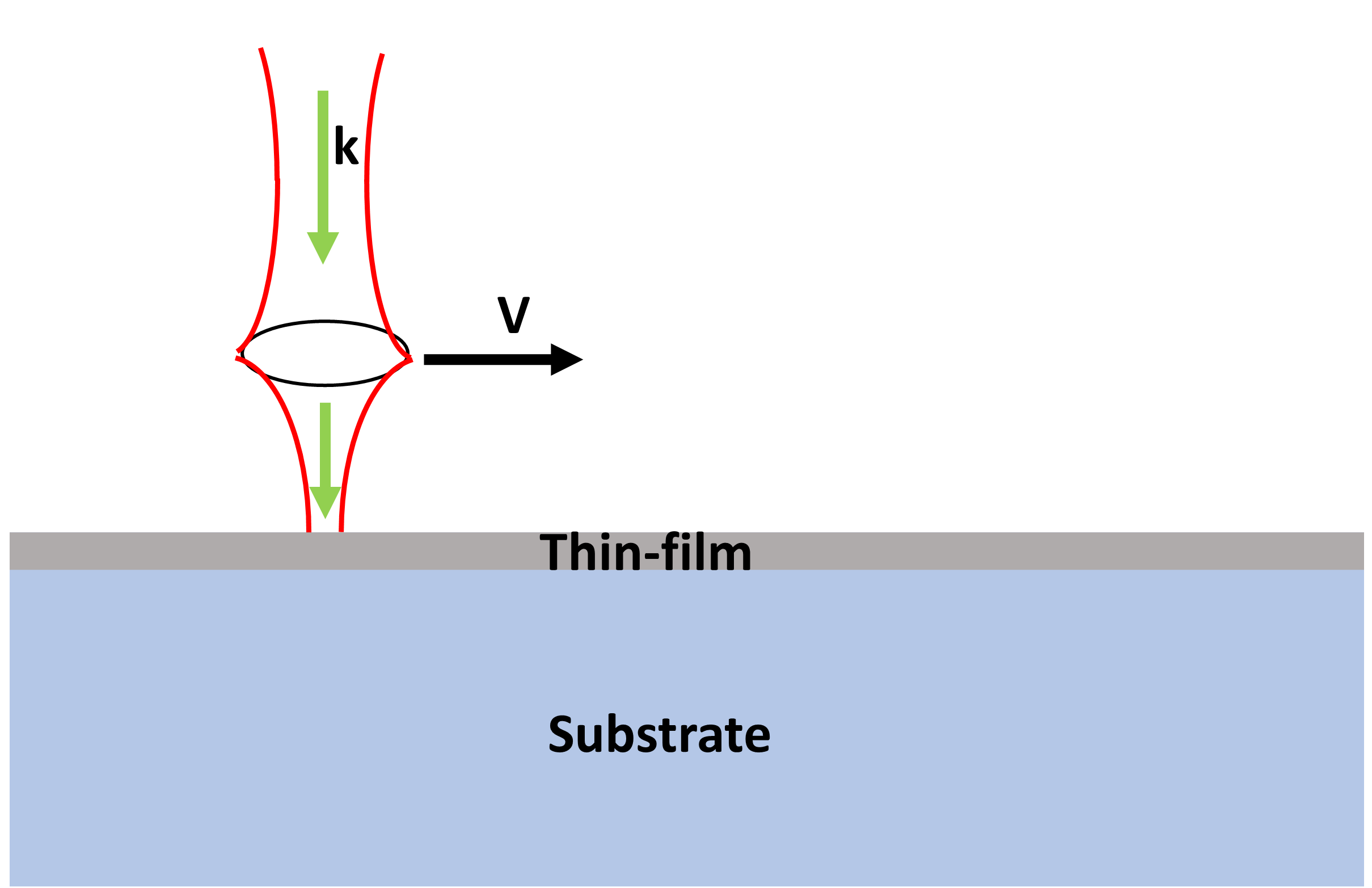
In this tutorial, the studied problem is to simulate temperature distributions of a sample under a moving laser. Light penetrates the substrate without loss. The top-covered thin-film is, however, a light absorbing material. For simplicity, the thin-film is assumed to be TiO$_2$ mixed with silver nanoparticles, which supports light heating of the material by absorbing light energy. For this tutorial, we only consider the isotropic absorption. Figure \ref{fgr:s1} illustrates the sketch of the problem. The absorption coefficient is assumed to be $10^4 m^{-1}$. The substrate is glass. The thickness of the thin-film is assumed to be 400 nm. The spot size at the top of thin film is $20 \mu m$ at $e^{-2}$. The writing speed is assumed to be 10 mm/s. The laser power is 0.4 W. The time step is set as 10 $\mu s$. The initial position of laser center is $-50 \mu m$ with 50 $\mu m$ distance away from the left boundary to avoid boundary effects.
## Illustration of the problem
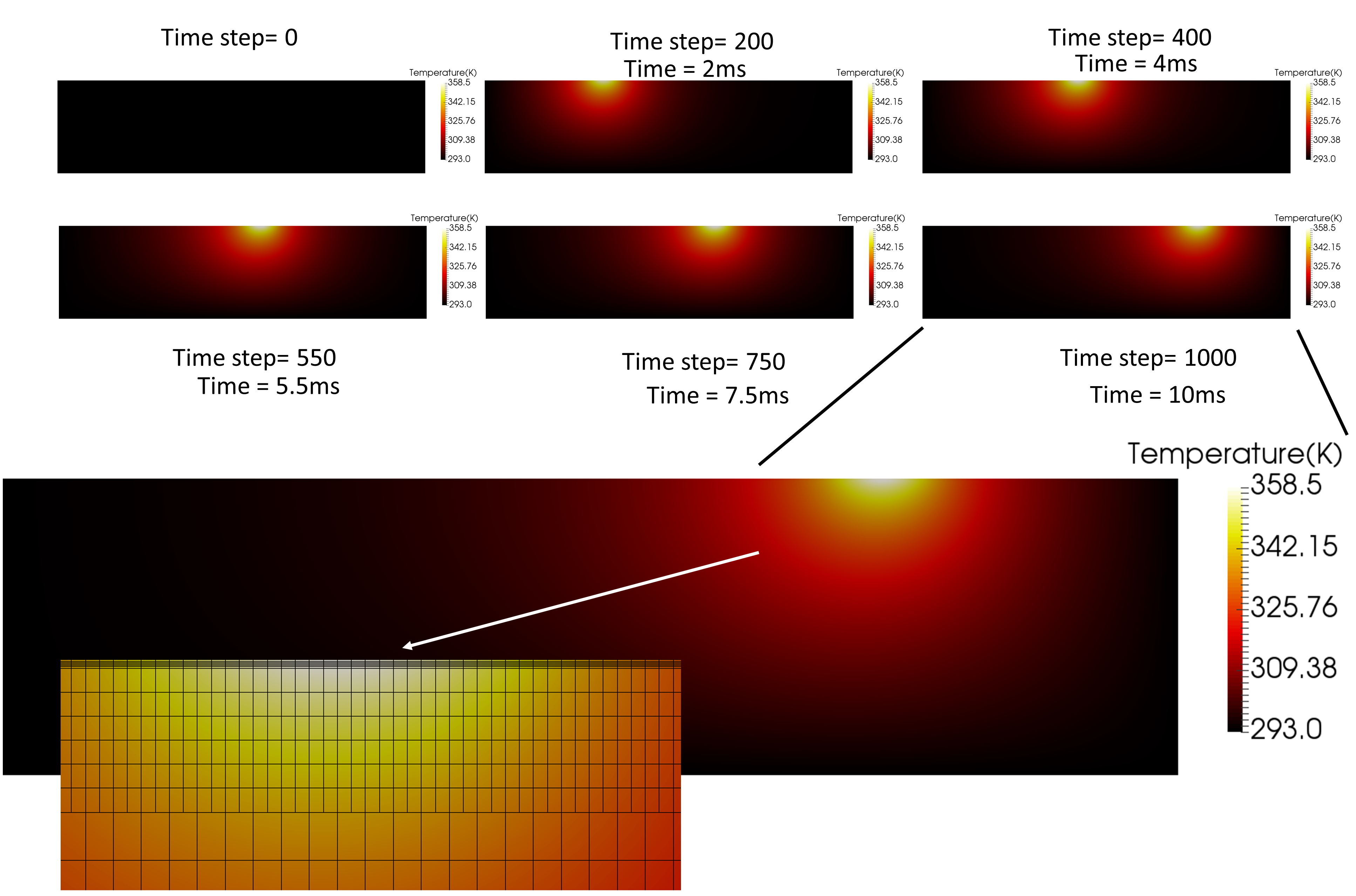
## Numerical results

# Discretization of the non-uniform isotropic heat equation
In general, the non-uniform isotropic heat equation is as following
@f{align*}
\rho C_m \frac{\partial T}{\partial t} -\nabla \cdot (k\nabla T) = f(\textbf{x})
@f}
Now, we discretize the equation in time with the theta-scheme as
@f{align*}
\rho C_m \frac{T^{n} - T^{n-1}}{dt} - [(1-\theta) \nabla \cdot (k \nabla T^{n-1}) + \theta \nabla \cdot (k \nabla T^n)] = (1-\theta) f^{n-1}(\textbf{x}) + \theta f^n(\textbf{x})
@f}
where $\theta$ is a parameter; if $\theta = 0 (\text{or} = 1)$, it becomes forward (backward) explicit Euler method; the Crank-Nicolson method is when $\theta = 0.5$. Integrating by the test function $T^{'}$ and do integration by parts
@f{align*}
\int T^{'} \nabla \cdot (k \nabla T) dV = T^{'} k \nabla T |^a_b - \int k \nabla T \cdot \nabla T^{'} dV
@f}
since the test function is time invariant (because the grid is not changed), we have $T^{'n}$ = $T^{'n-1}$.
@f{align*}
T &= \sum{_i} {u_i} T^{'}_{i} \\
\int T T^{'}_{i} dV &= u_{i}
@f}
\noindent let
@f{align*}
M &= \int \rho C_m T^{'_i} T^{'_j} dV \\
A & = \int k \nabla T^{'_i} \cdot \nabla T^{'_j} dV \\
F^n & = \int T' f^{n}(\textbf{x})
@f}
we have the following term,
@f{align*}
\int T^{'} \rho C_m [T^{n} - T^{n-1}] - dt \int T^{'} [(1-\theta) \nabla \cdot (k \nabla T^{n-1}) + \theta \nabla \cdot (k \nabla T^n)] \\ = dt \int T^{'} (1-\theta) f^{n-1}(\textbf{x}) + dt \int T^{'} \theta f^n(\textbf{x})
@f}
@f{align*}
M U^n - M U^{n-1} - dt \int T^{'} [(1-\theta) \nabla \cdot (k \nabla T^{n-1}) + \theta \nabla \cdot (k \nabla T^n)] \\ = dt \int T^{'} (1-\theta) f^{n-1}(\textbf{x}) + dt \int T^{'} \theta f^n(\textbf{x})
@f}
@f{align*}
M U^n - M U^{n-1} + dt [(1-\theta) A U^{n-1} + \theta A U^n] \\ = dt (1-\theta) F^{n-1} + dt \theta F^{n}
@f}
the final equation becomes
@f{align*}
(M + dt \theta A) U^n = [M - dt (1-\theta) A] U^{n-1} + dt (1-\theta) F^{n-1} + dt \theta F^{n}
@f}
# Initial temperature
The initial temperature can be interpolated over each vertex as follows,
@f{align*}
M_0 &= \int T^{'_i} T^{'_j} dV \\
T_0 &= \sum_i u_i T^{'i} = g_0(x) \\
M_0 U &= \int g_0(\textbf{x}) T^{'i} dV
@f}
which is robust for general use. In fact, Deal.II provides a function (VectorTools::interpolate) doing the same thing, which is, however, may not necessary work for parallel version.
## Mesh

## Results
To simplify the question, the heat equation is solved in two-dimensions (x-y) by assuming that the z-axis is homogeneous. Following is part of the running results in 4-threads:
Solving problem in 2 space dimensions.
Number of active cells: 6567
Total number of cells: 6567
Number of degrees of freedom: 11185
9 CG iterations needed to obtain convergence.
initial convergence value = nan
final convergence value = 2.31623e-20
Time step 1 at t=1e-05 time_step = 1e-05
80 CG iterations needed to obtain convergence.
initial convergence value = nan
final convergence value = 1.66925e-13
+------------------------------------------+------------+------+
| Total wallclock time elapsed since start | 2.98s | |
| | | | |
| Section | no. calls | wall time| % |
+------------------------------+-----------+------------+------+
| assemble_rhs_T() | 1 | 0.107s | 3.6% |
| assemble_system_matrix_init() | 1 | 0.245s | 8.2% |
| make_grid() | 1 | 1.11s | 37% |
| refine_mesh_at_beginning | 1 | 0.652s | 22% |
| setup_system() | 1 | 0.276s | 9.3% |
| solve_T() | 2 | 0.426s | 14% |
+-------------------------------+-----------+-----------+------+
Time step 2 at t=2e-05 time_step = 1e-05
79 CG iterations needed to obtain convergence.
initial convergence value = nan
final convergence value = 2.06942e-13
+------------------------------------------+------------+------+
| Total wallclock time elapsed since start | 0.293s | |
| | | |
| Section | no. calls | wall time | % |
+---------------------------------+--------+------------+------+
| assemble_rhs_T() | 1 | 0.0969s | 33% |
| solve_T() | 1 | 0.161s | 55% |
+------------------------------+-----------+------------+------+
Time step 3 at t=3e-05 time_step = 1e-05
80 CG iterations needed to obtain convergence.
initial convergence value = nan
final convergence value = 1.71207e-13
## Temperature distribution
## 8-threads
The colors stand for different cores.
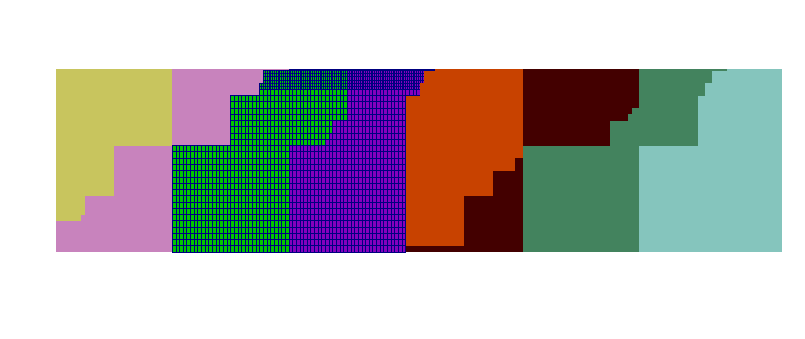
# References
@article{ma2021numerical,
title={Numerical study of laser micro-and nano-processing of nanocomposite porous materials},
author={Ma, Hongfeng},
journal={arXiv preprint arXiv:2103.07334},
year={2021}
}
@article{ma2019laser,
title={Laser-generated ag nanoparticles in mesoporous tio2 films: Formation processes and modeling-based size prediction},
author={Ma, Hongfeng and Bakhti, Said and Rudenko, Anton and Vocanson, Francis and Slaughter, Daniel S and Destouches, Nathalie and Itina, Tatiana E},
journal={The Journal of Physical Chemistry C},
volume={123},
number={42},
pages={25898--25907},
year={2019},
publisher={ACS Publications}
}
@article{dealII93,
title = {The \texttt{deal.II} Library, Version 9.3},
author = {Daniel Arndt and Wolfgang Bangerth and Bruno Blais and
Marc Fehling and Rene Gassm{\"o}ller and Timo Heister
and Luca Heltai and Uwe K{\"o}cher and Martin
Kronbichler and Matthias Maier and Peter Munch and
Jean-Paul Pelteret and Sebastian Proell and Konrad
Simon and Bruno Turcksin and David Wells and Jiaqi
Zhang},
journal = {Journal of Numerical Mathematics},
year = {2021, accepted for publication},
url = {https://dealii.org/deal93-preprint.pdf}
}
@inproceedings{crank1947practical,
title={A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type},
author={Crank, John and Nicolson, Phyllis},
booktitle={Mathematical Proceedings of the Cambridge Philosophical Society},
volume={43},
number={1},
pages={50--67},
year={1947},
organization={Cambridge University Press}
}