 |
Reference documentation for deal.II version 9.6.0
|
 |
Reference documentation for deal.II version 9.6.0
|
This tutorial depends on step-8, step-22, step-27.
| Table of contents | |
|---|---|
This program was contributed by Wolfgang Bangerth.
This material is based upon work partly supported by the National Science Foundation under Award No. EAR-0949446 and The University of California – Davis. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the author and do not necessarily reflect the views of the National Science Foundation or of The University of California – Davis.
This program deals with the problem of coupling different physics in different parts of the domain. Specifically, let us consider the following situation that couples a Stokes fluid with an elastic solid (these two problems were previously discussed separately in step-22 and step-8, where you may want to read up on the individual equations):
\begin{align*} -2\eta\nabla \cdot \varepsilon(\mathbf v) + \nabla p &= 0, \qquad \qquad && \text{in}\ \Omega_f\\ -\nabla \cdot \mathbf v &= 0 && \text{in}\ \Omega_f. \end{align*}
Here, \(\mathbf v, p\) are the fluid velocity and pressure, respectively. We prescribe the velocity on part of the external boundary,\begin{align*} \mathbf v = \mathbf v_0 \qquad\qquad \text{on}\ \Gamma_{f,1} \subset \partial\Omega \cap \partial\Omega_f \end{align*}
while we assume free-flow conditions on the remainder of the external boundary,\begin{align*} (2\eta \varepsilon(\mathbf v) - p \mathbf 1) \cdot \mathbf n = 0 \qquad\qquad \text{on}\ \Gamma_{f,2} = \partial\Omega \cap \partial\Omega_f \backslash \Gamma_{f,1}. \end{align*}
\begin{align*} -\nabla \cdot C \varepsilon(\mathbf u) = 0 \qquad\qquad & \text{in}\ \Omega_s, \end{align*}
where \(C\) is the rank-4 elasticity tensor (for which we will use a particularly simple form by assuming that the solid is isotropic). It deforms in reaction to the forces exerted by the fluid flowing along the boundary of the solid. We assume this deformation to be so small that it has no feedback effect on the fluid, i.e. the coupling is only in one direction. For simplicity, we will assume that the solid's external boundary is clamped, i.e.\begin{align*} \mathbf u = \mathbf 0 \qquad\qquad \text{on}\ \Gamma_{s,1} = \partial\Omega \cap \partial\Omega_s \end{align*}
\begin{align*} \mathbf v = \mathbf 0 \qquad\qquad \text{on}\ \Gamma_{i} = \partial\Omega_s \cap \partial\Omega_f. \end{align*}
Secondly, the forces (traction) on the solid equal the normal stress from the fluid,\begin{align*} (C \varepsilon(\mathbf u)) \mathbf n = (2 \eta \varepsilon(\mathbf v) - p \mathbf 1) \mathbf n \qquad\qquad \text{on}\ \Gamma_{i} = \partial\Omega_s \cap \partial\Omega_f, \end{align*}
where \(\mathbf{n}\) is the normal vector on \(\Gamma_{i}\) pointing from the solid to the fluid.We get a weak formulation of this problem by following our usual rule of multiplying from the left by a test function and integrating over the domain. It then looks like this: Find \(y = \{\mathbf v, p, \mathbf u\} \in Y \subset H^1(\Omega_f)^d \times L_2(\Omega_f) \times H^1(\Omega_s)^d\) such that
\begin{align*} 2 \eta (\varepsilon(\mathbf a), \varepsilon(\mathbf v))_{\Omega_f} - (\nabla \cdot \mathbf a, p)_{\Omega_f} - (q, \nabla \cdot \mathbf v)_{\Omega_f} & \\ + (\varepsilon(\mathbf b), C \varepsilon(\mathbf u))_{\Omega_s} & \\ - (\mathbf b, (2 \eta \varepsilon(\mathbf v) - p \mathbf 1) \mathbf n)_{\Gamma_i} &= 0, \end{align*}
for all test functions \(\mathbf a, q, \mathbf b\); the first, second, and third lines correspond to the fluid, solid, and interface contributions, respectively. Note that \(Y\) is only a subspace of the spaces listed above to accommodate for the various Dirichlet boundary conditions.
This sort of coupling is of course possible by simply having two Triangulation and two DoFHandler objects, one each for each of the two subdomains. On the other hand, deal.II is much simpler to use if there is a single DoFHandler object that knows about the discretization of the entire problem.
This program is about how this can be achieved. Note that the goal is not to present a particularly useful physical model (a realistic fluid-structure interaction model would have to take into account the finite deformation of the solid and the effect this has on the fluid): this is, after all, just a tutorial program intended to demonstrate techniques, not to solve actual problems. Furthermore, we will make the assumption that the interface between the subdomains is aligned with coarse mesh cell faces.
Before going into more details let us state the obvious: this is a problem with multiple solution variables; for this, you will probably want to read the Handling vector valued problems documentation topic first, which presents the basic philosophical framework in which we address problems with more than one solution variable. But back to the problem at hand:
The fundamental idea to implement these sort of problems in deal.II goes as follows: in the problem formulation, the velocity and pressure variables \(\mathbf v, p\) only live in the fluid subdomain \(\Omega_f\). But let's assume that we extend them by zero to the entire domain \(\Omega\) (in the general case this means that they will be discontinuous along \(\Gamma_i\)). So what is the appropriate function space for these variables? We know that on \(\Omega_f\) we should require \(\mathbf v \in H^1(\Omega_f)^d, p \in L_2(\Omega_f)\), so for the extensions \(\tilde{\mathbf v}, \tilde p\) to the whole domain the following appears a useful set of function spaces:
\begin{align*} \tilde {\mathbf v} &\in V = \{\tilde {\mathbf v}|_{\Omega_f} \in H^1(\Omega_f)^d, \quad \tilde {\mathbf v}|_{\Omega_s} = 0 \} \\ \tilde p &\in P = \{\tilde p|_{\Omega_f} \in L_2(\Omega_f), \quad \tilde p|_{\Omega_s} = 0 \}. \end{align*}
(Since this is not important for the current discussion, we have omitted the question of boundary values from the choice of function spaces; this question also affects whether we can choose \(L_2\) for the pressure or whether we have to choose the space \(L_{2,0}(\Omega_f)=\{q\in L_2(\Omega_f): \int_{\Omega_f} q = 0\}\) for the pressure. None of these questions are relevant to the following discussion, however.)
Note that these are indeed a linear function spaces with obvious norm. Since no confusion is possible in practice, we will henceforth omit the tilde again to denote the extension of a function to the whole domain and simply refer by \(\mathbf v, p\) to both the original and the extended function.
For discretization, we need finite dimensional subspaces \(V_h,P_h\) of \(V, P\). For Stokes, we know from step-22 that an appropriate choice is \(Q_{p+1}^d\times Q_P\) but this only holds for that part of the domain occupied by the fluid. For the extended field, let's use the following subspaces defined on the triangulation \(\mathbb T\):
\begin{align*} V_h &= \{{\mathbf v}_h \quad | \quad \forall K \in {\mathbb T}: {\mathbf v}_h|_K \in Q_{p+1}^d\ \text{if}\ K\subset {\Omega_f}, \quad {\mathbf v}_h|_{\Omega_f}\ \text{is continuous}, \quad {\mathbf v}_h|_K = 0\ \text{if}\ K\subset {\Omega_s}\} && \subset V \\ P_h &= \{ p_h \quad | \quad \forall K \in {\mathbb T}: p_h|_K \in Q_p\ \text{if}\ K\subset {\Omega_f}, \quad p_h|_{\Omega_f}\ \text{is continuous}, \quad p_h|_K = 0\ \text{if}\ K\subset {\Omega_s}\ \} && \subset P. \end{align*}
In other words, on \(\Omega_f\) we choose the usual discrete spaces but we keep the (discontinuous) extension by zero. The point to make is that we now need a description of a finite element space for functions that are zero on a cell — and this is where the FE_Nothing class comes in: it describes a finite dimensional function space of functions that are constant zero. A particular property of this peculiar linear vector space is that it has no degrees of freedom: it isn't just finite dimensional, it is in fact zero dimensional, and consequently for objects of this type, FiniteElement::n_dofs_per_cell() will return zero. For discussion below, let us give this space a proper symbol:
\[ Z = \{ \varphi: \varphi(x)=0 \}. \]
The symbol \(Z\) reminds of the fact that functions in this space are zero. Obviously, we choose \(Z_h=Z\).
This entire discussion above can be repeated for the variables we use to describe the elasticity equation. Here, for the extended variables, we have
\begin{align*} \tilde {\mathbf u} &\in U = \{\tilde {\mathbf u}|_{\Omega_s} \in H^1(\Omega_f)^d, \quad \tilde {\mathbf u}|_{\Omega_f} \in Z(\Omega_s)^d \}, \end{align*}
and we will typically use a finite element space of the kind
\begin{align*} U_h &= \{{\mathbf u}_h \quad | \quad \forall K \in {\mathbb T}: {\mathbf u}_h|_K \in Q_r^d\ \text{if}\ K\subset {\Omega_s}, \quad {\mathbf u}_h|_{\Omega_f}\ \text{is continuous}, \quad {\mathbf u}_h|_K \in Z^d\ \text{if}\ K\subset {\Omega_f}\} && \subset U \end{align*}
of polynomial degree \(r\).
So to sum up, we are going to look for a discrete vector-valued solution \(y_h = \{\mathbf v_h, p_h, \mathbf u_h\}\) in the following space:
\begin{align*} Y_h = \{ & y_h = \{\mathbf v_h, p_h, \mathbf u_h\} : \\ & y_h|_{\Omega_f} \in Q_{p+1}^d \times Q_p \times Z^d, \\ & y_h|_{\Omega_s} \in Z^d \times Z \times Q_r^d \}. \end{align*}
So how do we implement this sort of thing? First, we realize that the discrete space \(Y_h\) essentially calls for two different finite elements: First, on the fluid subdomain, we need the element \(Q_{p+1}^d \times Q_p \times Z^d\) which in deal.II is readily implemented by
where FE_Nothing implements the space of functions that are always zero. Second, on the solid subdomain, we need the element \(\in Z^d \times Z \times Q_r^d\), which we get using
The next step is that we associate each of these two elements with the cells that occupy each of the two subdomains. For this we realize that in a sense the two elements are just variations of each other in that they have the same number of vector components but have different polynomial degrees — this smells very much like what one would do in \(hp\) finite element methods, and it is exactly what we are going to do here: we are going to (ab)use the classes and facilities of the hp-namespace to assign different elements to different cells. In other words, we will use collect the two finite elements in an hp::FECollection, will integrate with an appropriate hp::QCollection using an hp::FEValues object, and our DoFHandler will be in hp-mode. You may wish to take a look at step-27 for an overview of all of these concepts.
Before going on describing the testcase, let us clarify a bit why this approach of extending the functions by zero to the entire domain and then mapping the problem on to the hp-framework makes sense:
2*dim+1). This makes all sorts of things possible since a uniform description allows for code re-use. For example, counting degrees of freedom per vector component (DoFTools::count_dofs_per_fe_component), sorting degrees of freedom by component (DoFRenumbering::component_wise), subsequent partitioning of matrices and vectors into blocks and many other functions work as they always did without the need to add special logic to them that describes cases where some of the variables only live on parts of the domain. Consequently, you have all sorts of tools already available to you in programs like the current one that weren't originally written for the multiphysics case but work just fine in the current context.More specifically, in the program we have to address the following points:
Let us first discuss implementing the bilinear form, which at the discrete level we recall to be
\begin{align*} 2 \eta (\varepsilon(\mathbf a_h), \varepsilon(\mathbf v_h))_{\Omega_f} - (\nabla \cdot \mathbf a_h, p_h)_{\Omega_f} - (q_h, \nabla \cdot \mathbf v_h)_{\Omega_f} & \\ + (\varepsilon(\mathbf b_h), C \varepsilon(\mathbf u_h))_{\Omega_s} & \\ - (\mathbf b_h, (2 \eta \varepsilon(\mathbf v_h) - p \mathbf 1) \mathbf n)_{\Gamma_i} &= 0, \end{align*}
Given that we have extended the fields by zero, we could in principle write the integrals over subdomains to the entire domain \(\Omega\), though it is little additional effort to first ask whether a cell is part of the elastic or fluid region before deciding which terms to integrate. Actually integrating these terms is not very difficult; for the Stokes equations, the relevant steps have been shown in step-22, whereas for the elasticity equation we take essentially the form shown in the Handling vector valued problems topic (rather than the one from step-8).
The term that is of more interest is the interface term,
\[ -(\mathbf b_h, (2 \eta \varepsilon(\mathbf v_h) - p \mathbf 1) \mathbf n)_{\Gamma_i}. \]
Based on our assumption that the interface \(\Gamma_i\) coincides with cell boundaries, this can in fact be written as a set of face integrals. If we denote the velocity, pressure and displacement components of shape function \(\psi_i\in Y_h\) using the extractor notation \(\psi_i[\mathbf v],\psi_i[p], \psi_i[\mathbf u]\), then the term above yields the following contribution to the global matrix entry \(i,j\):
\[ -\sum_K (\psi_i[\mathbf u], (2 \eta \varepsilon(\psi_j[\mathbf v]) - \psi_j[p] \mathbf 1) \mathbf n)_{\partial K \cap \Gamma_i}. \]
Although it isn't immediately obvious, this term presents a slight complication: while \(\psi_i[\mathbf u]\) and \(\mathbf n\) are evaluated on the solid side of the interface (they are test functions for the displacement and the normal vector to \(\Omega_s\), respectively, we need to evaluate \(\psi_j[\mathbf v],\psi_j[p]\) on the fluid side of the interface since they correspond to the stress/force exerted by the fluid. In other words, in our implementation, we will need FEFaceValue objects for both sides of the interface. To make things slightly worse, we may also have to deal with the fact that one side or the other may be refined, leaving us with the need to integrate over parts of a face. Take a look at the implementation below on how to deal with this.
As an additional complication, the matrix entries that result from this term need to be added to the sparsity pattern of the matrix somehow. This is the realm of various functions in the DoFTools namespace like DoFTools::make_sparsity_pattern and DoFTools::make_flux_sparsity_pattern. Essentially, what these functions do is simulate what happens during assembly of the system matrix: whenever assembly would write a nonzero entry into the global matrix, the functions in DoFTools would add an entry to the sparsity pattern. We could therefore do the following: let DoFTools::make_sparsity_pattern add all those entries to the sparsity pattern that arise from the regular cell-by-cell integration, and then do the same by hand that arise from the interface terms. If you look at the implementation of the interface integrals in the program below, it should be obvious how to do that and would require no more than maybe 100 lines of code at most.
But we're lazy people: the interface term couples degrees of freedom from two adjacent cells along a face, which is exactly the kind of thing one would do in discontinuous Galerkin schemes for which the function DoFTools::make_flux_sparsity_pattern was written. This is a superset of matrix entries compared to the usual DoFTools::make_sparsity_pattern: it will also add all entries that result from computing terms coupling the degrees of freedom from both sides of all faces. Unfortunately, for the simplest version of this function, this is a pretty big superset. Consider for example the following mesh with two cells and a \(Q_1\) finite element:
Here, the sparsity pattern produced by DoFTools::make_sparsity_pattern will only have entries for degrees of freedom that couple on a cell. However, it will not have sparsity pattern entries \((0,4),(0,5),(2,4),(2,5)\). The sparsity pattern generated by DoFTools::make_flux_sparsity_pattern will have these entries, however: it assumes that you want to build a sparsity pattern for a bilinear form that couples all degrees of freedom from adjacent cells. This is not what we want: our interface term acts only on a small subset of cells, and we certainly don't need all the extra couplings between two adjacent fluid cells, or two adjacent solid cells. Furthermore, the fact that we use higher order elements means that we would really generate many many more entries than we actually need: on the coarsest mesh, in 2d, 44,207 nonzero entries instead of 16,635 for DoFTools::make_sparsity_pattern, leading to plenty of zeros in the matrix we later build (of course, the 16,635 are not enough since they don't include the interface entries). This ratio would be even worse in 3d.
So being extremely lazy comes with a cost: too many entries in the matrix. But we can get away with being moderately lazy: there is a variant of DoFTools::make_flux_sparsity_pattern that allows us to specify which vector components of the finite element couple with which other components, both in cell terms as well as in face terms. For cells that are in the solid subdomain, we couple all displacements with each other; for fluid cells, all velocities with all velocities and the pressure, but not the pressure with itself. Since no cell has both sets of variables, there is no need to distinguish between the two kinds of cells, so we can write the mask like this:
Here, we have used the fact that the first dim components of the finite element are the velocities, then the pressure, and then the dim displacements. (We could as well have stated that the velocities/pressure also couple with the displacements since no cell ever has both sets of variables.) On the other hand, the interface terms require a mask like this:
In other words, all displacement test functions (components c>=dim+1) couple with all velocity and pressure shape functions on the other side of an interface. This is not entirely true, though close: in fact, the exact form of the interface term only those pressure displacement shape functions that are indeed nonzero on the common interface, which is not true for all shape functions; on the other hand, it really couples all velocities (since the integral involves gradients of the velocity shape functions, which are all nonzero on all faces of the cell). However, the mask we build above, is not capable of these subtleties. Nevertheless, through these masks we manage to get the number of sparsity pattern entries down to 21,028 — good enough for now.
The second difficulty is that while we know how to enforce a zero velocity or stress on the external boundary (using VectorTools::interpolate_boundary_values, called with an appropriate component mask and setting different boundary indicators for solid and fluid external boundaries), we now also needed the velocity to be zero on the interior interface, i.e. \(\mathbf v|_{\Gamma_i}=0\). At the time of writing this, there is no function in deal.II that handles this part, but it isn't particularly difficult to implement by hand: essentially, we just have to loop over all cells, and if it is a fluid cell and its neighbor is a solid cell, then add constraints that ensure that the velocity degrees of freedom on this face are zero. Some care is necessary to deal with the case that the adjacent solid cell is refined, yielding the following code:
The last line adds the constraint xlocal_face_dof_indices[i]=0, which is exactly what we need in the current context. The call to FiniteElement::face_system_to_component_index() makes sure that we only set boundary values to zero for velocity but not pressure components.
Note that there are cases where this may yield incorrect results: notably, once we find a solid neighbor child to a current fluid cell, we assume that all neighbor children on the common face are in the solid subdomain. But that need not be so; consider, for example, the following mesh:
In this case, we would set all velocity degrees of freedom on the right face of the left cell to zero, which is incorrect for the top degree of freedom on that face. That said, that can only happen if the fluid and solid subdomains do not coincide with a set of complete coarse mesh cells — but this is a contradiction to the assumption stated at the end of the first section of this introduction.
We will consider the following situation as a testcase:
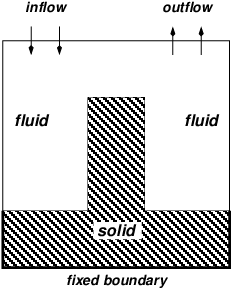
As discussed at the top of this document, we need to assume in a few places that a cell is either entirely in the fluid or solid part of the domain and, furthermore, that all children of an inactive cell also belong to the same subdomain. This can definitely be ensured if the coarse mesh already subdivides the mesh into solid and fluid coarse mesh cells; given the geometry outlined above, we can do that by using an \(8\times 8\) coarse mesh, conveniently provided by the GridGenerator::subdivided_hyper_rectangle function.
The fixed boundary at the bottom implies \(\mathbf u=0\), and we also prescribe Dirichlet conditions for the flow at the top so that we get inflow at the left and outflow at the right. At the left and right boundaries, no boundary conditions are imposed explicitly for the flow, yielding the implicit no-stress condition \((2\eta \varepsilon(\mathbf v) - p \mathbf 1) \cdot \mathbf n = 0\). The conditions on the interface between the two domains has already been discussed above.
For simplicity, we choose the material parameters to be \(\eta=\lambda=\mu=1\). In the results section below, we will also show a 3d simulation that can be obtained from the same program. The boundary conditions and geometry are defined nearly analogously to the 2d situation above.
In the program, we need a way to identify which part of the domain a cell is in. There are many different ways of doing this. A typical way would be to use the subdomain_id tag available with each cell, though this field has a special meaning in parallel computations. An alternative is the material_id field also available with every cell. It has the additional advantage that it is inherited from the mother to the child cell upon mesh refinement; in other words, we would set the material id once upon creating the mesh and it will be correct for all active cells even after several refinement cycles. We therefore go with this alternative: we define an enum with symbolic names for material_id numbers and will use them to identify which part of the domain a cell is on.
Secondly, we use an object of type DoFHandler operating in hp-mode. This class needs to know which cells will use the Stokes and which the elasticity finite element. At the beginning of each refinement cycle we will therefore have to walk over all cells and set the (in hp-parlance) active FE index to whatever is appropriate in the current situation. While we can use symbolic names for the material id, the active FE index is in fact a number that will frequently be used to index into collections of objects (e.g. of type hp::FECollection and hp::QCollection); that means that the active FE index actually has to have value zero for the fluid and one for the elastic part of the domain.
This program is primarily intended to show how to deal with different physics in different parts of the domain, and how to implement such models in deal.II. As a consequence, we won't bother coming up with a good solver: we'll just use the SparseDirectUMFPACK class which always works, even if not with optimal complexity. We will, however, comment on possible other solvers in the results section.
One of the trickier aspects of this program is how to estimate the error. Because it works on almost any program, we'd like to use the KellyErrorEstimator, and we can relatively easily do that here as well using code like the following:
This gives us two sets of error indicators for each cell. We would then somehow combine them into one for mesh refinement, for example using something like the following (note that we normalize the squared error indicator in the two vectors because error quantities have physical units that do not match in the current situation, leading to error indicators that may differ by orders of magnitude between the two subdomains):
(In the code, we actually weigh the error indicators 4:1 in favor of the ones computed on the Stokes subdomain since refinement is otherwise heavily biased towards the elastic subdomain, but this is just a technicality. The factor 4 has been determined heuristically to work reasonably well.)
While this principle is sound, it doesn't quite work as expected. The reason is that the KellyErrorEstimator class computes error indicators by integrating the jump in the solution's gradient around the faces of each cell. This jump is likely to be very large at the locations where the solution is discontinuous and extended by zero; it also doesn't become smaller as the mesh is refined. The KellyErrorEstimator class can't just ignore the interface because it essentially only sees a DoFHandler in hp-mode where the element type changes from one cell to another — precisely the thing that the hp-mode was designed for, the interface in the current program looks no different than the interfaces in step-27, for example, and certainly no less legitimate. Be that as it may, the end results is that there is a layer of cells on both sides of the interface between the two subdomains where error indicators are irrationally large. Consequently, most of the mesh refinement is focused on the interface.
This clearly wouldn't happen if we had a refinement indicator that actually understood something about the problem and simply ignore the interface between subdomains when integrating jump terms. On the other hand, this program is about showing how to represent problems where we have different physics in different subdomains, not about the peculiarities of the KellyErrorEstimator, and so we resort to the big hammer called "heuristics": we simply set the error indicators of cells at the interface to zero. This cuts off the spikes in the error indicators. At first sight one would also think that it prevents the mesh from being refined at the interface, but the requirement that neighboring cells may only differ by one level of refinement will still lead to a reasonably refined mesh.
While this is clearly a suboptimal solution, it works for now and leaves room for future improvement.
The include files for this program are the same as for many others before. The only new one is the one that declares FE_Nothing as discussed in the introduction. The ones in the hp directory have already been discussed in step-27.
FluidStructureProblem class templateThis is the main class. It is, if you want, a combination of step-8 and step-22 in that it has member variables that either address the global problem (the Triangulation and DoFHandler objects, as well as the hp::FECollection and various linear algebra objects) or that pertain to either the elasticity or Stokes sub-problems. The general structure of the class, however, is like that of most of the other programs implementing stationary problems.
There are a few helper functions (cell_is_in_fluid_domain, cell_is_in_solid_domain) of self-explanatory nature (operating on the symbolic names for the two subdomains that will be used as material_ids for cells belonging to the subdomains, as explained in the introduction) and a few functions (make_grid, set_active_fe_indices, assemble_interface_terms) that have been broken out of other functions that can be found in many of the other tutorial programs and that will be discussed as we get to their implementation.
The final set of variables (viscosity, lambda, eta) describes the material properties used for the two physics models.
The following class does as its name suggests. The boundary values for the velocity are \(\mathbf u=(0, \sin(\pi x))^T\) in 2d and \(\mathbf u=(0, 0, \sin(\pi x)\sin(\pi y))^T\) in 3d, respectively. The remaining boundary conditions for this problem are all homogeneous and have been discussed in the introduction. The right hand side forcing term is zero for both the fluid and the solid so we don't need an extra class for it.
FluidStructureProblem implementationLet's now get to the implementation of the primary class of this program. The first few functions are the constructor and the helper functions that can be used to determine which part of the domain a cell is in. Given the discussion of these topics in the introduction, their implementation is rather obvious. In the constructor, note that we have to construct the hp::FECollection object from the base elements for Stokes and elasticity; using the hp::FECollection::push_back function assigns them spots zero and one in this collection, an order that we have to remember and use consistently in the rest of the program.
The next pair of functions deals with generating a mesh and making sure all flags that denote subdomains are correct. make_grid, as discussed in the introduction, generates an \(8\times 8\) mesh (or an \(8\times 8\times 8\) mesh in 3d) to make sure that each coarse mesh cell is completely within one of the subdomains. After generating this mesh, we loop over its boundary and set the boundary indicator to one at the top boundary, the only place where we set nonzero Dirichlet boundary conditions. After this, we loop again over all cells to set the material indicator — used to denote which part of the domain we are in, to either the fluid or solid indicator.
The second part of this pair of functions determines which finite element to use on each cell. Above we have set the material indicator for each coarse mesh cell, and as mentioned in the introduction, this information is inherited from mother to child cell upon mesh refinement.
In other words, whenever we have refined (or created) the mesh, we can rely on the material indicators to be a correct description of which part of the domain a cell is in. We then use this to set the active FE index of the cell to the corresponding element of the hp::FECollection member variable of this class: zero for fluid cells, one for solid cells.
FluidStructureProblem::setup_dofsThe next step is to set up the data structures for the linear system. To this end, we first have to set the active FE indices with the function immediately above, then distribute degrees of freedom, and then determine constraints on the linear system. The latter includes hanging node constraints as usual, but also the inhomogeneous boundary values at the top fluid boundary, and zero boundary values along the perimeter of the solid subdomain.
There are more constraints we have to handle, though: we have to make sure that the velocity is zero at the interface between fluid and solid. The following piece of code was already presented in the introduction:
At the end of all this, we can declare to the constraints object that we now have all constraints ready to go and that the object can rebuild its internal data structures for better efficiency:
In the rest of this function we create a sparsity pattern as discussed extensively in the introduction, and use it to initialize the matrix; then also set vectors to their correct sizes:
FluidStructureProblem::assemble_systemFollowing is the central function of this program: the one that assembles the linear system. It has a long section of setting up auxiliary functions at the beginning: from creating the quadrature formulas and setting up the FEValues, FEFaceValues and FESubfaceValues objects necessary to integrate the cell terms as well as the interface terms for the case where cells along the interface come together at same size or with differing levels of refinement...
...to objects that are needed to describe the local contributions to the global linear system...
...to variables that allow us to extract certain components of the shape functions and cache their values rather than having to recompute them at every quadrature point:
Then comes the main loop over all cells and, as in step-27, the initialization of the hp::FEValues object for the current cell and the extraction of a FEValues object that is appropriate for the current cell:
With all of this done, we continue to assemble the cell terms for cells that are part of the Stokes and elastic regions. While we could in principle do this in one formula, in effect implementing the one bilinear form stated in the introduction, we realize that our finite element spaces are chosen in such a way that on each cell, one set of variables (either velocities and pressure, or displacements) are always zero, and consequently a more efficient way of computing local integrals is to do only what's necessary based on an if clause that tests which part of the domain we are in.
The actual computation of the local matrix is the same as in step-22 as well as that given in the Handling vector valued problems documentation topic for the elasticity equations:
Once we have the contributions from cell integrals, we copy them into the global matrix (taking care of constraints right away, through the AffineConstraints::distribute_local_to_global function). Note that we have not written anything into the local_rhs variable, though we still need to pass it along since the elimination of nonzero boundary values requires the modification of local and consequently also global right hand side values:
The more interesting part of this function is where we see about face terms along the interface between the two subdomains. To this end, we first have to make sure that we only assemble them once even though a loop over all faces of all cells would encounter each part of the interface twice. We arbitrarily make the decision that we will only evaluate interface terms if the current cell is part of the solid subdomain and if, consequently, a face is not at the boundary and the potential neighbor behind it is part of the fluid domain. Let's start with these conditions:
At this point we know that the current cell is a candidate for integration and that a neighbor behind face f exists. There are now three possibilities:
In all three cases, we are only interested in it if it is part of the fluid subdomain. So let us start with the first and simplest case: if the neighbor is at the same level, has no children, and is a fluid cell, then the two cells share a boundary that is part of the interface along which we want to integrate interface terms. All we have to do is initialize two FEFaceValues object with the current face and the face of the neighboring cell (note how we find out which face of the neighboring cell borders on the current cell) and pass things off to the function that evaluates the interface terms (the third through fifth arguments to this function provide it with scratch arrays). The result is then again copied into the global matrix, using a function that knows that the DoF indices of rows and columns of the local matrix result from different cells:
The second case is if the neighbor has further children. In that case, we have to loop over all the children of the neighbor to see if they are part of the fluid subdomain. If they are, then we integrate over the common interface, which is a face for the neighbor and a subface of the current cell, requiring us to use an FEFaceValues for the neighbor and an FESubfaceValues for the current cell:
The last option is that the neighbor is coarser. In that case we have to use an FESubfaceValues object for the neighbor and a FEFaceValues for the current cell; the rest is the same as before:
In the function that assembles the global system, we passed computing interface terms to a separate function we discuss here. The key is that even though we can't predict the combination of FEFaceValues and FESubfaceValues objects, they are both derived from the FEFaceValuesBase class and consequently we don't have to care: the function is simply called with two such objects denoting the values of the shape functions on the quadrature points of the two sides of the face. We then do what we always do: we fill the scratch arrays with the values of shape functions and their derivatives, and then loop over all entries of the matrix to compute the local integrals. The details of the bilinear form we evaluate here are given in the introduction.
FluidStructureProblem::solveAs discussed in the introduction, we use a rather trivial solver here: we just pass the linear system off to the SparseDirectUMFPACK direct solver (see, for example, step-29). The only thing we have to do after solving is ensure that hanging node and boundary value constraints are correct.
FluidStructureProblem::output_resultsGenerating graphical output is rather trivial here: all we have to do is identify which components of the solution vector belong to scalars and/or vectors (see, for example, step-22 for a previous example), and then pass it all on to the DataOut class:
FluidStructureProblem::refine_meshThe next step is to refine the mesh. As was discussed in the introduction, this is a bit tricky primarily because the fluid and the solid subdomains use variables that have different physical dimensions and for which the absolute magnitude of error estimates is consequently not directly comparable. We will therefore have to scale them. At the top of the function, we therefore first compute error estimates for the different variables separately (using the velocities but not the pressure for the fluid domain, and the displacements in the solid domain):
We then normalize error estimates by dividing by their norm and scale the fluid error indicators by a factor of 4 as discussed in the introduction. The results are then added together into a vector that contains error indicators for all cells:
The second to last part of the function, before actually refining the mesh, involves a heuristic that we have already mentioned in the introduction: because the solution is discontinuous, the KellyErrorEstimator class gets all confused about cells that sit at the boundary between subdomains: it believes that the error is large there because the jump in the gradient is large, even though this is entirely expected and a feature that is in fact present in the exact solution as well and therefore not indicative of any numerical error.
Consequently, we set the error indicators to zero for all cells at the interface; the conditions determining which cells this affects are slightly awkward because we have to account for the possibility of adaptively refined meshes, meaning that the neighboring cell can be coarser than the current one, or could in fact be refined some more. The structure of these nested conditions is much the same as we encountered when assembling interface terms in assemble_system.
FluidStructureProblem::runThis is, as usual, the function that controls the overall flow of operation. If you've read through tutorial programs step-1 through step-6, for example, then you are already quite familiar with the following structure:
main() functionThis, final, function contains pretty much exactly what most of the other tutorial programs have:
When running the program, you should get output like the following:
The results are easily visualized:
Magnitude and vectors for the fluid velocity. |
Fluid pressure. The dynamic range has been truncated to cut off the pressure singularities at the top left and right corners of the domain as well as the top corners of the solid that forms re-entrant corners into the fluid domain. |
Magnitude and vectors for the solid displacement. |
The plots are easily interpreted: as the flow drives down on the left side and up on the right side of the upright part of the solid, it produces a pressure that is high on the left and low on the right, and these forces bend the vertical part of the solid to the right.
By changing the dimension of the FluidStructureProblem class in main() to 3, we can also run the same problem 3d. You'd get output along the following lines:
You'll notice that the big bottleneck is the solver: SparseDirectUmfpack needs nearly 5 hours and some 80 GB of memory to solve the last iteration of this problem on a 2016 workstation (the second to last iteration took only 16 minutes). Clearly a better solver is needed here, a topic discussed below.
The results can also be visualized and yield good pictures as well. Here is one, showing both a vector plot for the velocity (in oranges), the solid displacement (in blues), and shading the solid region:
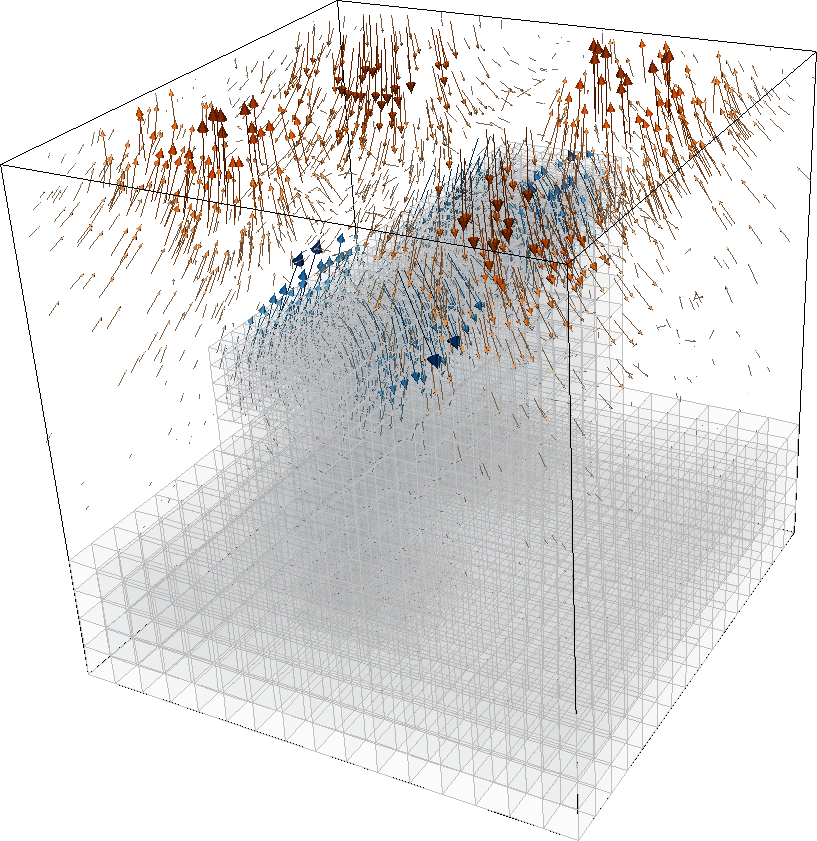
In addition to the lack of a good solver, the mesh is a bit unbalanced: mesh refinement heavily favors the fluid subdomain (in 2d, it was the other way around, prompting us to weigh the fluid error indicators higher). Clearly, some tweaking of the relative importance of error indicators in the two subdomains is important if one wanted to go on doing more 3d computations.
An obvious place to improve the program would be to use a more sophisticated solver — in particular one that scales well and will also work for realistic 3d problems. This shouldn't actually be too hard to achieve here, because of the one-way coupling from fluid into solid. To this end, assume we had re-ordered degrees of freedom in such a way that we first have all velocity and pressure degrees of freedom, and then all displacements (this is easily possible using DoFRenumbering::component_wise). Then the system matrix could be split into the following block form:
\[ A_\text{global} = \begin{pmatrix} A_{\text{fluid}} & 0 \\ B & A_{\text{solid}} \end{pmatrix} \]
where \(A_{\text{fluid}}\) is the Stokes matrix for velocity and pressure (it could be further subdivided into a \(2\times 2\) matrix as in step-22, though this is immaterial for the current purpose), \(A_{\text{solid}}\) results from the elasticity equations for the displacements, and \(B\) is the matrix that comes from the interface conditions. Now notice that the matrix
\[ A_\text{global}^{-1} = \begin{pmatrix} A_{\text{fluid}}^{-1} & 0 \\ -A_\text{solid}^{-1} B A_\text{fluid}^{-1} & A_{\text{solid}}^{-1} \end{pmatrix} \]
is the inverse of \(A_\text{global}\). Applying this matrix requires only one solve with \(A_\text{fluid}\) and \(A_\text{solid}\) each since
\[ \begin{pmatrix} p_x \\ p_y \end{pmatrix} = \begin{pmatrix} A_{\text{fluid}}^{-1} & 0 \\ -A_\text{solid}^{-1} B A_\text{fluid}^{-1} & A_{\text{solid}}^{-1} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \]
can be computed as \(p_x = A_{\text{fluid}}^{-1} x\) followed by \(p_y = A_{\text{solid}}^{-1} (y-Bp_x)\).
One can therefore expect that
\[ \widetilde{A_\text{global}^{-1}} = \begin{pmatrix} \widetilde{A_{\text{fluid}}^{-1}} & 0 \\ -\widetilde{A_\text{solid}^{-1}} B \widetilde{A_\text{fluid}^{-1}} & \widetilde{A_{\text{solid}}^{-1}} \end{pmatrix} \]
would be a good preconditioner if \(\widetilde{A_{\text{fluid}}^{-1}} \approx A_{\text{fluid}}^{-1}, \widetilde{A_{\text{solid}}^{-1}} \approx A_{\text{solid}}^{-1}\).
That means, we only need good preconditioners for Stokes and the elasticity equations separately. These are well known: for Stokes, we can use the preconditioner discussed in the results section of step-22; for elasticity, a good preconditioner would be a single V-cycle of a geometric or algebraic multigrid. There are more open questions, however: For an "optimized" solver block-triangular preconditioner built from two sub-preconditioners, one point that often comes up is that, when choosing parameters for the sub-preconditioners, values that work well when solving the two problems separately may not be optimal when combined into a multiphysics preconditioner. In particular, when solving just a solid or fluid mechanics problem separately, the balancing act between the number of iterations to convergence and the cost of applying the preconditioner on a per iteration basis may lead one to choose an expensive preconditioner for the Stokes problem and a cheap preconditioner for the elasticity problem (or vice versa). When combined, however, there is the additional constraint that you want the two sub-preconditioners to converge at roughly the same rate, or else the cheap one may drive up the global number of iterations while the expensive one drives up the cost-per-iteration. For example, while a single AMG V-cycle is a good approach for elasticity by itself, when combined into a multiphysics problem there may be an incentive to using a full W-cycle or multiple cycles to help drive down the total solve time.
As mentioned in the introduction, the refinement indicator we use for this program is rather ad hoc. A better one would understand that the jump in the gradient of the solution across the interface is not indicative of the error but to be expected and ignore the interface when integrating the jump terms. Nevertheless, this is not what the KellyErrorEstimator class does. Another, bigger question, is whether this kind of estimator is a good strategy in the first place: for example, if we want to have maximal accuracy in one particular aspect of the displacement (e.g. the displacement at the top right corner of the solid), then is it appropriate to scale the error indicators for fluid and solid to the same magnitude? Maybe it is necessary to solve the fluid problem with more accuracy than the solid because the fluid solution directly affects the solids solution? Maybe the other way around?
Consequently, an obvious possibility for improving the program would be to implement a better refinement criterion. There is some literature on this topic; one of a variety of possible starting points would be the paper by Thomas Wick on "Adaptive finite elements for monolithic fluid-structure interaction on a prolongated domain: Applied to an heart valve simulation", Proceedings of the Computer Methods in Mechanics Conference 2011 (CMM-2011), 9-12 May 2011, Warszaw, Poland.
The results above are purely qualitative as there is no evidence that our scheme in fact converges. An obvious thing to do would therefore be to add some quantitative measures to check that the scheme at least converges to something. For example, we could output for each refinement cycle the deflection of the top right corner of the part of the solid that protrudes into the fluid subdomain. Or we could compute the net force vector or torque the fluid exerts on the solid.
In reality, most fluid structure interaction problems are so that the movement of the solid does affect the flow of the fluid. For example, the forces of the air around an air foil cause it to flex and to change its shape. Likewise, a flag flaps in the wind, completely changing its shape.
Such problems where the coupling goes both ways are typically handled in an Arbitrary Lagrangian Eulerian (ALE) framework, in which the displacement of the solid is extended into the fluid domain in some smooth way, rather than by zero as we do here. The extended displacement field is then used to deform the mesh on which we compute the fluid flow. Furthermore, the boundary conditions for the fluid on the interface are no longer that the velocity is zero; rather, in a time dependent program, the fluid velocity must be equal to the time derivative of the displacement along the interface.