 |
Reference documentation for deal.II version 9.6.0
|
 |
Reference documentation for deal.II version 9.6.0
|
This tutorial depends on step-4.
| Table of contents | |
|---|---|
This is the first of a number of tutorial programs that will finally cover "real" time-dependent problems, not the slightly odd form of time dependence found in step-18 or the DAE model of step-21. In particular, this program introduces the wave equation in a bounded domain. Later, step-24 will consider an example of absorbing boundary conditions, and step-25 a kind of nonlinear wave equation producing solutions called solitons.
The wave equation in its prototypical form reads as follows: find u(x,t), x\in\Omega, t\in[0,T] that satisfies
\begin{eqnarray*} \frac{\partial^2 u}{\partial t^2} - \Delta u &=& f \qquad \textrm{in}\ \Omega\times [0,T], \\ u(x,t) &=& g \qquad \textrm{on}\ \partial\Omega\times [0,T], \\ u(x,0) &=& u_0(x) \qquad \textrm{in}\ \Omega, \\ \frac{\partial u(x,0)}{\partial t} &=& u_1(x) \qquad \textrm{in}\ \Omega. \end{eqnarray*}
Note that since this is an equation with second-order time derivatives, we need to pose two initial conditions, one for the value and one for the time derivative of the solution.
Physically, the equation describes the motion of an elastic medium. In 2-d, one can think of how a membrane moves if subjected to a force. The Dirichlet boundary conditions above indicate that the membrane is clamped at the boundary at a height g(x,t) (this height might be moving as well — think of people holding a blanket and shaking it up and down). The first initial condition equals the initial deflection of the membrane, whereas the second one gives its velocity. For example, one could think of pushing the membrane down with a finger and then letting it go at t=0 (nonzero deflection but zero initial velocity), or hitting it with a hammer at t=0 (zero deflection but nonzero velocity). Both cases would induce motion in the membrane.
There is a long-standing debate in the numerical analysis community over whether a discretization of time dependent equations should involve first discretizing the time variable leading to a stationary PDE at each time step that is then solved using standard finite element techniques (this is called the Rothe method), or whether one should first discretize the spatial variables, leading to a large system of ordinary differential equations that can then be handled by one of the usual ODE solvers (this is called the method of lines).
Both of these methods have advantages and disadvantages. Traditionally, people have preferred the method of lines, since it allows to use the very well developed machinery of high-order ODE solvers available for the rather stiff ODEs resulting from this approach, including step length control and estimation of the temporal error.
On the other hand, Rothe's method becomes awkward when using higher-order time stepping method, since one then has to write down a PDE that couples the solution of the present time step not only with that at the previous time step, but possibly also even earlier solutions, leading to a significant number of terms.
For these reasons, the method of lines was the method of choice for a long time. However, it has one big drawback: if we discretize the spatial variable first, leading to a large ODE system, we have to choose a mesh once and for all. If we are willing to do this, then this is a legitimate and probably superior approach.
If, on the other hand, we are looking at the wave equation and many other time dependent problems, we find that the character of a solution changes as time progresses. For example, for the wave equation, we may have a single wave travelling through the domain, where the solution is smooth or even constant in front of and behind the wave — adaptivity would be really useful for such cases, but the key is that the area where we need to refine the mesh changes from time step to time step!
If we intend to go that way, i.e. choose a different mesh for each time step (or set of time steps), then the method of lines is not appropriate any more: instead of getting one ODE system with a number of variables equal to the number of unknowns in the finite element mesh, our number of unknowns now changes all the time, a fact that standard ODE solvers are certainly not prepared to deal with at all. On the other hand, for the Rothe method, we just get a PDE for each time step that we may choose to discretize independently of the mesh used for the previous time step; this approach is not without perils and difficulties, but at least is a sensible and well-defined procedure.
For all these reasons, for the present program, we choose to use the Rothe method for discretization, i.e. we first discretize in time and then in space. We will not actually use adaptive meshes at all, since this involves a large amount of additional code, but we will comment on this some more in the results section below.
Given these considerations, here is how we will proceed: let us first define a simple time stepping method for this second order problem, and then in a second step do the spatial discretization, i.e. we will follow Rothe's approach.
For the first step, let us take a little detour first: in order to discretize a second time derivative, we can either discretize it directly, or we can introduce an additional variable and transform the system into a first order system. In many cases, this turns out to be equivalent, but dealing with first order systems is often simpler. To this end, let us introduce
v = \frac{\partial u}{\partial t},
and call this variable the velocity for obvious reasons. We can then reformulate the original wave equation as follows:
\begin{eqnarray*} \frac{\partial u}{\partial t} - v &=& 0 \qquad \textrm{in}\ \Omega\times [0,T], \\ \frac{\partial v}{\partial t} - \Delta u &=& f \qquad \textrm{in}\ \Omega\times [0,T], \\ u(x,t) &=& g \qquad \textrm{on}\ \partial\Omega\times [0,T], \\ u(x,0) &=& u_0(x) \qquad \textrm{in}\ \Omega, \\ v(x,0) &=& u_1(x) \qquad \textrm{in}\ \Omega. \end{eqnarray*}
The advantage of this formulation is that it now only contains first time derivatives for both variables, for which it is simple to write down time stepping schemes. Note that we do not have boundary conditions for v at first. However, we could enforce v=\frac{\partial g}{\partial t} on the boundary. It turns out in numerical examples that this is actually necessary: without doing so the solution doesn't look particularly wrong, but the Crank-Nicolson scheme does not conserve energy if one doesn't enforce these boundary conditions.
With this formulation, let us introduce the following time discretization where a superscript n indicates the number of a time step and k=t_n-t_{n-1} is the length of the present time step:
\begin{eqnarray*} \frac{u^n - u^{n-1}}{k} - \left[\theta v^n + (1-\theta) v^{n-1}\right] &=& 0, \\ \frac{v^n - v^{n-1}}{k} - \Delta\left[\theta u^n + (1-\theta) u^{n-1}\right] &=& \theta f^n + (1-\theta) f^{n-1}. \end{eqnarray*}
Note how we introduced a parameter \theta here. If we chose \theta=0, for example, the first equation would reduce to \frac{u^n - u^{n-1}}{k} - v^{n-1} = 0, which is well-known as the forward or explicit Euler method. On the other hand, if we set \theta=1, then we would get \frac{u^n - u^{n-1}}{k} - v^n = 0, which corresponds to the backward or implicit Euler method. Both these methods are first order accurate methods. They are simple to implement, but they are not really very accurate.
The third case would be to choose \theta=\frac 12. The first of the equations above would then read \frac{u^n - u^{n-1}}{k} - \frac 12 \left[v^n + v^{n-1}\right] = 0. This method is known as the Crank-Nicolson method and has the advantage that it is second order accurate. In addition, it has the nice property that it preserves the energy in the solution (physically, the energy is the sum of the kinetic energy of the particles in the membrane plus the potential energy present due to the fact that it is locally stretched; this quantity is a conserved one in the continuous equation, but most time stepping schemes do not conserve it after time discretization). Since v^n also appears in the equation for u^n, the Crank-Nicolson scheme is also implicit.
In the program, we will leave \theta as a parameter, so that it will be easy to play with it. The results section will show some numerical evidence comparing the different schemes.
The equations above (called the semidiscretized equations because we have only discretized the time, but not space), can be simplified a bit by eliminating v^n from the first equation and rearranging terms. We then get
\begin{eqnarray*} \left[ 1-k^2\theta^2\Delta \right] u^n &=& \left[ 1+k^2\theta(1-\theta)\Delta\right] u^{n-1} + k v^{n-1} + k^2\theta\left[\theta f^n + (1-\theta) f^{n-1}\right],\\ v^n &=& v^{n-1} + k\Delta\left[ \theta u^n + (1-\theta) u^{n-1}\right] + k\left[\theta f^n + (1-\theta) f^{n-1}\right]. \end{eqnarray*}
In this form, we see that if we are given the solution u^{n-1},v^{n-1} of the previous timestep, that we can then solve for the variables u^n,v^n separately, i.e. one at a time. This is convenient. In addition, we recognize that the operator in the first equation is positive definite, and the second equation looks particularly simple.
We have now derived equations that relate the approximate (semi-discrete) solution u^n(x) and its time derivative v^n(x) at time t_n with the solutions u^{n-1}(x),v^{n-1}(x) of the previous time step at t_{n-1}. The next step is to also discretize the spatial variable using the usual finite element methodology. To this end, we multiply each equation with a test function, integrate over the entire domain, and integrate by parts where necessary. This leads to
\begin{eqnarray*} (u^n,\varphi) + k^2\theta^2(\nabla u^n,\nabla \varphi) &=& (u^{n-1},\varphi) - k^2\theta(1-\theta)(\nabla u^{n-1},\nabla \varphi) + k(v^{n-1},\varphi) + k^2\theta \left[ \theta (f^n,\varphi) + (1-\theta) (f^{n-1},\varphi) \right], \\ (v^n,\varphi) &=& (v^{n-1},\varphi) - k\left[ \theta (\nabla u^n,\nabla\varphi) + (1-\theta) (\nabla u^{n-1},\nabla \varphi)\right] + k \left[ \theta (f^n,\varphi) + (1-\theta) (f^{n-1},\varphi) \right]. \end{eqnarray*}
It is then customary to approximate u^n(x) \approx u^n_h(x) = \sum_i U_i^n\phi_i^n(x), where \phi_i^n(x) are the shape functions used for the discretization of the n-th time step and U_i^n are the unknown nodal values of the solution. Similarly, v^n(x) \approx v^n_h(x) = \sum_i V_i^n\phi_i^n(x). Finally, we have the solutions of the previous time step, u^{n-1}(x) \approx u^{n-1}_h(x) = \sum_i U_i^{n-1}\phi_i^{n-1}(x) and v^{n-1}(x) \approx v^{n-1}_h(x) = \sum_i V_i^{n-1}\phi_i^{n-1}(x). Note that since the solution of the previous time step has already been computed by the time we get to time step n, U^{n-1},V^{n-1} are known. Furthermore, note that the solutions of the previous step may have been computed on a different mesh, so we have to use shape functions \phi^{n-1}_i(x).
If we plug these expansions into above equations and test with the test functions from the present mesh, we get the following linear system:
\begin{eqnarray*} (M^n + k^2\theta^2 A^n)U^n &=& M^{n,n-1}U^{n-1} - k^2\theta(1-\theta) A^{n,n-1}U^{n-1} + kM^{n,n-1}V^{n-1} + k^2\theta \left[ \theta F^n + (1-\theta) F^{n-1} \right], \\ M^nV^n &=& M^{n,n-1}V^{n-1} - k\left[ \theta A^n U^n + (1-\theta) A^{n,n-1} U^{n-1}\right] + k \left[ \theta F^n + (1-\theta) F^{n-1} \right], \end{eqnarray*}
where
\begin{eqnarray*} M^n_{ij} &=& (\phi_i^n, \phi_j^n), \\ A^n_{ij} &=& (\nabla\phi_i^n, \nabla\phi_j^n), \\ M^{n,n-1}_{ij} &=& (\phi_i^n, \phi_j^{n-1}), \\ A^{n,n-1}_{ij} &=& (\nabla\phi_i^n, \nabla\phi_j^{n-1}), \\ F^n_{i} &=& (f^n,\phi_i^n), \\ F^{n-1}_{i} &=& (f^{n-1},\phi_i^n). \end{eqnarray*}
If we solve these two equations, we can move the solution one step forward and go on to the next time step.
It is worth noting that if we choose the same mesh on each time step (as we will in fact do in the program below), then we have the same shape functions on time step n and n-1, i.e. \phi^n_i=\phi_i^{n-1}=\phi_i. Consequently, we get M^n=M^{n,n-1}=M and A^n=A^{n,n-1}=A. On the other hand, if we had used different shape functions, then we would have to compute integrals that contain shape functions defined on two meshes. This is a somewhat messy process that we omit here, but that is treated in some detail in step-28.
Under these conditions (i.e. a mesh that doesn't change), one can optimize the solution procedure a bit by basically eliminating the solution of the second linear system. We will discuss this in the introduction of the step-25 program.
One way to compare the quality of a time stepping scheme is to see whether the numerical approximation preserves conservation properties of the continuous equation. For the wave equation, the natural quantity to look at is the energy. By multiplying the wave equation by u_t, integrating over \Omega, and integrating by parts where necessary, we find that
\frac{d}{d t} \left[\frac 12 \int_\Omega \left(\frac{\partial u}{\partial t}\right)^2 + (\nabla u)^2 \; dx\right] = \int_\Omega f \frac{\partial u}{\partial t} \; dx + \int_{\partial\Omega} n\cdot\nabla u \frac{\partial g}{\partial t} \; dx.
By consequence, in absence of body forces and constant boundary values, we get that
E(t) = \frac 12 \int_\Omega \left(\frac{\partial u}{\partial t}\right)^2 + (\nabla u)^2 \; dx
is a conserved quantity, i.e. one that doesn't change with time. We will compute this quantity after each time step. It is straightforward to see that if we replace u by its finite element approximation, and \frac{\partial u}{\partial t} by the finite element approximation of the velocity v, then
E(t_n) = \frac 12 \left<V^n, M^n V^n\right> + \frac 12 \left<U^n, A^n U^n\right>.
As we will see in the results section, the Crank-Nicolson scheme does indeed conserve the energy, whereas neither the forward nor the backward Euler scheme do.
One of the reasons why the wave equation is not easy to solve numerically is that explicit time discretizations are only stable if the time step is small enough. In particular, it is coupled to the spatial mesh width h. For the lowest order discretization we use here, the relationship reads
k\le \frac hc
where c is the wave speed, which in our formulation of the wave equation has been normalized to one. Consequently, unless we use the implicit schemes with \theta>0, our solutions will not be numerically stable if we violate this restriction. Implicit schemes do not have this restriction for stability, but they become inaccurate if the time step is too large.
This condition was first recognized by Courant, Friedrichs, and Lewy — in 1928, long before computers became available for numerical computations! (This result appeared in the German language article R. Courant, K. Friedrichs and H. Lewy: Über die partiellen Differenzengleichungen der mathematischen Physik, Mathematische Annalen, vol. 100, no. 1, pages 32-74, 1928.) This condition on the time step is most frequently just referred to as the CFL condition. Intuitively, the CFL condition says that the time step must not be larger than the time it takes a wave to cross a single cell.
In the program, we will refine the square [-1,1]^2 seven times uniformly, giving a mesh size of h=\frac 1{64}, which is what we set the time step to. The fact that we set the time step and mesh size individually in two different places is error prone: it is too easy to refine the mesh once more but forget to also adjust the time step. step-24 shows a better way how to keep these things in sync.
Although the program has all the hooks to deal with nonzero initial and boundary conditions and body forces, we take a simple case where the domain is a square [-1,1]^2 and
\begin{eqnarray*} f &=& 0, \\ u_0 &=& 0, \\ u_1 &=& 0, \\ g &=& \left\{\begin{matrix}\sin (4\pi t) &\qquad& \text{for }\ t\le \frac 12, x=-1, -\frac 13<y<\frac 13 \\ 0 &&\text{otherwise} \end{matrix} \right. \end{eqnarray*}
This corresponds to a membrane initially at rest and clamped all around, where someone is waving a part of the clamped boundary once up and down, thereby shooting a wave into the domain.
We start with the usual assortment of include files that we've seen in so many of the previous tests:
Here are the only three include files of some new interest: The first one is already used, for example, for the VectorTools::interpolate_boundary_values and MatrixTools::apply_boundary_values functions. However, we here use another function in that class, VectorTools::project to compute our initial values as the L^2 projection of the continuous initial values. Furthermore, we use VectorTools::create_right_hand_side to generate the integrals (f^n,\phi^n_i). These were previously always generated by hand in assemble_system or similar functions in application code. However, we're too lazy to do that here, so simply use a library function:
In a very similar vein, we are also too lazy to write the code to assemble mass and Laplace matrices, although it would have only taken copying the relevant code from any number of previous tutorial programs. Rather, we want to focus on the things that are truly new to this program and therefore use the MatrixCreator::create_mass_matrix() and MatrixCreator::create_laplace_matrix() functions. They are declared here:
Finally, here is an include file that contains all sorts of tool functions that one sometimes needs. In particular, we need the Utilities::int_to_string class that, given an integer argument, returns a string representation of it. It is particularly useful since it allows for a second parameter indicating the number of digits to which we want the result padded with leading zeros. We will use this to write output files that have the form solution-XXX.vtu where XXX denotes the number of the time step and always consists of three digits even if we are still in the single or double digit time steps.
The last step is as in all previous programs:
WaveEquation classNext comes the declaration of the main class. It's public interface of functions is like in most of the other tutorial programs. Worth mentioning is that we now have to store four matrices instead of one: the mass matrix M, the Laplace matrix A, the matrix M+k^2\theta^2A used for solving for U^n, and a copy of the mass matrix with boundary conditions applied used for solving for V^n. Note that it is a bit wasteful to have an additional copy of the mass matrix around. We will discuss strategies for how to avoid this in the section on possible improvements.
Likewise, we need solution vectors for U^n,V^n as well as for the corresponding vectors at the previous time step, U^{n-1},V^{n-1}. The system_rhs will be used for whatever right hand side vector we have when solving one of the two linear systems in each time step. These will be solved in the two functions solve_u and solve_v.
Finally, the variable theta is used to indicate the parameter \theta that is used to define which time stepping scheme to use, as explained in the introduction. The rest is self-explanatory.
Before we go on filling in the details of the main class, let us define the equation data corresponding to the problem, i.e. initial and boundary values for both the solution u and its time derivative v, as well as a right hand side class. We do so using classes derived from the Function class template that has been used many times before, so the following should not be a surprise.
Let's start with initial values and choose zero for both the value u as well as its time derivative, the velocity v:
Secondly, we have the right hand side forcing term. Boring as we are, we choose zero here as well:
Finally, we have boundary values for u and v. They are as described in the introduction, one being the time derivative of the other:
WaveEquation classThe implementation of the actual logic is actually fairly short, since we relegate things like assembling the matrices and right hand side vectors to the library. The rest boils down to not much more than 130 lines of actual code, a significant fraction of which is boilerplate code that can be taken from previous example programs (e.g. the functions that solve linear systems, or that generate output).
Let's start with the constructor (for an explanation of the choice of time step, see the section on Courant, Friedrichs, and Lewy in the introduction):
The next function is the one that sets up the mesh, DoFHandler, and matrices and vectors at the beginning of the program, i.e. before the first time step. The first few lines are pretty much standard if you've read through the tutorial programs at least up to step-6:
Then comes a block where we have to initialize the 3 matrices we need in the course of the program: the mass matrix, the Laplace matrix, and the matrix M+k^2\theta^2A used when solving for U^n in each time step.
When setting up these matrices, note that they all make use of the same sparsity pattern object. Finally, the reason why matrices and sparsity patterns are separate objects in deal.II (unlike in many other finite element or linear algebra classes) becomes clear: in a significant fraction of applications, one has to hold several matrices that happen to have the same sparsity pattern, and there is no reason for them not to share this information, rather than re-building and wasting memory on it several times.
After initializing all of these matrices, we call library functions that build the Laplace and mass matrices. All they need is a DoFHandler object and a quadrature formula object that is to be used for numerical integration. Note that in many respects these functions are better than what we would usually do in application programs, for example because they automatically parallelize building the matrices if multiple processors are available in a machine: for more information see the documentation of WorkStream or the Parallel computing with multiple processors topic. The matrices for solving linear systems will be filled in the run() method because we need to re-apply boundary conditions every time step.
The rest of the function is spent on setting vector sizes to the correct value. The final line closes the hanging node constraints object. Since we work on a uniformly refined mesh, no constraints exist or have been computed (i.e. there was no need to call DoFTools::make_hanging_node_constraints as in other programs), but we need a constraints object in one place further down below anyway.
The next two functions deal with solving the linear systems associated with the equations for U^n and V^n. Both are not particularly interesting as they pretty much follow the scheme used in all the previous tutorial programs.
One can make little experiments with preconditioners for the two matrices we have to invert. As it turns out, however, for the matrices at hand here, using Jacobi or SSOR preconditioners reduces the number of iterations necessary to solve the linear system slightly, but due to the cost of applying the preconditioner it is no win in terms of run-time. It is not much of a loss either, but let's keep it simple and just do without:
Likewise, the following function is pretty much what we've done before. The only thing worth mentioning is how here we generate a string representation of the time step number padded with leading zeros to 3 character length using the Utilities::int_to_string function's second argument.
Like step-15, since we write output at every time step (and the system we have to solve is relatively easy), we instruct DataOut to use the zlib compression algorithm that is optimized for speed instead of disk usage since otherwise plotting the output becomes a bottleneck:
The following is really the only interesting function of the program. It contains the loop over all time steps, but before we get to that we have to set up the grid, DoFHandler, and matrices. In addition, we have to somehow get started with initial values. To this end, we use the VectorTools::project function that takes an object that describes a continuous function and computes the L^2 projection of this function onto the finite element space described by the DoFHandler object. Can't be any simpler than that:
The next thing is to loop over all the time steps until we reach the end time ( T=5 in this case). In each time step, we first have to solve for U^n, using the equation (M^n + k^2\theta^2 A^n)U^n = (M^{n,n-1} - k^2\theta(1-\theta) A^{n,n-1})U^{n-1} + kM^{n,n-1}V^{n-1}
+ k\theta \left[k \theta F^n + k(1-\theta) F^{n-1} \right]. Note that we use the same mesh for all time steps, so that M^n=M^{n,n-1}=M and A^n=A^{n,n-1}=A. What we therefore have to do first is to add up MU^{n-1} - k^2\theta(1-\theta) AU^{n-1} + kMV^{n-1} and the forcing terms, and put the result into the system_rhs vector. (For these additions, we need a temporary vector that we declare before the loop to avoid repeated memory allocations in each time step.)
The one thing to realize here is how we communicate the time variable to the object describing the right hand side: each object derived from the Function class has a time field that can be set using the Function::set_time and read by Function::get_time. In essence, using this mechanism, all functions of space and time are therefore considered functions of space evaluated at a particular time. This matches well what we typically need in finite element programs, where we almost always work on a single time step at a time, and where it never happens that, for example, one would like to evaluate a space-time function for all times at any given spatial location.
After so constructing the right hand side vector of the first equation, all we have to do is apply the correct boundary values. As for the right hand side, this is a space-time function evaluated at a particular time, which we interpolate at boundary nodes and then use the result to apply boundary values as we usually do. The result is then handed off to the solve_u() function:
The matrix for solve_u() is the same in every time steps, so one could think that it is enough to do this only once at the beginning of the simulation. However, since we need to apply boundary values to the linear system (which eliminate some matrix rows and columns and give contributions to the right hand side), we have to refill the matrix in every time steps before we actually apply boundary data. The actual content is very simple: it is the sum of the mass matrix and a weighted Laplace matrix:
The second step, i.e. solving for V^n, works similarly, except that this time the matrix on the left is the mass matrix (which we copy again in order to be able to apply boundary conditions, and the right hand side is MV^{n-1} - k\left[ \theta A U^n + (1-\theta) AU^{n-1}\right] plus forcing terms. Boundary values are applied in the same way as before, except that now we have to use the BoundaryValuesV class:
Finally, after both solution components have been computed, we output the result, compute the energy in the solution, and go on to the next time step after shifting the present solution into the vectors that hold the solution at the previous time step. Note the function SparseMatrix::matrix_norm_square that can compute \left<V^n,MV^n\right> and \left<U^n,AU^n\right> in one step, saving us the expense of a temporary vector and several lines of code:
main functionWhat remains is the main function of the program. There is nothing here that hasn't been shown in several of the previous programs:
When the program is run, it produces the following output:
What we see immediately is that the energy is a constant at least after t=\frac 12 (until which the boundary source term g is nonzero, injecting energy into the system).
In addition to the screen output, the program writes the solution of each time step to an output file. If we process them adequately and paste them into a movie, we get the following:
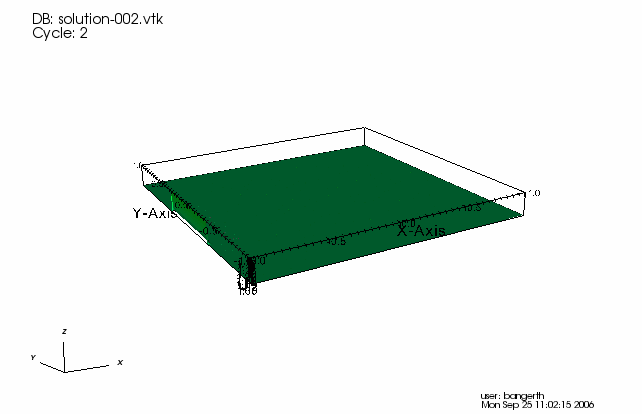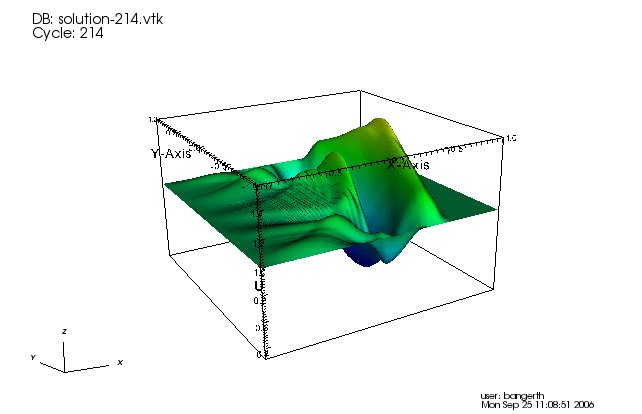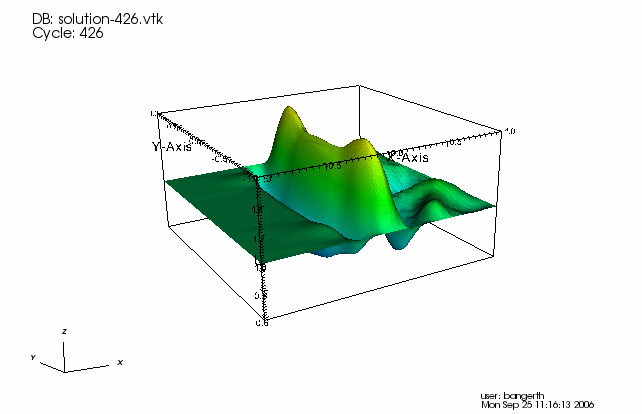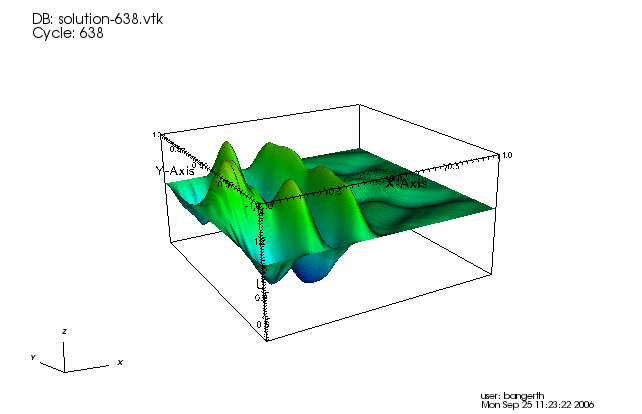
The movie shows the generated wave nice traveling through the domain and back, being reflected at the clamped boundary. Some numerical noise is trailing the wave, an artifact of a too-large mesh size that can be reduced by reducing the mesh width and the time step.
If you want to explore a bit, try out some of the following things:
Varying \theta. This gives different time stepping schemes, some of which are stable while others are not. Take a look at how the energy evolves.
Different initial and boundary conditions, right hand sides.
More complicated domains or more refined meshes. Remember that the time step needs to be bounded by the mesh width, so changing the mesh should always involve also changing the time step. We will come back to this issue in step-24.
Variable coefficients: In real media, the wave speed is often variable. In particular, the "real" wave equation in realistic media would read
\rho(x) \frac{\partial^2 u}{\partial t^2} - \nabla \cdot a(x) \nabla u = f,
where \rho(x) is the density of the material, and a(x) is related to the stiffness coefficient. The wave speed is then c=\sqrt{a/\rho}.
To make such a change, we would have to compute the mass and Laplace matrices with a variable coefficient. Fortunately, this isn't too hard: the functions MatrixCreator::create_laplace_matrix and MatrixCreator::create_mass_matrix have additional default parameters that can be used to pass non-constant coefficient functions to them. The required changes are therefore relatively small. On the other hand, care must be taken again to make sure the time step is within the allowed range.
In the in-code comments, we discussed the fact that the matrices for solving for U^n and V^n need to be reset in every time because of boundary conditions, even though the actual content does not change. It is possible to avoid copying by not eliminating columns in the linear systems, which is implemented by appending a false argument to the call:
deal.II being a library that supports adaptive meshes it would of course be nice if this program supported change the mesh every few time steps. Given the structure of the solution — a wave that travels through the domain — it would seem appropriate if we only refined the mesh where the wave currently is, and not simply everywhere. It is intuitively clear that we should be able to save a significant amount of cells this way. (Though upon further thought one realizes that this is really only the case in the initial stages of the simulation. After some time, for wave phenomena, the domain is filled with reflections of the initial wave going in every direction and filling every corner of the domain. At this point, there is in general little one can gain using local mesh refinement.)
To make adaptively changing meshes possible, there are basically two routes. The "correct" way would be to go back to the weak form we get using Rothe's method. For example, the first of the two equations to be solved in each time step looked like this:
\begin{eqnarray*} (u^n,\varphi) + k^2\theta^2(\nabla u^n,\nabla \varphi) &=& (u^{n-1},\varphi) - k^2\theta(1-\theta)(\nabla u^{n-1},\nabla \varphi) + k(v^{n-1},\varphi) + k^2\theta \left[ \theta (f^n,\varphi) + (1-\theta) (f^{n-1},\varphi) \right]. \end{eqnarray*}
Now, note that we solve for u^n on mesh {\mathbb T}^n, and consequently the test functions \varphi have to be from the space V_h^n as well. As discussed in the introduction, terms like (u^{n-1},\varphi) then require us to integrate the solution of the previous step (which may have been computed on a different mesh {\mathbb T}^{n-1}) against the test functions of the current mesh, leading to a matrix M^{n,n-1}. This process of integrating shape functions from different meshes is, at best, awkward. It can be done but because it is difficult to ensure that {\mathbb T}^{n-1} and {\mathbb T}^{n} differ by at most one level of refinement, one has to recursively match cells from both meshes. It is feasible to do this, but it leads to lengthy and not entirely obvious code.
The second approach is the following: whenever we change the mesh, we simply interpolate the solution from the last time step on the old mesh to the new mesh, using the SolutionTransfer class. In other words, instead of the equation above, we would solve
\begin{eqnarray*} (u^n,\varphi) + k^2\theta^2(\nabla u^n,\nabla \varphi) &=& (I^n u^{n-1},\varphi) - k^2\theta(1-\theta)(\nabla I^n u^{n-1},\nabla \varphi) + k(I^n v^{n-1},\varphi) + k^2\theta \left[ \theta (f^n,\varphi) + (1-\theta) (f^{n-1},\varphi) \right], \end{eqnarray*}
where I^n interpolates a given function onto mesh {\mathbb T}^n. This is a much simpler approach because, in each time step, we no longer have to worry whether u^{n-1},v^{n-1} were computed on the same mesh as we are using now or on a different mesh. Consequently, the only changes to the code necessary are the addition of a function that computes the error, marks cells for refinement, sets up a SolutionTransfer object, transfers the solution to the new mesh, and rebuilds matrices and right hand side vectors on the new mesh. Neither the functions building the matrices and right hand sides, nor the solvers need to be changed.
While this second approach is, strictly speaking, not quite correct in the Rothe framework (it introduces an addition source of error, namely the interpolation), it is nevertheless what almost everyone solving time dependent equations does. We will use this method in step-31, for example.