 |
Reference documentation for deal.II version 9.6.0
|
 |
Reference documentation for deal.II version 9.6.0
|
This tutorial depends on step-6.
This program was contributed by Wolfgang Bangerth, Rene Gassmoeller, and Peter Munch.
Wolfgang Bangerth acknowledges support through NSF awards DMS-1821210, EAR-1550901, and OAC-1835673.
The finite element method in general, and deal.II in particular, were invented to solve partial differential equations – in other words, to solve continuum mechanics problems. On the other hand, sometimes one wants to solve problems in which it is useful to track individual objects ("particles") and how their positions evolve. If this simply leads to a set of ordinary differential equations, for example if you want to track the positions of the planets in the solar system over time, then deal.II is clearly not the right tool. On the other hand, if this evolution is due to the interaction with the solution of partial differential equations, or if having a mesh to determine which particles interact with others (such as in the smoothed particle hydrodynamics (SPH) method), then deal.II has support for you.
The case we will consider here is how electrically charged particles move through an electric field. As motivation, we will consider cathode rays: Electrons emitted by a heated piece of metal that is negatively charged (the "cathode"), and that are then accelerated by an electric field towards the positively charged electrode (the "anode"). The anode is typically ring-shaped so that the majority of electrons can fly through the hole in the form of an electron beam. In the olden times, they might then have illuminated the screen of a TV built from a cathode ray tube. Today, instead, electron beams are useful in X-ray machines, electron beam lithography, electron beam welding, and a number of other areas.
The equations we will then consider are as follows: First, we need to describe the electric field. This is most easily accomplished by noting that the electric potential V satisfied the equation
-\epsilon_0 \Delta V = \rho
where \epsilon_0 is the dielectric constant of vacuum, and \rho is the charge density. This is augmented by boundary conditions that we will choose as follows:
\begin{align*} V &= -V_0 && \text{on}\; \Gamma_\text{cathode}\subset\partial\Omega \\ V &= +V_0 && \text{on}\; \Gamma_\text{anode}\subset\partial\Omega \\ \epsilon\frac{\partial V}{\partial n} &= 0 && \text{on}\; \partial\Omega\setminus\Gamma_\text{cathode}\setminus\Gamma_\text{anode}. \end{align*}
In other words, we prescribe voltages +V_0 and -V_0 at the two electrodes and insulating (Neumann) boundary conditions elsewhere. Since the dynamics of the particles are purely due to the electric field \mathbf E=\nabla V, we could as well have prescribed 2V_0 and 0 at the two electrodes – all that matters is the voltage difference at the two electrodes.
Given this electric potential V and the electric field \mathbf E=\nabla V, we can describe the trajectory of the ith particle using the differential equation
m {\ddot {\mathbf x}}_i = e\mathbf E,
where m,e are the mass and electric charge of each particle. In practice, it is convenient to write this as a system of first-order differential equations in the position \mathbf x and velocity \mathbf v:
\begin{align*} {\dot {\mathbf v}}_i &= \frac{e\mathbf E}{m}, \\ {\dot {\mathbf x}}_i &= {\mathbf v}_i. \end{align*}
The deal.II class we will use to deal with particles, Particles::ParticleHandler, stores particles in a way so that the position \mathbf x_i is part of the Particles::ParticleHandler data structures. (It stores particles sorted by cell they are in, and consequently needs to know where each particle is.) The velocity \mathbf v_i, on the other hand, is of no concern to Particles::ParticleHandler and consequently we will store it as a "property" of each particle that we will update in each time step. Properties can also be used to store any other quantity we might care about each particle: its charge, or if they were larger than just an electron, its color, mass, attitude in space, chemical composition, etc.
There remain two things to discuss to complete the model: Where particles start and what the charge density \rho is.
First, historically, cathode rays used very large electric fields to pull electrons out of the metal. This produces only a relatively small current. One can do better by heating the cathode: a statistical fraction of electrons in that case have enough thermal energy to leave the metal; the electric field then just has to be strong enough to pull them away from the attraction of their host body. We will model this in the following way: We will create a new particle if (i) the electric field points away from the electrode, i.e., if \mathbf E \cdot \mathbf n < 0 where \mathbf n is the normal vector at a face pointing out of the domain (into the electrode), and (ii) the electric field exceeds a threshold value |\mathbf E|\ge E_\text{threshold}. This is surely not a sufficiently accurate model for what really happens, but is good enough for our current tutorial program.
Second, in principle we would have to model the charge density via
\rho(\mathbf x) = \sum_i e\delta(\mathbf x-\mathbf x_i).
The issue now is that in reality, a cathode ray tube in an old television yields a current of somewhere around a few milli-Amperes. In the much higher energy beams of particle accelerators, the current may only be a few nano-Ampere. But an Ampere is 6\times 10^{18} electrons flowing per second. Now, as you will see in the results section, we really only simulate a few microseconds ( 10^{-6} seconds), but that still results in very very large numbers of electrons – far more than we can hope to simulate with a program as small as the current one. As a consequence, let us presume that each particle represents N electrons. Then the particle mass and charge are also Nm and Ne and the equations we have to solve are
(Nm) {\ddot {\mathbf x}}_i = (Ne)\mathbf E,
which is of course exactly the same as above after dividing both sides by N. On the other hand, the charge density for these "clumps" of electrons is given by
\rho(\mathbf x) = \sum_i (Ne)\delta(\mathbf x-\mathbf x_i).
It is this form that we will implement in the program, where N is chosen rather large in the program to ensure that the particles actually affect the electric field. (This may not be realistic in practice: In most cases, there are just not enough electrons to actually affect the overall electric field. But realism is not our goal here.)
As a final thought about the model, one may wonder why the equation for the electric field (or, rather, the electric potential) has no time derivative whereas the equations for the electron positions do. In essence, this is a modeling assumption: We assume that the particles move so slowly that at any given time the electric field is in equilibrium. This is saying, in other words, that the velocity of the electrons is much less than the speed of light. In yet other words, we can rephrase this in terms of the electrode voltage V_0: Since every volt of electric potential accelerates electrons by approximately 600 km/s (neglecting relativistic effects), requiring |\mathbf v_i\|\ll c is equivalent to saying that 2V_0 \ll 500 \text{V}. Under this assumption (and the assumption that the total number of electrons is small), one can also neglect the creation of magnetic fields by the moving charges, which would otherwise also affect the movement of the electrons.
The equations outlined above then form a set of coupled differential equations. Let us bring them all together in one place again to make that clear:
\begin{align*} -\epsilon_0 \Delta V &= \sum_i e\delta(\mathbf x-\mathbf x_i) \\ {\dot {\mathbf x}}_i &= {\mathbf v}_i, \\ {\dot {\mathbf v}}_i &= \frac{e\mathbf E}{m} = \frac{e\mathbf \nabla V}{m}. \end{align*}
Because of the awkward dependence of the electric potential on the particle locations, we don't want to solve this as a coupled system but instead use a decoupled approach where we first solve for the potential in each time step and then the particle locations. (One could also do it the other way around, of course.) This is very much in the same spirit as we do in step-21, step-31, and step-32, to name just a few, and can all be understood in the context of the operator splitting methods discussed in step-58.
So, if we denote by an upper index n the time step, and if we use a simple time discretization for the ODE, then this means that we have to solve the following set of equations in each time step:
\begin{align*} -\epsilon_0 \Delta V^{(n)} &= \sum_i e\delta(\mathbf x-\mathbf x_i^{(n-1)}) \\ \frac{{\mathbf v}_i^{(n)}-{\mathbf v}_i^{(n-1)}}{\Delta t} &= \frac{e\nabla V^{(n)}}{m} \\ \frac{{\mathbf x}_i^{(n)}-{\mathbf x}_i^{(n-1)}}{\Delta t} &= {\mathbf v}_i^{(n)}. \end{align*}
This scheme can be understood in the framework of operator splitting methods (specifically, the "Lie splitting" method) wherein a coupled system is solved by updating one variable at a time, using either the old values of other variables (e.g., using \mathbf x_i^{(n-1)} in the first equation) or the values of variables that have already been updated in a previous sub-step (e.g., using V^{(n)} in the second equation). There are of course many better ways to do a time discretization (for example the simple leapfrog scheme when updating the velocity, or more general Strang splitting methods for the coupled system) but this isn't the point of the tutorial program, and so we will be content with what we have here. (We will comment on a piece of this puzzle in the possibilities for extensions section of this program, however.)
There remains the question of how we should choose the time step size \Delta t. The limitation here is that the Particles::ParticleHandler class needs to keep track of which cell each particle is in. This is particularly an issue if we are running computations in parallel (say, in step-70) because in that case every process only stores those cells it owns plus one layer of "ghost cells". That's not relevant here, but in general we should make sure that over the course of each time step, a particle moves only from one cell to any of its immediate neighbors (face, edge, or vertex neighbors). If we can ensure that, then Particles::ParticleHandler is guaranteed to be able to figure out which cell a particle ends up in. To do this, a useful rule of thumb is that we should choose the time step so that for all particles the expected distance the particle moves by is less than one cell diameter:
\Delta t \le \frac{h_i}{\|\mathbf v_i\|} \qquad\qquad \forall i,
or equivalently
\Delta t \le \min_i \frac{h_i}{\|\mathbf v_i\|}.
Here, h_i is the length of the shortest edge of the cell on which particle i is located – in essence, a measure of the size of a cell.
On the other hand, a particle might already be at the boundary of one cell and the neighboring cell might be once further refined. So then the time to cross that neighboring cell would actually be half the amount above, suggesting
\Delta t \le \min_i \frac{\tfrac 12 h_i}{\|\mathbf v_i\|}.
But even that is not good enough: The formula above updates the particle positions in each time using the formula
\frac{{\mathbf x}_i^{(n)}-{\mathbf x}_i^{(n-1)}}{\Delta t} = {\mathbf v}_i^{(n)},
that is, using the current velocity {\mathbf v}_i^{n}. But we don't have the current velocity yet at the time when we need to choose \Delta t – which is after we have updated the potential V^{(n)} but before we update the velocity from {\mathbf v}_i^{(n-1)} to {\mathbf v}_i^{(n)}. All we have is {\mathbf v}_i^{(n-1)}. So we need an additional safety factor for our final choice:
\Delta t^{(n)} = c_\text{safety} \min_i \frac{\tfrac 12 h_i}{\|\mathbf v_i^{(n-1)}\|}.
How large should c_\text{safety} be? That depends on how much of underestimate \|\mathbf v_i^{(n-1)}\| might be compared to \|\mathbf v_i^{(n)}\|, and that is actually quite easy to assess: A particle created in one time step with zero velocity will roughly pick up equal velocity increments in each successive time step if the electric field it encounters along the way were roughly constant. So the maximal difference between \|\mathbf v_i^{(n-1)}\| and \|\mathbf v_i^{(n)}\| would be a factor of two. As a consequence, we will choose c_\text{safety}=0.5.
There is only one other case we ought to consider: What happens in the very first time step? There, any particles to be moved along have just been created, but they have a zero velocity. So we don't know what velocity we should choose for them. Of course, in all other time steps there are also particles that have just been created, but in general, the particles with the highest velocity limit the time step size and so the newly created particles with their zero velocity don't matter. But if we only have such particles?
In that case, we can use the following approximation: If a particle starts at \mathbf v^{(0)}=0, then the update formula tells us that
{\mathbf v}_i^{(1)} = \frac{e\nabla V^{(1)}}{m} \Delta t,
and consequently
\frac{{\mathbf x}_i^{(1)}-{\mathbf x}_i^{(0)}}{\Delta t} = {\mathbf v}_i^{(1)},
which we can write as
{\mathbf x}_i^{(1)} - {\mathbf x}_i^{(0)} = \frac{e\nabla V^{(1)}}{m} \Delta t^2.
Not wanting to move a particle by more than \frac 12 h_i then implies that we should choose the time step as
\Delta t \le \min_i \sqrt{ \frac{h_i m}{e \|\nabla V^{(1)}\| }}.
Using the same argument about neighboring cells possibly being smaller by a factor of two then leads to the final formula for time step zero:
\Delta t = \min_i \sqrt{ \frac{\frac 12 h_i m}{e \|\nabla V^{(1)}\| } }.
Strictly speaking, we would have to evaluate the electric potential V^{(1)} at the location of each particle, but a good enough approximation is to use the maximum of the values at the vertices of the respective cell. (Why the vertices and not the midpoint? Because the gradient of the solution of the Laplace equation, i.e., the electric field, is largest in corner singularities which are located at the vertices of cells.) This has the advantage that we can make good use of the FEValues functionality which can recycle pre-computed material as long as the quadrature points are the same from one cell to the next.
We could always run this kind of scheme to estimate the difference between \mathbf v_i^{(n-1)} and \mathbf v_i^{(n)}, but it relies on evaluating the electric field \mathbf E on each cell, and that is expensive. As a consequence, we will limit this approach to the very first time step.
Having discussed the time discretization, the discussion of the spatial discretization is going to be short: We use quadratic finite elements, i.e., the space Q_2, to approximate the electric potential V. The mesh is adapted a couple of times during the initial time step. All of this is entirely standard if you have read step-6, and the implementation does not provide for any kind of surprise.
Adding and moving particles is, in practice, not very difficult in deal.II. To add one, the create_particles() function of this program simply uses a code snippet of the following form:
In other words, it is not all that different from inserting an object into a std::set or std::map: Create the object, set its properties (here, the current location, its reference cell location, and its id) and call insert_particle. The only thing that may be surprising is the reference location: In order to evaluate things such as \nabla V(\mathbf x_i), it is necessary to evaluate finite element fields at locations \mathbf x_i. But this requires evaluating the finite element shape functions at points on the reference cell \hat{\mathbf x}_i. To make this efficient, every particle doesn't just store its location and the cell it is on, but also what location that point corresponds to in the cell's reference coordinate system.
Updating a particle's position is then no more difficult: One just has to call
We do this in the move_particles() function. The only difference is that we then have to tell the Particles::ParticleHandler class to also find what cell that position corresponds to (and, when computing in parallel, which process owns this cell). For efficiency reason, this is most easily done after updating all particles' locations, and is achieved via the Particles::ParticleHandler::sort_particles_into_subdomains_and_cells() function.
There are, of course, times where a particle may leave the domain in question. In that case, Particles::ParticleHandler::sort_particles_into_subdomains_and_cells() can not find a surrounding cell and simply deletes the particle. But, it is often useful to track the number of particles that have been lost this way, and for this the Particles::ParticleHandler class offers a "signal" that one can attach to. We show how to do this in the constructor of the main class to count how many particles were lost in each time step. Specifically, the way this works is that the Particles::ParticleHandler class has a "signal" to which one can attach a function that will be executed whenever the signal is triggered. Here, this looks as follows:
That's a bit of a mouthful, but what's happening is this: We declare a lambda function that "captures" the this pointer (so that we can access member functions of the surrounding object inside the lambda function), and that takes two arguments:
CathodeRaySimulator::track_lost_particle function with these arguments. When we attach this lambda function to the signal, the Particles::ParticleHandler::sort_particles_into_subdomains_and_cells() function will trigger the signal for every particle for which it can't find a new home. This gives us the chance to record where the particle is, and to record statistics on it.The test case here is not meant to be a realistic depiction of a cathode ray tube, but it has the right general characteristics and the point is, in any case, only to demonstrate how one would implement deal.II codes that use particles.
The following picture shows the geometry that we're going to use:
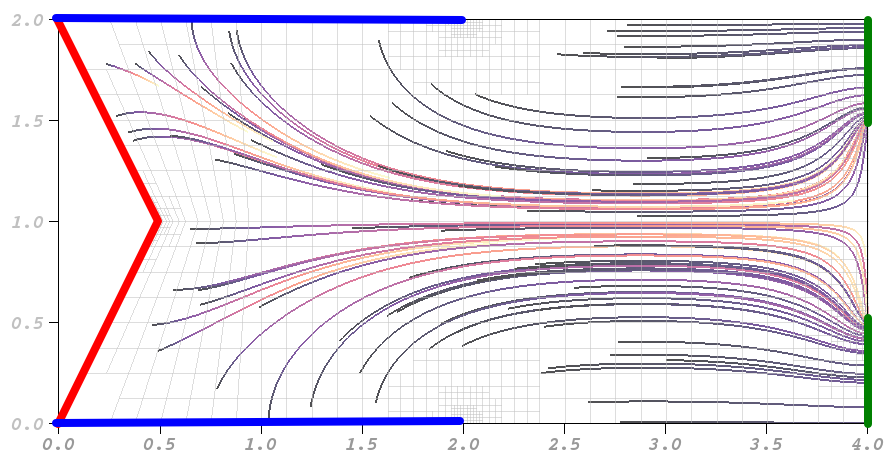
In this picture, the parts of the boundary marked in red and blue are the cathode, held at an electric potential V=-V_0. The part of the cathode shown in red is the part that is heated, leading to electrons leaving the metal and then being accelerated by the electric field (a few electric field lines are also shown). The green part of the boundary is the anode, held at V=+V_0. The rest of the boundary satisfies a Neumann boundary condition.
This setup mimics real devices. The re-entrant corner results in an electric potential V whose derivative (the electric field \mathbf E) has a singularity – in other words, it becomes very large in the vicinity of the corner, allowing it to rip electrons away from the metal. These electrons are then accelerated towards the (green) anode which has a hole in the middle through which the electrons can escape the device and fly on to hit the screen, where they excite the "phosphor" to then emit the light that we see from these old-style TV screens. The non-heated part of the cathode is not subject to the emission of electrons – in the code, we will mark this as the "focussing element" of the tube, because its negative electric voltage repels the electrons and makes sure that they do not just fly away from the heated part of the cathode perpendicular to the boundary, but in fact bend their paths towards the anode on the right.
The electric field lines also shown in the picture illustrate that the electric field connects the negative and positive electrodes, respectively. The accelerating force the electrons experience is along these field lines. Finally, the picture shows the mesh used in the computation, illustrating that there are singularities at the tip of the re-rentrant corner as well as at all places where the boundary conditions change; these singularities are visible because the mesh is refined in these locations.
Of practical interest is to figure out which fraction of the electrons emitted from the cathode actually make it through the hole in the anode – electrons that just bounce into the anode itself are not actually doing anything useful other than converting electricity into heat. As a consequence, in the track_lost_particle() function (which is called for each particle that leaves the domain, see above), we will estimate where it might have left the domain and report this in the output.
The majority of the include files used in this program are well known from step-6 and similar programs:
The ones that are new are only the following three: The first declares the DiscreteTime class that helps us keep track of time in a time-dependent simulation. The latter two provide all of the particle functionality, namely a way to keep track of particles located on a mesh (the Particles::ParticleHandler class) and the ability to output these particles' locations and their properties for the purposes of visualization (the Particles::DataOut class).
As is customary, we put everything that corresponds to the details of the program into a namespace of its own. At the top, we define a few constants for which we would rather use symbolic names than hard-coded numbers.
Specifically, we define numbers for boundary indicators for the various parts of the geometry, as well as the physical properties of electrons and other specifics of the setup we use here.
For the boundary indicators, let us start enumerating at some random value 101. The principle here is to use numbers that are uncommon. If there are pre-defined boundary indicators previously set by the GridGenerator functions, they will likely be small integers starting from zero, but not in this rather randomly chosen range. Using numbers such as those below avoids the possibility for conflicts, and also reduces the temptation to just spell these numbers out in the program (because you will probably never remember which is which, whereas you might have been tempted if they had started at 0).
The following is then the main class of this program. It has, fundamentally, the same structure as step-6 and many other tutorial programs. This includes the majority of the member functions (with the purpose of the rest probably self-explanatory from their names) as well as only a small number of member variables beyond those of step-6, all of which are related to dealing with particles.
CathodeRaySimulator class implementationCathodeRaySimulator constructorSo then let us get started on the implementation. What the constructor does is really only a straight-forward initialization of all of the member variables at the top. The only two worth mentioning are the particle_handler, which is handed a reference to the triangulation on which the particles will live (currently of course still empty, but the particle handler stores the reference and will use it once particles are added – which happens after the triangulation is built). The other piece of information it gets is how many "properties" each particle needs to store. Here, all we need each particle to remember is its current velocity, i.e., a vector with dim components. There are, however, other intrinsic properties that each particle has and that the Particles::ParticleHandler class automatically and always makes sure are available; in particular, these are the current location of a particle, the cell it is on, it's reference location within that cell, and the particle's ID.
The only other variable of interest is time, an object of type DiscreteTime. It keeps track of the current time we are in a time-dependent simulation, and is initialized with the start time (zero) and end time ( 10^{-4}). We will later set the time step size in update_timestep_size().
The body of the constructor consists of a piece of code we have already discussed in the introduction. Namely, we make sure that the track_lost_particle() function is called by the particle_handler object every time a particle leaves the domain.
CathodeRaySimulator::make_grid functionThe next function is then responsible for generating the mesh on which we want to solve. Recall how the domain looks like:

We subdivide this geometry into a mesh of 4\times 2 cells that looks like this:
The way this is done is by first defining where the 15=5\times 3 vertices are located – here, we say that they are on integer points with the middle one on the left side moved to the right by a value of delta=0.5.
In the following, we then have to say which vertices together form the 8 cells. The following code is then entirely equivalent to what we also do in step-14:
With these arrays out of the way, we can move to slightly higher higher-level data structures. We create a vector of CellData objects that store for each cell to be created the vertices in question as well as the material id (which we will here simply set to zero since we don't use it in the program).
This information is then handed to the Triangulation::create_triangulation() function, and the mesh is twice globally refined. As discussed in the corresponding place in step-14, the inputs to Triangulation::create_triangulation() need to be consistently oriented, which a function in namespace GridTools does for us.
The remaining part of the function loops over all cells and their faces, and if a face is at the boundary determines which boundary indicator should be applied to it. The various conditions should make sense if you compare the code with the picture of the geometry above.
Once done with this step, we refine the mesh once more globally.
CathodeRaySimulator::setup_system functionThe next function in this program deals with setting up the various objects related to solving the partial differential equations. It is in essence a copy of the corresponding function in step-6 and requires no further discussion.
CathodeRaySimulator::assemble_system functionThe function that computes the matrix entries is again in essence a copy of the corresponding function in step-6:
The only interesting part of this function is how it forms the right hand side of the linear system. Recall that the right hand side of the PDE is
\sum_p (N e)\delta(\mathbf x-\mathbf x_p),
where we have used p to index the particles here to avoid confusion with the shape function \varphi_i; \mathbf x_p is the position of the pth particle.
When multiplied by a test function \varphi_i and integrated over the domain results in a right hand side vector
\begin{align*} F_i &= \int_\Omega \varphi_i (\mathbf x)\left[ \sum_p (N e)\delta(\mathbf x-\mathbf x_p) \right] dx \\ &= \sum_p (N e) \varphi_i(\mathbf x_p). \end{align*}
Note that the final line no longer contains an integral, and consequently also no occurrence of dx which would require the appearance of the JxW symbol in our code.
For a given cell K, this cell's contribution to the right hand side is then
\begin{align*} F_i^K &= \sum_{p, \mathbf x_p\in K} (N e) \varphi_i(\mathbf x_p), \end{align*}
i.e., we only have to worry about those particles that are actually located on the current cell K.
In practice, what we do here is the following: If there are any particles on the current cell, then we first obtain an iterator range pointing to the first particle of that cell as well as the particle past the last one on this cell (or the end iterator) – i.e., a half-open range as is common for C++ functions. Knowing now the list of particles, we query their reference locations (with respect to the reference cell), evaluate the shape functions in these reference locations, and compute the force according to the formula above (without any FEValues::JxW).
Finally, we can copy the contributions of this cell into the global matrix and right hand side vector:
The function that solves the linear system is then again exactly as in step-6:
The final field-related function is the one that refines the grid. We will call it a number of times in the first time step to obtain a mesh that is well-adapted to the structure of the solution and, in particular, resolves the various singularities in the solution that are due to re-entrant corners and places where the boundary condition type changes. You might want to refer to step-6 again for more details:
Let us now turn to the functions that deal with particles. The first one is about the creation of particles. As mentioned in the introduction, we want to create a particle at points of the cathode if the electric field \mathbf E=\nabla V exceeds a certain threshold, i.e., if |\mathbf E| \ge E_\text{threshold}, and if furthermore the electric field points into the domain (i.e., if \mathbf E \cdot \mathbf n < 0). As is common in the finite element method, we evaluate fields (and their derivatives) at specific evaluation points; typically, these are "quadrature points", and so we create a "quadrature formula" that we will use to designate the points at which we want to evaluate the solution. Here, we will simply take QMidpoint implying that we will only check the threshold condition at the midpoints of faces. We then use this to initialize an object of type FEFaceValues to evaluate the solution at these points.
All of this will then be used in a loop over all cells, their faces, and specifically those faces that are at the boundary and, moreover, the cathode part of the boundary.
So we have found a face on the cathode. Next, we let the FEFaceValues object compute the gradient of the solution at each "quadrature" point, and extract the electric field vector from the gradient in the form of a Tensor variable through the methods discussed in the vector-valued problems documentation topic.
Electrons can only escape the cathode if the electric field strength exceeds a threshold and, crucially, if the electric field points into the domain. Once we have that checked, we create a new Particles::Particle object at this location and insert it into the Particles::ParticleHandler object with a unique ID.
The only thing that may be not obvious here is that we also associate with this particle the location in the reference coordinates of the cell we are currently on. This is done because we will in downstream functions compute quantities such as the electric field at the location of the particle (e.g., to compute the forces that act on it when updating its position in each time step). Evaluating a finite element field at arbitrary coordinates is quite an expensive operation because shape functions are really only defined on the reference cell, and so when asking for the electric field at an arbitrary point requires us first to determine what the reference coordinates of that point are. To avoid having to do this over and over, we determine these coordinates once and for all and then store these reference coordinates directly with the particle.
At the end of all of these insertions, we let the particle_handler update some internal statistics about the particles it stores.
The second particle-related function is the one that moves the particles in each time step. To do this, we have to loop over all cells, the particles in each cell, and evaluate the electric field at each of the particles' positions.
The approach used here is conceptually the same used in the assemble_system() function: We loop over all cells, find the particles located there (with the same caveat about the inefficiency of the algorithm used here to find these particles), and use FEPointEvaluation object to evaluate the gradient at these positions:
Then we can ask the FEPointEvaluation object for the gradients of the solution (i.e., the electric field \mathbf E) at these locations and loop over the individual particles:
Having now obtained the electric field at the location of one of the particles, we use this to update first the velocity and then the position. To do so, let us first get the old velocity out of the properties stored with the particle, compute the acceleration, update the velocity, and store this new velocity again in the properties of the particle. Recall that this corresponds to the first of the following set of update equations discussed in the introduction:
\begin{align*} \frac{{\mathbf v}_i^{(n)} -{\mathbf v}_i^{(n-1)}}{\Delta t} &= \frac{e\nabla V^{(n)}}{m} \\ \frac{{\mathbf x}_i^{(n)}-{\mathbf x}_i^{(n-1)}} {\Delta t} &= {\mathbf v}_i^{(n)}. \end{align*}
With the new velocity, we can then also update the location of the particle and tell the particle about it.
Having updated the locations and properties (i.e., velocities) of all particles, we need to make sure that the particle_handler again knows which cells they are in, and what their locations in the coordinate system of the reference cell are. The following function does that. (It also makes sure that, in parallel computations, particles are moved from one processor to another processor if a particle moves from the subdomain owned by the former to the subdomain owned by the latter.)
The final particle-related function is the one that is called whenever a particle is lost from the simulation. This typically happens if it leaves the domain. If that happens, this function is called both the cell (which we can ask for its new location) and the cell it was previously on. The function then keeps track of updating the number of particles lost in this time step, the total number of lost particles, and then estimates whether the particle left through the hole in the middle of the anode. We do so by first checking whether the cell it was in last had an x coordinate to the left of the right boundary (located at x=4) and the particle now has a position to the right of the right boundary. If that is so, we compute a direction vector of its motion that is normalized so that the x component of the direction vector is equal to 1. With this direction vector, we can compute where it would have intersected the line x=4. If this intersect is between 0.5 and 1.5, then we claim that the particle left through the hole and increment a counter.
As discussed at length in the introduction, we need to respect a time step condition whereby particles can not move further than one cell in one time step. To ensure that this is the case, we again first compute the maximal speed of all particles on each cell, and divide the cell size by that speed. We then compute the next time step size as the minimum of this quantity over all cells, using the safety factor discussed in the introduction, and set this as the desired time step size using the DiscreteTime::set_desired_time_step_size() function.
As mentioned in the introduction, we have to treat the very first time step differently since there, particles are not available yet or do not yet have the information associated that we need for the computation of a reasonable step length. The formulas below follow the discussion in the introduction.
CathodeRaySimulator::output_results() functionThe final function implementing pieces of the overall algorithm is the one that generates graphical output. In the current context, we want to output both the electric potential field as well as the particle locations and velocities. But we also want to output the electric field, i.e., the gradient of the solution.
deal.II has a general way how one can compute derived quantities from the solution and output those as well. Here, this is the electric field, but it could also be some other quantity – say, the norm of the electric field, or in fact anything else one could want to compute from the solution V_h(\mathbf x) or its derivatives. This general solution uses the DataPostprocessor class and, in cases like the one here where we want to output a quantity that represents a vector field, the DataPostprocessorVector class.
Rather than try and explain how this class works, let us simply refer to the documentation of the DataPostprocessorVector class that has essentially this case as a well-documented example.
With this, the output_results() function becomes relatively straightforward: We use the DataOut class as we have in almost every one of the previous tutorial programs to output the solution (the "electric potential") and we use the postprocessor defined above to also output its gradient (the "electric
field"). This all is then written into a file in VTU format after also associating the current time and time step number with this file, and providing physical units for the two fields to be output.
Output the particle positions and properties is not more complicated. The Particles::DataOut class plays the role of the DataOut class for particles, and all we have to do is tell that class where to take particles from and how to interpret the dim components of the properties – namely, as a single vector indicating the velocity, rather than as dim scalar properties. The rest is then the same as above:
The last member function of the principal class of this program is then the driver. At the top, it refines the mesh a number of times by solving the problem (with no particles yet created) on a sequence of finer and finer meshes.
Now do the loop over time. The sequence of steps follows closely the outline of the algorithm discussed in the introduction. As discussed in great detail in the documentation of the DiscreteTime class, while we move the field and particle information forward by one time step, the time stored in the time variable is not consistent with where (some of) these quantities are (in the diction of DiscreteTime, this is the "update
stage"). The call to time.advance_time() makes everything consistent again by setting the time variable to the time at which the field and particles already are, and once we are in this "consistent stage", we can generate graphical output and write information about the current state of the simulation to screen.
main functionThe final function of the program is then again the main() function. It is unchanged in all tutorial programs since step-6 and so there is nothing new to discuss:
When this program is run, it produces output that looks as follows:
Picking a random few time steps, we can visualize the solution in the form of streamlines for the electric field and dots for the electrons (the pictures were created with an earlier version of the program and are no longer exact representations of the solution as currently computed – but they are conceptually still correct):




That said, a more appropriate way to visualize the results of this program are by creating a video that shows how these electrons move, and how the electric field changes in response to their motion (again showing results of an earlier version of the program):
What you can see here is how the "focus element" of the boundary with its negative voltage repels the electrons and makes sure that they do not just fly away perpendicular from the cathode (as they do in the initial part of their trajectories). It also shows how the electric field lines move around over time, in response to the charges flying by – in other words, the feedback the particles have on the electric field that itself drives the motion of the electrons.
The movie suggests that electrons move in "bunches" or "bursts". One element of this appearance is an artifact of how the movie was created: Every frame of the movie corresponds to one time step, but the time step length varies. More specifically, the fastest particle moving through the smallest cell determines the length of the time step (see the discussion in the introduction), and consequently time steps are small whenever a (fast) particle moves through the small cells at the right edge of the domain; time steps are longer again once the particle has left the domain. This slowing-accelerating effect can easily be visualized by plotting the time step length shown in the screen output.
The second part of this is real, however: The simulation creates a large group of particles in the beginning, and fewer after about the 300th time step. This is probably because of the negative charge of the particles in the simulation: They reduce the magnitude of the electric field at the (also negatively charged electrode) and consequently reduce the number of points on the cathode at which the magnitude exceeds the threshold necessary to draw an electron out of the electrode.
At the end of the day, we are rarely interested in the solution of an equation, but in numbers that can be extracted from it – in other words, we want to postprocess* the solution (see the results section of step-4 for an extensive discussion of this concept). Here, what one would likely be most interested in assessing are some statistics about the particles.
The program already computes the fraction of the electrons that leave the domain through the hole in the anode. But there are other quantities one might be interested in. For example, the average velocity of these particles. It would not be very difficult to obtain each particle's velocity from its properties, in the same way as we do in the move_particles() function, and compute statistics from it.
As discussed above, there is a varying time difference between different frames of the video because we create output for every time step. A better way to create movies would be to generate a new output file in fixed time intervals, regardless of how many time steps lie between each such point.
The problem we are considering in this program is a coupled, multiphysics problem. But the way we solve it is by first computing the (electric) potential field and then updating first the particle velocity and finally the particle locations. This is what is called an "operator-splitting method", a concept we will investigate in more detail in step-58.
While it is awkward to think of a way to solve this problem that does not involve splitting the problem into a PDE piece and a particles piece, one can (and probably should!) think of a better way to update the particle locations. Specifically, the equations we use to update the particle location are
\begin{align*} \frac{{\mathbf v}_i^{(n)}-{\mathbf v}_i^{(n-1)}}{\Delta t} &= \frac{e\nabla V^{(n)}}{m} \\ \frac{{\mathbf x}_i^{(n)}-{\mathbf x}_i^{(n-1)}}{\Delta t} &= {\mathbf v}_i^{(n)}. \end{align*}
This corresponds to a Lie splitting where we first update one variable (the velocity) and then, using the already-updated value of the one variable to update the other (the position). It is well understood that the Lie splitting incurs a first order error accuracy in the time step (i.e., the error introduced by the splitting is {\cal O}(\Delta t)) that we know we should avoid because we can do better. Independently, of course, we incur an error of the same rate a second time because we use an Euler-like scheme for each of the two updates (we replace the time derivative by a simple finite difference quotient containing the old and new value, and we evaluate the right hand side only at the end time of the interval, at t_n), and a better scheme would also use a better way to do this kind of update.
Better strategies would replace the Lie splitting by something like a Strang splitting, and the update of the particle position and velocity by a scheme such as the leapfrog scheme or more generally symplectic integrators such as the Verlet scheme.
In release mode, the program runs in about 3.5 minutes on one of the author's laptops at the time of writing this. That's acceptable. But what if we wanted to make the simulation three-dimensional? If we wanted to not use a maximum of around 100 particles at any given time (as happens with the parameters used here) but 100,000? If we needed a substantially finer mesh?
In those cases, one would want to run the program not just on a single processor, but in fact on as many as one has available. This requires parallelization of both the PDE solution as well as over particles. In practice, while there are substantial challenges to making this efficient and scale well, these challenges are all addressed in deal.II itself, and have been demonstrated on simulations running on 10,000 or more cores. For example, step-40 shows how to parallelize the finite element part, and step-70 shows how one can then also parallelize the particles part.