This tutorial depends on step-6.
Introduction
This example shows the basic usage of the multilevel functions in deal.II. It solves almost the same problem as used in step-6, but demonstrating the things one has to provide when using multigrid as a preconditioner. In particular, this requires that we define a hierarchy of levels, provide transfer operators from one level to the next and back, and provide representations of the Laplace operator on each level.
In order to allow sufficient flexibility in conjunction with systems of differential equations and block preconditioners, quite a few different objects have to be created before starting the multilevel method, although most of what needs to be done is provided by deal.II itself. These are
- the object handling transfer between grids; we use the MGTransferPrebuilt class for this that does almost all of the work inside the library,
- the solver on the coarsest level; here, we use MGCoarseGridHouseholder,
- the smoother on all other levels, which in our case will be the mg::SmootherRelaxation class using SOR as the underlying method,
- and mg::Matrix, a class having a special level multiplication, i.e. we basically store one matrix per grid level and allow multiplication with it.
Most of these objects will only be needed inside the function that actually solves the linear system. There, these objects are combined in an object of type Multigrid, containing the implementation of the V-cycle, which is in turn used by the preconditioner PreconditionMG, ready for plug-in into a linear solver of the LAC library.
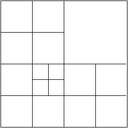
The multigrid method implemented here for adaptively refined meshes follows the outline in the Multigrid paper, which describes the underlying implementation in deal.II and also introduces a lot of the nomenclature. First, we have to distinguish between level meshes, namely cells that have the same refinement distance from the coarse mesh, and the leaf mesh consisting of active cells of the hierarchy (in older work we refer to this as the global mesh, but this term is overused). Most importantly, the leaf mesh is not identical with the level mesh on the finest level. The following image shows what we consider to be a "level mesh":

The fine level in this mesh consists only of the degrees of freedom that are defined on the refined cells, but does not extend to that part of the domain that is not refined. While this guarantees that the overall effort grows as {\cal O}(N) as necessary for optimal multigrid complexity, it leads to problems when defining where to smooth and what boundary conditions to pose for the operators defined on individual levels if the level boundary is not an external boundary. These questions are discussed in detail in the article cited above.
The testcase
The problem we solve here is similar to step-6, with two main differences: first, the multigrid preconditioner, obviously. We also change the discontinuity of the coefficients such that the local assembler does not look more complicated than necessary.
The commented program
Include files
Again, the first few include files are already known, so we won't comment on them:
#include <deal.II/base/quadrature_lib.h>
#include <deal.II/base/function.h>
#include <deal.II/base/utilities.h>
#include <deal.II/lac/affine_constraints.h>
#include <deal.II/lac/vector.h>
#include <deal.II/lac/full_matrix.h>
#include <deal.II/lac/sparse_matrix.h>
#include <deal.II/lac/solver_cg.h>
#include <deal.II/lac/precondition.h>
#include <deal.II/grid/tria.h>
#include <deal.II/grid/grid_generator.h>
#include <deal.II/grid/grid_refinement.h>
#include <deal.II/dofs/dof_tools.h>
#include <deal.II/fe/fe_q.h>
#include <deal.II/fe/fe_values.h>
#include <deal.II/fe/mapping_q1.h>
#include <deal.II/numerics/vector_tools.h>
#include <deal.II/numerics/data_out.h>
#include <deal.II/numerics/error_estimator.h>
These, now, are the include necessary for the multilevel methods. The first one declares how to handle Dirichlet boundary conditions on each of the levels of the multigrid method. For the actual description of the degrees of freedom, we do not need any new include file because DoFHandler already has all necessary methods implemented. We will only need to distribute the DoFs for the levels further down.
The rest of the include files deals with the mechanics of multigrid as a linear operator (solver or preconditioner).
#include <deal.II/multigrid/mg_constrained_dofs.h>
#include <deal.II/multigrid/multigrid.h>
#include <deal.II/multigrid/mg_transfer.h>
#include <deal.II/multigrid/mg_tools.h>
#include <deal.II/multigrid/mg_coarse.h>
#include <deal.II/multigrid/mg_smoother.h>
#include <deal.II/multigrid/mg_matrix.h>
We will be using MeshWorker::mesh_loop to loop over the cells, so include it here:
#include <deal.II/meshworker/mesh_loop.h>
This is C++:
#include <iostream>
#include <fstream>
namespace Step16
{
The Scratch and Copy objects
We use MeshWorker::mesh_loop() to assemble our matrices. For this, we need a ScratchData object to store temporary data on each cell (this is just the FEValues object) and a CopyData object that will contain the output of each cell assembly. For more details about the usage of scratch and copy objects, see the WorkStream namespace.
template <int dim>
struct ScratchData
{
const unsigned int quadrature_degree,
: fe_values(mapping, fe,
QGauss<dim>(quadrature_degree), update_flags)
{}
ScratchData(const ScratchData<dim> &scratch_data)
: fe_values(scratch_data.fe_values.get_mapping(),
scratch_data.fe_values.get_fe(),
scratch_data.fe_values.get_quadrature(),
scratch_data.fe_values.get_update_flags())
{}
};
struct CopyData
{
std::vector<types::global_dof_index> local_dof_indices;
template <class Iterator>
void reinit(const Iterator &cell, unsigned int dofs_per_cell)
{
cell_matrix.reinit(dofs_per_cell, dofs_per_cell);
cell_rhs.reinit(dofs_per_cell);
local_dof_indices.resize(dofs_per_cell);
cell->get_active_or_mg_dof_indices(local_dof_indices);
}
};
Abstract base class for mapping classes.
The LaplaceProblem class template
This main class is similar to the same class in step-6. As far as member functions is concerned, the only additions are:
- The
assemble_multigrid function that assembles the matrices that correspond to the discrete operators on intermediate levels.
- The
cell_worker function that assembles our PDE on a single cell.
template <int dim>
class LaplaceProblem
{
public:
LaplaceProblem(const unsigned int degree);
void run();
private:
template <class Iterator>
void cell_worker(const Iterator &cell,
ScratchData<dim> &scratch_data,
CopyData ©_data);
void setup_system();
void assemble_system();
void assemble_multigrid();
void solve();
void refine_grid();
void output_results(const unsigned int cycle) const;
const unsigned int degree;
const ::parallel::distributed::Triangulation< dim, spacedim > * triangulation
The following members are the essential data structures for the multigrid method. The first four represent the sparsity patterns and the matrices on individual levels of the multilevel hierarchy, very much like the objects for the global mesh above.
Then we have two new matrices only needed for multigrid methods with local smoothing on adaptive meshes. They convey data between the interior part of the refined region and the refinement edge, as outlined in detail in the multigrid paper.
The last object stores information about the boundary indices on each level and information about indices lying on a refinement edge between two different refinement levels. It thus serves a similar purpose as AffineConstraints, but on each level.
The LaplaceProblem class implementation
Just one short remark about the constructor of the Triangulation: by convention, all adaptively refined triangulations in deal.II never change by more than one level across a face between cells. For our multigrid algorithms, however, we need a slightly stricter guarantee, namely that the mesh also does not change by more than refinement level across vertices that might connect two cells. In other words, we must prevent the following situation:
This is achieved by passing the Triangulation::limit_level_difference_at_vertices flag to the constructor of the triangulation class.
template <int dim>
LaplaceProblem<dim>::LaplaceProblem(const unsigned int degree)
, fe(degree)
, degree(degree)
{}
LaplaceProblem::setup_system
In addition to just distributing the degrees of freedom in the DoFHandler, we do the same on each level. Then, we follow the same procedure as before to set up the system on the leaf mesh.
template <int dim>
void LaplaceProblem<dim>::setup_system()
{
dof_handler.distribute_dofs(fe);
dof_handler.distribute_mg_dofs();
std::cout << " Number of degrees of freedom: " << dof_handler.n_dofs()
<< " (by level: ";
std::cout << dof_handler.n_dofs(
level)
std::cout << std::endl;
solution.reinit(dof_handler.n_dofs());
system_rhs.reinit(dof_handler.n_dofs());
constraints.clear();
std::set<types::boundary_id> dirichlet_boundary_ids = {0};
const std::map<types::boundary_id, const Function<dim> *>
dirichlet_boundary_functions = {
dirichlet_boundary_functions,
constraints);
constraints.close();
{
sparsity_pattern.copy_from(dsp);
}
system_matrix.reinit(sparsity_pattern);
unsigned int n_levels() const
void make_hanging_node_constraints(const DoFHandler< dim, spacedim > &dof_handler, AffineConstraints< number > &constraints)
void make_sparsity_pattern(const DoFHandler< dim, spacedim > &dof_handler, SparsityPatternBase &sparsity_pattern, const AffineConstraints< number > &constraints={}, const bool keep_constrained_dofs=true, const types::subdomain_id subdomain_id=numbers::invalid_subdomain_id)
The multigrid constraints have to be initialized. They need to know where Dirichlet boundary conditions are prescribed.
mg_constrained_dofs.clear();
mg_constrained_dofs.initialize(dof_handler);
mg_constrained_dofs.make_zero_boundary_constraints(dof_handler,
dirichlet_boundary_ids);
Now for the things that concern the multigrid data structures. First, we resize the multilevel objects to hold matrices and sparsity patterns for every level. The coarse level is zero (this is mandatory right now but may change in a future revision). Note that these functions take a complete, inclusive range here (not a starting index and size), so the finest level is n_levels-1. We first have to resize the container holding the SparseMatrix classes, since they have to release their SparsityPattern before they can be destroyed upon resizing.
mg_interface_matrices.resize(0, n_levels - 1);
mg_matrices.resize(0, n_levels - 1);
mg_sparsity_patterns.resize(0, n_levels - 1);
mg_interface_sparsity_patterns.resize(0, n_levels - 1);
Now, we have to provide a matrix on each level. To this end, we first use the MGTools::make_sparsity_pattern function to generate a preliminary compressed sparsity pattern on each level (see the Sparsity patterns topic for more information on this topic) and then copy it over to the one we really want. The next step is to initialize the interface matrices with the fitting sparsity pattern.
It may be worth pointing out that the interface matrices only have entries for degrees of freedom that sit at or next to the interface between coarser and finer levels of the mesh. They are therefore even sparser than the matrices on the individual levels of our multigrid hierarchy. Therefore, we use a function specifically build for this purpose to generate it.
{
{
dof_handler.n_dofs(
level));
mg_sparsity_patterns[
level].copy_from(dsp);
mg_matrices[
level].reinit(mg_sparsity_patterns[
level]);
}
{
dof_handler.n_dofs(
level));
mg_constrained_dofs,
dsp,
mg_interface_sparsity_patterns[
level].copy_from(dsp);
mg_interface_matrices[
level].reinit(
mg_interface_sparsity_patterns[
level]);
}
}
}
LaplaceProblem::cell_worker
The cell_worker function is used to assemble the matrix and right-hand side on the given cell. This function is used for the active cells to generate the system_matrix and on each level to build the level matrices.
Note that we also assemble a right-hand side when called from assemble_multigrid() even though it is not used.
template <int dim>
template <class Iterator>
void LaplaceProblem<dim>::cell_worker(const Iterator &cell,
ScratchData<dim> &scratch_data,
CopyData ©_data)
{
const unsigned int dofs_per_cell = fe_values.get_fe().n_dofs_per_cell();
const unsigned int n_q_points = fe_values.get_quadrature().size();
copy_data.reinit(cell, dofs_per_cell);
const std::vector<double> &JxW = fe_values.get_JxW_values();
for (unsigned int q = 0; q < n_q_points; ++q)
{
const double coefficient =
(fe_values.get_quadrature_points()[q][0] < 0.0) ? 1.0 : 0.1;
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
for (unsigned int j = 0; j < dofs_per_cell; ++j)
{
copy_data.cell_matrix(i, j) +=
coefficient *
(fe_values.shape_grad(i, q) * fe_values.shape_grad(j, q)) *
JxW[q];
}
copy_data.cell_rhs(i) += 1.0 * fe_values.shape_value(i, q) * JxW[q];
}
}
}
void reinit(const TriaIterator< DoFCellAccessor< dim, spacedim, level_dof_access > > &cell)
LaplaceProblem::assemble_system
The following function assembles the linear system on the active cells of the mesh. For this, we pass two lambda functions to the mesh_loop() function. The cell_worker function redirects to the class member function of the same name, while the copier is specific to this function and copies local matrix and vector to the corresponding global ones using the constraints.
template <int dim>
void LaplaceProblem<dim>::assemble_system()
{
auto cell_worker =
ScratchData<dim> &scratch_data,
CopyData ©_data) {
this->cell_worker(cell, scratch_data, copy_data);
};
auto copier = [&](const CopyData &cd) {
this->constraints.distribute_local_to_global(cd.cell_matrix,
cd.cell_rhs,
cd.local_dof_indices,
system_matrix,
system_rhs);
};
const unsigned int n_gauss_points = degree + 1;
ScratchData<dim> scratch_data(mapping,
fe,
n_gauss_points,
dof_handler.end(),
cell_worker,
copier,
scratch_data,
CopyData(),
}
typename ActiveSelector::active_cell_iterator active_cell_iterator
void mesh_loop(const CellIteratorType &begin, const CellIteratorType &end, const CellWorkerFunctionType &cell_worker, const CopierType &copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const AssembleFlags flags=assemble_own_cells, const BoundaryWorkerFunctionType &boundary_worker=BoundaryWorkerFunctionType(), const FaceWorkerFunctionType &face_worker=FaceWorkerFunctionType(), const unsigned int queue_length=2 *MultithreadInfo::n_threads(), const unsigned int chunk_size=8)
@ update_values
Shape function values.
@ update_JxW_values
Transformed quadrature weights.
@ update_gradients
Shape function gradients.
@ update_quadrature_points
Transformed quadrature points.
LaplaceProblem::assemble_multigrid
The next function is the one that builds the matrices that define the multigrid method on each level of the mesh. The integration core is the same as above, but the loop below will go over all existing cells instead of just the active ones, and the results must be entered into the correct level matrices. Fortunately, MeshWorker hides most of that from us, and thus the difference between this function and the previous lies only in the setup of the assembler and the different iterators in the loop.
We generate an AffineConstraints object for each level containing the boundary and interface dofs as constrained entries. The corresponding object is then used to generate the level matrices.
template <int dim>
void LaplaceProblem<dim>::assemble_multigrid()
{
std::vector<AffineConstraints<double>> boundary_constraints(n_levels);
{
boundary_constraints[
level].reinit(
dof_handler.locally_owned_mg_dofs(
level),
mg_constrained_dofs.get_refinement_edge_indices(
level))
boundary_constraints[
level].constrain_dof_to_zero(dof_index);
mg_constrained_dofs.get_boundary_indices(
level))
boundary_constraints[
level].constrain_dof_to_zero(dof_index);
boundary_constraints[
level].close();
}
auto cell_worker =
ScratchData<dim> &scratch_data,
CopyData ©_data) {
this->cell_worker(cell, scratch_data, copy_data);
};
auto copier = [&](const CopyData &cd) {
boundary_constraints[cd.level].distribute_local_to_global(
cd.cell_matrix, cd.local_dof_indices, mg_matrices[cd.level]);
const unsigned int dofs_per_cell = cd.local_dof_indices.size();
typename LevelSelector::cell_iterator level_cell_iterator
Interface entries are ignored by the boundary_constraints object above when filling the mg_matrices[cd.level]. Instead, we copy these entries into the interface matrix of the current level manually:
for (unsigned int i = 0; i < dofs_per_cell; ++i)
for (unsigned int j = 0; j < dofs_per_cell; ++j)
if (mg_constrained_dofs.is_interface_matrix_entry(
cd.level, cd.local_dof_indices[i], cd.local_dof_indices[j]))
{
mg_interface_matrices[cd.level].add(cd.local_dof_indices[i],
cd.local_dof_indices[j],
cd.cell_matrix(i, j));
}
};
const unsigned int n_gauss_points = degree + 1;
ScratchData<dim> scratch_data(mapping,
fe,
n_gauss_points,
dof_handler.end_mg(),
cell_worker,
copier,
scratch_data,
CopyData(),
}
LaplaceProblem::solve
This is the other function that is significantly different in support of the multigrid solver (or, in fact, the preconditioner for which we use the multigrid method).
Let us start out by setting up two of the components of multilevel methods: transfer operators between levels, and a solver on the coarsest level. In finite element methods, the transfer operators are derived from the finite element function spaces involved and can often be computed in a generic way independent of the problem under consideration. In that case, we can use the MGTransferPrebuilt class that, given the constraints of the final linear system and the MGConstrainedDoFs object that knows about the boundary conditions on the each level and the degrees of freedom on interfaces between different refinement level can build the matrices for those transfer operations from a DoFHandler object with level degrees of freedom.
The second part of the following lines deals with the coarse grid solver. Since our coarse grid is very coarse indeed, we decide for a direct solver (a Householder decomposition of the coarsest level matrix), even if its implementation is not particularly sophisticated. If our coarse mesh had many more cells than the five we have here, something better suited would obviously be necessary here.
template <int dim>
void LaplaceProblem<dim>::solve()
{
mg_transfer.build(dof_handler);
void copy_from(const MatrixType &)
void initialize(const FullMatrix< number > &A)
The next component of a multilevel solver or preconditioner is that we need a smoother on each level. A common choice for this is to use the application of a relaxation method (such as the SOR, Jacobi or Richardson method) or a small number of iterations of a solver method (such as CG or GMRES). The mg::SmootherRelaxation and MGSmootherPrecondition classes provide support for these two kinds of smoothers. Here, we opt for the application of a single SOR iteration. To this end, we define an appropriate alias and then setup a smoother object.
The last step is to initialize the smoother object with our level matrices and to set some smoothing parameters. The initialize() function can optionally take additional arguments that will be passed to the smoother object on each level. In the current case for the SOR smoother, this could, for example, include a relaxation parameter. However, we here leave these at their default values. The call to set_steps() indicates that we will use two pre- and two post-smoothing steps on each level; to use a variable number of smoother steps on different levels, more options can be set in the constructor call to the mg_smoother object.
The last step results from the fact that we use the SOR method as a smoother - which is not symmetric - but we use the conjugate gradient iteration (which requires a symmetric preconditioner) below, we need to let the multilevel preconditioner make sure that we get a symmetric operator even for nonsymmetric smoothers:
mg_smoother.set_steps(2);
mg_smoother.set_symmetric(true);
void initialize(const MGLevelObject< MatrixType2 > &matrices, const typename RelaxationType::AdditionalData &additional_data=typename RelaxationType::AdditionalData())
The next preparatory step is that we must wrap our level and interface matrices in an object having the required multiplication functions. We will create two objects for the interface objects going from coarse to fine and the other way around; the multigrid algorithm will later use the transpose operator for the latter operation, allowing us to initialize both up and down versions of the operator with the matrices we already built:
Now, we are ready to set up the V-cycle operator and the multilevel preconditioner.
mg_matrix, coarse_grid_solver, mg_transfer, mg_smoother, mg_smoother);
mg.set_edge_matrices(mg_interface_down, mg_interface_up);
preconditioner(dof_handler,
mg, mg_transfer);
With all this together, we can finally get about solving the linear system in the usual way:
solution = 0;
solver.solve(system_matrix, solution, system_rhs, preconditioner);
std::cout << " Number of CG iterations: " << solver_control.last_step()
<< '\n'
<< std::endl;
constraints.distribute(solution);
}
Postprocessing
The following two functions postprocess a solution once it is computed. In particular, the first one refines the mesh at the beginning of each cycle while the second one outputs results at the end of each such cycle. The functions are almost unchanged from those in step-6.
template <int dim>
void LaplaceProblem<dim>::refine_grid()
{
dof_handler,
solution,
estimated_error_per_cell);
estimated_error_per_cell,
0.3,
0.03);
}
template <int dim>
void LaplaceProblem<dim>::output_results(const unsigned int cycle) const
{
data_out.add_data_vector(solution, "solution");
data_out.build_patches();
std::ofstream output("solution-" + std::to_string(cycle) + ".vtk");
data_out.write_vtk(output);
}
void attach_dof_handler(const DoFHandler< dim, spacedim > &)
static void estimate(const Mapping< dim, spacedim > &mapping, const DoFHandler< dim, spacedim > &dof, const Quadrature< dim - 1 > &quadrature, const std::map< types::boundary_id, const Function< spacedim, Number > * > &neumann_bc, const ReadVector< Number > &solution, Vector< float > &error, const ComponentMask &component_mask={}, const Function< spacedim > *coefficients=nullptr, const unsigned int n_threads=numbers::invalid_unsigned_int, const types::subdomain_id subdomain_id=numbers::invalid_subdomain_id, const types::material_id material_id=numbers::invalid_material_id, const Strategy strategy=cell_diameter_over_24)
unsigned int n_active_cells() const
virtual void execute_coarsening_and_refinement() override
void refine_and_coarsen_fixed_number(Triangulation< dim, spacedim > &triangulation, const Vector< Number > &criteria, const double top_fraction_of_cells, const double bottom_fraction_of_cells, const unsigned int max_n_cells=std::numeric_limits< unsigned int >::max())
LaplaceProblem::run
Like several of the functions above, this is almost exactly a copy of the corresponding function in step-6. The only difference is the call to assemble_multigrid that takes care of forming the matrices on every level that we need in the multigrid method.
template <int dim>
void LaplaceProblem<dim>::run()
{
for (unsigned int cycle = 0; cycle < 8; ++cycle)
{
std::cout << "Cycle " << cycle << std::endl;
if (cycle == 0)
{
}
else
refine_grid();
std::cout << " Number of active cells: "
setup_system();
assemble_system();
assemble_multigrid();
solve();
output_results(cycle);
}
}
}
void refine_global(const unsigned int times=1)
void hyper_ball(Triangulation< dim > &tria, const Point< dim > ¢er=Point< dim >(), const double radius=1., const bool attach_spherical_manifold_on_boundary_cells=false)
The main() function
This is again the same function as in step-6:
int main()
{
try
{
using namespace Step16;
LaplaceProblem<2> laplace_problem(1);
laplace_problem.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
Results
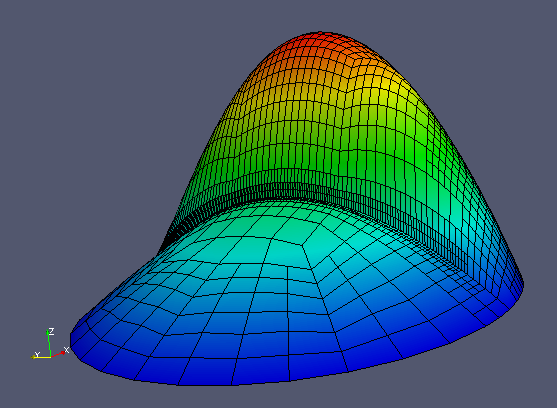
On the finest mesh, the solution looks like this:
More importantly, we would like to see if the multigrid method really improved the solver performance. Therefore, here is the textual output:
Cycle 0
Number of active cells: 80
Number of degrees of freedom: 89 (by level: 8, 25, 89)
Number of CG iterations: 5
Cycle 1
Number of active cells: 152
Number of degrees of freedom: 174 (by level: 8, 25, 89, 123)
Number of CG iterations: 5
Cycle 2
Number of active cells: 287
Number of degrees of freedom: 331 (by level: 8, 25, 89, 223, 127)
Number of CG iterations: 6
Cycle 3
Number of active cells: 545
Number of degrees of freedom: 608 (by level: 8, 25, 89, 231, 476, 24)
Number of CG iterations: 6
Cycle 4
Number of active cells: 1034
Number of degrees of freedom: 1137 (by level: 8, 25, 89, 274, 756, 417, 15)
Number of CG iterations: 6
Cycle 5
Number of active cells: 1964
Number of degrees of freedom: 2181 (by level: 8, 25, 89, 304, 779, 1030, 817)
Number of CG iterations: 6
Cycle 6
Number of active cells: 3734
Number of degrees of freedom: 4101 (by level: 8, 25, 89, 337, 779, 2046, 885, 1545)
Number of CG iterations: 6
Cycle 7
Number of active cells: 7094
Number of degrees of freedom: 7833 (by level: 8, 25, 89, 337, 1056, 2835, 1740, 1765, 3085)
Number of CG iterations: 6
That's almost perfect multigrid performance: the linear residual gets reduced by 6 orders of magnitude in 5 or 6 iterations, and the results are almost independent of the mesh size. That's obviously in part due to the simple nature of the problem solved, but it also shows the power of multigrid methods.
Possibilities for extensions
We encourage you to generate timings for the solve() call and compare to step-6. You will see that the multigrid method has quite an overhead on coarse meshes, but that it always beats other methods on fine meshes because of its optimal complexity.
A close inspection of this program's performance shows that it is mostly dominated by matrix-vector operations. step-37 shows one way how this can be avoided by working with matrix-free methods.
Another avenue would be to use algebraic multigrid methods. The geometric multigrid method used here can at times be a bit awkward to implement because it needs all those additional data structures, and it becomes even more difficult if the program is to run in parallel on machines coupled through MPI, for example. In that case, it would be simpler if one could use a black-box preconditioner that uses some sort of multigrid hierarchy for good performance but can figure out level matrices and similar things by itself. Algebraic multigrid methods do exactly this, and we will use them in step-31 for the solution of a Stokes problem and in step-32 and step-40 for a parallel variation. That said, a parallel version of this example program with MPI can be found in step-50.
Finally, one may want to think how to use geometric multigrid for other kinds of problems, specifically vector valued problems. This is the topic of step-56 where we use the techniques shown here for the Stokes equation.
The plain program
#include <iostream>
#include <fstream>
namespace Step16
{
template <int dim>
struct ScratchData
{
const unsigned int quadrature_degree,
: fe_values(mapping, fe,
QGauss<dim>(quadrature_degree), update_flags)
{}
ScratchData(const ScratchData<dim> &scratch_data)
: fe_values(scratch_data.fe_values.get_mapping(),
scratch_data.fe_values.get_fe(),
scratch_data.fe_values.get_quadrature(),
scratch_data.fe_values.get_update_flags())
{}
};
struct CopyData
{
std::vector<types::global_dof_index> local_dof_indices;
template <class Iterator>
void reinit(
const Iterator &cell,
unsigned int dofs_per_cell)
{
cell_rhs.
reinit(dofs_per_cell);
local_dof_indices.resize(dofs_per_cell);
cell->get_active_or_mg_dof_indices(local_dof_indices);
}
};
template <int dim>
class LaplaceProblem
{
public:
LaplaceProblem(const unsigned int degree);
private:
template <class Iterator>
void cell_worker(const Iterator &cell,
ScratchData<dim> &scratch_data,
CopyData ©_data);
void setup_system();
void assemble_system();
void assemble_multigrid();
void solve();
void refine_grid();
void output_results(const unsigned int cycle) const;
const unsigned int degree;
};
template <int dim>
LaplaceProblem<dim>::LaplaceProblem(const unsigned int degree)
, fe(degree)
, degree(degree)
{}
template <int dim>
void LaplaceProblem<dim>::setup_system()
{
dof_handler.distribute_dofs(fe);
dof_handler.distribute_mg_dofs();
std::cout << " Number of degrees of freedom: " << dof_handler.n_dofs()
<< " (by level: ";
std::cout << dof_handler.n_dofs(
level)
std::cout << std::endl;
solution.reinit(dof_handler.n_dofs());
system_rhs.reinit(dof_handler.n_dofs());
constraints.clear();
std::set<types::boundary_id> dirichlet_boundary_ids = {0};
const std::map<types::boundary_id, const Function<dim> *>
dirichlet_boundary_functions = {
dirichlet_boundary_functions,
constraints);
constraints.close();
{
sparsity_pattern.copy_from(dsp);
}
system_matrix.reinit(sparsity_pattern);
mg_constrained_dofs.clear();
mg_constrained_dofs.initialize(dof_handler);
mg_constrained_dofs.make_zero_boundary_constraints(dof_handler,
dirichlet_boundary_ids);
mg_interface_matrices.resize(0, n_levels - 1);
mg_matrices.resize(0, n_levels - 1);
mg_sparsity_patterns.resize(0, n_levels - 1);
mg_interface_sparsity_patterns.resize(0, n_levels - 1);
{
{
dof_handler.n_dofs(
level));
mg_sparsity_patterns[
level].copy_from(dsp);
mg_matrices[
level].reinit(mg_sparsity_patterns[
level]);
}
{
dof_handler.n_dofs(
level));
mg_constrained_dofs,
dsp,
mg_interface_sparsity_patterns[
level].copy_from(dsp);
mg_interface_matrices[
level].reinit(
mg_interface_sparsity_patterns[
level]);
}
}
}
template <int dim>
template <class Iterator>
void LaplaceProblem<dim>::cell_worker(const Iterator &cell,
ScratchData<dim> &scratch_data,
CopyData ©_data)
{
copy_data.reinit(cell, dofs_per_cell);
for (unsigned int q = 0; q < n_q_points; ++q)
{
const double coefficient =
for (unsigned int i = 0; i < dofs_per_cell; ++i)
{
for (unsigned int j = 0; j < dofs_per_cell; ++j)
{
copy_data.cell_matrix(i, j) +=
coefficient *
JxW[q];
}
copy_data.cell_rhs(i) += 1.0 * fe_values.
shape_value(i, q) * JxW[q];
}
}
}
template <int dim>
void LaplaceProblem<dim>::assemble_system()
{
auto cell_worker =
ScratchData<dim> &scratch_data,
CopyData ©_data) {
this->cell_worker(cell, scratch_data, copy_data);
};
auto copier = [&](const CopyData &cd) {
this->constraints.distribute_local_to_global(cd.cell_matrix,
cd.cell_rhs,
cd.local_dof_indices,
system_matrix,
system_rhs);
};
const unsigned int n_gauss_points = degree + 1;
ScratchData<dim> scratch_data(mapping,
fe,
n_gauss_points,
dof_handler.end(),
cell_worker,
copier,
scratch_data,
CopyData(),
}
template <int dim>
void LaplaceProblem<dim>::assemble_multigrid()
{
std::vector<AffineConstraints<double>> boundary_constraints(n_levels);
{
boundary_constraints[
level].reinit(
dof_handler.locally_owned_mg_dofs(
level),
mg_constrained_dofs.get_refinement_edge_indices(
level))
boundary_constraints[
level].constrain_dof_to_zero(dof_index);
mg_constrained_dofs.get_boundary_indices(
level))
boundary_constraints[
level].constrain_dof_to_zero(dof_index);
boundary_constraints[
level].close();
}
auto cell_worker =
ScratchData<dim> &scratch_data,
CopyData ©_data) {
this->cell_worker(cell, scratch_data, copy_data);
};
auto copier = [&](const CopyData &cd) {
boundary_constraints[cd.level].distribute_local_to_global(
cd.cell_matrix, cd.local_dof_indices, mg_matrices[cd.level]);
const unsigned int dofs_per_cell = cd.local_dof_indices.size();
for (unsigned int i = 0; i < dofs_per_cell; ++i)
for (unsigned int j = 0; j < dofs_per_cell; ++j)
if (mg_constrained_dofs.is_interface_matrix_entry(
cd.level, cd.local_dof_indices[i], cd.local_dof_indices[j]))
{
mg_interface_matrices[cd.level].add(cd.local_dof_indices[i],
cd.local_dof_indices[j],
cd.cell_matrix(i, j));
}
};
const unsigned int n_gauss_points = degree + 1;
ScratchData<dim> scratch_data(mapping,
fe,
n_gauss_points,
dof_handler.end_mg(),
cell_worker,
copier,
scratch_data,
CopyData(),
}
template <int dim>
void LaplaceProblem<dim>::solve()
{
mg_transfer.build(dof_handler);
mg_matrix, coarse_grid_solver, mg_transfer, mg_smoother, mg_smoother);
mg.set_edge_matrices(mg_interface_down, mg_interface_up);
preconditioner(dof_handler,
mg, mg_transfer);
solution = 0;
solver.solve(system_matrix, solution, system_rhs, preconditioner);
std::cout << " Number of CG iterations: " << solver_control.last_step()
<< '\n'
<< std::endl;
constraints.distribute(solution);
}
template <int dim>
void LaplaceProblem<dim>::refine_grid()
{
dof_handler,
solution,
estimated_error_per_cell);
estimated_error_per_cell,
0.3,
0.03);
}
template <int dim>
void LaplaceProblem<dim>::output_results(const unsigned int cycle) const
{
std::ofstream output("solution-" + std::to_string(cycle) + ".vtk");
}
template <int dim>
void LaplaceProblem<dim>::run()
{
for (unsigned int cycle = 0; cycle < 8; ++cycle)
{
std::cout << "Cycle " << cycle << std::endl;
if (cycle == 0)
{
}
else
refine_grid();
std::cout << " Number of active cells: "
setup_system();
assemble_system();
assemble_multigrid();
solve();
output_results(cycle);
}
}
}
int main()
{
try
{
using namespace Step16;
LaplaceProblem<2> laplace_problem(1);
laplace_problem.run();
}
catch (std::exception &exc)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Exception on processing: " << std::endl
<< exc.what() << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
catch (...)
{
std::cerr << std::endl
<< std::endl
<< "----------------------------------------------------"
<< std::endl;
std::cerr << "Unknown exception!" << std::endl
<< "Aborting!" << std::endl
<< "----------------------------------------------------"
<< std::endl;
return 1;
}
return 0;
}
void write_vtk(std::ostream &out) const
void add_data_vector(const VectorType &data, const std::vector< std::string > &names, const DataVectorType type=type_automatic, const std::vector< DataComponentInterpretation::DataComponentInterpretation > &data_component_interpretation={})
virtual void build_patches(const unsigned int n_subdivisions=0)
const std::vector< double > & get_JxW_values() const
const std::vector< Point< spacedim > > & get_quadrature_points() const
const Tensor< 1, spacedim > & shape_grad(const unsigned int i, const unsigned int q_point) const
const FiniteElement< dim, spacedim > & get_fe() const
const double & shape_value(const unsigned int i, const unsigned int q_point) const
const Quadrature< dim > & get_quadrature() const
unsigned int n_dofs_per_cell() const
void set_steps(const unsigned int)
void set_symmetric(const bool)
virtual void reinit(const size_type N, const bool omit_zeroing_entries=false)
void cell_matrix(FullMatrix< double > &M, const FEValuesBase< dim > &fe, const FEValuesBase< dim > &fetest, const ArrayView< const std::vector< double > > &velocity, const double factor=1.)
void run(const Iterator &begin, const std_cxx20::type_identity_t< Iterator > &end, Worker worker, Copier copier, const ScratchData &sample_scratch_data, const CopyData &sample_copy_data, const unsigned int queue_length, const unsigned int chunk_size)
void reinit(MatrixBlock< MatrixType > &v, const BlockSparsityPattern &p)